Type tf
Namespace tensorflow
Bring in all of the public TensorFlow interface into this module.
Methods
- a
- a_dyn
- abs
- abs_dyn
- accumulate_n
- accumulate_n
- accumulate_n
- accumulate_n
- accumulate_n_dyn
- acos
- acos_dyn
- acosh
- acosh_dyn
- add
- add
- add_check_numerics_ops
- add_check_numerics_ops_dyn
- add_dyn
- add_n
- add_n
- add_n_dyn
- add_to_collection
- add_to_collection
- add_to_collection
- add_to_collection
- add_to_collections
- add_to_collections
- adjust_hsv_in_yiq
- adjust_hsv_in_yiq_dyn
- all_variables
- all_variables_dyn
- angle
- angle_dyn
- arg_max
- arg_max
- arg_max_dyn
- arg_min
- arg_min
- arg_min_dyn
- argmax
- argmax
- argmax
- argmax
- argmax
- argmax
- argmax
- argmax
- argmax
- argmax
- argmax
- argmax
- argmax_dyn
- argmin
- argmin
- argmin
- argmin
- argmin
- argmin
- argmin
- argmin
- argmin
- argmin
- argmin
- argmin
- argmin_dyn
- argsort
- argsort
- argsort
- argsort
- argsort
- argsort_dyn
- as_dtype
- as_dtype
- as_dtype_dyn
- as_string
- as_string_dyn
- asin
- asin_dyn
- asinh
- asinh_dyn
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert
- Assert_dyn
- assert_equal
- assert_equal
- assert_equal
- assert_equal
- assert_equal
- assert_equal
- assert_equal
- assert_equal
- assert_equal
- assert_equal
- assert_equal_dyn
- assert_greater
- assert_greater
- assert_greater
- assert_greater
- assert_greater
- assert_greater
- assert_greater
- assert_greater
- assert_greater
- assert_greater
- assert_greater_dyn
- assert_greater_equal
- assert_greater_equal
- assert_greater_equal
- assert_greater_equal
- assert_greater_equal
- assert_greater_equal
- assert_greater_equal
- assert_greater_equal
- assert_greater_equal
- assert_greater_equal
- assert_greater_equal_dyn
- assert_integer
- assert_integer
- assert_integer_dyn
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less
- assert_less_dyn
- assert_less_equal
- assert_less_equal
- assert_less_equal_dyn
- assert_near
- assert_near
- assert_near_dyn
- assert_negative
- assert_negative
- assert_negative_dyn
- assert_non_negative
- assert_non_negative
- assert_non_negative
- assert_non_negative
- assert_non_negative
- assert_non_negative
- assert_non_negative_dyn
- assert_non_positive
- assert_non_positive
- assert_non_positive_dyn
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal
- assert_none_equal_dyn
- assert_positive
- assert_positive
- assert_positive_dyn
- assert_proper_iterable
- assert_proper_iterable
- assert_proper_iterable
- assert_proper_iterable
- assert_proper_iterable
- assert_proper_iterable
- assert_proper_iterable
- assert_proper_iterable_dyn
- assert_rank
- assert_rank
- assert_rank
- assert_rank
- assert_rank
- assert_rank
- assert_rank
- assert_rank
- assert_rank_at_least
- assert_rank_at_least
- assert_rank_at_least
- assert_rank_at_least
- assert_rank_at_least
- assert_rank_at_least
- assert_rank_at_least_dyn
- assert_rank_dyn
- assert_rank_in
- assert_rank_in
- assert_rank_in
- assert_rank_in
- assert_rank_in
- assert_rank_in
- assert_rank_in
- assert_rank_in
- assert_rank_in
- assert_rank_in
- assert_rank_in_dyn
- assert_same_float_dtype
- assert_same_float_dtype
- assert_same_float_dtype
- assert_same_float_dtype_dyn
- assert_scalar
- assert_scalar_dyn
- assert_type
- assert_type
- assert_type_dyn
- assert_variables_initialized
- assert_variables_initialized_dyn
- assign
- assign
- assign_add
- assign_add
- assign_add
- assign_add
- assign_add_dyn
- assign_dyn
- assign_sub
- assign_sub
- assign_sub
- assign_sub
- assign_sub_dyn
- atan
- atan_dyn
- atan2
- atan2_dyn
- atanh
- atanh_dyn
- attr
- attr_bool
- attr_bool_dyn
- attr_bool_list
- attr_bool_list_dyn
- attr_default
- attr_default_dyn
- attr_dyn
- attr_empty_list_default
- attr_empty_list_default_dyn
- attr_enum
- attr_enum_dyn
- attr_enum_list
- attr_enum_list_dyn
- attr_float
- attr_float_dyn
- attr_list_default
- attr_list_default_dyn
- attr_list_min
- attr_list_min_dyn
- attr_list_type_default
- attr_list_type_default_dyn
- attr_min
- attr_min_dyn
- attr_partial_shape
- attr_partial_shape_dyn
- attr_partial_shape_list
- attr_partial_shape_list_dyn
- attr_shape
- attr_shape_dyn
- attr_shape_list
- attr_shape_list_dyn
- attr_type_default
- attr_type_default_dyn
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend
- audio_microfrontend_dyn
- b
- b_dyn
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather
- batch_gather_dyn
- batch_scatter_update
- batch_scatter_update
- batch_scatter_update
- batch_scatter_update
- batch_scatter_update
- batch_scatter_update
- batch_scatter_update
- batch_scatter_update
- batch_scatter_update
- batch_scatter_update_dyn
- batch_to_space
- batch_to_space_dyn
- batch_to_space_nd
- batch_to_space_nd_dyn
- betainc
- betainc_dyn
- binary
- binary_dyn
- bincount
- bincount_dyn
- bipartite_match
- bipartite_match_dyn
- bitcast
- bitcast_dyn
- boolean_mask
- boolean_mask
- boolean_mask_dyn
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape
- broadcast_dynamic_shape_dyn
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape
- broadcast_static_shape_dyn
- broadcast_to
- broadcast_to_dyn
- bucketize_with_input_boundaries
- bucketize_with_input_boundaries_dyn
- build_categorical_equality_splits
- build_categorical_equality_splits_dyn
- build_dense_inequality_splits
- build_dense_inequality_splits_dyn
- build_sparse_inequality_splits
- build_sparse_inequality_splits_dyn
- bytes_in_use
- bytes_in_use_dyn
- bytes_limit
- bytes_limit_dyn
- case
- case
- case
- case
- case
- case
- case_dyn
- cast
- cast
- cast
- cast
- cast
- cast
- cast
- cast
- cast
- cast
- cast
- cast
- cast
- cast
- cast
- cast
- cast_dyn
- cast<T>
- ceil
- ceil_dyn
- center_tree_ensemble_bias
- center_tree_ensemble_bias_dyn
- check_numerics
- check_numerics_dyn
- cholesky
- cholesky_dyn
- cholesky_solve
- cholesky_solve_dyn
- clip_by_average_norm
- clip_by_average_norm
- clip_by_average_norm_dyn
- clip_by_global_norm
- clip_by_global_norm
- clip_by_global_norm
- clip_by_global_norm
- clip_by_global_norm_dyn
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm
- clip_by_norm_dyn
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value
- clip_by_value_dyn
- complex
- complex_dyn
- complex_struct
- complex_struct_dyn
- concat
- concat
- concat_dyn
- cond
- cond
- cond
- cond
- cond
- cond
- cond
- cond
- cond
- cond
- cond
- cond
- cond
- cond
- cond
- cond
- cond_dyn
- confusion_matrix
- confusion_matrix_dyn
- conj
- conj
- conj
- conj_dyn
- constant
- constant
- constant
- constant_dyn
- constant_scalar<T>
- constant<T>
- constant<T>
- constant<T>
- constant<T>
- constant<T>
- constant<T>
- constant<T>
- container
- container_dyn
- control_dependencies
- control_dependencies
- control_dependencies_dyn
- control_flow_v2_enabled
- control_flow_v2_enabled_dyn
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor
- convert_to_tensor_dyn
- convert_to_tensor_or_indexed_slices
- convert_to_tensor_or_indexed_slices_dyn
- convert_to_tensor_or_sparse_tensor
- convert_to_tensor_or_sparse_tensor
- convert_to_tensor_or_sparse_tensor_dyn
- copy_op
- copy_op_dyn
- cos
- cos_dyn
- cosh
- cosh_dyn
- count_nonzero
- count_nonzero
- count_nonzero
- count_nonzero
- count_nonzero
- count_nonzero
- count_nonzero
- count_nonzero
- count_nonzero
- count_nonzero
- count_nonzero
- count_nonzero
- count_nonzero_dyn
- count_up_to
- count_up_to
- count_up_to
- count_up_to_dyn
- create_fertile_stats_variable
- create_fertile_stats_variable_dyn
- create_partitioned_variables
- create_partitioned_variables
- create_partitioned_variables
- create_partitioned_variables
- create_partitioned_variables
- create_partitioned_variables
- create_partitioned_variables_dyn
- create_quantile_accumulator
- create_quantile_accumulator
- create_quantile_accumulator_dyn
- create_stats_accumulator_scalar
- create_stats_accumulator_scalar_dyn
- create_stats_accumulator_tensor
- create_stats_accumulator_tensor_dyn
- create_tree_ensemble_variable
- create_tree_ensemble_variable_dyn
- create_tree_variable
- create_tree_variable_dyn
- cross
- cross_dyn
- cumprod
- cumprod_dyn
- cumsum
- cumsum_dyn
- custom_gradient
- custom_gradient_dyn
- decision_tree_ensemble_resource_handle_op
- decision_tree_ensemble_resource_handle_op_dyn
- decision_tree_resource_handle_op
- decision_tree_resource_handle_op_dyn
- decode_base64
- decode_base64_dyn
- decode_compressed
- decode_compressed_dyn
- decode_csv
- decode_csv_dyn
- decode_json_example
- decode_json_example_dyn
- decode_libsvm
- decode_libsvm_dyn
- decode_raw
- decode_raw
- decode_raw
- decode_raw
- decode_raw_dyn
- default_attrs
- default_attrs_dyn
- delete_session_tensor
- delete_session_tensor_dyn
- depth_to_space
- depth_to_space
- depth_to_space
- depth_to_space
- depth_to_space_dyn
- dequantize
- dequantize_dyn
- deserialize_many_sparse
- deserialize_many_sparse_dyn
- device
- device
- device_dyn
- device_placement_op
- device_placement_op_dyn
- diag
- diag_dyn
- diag_part
- diag_part_dyn
- digamma
- digamma_dyn
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index
- dimension_at_index_dyn
- dimension_value
- dimension_value
- dimension_value
- dimension_value_dyn
- disable_control_flow_v2
- disable_control_flow_v2_dyn
- disable_eager_execution
- disable_eager_execution_dyn
- disable_tensor_equality
- disable_tensor_equality_dyn
- disable_v2_behavior
- disable_v2_behavior_dyn
- disable_v2_tensorshape
- disable_v2_tensorshape_dyn
- div
- div
- div
- div
- div
- div
- div_dyn
- div_no_nan
- div_no_nan_dyn
- divide
- divide
- divide
- divide
- divide
- divide_dyn
- dynamic_partition
- dynamic_partition
- dynamic_partition_dyn
- dynamic_stitch
- dynamic_stitch
- dynamic_stitch_dyn
- edit_distance
- edit_distance
- edit_distance
- edit_distance
- edit_distance_dyn
- einsum
- einsum
- einsum_dyn
- einsum_dyn
- enable_control_flow_v2
- enable_control_flow_v2_dyn
- enable_eager_execution
- enable_eager_execution_dyn
- enable_tensor_equality
- enable_tensor_equality_dyn
- enable_v2_behavior
- enable_v2_behavior_dyn
- enable_v2_tensorshape
- enable_v2_tensorshape_dyn
- encode_base64
- encode_base64_dyn
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal
- equal_dyn
- erf
- erf_dyn
- erfc
- erfc_dyn
- executing_eagerly
- executing_eagerly_dyn
- exp
- exp_dyn
- expand_dims
- expand_dims
- expand_dims
- expand_dims
- expand_dims
- expand_dims
- expand_dims_dyn
- expm1
- expm1_dyn
- extract_image_patches
- extract_image_patches
- extract_image_patches
- extract_image_patches
- extract_image_patches
- extract_image_patches
- extract_image_patches_dyn
- extract_volume_patches
- extract_volume_patches_dyn
- eye
- eye
- eye
- eye
- eye
- eye
- eye
- eye
- eye
- eye
- eye
- eye
- eye
- eye
- eye_dyn
- fake_quant_with_min_max_args
- fake_quant_with_min_max_args
- fake_quant_with_min_max_args
- fake_quant_with_min_max_args
- fake_quant_with_min_max_args_dyn
- fake_quant_with_min_max_args_gradient
- fake_quant_with_min_max_args_gradient
- fake_quant_with_min_max_args_gradient
- fake_quant_with_min_max_args_gradient
- fake_quant_with_min_max_args_gradient_dyn
- fake_quant_with_min_max_vars
- fake_quant_with_min_max_vars_dyn
- fake_quant_with_min_max_vars_gradient
- fake_quant_with_min_max_vars_gradient_dyn
- fake_quant_with_min_max_vars_per_channel
- fake_quant_with_min_max_vars_per_channel_dyn
- fake_quant_with_min_max_vars_per_channel_gradient
- fake_quant_with_min_max_vars_per_channel_gradient_dyn
- feature_usage_counts
- feature_usage_counts_dyn
- fertile_stats_deserialize
- fertile_stats_deserialize_dyn
- fertile_stats_is_initialized_op
- fertile_stats_is_initialized_op_dyn
- fertile_stats_resource_handle_op
- fertile_stats_resource_handle_op_dyn
- fertile_stats_serialize
- fertile_stats_serialize_dyn
- fft
- fft_dyn
- fft2d
- fft2d_dyn
- fft3d
- fft3d_dyn
- fill
- fill
- fill_dyn
- finalize_tree
- finalize_tree_dyn
- fingerprint
- fingerprint_dyn
- five_float_outputs
- five_float_outputs_dyn
- fixed_size_partitioner
- fixed_size_partitioner_dyn
- float_input
- float_input_dyn
- float_output
- float_output_dyn
- float_output_string_output
- float_output_string_output_dyn
- floor
- floor_div
- floor_div
- floor_div_dyn
- floor_dyn
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv
- floordiv_dyn
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl
- foldl_dyn
- foldr
- foldr
- foldr
- foldr
- foldr
- foldr
- foldr
- foldr
- foldr
- foldr_dyn
- foo1
- foo1_dyn
- foo2
- foo2_dyn
- foo3
- foo3_dyn
- func_attr
- func_attr
- func_attr
- func_attr_dyn
- func_list_attr
- func_list_attr_dyn
- function
- function
- function
- function
- function
- function_dyn
- gather
- gather
- gather
- gather
- gather
- gather
- gather
- gather
- gather
- gather
- gather
- gather
- gather_dyn
- gather_nd
- gather_nd
- gather_nd_dyn
- gather_tree
- gather_tree_dyn
- get_collection
- get_collection
- get_collection
- get_collection
- get_collection
- get_collection
- get_default_graph
- get_default_graph_dyn
- get_default_session
- get_default_session_dyn
- get_local_variable
- get_local_variable
- get_local_variable
- get_local_variable
- get_local_variable
- get_local_variable_dyn
- get_logger
- get_logger_dyn
- get_seed
- get_seed
- get_seed
- get_seed_dyn
- get_session_handle
- get_session_handle
- get_session_handle_dyn
- get_session_tensor
- get_session_tensor_dyn
- get_static_value
- get_static_value
- get_static_value
- get_static_value_dyn
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable
- get_variable_dyn
- get_variable_scope
- get_variable_scope_dyn
- global_norm
- global_norm
- global_norm_dyn
- global_variables
- global_variables_dyn
- global_variables_initializer
- global_variables_initializer_dyn
- grad_pass_through
- grad_pass_through
- grad_pass_through_dyn
- gradient_trees_partition_examples
- gradient_trees_partition_examples_dyn
- gradient_trees_prediction
- gradient_trees_prediction
- gradient_trees_prediction_dyn
- gradient_trees_prediction_verbose
- gradient_trees_prediction_verbose
- gradient_trees_prediction_verbose_dyn
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients
- gradients_dyn
- graph_def_version
- graph_def_version_dyn
- greater
- greater
- greater
- greater
- greater
- greater
- greater
- greater
- greater
- greater_dyn
- greater_equal
- greater_equal
- greater_equal
- greater_equal
- greater_equal
- greater_equal
- greater_equal
- greater_equal
- greater_equal
- greater_equal_dyn
- group
- group
- group_dyn
- group_dyn
- grow_tree_ensemble
- grow_tree_ensemble
- grow_tree_ensemble_dyn
- grow_tree_v4
- grow_tree_v4_dyn
- guarantee_const
- guarantee_const_dyn
- hard_routing_function
- hard_routing_function_dyn
- hessians
- hessians
- hessians
- hessians
- hessians_dyn
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width
- histogram_fixed_width_bins
- histogram_fixed_width_bins
- histogram_fixed_width_bins
- histogram_fixed_width_bins
- histogram_fixed_width_bins
- histogram_fixed_width_bins
- histogram_fixed_width_bins_dyn
- histogram_fixed_width_dyn
- identity
- identity
- identity_dyn
- identity_n
- identity_n_dyn
- ifft
- ifft_dyn
- ifft2d
- ifft2d_dyn
- ifft3d
- ifft3d_dyn
- igamma
- igamma_dyn
- igammac
- igammac_dyn
- imag
- imag_dyn
- image_connected_components
- image_connected_components_dyn
- image_projective_transform
- image_projective_transform_dyn
- image_projective_transform_v2
- image_projective_transform_v2_dyn
- import_graph_def
- import_graph_def
- import_graph_def
- import_graph_def
- import_graph_def
- import_graph_def
- import_graph_def_dyn
- in_polymorphic_twice
- in_polymorphic_twice_dyn
- init_scope
- init_scope_dyn
- initialize_all_tables
- initialize_all_tables_dyn
- initialize_all_variables
- initialize_all_variables_dyn
- initialize_local_variables
- initialize_local_variables_dyn
- initialize_variables
- initialize_variables_dyn
- int_attr
- int_attr_dyn
- int_input
- int_input_dyn
- int_input_float_input
- int_input_float_input_dyn
- int_input_int_output
- int_input_int_output_dyn
- int_output
- int_output_dyn
- int_output_float_output
- int_output_float_output_dyn
- int64_output
- int64_output_dyn
- invert_permutation
- invert_permutation_dyn
- is_finite
- is_finite_dyn
- is_inf
- is_inf_dyn
- is_nan
- is_nan_dyn
- is_non_decreasing
- is_non_decreasing_dyn
- is_numeric_tensor
- is_numeric_tensor
- is_numeric_tensor_dyn
- is_strictly_increasing
- is_strictly_increasing_dyn
- is_tensor
- is_tensor
- is_tensor
- is_tensor_dyn
- is_variable_initialized
- is_variable_initialized_dyn
- k_feature_gradient
- k_feature_gradient_dyn
- k_feature_routing_function
- k_feature_routing_function_dyn
- kernel_label
- kernel_label_dyn
- kernel_label_required
- kernel_label_required_dyn
- lbeta
- lbeta
- lbeta
- lbeta
- lbeta_dyn
- less
- less
- less
- less
- less
- less
- less
- less
- less
- less_dyn
- less_equal
- less_equal
- less_equal
- less_equal
- less_equal
- less_equal
- less_equal
- less_equal
- less_equal
- less_equal_dyn
- lgamma
- lgamma_dyn
- linspace
- linspace_dyn
- list_input
- list_input_dyn
- list_output
- list_output_dyn
- load_file_system_library
- load_file_system_library_dyn
- load_library
- load_library_dyn
- load_op_library
- load_op_library
- load_op_library_dyn
- local_variables
- local_variables_dyn
- local_variables_initializer
- local_variables_initializer_dyn
- log
- log_dyn
- log_sigmoid
- log_sigmoid
- log_sigmoid
- log_sigmoid_dyn
- log1p
- log1p_dyn
- logical_and
- logical_and
- logical_and
- logical_and
- logical_and_dyn
- logical_not
- logical_not_dyn
- logical_or
- logical_or
- logical_or
- logical_or
- logical_or_dyn
- logical_xor
- logical_xor
- logical_xor_dyn
- make_ndarray
- make_ndarray_dyn
- make_quantile_summaries
- make_quantile_summaries_dyn
- make_template
- make_template_dyn
- make_tensor_proto
- make_tensor_proto
- make_tensor_proto
- make_tensor_proto
- make_tensor_proto
- make_tensor_proto
- make_tensor_proto
- make_tensor_proto
- make_tensor_proto_dyn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn
- map_fn_dyn
- masked_matmul
- masked_matmul_dyn
- matching_files
- matching_files_dyn
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul
- matmul_dyn
- matrix_band_part
- matrix_band_part_dyn
- matrix_determinant
- matrix_determinant_dyn
- matrix_diag
- matrix_diag
- matrix_diag_dyn
- matrix_diag_part
- matrix_diag_part
- matrix_diag_part_dyn
- matrix_inverse
- matrix_inverse_dyn
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag
- matrix_set_diag_dyn
- matrix_solve
- matrix_solve_dyn
- matrix_solve_ls
- matrix_solve_ls
- matrix_solve_ls
- matrix_solve_ls
- matrix_solve_ls_dyn
- matrix_square_root
- matrix_square_root_dyn
- matrix_transpose
- matrix_transpose_dyn
- matrix_triangular_solve
- matrix_triangular_solve_dyn
- max_bytes_in_use
- max_bytes_in_use_dyn
- maximum
- maximum
- maximum
- maximum
- maximum
- maximum
- maximum
- maximum
- maximum
- maximum_dyn
- meshgrid
- meshgrid
- meshgrid_dyn
- meshgrid_dyn
- min_max_variable_partitioner
- min_max_variable_partitioner
- min_max_variable_partitioner
- min_max_variable_partitioner
- min_max_variable_partitioner_dyn
- minimum
- minimum
- minimum
- minimum
- minimum
- minimum
- minimum
- minimum
- minimum
- minimum_dyn
- mixed_struct
- mixed_struct_dyn
- mod
- mod
- mod_dyn
- model_variables
- model_variables_dyn
- moving_average_variables
- moving_average_variables_dyn
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial
- multinomial_dyn
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply
- multiply_dyn
- n_in_polymorphic_twice
- n_in_polymorphic_twice_dyn
- n_in_twice
- n_in_twice_dyn
- n_in_two_type_variables
- n_in_two_type_variables_dyn
- n_ints_in
- n_ints_in_dyn
- n_ints_out
- n_ints_out_default
- n_ints_out_default_dyn
- n_ints_out_dyn
- n_polymorphic_in
- n_polymorphic_in_dyn
- n_polymorphic_out
- n_polymorphic_out_default
- n_polymorphic_out_default_dyn
- n_polymorphic_out_dyn
- n_polymorphic_restrict_in
- n_polymorphic_restrict_in_dyn
- n_polymorphic_restrict_out
- n_polymorphic_restrict_out_dyn
- negative
- negative_dyn
- no_op
- no_op
- no_op_dyn
- no_regularizer
- no_regularizer_dyn
- NoGradient
- NoGradient_dyn
- nondifferentiable_batch_function
- nondifferentiable_batch_function_dyn
- none
- none_dyn
- norm
- norm
- norm
- norm
- norm
- norm
- norm
- norm
- norm
- norm
- norm
- norm
- norm_dyn
- not_equal
- not_equal
- not_equal
- not_equal
- not_equal_dyn
- numpy_function
- numpy_function
- numpy_function
- numpy_function
- numpy_function
- numpy_function
- numpy_function
- numpy_function
- numpy_function_dyn
- obtain_next
- obtain_next_dyn
- old
- old_dyn
- one_hot
- one_hot
- one_hot
- one_hot
- one_hot
- one_hot
- one_hot
- one_hot_dyn
- ones
- ones
- ones
- ones
- ones_dyn
- ones_like
- ones_like
- ones_like
- ones_like_dyn
- op_scope
- op_scope_dyn
- op_with_default_attr
- op_with_default_attr_dyn
- op_with_future_default_attr
- op_with_future_default_attr_dyn
- out_t
- out_t_dyn
- out_type_list
- out_type_list_dyn
- out_type_list_restrict
- out_type_list_restrict_dyn
- pad
- pad
- pad
- pad
- pad
- pad
- pad
- pad
- pad
- pad
- pad
- pad
- pad_dyn
- parallel_stack
- parallel_stack_dyn
- parse_example
- parse_example
- parse_example
- parse_example
- parse_example_dyn
- parse_single_example
- parse_single_example
- parse_single_example
- parse_single_example_dyn
- parse_single_sequence_example
- parse_single_sequence_example_dyn
- parse_tensor
- parse_tensor_dyn
- periodic_resample
- periodic_resample_dyn
- periodic_resample_op_grad
- periodic_resample_op_grad_dyn
- placeholder
- placeholder
- placeholder
- placeholder
- placeholder_dyn
- placeholder_with_default
- placeholder_with_default
- placeholder_with_default_dyn
- polygamma
- polygamma_dyn
- polymorphic
- polymorphic_default_out
- polymorphic_default_out_dyn
- polymorphic_dyn
- polymorphic_out
- polymorphic_out_dyn
- pow
- pow
- pow
- pow
- pow
- pow
- pow
- pow
- pow
- pow_dyn
- print_dyn
- print_dyn
- Print_dyn
- process_input_v4
- process_input_v4_dyn
- py_func
- py_func
- py_func
- py_func_dyn
- py_function
- py_function
- py_function
- py_function
- py_function
- py_function
- py_function
- py_function
- py_function_dyn
- qr
- qr_dyn
- quantile_accumulator_add_summaries
- quantile_accumulator_add_summaries_dyn
- quantile_accumulator_deserialize
- quantile_accumulator_deserialize_dyn
- quantile_accumulator_flush
- quantile_accumulator_flush_dyn
- quantile_accumulator_flush_summary
- quantile_accumulator_flush_summary_dyn
- quantile_accumulator_get_buckets
- quantile_accumulator_get_buckets_dyn
- quantile_accumulator_is_initialized
- quantile_accumulator_is_initialized_dyn
- quantile_accumulator_serialize
- quantile_accumulator_serialize_dyn
- quantile_buckets
- quantile_buckets_dyn
- quantile_stream_resource_handle_op
- quantile_stream_resource_handle_op
- quantile_stream_resource_handle_op
- quantile_stream_resource_handle_op_dyn
- quantiles
- quantiles_dyn
- quantize
- quantize_dyn
- quantize_v2
- quantize_v2_dyn
- quantized_concat
- quantized_concat_dyn
- random_crop
- random_crop
- random_crop
- random_crop
- random_crop_dyn
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma
- random_gamma_dyn
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal
- random_normal_dyn
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson
- random_poisson_dyn
- random_shuffle
- random_shuffle
- random_shuffle_dyn
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform
- random_uniform_dyn
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range
- range_dyn
- rank
- rank
- rank
- rank
- rank
- rank
- rank_dyn
- read_file
- read_file_dyn
- real
- real_dyn
- realdiv
- realdiv
- realdiv_dyn
- reciprocal
- reciprocal_dyn
- recompute_grad
- recompute_grad
- recompute_grad_dyn
- reduce_all
- reduce_all
- reduce_all_dyn
- reduce_any
- reduce_any
- reduce_any_dyn
- reduce_join
- reduce_join
- reduce_join
- reduce_join
- reduce_join
- reduce_join
- reduce_join_dyn
- reduce_logsumexp
- reduce_logsumexp_dyn
- reduce_max
- reduce_max
- reduce_max
- reduce_max
- reduce_max_dyn
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean
- reduce_mean_dyn
- reduce_min
- reduce_min_dyn
- reduce_prod
- reduce_prod_dyn
- reduce_slice_max
- reduce_slice_max_dyn
- reduce_slice_min
- reduce_slice_min_dyn
- reduce_slice_prod
- reduce_slice_prod_dyn
- reduce_slice_sum
- reduce_slice_sum_dyn
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum
- reduce_sum_dyn
- ref_in
- ref_in_dyn
- ref_input_float_input
- ref_input_float_input_dyn
- ref_input_float_input_int_output
- ref_input_float_input_int_output_dyn
- ref_input_int_input
- ref_input_int_input_dyn
- ref_out
- ref_out_dyn
- ref_output
- ref_output_dyn
- ref_output_float_output
- ref_output_float_output_dyn
- regex_replace
- regex_replace_dyn
- register_tensor_conversion_function
- register_tensor_conversion_function
- register_tensor_conversion_function_dyn
- reinterpret_string_to_float
- reinterpret_string_to_float_dyn
- remote_fused_graph_execute
- remote_fused_graph_execute_dyn
- repeat
- repeat
- repeat
- repeat_dyn
- report_uninitialized_variables
- report_uninitialized_variables_dyn
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings
- required_space_to_batch_paddings_dyn
- requires_older_graph_version
- requires_older_graph_version_dyn
- resampler
- resampler_dyn
- resampler_grad
- resampler_grad_dyn
- reserved_attr
- reserved_attr_dyn
- reserved_input
- reserved_input_dyn
- reset_default_graph
- reset_default_graph_dyn
- reshape
- reshape
- reshape
- reshape
- reshape
- reshape_dyn
- reshape<T>
- reshape<T>
- resource_create_op
- resource_create_op_dyn
- resource_initialized_op
- resource_initialized_op_dyn
- resource_using_op
- resource_using_op_dyn
- restrict
- restrict_dyn
- reverse
- reverse_dyn
- reverse_sequence
- reverse_sequence
- reverse_sequence
- reverse_sequence
- reverse_sequence
- reverse_sequence
- reverse_sequence_dyn
- rint
- rint_dyn
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll
- roll_dyn
- round
- round_dyn
- routing_function
- routing_function_dyn
- routing_gradient
- routing_gradient_dyn
- rpc
- rpc_dyn
- rsqrt
- rsqrt_dyn
- saturate_cast
- saturate_cast
- saturate_cast_dyn
- scalar_mul
- scalar_mul
- scalar_mul
- scalar_mul
- scalar_mul
- scalar_mul
- scalar_mul
- scalar_mul
- scalar_mul
- scalar_mul
- scalar_mul
- scalar_mul
- scalar_mul_dyn
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan
- scan_dyn
- scatter_add
- scatter_add
- scatter_add
- scatter_add_dyn
- scatter_add_ndim
- scatter_add_ndim_dyn
- scatter_div
- scatter_div_dyn
- scatter_max
- scatter_max_dyn
- scatter_min
- scatter_min_dyn
- scatter_mul
- scatter_mul_dyn
- scatter_nd
- scatter_nd_add
- scatter_nd_add_dyn
- scatter_nd_dyn
- scatter_nd_sub
- scatter_nd_sub_dyn
- scatter_nd_update
- scatter_nd_update_dyn
- scatter_sub
- scatter_sub_dyn
- scatter_update
- scatter_update
- scatter_update_dyn
- searchsorted
- searchsorted
- searchsorted
- searchsorted
- searchsorted_dyn
- segment_max
- segment_max_dyn
- segment_mean
- segment_mean_dyn
- segment_min
- segment_min_dyn
- segment_prod
- segment_prod_dyn
- segment_sum
- segment_sum
- segment_sum_dyn
- self_adjoint_eig
- self_adjoint_eig_dyn
- self_adjoint_eigvals
- self_adjoint_eigvals_dyn
- sequence_file_dataset
- sequence_file_dataset_dyn
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask
- sequence_mask_dyn
- serialize_many_sparse
- serialize_many_sparse_dyn
- serialize_sparse
- serialize_sparse
- serialize_sparse_dyn
- serialize_tensor
- serialize_tensor_dyn
- set_random_seed
- set_random_seed_dyn
- setdiff1d
- setdiff1d
- setdiff1d
- setdiff1d
- setdiff1d_dyn
- shape
- shape
- shape
- shape
- shape
- shape
- shape_dyn
- shape_n
- shape_n_dyn
- sigmoid
- sigmoid_dyn
- sign
- sign_dyn
- simple
- simple_dyn
- simple_struct
- simple_struct_dyn
- sin
- sin_dyn
- single_image_random_dot_stereograms
- single_image_random_dot_stereograms_dyn
- sinh
- sinh_dyn
- size
- size
- size
- size
- size
- size
- size_dyn
- skip_gram_generate_candidates
- skip_gram_generate_candidates_dyn
- slice
- slice
- slice
- slice
- slice
- slice
- slice
- slice
- slice
- slice
- slice
- slice
- slice_dyn
- sort
- sort_dyn
- space_to_batch
- space_to_batch_dyn
- space_to_batch_nd
- space_to_batch_nd_dyn
- space_to_depth
- space_to_depth
- space_to_depth
- space_to_depth
- space_to_depth_dyn
- sparse_add
- sparse_add
- sparse_add
- sparse_add
- sparse_add_dyn
- sparse_concat
- sparse_concat
- sparse_concat_dyn
- sparse_feature_cross
- sparse_feature_cross
- sparse_feature_cross_dyn
- sparse_feature_cross_v2
- sparse_feature_cross_v2
- sparse_feature_cross_v2_dyn
- sparse_fill_empty_rows
- sparse_fill_empty_rows
- sparse_fill_empty_rows
- sparse_fill_empty_rows
- sparse_fill_empty_rows
- sparse_fill_empty_rows
- sparse_fill_empty_rows
- sparse_fill_empty_rows
- sparse_fill_empty_rows_dyn
- sparse_mask
- sparse_mask_dyn
- sparse_matmul
- sparse_matmul_dyn
- sparse_maximum
- sparse_maximum_dyn
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge
- sparse_merge_dyn
- sparse_minimum
- sparse_minimum_dyn
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder
- sparse_placeholder_dyn
- sparse_reduce_max
- sparse_reduce_max
- sparse_reduce_max_dyn
- sparse_reduce_max_sparse
- sparse_reduce_max_sparse
- sparse_reduce_max_sparse_dyn
- sparse_reduce_sum
- sparse_reduce_sum
- sparse_reduce_sum_dyn
- sparse_reduce_sum_sparse
- sparse_reduce_sum_sparse
- sparse_reduce_sum_sparse_dyn
- sparse_reorder
- sparse_reorder
- sparse_reorder_dyn
- sparse_reset_shape
- sparse_reset_shape
- sparse_reset_shape
- sparse_reset_shape
- sparse_reset_shape_dyn
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape
- sparse_reshape_dyn
- sparse_retain
- sparse_retain
- sparse_retain
- sparse_retain
- sparse_retain_dyn
- sparse_segment_mean
- sparse_segment_mean
- sparse_segment_mean
- sparse_segment_mean
- sparse_segment_mean
- sparse_segment_mean
- sparse_segment_mean
- sparse_segment_mean
- sparse_segment_mean
- sparse_segment_mean
- sparse_segment_mean_dyn
- sparse_segment_sqrt_n
- sparse_segment_sqrt_n
- sparse_segment_sqrt_n
- sparse_segment_sqrt_n
- sparse_segment_sqrt_n
- sparse_segment_sqrt_n
- sparse_segment_sqrt_n
- sparse_segment_sqrt_n
- sparse_segment_sqrt_n
- sparse_segment_sqrt_n
- sparse_segment_sqrt_n_dyn
- sparse_segment_sum
- sparse_segment_sum
- sparse_segment_sum
- sparse_segment_sum
- sparse_segment_sum
- sparse_segment_sum
- sparse_segment_sum
- sparse_segment_sum
- sparse_segment_sum
- sparse_segment_sum
- sparse_segment_sum_dyn
- sparse_slice
- sparse_slice
- sparse_slice_dyn
- sparse_softmax
- sparse_softmax_dyn
- sparse_split
- sparse_split
- sparse_split
- sparse_split
- sparse_split
- sparse_split
- sparse_split_dyn
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul
- sparse_tensor_dense_matmul_dyn
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense
- sparse_tensor_to_dense_dyn
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense
- sparse_to_dense_dyn
- sparse_to_indicator
- sparse_to_indicator_dyn
- sparse_transpose
- sparse_transpose_dyn
- split
- split
- split
- split
- split
- split
- split
- split
- split
- split
- split
- split
- split_dyn
- sqrt
- sqrt_dyn
- square
- square_dyn
- squared_difference
- squared_difference
- squared_difference
- squared_difference
- squared_difference
- squared_difference
- squared_difference
- squared_difference
- squared_difference
- squared_difference_dyn
- squeeze
- squeeze
- squeeze
- squeeze_dyn
- stack
- stack
- stack_dyn
- stats_accumulator_scalar_add
- stats_accumulator_scalar_add_dyn
- stats_accumulator_scalar_deserialize
- stats_accumulator_scalar_deserialize_dyn
- stats_accumulator_scalar_flush
- stats_accumulator_scalar_flush_dyn
- stats_accumulator_scalar_is_initialized
- stats_accumulator_scalar_is_initialized_dyn
- stats_accumulator_scalar_make_summary
- stats_accumulator_scalar_make_summary_dyn
- stats_accumulator_scalar_resource_handle_op
- stats_accumulator_scalar_resource_handle_op
- stats_accumulator_scalar_resource_handle_op
- stats_accumulator_scalar_resource_handle_op_dyn
- stats_accumulator_scalar_serialize
- stats_accumulator_scalar_serialize_dyn
- stats_accumulator_tensor_add
- stats_accumulator_tensor_add_dyn
- stats_accumulator_tensor_deserialize
- stats_accumulator_tensor_deserialize_dyn
- stats_accumulator_tensor_flush
- stats_accumulator_tensor_flush_dyn
- stats_accumulator_tensor_is_initialized
- stats_accumulator_tensor_is_initialized_dyn
- stats_accumulator_tensor_make_summary
- stats_accumulator_tensor_make_summary_dyn
- stats_accumulator_tensor_resource_handle_op
- stats_accumulator_tensor_resource_handle_op
- stats_accumulator_tensor_resource_handle_op
- stats_accumulator_tensor_resource_handle_op_dyn
- stats_accumulator_tensor_serialize
- stats_accumulator_tensor_serialize_dyn
- stochastic_hard_routing_function
- stochastic_hard_routing_function_dyn
- stochastic_hard_routing_gradient
- stochastic_hard_routing_gradient_dyn
- stop_gradient
- stop_gradient_dyn
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice
- strided_slice_dyn
- string_join
- string_join_dyn
- string_list_attr
- string_list_attr_dyn
- string_split
- string_split_dyn
- string_strip
- string_strip_dyn
- string_to_hash_bucket
- string_to_hash_bucket_dyn
- string_to_hash_bucket_fast
- string_to_hash_bucket_fast_dyn
- string_to_hash_bucket_strong
- string_to_hash_bucket_strong_dyn
- string_to_number
- string_to_number
- string_to_number
- string_to_number_dyn
- stub_resource_handle_op
- stub_resource_handle_op_dyn
- substr
- substr_dyn
- subtract
- subtract_dyn
- svd
- svd
- svd_dyn
- switch_case
- switch_case
- switch_case
- switch_case
- switch_case_dyn
- tables_initializer
- tables_initializer_dyn
- tan
- tan_dyn
- tanh
- tanh_dyn
- tensor_scatter_add
- tensor_scatter_add_dyn
- tensor_scatter_sub
- tensor_scatter_sub_dyn
- tensor_scatter_update
- tensor_scatter_update_dyn
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot
- tensordot_dyn
- test_attr
- test_attr_dyn
- test_string_output
- test_string_output_dyn
- tile
- tile
- tile_dyn
- timestamp
- timestamp_dyn
- to_bfloat16
- to_bfloat16_dyn
- to_complex128
- to_complex128_dyn
- to_complex64
- to_complex64_dyn
- to_double
- to_double_dyn
- to_float
- to_float_dyn
- to_int32
- to_int32_dyn
- to_int64
- to_int64_dyn
- trace
- trace
- trace
- trace_dyn
- trainable_variables
- trainable_variables_dyn
- transpose
- transpose
- transpose
- transpose
- transpose
- transpose
- transpose_dyn
- traverse_tree_v4
- traverse_tree_v4_dyn
- tree_deserialize
- tree_deserialize_dyn
- tree_ensemble_deserialize
- tree_ensemble_deserialize_dyn
- tree_ensemble_is_initialized_op
- tree_ensemble_is_initialized_op_dyn
- tree_ensemble_serialize
- tree_ensemble_serialize_dyn
- tree_ensemble_stamp_token
- tree_ensemble_stamp_token_dyn
- tree_ensemble_stats
- tree_ensemble_stats_dyn
- tree_ensemble_used_handlers
- tree_ensemble_used_handlers_dyn
- tree_is_initialized_op
- tree_is_initialized_op_dyn
- tree_predictions_v4
- tree_predictions_v4_dyn
- tree_serialize
- tree_serialize_dyn
- tree_size
- tree_size_dyn
- truediv
- truediv
- truediv
- truediv_dyn
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal
- truncated_normal_dyn
- truncatediv
- truncatediv
- truncatediv
- truncatediv
- truncatediv
- truncatediv
- truncatediv
- truncatediv
- truncatediv
- truncatediv_dyn
- truncatemod
- truncatemod
- truncatemod
- truncatemod
- truncatemod
- truncatemod
- truncatemod
- truncatemod
- truncatemod
- truncatemod_dyn
- try_rpc
- try_rpc_dyn
- tuple
- tuple
- tuple
- tuple_dyn
- two_float_inputs
- two_float_inputs_dyn
- two_float_inputs_float_output
- two_float_inputs_float_output_dyn
- two_float_inputs_int_output
- two_float_inputs_int_output_dyn
- two_float_outputs
- two_float_outputs_dyn
- two_int_inputs
- two_int_inputs_dyn
- two_int_outputs
- two_int_outputs_dyn
- two_refs_in
- two_refs_in_dyn
- type_list
- type_list_dyn
- type_list_restrict
- type_list_restrict_dyn
- type_list_twice
- type_list_twice_dyn
- unary
- unary_dyn
- unique
- unique
- unique_dyn
- unique_with_counts
- unique_with_counts
- unique_with_counts_dyn
- unpack_path
- unpack_path_dyn
- unravel_index
- unravel_index_dyn
- unsorted_segment_max
- unsorted_segment_max_dyn
- unsorted_segment_mean
- unsorted_segment_mean_dyn
- unsorted_segment_min
- unsorted_segment_min_dyn
- unsorted_segment_prod
- unsorted_segment_prod_dyn
- unsorted_segment_sqrt_n
- unsorted_segment_sqrt_n_dyn
- unsorted_segment_sum
- unsorted_segment_sum_dyn
- unstack
- unstack
- unstack
- unstack
- unstack
- unstack
- unstack_dyn
- update_model_v4
- update_model_v4_dyn
- variable_axis_size_partitioner
- variable_axis_size_partitioner_dyn
- variable_op_scope
- variable_op_scope_dyn
- variables_initializer
- variables_initializer
- variables_initializer_dyn
- vectorized_map
- vectorized_map
- vectorized_map_dyn
- verify_tensor_all_finite
- verify_tensor_all_finite
- verify_tensor_all_finite
- verify_tensor_all_finite_dyn
- wals_compute_partial_lhs_and_rhs
- wals_compute_partial_lhs_and_rhs_dyn
- where
- where
- where
- where
- where
- where
- where
- where
- where
- where
- where
- where
- where
- where
- where
- where
- where
- where
- where_dyn
- where_v2
- where_v2
- where_v2
- where_v2
- where_v2
- where_v2
- where_v2_dyn
- while_loop
- while_loop_dyn
- wrap_function
- wrap_function
- write_file
- write_file_dyn
- xla_broadcast_helper
- xla_broadcast_helper_dyn
- xla_cluster_output
- xla_cluster_output_dyn
- xla_conv
- xla_conv_dyn
- xla_dequantize
- xla_dequantize_dyn
- xla_dot
- xla_dot_dyn
- xla_dynamic_slice
- xla_dynamic_slice_dyn
- xla_dynamic_update_slice
- xla_dynamic_update_slice_dyn
- xla_einsum
- xla_einsum_dyn
- xla_if
- xla_if_dyn
- xla_key_value_sort
- xla_key_value_sort_dyn
- xla_launch
- xla_launch_dyn
- xla_pad
- xla_pad_dyn
- xla_recv
- xla_recv_dyn
- xla_reduce
- xla_reduce
- xla_reduce
- xla_reduce_dyn
- xla_reduce_window
- xla_reduce_window_dyn
- xla_replica_id
- xla_replica_id_dyn
- xla_select_and_scatter
- xla_select_and_scatter
- xla_select_and_scatter
- xla_select_and_scatter
- xla_select_and_scatter
- xla_select_and_scatter
- xla_select_and_scatter
- xla_select_and_scatter
- xla_select_and_scatter
- xla_select_and_scatter_dyn
- xla_self_adjoint_eig
- xla_self_adjoint_eig_dyn
- xla_send
- xla_send_dyn
- xla_sort
- xla_sort_dyn
- xla_svd
- xla_svd_dyn
- xla_while
- xla_while
- xla_while
- xla_while
- xla_while
- xla_while
- xla_while
- xla_while
- xla_while
- xla_while_dyn
- zero_initializer
- zero_initializer_dyn
- zero_var_initializer
- zero_var_initializer_dyn
- zeros
- zeros
- zeros
- zeros
- zeros_dyn
- zeros_like
- zeros_like
- zeros_like
- zeros_like
- zeros_like_dyn
- zeta
- zeta_dyn
Properties
- a_fn
- abs_fn
- accumulate_n_fn
- acos_fn
- acosh_fn
- add_check_numerics_ops_fn
- add_fn
- add_n_fn
- add_to_collection_fn
- add_to_collections_fn
- adjust_hsv_in_yiq_fn
- all_variables_fn
- angle_fn
- arg_max_fn
- arg_min_fn
- argmax_fn
- argmin_fn
- argsort_fn
- as_dtype_fn
- as_string_fn
- asin_fn
- asinh_fn
- assert_equal_fn
- Assert_fn
- assert_greater_equal_fn
- assert_greater_fn
- assert_integer_fn
- assert_less_equal_fn
- assert_less_fn
- assert_near_fn
- assert_negative_fn
- assert_non_negative_fn
- assert_non_positive_fn
- assert_none_equal_fn
- assert_positive_fn
- assert_proper_iterable_fn
- assert_rank_at_least_fn
- assert_rank_fn
- assert_rank_in_fn
- assert_same_float_dtype_fn
- assert_scalar_fn
- assert_type_fn
- assert_variables_initialized_fn
- assign_add_fn
- assign_fn
- assign_sub_fn
- atan_fn
- atan2_fn
- atanh_fn
- attr_bool_fn
- attr_bool_list_fn
- attr_default_fn
- attr_empty_list_default_fn
- attr_enum_fn
- attr_enum_list_fn
- attr_float_fn
- attr_fn
- attr_list_default_fn
- attr_list_min_fn
- attr_list_type_default_fn
- attr_min_fn
- attr_partial_shape_fn
- attr_partial_shape_list_fn
- attr_shape_fn
- attr_shape_list_fn
- attr_type_default_fn
- audio_microfrontend_fn
- b_fn
- batch_gather_fn
- batch_scatter_update_fn
- batch_to_space_fn
- batch_to_space_nd_fn
- betainc_fn
- bfloat16
- binary_fn
- bincount_fn_
- bipartite_match_fn
- bitcast_fn
- bool
- boolean_mask_fn
- broadcast_dynamic_shape_fn
- broadcast_static_shape_fn
- broadcast_to_fn
- bucketize_with_input_boundaries_fn
- build_categorical_equality_splits_fn
- build_dense_inequality_splits_fn
- build_sparse_inequality_splits_fn
- bytes_in_use_fn
- bytes_limit_fn
- case_fn
- cast_fn
- ceil_fn
- center_tree_ensemble_bias_fn
- check_numerics_fn
- cholesky_fn
- cholesky_solve_fn
- clip_by_average_norm_fn
- clip_by_global_norm_fn
- clip_by_norm_fn
- clip_by_value_fn
- complex_fn
- complex_struct_fn
- complex128
- complex64
- concat_fn
- cond_fn
- confusion_matrix_fn_
- conj_fn
- constant_fn_
- container_fn
- contrib
- contrib_dyn
- control_dependencies_fn
- control_flow_v2_enabled_fn
- convert_to_tensor_fn
- convert_to_tensor_or_indexed_slices_fn
- convert_to_tensor_or_sparse_tensor_fn
- copy_op_fn
- cos_fn
- cosh_fn
- count_nonzero_fn
- count_up_to_fn
- create_fertile_stats_variable_fn
- create_partitioned_variables_fn
- create_quantile_accumulator_fn
- create_stats_accumulator_scalar_fn
- create_stats_accumulator_tensor_fn
- create_tree_ensemble_variable_fn
- create_tree_variable_fn
- cross_fn
- cumprod_fn
- cumsum_fn
- custom_gradient_fn
- decision_tree_ensemble_resource_handle_op_fn
- decision_tree_resource_handle_op_fn
- decode_base64_fn
- decode_compressed_fn
- decode_csv_fn
- decode_json_example_fn
- decode_libsvm_fn
- decode_raw_fn_
- default_attrs_fn
- delete_session_tensor_fn
- depth_to_space_fn
- dequantize_fn
- deserialize_many_sparse_fn
- device_fn
- device_placement_op_fn
- diag_fn
- diag_part_fn
- digamma_fn
- dimension_at_index_fn
- dimension_value_fn
- disable_control_flow_v2_fn
- disable_eager_execution_fn
- disable_tensor_equality_fn
- disable_v2_behavior_fn
- disable_v2_tensorshape_fn
- div_fn
- div_no_nan_fn
- divide_fn
- dynamic_partition_fn
- dynamic_stitch_fn
- edit_distance_fn
- einsum_fn
- enable_control_flow_v2_fn
- enable_eager_execution_fn
- enable_tensor_equality_fn
- enable_v2_behavior_fn
- enable_v2_tensorshape_fn
- encode_base64_fn
- equal_fn
- erf_fn
- erfc_fn
- executing_eagerly_fn
- exp_fn
- expand_dims_fn
- expm1_fn
- extract_image_patches_fn
- extract_volume_patches_fn
- eye_fn
- fake_quant_with_min_max_args_fn
- fake_quant_with_min_max_args_gradient_fn
- fake_quant_with_min_max_vars_fn
- fake_quant_with_min_max_vars_gradient_fn
- fake_quant_with_min_max_vars_per_channel_fn
- fake_quant_with_min_max_vars_per_channel_gradient_fn
- feature_usage_counts_fn
- fertile_stats_deserialize_fn
- fertile_stats_is_initialized_op_fn
- fertile_stats_resource_handle_op_fn
- fertile_stats_serialize_fn
- fft_fn
- fft2d_fn
- fft3d_fn
- fill_fn
- finalize_tree_fn
- fingerprint_fn
- five_float_outputs_fn
- fixed_size_partitioner_fn
- float_input_fn
- float_output_fn
- float_output_string_output_fn
- float16
- float32
- float64
- floor_div_fn
- floor_fn
- floordiv_fn
- foldl_fn
- foldr_fn
- foo1_fn
- foo2_fn
- foo3_fn
- func_attr_fn
- func_list_attr_fn
- function_fn
- gather_fn
- gather_nd_fn
- gather_tree_fn
- get_collection_fn
- get_collection_ref_fn
- get_default_graph_fn
- get_default_session__fn
- get_local_variable_fn
- get_logger_fn
- get_seed_fn
- get_session_handle_fn
- get_session_tensor_fn
- get_static_value_fn
- get_variable_fn
- get_variable_scope_fn
- global_norm_fn
- global_variables_fn
- global_variables_initializer_fn
- grad_pass_through_fn
- gradient_trees_partition_examples_fn
- gradient_trees_prediction_fn
- gradient_trees_prediction_verbose_fn
- gradients_fn
- graph_def_version_fn
- greater_equal_fn
- greater_fn
- group_fn
- grow_tree_ensemble_fn
- grow_tree_v4_fn
- guarantee_const_fn
- hard_routing_function_fn
- hessians_fn
- histogram_fixed_width_bins_fn
- histogram_fixed_width_fn
- identity_fn
- identity_n_fn
- ifft_fn
- ifft2d_fn
- ifft3d_fn
- igamma_fn
- igammac_fn
- imag_fn
- image_connected_components_fn
- image_projective_transform_fn
- image_projective_transform_v2_fn
- import_graph_def_fn
- in_polymorphic_twice_fn
- init_scope_fn
- initialize_all_tables_fn
- initialize_all_variables_fn
- initialize_local_variables_fn
- initialize_variables_fn
- int_attr_fn
- int_input_float_input_fn
- int_input_fn
- int_input_int_output_fn
- int_output_float_output_fn
- int_output_fn
- int16
- int32
- int64
- int64_output_fn
- int8
- invert_permutation_fn
- is_finite_fn
- is_inf_fn
- is_nan_fn
- is_non_decreasing_fn
- is_numeric_tensor_fn
- is_strictly_increasing_fn
- is_tensor_fn
- is_variable_initialized_fn
- k_feature_gradient_fn
- k_feature_routing_function_fn
- kernel_label_fn
- kernel_label_required_fn
- lbeta_fn
- less_equal_fn
- less_fn
- lgamma_fn
- linspace_fn
- list_input_fn
- list_output_fn
- load_file_system_library_fn
- load_library_fn
- load_op_library_fn
- local_variables_fn
- local_variables_initializer_fn
- log_fn
- log_sigmoid_fn
- log1p_fn
- logical_and_fn
- logical_not_fn
- logical_or_fn
- logical_xor_fn
- make_ndarray_fn
- make_quantile_summaries_fn
- make_template_fn
- make_tensor_proto_fn
- map_fn_fn
- masked_matmul_fn
- matching_files_fn
- matmul_fn
- matrix_band_part_fn
- matrix_determinant_fn
- matrix_diag_fn
- matrix_diag_part_fn
- matrix_inverse_fn
- matrix_set_diag_fn
- matrix_solve_fn
- matrix_solve_ls_fn
- matrix_square_root_fn
- matrix_transpose_fn
- matrix_triangular_solve_fn
- max_bytes_in_use_fn
- maximum_fn
- meshgrid_fn
- min_max_variable_partitioner_fn
- minimum_fn
- mixed_struct_fn
- mod_fn
- model_variables_fn
- moving_average_variables_fn
- multinomial_fn
- multiply_fn
- n_in_polymorphic_twice_fn
- n_in_twice_fn
- n_in_two_type_variables_fn
- n_ints_in_fn
- n_ints_out_default_fn
- n_ints_out_fn
- n_polymorphic_in_fn
- n_polymorphic_out_default_fn
- n_polymorphic_out_fn
- n_polymorphic_restrict_in_fn
- n_polymorphic_restrict_out_fn
- negative_fn
- no_op_fn
- no_regularizer_fn
- NoGradient_fn
- nondifferentiable_batch_function_fn
- none_fn
- norm_fn
- not_equal_fn
- numpy_function_fn
- obtain_next_fn
- old_fn
- one_hot_fn
- ones_fn
- ones_like_fn
- op_scope_fn
- op_with_default_attr_fn
- op_with_future_default_attr_fn
- out_t_fn
- out_type_list_fn
- out_type_list_restrict_fn
- pad_fn
- parallel_stack_fn
- parse_example_fn
- parse_single_example_fn
- parse_single_sequence_example_fn
- parse_tensor_fn
- periodic_resample_fn
- periodic_resample_op_grad_fn
- placeholder_fn
- placeholder_with_default_fn
- plugin_dir
- plugin_dir_dyn
- polygamma_fn
- polymorphic_default_out_fn
- polymorphic_fn
- polymorphic_out_fn
- pow_fn
- print_fn
- Print_fn
- process_input_v4_fn
- py_func_fn
- py_function_fn
- qint16
- qint32
- qint8
- qr_fn
- quantile_accumulator_add_summaries_fn
- quantile_accumulator_deserialize_fn
- quantile_accumulator_flush_fn
- quantile_accumulator_flush_summary_fn
- quantile_accumulator_get_buckets_fn
- quantile_accumulator_is_initialized_fn
- quantile_accumulator_serialize_fn
- quantile_buckets_fn
- quantile_stream_resource_handle_op_fn
- quantiles_fn
- quantize_fn
- quantize_v2_fn
- quantized_concat_fn
- QUANTIZED_DTYPES
- quint16
- quint8
- random_crop_fn
- random_gamma_fn
- random_normal_fn
- random_poisson_fn
- random_shuffle_fn
- random_uniform_fn
- range_fn
- rank_fn
- read_file_fn
- real_fn
- realdiv_fn
- reciprocal_fn
- recompute_grad_fn
- reduce_all_fn_
- reduce_any_fn_
- reduce_join_fn
- reduce_logsumexp_fn_
- reduce_max_fn_
- reduce_mean_fn_
- reduce_min_fn_
- reduce_prod_fn_
- reduce_slice_max_fn
- reduce_slice_min_fn
- reduce_slice_prod_fn
- reduce_slice_sum_fn
- reduce_sum_fn_
- ref_in_fn
- ref_input_float_input_fn
- ref_input_float_input_int_output_fn
- ref_input_int_input_fn
- ref_out_fn
- ref_output_float_output_fn
- ref_output_fn
- regex_replace_fn
- register_tensor_conversion_function_fn
- reinterpret_string_to_float_fn
- remote_fused_graph_execute_fn
- repeat_fn
- report_uninitialized_variables_fn
- required_space_to_batch_paddings_fn
- requires_older_graph_version_fn
- resampler_fn
- resampler_grad_fn
- reserved_attr_fn
- reserved_input_fn
- reset_default_graph_fn
- reshape_fn
- resource
- resource_create_op_fn
- resource_initialized_op_fn
- resource_using_op_fn
- rest_of_the_axes
- restrict_fn
- reverse_fn_
- reverse_sequence_fn
- rint_fn
- roll_fn
- round_fn
- routing_function_fn
- routing_gradient_fn
- rpc_fn
- rsqrt_fn
- s
- s_dyn
- saturate_cast_fn
- scalar_mul_fn
- scan_fn
- scatter_add_fn
- scatter_add_ndim_fn
- scatter_div_fn
- scatter_max_fn
- scatter_min_fn
- scatter_mul_fn
- scatter_nd_add_fn
- scatter_nd_fn
- scatter_nd_sub_fn
- scatter_nd_update_fn
- scatter_sub_fn
- scatter_update_fn
- searchsorted_fn
- segment_max_fn
- segment_mean_fn
- segment_min_fn
- segment_prod_fn
- segment_sum_fn
- self_adjoint_eig_fn
- self_adjoint_eigvals_fn
- sequence_file_dataset_fn
- sequence_mask_fn
- serialize_many_sparse_fn
- serialize_sparse_fn
- serialize_tensor_fn
- set_random_seed_fn
- setdiff1d_fn
- shape_fn
- shape_n_fn
- sigmoid_fn
- sign_fn
- simple_fn
- simple_struct_fn
- sin_fn
- single_image_random_dot_stereograms_fn
- sinh_fn
- size_fn
- skip_gram_generate_candidates_fn
- slice_fn
- sort_fn
- space_to_batch_fn
- space_to_batch_nd_fn
- space_to_depth_fn
- sparse_add_fn
- sparse_concat_fn
- sparse_feature_cross_fn
- sparse_feature_cross_v2_fn
- sparse_fill_empty_rows_fn
- sparse_mask_fn
- sparse_matmul_fn
- sparse_maximum_fn
- sparse_merge_fn
- sparse_minimum_fn
- sparse_placeholder_fn
- sparse_reduce_max_fn
- sparse_reduce_max_sparse_fn
- sparse_reduce_sum_fn
- sparse_reduce_sum_sparse_fn
- sparse_reorder_fn
- sparse_reset_shape_fn
- sparse_reshape_fn
- sparse_retain_fn
- sparse_segment_mean_fn
- sparse_segment_sqrt_n_fn
- sparse_segment_sum_fn
- sparse_slice_fn
- sparse_softmax_fn
- sparse_split_fn
- sparse_tensor_dense_matmul_fn
- sparse_tensor_to_dense_fn
- sparse_to_dense_fn
- sparse_to_indicator_fn
- sparse_transpose_fn
- split_fn
- sqrt_fn
- square_fn
- squared_difference_fn
- squeeze_fn
- stack_fn
- stats_accumulator_scalar_add_fn
- stats_accumulator_scalar_deserialize_fn
- stats_accumulator_scalar_flush_fn
- stats_accumulator_scalar_is_initialized_fn
- stats_accumulator_scalar_make_summary_fn
- stats_accumulator_scalar_resource_handle_op_fn
- stats_accumulator_scalar_serialize_fn
- stats_accumulator_tensor_add_fn
- stats_accumulator_tensor_deserialize_fn
- stats_accumulator_tensor_flush_fn
- stats_accumulator_tensor_is_initialized_fn
- stats_accumulator_tensor_make_summary_fn
- stats_accumulator_tensor_resource_handle_op_fn
- stats_accumulator_tensor_serialize_fn
- stochastic_hard_routing_function_fn
- stochastic_hard_routing_gradient_fn
- stop_gradient_fn
- strided_slice_fn
- string
- string_join_fn
- string_list_attr_fn
- string_split_fn
- string_strip_fn
- string_to_hash_bucket_fast_fn
- string_to_hash_bucket_fn
- string_to_hash_bucket_strong_fn
- string_to_number_fn
- stub_resource_handle_op_fn
- substr_fn_
- subtract_fn
- svd_fn
- switch_case_fn
- tables_initializer_fn
- tan_fn
- tanh_fn
- tensor_scatter_add_fn
- tensor_scatter_sub_fn
- tensor_scatter_update_fn
- tensordot_fn
- test_attr_fn
- test_string_output_fn
- tile_fn
- timestamp_fn
- to_bfloat16_fn
- to_complex128_fn
- to_complex64_fn
- to_double_fn
- to_float_fn
- to_int32_fn
- to_int64_fn
- trace_fn
- trainable_variables_fn
- transpose_fn
- traverse_tree_v4_fn
- tree_deserialize_fn
- tree_ensemble_deserialize_fn
- tree_ensemble_is_initialized_op_fn
- tree_ensemble_serialize_fn
- tree_ensemble_stamp_token_fn
- tree_ensemble_stats_fn
- tree_ensemble_used_handlers_fn
- tree_is_initialized_op_fn
- tree_predictions_v4_fn
- tree_serialize_fn
- tree_size_fn
- truediv_fn
- truncated_normal_fn
- truncatediv_fn
- truncatemod_fn
- try_rpc_fn
- tuple_fn
- two_float_inputs_float_output_fn
- two_float_inputs_fn
- two_float_inputs_int_output_fn
- two_float_outputs_fn
- two_int_inputs_fn
- two_int_outputs_fn
- two_refs_in_fn
- type_list_fn
- type_list_restrict_fn
- type_list_twice_fn
- uint16
- uint32
- uint64
- uint8
- unary_fn
- unique_fn
- unique_with_counts_fn
- unpack_path_fn
- unravel_index_fn
- unsorted_segment_max_fn
- unsorted_segment_mean_fn
- unsorted_segment_min_fn
- unsorted_segment_prod_fn
- unsorted_segment_sqrt_n_fn
- unsorted_segment_sum_fn
- unstack_fn
- update_model_v4_fn
- variable_axis_size_partitioner_fn
- variable_op_scope_fn
- variables_initializer_fn
- variant
- vectorized_map_fn
- verify_tensor_all_finite_fn
- Version
- wals_compute_partial_lhs_and_rhs_fn
- where_fn
- where_v2_fn
- while_loop_fn
- wrap_function_fn
- write_file_fn
- xla_broadcast_helper_fn
- xla_cluster_output_fn
- xla_conv_fn
- xla_dequantize_fn
- xla_dot_fn
- xla_dynamic_slice_fn
- xla_dynamic_update_slice_fn
- xla_einsum_fn
- xla_if_fn
- xla_key_value_sort_fn
- xla_launch_fn
- xla_pad_fn
- xla_recv_fn
- xla_reduce_fn
- xla_reduce_window_fn
- xla_replica_id_fn
- xla_select_and_scatter_fn
- xla_self_adjoint_eig_fn
- xla_send_fn
- xla_sort_fn
- xla_svd_fn
- xla_while_fn
- zero_initializer_fn
- zero_var_initializer_fn
- zeros_fn
- zeros_like_fn
- zeta_fn
Fields
Public static methods
Tensor a(string name)
object a_dyn(object name)
object abs(IGraphNodeBase x, string name)
object abs_dyn(object x, object name)
Tensor accumulate_n(IEnumerable<IGraphNodeBase> inputs, IEnumerable<object> shape, PythonClassContainer tensor_dtype, string name)
Returns the element-wise sum of a list of tensors. Optionally, pass `shape` and `tensor_dtype` for shape and type checking,
otherwise, these are inferred. `accumulate_n` performs the same operation as
tf.math.add_n, but
does not wait for all of its inputs to be ready before beginning to sum.
This approach can save memory if inputs are ready at different times, since
minimum temporary storage is proportional to the output size rather than the
inputs' size. `accumulate_n` is differentiable (but wasn't previous to TensorFlow 1.7).
Parameters
-
IEnumerable<IGraphNodeBase>inputs - A list of `Tensor` objects, each with same shape and type.
-
IEnumerable<object>shape - Expected shape of elements of `inputs` (optional). Also controls the output shape of this op, which may affect type inference in other ops. A value of `None` means "infer the input shape from the shapes in `inputs`".
-
PythonClassContainertensor_dtype - Expected data type of `inputs` (optional). A value of `None` means "infer the input dtype from `inputs[0]`".
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of same shape and type as the elements of `inputs`.
Show Example
a = tf.constant([[1, 2], [3, 4]])
b = tf.constant([[5, 0], [0, 6]])
tf.math.accumulate_n([a, b, a]) # [[7, 4], [6, 14]] # Explicitly pass shape and type
tf.math.accumulate_n([a, b, a], shape=[2, 2], tensor_dtype=tf.int32)
# [[7, 4],
# [6, 14]]
Tensor accumulate_n(ValueTuple<PythonClassContainer, PythonClassContainer> inputs, TensorShape shape, PythonClassContainer tensor_dtype, string name)
Returns the element-wise sum of a list of tensors. Optionally, pass `shape` and `tensor_dtype` for shape and type checking,
otherwise, these are inferred. `accumulate_n` performs the same operation as
tf.math.add_n, but
does not wait for all of its inputs to be ready before beginning to sum.
This approach can save memory if inputs are ready at different times, since
minimum temporary storage is proportional to the output size rather than the
inputs' size. `accumulate_n` is differentiable (but wasn't previous to TensorFlow 1.7).
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>inputs - A list of `Tensor` objects, each with same shape and type.
-
TensorShapeshape - Expected shape of elements of `inputs` (optional). Also controls the output shape of this op, which may affect type inference in other ops. A value of `None` means "infer the input shape from the shapes in `inputs`".
-
PythonClassContainertensor_dtype - Expected data type of `inputs` (optional). A value of `None` means "infer the input dtype from `inputs[0]`".
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of same shape and type as the elements of `inputs`.
Show Example
a = tf.constant([[1, 2], [3, 4]])
b = tf.constant([[5, 0], [0, 6]])
tf.math.accumulate_n([a, b, a]) # [[7, 4], [6, 14]] # Explicitly pass shape and type
tf.math.accumulate_n([a, b, a], shape=[2, 2], tensor_dtype=tf.int32)
# [[7, 4],
# [6, 14]]
Tensor accumulate_n(ValueTuple<PythonClassContainer, PythonClassContainer> inputs, IEnumerable<object> shape, PythonClassContainer tensor_dtype, string name)
Returns the element-wise sum of a list of tensors. Optionally, pass `shape` and `tensor_dtype` for shape and type checking,
otherwise, these are inferred. `accumulate_n` performs the same operation as
tf.math.add_n, but
does not wait for all of its inputs to be ready before beginning to sum.
This approach can save memory if inputs are ready at different times, since
minimum temporary storage is proportional to the output size rather than the
inputs' size. `accumulate_n` is differentiable (but wasn't previous to TensorFlow 1.7).
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>inputs - A list of `Tensor` objects, each with same shape and type.
-
IEnumerable<object>shape - Expected shape of elements of `inputs` (optional). Also controls the output shape of this op, which may affect type inference in other ops. A value of `None` means "infer the input shape from the shapes in `inputs`".
-
PythonClassContainertensor_dtype - Expected data type of `inputs` (optional). A value of `None` means "infer the input dtype from `inputs[0]`".
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of same shape and type as the elements of `inputs`.
Show Example
a = tf.constant([[1, 2], [3, 4]])
b = tf.constant([[5, 0], [0, 6]])
tf.math.accumulate_n([a, b, a]) # [[7, 4], [6, 14]] # Explicitly pass shape and type
tf.math.accumulate_n([a, b, a], shape=[2, 2], tensor_dtype=tf.int32)
# [[7, 4],
# [6, 14]]
Tensor accumulate_n(IEnumerable<IGraphNodeBase> inputs, TensorShape shape, PythonClassContainer tensor_dtype, string name)
Returns the element-wise sum of a list of tensors. Optionally, pass `shape` and `tensor_dtype` for shape and type checking,
otherwise, these are inferred. `accumulate_n` performs the same operation as
tf.math.add_n, but
does not wait for all of its inputs to be ready before beginning to sum.
This approach can save memory if inputs are ready at different times, since
minimum temporary storage is proportional to the output size rather than the
inputs' size. `accumulate_n` is differentiable (but wasn't previous to TensorFlow 1.7).
Parameters
-
IEnumerable<IGraphNodeBase>inputs - A list of `Tensor` objects, each with same shape and type.
-
TensorShapeshape - Expected shape of elements of `inputs` (optional). Also controls the output shape of this op, which may affect type inference in other ops. A value of `None` means "infer the input shape from the shapes in `inputs`".
-
PythonClassContainertensor_dtype - Expected data type of `inputs` (optional). A value of `None` means "infer the input dtype from `inputs[0]`".
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of same shape and type as the elements of `inputs`.
Show Example
a = tf.constant([[1, 2], [3, 4]])
b = tf.constant([[5, 0], [0, 6]])
tf.math.accumulate_n([a, b, a]) # [[7, 4], [6, 14]] # Explicitly pass shape and type
tf.math.accumulate_n([a, b, a], shape=[2, 2], tensor_dtype=tf.int32)
# [[7, 4],
# [6, 14]]
object accumulate_n_dyn(object inputs, object shape, object tensor_dtype, object name)
Returns the element-wise sum of a list of tensors. Optionally, pass `shape` and `tensor_dtype` for shape and type checking,
otherwise, these are inferred. `accumulate_n` performs the same operation as
tf.math.add_n, but
does not wait for all of its inputs to be ready before beginning to sum.
This approach can save memory if inputs are ready at different times, since
minimum temporary storage is proportional to the output size rather than the
inputs' size. `accumulate_n` is differentiable (but wasn't previous to TensorFlow 1.7).
Parameters
-
objectinputs - A list of `Tensor` objects, each with same shape and type.
-
objectshape - Expected shape of elements of `inputs` (optional). Also controls the output shape of this op, which may affect type inference in other ops. A value of `None` means "infer the input shape from the shapes in `inputs`".
-
objecttensor_dtype - Expected data type of `inputs` (optional). A value of `None` means "infer the input dtype from `inputs[0]`".
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of same shape and type as the elements of `inputs`.
Show Example
a = tf.constant([[1, 2], [3, 4]])
b = tf.constant([[5, 0], [0, 6]])
tf.math.accumulate_n([a, b, a]) # [[7, 4], [6, 14]] # Explicitly pass shape and type
tf.math.accumulate_n([a, b, a], shape=[2, 2], tensor_dtype=tf.int32)
# [[7, 4],
# [6, 14]]
Tensor acos(IGraphNodeBase x, string name)
Computes acos of x element-wise.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
object acos_dyn(object x, object name)
Computes acos of x element-wise.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Tensor acosh(IGraphNodeBase x, string name)
Computes inverse hyperbolic cosine of x element-wise. Given an input tensor, the function computes inverse hyperbolic cosine of every element.
Input range is `[1, inf]`. It returns `nan` if the input lies outside the range.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-2, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.acosh(x) ==> [nan nan 0. 0.62236255 5.9914584 9.903487 inf]
object acosh_dyn(object x, object name)
Computes inverse hyperbolic cosine of x element-wise. Given an input tensor, the function computes inverse hyperbolic cosine of every element.
Input range is `[1, inf]`. It returns `nan` if the input lies outside the range.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-2, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.acosh(x) ==> [nan nan 0. 0.62236255 5.9914584 9.903487 inf]
Tensor add(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns x + y element-wise. *NOTE*: `math.add` supports broadcasting. `AddN` does not. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `int16`, `int32`, `int64`, `complex64`, `complex128`, `string`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Tensor add(IGraphNodeBase x, IGraphNodeBase y, PythonFunctionContainer name)
Returns x + y element-wise. *NOTE*: `math.add` supports broadcasting. `AddN` does not. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `int16`, `int32`, `int64`, `complex64`, `complex128`, `string`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
object add_check_numerics_ops()
Connect a
tf.debugging.check_numerics to every floating point tensor. `check_numerics` operations themselves are added for each `half`, `float`,
or `double` tensor in the current default graph. For all ops in the graph, the
`check_numerics` op for all of its (`half`, `float`, or `double`) inputs
is guaranteed to run before the `check_numerics` op on any of its outputs. Note: This API is not compatible with the use of tf.cond or
tf.while_loop, and will raise a `ValueError` if you attempt to call it
in such a graph.
Returns
-
object - A `group` op depending on all `check_numerics` ops added.
object add_check_numerics_ops_dyn()
Connect a
tf.debugging.check_numerics to every floating point tensor. `check_numerics` operations themselves are added for each `half`, `float`,
or `double` tensor in the current default graph. For all ops in the graph, the
`check_numerics` op for all of its (`half`, `float`, or `double`) inputs
is guaranteed to run before the `check_numerics` op on any of its outputs. Note: This API is not compatible with the use of tf.cond or
tf.while_loop, and will raise a `ValueError` if you attempt to call it
in such a graph.
Returns
-
object - A `group` op depending on all `check_numerics` ops added.
object add_dyn(object x, object y, object name)
Returns x + y element-wise. *NOTE*: `math.add` supports broadcasting. `AddN` does not. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `int16`, `int32`, `int64`, `complex64`, `complex128`, `string`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Tensor add_n(object inputs, string name)
Adds all input tensors element-wise. Converts `IndexedSlices` objects into dense tensors prior to adding.
tf.math.add_n performs the same operation as tf.math.accumulate_n, but it
waits for all of its inputs to be ready before beginning to sum.
This buffering can result in higher memory consumption when inputs are ready
at different times, since the minimum temporary storage required is
proportional to the input size rather than the output size. This op does not [broadcast](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
its inputs. If you need broadcasting, use tf.math.add (or the `+` operator)
instead.
Parameters
-
objectinputs - A list of
tf.Tensorortf.IndexedSlicesobjects, each with same shape and type. -
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of same shape and type as the elements of `inputs`.
Show Example
a = tf.constant([[3, 5], [4, 8]])
b = tf.constant([[1, 6], [2, 9]])
tf.math.add_n([a, b, a]) # [[7, 16], [10, 25]]
Tensor add_n(PythonFunctionContainer inputs, string name)
Adds all input tensors element-wise. Converts `IndexedSlices` objects into dense tensors prior to adding.
tf.math.add_n performs the same operation as tf.math.accumulate_n, but it
waits for all of its inputs to be ready before beginning to sum.
This buffering can result in higher memory consumption when inputs are ready
at different times, since the minimum temporary storage required is
proportional to the input size rather than the output size. This op does not [broadcast](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
its inputs. If you need broadcasting, use tf.math.add (or the `+` operator)
instead.
Parameters
-
PythonFunctionContainerinputs - A list of
tf.Tensorortf.IndexedSlicesobjects, each with same shape and type. -
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of same shape and type as the elements of `inputs`.
Show Example
a = tf.constant([[3, 5], [4, 8]])
b = tf.constant([[1, 6], [2, 9]])
tf.math.add_n([a, b, a]) # [[7, 16], [10, 25]]
object add_n_dyn(object inputs, object name)
Adds all input tensors element-wise. Converts `IndexedSlices` objects into dense tensors prior to adding.
tf.math.add_n performs the same operation as tf.math.accumulate_n, but it
waits for all of its inputs to be ready before beginning to sum.
This buffering can result in higher memory consumption when inputs are ready
at different times, since the minimum temporary storage required is
proportional to the input size rather than the output size. This op does not [broadcast](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
its inputs. If you need broadcasting, use tf.math.add (or the `+` operator)
instead.
Parameters
-
objectinputs - A list of
tf.Tensorortf.IndexedSlicesobjects, each with same shape and type. -
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of same shape and type as the elements of `inputs`.
Show Example
a = tf.constant([[3, 5], [4, 8]])
b = tf.constant([[1, 6], [2, 9]])
tf.math.add_n([a, b, a]) # [[7, 16], [10, 25]]
void add_to_collection(Saver name, object value)
Wrapper for `Graph.add_to_collection()` using the default graph. See
tf.Graph.add_to_collection
for more details.
Parameters
-
Savername - The key for the collection. For example, the `GraphKeys` class contains many standard names for collections.
-
objectvalue - The value to add to the collection.
void add_to_collection(Saver name, IEnumerable<object> value)
Wrapper for `Graph.add_to_collection()` using the default graph. See
tf.Graph.add_to_collection
for more details.
Parameters
-
Savername - The key for the collection. For example, the `GraphKeys` class contains many standard names for collections.
-
IEnumerable<object>value - The value to add to the collection.
void add_to_collection(IEnumerable<string> name, object value)
Wrapper for `Graph.add_to_collection()` using the default graph. See
tf.Graph.add_to_collection
for more details.
Parameters
-
IEnumerable<string>name - The key for the collection. For example, the `GraphKeys` class contains many standard names for collections.
-
objectvalue - The value to add to the collection.
void add_to_collection(IEnumerable<string> name, IEnumerable<object> value)
Wrapper for `Graph.add_to_collection()` using the default graph. See
tf.Graph.add_to_collection
for more details.
Parameters
-
IEnumerable<string>name - The key for the collection. For example, the `GraphKeys` class contains many standard names for collections.
-
IEnumerable<object>value - The value to add to the collection.
void add_to_collections(ValueTuple names, object value)
Wrapper for `Graph.add_to_collections()` using the default graph. See
tf.Graph.add_to_collections
for more details.
Parameters
-
ValueTuplenames - The key for the collections. The `GraphKeys` class contains many standard names for collections.
-
objectvalue - The value to add to the collections.
void add_to_collections(ValueTuple names, IEnumerable<IGraphNodeBase> value)
Wrapper for `Graph.add_to_collections()` using the default graph. See
tf.Graph.add_to_collections
for more details.
Parameters
-
ValueTuplenames - The key for the collections. The `GraphKeys` class contains many standard names for collections.
-
IEnumerable<IGraphNodeBase>value - The value to add to the collections.
Tensor adjust_hsv_in_yiq(IGraphNodeBase images, IGraphNodeBase delta_h, IGraphNodeBase scale_s, IGraphNodeBase scale_v, string name)
object adjust_hsv_in_yiq_dyn(object images, object delta_h, object scale_s, object scale_v, object name)
object all_variables()
Use `tf.compat.v1.global_variables` instead. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Please use tf.global_variables instead.
object all_variables_dyn()
Use `tf.compat.v1.global_variables` instead. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Please use tf.global_variables instead.
Tensor angle(IGraphNodeBase input, string name)
Returns the element-wise argument of a complex (or real) tensor. Given a tensor `input`, this operation returns a tensor of type `float` that
is the argument of each element in `input` considered as a complex number. The elements in `input` are considered to be complex numbers of the form
\\(a + bj\\), where *a* is the real part and *b* is the imaginary part.
If `input` is real then *b* is zero by definition. The argument returned by this function is of the form \\(atan2(b, a)\\).
If `input` is real, a tensor of all zeros is returned. For example: ```
input = tf.constant([-2.25 + 4.75j, 3.25 + 5.75j], dtype=tf.complex64)
tf.math.angle(input).numpy()
# ==> array([2.0131705, 1.056345 ], dtype=float32)
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float`, `double`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32` or `float64`.
object angle_dyn(object input, object name)
Returns the element-wise argument of a complex (or real) tensor. Given a tensor `input`, this operation returns a tensor of type `float` that
is the argument of each element in `input` considered as a complex number. The elements in `input` are considered to be complex numbers of the form
\\(a + bj\\), where *a* is the real part and *b* is the imaginary part.
If `input` is real then *b* is zero by definition. The argument returned by this function is of the form \\(atan2(b, a)\\).
If `input` is real, a tensor of all zeros is returned. For example: ```
input = tf.constant([-2.25 + 4.75j, 3.25 + 5.75j], dtype=tf.complex64)
tf.math.angle(input).numpy()
# ==> array([2.0131705, 1.056345 ], dtype=float32)
```
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float`, `double`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `float32` or `float64`.
Tensor arg_max(IGraphNodeBase input, IGraphNodeBase dimension, ndarray output_type, string name)
Returns the index with the largest value across dimensions of a tensor. Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasedimension - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which dimension of the input Tensor to reduce across. For vectors, use dimension = 0.
-
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64. -
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor arg_max(IGraphNodeBase input, IGraphNodeBase dimension, ImplicitContainer<T> output_type, string name)
Returns the index with the largest value across dimensions of a tensor. Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasedimension - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which dimension of the input Tensor to reduce across. For vectors, use dimension = 0.
-
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64. -
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
object arg_max_dyn(object input, object dimension, ImplicitContainer<T> output_type, object name)
Returns the index with the largest value across dimensions of a tensor. Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
objectdimension - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which dimension of the input Tensor to reduce across. For vectors, use dimension = 0.
-
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64. -
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor arg_min(IGraphNodeBase input, IGraphNodeBase dimension, ImplicitContainer<T> output_type, string name)
Returns the index with the smallest value across dimensions of a tensor. Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasedimension - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which dimension of the input Tensor to reduce across. For vectors, use dimension = 0.
-
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64. -
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor arg_min(IGraphNodeBase input, IGraphNodeBase dimension, ndarray output_type, string name)
Returns the index with the smallest value across dimensions of a tensor. Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasedimension - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which dimension of the input Tensor to reduce across. For vectors, use dimension = 0.
-
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64. -
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
object arg_min_dyn(object input, object dimension, ImplicitContainer<T> output_type, object name)
Returns the index with the smallest value across dimensions of a tensor. Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
objectdimension - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which dimension of the input Tensor to reduce across. For vectors, use dimension = 0.
-
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64. -
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmax(IEnumerable<IGraphNodeBase> input, ValueTuple<object, ndarray, object> axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
ValueTuple<object, ndarray, object>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(IEnumerable<IGraphNodeBase> input, int axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(IEnumerable<IGraphNodeBase> input, int axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(IEnumerable<IGraphNodeBase> input, IGraphNodeBase axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(object input, IGraphNodeBase axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(IEnumerable<IGraphNodeBase> input, IGraphNodeBase axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(object input, IGraphNodeBase axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(object input, int axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(object input, int axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(IEnumerable<IGraphNodeBase> input, ValueTuple<object, ndarray, object> axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
ValueTuple<object, ndarray, object>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(object input, ValueTuple<object, ndarray, object> axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
ValueTuple<object, ndarray, object>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmax(object input, ValueTuple<object, ndarray, object> axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
ValueTuple<object, ndarray, object>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
object argmax_dyn(object input, object axis, object name, object dimension, ImplicitContainer<T> output_type)
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
objectaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
objectname - A name for the operation (optional).
-
objectdimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
object - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
Tensor argmin(ndarray input, ValueTuple<object, ndarray, object> axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
ndarrayinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
ValueTuple<object, ndarray, object>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(IEnumerable<int> input, Nullable<int> axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IEnumerable<int>input - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
Nullable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(IEnumerable<int> input, Nullable<int> axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IEnumerable<int>input - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
Nullable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(IGraphNodeBase input, ValueTuple<object, ndarray, object> axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
ValueTuple<object, ndarray, object>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(IGraphNodeBase input, Nullable<int> axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
Nullable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(IGraphNodeBase input, Nullable<int> axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
Nullable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(IEnumerable<int> input, ValueTuple<object, ndarray, object> axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IEnumerable<int>input - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
ValueTuple<object, ndarray, object>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(ndarray input, Nullable<int> axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
ndarrayinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
Nullable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(ndarray input, Nullable<int> axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
ndarrayinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
Nullable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(ndarray input, ValueTuple<object, ndarray, object> axis, string name, Nullable<int> dimension, ndarray output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
ndarrayinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
ValueTuple<object, ndarray, object>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ndarrayoutput_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(IEnumerable<int> input, ValueTuple<object, ndarray, object> axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IEnumerable<int>input - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
ValueTuple<object, ndarray, object>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
Tensor argmin(IGraphNodeBase input, ValueTuple<object, ndarray, object> axis, string name, Nullable<int> dimension, ImplicitContainer<T> output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
ValueTuple<object, ndarray, object>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
stringname - A name for the operation (optional).
-
Nullable<int>dimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
Tensor - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
object argmin_dyn(object input, object axis, object name, object dimension, ImplicitContainer<T> output_type)
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
objectaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. int32 or int64, must be in the range `[-rank(input), rank(input))`. Describes which axis of the input Tensor to reduce across. For vectors, use axis = 0.
-
objectname - A name for the operation (optional).
-
objectdimension -
ImplicitContainer<T>output_type - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int64.
Returns
-
object - A `Tensor` of type `output_type`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
object argsort(int values, int axis, string direction, bool stable, string name)
Returns the indices of a tensor that give its sorted order along an axis. For a 1D tensor, `tf.gather(values, tf.argsort(values))` is equivalent to
`tf.sort(values)`. For higher dimensions, the output has the same shape as
`values`, but along the given axis, values represent the index of the sorted
element in that slice of the tensor at the given position. Usage:
Parameters
-
intvalues - 1-D or higher numeric `Tensor`.
-
intaxis - The axis along which to sort. The default is -1, which sorts the last axis.
-
stringdirection - The direction in which to sort the values (`'ASCENDING'` or `'DESCENDING'`).
-
boolstable - If True, equal elements in the original tensor will not be re-ordered in the returned order. Unstable sort is not yet implemented, but will eventually be the default for performance reasons. If you require a stable order, pass `stable=True` for forwards compatibility.
-
stringname - Optional name for the operation.
Returns
-
object - An int32 `Tensor` with the same shape as `values`. The indices that would sort each slice of the given `values` along the given `axis`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.argsort(a,axis=-1,direction='ASCENDING',stable=False,name=None)
c = tf.keras.backend.eval(b)
# Here, c = [0 3 1 2 5 4]
object argsort(IEnumerable<object> values, int axis, string direction, bool stable, string name)
Returns the indices of a tensor that give its sorted order along an axis. For a 1D tensor, `tf.gather(values, tf.argsort(values))` is equivalent to
`tf.sort(values)`. For higher dimensions, the output has the same shape as
`values`, but along the given axis, values represent the index of the sorted
element in that slice of the tensor at the given position. Usage:
Parameters
-
IEnumerable<object>values - 1-D or higher numeric `Tensor`.
-
intaxis - The axis along which to sort. The default is -1, which sorts the last axis.
-
stringdirection - The direction in which to sort the values (`'ASCENDING'` or `'DESCENDING'`).
-
boolstable - If True, equal elements in the original tensor will not be re-ordered in the returned order. Unstable sort is not yet implemented, but will eventually be the default for performance reasons. If you require a stable order, pass `stable=True` for forwards compatibility.
-
stringname - Optional name for the operation.
Returns
-
object - An int32 `Tensor` with the same shape as `values`. The indices that would sort each slice of the given `values` along the given `axis`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.argsort(a,axis=-1,direction='ASCENDING',stable=False,name=None)
c = tf.keras.backend.eval(b)
# Here, c = [0 3 1 2 5 4]
object argsort(CompositeTensor values, int axis, string direction, bool stable, string name)
Returns the indices of a tensor that give its sorted order along an axis. For a 1D tensor, `tf.gather(values, tf.argsort(values))` is equivalent to
`tf.sort(values)`. For higher dimensions, the output has the same shape as
`values`, but along the given axis, values represent the index of the sorted
element in that slice of the tensor at the given position. Usage:
Parameters
-
CompositeTensorvalues - 1-D or higher numeric `Tensor`.
-
intaxis - The axis along which to sort. The default is -1, which sorts the last axis.
-
stringdirection - The direction in which to sort the values (`'ASCENDING'` or `'DESCENDING'`).
-
boolstable - If True, equal elements in the original tensor will not be re-ordered in the returned order. Unstable sort is not yet implemented, but will eventually be the default for performance reasons. If you require a stable order, pass `stable=True` for forwards compatibility.
-
stringname - Optional name for the operation.
Returns
-
object - An int32 `Tensor` with the same shape as `values`. The indices that would sort each slice of the given `values` along the given `axis`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.argsort(a,axis=-1,direction='ASCENDING',stable=False,name=None)
c = tf.keras.backend.eval(b)
# Here, c = [0 3 1 2 5 4]
object argsort(ValueTuple<PythonClassContainer, PythonClassContainer> values, int axis, string direction, bool stable, string name)
Returns the indices of a tensor that give its sorted order along an axis. For a 1D tensor, `tf.gather(values, tf.argsort(values))` is equivalent to
`tf.sort(values)`. For higher dimensions, the output has the same shape as
`values`, but along the given axis, values represent the index of the sorted
element in that slice of the tensor at the given position. Usage:
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>values - 1-D or higher numeric `Tensor`.
-
intaxis - The axis along which to sort. The default is -1, which sorts the last axis.
-
stringdirection - The direction in which to sort the values (`'ASCENDING'` or `'DESCENDING'`).
-
boolstable - If True, equal elements in the original tensor will not be re-ordered in the returned order. Unstable sort is not yet implemented, but will eventually be the default for performance reasons. If you require a stable order, pass `stable=True` for forwards compatibility.
-
stringname - Optional name for the operation.
Returns
-
object - An int32 `Tensor` with the same shape as `values`. The indices that would sort each slice of the given `values` along the given `axis`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.argsort(a,axis=-1,direction='ASCENDING',stable=False,name=None)
c = tf.keras.backend.eval(b)
# Here, c = [0 3 1 2 5 4]
object argsort(IGraphNodeBase values, int axis, string direction, bool stable, string name)
Returns the indices of a tensor that give its sorted order along an axis. For a 1D tensor, `tf.gather(values, tf.argsort(values))` is equivalent to
`tf.sort(values)`. For higher dimensions, the output has the same shape as
`values`, but along the given axis, values represent the index of the sorted
element in that slice of the tensor at the given position. Usage:
Parameters
-
IGraphNodeBasevalues - 1-D or higher numeric `Tensor`.
-
intaxis - The axis along which to sort. The default is -1, which sorts the last axis.
-
stringdirection - The direction in which to sort the values (`'ASCENDING'` or `'DESCENDING'`).
-
boolstable - If True, equal elements in the original tensor will not be re-ordered in the returned order. Unstable sort is not yet implemented, but will eventually be the default for performance reasons. If you require a stable order, pass `stable=True` for forwards compatibility.
-
stringname - Optional name for the operation.
Returns
-
object - An int32 `Tensor` with the same shape as `values`. The indices that would sort each slice of the given `values` along the given `axis`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.argsort(a,axis=-1,direction='ASCENDING',stable=False,name=None)
c = tf.keras.backend.eval(b)
# Here, c = [0 3 1 2 5 4]
object argsort_dyn(object values, ImplicitContainer<T> axis, ImplicitContainer<T> direction, ImplicitContainer<T> stable, object name)
Returns the indices of a tensor that give its sorted order along an axis. For a 1D tensor, `tf.gather(values, tf.argsort(values))` is equivalent to
`tf.sort(values)`. For higher dimensions, the output has the same shape as
`values`, but along the given axis, values represent the index of the sorted
element in that slice of the tensor at the given position. Usage:
Parameters
-
objectvalues - 1-D or higher numeric `Tensor`.
-
ImplicitContainer<T>axis - The axis along which to sort. The default is -1, which sorts the last axis.
-
ImplicitContainer<T>direction - The direction in which to sort the values (`'ASCENDING'` or `'DESCENDING'`).
-
ImplicitContainer<T>stable - If True, equal elements in the original tensor will not be re-ordered in the returned order. Unstable sort is not yet implemented, but will eventually be the default for performance reasons. If you require a stable order, pass `stable=True` for forwards compatibility.
-
objectname - Optional name for the operation.
Returns
-
object - An int32 `Tensor` with the same shape as `values`. The indices that would sort each slice of the given `values` along the given `axis`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.argsort(a,axis=-1,direction='ASCENDING',stable=False,name=None)
c = tf.keras.backend.eval(b)
# Here, c = [0 3 1 2 5 4]
DType as_dtype(object type_value)
Converts the given `type_value` to a `DType`.
Parameters
Returns
-
DType - A `DType` corresponding to `type_value`.
DType as_dtype(PythonFunctionContainer type_value)
Converts the given `type_value` to a `DType`.
Parameters
-
PythonFunctionContainertype_value - A value that can be converted to a
tf.DTypeobject. This may currently be atf.DTypeobject, a [`DataType` enum](https://www.tensorflow.org/code/tensorflow/core/framework/types.proto), a string type name, or a `numpy.dtype`.
Returns
-
DType - A `DType` corresponding to `type_value`.
object as_dtype_dyn(object type_value)
Converts the given `type_value` to a `DType`.
Parameters
Returns
-
object - A `DType` corresponding to `type_value`.
Tensor as_string(IGraphNodeBase input, int precision, bool scientific, bool shortest, int width, string fill, string name)
Converts each entry in the given tensor to strings. Supports many numeric types and boolean. For Unicode, see the
[https://www.tensorflow.org/tutorials/representation/unicode](Working with Unicode text)
tutorial.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `int8`, `int16`, `int32`, `int64`, `complex64`, `complex128`, `float32`, `float64`, `bool`.
-
intprecision - An optional `int`. Defaults to `-1`. The post-decimal precision to use for floating point numbers. Only used if precision > -1.
-
boolscientific - An optional `bool`. Defaults to `False`. Use scientific notation for floating point numbers.
-
boolshortest - An optional `bool`. Defaults to `False`. Use shortest representation (either scientific or standard) for floating point numbers.
-
intwidth - An optional `int`. Defaults to `-1`. Pad pre-decimal numbers to this width. Applies to both floating point and integer numbers. Only used if width > -1.
-
stringfill - An optional `string`. Defaults to `""`. The value to pad if width > -1. If empty, pads with spaces. Another typical value is '0'. String cannot be longer than 1 character.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `string`.
object as_string_dyn(object input, ImplicitContainer<T> precision, ImplicitContainer<T> scientific, ImplicitContainer<T> shortest, ImplicitContainer<T> width, ImplicitContainer<T> fill, object name)
Converts each entry in the given tensor to strings. Supports many numeric types and boolean. For Unicode, see the
[https://www.tensorflow.org/tutorials/representation/unicode](Working with Unicode text)
tutorial.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `int8`, `int16`, `int32`, `int64`, `complex64`, `complex128`, `float32`, `float64`, `bool`.
-
ImplicitContainer<T>precision - An optional `int`. Defaults to `-1`. The post-decimal precision to use for floating point numbers. Only used if precision > -1.
-
ImplicitContainer<T>scientific - An optional `bool`. Defaults to `False`. Use scientific notation for floating point numbers.
-
ImplicitContainer<T>shortest - An optional `bool`. Defaults to `False`. Use shortest representation (either scientific or standard) for floating point numbers.
-
ImplicitContainer<T>width - An optional `int`. Defaults to `-1`. Pad pre-decimal numbers to this width. Applies to both floating point and integer numbers. Only used if width > -1.
-
ImplicitContainer<T>fill - An optional `string`. Defaults to `""`. The value to pad if width > -1. If empty, pads with spaces. Another typical value is '0'. String cannot be longer than 1 character.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `string`.
Tensor asin(IGraphNodeBase x, string name)
Computes the trignometric inverse sine of x element-wise. The
tf.math.asin operation returns the inverse of tf.math.sin, such that
if `y = tf.math.sin(x)` then, `x = tf.math.asin(y)`. **Note**: The output of tf.math.asin will lie within the invertible range
of sine, i.e [-pi/2, pi/2].
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Show Example
# Note: [1.047, 0.785] ~= [(pi/3), (pi/4)]
x = tf.constant([1.047, 0.785])
y = tf.math.sin(x) # [0.8659266, 0.7068252] tf.math.asin(y) # [1.047, 0.785] = x
object asin_dyn(object x, object name)
Computes the trignometric inverse sine of x element-wise. The
tf.math.asin operation returns the inverse of tf.math.sin, such that
if `y = tf.math.sin(x)` then, `x = tf.math.asin(y)`. **Note**: The output of tf.math.asin will lie within the invertible range
of sine, i.e [-pi/2, pi/2].
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
# Note: [1.047, 0.785] ~= [(pi/3), (pi/4)]
x = tf.constant([1.047, 0.785])
y = tf.math.sin(x) # [0.8659266, 0.7068252] tf.math.asin(y) # [1.047, 0.785] = x
Tensor asinh(IGraphNodeBase x, string name)
Computes inverse hyperbolic sine of x element-wise. Given an input tensor, this function computes inverse hyperbolic sine
for every element in the tensor. Both input and output has a range of
`[-inf, inf]`.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -2, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.asinh(x) ==> [-inf -1.4436355 -0.4812118 0.8813736 1.0159732 5.991471 9.903487 inf]
object asinh_dyn(object x, object name)
Computes inverse hyperbolic sine of x element-wise. Given an input tensor, this function computes inverse hyperbolic sine
for every element in the tensor. Both input and output has a range of
`[-inf, inf]`.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -2, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.asinh(x) ==> [-inf -1.4436355 -0.4812118 0.8813736 1.0159732 5.991471 9.903487 inf]
object Assert(IEnumerable<object> condition, ValueTuple<string, IGraphNodeBase> data, int summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
ValueTuple<string, IGraphNodeBase>data - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, object data, Nullable<double> summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
objectdata - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, object data, int summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
objectdata - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, object data, Nullable<double> summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
objectdata - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, object data, int summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
objectdata - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, IEnumerable<object> data, Nullable<double> summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
IEnumerable<object>data - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, IEnumerable<object> data, Nullable<double> summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
IEnumerable<object>data - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, ValueTuple<string, IGraphNodeBase> data, Nullable<double> summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
ValueTuple<string, IGraphNodeBase>data - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, IEnumerable<object> data, Nullable<double> summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
IEnumerable<object>data - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, IEnumerable<object> data, int summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
IEnumerable<object>data - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, IEnumerable<object> data, int summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
IEnumerable<object>data - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, object data, int summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
objectdata - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, object data, int summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
objectdata - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, IEnumerable<object> data, int summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
IEnumerable<object>data - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, object data, Nullable<double> summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
objectdata - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, IEnumerable<object> data, int summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
IEnumerable<object>data - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, object data, Nullable<double> summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
objectdata - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, ValueTuple<string, IGraphNodeBase> data, int summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
ValueTuple<string, IGraphNodeBase>data - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, ValueTuple<string, IGraphNodeBase> data, Nullable<double> summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
ValueTuple<string, IGraphNodeBase>data - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, ValueTuple<string, IGraphNodeBase> data, int summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
ValueTuple<string, IGraphNodeBase>data - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, ValueTuple<string, IGraphNodeBase> data, Nullable<double> summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
ValueTuple<string, IGraphNodeBase>data - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(object condition, ValueTuple<string, IGraphNodeBase> data, Nullable<double> summarize, PythonFunctionContainer name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
ValueTuple<string, IGraphNodeBase>data - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
PythonFunctionContainername - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, IEnumerable<object> data, Nullable<double> summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
IEnumerable<object>data - The tensors to print out when condition is false.
-
Nullable<double>summarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert(IEnumerable<object> condition, ValueTuple<string, IGraphNodeBase> data, int summarize, string name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
IEnumerable<object>condition - The condition to evaluate.
-
ValueTuple<string, IGraphNodeBase>data - The tensors to print out when condition is false.
-
intsummarize - Print this many entries of each tensor.
-
stringname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object Assert_dyn(object condition, object data, object summarize, object name)
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Parameters
-
objectcondition - The condition to evaluate.
-
objectdata - The tensors to print out when condition is false.
-
objectsummarize - Print this many entries of each tensor.
-
objectname - A name for this operation (optional).
Returns
-
object
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
object assert_equal(PythonClassContainer x, object y, IEnumerable<object> data, Nullable<int> summarize, object message, string name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
PythonClassContainerx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_equal(PythonClassContainer x, object y, IEnumerable<object> data, Nullable<int> summarize, string message, string name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
PythonClassContainerx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_equal(PythonClassContainer x, object y, IEnumerable<object> data, Nullable<int> summarize, IGraphNodeBase message, string name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
PythonClassContainerx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
IGraphNodeBasemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_equal(object x, object y, IEnumerable<object> data, Nullable<int> summarize, int message, string name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
intmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_equal(object x, object y, IEnumerable<object> data, Nullable<int> summarize, double message, string name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
doublemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_equal(PythonClassContainer x, object y, IEnumerable<object> data, Nullable<int> summarize, double message, string name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
PythonClassContainerx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
doublemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_equal(object x, object y, IEnumerable<object> data, Nullable<int> summarize, object message, string name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_equal(object x, object y, IEnumerable<object> data, Nullable<int> summarize, IGraphNodeBase message, string name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
IGraphNodeBasemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_equal(PythonClassContainer x, object y, IEnumerable<object> data, Nullable<int> summarize, int message, string name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
PythonClassContainerx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
intmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_equal(object x, object y, IEnumerable<object> data, Nullable<int> summarize, string message, string name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_equal_dyn(object x, object y, object data, object summarize, object message, object name)
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x == y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater(int x, IndexedSlices y, object data, object summarize, string message, string name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
intx - Numeric `Tensor`.
-
IndexedSlicesy - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater(IGraphNodeBase x, int y, object data, object summarize, string message, string name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
inty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater(IGraphNodeBase x, ValueTuple<PythonClassContainer, PythonClassContainer> y, object data, object summarize, string message, string name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
ValueTuple<PythonClassContainer, PythonClassContainer>y - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater(int x, double y, object data, object summarize, string message, string name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
intx - Numeric `Tensor`.
-
doubley - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater(int x, int y, object data, object summarize, string message, string name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
intx - Numeric `Tensor`.
-
inty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater(IGraphNodeBase x, IGraphNodeBase y, object data, object summarize, string message, string name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
IGraphNodeBasey - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater(IGraphNodeBase x, double y, object data, object summarize, string message, string name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
doubley - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater(int x, IGraphNodeBase y, object data, object summarize, string message, string name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
intx - Numeric `Tensor`.
-
IGraphNodeBasey - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater(IGraphNodeBase x, IndexedSlices y, object data, object summarize, string message, string name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
IndexedSlicesy - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater(int x, ValueTuple<PythonClassContainer, PythonClassContainer> y, object data, object summarize, string message, string name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
intx - Numeric `Tensor`.
-
ValueTuple<PythonClassContainer, PythonClassContainer>y - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_dyn(object x, object y, object data, object summarize, object message, object name)
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_greater".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal(object x, object y, object data, object summarize, string message, string name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal(object x, object y, object data, object summarize, IGraphNodeBase message, string name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
IGraphNodeBasemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal(object x, object y, object data, object summarize, TensorShape message, string name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
TensorShapemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal(object x, object y, IEnumerable<object> data, object summarize, TensorShape message, string name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
TensorShapemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal(object x, object y, IEnumerable<object> data, object summarize, IEnumerable<int> message, string name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
IEnumerable<int>message - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal(object x, object y, object data, object summarize, IEnumerable<int> message, string name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
IEnumerable<int>message - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal(object x, object y, IEnumerable<object> data, object summarize, string message, string name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal(object x, object y, IEnumerable<object> data, object summarize, IGraphNodeBase message, string name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
IGraphNodeBasemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal(object x, object y, IEnumerable<object> data, object summarize, int message, string name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
intmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal(object x, object y, object data, object summarize, int message, string name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
intmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_greater_equal_dyn(object x, object y, object data, object summarize, object message, object name)
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_greater_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_integer(IEnumerable<IGraphNodeBase> x, string message, string name)
Assert that `x` is of integer dtype. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<IGraphNodeBase>x - `Tensor` whose basetype is integer and is not quantized.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_integer".
Returns
-
object - A `no_op` that does nothing. Type can be determined statically.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_integer(x)]):
output = tf.reduce_sum(x)
object assert_integer(object x, string message, string name)
Assert that `x` is of integer dtype. Example of adding a dependency to an operation:
Parameters
-
objectx - `Tensor` whose basetype is integer and is not quantized.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_integer".
Returns
-
object - A `no_op` that does nothing. Type can be determined statically.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_integer(x)]):
output = tf.reduce_sum(x)
object assert_integer_dyn(object x, object message, object name)
Assert that `x` is of integer dtype. Example of adding a dependency to an operation:
Parameters
-
objectx - `Tensor` whose basetype is integer and is not quantized.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_integer".
Returns
-
object - A `no_op` that does nothing. Type can be determined statically.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_integer(x)]):
output = tf.reduce_sum(x)
object assert_less(object x, object y, object data, Nullable<int> summarize, string message, string name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(IEnumerable<IGraphNodeBase> x, object y, IEnumerable<object> data, Nullable<int> summarize, IEnumerable<object> message, PythonFunctionContainer name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
IEnumerable<object>message - A string to prefix to the default message.
-
PythonFunctionContainername - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(object x, object y, IEnumerable<object> data, Nullable<int> summarize, string message, string name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(object x, object y, object data, Nullable<int> summarize, string message, PythonFunctionContainer name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
PythonFunctionContainername - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(object x, object y, IEnumerable<object> data, Nullable<int> summarize, string message, PythonFunctionContainer name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
PythonFunctionContainername - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(object x, object y, object data, Nullable<int> summarize, IEnumerable<object> message, PythonFunctionContainer name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
IEnumerable<object>message - A string to prefix to the default message.
-
PythonFunctionContainername - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(object x, object y, object data, Nullable<int> summarize, IEnumerable<object> message, string name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
IEnumerable<object>message - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(IEnumerable<IGraphNodeBase> x, object y, IEnumerable<object> data, Nullable<int> summarize, string message, PythonFunctionContainer name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
PythonFunctionContainername - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(IEnumerable<IGraphNodeBase> x, object y, IEnumerable<object> data, Nullable<int> summarize, IEnumerable<object> message, string name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
IEnumerable<object>message - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(object x, object y, IEnumerable<object> data, Nullable<int> summarize, IEnumerable<object> message, string name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
IEnumerable<object>message - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(IEnumerable<IGraphNodeBase> x, object y, IEnumerable<object> data, Nullable<int> summarize, string message, string name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(object x, object y, IEnumerable<object> data, Nullable<int> summarize, IEnumerable<object> message, PythonFunctionContainer name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
IEnumerable<object>message - A string to prefix to the default message.
-
PythonFunctionContainername - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(IEnumerable<IGraphNodeBase> x, object y, object data, Nullable<int> summarize, IEnumerable<object> message, string name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
IEnumerable<object>message - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(IEnumerable<IGraphNodeBase> x, object y, object data, Nullable<int> summarize, string message, PythonFunctionContainer name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
PythonFunctionContainername - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(IEnumerable<IGraphNodeBase> x, object y, object data, Nullable<int> summarize, IEnumerable<object> message, PythonFunctionContainer name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
IEnumerable<object>message - A string to prefix to the default message.
-
PythonFunctionContainername - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less(IEnumerable<IGraphNodeBase> x, object y, object data, Nullable<int> summarize, string message, string name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less_dyn(object x, object y, object data, object summarize, object message, object name)
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_less".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
object assert_less_equal(object x, object y, IEnumerable<object> data, object summarize, object message, string name)
Assert the condition `x <= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] <= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_less_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x <= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_less_equal(object x, IEnumerable<object> y, IEnumerable<object> data, object summarize, object message, string name)
Assert the condition `x <= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] <= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
IEnumerable<object>y - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_less_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x <= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_less_equal_dyn(object x, object y, object data, object summarize, object message, object name)
Assert the condition `x <= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] <= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_less_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x <= y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_near(IEnumerable<object> x, IGraphNodeBase y, Nullable<double> rtol, Nullable<double> atol, object data, object summarize, string message, string name)
Assert the condition `x` and `y` are close element-wise. Example of adding a dependency to an operation:
This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have ```tf.abs(x[i] - y[i]) <= atol + rtol * tf.abs(y[i])```. If both `x` and `y` are empty, this is trivially satisfied. The default `atol` and `rtol` is `10 * eps`, where `eps` is the smallest
representable positive number such that `1 + eps != 1`. This is about
`1.2e-6` in `32bit`, `2.22e-15` in `64bit`, and `0.00977` in `16bit`.
See `numpy.finfo`.
Parameters
-
IEnumerable<object>x - Float or complex `Tensor`.
-
IGraphNodeBasey - Float or complex `Tensor`, same `dtype` as, and broadcastable to, `x`.
-
Nullable<double>rtol - `Tensor`. Same `dtype` as, and broadcastable to, `x`. The relative tolerance. Default is `10 * eps`.
-
Nullable<double>atol - `Tensor`. Same `dtype` as, and broadcastable to, `x`. The absolute tolerance. Default is `10 * eps`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_near".
Returns
-
object - Op that raises `InvalidArgumentError` if `x` and `y` are not close enough.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_near(x, y)]):
output = tf.reduce_sum(x)
object assert_near(IGraphNodeBase x, IGraphNodeBase y, Nullable<double> rtol, Nullable<double> atol, object data, object summarize, string message, string name)
Assert the condition `x` and `y` are close element-wise. Example of adding a dependency to an operation:
This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have ```tf.abs(x[i] - y[i]) <= atol + rtol * tf.abs(y[i])```. If both `x` and `y` are empty, this is trivially satisfied. The default `atol` and `rtol` is `10 * eps`, where `eps` is the smallest
representable positive number such that `1 + eps != 1`. This is about
`1.2e-6` in `32bit`, `2.22e-15` in `64bit`, and `0.00977` in `16bit`.
See `numpy.finfo`.
Parameters
-
IGraphNodeBasex - Float or complex `Tensor`.
-
IGraphNodeBasey - Float or complex `Tensor`, same `dtype` as, and broadcastable to, `x`.
-
Nullable<double>rtol - `Tensor`. Same `dtype` as, and broadcastable to, `x`. The relative tolerance. Default is `10 * eps`.
-
Nullable<double>atol - `Tensor`. Same `dtype` as, and broadcastable to, `x`. The absolute tolerance. Default is `10 * eps`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_near".
Returns
-
object - Op that raises `InvalidArgumentError` if `x` and `y` are not close enough.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_near(x, y)]):
output = tf.reduce_sum(x)
object assert_near_dyn(object x, object y, object rtol, object atol, object data, object summarize, object message, object name)
Assert the condition `x` and `y` are close element-wise. Example of adding a dependency to an operation:
This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have ```tf.abs(x[i] - y[i]) <= atol + rtol * tf.abs(y[i])```. If both `x` and `y` are empty, this is trivially satisfied. The default `atol` and `rtol` is `10 * eps`, where `eps` is the smallest
representable positive number such that `1 + eps != 1`. This is about
`1.2e-6` in `32bit`, `2.22e-15` in `64bit`, and `0.00977` in `16bit`.
See `numpy.finfo`.
Parameters
-
objectx - Float or complex `Tensor`.
-
objecty - Float or complex `Tensor`, same `dtype` as, and broadcastable to, `x`.
-
objectrtol - `Tensor`. Same `dtype` as, and broadcastable to, `x`. The relative tolerance. Default is `10 * eps`.
-
objectatol - `Tensor`. Same `dtype` as, and broadcastable to, `x`. The absolute tolerance. Default is `10 * eps`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_near".
Returns
-
object - Op that raises `InvalidArgumentError` if `x` and `y` are not close enough.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_near(x, y)]):
output = tf.reduce_sum(x)
object assert_negative(int x, object data, object summarize, string message, string name)
Assert the condition `x < 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Negative means, for every element `x[i]` of `x`, we have `x[i] < 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
intx - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_negative".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_negative(x, y)]):
output = tf.reduce_sum(x)
object assert_negative(IGraphNodeBase x, object data, object summarize, string message, string name)
Assert the condition `x < 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Negative means, for every element `x[i]` of `x`, we have `x[i] < 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_negative".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_negative(x, y)]):
output = tf.reduce_sum(x)
object assert_negative_dyn(object x, object data, object summarize, object message, object name)
Assert the condition `x < 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Negative means, for every element `x[i]` of `x`, we have `x[i] < 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
objectx - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_negative".
Returns
-
object - Op that raises `InvalidArgumentError` if `x < 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_negative(x, y)]):
output = tf.reduce_sum(x)
object assert_non_negative(IEnumerable<IGraphNodeBase> x, object data, object summarize, string message, string name)
Assert the condition `x >= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-negative means, for every element `x[i]` of `x`, we have `x[i] >= 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_non_negative".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_negative(x, y)]):
output = tf.reduce_sum(x)
object assert_non_negative(IEnumerable<IGraphNodeBase> x, object data, object summarize, IGraphNodeBase message, string name)
Assert the condition `x >= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-negative means, for every element `x[i]` of `x`, we have `x[i] >= 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
IGraphNodeBasemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_non_negative".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_negative(x, y)]):
output = tf.reduce_sum(x)
object assert_non_negative(object x, object data, object summarize, IGraphNodeBase message, string name)
Assert the condition `x >= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-negative means, for every element `x[i]` of `x`, we have `x[i] >= 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
objectx - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
IGraphNodeBasemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_non_negative".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_negative(x, y)]):
output = tf.reduce_sum(x)
object assert_non_negative(object x, object data, object summarize, double message, string name)
Assert the condition `x >= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-negative means, for every element `x[i]` of `x`, we have `x[i] >= 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
objectx - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
doublemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_non_negative".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_negative(x, y)]):
output = tf.reduce_sum(x)
object assert_non_negative(IEnumerable<IGraphNodeBase> x, object data, object summarize, double message, string name)
Assert the condition `x >= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-negative means, for every element `x[i]` of `x`, we have `x[i] >= 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
IEnumerable<IGraphNodeBase>x - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
doublemessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_non_negative".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_negative(x, y)]):
output = tf.reduce_sum(x)
object assert_non_negative(object x, object data, object summarize, string message, string name)
Assert the condition `x >= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-negative means, for every element `x[i]` of `x`, we have `x[i] >= 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
objectx - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_non_negative".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_negative(x, y)]):
output = tf.reduce_sum(x)
object assert_non_negative_dyn(object x, object data, object summarize, object message, object name)
Assert the condition `x >= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-negative means, for every element `x[i]` of `x`, we have `x[i] >= 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
objectx - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_non_negative".
Returns
-
object - Op that raises `InvalidArgumentError` if `x >= 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_negative(x, y)]):
output = tf.reduce_sum(x)
object assert_non_positive(int x, object data, object summarize, string message, string name)
Assert the condition `x <= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-positive means, for every element `x[i]` of `x`, we have `x[i] <= 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
intx - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_non_positive".
Returns
-
object - Op that raises `InvalidArgumentError` if `x <= 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_positive(x, y)]):
output = tf.reduce_sum(x)
object assert_non_positive(IGraphNodeBase x, object data, object summarize, string message, string name)
Assert the condition `x <= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-positive means, for every element `x[i]` of `x`, we have `x[i] <= 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_non_positive".
Returns
-
object - Op that raises `InvalidArgumentError` if `x <= 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_positive(x, y)]):
output = tf.reduce_sum(x)
object assert_non_positive_dyn(object x, object data, object summarize, object message, object name)
Assert the condition `x <= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-positive means, for every element `x[i]` of `x`, we have `x[i] <= 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
objectx - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_non_positive".
Returns
-
object - Op that raises `InvalidArgumentError` if `x <= 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_positive(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(double x, IGraphNodeBase y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
doublex - Numeric `Tensor`.
-
IGraphNodeBasey - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(float32 x, int y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
float32x - Numeric `Tensor`.
-
inty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(double x, int y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
doublex - Numeric `Tensor`.
-
inty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(IGraphNodeBase x, IGraphNodeBase y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
IGraphNodeBasey - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(IGraphNodeBase x, int y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
inty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(float64 x, int y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
float64x - Numeric `Tensor`.
-
inty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(float64 x, IGraphNodeBase y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
float64x - Numeric `Tensor`.
-
IGraphNodeBasey - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(int x, IGraphNodeBase y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
intx - Numeric `Tensor`.
-
IGraphNodeBasey - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(int x, int y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
intx - Numeric `Tensor`.
-
inty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(float32 x, IGraphNodeBase y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
float32x - Numeric `Tensor`.
-
IGraphNodeBasey - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(ndarray x, IGraphNodeBase y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
ndarrayx - Numeric `Tensor`.
-
IGraphNodeBasey - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(IEnumerable<double> x, int y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<double>x - Numeric `Tensor`.
-
inty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(ndarray x, int y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
ndarrayx - Numeric `Tensor`.
-
inty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal(IEnumerable<double> x, IGraphNodeBase y, IEnumerable<string> data, Nullable<int> summarize, string message, string name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
IEnumerable<double>x - Numeric `Tensor`.
-
IGraphNodeBasey - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
Nullable<int>summarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_none_equal_dyn(object x, object y, object data, object summarize, object message, object name)
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objecty - Numeric `Tensor`, same dtype as and broadcastable to `x`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`, `y`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_none_equal".
Returns
-
object - Op that raises `InvalidArgumentError` if `x != y` is False.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
object assert_positive(object x, IEnumerable<string> data, object summarize, object message, string name)
Assert the condition `x > 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Positive means, for every element `x[i]` of `x`, we have `x[i] > 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
objectx - Numeric `Tensor`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_positive".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_positive(x, y)]):
output = tf.reduce_sum(x)
object assert_positive(object x, IEnumerable<string> data, object summarize, string message, string name)
Assert the condition `x > 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Positive means, for every element `x[i]` of `x`, we have `x[i] > 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
objectx - Numeric `Tensor`.
-
IEnumerable<string>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_positive".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_positive(x, y)]):
output = tf.reduce_sum(x)
object assert_positive_dyn(object x, object data, object summarize, object message, object name)
Assert the condition `x > 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Positive means, for every element `x[i]` of `x`, we have `x[i] > 0`.
If `x` is empty this is trivially satisfied.
Parameters
-
objectx - Numeric `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_positive".
Returns
-
object - Op that raises `InvalidArgumentError` if `x > 0` is False.
Show Example
with tf.control_dependencies([tf.debugging.assert_positive(x, y)]):
output = tf.reduce_sum(x)
void assert_proper_iterable(string values)
Static assert that values is a "proper" iterable. `Ops` that expect iterables of `Tensor` can call this to validate input.
Useful since `Tensor`, `ndarray`, byte/text type are all iterables themselves.
Parameters
-
stringvalues - Object to be checked.
void assert_proper_iterable(IGraphNodeBase values)
Static assert that values is a "proper" iterable. `Ops` that expect iterables of `Tensor` can call this to validate input.
Useful since `Tensor`, `ndarray`, byte/text type are all iterables themselves.
Parameters
-
IGraphNodeBasevalues - Object to be checked.
void assert_proper_iterable(int values)
Static assert that values is a "proper" iterable. `Ops` that expect iterables of `Tensor` can call this to validate input.
Useful since `Tensor`, `ndarray`, byte/text type are all iterables themselves.
Parameters
-
intvalues - Object to be checked.
void assert_proper_iterable(ValueTuple<IGraphNodeBase, object> values)
Static assert that values is a "proper" iterable. `Ops` that expect iterables of `Tensor` can call this to validate input.
Useful since `Tensor`, `ndarray`, byte/text type are all iterables themselves.
Parameters
-
ValueTuple<IGraphNodeBase, object>values - Object to be checked.
void assert_proper_iterable(IEnumerable<IGraphNodeBase> values)
Static assert that values is a "proper" iterable. `Ops` that expect iterables of `Tensor` can call this to validate input.
Useful since `Tensor`, `ndarray`, byte/text type are all iterables themselves.
Parameters
-
IEnumerable<IGraphNodeBase>values - Object to be checked.
void assert_proper_iterable(ndarray values)
Static assert that values is a "proper" iterable. `Ops` that expect iterables of `Tensor` can call this to validate input.
Useful since `Tensor`, `ndarray`, byte/text type are all iterables themselves.
Parameters
-
ndarrayvalues - Object to be checked.
void assert_proper_iterable(object values)
Static assert that values is a "proper" iterable. `Ops` that expect iterables of `Tensor` can call this to validate input.
Useful since `Tensor`, `ndarray`, byte/text type are all iterables themselves.
Parameters
-
objectvalues - Object to be checked.
object assert_proper_iterable_dyn(object values)
Static assert that values is a "proper" iterable. `Ops` that expect iterables of `Tensor` can call this to validate input.
Useful since `Tensor`, `ndarray`, byte/text type are all iterables themselves.
Parameters
-
objectvalues - Object to be checked.
object assert_rank(object x, double rank, IEnumerable<object> data, object summarize, string message, string name)
Assert `x` has rank equal to `rank`. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
doublerank - Scalar integer `Tensor`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and the shape of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank(object x, IGraphNodeBase rank, IEnumerable<object> data, object summarize, string message, string name)
Assert `x` has rank equal to `rank`. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
IGraphNodeBaserank - Scalar integer `Tensor`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and the shape of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank(object x, ndarray rank, IEnumerable<object> data, object summarize, string message, string name)
Assert `x` has rank equal to `rank`. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
ndarrayrank - Scalar integer `Tensor`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and the shape of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank(PythonClassContainer x, ndarray rank, IEnumerable<object> data, object summarize, string message, string name)
Assert `x` has rank equal to `rank`. Example of adding a dependency to an operation:
Parameters
-
PythonClassContainerx - Numeric `Tensor`.
-
ndarrayrank - Scalar integer `Tensor`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and the shape of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank(object x, int rank, IEnumerable<object> data, object summarize, string message, string name)
Assert `x` has rank equal to `rank`. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
intrank - Scalar integer `Tensor`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and the shape of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank(PythonClassContainer x, double rank, IEnumerable<object> data, object summarize, string message, string name)
Assert `x` has rank equal to `rank`. Example of adding a dependency to an operation:
Parameters
-
PythonClassContainerx - Numeric `Tensor`.
-
doublerank - Scalar integer `Tensor`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and the shape of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank(PythonClassContainer x, int rank, IEnumerable<object> data, object summarize, string message, string name)
Assert `x` has rank equal to `rank`. Example of adding a dependency to an operation:
Parameters
-
PythonClassContainerx - Numeric `Tensor`.
-
intrank - Scalar integer `Tensor`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and the shape of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank(PythonClassContainer x, IGraphNodeBase rank, IEnumerable<object> data, object summarize, string message, string name)
Assert `x` has rank equal to `rank`. Example of adding a dependency to an operation:
Parameters
-
PythonClassContainerx - Numeric `Tensor`.
-
IGraphNodeBaserank - Scalar integer `Tensor`.
-
IEnumerable<object>data - The tensors to print out if the condition is False. Defaults to error message and the shape of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank_at_least(object x, int rank, IEnumerable<IGraphNodeBase> data, object summarize, object message, string name)
Assert `x` has rank equal to `rank` or higher. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
intrank - Scalar `Tensor`.
-
IEnumerable<IGraphNodeBase>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_at_least".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank or higher. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_at_least(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank_at_least(object x, int rank, IEnumerable<IGraphNodeBase> data, object summarize, int message, string name)
Assert `x` has rank equal to `rank` or higher. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
intrank - Scalar `Tensor`.
-
IEnumerable<IGraphNodeBase>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
intmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_at_least".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank or higher. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_at_least(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank_at_least(object x, object rank, IEnumerable<IGraphNodeBase> data, object summarize, string message, string name)
Assert `x` has rank equal to `rank` or higher. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objectrank - Scalar `Tensor`.
-
IEnumerable<IGraphNodeBase>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_at_least".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank or higher. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_at_least(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank_at_least(object x, object rank, IEnumerable<IGraphNodeBase> data, object summarize, int message, string name)
Assert `x` has rank equal to `rank` or higher. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objectrank - Scalar `Tensor`.
-
IEnumerable<IGraphNodeBase>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
intmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_at_least".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank or higher. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_at_least(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank_at_least(object x, object rank, IEnumerable<IGraphNodeBase> data, object summarize, object message, string name)
Assert `x` has rank equal to `rank` or higher. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objectrank - Scalar `Tensor`.
-
IEnumerable<IGraphNodeBase>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_at_least".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank or higher. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_at_least(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank_at_least(object x, int rank, IEnumerable<IGraphNodeBase> data, object summarize, string message, string name)
Assert `x` has rank equal to `rank` or higher. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
intrank - Scalar `Tensor`.
-
IEnumerable<IGraphNodeBase>data - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_at_least".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank or higher. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_at_least(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank_at_least_dyn(object x, object rank, object data, object summarize, object message, object name)
Assert `x` has rank equal to `rank` or higher. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objectrank - Scalar `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_rank_at_least".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank or higher. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_at_least(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank_dyn(object x, object rank, object data, object summarize, object message, object name)
Assert `x` has rank equal to `rank`. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objectrank - Scalar integer `Tensor`.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and the shape of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_rank".
Returns
-
object - Op raising `InvalidArgumentError` unless `x` has specified rank. If static checks determine `x` has correct rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank(x, 2)]):
output = tf.reduce_sum(x)
object assert_rank_in(IGraphNodeBase x, IEnumerable<int> ranks, object data, object summarize, string message, string name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
IEnumerable<int>ranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
object assert_rank_in(ValueTuple<PythonClassContainer, PythonClassContainer> x, IEnumerable<int> ranks, object data, object summarize, string message, string name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>x - Numeric `Tensor`.
-
IEnumerable<int>ranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
object assert_rank_in(IndexedSlices x, IEnumerable<int> ranks, object data, object summarize, string message, string name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
IndexedSlicesx - Numeric `Tensor`.
-
IEnumerable<int>ranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
object assert_rank_in(IGraphNodeBase x, ValueTuple<ndarray, object> ranks, object data, object summarize, string message, string name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
IGraphNodeBasex - Numeric `Tensor`.
-
ValueTuple<ndarray, object>ranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
object assert_rank_in(ValueTuple<PythonClassContainer, PythonClassContainer> x, ValueTuple<ndarray, object> ranks, object data, object summarize, string message, string name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>x - Numeric `Tensor`.
-
ValueTuple<ndarray, object>ranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
object assert_rank_in(int x, ValueTuple<ndarray, object> ranks, object data, object summarize, string message, string name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
intx - Numeric `Tensor`.
-
ValueTuple<ndarray, object>ranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
object assert_rank_in(double x, ValueTuple<ndarray, object> ranks, object data, object summarize, string message, string name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
doublex - Numeric `Tensor`.
-
ValueTuple<ndarray, object>ranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
object assert_rank_in(IndexedSlices x, ValueTuple<ndarray, object> ranks, object data, object summarize, string message, string name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
IndexedSlicesx - Numeric `Tensor`.
-
ValueTuple<ndarray, object>ranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
object assert_rank_in(int x, IEnumerable<int> ranks, object data, object summarize, string message, string name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
intx - Numeric `Tensor`.
-
IEnumerable<int>ranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
object assert_rank_in(double x, IEnumerable<int> ranks, object data, object summarize, string message, string name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
doublex - Numeric `Tensor`.
-
IEnumerable<int>ranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
stringmessage - A string to prefix to the default message.
-
stringname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
object assert_rank_in_dyn(object x, object ranks, object data, object summarize, object message, object name)
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Parameters
-
objectx - Numeric `Tensor`.
-
objectranks - Iterable of scalar `Tensor` objects.
-
objectdata - The tensors to print out if the condition is False. Defaults to error message and first few entries of `x`.
-
objectsummarize - Print this many entries of each tensor.
-
objectmessage - A string to prefix to the default message.
-
objectname - A name for this operation (optional). Defaults to "assert_rank_in".
Returns
-
object - Op raising `InvalidArgumentError` unless rank of `x` is in `ranks`. If static checks determine `x` has matching rank, a `no_op` is returned.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
DType assert_same_float_dtype(ValueTuple<IGraphNodeBase, object, object> tensors, DType dtype)
Validate and return float type based on `tensors` and `dtype`. For ops such as matrix multiplication, inputs and weights must be of the
same float type. This function validates that all `tensors` are the same type,
validates that type is `dtype` (if supplied), and returns the type. Type must
be a floating point type. If neither `tensors` nor `dtype` is supplied,
the function will return `dtypes.float32`.
Parameters
-
ValueTuple<IGraphNodeBase, object, object>tensors - Tensors of input values. Can include `None` elements, which will be ignored.
-
DTypedtype - Expected type.
Returns
-
DType - Validated type.
DType assert_same_float_dtype(IEnumerable<object> tensors, DType dtype)
Validate and return float type based on `tensors` and `dtype`. For ops such as matrix multiplication, inputs and weights must be of the
same float type. This function validates that all `tensors` are the same type,
validates that type is `dtype` (if supplied), and returns the type. Type must
be a floating point type. If neither `tensors` nor `dtype` is supplied,
the function will return `dtypes.float32`.
Parameters
-
IEnumerable<object>tensors - Tensors of input values. Can include `None` elements, which will be ignored.
-
DTypedtype - Expected type.
Returns
-
DType - Validated type.
DType assert_same_float_dtype(object tensors, DType dtype)
Validate and return float type based on `tensors` and `dtype`. For ops such as matrix multiplication, inputs and weights must be of the
same float type. This function validates that all `tensors` are the same type,
validates that type is `dtype` (if supplied), and returns the type. Type must
be a floating point type. If neither `tensors` nor `dtype` is supplied,
the function will return `dtypes.float32`.
Parameters
-
objecttensors - Tensors of input values. Can include `None` elements, which will be ignored.
-
DTypedtype - Expected type.
Returns
-
DType - Validated type.
object assert_same_float_dtype_dyn(object tensors, object dtype)
Validate and return float type based on `tensors` and `dtype`. For ops such as matrix multiplication, inputs and weights must be of the
same float type. This function validates that all `tensors` are the same type,
validates that type is `dtype` (if supplied), and returns the type. Type must
be a floating point type. If neither `tensors` nor `dtype` is supplied,
the function will return `dtypes.float32`.
Parameters
-
objecttensors - Tensors of input values. Can include `None` elements, which will be ignored.
-
objectdtype - Expected type.
Returns
-
object - Validated type.
Tensor assert_scalar(IGraphNodeBase tensor, string name, object message)
Asserts that the given `tensor` is a scalar (i.e. zero-dimensional). This function raises `ValueError` unless it can be certain that the given
`tensor` is a scalar. `ValueError` is also raised if the shape of `tensor` is
unknown.
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
stringname - A name for this operation. Defaults to "assert_scalar"
-
objectmessage - A string to prefix to the default message.
Returns
-
Tensor - The input tensor (potentially converted to a `Tensor`).
object assert_scalar_dyn(object tensor, object name, object message)
Asserts that the given `tensor` is a scalar (i.e. zero-dimensional). This function raises `ValueError` unless it can be certain that the given
`tensor` is a scalar. `ValueError` is also raised if the shape of `tensor` is
unknown.
Parameters
-
objecttensor - A `Tensor`.
-
objectname - A name for this operation. Defaults to "assert_scalar"
-
objectmessage - A string to prefix to the default message.
Returns
-
object - The input tensor (potentially converted to a `Tensor`).
object assert_type(IGraphNodeBase tensor, DType tf_type, string message, string name)
Statically asserts that the given `Tensor` is of the specified type.
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
DTypetf_type - A tensorflow type (`dtypes.float32`,
tf.int64, `dtypes.bool`, etc). -
stringmessage - A string to prefix to the default message.
-
stringname - A name to give this `Op`. Defaults to "assert_type"
Returns
-
object - A `no_op` that does nothing. Type can be determined statically.
object assert_type(IGraphNodeBase tensor, DType tf_type, DType message, string name)
Statically asserts that the given `Tensor` is of the specified type.
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
DTypetf_type - A tensorflow type (`dtypes.float32`,
tf.int64, `dtypes.bool`, etc). -
DTypemessage - A string to prefix to the default message.
-
stringname - A name to give this `Op`. Defaults to "assert_type"
Returns
-
object - A `no_op` that does nothing. Type can be determined statically.
object assert_type_dyn(object tensor, object tf_type, object message, object name)
Statically asserts that the given `Tensor` is of the specified type.
Parameters
-
objecttensor - A `Tensor`.
-
objecttf_type - A tensorflow type (`dtypes.float32`,
tf.int64, `dtypes.bool`, etc). -
objectmessage - A string to prefix to the default message.
-
objectname - A name to give this `Op`. Defaults to "assert_type"
Returns
-
object - A `no_op` that does nothing. Type can be determined statically.
Tensor assert_variables_initialized(IEnumerable<Variable> var_list)
Returns an Op to check if variables are initialized. NOTE: This function is obsolete and will be removed in 6 months. Please
change your implementation to use `report_uninitialized_variables()`. When run, the returned Op will raise the exception `FailedPreconditionError`
if any of the variables has not yet been initialized. Note: This function is implemented by trying to fetch the values of the
variables. If one of the variables is not initialized a message may be
logged by the C++ runtime. This is expected.
Parameters
-
IEnumerable<Variable>var_list - List of `Variable` objects to check. Defaults to the value of `global_variables().`
Returns
-
Tensor - An Op, or None if there are no variables. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
object assert_variables_initialized_dyn(object var_list)
Returns an Op to check if variables are initialized. NOTE: This function is obsolete and will be removed in 6 months. Please
change your implementation to use `report_uninitialized_variables()`. When run, the returned Op will raise the exception `FailedPreconditionError`
if any of the variables has not yet been initialized. Note: This function is implemented by trying to fetch the values of the
variables. If one of the variables is not initialized a message may be
logged by the C++ runtime. This is expected.
Parameters
-
objectvar_list - List of `Variable` objects to check. Defaults to the value of `global_variables().`
Returns
-
object - An Op, or None if there are no variables. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
Tensor assign(PartitionedVariable ref, IGraphNodeBase value, Nullable<bool> validate_shape, Nullable<bool> use_locking, string name)
Update `ref` by assigning `value` to it. This operation outputs a Tensor that holds the new value of `ref` after
the value has been assigned. This makes it easier to chain operations that
need to use the reset value.
Parameters
-
PartitionedVariableref - A mutable `Tensor`. Should be from a `Variable` node. May be uninitialized.
-
IGraphNodeBasevalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be assigned to the variable.
-
Nullable<bool>validate_shape - An optional `bool`. Defaults to `True`. If true, the operation will validate that the shape of 'value' matches the shape of the Tensor being assigned to. If false, 'ref' will take on the shape of 'value'.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `True`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` that will hold the new value of `ref` after the assignment has completed.
Tensor assign(Variable ref, IGraphNodeBase value, Nullable<bool> validate_shape, Nullable<bool> use_locking, string name)
Update `ref` by assigning `value` to it. This operation outputs a Tensor that holds the new value of `ref` after
the value has been assigned. This makes it easier to chain operations that
need to use the reset value.
Parameters
-
Variableref - A mutable `Tensor`. Should be from a `Variable` node. May be uninitialized.
-
IGraphNodeBasevalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be assigned to the variable.
-
Nullable<bool>validate_shape - An optional `bool`. Defaults to `True`. If true, the operation will validate that the shape of 'value' matches the shape of the Tensor being assigned to. If false, 'ref' will take on the shape of 'value'.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `True`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` that will hold the new value of `ref` after the assignment has completed.
Tensor assign_add(IEnumerable<object> ref, IGraphNodeBase value, Nullable<bool> use_locking, PythonFunctionContainer name)
Update `ref` by adding `value` to it. This operation outputs "ref" after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.add, this op does not broadcast. `ref` and `value` must have
the same shape.
Parameters
-
IEnumerable<object>ref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`. Should be from a `Variable` node.
-
IGraphNodeBasevalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be added to the variable.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the addition will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - Same as "ref". Returned as a convenience for operations that want to use the new value after the variable has been updated.
Tensor assign_add(IEnumerable<object> ref, IGraphNodeBase value, Nullable<bool> use_locking, string name)
Update `ref` by adding `value` to it. This operation outputs "ref" after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.add, this op does not broadcast. `ref` and `value` must have
the same shape.
Parameters
-
IEnumerable<object>ref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`. Should be from a `Variable` node.
-
IGraphNodeBasevalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be added to the variable.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the addition will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Same as "ref". Returned as a convenience for operations that want to use the new value after the variable has been updated.
Tensor assign_add(object ref, IGraphNodeBase value, Nullable<bool> use_locking, PythonFunctionContainer name)
Update `ref` by adding `value` to it. This operation outputs "ref" after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.add, this op does not broadcast. `ref` and `value` must have
the same shape.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`. Should be from a `Variable` node.
-
IGraphNodeBasevalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be added to the variable.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the addition will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - Same as "ref". Returned as a convenience for operations that want to use the new value after the variable has been updated.
Tensor assign_add(object ref, IGraphNodeBase value, Nullable<bool> use_locking, string name)
Update `ref` by adding `value` to it. This operation outputs "ref" after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.add, this op does not broadcast. `ref` and `value` must have
the same shape.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`. Should be from a `Variable` node.
-
IGraphNodeBasevalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be added to the variable.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the addition will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Same as "ref". Returned as a convenience for operations that want to use the new value after the variable has been updated.
object assign_add_dyn(object ref, object value, object use_locking, object name)
Update `ref` by adding `value` to it. This operation outputs "ref" after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.add, this op does not broadcast. `ref` and `value` must have
the same shape.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`. Should be from a `Variable` node.
-
objectvalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be added to the variable.
-
objectuse_locking - An optional `bool`. Defaults to `False`. If True, the addition will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - Same as "ref". Returned as a convenience for operations that want to use the new value after the variable has been updated.
object assign_dyn(object ref, object value, object validate_shape, object use_locking, object name)
Update `ref` by assigning `value` to it. This operation outputs a Tensor that holds the new value of `ref` after
the value has been assigned. This makes it easier to chain operations that
need to use the reset value.
Parameters
-
objectref - A mutable `Tensor`. Should be from a `Variable` node. May be uninitialized.
-
objectvalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be assigned to the variable.
-
objectvalidate_shape - An optional `bool`. Defaults to `True`. If true, the operation will validate that the shape of 'value' matches the shape of the Tensor being assigned to. If false, 'ref' will take on the shape of 'value'.
-
objectuse_locking - An optional `bool`. Defaults to `True`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` that will hold the new value of `ref` after the assignment has completed.
object assign_sub(AutoCastVariable ref, IGraphNodeBase value, Nullable<bool> use_locking, string name)
Update `ref` by subtracting `value` from it. This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.subtract, this op does not broadcast. `ref` and `value`
must have the same shape.
Parameters
-
AutoCastVariableref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`. Should be from a `Variable` node.
-
IGraphNodeBasevalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be subtracted to the variable.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the subtraction will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - Same as "ref". Returned as a convenience for operations that want to use the new value after the variable has been updated.
object assign_sub(Operation ref, IGraphNodeBase value, Nullable<bool> use_locking, string name)
Update `ref` by subtracting `value` from it. This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.subtract, this op does not broadcast. `ref` and `value`
must have the same shape.
Parameters
-
Operationref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`. Should be from a `Variable` node.
-
IGraphNodeBasevalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be subtracted to the variable.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the subtraction will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - Same as "ref". Returned as a convenience for operations that want to use the new value after the variable has been updated.
object assign_sub(DistributedVariable ref, IGraphNodeBase value, Nullable<bool> use_locking, string name)
Update `ref` by subtracting `value` from it. This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.subtract, this op does not broadcast. `ref` and `value`
must have the same shape.
Parameters
-
DistributedVariableref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`. Should be from a `Variable` node.
-
IGraphNodeBasevalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be subtracted to the variable.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the subtraction will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - Same as "ref". Returned as a convenience for operations that want to use the new value after the variable has been updated.
object assign_sub(IGraphNodeBase ref, IGraphNodeBase value, Nullable<bool> use_locking, string name)
Update `ref` by subtracting `value` from it. This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.subtract, this op does not broadcast. `ref` and `value`
must have the same shape.
Parameters
-
IGraphNodeBaseref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`. Should be from a `Variable` node.
-
IGraphNodeBasevalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be subtracted to the variable.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the subtraction will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - Same as "ref". Returned as a convenience for operations that want to use the new value after the variable has been updated.
object assign_sub_dyn(object ref, object value, object use_locking, object name)
Update `ref` by subtracting `value` from it. This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.subtract, this op does not broadcast. `ref` and `value`
must have the same shape.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`. Should be from a `Variable` node.
-
objectvalue - A `Tensor`. Must have the same shape and dtype as `ref`. The value to be subtracted to the variable.
-
objectuse_locking - An optional `bool`. Defaults to `False`. If True, the subtraction will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - Same as "ref". Returned as a convenience for operations that want to use the new value after the variable has been updated.
Tensor atan(IGraphNodeBase x, string name)
Computes the trignometric inverse tangent of x element-wise. The
tf.math.atan operation returns the inverse of tf.math.tan, such that
if `y = tf.math.tan(x)` then, `x = tf.math.atan(y)`. **Note**: The output of tf.math.atan will lie within the invertible range
of tan, i.e (-pi/2, pi/2).
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Show Example
# Note: [1.047, 0.785] ~= [(pi/3), (pi/4)]
x = tf.constant([1.047, 0.785])
y = tf.math.tan(x) # [1.731261, 0.99920404] tf.math.atan(y) # [1.047, 0.785] = x
object atan_dyn(object x, object name)
Computes the trignometric inverse tangent of x element-wise. The
tf.math.atan operation returns the inverse of tf.math.tan, such that
if `y = tf.math.tan(x)` then, `x = tf.math.atan(y)`. **Note**: The output of tf.math.atan will lie within the invertible range
of tan, i.e (-pi/2, pi/2).
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
# Note: [1.047, 0.785] ~= [(pi/3), (pi/4)]
x = tf.constant([1.047, 0.785])
y = tf.math.tan(x) # [1.731261, 0.99920404] tf.math.atan(y) # [1.047, 0.785] = x
Tensor atan2(IGraphNodeBase y, IGraphNodeBase x, string name)
Computes arctangent of `y/x` element-wise, respecting signs of the arguments. This is the angle \( \theta \in [-\pi, \pi] \) such that
\[ x = r \cos(\theta) \]
and
\[ y = r \sin(\theta) \]
where \(r = \sqrt(x^2 + y^2) \).
Parameters
-
IGraphNodeBasey - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
IGraphNodeBasex - A `Tensor`. Must have the same type as `y`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `y`.
object atan2_dyn(object y, object x, object name)
Computes arctangent of `y/x` element-wise, respecting signs of the arguments. This is the angle \( \theta \in [-\pi, \pi] \) such that
\[ x = r \cos(\theta) \]
and
\[ y = r \sin(\theta) \]
where \(r = \sqrt(x^2 + y^2) \).
Parameters
-
objecty - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectx - A `Tensor`. Must have the same type as `y`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `y`.
Tensor atanh(IGraphNodeBase x, string name)
Computes inverse hyperbolic tangent of x element-wise. Given an input tensor, this function computes inverse hyperbolic tangent
for every element in the tensor. Input range is `[-1,1]` and output range is
`[-inf, inf]`. If input is `-1`, output will be `-inf` and if the
input is `1`, output will be `inf`. Values outside the range will have
`nan` as output.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -1, -0.5, 1, 0, 0.5, 10, float("inf")])
tf.math.atanh(x) ==> [nan -inf -0.54930615 inf 0. 0.54930615 nan nan]
object atanh_dyn(object x, object name)
Computes inverse hyperbolic tangent of x element-wise. Given an input tensor, this function computes inverse hyperbolic tangent
for every element in the tensor. Input range is `[-1,1]` and output range is
`[-inf, inf]`. If input is `-1`, output will be `-inf` and if the
input is `1`, output will be `inf`. Values outside the range will have
`nan` as output.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -1, -0.5, 1, 0, 0.5, 10, float("inf")])
tf.math.atanh(x) ==> [nan -inf -0.54930615 inf 0. 0.54930615 nan nan]
object attr(object a, string name)
object attr_bool(object a, string name)
object attr_bool_dyn(object a, object name)
object attr_bool_list(object a, string name)
object attr_bool_list_dyn(object a, object name)
object attr_default(string a, string name)
object attr_default_dyn(ImplicitContainer<T> a, object name)
object attr_dyn(object a, object name)
object attr_empty_list_default(ImplicitContainer<T> a, string name)
object attr_empty_list_default_dyn(ImplicitContainer<T> a, object name)
object attr_enum(object a, string name)
object attr_enum_dyn(object a, object name)
object attr_enum_list(object a, string name)
object attr_enum_list_dyn(object a, object name)
object attr_float(object a, string name)
object attr_float_dyn(object a, object name)
object attr_list_default(ImplicitContainer<T> a, string name)
object attr_list_default_dyn(ImplicitContainer<T> a, object name)
object attr_list_min(object a, string name)
object attr_list_min_dyn(object a, object name)
object attr_list_type_default(object a, object b, string name)
object attr_list_type_default_dyn(object a, object b, object name)
object attr_min(object a, string name)
object attr_min_dyn(object a, object name)
object attr_partial_shape(object a, string name)
object attr_partial_shape_dyn(object a, object name)
object attr_partial_shape_list(object a, string name)
object attr_partial_shape_list_dyn(object a, object name)
object attr_shape(object a, string name)
object attr_shape_dyn(object a, object name)
object attr_shape_list(object a, string name)
object attr_shape_list_dyn(object a, object name)
object attr_type_default(IGraphNodeBase a, string name)
object attr_type_default_dyn(object a, object name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, int window_size, int window_step, int num_channels, int upper_band_limit, int lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, int pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, double window_size, int window_step, int num_channels, double upper_band_limit, double lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, double pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, int window_size, int window_step, int num_channels, int upper_band_limit, int lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, double pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, double window_size, int window_step, int num_channels, double upper_band_limit, double lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, int pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, double window_size, int window_step, int num_channels, double upper_band_limit, int lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, double pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, double window_size, int window_step, int num_channels, double upper_band_limit, int lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, int pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, int window_size, int window_step, int num_channels, int upper_band_limit, double lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, int pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, double window_size, int window_step, int num_channels, int upper_band_limit, double lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, double pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, double window_size, int window_step, int num_channels, int upper_band_limit, double lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, int pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, double window_size, int window_step, int num_channels, int upper_band_limit, int lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, double pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, double window_size, int window_step, int num_channels, int upper_band_limit, int lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, int pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, int window_size, int window_step, int num_channels, double upper_band_limit, double lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, double pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, int window_size, int window_step, int num_channels, double upper_band_limit, double lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, int pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, int window_size, int window_step, int num_channels, double upper_band_limit, int lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, double pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, int window_size, int window_step, int num_channels, double upper_band_limit, int lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, int pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
Tensor audio_microfrontend(IGraphNodeBase audio, int sample_rate, int window_size, int window_step, int num_channels, int upper_band_limit, double lower_band_limit, int smoothing_bits, double even_smoothing, double odd_smoothing, double min_signal_remaining, bool enable_pcan, double pcan_strength, double pcan_offset, int gain_bits, bool enable_log, int scale_shift, int left_context, int right_context, int frame_stride, bool zero_padding, int out_scale, ImplicitContainer<T> out_type, string name)
object audio_microfrontend_dyn(object audio, ImplicitContainer<T> sample_rate, ImplicitContainer<T> window_size, ImplicitContainer<T> window_step, ImplicitContainer<T> num_channels, ImplicitContainer<T> upper_band_limit, ImplicitContainer<T> lower_band_limit, ImplicitContainer<T> smoothing_bits, ImplicitContainer<T> even_smoothing, ImplicitContainer<T> odd_smoothing, ImplicitContainer<T> min_signal_remaining, ImplicitContainer<T> enable_pcan, ImplicitContainer<T> pcan_strength, ImplicitContainer<T> pcan_offset, ImplicitContainer<T> gain_bits, ImplicitContainer<T> enable_log, ImplicitContainer<T> scale_shift, ImplicitContainer<T> left_context, ImplicitContainer<T> right_context, ImplicitContainer<T> frame_stride, ImplicitContainer<T> zero_padding, ImplicitContainer<T> out_scale, ImplicitContainer<T> out_type, object name)
Tensor b(string name)
object b_dyn(object name)
Tensor batch_gather(RaggedTensor params, RaggedTensor indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(ndarray params, IGraphNodeBase indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(ndarray params, IEnumerable<int> indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(IGraphNodeBase params, RaggedTensor indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(IGraphNodeBase params, ndarray indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(IGraphNodeBase params, IGraphNodeBase indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(ndarray params, ndarray indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(RaggedTensor params, IGraphNodeBase indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(IGraphNodeBase params, IEnumerable<int> indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(ndarray params, RaggedTensor indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(ndarray params, ValueTuple<object> indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(RaggedTensor params, ValueTuple<object> indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(RaggedTensor params, IEnumerable<int> indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(IEnumerable<object> params, ndarray indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(IEnumerable<object> params, IEnumerable<int> indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(IEnumerable<object> params, ValueTuple<object> indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(IEnumerable<object> params, RaggedTensor indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(RaggedTensor params, ndarray indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(IGraphNodeBase params, ValueTuple<object> indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
Tensor batch_gather(IEnumerable<object> params, IGraphNodeBase indices, string name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
object batch_gather_dyn(object params, object indices, object name)
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
object batch_scatter_update(Variable ref, IEnumerable<int> indices, object updates, bool use_locking, string name)
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
Parameters
-
Variableref - `Variable` to scatter onto.
-
IEnumerable<int>indices - Tensor containing indices as described above.
-
objectupdates - Tensor of updates to apply to `ref`.
-
booluse_locking - Boolean indicating whether to lock the writing operation.
-
stringname - Optional scope name string.
Returns
-
object - Ref to `variable` after it has been modified.
object batch_scatter_update(Variable ref, ValueTuple<PythonClassContainer, PythonClassContainer> indices, object updates, bool use_locking, string name)
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
Parameters
-
Variableref - `Variable` to scatter onto.
-
ValueTuple<PythonClassContainer, PythonClassContainer>indices - Tensor containing indices as described above.
-
objectupdates - Tensor of updates to apply to `ref`.
-
booluse_locking - Boolean indicating whether to lock the writing operation.
-
stringname - Optional scope name string.
Returns
-
object - Ref to `variable` after it has been modified.
object batch_scatter_update(Variable ref, int indices, object updates, bool use_locking, string name)
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
Parameters
-
Variableref - `Variable` to scatter onto.
-
intindices - Tensor containing indices as described above.
-
objectupdates - Tensor of updates to apply to `ref`.
-
booluse_locking - Boolean indicating whether to lock the writing operation.
-
stringname - Optional scope name string.
Returns
-
object - Ref to `variable` after it has been modified.
object batch_scatter_update(Variable ref, IDictionary<object, object> indices, object updates, bool use_locking, string name)
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
Parameters
-
Variableref - `Variable` to scatter onto.
-
IDictionary<object, object>indices - Tensor containing indices as described above.
-
objectupdates - Tensor of updates to apply to `ref`.
-
booluse_locking - Boolean indicating whether to lock the writing operation.
-
stringname - Optional scope name string.
Returns
-
object - Ref to `variable` after it has been modified.
object batch_scatter_update(Variable ref, ndarray indices, object updates, bool use_locking, string name)
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
Parameters
Returns
-
object - Ref to `variable` after it has been modified.
object batch_scatter_update(Variable ref, float64 indices, object updates, bool use_locking, string name)
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
Parameters
Returns
-
object - Ref to `variable` after it has been modified.
object batch_scatter_update(Variable ref, float32 indices, object updates, bool use_locking, string name)
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
Parameters
Returns
-
object - Ref to `variable` after it has been modified.
object batch_scatter_update(Variable ref, IGraphNodeBase indices, object updates, bool use_locking, string name)
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
Parameters
-
Variableref - `Variable` to scatter onto.
-
IGraphNodeBaseindices - Tensor containing indices as described above.
-
objectupdates - Tensor of updates to apply to `ref`.
-
booluse_locking - Boolean indicating whether to lock the writing operation.
-
stringname - Optional scope name string.
Returns
-
object - Ref to `variable` after it has been modified.
object batch_scatter_update(Variable ref, IndexedSlices indices, object updates, bool use_locking, string name)
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
Parameters
-
Variableref - `Variable` to scatter onto.
-
IndexedSlicesindices - Tensor containing indices as described above.
-
objectupdates - Tensor of updates to apply to `ref`.
-
booluse_locking - Boolean indicating whether to lock the writing operation.
-
stringname - Optional scope name string.
Returns
-
object - Ref to `variable` after it has been modified.
object batch_scatter_update_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
Parameters
-
objectref - `Variable` to scatter onto.
-
objectindices - Tensor containing indices as described above.
-
objectupdates - Tensor of updates to apply to `ref`.
-
ImplicitContainer<T>use_locking - Boolean indicating whether to lock the writing operation.
-
objectname - Optional scope name string.
Returns
-
object - Ref to `variable` after it has been modified.
Tensor batch_to_space(IGraphNodeBase input, IEnumerable<object> crops, int block_size, string name, object block_shape)
BatchToSpace for 4-D tensors of type T. This is a legacy version of the more general BatchToSpaceND. Rearranges (permutes) data from batch into blocks of spatial data, followed by
cropping. This is the reverse transformation of SpaceToBatch. More specifically,
this op outputs a copy of the input tensor where values from the `batch`
dimension are moved in spatial blocks to the `height` and `width` dimensions,
followed by cropping along the `height` and `width` dimensions.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. 4-D tensor with shape `[batch*block_size*block_size, height_pad/block_size, width_pad/block_size, depth]`. Note that the batch size of the input tensor must be divisible by `block_size * block_size`.
-
IEnumerable<object>crops - A `Tensor`. Must be one of the following types: `int32`, `int64`. 2-D tensor of non-negative integers with shape `[2, 2]`. It specifies how many elements to crop from the intermediate result across the spatial dimensions as follows: crops = [[crop_top, crop_bottom], [crop_left, crop_right]]
-
intblock_size - An `int` that is `>= 2`.
-
stringname - A name for the operation (optional).
-
objectblock_shape
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object batch_to_space_dyn(object input, object crops, object block_size, object name, object block_shape)
BatchToSpace for 4-D tensors of type T. This is a legacy version of the more general BatchToSpaceND. Rearranges (permutes) data from batch into blocks of spatial data, followed by
cropping. This is the reverse transformation of SpaceToBatch. More specifically,
this op outputs a copy of the input tensor where values from the `batch`
dimension are moved in spatial blocks to the `height` and `width` dimensions,
followed by cropping along the `height` and `width` dimensions.
Parameters
-
objectinput - A `Tensor`. 4-D tensor with shape `[batch*block_size*block_size, height_pad/block_size, width_pad/block_size, depth]`. Note that the batch size of the input tensor must be divisible by `block_size * block_size`.
-
objectcrops - A `Tensor`. Must be one of the following types: `int32`, `int64`. 2-D tensor of non-negative integers with shape `[2, 2]`. It specifies how many elements to crop from the intermediate result across the spatial dimensions as follows: crops = [[crop_top, crop_bottom], [crop_left, crop_right]]
-
objectblock_size - An `int` that is `>= 2`.
-
objectname - A name for the operation (optional).
-
objectblock_shape
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor batch_to_space_nd(IGraphNodeBase input, IGraphNodeBase block_shape, IGraphNodeBase crops, string name)
BatchToSpace for N-D tensors of type T. This operation reshapes the "batch" dimension 0 into `M + 1` dimensions of shape
`block_shape + [batch]`, interleaves these blocks back into the grid defined by
the spatial dimensions `[1,..., M]`, to obtain a result with the same rank as
the input. The spatial dimensions of this intermediate result are then
optionally cropped according to `crops` to produce the output. This is the
reverse of SpaceToBatch. See below for a precise description.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. N-D with shape `input_shape = [batch] + spatial_shape + remaining_shape`, where spatial_shape has M dimensions.
-
IGraphNodeBaseblock_shape - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with shape `[M]`, all values must be >= 1.
-
IGraphNodeBasecrops - A `Tensor`. Must be one of the following types: `int32`, `int64`. 2-D with shape `[M, 2]`, all values must be >= 0. `crops[i] = [crop_start, crop_end]` specifies the amount to crop from input dimension `i + 1`, which corresponds to spatial dimension `i`. It is required that `crop_start[i] + crop_end[i] <= block_shape[i] * input_shape[i + 1]`. This operation is equivalent to the following steps: 1. Reshape `input` to `reshaped` of shape: [block_shape[0],..., block_shape[M-1], batch / prod(block_shape), input_shape[1],..., input_shape[N-1]] 2. Permute dimensions of `reshaped` to produce `permuted` of shape [batch / prod(block_shape), input_shape[1], block_shape[0], ..., input_shape[M], block_shape[M-1], input_shape[M+1],..., input_shape[N-1]] 3. Reshape `permuted` to produce `reshaped_permuted` of shape [batch / prod(block_shape), input_shape[1] * block_shape[0], ..., input_shape[M] * block_shape[M-1], input_shape[M+1], ..., input_shape[N-1]] 4. Crop the start and end of dimensions `[1,..., M]` of `reshaped_permuted` according to `crops` to produce the output of shape: [batch / prod(block_shape), input_shape[1] * block_shape[0] - crops[0,0] - crops[0,1], ..., input_shape[M] * block_shape[M-1] - crops[M-1,0] - crops[M-1,1], input_shape[M+1],..., input_shape[N-1]] Some examples: (1) For the following input of shape `[4, 1, 1, 1]`, `block_shape = [2, 2]`, and `crops = [[0, 0], [0, 0]]`: ``` [[[[1]]], [[[2]]], [[[3]]], [[[4]]]] ``` The output tensor has shape `[1, 2, 2, 1]` and value: ``` x = [[[[1], [2]], [[3], [4]]]] ``` (2) For the following input of shape `[4, 1, 1, 3]`, `block_shape = [2, 2]`, and `crops = [[0, 0], [0, 0]]`: ``` [[[[1, 2, 3]]], [[[4, 5, 6]]], [[[7, 8, 9]]], [[[10, 11, 12]]]] ``` The output tensor has shape `[1, 2, 2, 3]` and value: ``` x = [[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]]] ``` (3) For the following input of shape `[4, 2, 2, 1]`, `block_shape = [2, 2]`, and `crops = [[0, 0], [0, 0]]`: ``` x = [[[[1], [3]], [[9], [11]]], [[[2], [4]], [[10], [12]]], [[[5], [7]], [[13], [15]]], [[[6], [8]], [[14], [16]]]] ``` The output tensor has shape `[1, 4, 4, 1]` and value: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]], [[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ``` (4) For the following input of shape `[8, 1, 3, 1]`, `block_shape = [2, 2]`, and `crops = [[0, 0], [2, 0]]`: ``` x = [[[[0], [1], [3]]], [[[0], [9], [11]]], [[[0], [2], [4]]], [[[0], [10], [12]]], [[[0], [5], [7]]], [[[0], [13], [15]]], [[[0], [6], [8]]], [[[0], [14], [16]]]] ``` The output tensor has shape `[2, 2, 4, 1]` and value: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]]], [[[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ```
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object batch_to_space_nd_dyn(object input, object block_shape, object crops, object name)
BatchToSpace for N-D tensors of type T. This operation reshapes the "batch" dimension 0 into `M + 1` dimensions of shape
`block_shape + [batch]`, interleaves these blocks back into the grid defined by
the spatial dimensions `[1,..., M]`, to obtain a result with the same rank as
the input. The spatial dimensions of this intermediate result are then
optionally cropped according to `crops` to produce the output. This is the
reverse of SpaceToBatch. See below for a precise description.
Parameters
-
objectinput - A `Tensor`. N-D with shape `input_shape = [batch] + spatial_shape + remaining_shape`, where spatial_shape has M dimensions.
-
objectblock_shape - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with shape `[M]`, all values must be >= 1.
-
objectcrops - A `Tensor`. Must be one of the following types: `int32`, `int64`. 2-D with shape `[M, 2]`, all values must be >= 0. `crops[i] = [crop_start, crop_end]` specifies the amount to crop from input dimension `i + 1`, which corresponds to spatial dimension `i`. It is required that `crop_start[i] + crop_end[i] <= block_shape[i] * input_shape[i + 1]`. This operation is equivalent to the following steps: 1. Reshape `input` to `reshaped` of shape: [block_shape[0],..., block_shape[M-1], batch / prod(block_shape), input_shape[1],..., input_shape[N-1]] 2. Permute dimensions of `reshaped` to produce `permuted` of shape [batch / prod(block_shape), input_shape[1], block_shape[0], ..., input_shape[M], block_shape[M-1], input_shape[M+1],..., input_shape[N-1]] 3. Reshape `permuted` to produce `reshaped_permuted` of shape [batch / prod(block_shape), input_shape[1] * block_shape[0], ..., input_shape[M] * block_shape[M-1], input_shape[M+1], ..., input_shape[N-1]] 4. Crop the start and end of dimensions `[1,..., M]` of `reshaped_permuted` according to `crops` to produce the output of shape: [batch / prod(block_shape), input_shape[1] * block_shape[0] - crops[0,0] - crops[0,1], ..., input_shape[M] * block_shape[M-1] - crops[M-1,0] - crops[M-1,1], input_shape[M+1],..., input_shape[N-1]] Some examples: (1) For the following input of shape `[4, 1, 1, 1]`, `block_shape = [2, 2]`, and `crops = [[0, 0], [0, 0]]`: ``` [[[[1]]], [[[2]]], [[[3]]], [[[4]]]] ``` The output tensor has shape `[1, 2, 2, 1]` and value: ``` x = [[[[1], [2]], [[3], [4]]]] ``` (2) For the following input of shape `[4, 1, 1, 3]`, `block_shape = [2, 2]`, and `crops = [[0, 0], [0, 0]]`: ``` [[[[1, 2, 3]]], [[[4, 5, 6]]], [[[7, 8, 9]]], [[[10, 11, 12]]]] ``` The output tensor has shape `[1, 2, 2, 3]` and value: ``` x = [[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]]] ``` (3) For the following input of shape `[4, 2, 2, 1]`, `block_shape = [2, 2]`, and `crops = [[0, 0], [0, 0]]`: ``` x = [[[[1], [3]], [[9], [11]]], [[[2], [4]], [[10], [12]]], [[[5], [7]], [[13], [15]]], [[[6], [8]], [[14], [16]]]] ``` The output tensor has shape `[1, 4, 4, 1]` and value: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]], [[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ``` (4) For the following input of shape `[8, 1, 3, 1]`, `block_shape = [2, 2]`, and `crops = [[0, 0], [2, 0]]`: ``` x = [[[[0], [1], [3]]], [[[0], [9], [11]]], [[[0], [2], [4]]], [[[0], [10], [12]]], [[[0], [5], [7]]], [[[0], [13], [15]]], [[[0], [6], [8]]], [[[0], [14], [16]]]] ``` The output tensor has shape `[2, 2, 4, 1]` and value: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]]], [[[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ```
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor betainc(IGraphNodeBase a, IGraphNodeBase b, IGraphNodeBase x, string name)
Compute the regularized incomplete beta integral \\(I_x(a, b)\\). The regularized incomplete beta integral is defined as: \\(I_x(a, b) = \frac{B(x; a, b)}{B(a, b)}\\) where \\(B(x; a, b) = \int_0^x t^{a-1} (1 - t)^{b-1} dt\\) is the incomplete beta function and \\(B(a, b)\\) is the *complete*
beta function.
Parameters
-
IGraphNodeBasea - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
IGraphNodeBaseb - A `Tensor`. Must have the same type as `a`.
-
IGraphNodeBasex - A `Tensor`. Must have the same type as `a`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `a`.
object betainc_dyn(object a, object b, object x, object name)
Compute the regularized incomplete beta integral \\(I_x(a, b)\\). The regularized incomplete beta integral is defined as: \\(I_x(a, b) = \frac{B(x; a, b)}{B(a, b)}\\) where \\(B(x; a, b) = \int_0^x t^{a-1} (1 - t)^{b-1} dt\\) is the incomplete beta function and \\(B(a, b)\\) is the *complete*
beta function.
Parameters
-
objecta - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
objectb - A `Tensor`. Must have the same type as `a`.
-
objectx - A `Tensor`. Must have the same type as `a`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `a`.
Tensor binary(IGraphNodeBase a, IGraphNodeBase b, string name)
object binary_dyn(object a, object b, object name)
Tensor bincount(object arr, object weights, object minlength, object maxlength, ImplicitContainer<T> dtype)
Counts the number of occurrences of each value in an integer array. If `minlength` and `maxlength` are not given, returns a vector with length
`tf.reduce_max(arr) + 1` if `arr` is non-empty, and length 0 otherwise.
If `weights` are non-None, then index `i` of the output stores the sum of the
value in `weights` at each index where the corresponding value in `arr` is
`i`.
Parameters
-
objectarr - An int32 tensor of non-negative values.
-
objectweights - If non-None, must be the same shape as arr. For each value in `arr`, the bin will be incremented by the corresponding weight instead of 1.
-
objectminlength - If given, ensures the output has length at least `minlength`, padding with zeros at the end if necessary.
-
objectmaxlength - If given, skips values in `arr` that are equal or greater than `maxlength`, ensuring that the output has length at most `maxlength`.
-
ImplicitContainer<T>dtype - If `weights` is None, determines the type of the output bins.
Returns
-
Tensor - A vector with the same dtype as `weights` or the given `dtype`. The bin values.
object bincount_dyn(object arr, object weights, object minlength, object maxlength, ImplicitContainer<T> dtype)
Counts the number of occurrences of each value in an integer array. If `minlength` and `maxlength` are not given, returns a vector with length
`tf.reduce_max(arr) + 1` if `arr` is non-empty, and length 0 otherwise.
If `weights` are non-None, then index `i` of the output stores the sum of the
value in `weights` at each index where the corresponding value in `arr` is
`i`.
Parameters
-
objectarr - An int32 tensor of non-negative values.
-
objectweights - If non-None, must be the same shape as arr. For each value in `arr`, the bin will be incremented by the corresponding weight instead of 1.
-
objectminlength - If given, ensures the output has length at least `minlength`, padding with zeros at the end if necessary.
-
objectmaxlength - If given, skips values in `arr` that are equal or greater than `maxlength`, ensuring that the output has length at most `maxlength`.
-
ImplicitContainer<T>dtype - If `weights` is None, determines the type of the output bins.
Returns
-
object - A vector with the same dtype as `weights` or the given `dtype`. The bin values.
object bipartite_match(IGraphNodeBase distance_mat, IGraphNodeBase num_valid_rows, int top_k, string name)
object bipartite_match_dyn(object distance_mat, object num_valid_rows, ImplicitContainer<T> top_k, object name)
Tensor bitcast(IGraphNodeBase input, DType type, string name)
Bitcasts a tensor from one type to another without copying data. Given a tensor `input`, this operation returns a tensor that has the same buffer
data as `input` with datatype `type`. If the input datatype `T` is larger than the output datatype `type` then the
shape changes from [...] to [..., sizeof(`T`)/sizeof(`type`)]. If `T` is smaller than `type`, the operator requires that the rightmost
dimension be equal to sizeof(`type`)/sizeof(`T`). The shape then goes from
[..., sizeof(`type`)/sizeof(`T`)] to [...]. tf.bitcast() and tf.cast() work differently when real dtype is casted as a complex dtype
(e.g. tf.complex64 or tf.complex128) as tf.cast() make imaginary part 0 while tf.bitcast()
gives module error.
For example, Example 1:
Example 2:
Example 3:
*NOTE*: Bitcast is implemented as a low-level cast, so machines with different
endian orderings will give different results.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `complex64`, `complex128`, `qint8`, `quint8`, `qint16`, `quint16`, `qint32`.
-
DTypetype - A
tf.DTypefrom: `tf.bfloat16, tf.half, tf.float32, tf.float64, tf.int64, tf.int32, tf.uint8, tf.uint16, tf.uint32, tf.uint64, tf.int8, tf.int16, tf.complex64, tf.complex128, tf.qint8, tf.quint8, tf.qint16, tf.quint16, tf.qint32`. -
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `type`.
Show Example
>>> a = [1., 2., 3.]
>>> equality_bitcast = tf.bitcast(a,tf.complex128)
tensorflow.python.framework.errors_impl.InvalidArgumentError: Cannot bitcast from float to complex128: shape [3] [Op:Bitcast]
>>> equality_cast = tf.cast(a,tf.complex128)
>>> print(equality_cast)
tf.Tensor([1.+0.j 2.+0.j 3.+0.j], shape=(3,), dtype=complex128)
object bitcast_dyn(object input, object type, object name)
Bitcasts a tensor from one type to another without copying data. Given a tensor `input`, this operation returns a tensor that has the same buffer
data as `input` with datatype `type`. If the input datatype `T` is larger than the output datatype `type` then the
shape changes from [...] to [..., sizeof(`T`)/sizeof(`type`)]. If `T` is smaller than `type`, the operator requires that the rightmost
dimension be equal to sizeof(`type`)/sizeof(`T`). The shape then goes from
[..., sizeof(`type`)/sizeof(`T`)] to [...]. tf.bitcast() and tf.cast() work differently when real dtype is casted as a complex dtype
(e.g. tf.complex64 or tf.complex128) as tf.cast() make imaginary part 0 while tf.bitcast()
gives module error.
For example, Example 1:
Example 2:
Example 3:
*NOTE*: Bitcast is implemented as a low-level cast, so machines with different
endian orderings will give different results.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `complex64`, `complex128`, `qint8`, `quint8`, `qint16`, `quint16`, `qint32`.
-
objecttype - A
tf.DTypefrom: `tf.bfloat16, tf.half, tf.float32, tf.float64, tf.int64, tf.int32, tf.uint8, tf.uint16, tf.uint32, tf.uint64, tf.int8, tf.int16, tf.complex64, tf.complex128, tf.qint8, tf.quint8, tf.qint16, tf.quint16, tf.qint32`. -
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `type`.
Show Example
>>> a = [1., 2., 3.]
>>> equality_bitcast = tf.bitcast(a,tf.complex128)
tensorflow.python.framework.errors_impl.InvalidArgumentError: Cannot bitcast from float to complex128: shape [3] [Op:Bitcast]
>>> equality_cast = tf.cast(a,tf.complex128)
>>> print(equality_cast)
tf.Tensor([1.+0.j 2.+0.j 3.+0.j], shape=(3,), dtype=complex128)
object boolean_mask(object tensor, object mask, string name, Nullable<int> axis)
Apply boolean mask to tensor. Numpy equivalent is `tensor[mask]`.
In general, `0 < dim(mask) = K <= dim(tensor)`, and `mask`'s shape must match
the first K dimensions of `tensor`'s shape. We then have:
`boolean_mask(tensor, mask)[i, j1,...,jd] = tensor[i1,...,iK,j1,...,jd]`
where `(i1,...,iK)` is the ith `True` entry of `mask` (row-major order).
The `axis` could be used with `mask` to indicate the axis to mask from.
In that case, `axis + dim(mask) <= dim(tensor)` and `mask`'s shape must match
the first `axis + dim(mask)` dimensions of `tensor`'s shape. See also:
tf.ragged.boolean_mask, which can be applied to both dense and
ragged tensors, and can be used if you need to preserve the masked dimensions
of `tensor` (rather than flattening them, as tf.boolean_mask does).
Parameters
-
objecttensor - N-D tensor.
-
objectmask - K-D boolean tensor, K <= N and K must be known statically.
-
stringname - A name for this operation (optional).
-
Nullable<int>axis - A 0-D int Tensor representing the axis in `tensor` to mask from. By default, axis is 0 which will mask from the first dimension. Otherwise K + axis <= N.
Returns
-
object - (N-K+1)-dimensional tensor populated by entries in `tensor` corresponding to `True` values in `mask`.
Show Example
# 1-D example
tensor = [0, 1, 2, 3]
mask = np.array([True, False, True, False])
boolean_mask(tensor, mask) # [0, 2]
object boolean_mask(IEnumerable<IGraphNodeBase> tensor, object mask, string name, Nullable<int> axis)
Apply boolean mask to tensor. Numpy equivalent is `tensor[mask]`.
In general, `0 < dim(mask) = K <= dim(tensor)`, and `mask`'s shape must match
the first K dimensions of `tensor`'s shape. We then have:
`boolean_mask(tensor, mask)[i, j1,...,jd] = tensor[i1,...,iK,j1,...,jd]`
where `(i1,...,iK)` is the ith `True` entry of `mask` (row-major order).
The `axis` could be used with `mask` to indicate the axis to mask from.
In that case, `axis + dim(mask) <= dim(tensor)` and `mask`'s shape must match
the first `axis + dim(mask)` dimensions of `tensor`'s shape. See also:
tf.ragged.boolean_mask, which can be applied to both dense and
ragged tensors, and can be used if you need to preserve the masked dimensions
of `tensor` (rather than flattening them, as tf.boolean_mask does).
Parameters
-
IEnumerable<IGraphNodeBase>tensor - N-D tensor.
-
objectmask - K-D boolean tensor, K <= N and K must be known statically.
-
stringname - A name for this operation (optional).
-
Nullable<int>axis - A 0-D int Tensor representing the axis in `tensor` to mask from. By default, axis is 0 which will mask from the first dimension. Otherwise K + axis <= N.
Returns
-
object - (N-K+1)-dimensional tensor populated by entries in `tensor` corresponding to `True` values in `mask`.
Show Example
# 1-D example
tensor = [0, 1, 2, 3]
mask = np.array([True, False, True, False])
boolean_mask(tensor, mask) # [0, 2]
object boolean_mask_dyn(object tensor, object mask, ImplicitContainer<T> name, object axis)
Apply boolean mask to tensor. Numpy equivalent is `tensor[mask]`.
In general, `0 < dim(mask) = K <= dim(tensor)`, and `mask`'s shape must match
the first K dimensions of `tensor`'s shape. We then have:
`boolean_mask(tensor, mask)[i, j1,...,jd] = tensor[i1,...,iK,j1,...,jd]`
where `(i1,...,iK)` is the ith `True` entry of `mask` (row-major order).
The `axis` could be used with `mask` to indicate the axis to mask from.
In that case, `axis + dim(mask) <= dim(tensor)` and `mask`'s shape must match
the first `axis + dim(mask)` dimensions of `tensor`'s shape. See also:
tf.ragged.boolean_mask, which can be applied to both dense and
ragged tensors, and can be used if you need to preserve the masked dimensions
of `tensor` (rather than flattening them, as tf.boolean_mask does).
Parameters
-
objecttensor - N-D tensor.
-
objectmask - K-D boolean tensor, K <= N and K must be known statically.
-
ImplicitContainer<T>name - A name for this operation (optional).
-
objectaxis - A 0-D int Tensor representing the axis in `tensor` to mask from. By default, axis is 0 which will mask from the first dimension. Otherwise K + axis <= N.
Returns
-
object - (N-K+1)-dimensional tensor populated by entries in `tensor` corresponding to `True` values in `mask`.
Show Example
# 1-D example
tensor = [0, 1, 2, 3]
mask = np.array([True, False, True, False])
boolean_mask(tensor, mask) # [0, 2]
Tensor broadcast_dynamic_shape(IGraphNodeBase shape_x, IGraphNodeBase shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
IGraphNodeBaseshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
IGraphNodeBaseshape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(IGraphNodeBase shape_x, TensorShape shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
IGraphNodeBaseshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
TensorShapeshape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(int shape_x, IEnumerable<int> shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
intshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
IEnumerable<int>shape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(IGraphNodeBase shape_x, IEnumerable<int> shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
IGraphNodeBaseshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
IEnumerable<int>shape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(int shape_x, IGraphNodeBase shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
intshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
IGraphNodeBaseshape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(int shape_x, TensorShape shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
intshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
TensorShapeshape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(TensorShape shape_x, IGraphNodeBase shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
TensorShapeshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
IGraphNodeBaseshape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(TensorShape shape_x, IEnumerable<int> shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
TensorShapeshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
IEnumerable<int>shape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(Dimension shape_x, TensorShape shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
Dimensionshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
TensorShapeshape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(Dimension shape_x, IGraphNodeBase shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
Dimensionshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
IGraphNodeBaseshape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(TensorShape shape_x, TensorShape shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
TensorShapeshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
TensorShapeshape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
Tensor broadcast_dynamic_shape(Dimension shape_x, IEnumerable<int> shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
Dimensionshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
IEnumerable<int>shape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
Tensor - A rank 1 integer `Tensor` representing the broadcasted shape.
object broadcast_dynamic_shape_dyn(object shape_x, object shape_y)
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
Parameters
-
objectshape_x - A rank 1 integer `Tensor`, representing the shape of x.
-
objectshape_y - A rank 1 integer `Tensor`, representing the shape of y.
Returns
-
object - A rank 1 integer `Tensor` representing the broadcasted shape.
TensorShape broadcast_static_shape(Dimension shape_x, int shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
Dimensionshape_x - A `TensorShape`
-
intshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(Dimension shape_x, TensorShape shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
Dimensionshape_x - A `TensorShape`
-
TensorShapeshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(TensorShape shape_x, int shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
TensorShapeshape_x - A `TensorShape`
-
intshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(Dimension shape_x, Dimension shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(int shape_x, IGraphNodeBase shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
intshape_x - A `TensorShape`
-
IGraphNodeBaseshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(IGraphNodeBase shape_x, IGraphNodeBase shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
IGraphNodeBaseshape_x - A `TensorShape`
-
IGraphNodeBaseshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(TensorShape shape_x, IGraphNodeBase shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
TensorShapeshape_x - A `TensorShape`
-
IGraphNodeBaseshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(IGraphNodeBase shape_x, TensorShape shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
IGraphNodeBaseshape_x - A `TensorShape`
-
TensorShapeshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(IGraphNodeBase shape_x, Dimension shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
IGraphNodeBaseshape_x - A `TensorShape`
-
Dimensionshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(Dimension shape_x, IGraphNodeBase shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
Dimensionshape_x - A `TensorShape`
-
IGraphNodeBaseshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(IGraphNodeBase shape_x, int shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
IGraphNodeBaseshape_x - A `TensorShape`
-
intshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(TensorShape shape_x, TensorShape shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
TensorShapeshape_x - A `TensorShape`
-
TensorShapeshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(int shape_x, Dimension shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
intshape_x - A `TensorShape`
-
Dimensionshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(int shape_x, int shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
intshape_x - A `TensorShape`
-
intshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(int shape_x, TensorShape shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
intshape_x - A `TensorShape`
-
TensorShapeshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
TensorShape broadcast_static_shape(TensorShape shape_x, Dimension shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
TensorShapeshape_x - A `TensorShape`
-
Dimensionshape_y - A `TensorShape`
Returns
-
TensorShape - A `TensorShape` representing the broadcasted shape.
object broadcast_static_shape_dyn(object shape_x, object shape_y)
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
Parameters
-
objectshape_x - A `TensorShape`
-
objectshape_y - A `TensorShape`
Returns
-
object - A `TensorShape` representing the broadcasted shape.
Tensor broadcast_to(IGraphNodeBase input, IGraphNodeBase shape, string name)
Broadcast an array for a compatible shape. Broadcasting is the process of making arrays to have compatible shapes
for arithmetic operations. Two shapes are compatible if for each
dimension pair they are either equal or one of them is one. When trying
to broadcast a Tensor to a shape, it starts with the trailing dimensions,
and works its way forward. For example,
In the above example, the input Tensor with the shape of `[1, 3]`
is broadcasted to output Tensor with shape of `[3, 3]`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. A Tensor to broadcast.
-
IGraphNodeBaseshape - A `Tensor`. Must be one of the following types: `int32`, `int64`. An 1-D `int` Tensor. The shape of the desired output.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Show Example
>>> x = tf.constant([1, 2, 3])
>>> y = tf.broadcast_to(x, [3, 3])
>>> sess.run(y)
array([[1, 2, 3],
[1, 2, 3],
[1, 2, 3]], dtype=int32)
object broadcast_to_dyn(object input, object shape, object name)
Broadcast an array for a compatible shape. Broadcasting is the process of making arrays to have compatible shapes
for arithmetic operations. Two shapes are compatible if for each
dimension pair they are either equal or one of them is one. When trying
to broadcast a Tensor to a shape, it starts with the trailing dimensions,
and works its way forward. For example,
In the above example, the input Tensor with the shape of `[1, 3]`
is broadcasted to output Tensor with shape of `[3, 3]`.
Parameters
-
objectinput - A `Tensor`. A Tensor to broadcast.
-
objectshape - A `Tensor`. Must be one of the following types: `int32`, `int64`. An 1-D `int` Tensor. The shape of the desired output.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Show Example
>>> x = tf.constant([1, 2, 3])
>>> y = tf.broadcast_to(x, [3, 3])
>>> sess.run(y)
array([[1, 2, 3],
[1, 2, 3],
[1, 2, 3]], dtype=int32)
Tensor bucketize_with_input_boundaries(IGraphNodeBase input, IGraphNodeBase boundaries, string name)
object bucketize_with_input_boundaries_dyn(object input, object boundaries, object name)
object build_categorical_equality_splits(IGraphNodeBase num_minibatches, IGraphNodeBase partition_ids, IGraphNodeBase feature_ids, IGraphNodeBase gradients, IGraphNodeBase hessians, IGraphNodeBase class_id, IGraphNodeBase feature_column_group_id, IGraphNodeBase bias_feature_id, IGraphNodeBase l1_regularization, IGraphNodeBase l2_regularization, IGraphNodeBase tree_complexity_regularization, IGraphNodeBase min_node_weight, IGraphNodeBase multiclass_strategy, IGraphNodeBase weak_learner_type, string name)
object build_categorical_equality_splits_dyn(object num_minibatches, object partition_ids, object feature_ids, object gradients, object hessians, object class_id, object feature_column_group_id, object bias_feature_id, object l1_regularization, object l2_regularization, object tree_complexity_regularization, object min_node_weight, object multiclass_strategy, object weak_learner_type, object name)
object build_dense_inequality_splits(IGraphNodeBase num_minibatches, IGraphNodeBase partition_ids, IGraphNodeBase bucket_ids, IGraphNodeBase gradients, IGraphNodeBase hessians, IGraphNodeBase bucket_boundaries, IGraphNodeBase class_id, IGraphNodeBase feature_column_group_id, IGraphNodeBase l1_regularization, IGraphNodeBase l2_regularization, IGraphNodeBase tree_complexity_regularization, IGraphNodeBase min_node_weight, IGraphNodeBase multiclass_strategy, IGraphNodeBase weak_learner_type, string name)
object build_dense_inequality_splits_dyn(object num_minibatches, object partition_ids, object bucket_ids, object gradients, object hessians, object bucket_boundaries, object class_id, object feature_column_group_id, object l1_regularization, object l2_regularization, object tree_complexity_regularization, object min_node_weight, object multiclass_strategy, object weak_learner_type, object name)
object build_sparse_inequality_splits(IGraphNodeBase num_minibatches, IGraphNodeBase partition_ids, IGraphNodeBase bucket_ids, IGraphNodeBase gradients, IGraphNodeBase hessians, IGraphNodeBase bucket_boundaries, IGraphNodeBase class_id, IGraphNodeBase feature_column_group_id, IGraphNodeBase bias_feature_id, IGraphNodeBase l1_regularization, IGraphNodeBase l2_regularization, IGraphNodeBase tree_complexity_regularization, IGraphNodeBase min_node_weight, IGraphNodeBase multiclass_strategy, string name)
object build_sparse_inequality_splits_dyn(object num_minibatches, object partition_ids, object bucket_ids, object gradients, object hessians, object bucket_boundaries, object class_id, object feature_column_group_id, object bias_feature_id, object l1_regularization, object l2_regularization, object tree_complexity_regularization, object min_node_weight, object multiclass_strategy, object name)
Tensor bytes_in_use(string name)
object bytes_in_use_dyn(object name)
Tensor bytes_limit(string name)
object bytes_limit_dyn(object name)
object case(IEnumerable<ValueTuple<object, object>> pred_fn_pairs, PythonFunctionContainer default, bool exclusive, bool strict, string name)
object case(ValueTuple<object, object> pred_fn_pairs, PythonFunctionContainer default, bool exclusive, bool strict, string name)
object case(IDictionary<object, object> pred_fn_pairs, PythonFunctionContainer default, bool exclusive, bool strict, PythonFunctionContainer name)
object case(IDictionary<object, object> pred_fn_pairs, PythonFunctionContainer default, bool exclusive, bool strict, string name)
object case(IEnumerable<ValueTuple<object, object>> pred_fn_pairs, PythonFunctionContainer default, bool exclusive, bool strict, PythonFunctionContainer name)
object case(ValueTuple<object, object> pred_fn_pairs, PythonFunctionContainer default, bool exclusive, bool strict, PythonFunctionContainer name)
object case_dyn(object pred_fn_pairs, object default, ImplicitContainer<T> exclusive, ImplicitContainer<T> strict, ImplicitContainer<T> name)
Create a case operation. See also
tf.switch_case. The `pred_fn_pairs` parameter is a dict or list of pairs of size N.
Each pair contains a boolean scalar tensor and a python callable that
creates the tensors to be returned if the boolean evaluates to True.
`default` is a callable generating a list of tensors. All the callables
in `pred_fn_pairs` as well as `default` (if provided) should return the same
number and types of tensors. If `exclusive==True`, all predicates are evaluated, and an exception is
thrown if more than one of the predicates evaluates to `True`.
If `exclusive==False`, execution stops at the first predicate which
evaluates to True, and the tensors generated by the corresponding function
are returned immediately. If none of the predicates evaluate to True, this
operation returns the tensors generated by `default`. tf.case supports nested structures as implemented in
tf.contrib.framework.nest. All of the callables must return the same
(possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
a callable, they are implicitly unpacked to single values. This
behavior is disabled by passing `strict=True`. If an unordered dictionary is used for `pred_fn_pairs`, the order of the
conditional tests is not guaranteed. However, the order is guaranteed to be
deterministic, so that variables created in conditional branches are created
in fixed order across runs. **Example 1:** Pseudocode: ```
if (x < y) return 17;
else return 23;
``` Expressions:
**Example 2:** Pseudocode: ```
if (x < y && x > z) raise OpError("Only one predicate may evaluate to True");
if (x < y) return 17;
else if (x > z) return 23;
else return -1;
``` Expressions:
Parameters
-
objectpred_fn_pairs - Dict or list of pairs of a boolean scalar tensor and a callable which returns a list of tensors.
-
objectdefault - Optional callable that returns a list of tensors.
-
ImplicitContainer<T>exclusive - True iff at most one predicate is allowed to evaluate to `True`.
-
ImplicitContainer<T>strict - A boolean that enables/disables 'strict' mode; see above.
-
ImplicitContainer<T>name - A name for this operation (optional).
Returns
-
object - The tensors returned by the first pair whose predicate evaluated to True, or those returned by `default` if none does.
Show Example
f1 = lambda: tf.constant(17)
f2 = lambda: tf.constant(23)
r = tf.case([(tf.less(x, y), f1)], default=f2)
object cast(PythonClassContainer x, PythonFunctionContainer dtype, PythonFunctionContainer name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
PythonClassContainerx - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
PythonFunctionContainerdtype - The destination type. The list of supported dtypes is the same as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(IEnumerator<IGraphNodeBase> x, DType dtype, string name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
IEnumerator<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
DTypedtype - The destination type. The list of supported dtypes is the same as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(IEnumerator<IGraphNodeBase> x, DType dtype, PythonFunctionContainer name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
IEnumerator<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
DTypedtype - The destination type. The list of supported dtypes is the same as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(object x, DType dtype, PythonFunctionContainer name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
DTypedtype - The destination type. The list of supported dtypes is the same as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(IEnumerator<IGraphNodeBase> x, PythonFunctionContainer dtype, string name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
IEnumerator<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
PythonFunctionContainerdtype - The destination type. The list of supported dtypes is the same as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(object x, PythonFunctionContainer dtype, PythonFunctionContainer name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
PythonFunctionContainerdtype - The destination type. The list of supported dtypes is the same as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(object x, PythonFunctionContainer dtype, string name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
PythonFunctionContainerdtype - The destination type. The list of supported dtypes is the same as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(object x, DType dtype, string name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
DTypedtype - The destination type. The list of supported dtypes is the same as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(PythonClassContainer x, PythonFunctionContainer dtype, string name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
PythonClassContainerx - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
PythonFunctionContainerdtype - The destination type. The list of supported dtypes is the same as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(IEnumerable<IGraphNodeBase> x, DType dtype, PythonFunctionContainer name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
DTypedtype - The destination type. The list of supported dtypes is the same as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(IEnumerable<IGraphNodeBase> x, PythonFunctionContainer dtype, string name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
PythonFunctionContainerdtype - The destination type. The list of supported dtypes is the same as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(PythonClassContainer x, DType dtype, string name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
PythonClassContainerx - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
DTypedtype - The destination type. The list of supported dtypes is the same as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(IEnumerable<IGraphNodeBase> x, DType dtype, string name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
DTypedtype - The destination type. The list of supported dtypes is the same as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(IEnumerable<IGraphNodeBase> x, PythonFunctionContainer dtype, PythonFunctionContainer name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
PythonFunctionContainerdtype - The destination type. The list of supported dtypes is the same as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(IEnumerator<IGraphNodeBase> x, PythonFunctionContainer dtype, PythonFunctionContainer name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
IEnumerator<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
PythonFunctionContainerdtype - The destination type. The list of supported dtypes is the same as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast(PythonClassContainer x, DType dtype, PythonFunctionContainer name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
PythonClassContainerx - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
DTypedtype - The destination type. The list of supported dtypes is the same as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
object cast_dyn(object x, object dtype, object name)
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices` of numeric type. It could be `uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`, `float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
-
objectdtype - The destination type. The list of supported dtypes is the same as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` and same type as `dtype`.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
Tensor<T> cast<T>(IGraphNodeBase value, string name)
Casts a tensor to a new type.
Tensor ceil(IGraphNodeBase x, string name)
Returns element-wise smallest integer not less than x.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
object ceil_dyn(object x, object name)
Returns element-wise smallest integer not less than x.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Tensor center_tree_ensemble_bias(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase stamp_token, IGraphNodeBase next_stamp_token, IGraphNodeBase delta_updates, object learner_config, double centering_epsilon, string name)
object center_tree_ensemble_bias_dyn(object tree_ensemble_handle, object stamp_token, object next_stamp_token, object delta_updates, object learner_config, ImplicitContainer<T> centering_epsilon, object name)
Tensor check_numerics(IGraphNodeBase tensor, string message, string name)
Checks a tensor for NaN and Inf values. When run, reports an `InvalidArgument` error if `tensor` has any values
that are not a number (NaN) or infinity (Inf). Otherwise, passes `tensor` as-is.
Parameters
-
IGraphNodeBasetensor - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringmessage - A `string`. Prefix of the error message.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
object check_numerics_dyn(object tensor, object message, object name)
Checks a tensor for NaN and Inf values. When run, reports an `InvalidArgument` error if `tensor` has any values
that are not a number (NaN) or infinity (Inf). Otherwise, passes `tensor` as-is.
Parameters
-
objecttensor - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectmessage - A `string`. Prefix of the error message.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `tensor`.
Tensor cholesky(IGraphNodeBase input, string name)
Computes the Cholesky decomposition of one or more square matrices. The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The input has to be symmetric and positive definite. Only the lower-triangular
part of the input will be used for this operation. The upper-triangular part
will not be read. The output is a tensor of the same shape as the input
containing the Cholesky decompositions for all input submatrices `[..., :, :]`. **Note**: The gradient computation on GPU is faster for large matrices but
not for large batch dimensions when the submatrices are small. In this
case it might be faster to use the CPU.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object cholesky_dyn(object input, object name)
Computes the Cholesky decomposition of one or more square matrices. The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The input has to be symmetric and positive definite. Only the lower-triangular
part of the input will be used for this operation. The upper-triangular part
will not be read. The output is a tensor of the same shape as the input
containing the Cholesky decompositions for all input submatrices `[..., :, :]`. **Note**: The gradient computation on GPU is faster for large matrices but
not for large batch dimensions when the submatrices are small. In this
case it might be faster to use the CPU.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor cholesky_solve(IGraphNodeBase chol, IGraphNodeBase rhs, string name)
Solves systems of linear eqns `A X = RHS`, given Cholesky factorizations.
Parameters
-
IGraphNodeBasechol - A `Tensor`. Must be `float32` or `float64`, shape is `[..., M, M]`. Cholesky factorization of `A`, e.g. `chol = tf.linalg.cholesky(A)`. For that reason, only the lower triangular parts (including the diagonal) of the last two dimensions of `chol` are used. The strictly upper part is assumed to be zero and not accessed.
-
IGraphNodeBaserhs - A `Tensor`, same type as `chol`, shape is `[..., M, K]`.
-
stringname - A name to give this `Op`. Defaults to `cholesky_solve`.
Returns
-
Tensor - Solution to `A x = rhs`, shape `[..., M, K]`.
Show Example
# Solve 10 separate 2x2 linear systems:
A =... # shape 10 x 2 x 2
RHS =... # shape 10 x 2 x 1
chol = tf.linalg.cholesky(A) # shape 10 x 2 x 2
X = tf.linalg.cholesky_solve(chol, RHS) # shape 10 x 2 x 1
# tf.matmul(A, X) ~ RHS
X[3, :, 0] # Solution to the linear system A[3, :, :] x = RHS[3, :, 0] # Solve five linear systems (K = 5) for every member of the length 10 batch.
A =... # shape 10 x 2 x 2
RHS =... # shape 10 x 2 x 5
...
X[3, :, 2] # Solution to the linear system A[3, :, :] x = RHS[3, :, 2]
object cholesky_solve_dyn(object chol, object rhs, object name)
Solves systems of linear eqns `A X = RHS`, given Cholesky factorizations.
Parameters
-
objectchol - A `Tensor`. Must be `float32` or `float64`, shape is `[..., M, M]`. Cholesky factorization of `A`, e.g. `chol = tf.linalg.cholesky(A)`. For that reason, only the lower triangular parts (including the diagonal) of the last two dimensions of `chol` are used. The strictly upper part is assumed to be zero and not accessed.
-
objectrhs - A `Tensor`, same type as `chol`, shape is `[..., M, K]`.
-
objectname - A name to give this `Op`. Defaults to `cholesky_solve`.
Returns
-
object - Solution to `A x = rhs`, shape `[..., M, K]`.
Show Example
# Solve 10 separate 2x2 linear systems:
A =... # shape 10 x 2 x 2
RHS =... # shape 10 x 2 x 1
chol = tf.linalg.cholesky(A) # shape 10 x 2 x 2
X = tf.linalg.cholesky_solve(chol, RHS) # shape 10 x 2 x 1
# tf.matmul(A, X) ~ RHS
X[3, :, 0] # Solution to the linear system A[3, :, :] x = RHS[3, :, 0] # Solve five linear systems (K = 5) for every member of the length 10 batch.
A =... # shape 10 x 2 x 2
RHS =... # shape 10 x 2 x 5
...
X[3, :, 2] # Solution to the linear system A[3, :, :] x = RHS[3, :, 2]
Tensor clip_by_average_norm(IGraphNodeBase t, IGraphNodeBase clip_norm, string name)
Clips tensor values to a maximum average L2-norm. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
clip_by_average_norm is deprecated in TensorFlow 2.0. Please use clip_by_norm(t, clip_norm * tf.cast(tf.size(t), tf.float32), name) instead. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its average L2-norm is less than or equal to
`clip_norm`. Specifically, if the average L2-norm is already less than or
equal to `clip_norm`, then `t` is not modified. If the average L2-norm is
greater than `clip_norm`, then this operation returns a tensor of the same
type and shape as `t` with its values set to: `t * clip_norm / l2norm_avg(t)` In this case, the average L2-norm of the output tensor is `clip_norm`. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
IGraphNodeBaset - A `Tensor`.
-
IGraphNodeBaseclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A clipped `Tensor`.
Tensor clip_by_average_norm(IGraphNodeBase t, double clip_norm, string name)
Clips tensor values to a maximum average L2-norm. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
clip_by_average_norm is deprecated in TensorFlow 2.0. Please use clip_by_norm(t, clip_norm * tf.cast(tf.size(t), tf.float32), name) instead. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its average L2-norm is less than or equal to
`clip_norm`. Specifically, if the average L2-norm is already less than or
equal to `clip_norm`, then `t` is not modified. If the average L2-norm is
greater than `clip_norm`, then this operation returns a tensor of the same
type and shape as `t` with its values set to: `t * clip_norm / l2norm_avg(t)` In this case, the average L2-norm of the output tensor is `clip_norm`. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
IGraphNodeBaset - A `Tensor`.
-
doubleclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A clipped `Tensor`.
object clip_by_average_norm_dyn(object t, object clip_norm, object name)
Clips tensor values to a maximum average L2-norm. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
clip_by_average_norm is deprecated in TensorFlow 2.0. Please use clip_by_norm(t, clip_norm * tf.cast(tf.size(t), tf.float32), name) instead. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its average L2-norm is less than or equal to
`clip_norm`. Specifically, if the average L2-norm is already less than or
equal to `clip_norm`, then `t` is not modified. If the average L2-norm is
greater than `clip_norm`, then this operation returns a tensor of the same
type and shape as `t` with its values set to: `t * clip_norm / l2norm_avg(t)` In this case, the average L2-norm of the output tensor is `clip_norm`. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor`.
-
objectclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
objectname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor`.
object clip_by_global_norm(ValueTuple<IGraphNodeBase, object> t_list, IGraphNodeBase clip_norm, object use_norm, string name)
Clips values of multiple tensors by the ratio of the sum of their norms. Given a tuple or list of tensors `t_list`, and a clipping ratio `clip_norm`,
this operation returns a list of clipped tensors `list_clipped`
and the global norm (`global_norm`) of all tensors in `t_list`. Optionally,
if you've already computed the global norm for `t_list`, you can specify
the global norm with `use_norm`. To perform the clipping, the values `t_list[i]` are set to: t_list[i] * clip_norm / max(global_norm, clip_norm) where: global_norm = sqrt(sum([l2norm(t)**2 for t in t_list])) If `clip_norm > global_norm` then the entries in `t_list` remain as they are,
otherwise they're all shrunk by the global ratio. If `global_norm == infinity` then the entries in `t_list` are all set to `NaN`
to signal that an error occurred. Any of the entries of `t_list` that are of type `None` are ignored. This is the correct way to perform gradient clipping (for example, see
[Pascanu et al., 2012](http://arxiv.org/abs/1211.5063)
([pdf](http://arxiv.org/pdf/1211.5063.pdf))). However, it is slower than `clip_by_norm()` because all the parameters must be
ready before the clipping operation can be performed.
Parameters
-
ValueTuple<IGraphNodeBase, object>t_list - A tuple or list of mixed `Tensors`, `IndexedSlices`, or None.
-
IGraphNodeBaseclip_norm - A 0-D (scalar) `Tensor` > 0. The clipping ratio.
-
objectuse_norm - A 0-D (scalar) `Tensor` of type `float` (optional). The global norm to use. If not provided, `global_norm()` is used to compute the norm.
-
stringname - A name for the operation (optional).
Returns
-
object
object clip_by_global_norm(ValueTuple<IGraphNodeBase, object> t_list, double clip_norm, object use_norm, string name)
Clips values of multiple tensors by the ratio of the sum of their norms. Given a tuple or list of tensors `t_list`, and a clipping ratio `clip_norm`,
this operation returns a list of clipped tensors `list_clipped`
and the global norm (`global_norm`) of all tensors in `t_list`. Optionally,
if you've already computed the global norm for `t_list`, you can specify
the global norm with `use_norm`. To perform the clipping, the values `t_list[i]` are set to: t_list[i] * clip_norm / max(global_norm, clip_norm) where: global_norm = sqrt(sum([l2norm(t)**2 for t in t_list])) If `clip_norm > global_norm` then the entries in `t_list` remain as they are,
otherwise they're all shrunk by the global ratio. If `global_norm == infinity` then the entries in `t_list` are all set to `NaN`
to signal that an error occurred. Any of the entries of `t_list` that are of type `None` are ignored. This is the correct way to perform gradient clipping (for example, see
[Pascanu et al., 2012](http://arxiv.org/abs/1211.5063)
([pdf](http://arxiv.org/pdf/1211.5063.pdf))). However, it is slower than `clip_by_norm()` because all the parameters must be
ready before the clipping operation can be performed.
Parameters
-
ValueTuple<IGraphNodeBase, object>t_list - A tuple or list of mixed `Tensors`, `IndexedSlices`, or None.
-
doubleclip_norm - A 0-D (scalar) `Tensor` > 0. The clipping ratio.
-
objectuse_norm - A 0-D (scalar) `Tensor` of type `float` (optional). The global norm to use. If not provided, `global_norm()` is used to compute the norm.
-
stringname - A name for the operation (optional).
Returns
-
object
object clip_by_global_norm(IEnumerable<IGraphNodeBase> t_list, IGraphNodeBase clip_norm, object use_norm, string name)
Clips values of multiple tensors by the ratio of the sum of their norms. Given a tuple or list of tensors `t_list`, and a clipping ratio `clip_norm`,
this operation returns a list of clipped tensors `list_clipped`
and the global norm (`global_norm`) of all tensors in `t_list`. Optionally,
if you've already computed the global norm for `t_list`, you can specify
the global norm with `use_norm`. To perform the clipping, the values `t_list[i]` are set to: t_list[i] * clip_norm / max(global_norm, clip_norm) where: global_norm = sqrt(sum([l2norm(t)**2 for t in t_list])) If `clip_norm > global_norm` then the entries in `t_list` remain as they are,
otherwise they're all shrunk by the global ratio. If `global_norm == infinity` then the entries in `t_list` are all set to `NaN`
to signal that an error occurred. Any of the entries of `t_list` that are of type `None` are ignored. This is the correct way to perform gradient clipping (for example, see
[Pascanu et al., 2012](http://arxiv.org/abs/1211.5063)
([pdf](http://arxiv.org/pdf/1211.5063.pdf))). However, it is slower than `clip_by_norm()` because all the parameters must be
ready before the clipping operation can be performed.
Parameters
-
IEnumerable<IGraphNodeBase>t_list - A tuple or list of mixed `Tensors`, `IndexedSlices`, or None.
-
IGraphNodeBaseclip_norm - A 0-D (scalar) `Tensor` > 0. The clipping ratio.
-
objectuse_norm - A 0-D (scalar) `Tensor` of type `float` (optional). The global norm to use. If not provided, `global_norm()` is used to compute the norm.
-
stringname - A name for the operation (optional).
Returns
-
object
object clip_by_global_norm(IEnumerable<IGraphNodeBase> t_list, double clip_norm, object use_norm, string name)
Clips values of multiple tensors by the ratio of the sum of their norms. Given a tuple or list of tensors `t_list`, and a clipping ratio `clip_norm`,
this operation returns a list of clipped tensors `list_clipped`
and the global norm (`global_norm`) of all tensors in `t_list`. Optionally,
if you've already computed the global norm for `t_list`, you can specify
the global norm with `use_norm`. To perform the clipping, the values `t_list[i]` are set to: t_list[i] * clip_norm / max(global_norm, clip_norm) where: global_norm = sqrt(sum([l2norm(t)**2 for t in t_list])) If `clip_norm > global_norm` then the entries in `t_list` remain as they are,
otherwise they're all shrunk by the global ratio. If `global_norm == infinity` then the entries in `t_list` are all set to `NaN`
to signal that an error occurred. Any of the entries of `t_list` that are of type `None` are ignored. This is the correct way to perform gradient clipping (for example, see
[Pascanu et al., 2012](http://arxiv.org/abs/1211.5063)
([pdf](http://arxiv.org/pdf/1211.5063.pdf))). However, it is slower than `clip_by_norm()` because all the parameters must be
ready before the clipping operation can be performed.
Parameters
-
IEnumerable<IGraphNodeBase>t_list - A tuple or list of mixed `Tensors`, `IndexedSlices`, or None.
-
doubleclip_norm - A 0-D (scalar) `Tensor` > 0. The clipping ratio.
-
objectuse_norm - A 0-D (scalar) `Tensor` of type `float` (optional). The global norm to use. If not provided, `global_norm()` is used to compute the norm.
-
stringname - A name for the operation (optional).
Returns
-
object
object clip_by_global_norm_dyn(object t_list, object clip_norm, object use_norm, object name)
Clips values of multiple tensors by the ratio of the sum of their norms. Given a tuple or list of tensors `t_list`, and a clipping ratio `clip_norm`,
this operation returns a list of clipped tensors `list_clipped`
and the global norm (`global_norm`) of all tensors in `t_list`. Optionally,
if you've already computed the global norm for `t_list`, you can specify
the global norm with `use_norm`. To perform the clipping, the values `t_list[i]` are set to: t_list[i] * clip_norm / max(global_norm, clip_norm) where: global_norm = sqrt(sum([l2norm(t)**2 for t in t_list])) If `clip_norm > global_norm` then the entries in `t_list` remain as they are,
otherwise they're all shrunk by the global ratio. If `global_norm == infinity` then the entries in `t_list` are all set to `NaN`
to signal that an error occurred. Any of the entries of `t_list` that are of type `None` are ignored. This is the correct way to perform gradient clipping (for example, see
[Pascanu et al., 2012](http://arxiv.org/abs/1211.5063)
([pdf](http://arxiv.org/pdf/1211.5063.pdf))). However, it is slower than `clip_by_norm()` because all the parameters must be
ready before the clipping operation can be performed.
Parameters
-
objectt_list - A tuple or list of mixed `Tensors`, `IndexedSlices`, or None.
-
objectclip_norm - A 0-D (scalar) `Tensor` > 0. The clipping ratio.
-
objectuse_norm - A 0-D (scalar) `Tensor` of type `float` (optional). The global norm to use. If not provided, `global_norm()` is used to compute the norm.
-
objectname - A name for the operation (optional).
Returns
-
object
object clip_by_norm(object t, ValueTuple<PythonClassContainer, PythonClassContainer> clip_norm, IGraphNodeBase axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
ValueTuple<PythonClassContainer, PythonClassContainer>clip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IGraphNodeBaseaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, int clip_norm, IGraphNodeBase axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
intclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IGraphNodeBaseaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, int clip_norm, IEnumerable<int> axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
intclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IEnumerable<int>axes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, _NumpyWrapper clip_norm, IGraphNodeBase axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
_NumpyWrapperclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IGraphNodeBaseaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, IGraphNodeBase clip_norm, IEnumerable<int> axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
IGraphNodeBaseclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IEnumerable<int>axes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, IGraphNodeBase clip_norm, int axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
IGraphNodeBaseclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
intaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, IGraphNodeBase clip_norm, IGraphNodeBase axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
IGraphNodeBaseclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IGraphNodeBaseaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, _NumpyWrapper clip_norm, int axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
_NumpyWrapperclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
intaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, ndarray clip_norm, IEnumerable<int> axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
ndarrayclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IEnumerable<int>axes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, _ArrayLike clip_norm, IGraphNodeBase axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
_ArrayLikeclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IGraphNodeBaseaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, _ArrayLike clip_norm, int axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
_ArrayLikeclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
intaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, int clip_norm, int axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
intclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
intaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, _ArrayLike clip_norm, IEnumerable<int> axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
_ArrayLikeclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IEnumerable<int>axes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, ValueTuple<PythonClassContainer, PythonClassContainer> clip_norm, int axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
ValueTuple<PythonClassContainer, PythonClassContainer>clip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
intaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, ValueTuple<PythonClassContainer, PythonClassContainer> clip_norm, IEnumerable<int> axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
ValueTuple<PythonClassContainer, PythonClassContainer>clip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IEnumerable<int>axes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, double clip_norm, IGraphNodeBase axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
doubleclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IGraphNodeBaseaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, double clip_norm, IEnumerable<int> axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
doubleclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IEnumerable<int>axes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, ndarray clip_norm, int axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
ndarrayclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
intaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, _NumpyWrapper clip_norm, IEnumerable<int> axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
_NumpyWrapperclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IEnumerable<int>axes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, ndarray clip_norm, IGraphNodeBase axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
ndarrayclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
IGraphNodeBaseaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm(object t, double clip_norm, int axes, string name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
doubleclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
intaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_norm_dyn(object t, object clip_norm, object axes, object name)
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
objectclip_norm - A 0-D (scalar) `Tensor` > 0. A maximum clipping value.
-
objectaxes - A 1-D (vector) `Tensor` of type int32 containing the dimensions to use for computing the L2-norm. If `None` (the default), uses all dimensions.
-
objectname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
object clip_by_value(IEnumerable<IGraphNodeBase> t, IGraphNodeBase clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IEnumerable<IGraphNodeBase>t - A `Tensor` or `IndexedSlices`.
-
IGraphNodeBaseclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(ValueTuple<PythonClassContainer, PythonClassContainer> t, double clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>t - A `Tensor` or `IndexedSlices`.
-
doubleclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(ValueTuple<PythonClassContainer, PythonClassContainer> t, ndarray clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>t - A `Tensor` or `IndexedSlices`.
-
ndarrayclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IGraphNodeBase t, IGraphNodeBase clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IGraphNodeBaset - A `Tensor` or `IndexedSlices`.
-
IGraphNodeBaseclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(ValueTuple<PythonClassContainer, PythonClassContainer> t, _ArrayLike clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>t - A `Tensor` or `IndexedSlices`.
-
_ArrayLikeclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(ValueTuple<PythonClassContainer, PythonClassContainer> t, _NumpyWrapper clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>t - A `Tensor` or `IndexedSlices`.
-
_NumpyWrapperclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(ValueTuple<PythonClassContainer, PythonClassContainer> t, ValueTuple<PythonClassContainer, PythonClassContainer> clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>t - A `Tensor` or `IndexedSlices`.
-
ValueTuple<PythonClassContainer, PythonClassContainer>clip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IEnumerable<IGraphNodeBase> t, int clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IEnumerable<IGraphNodeBase>t - A `Tensor` or `IndexedSlices`.
-
intclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(ValueTuple<PythonClassContainer, PythonClassContainer> t, int clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>t - A `Tensor` or `IndexedSlices`.
-
intclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IndexedSlices t, int clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IndexedSlicest - A `Tensor` or `IndexedSlices`.
-
intclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IGraphNodeBase t, int clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IGraphNodeBaset - A `Tensor` or `IndexedSlices`.
-
intclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IndexedSlices t, _NumpyWrapper clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IndexedSlicest - A `Tensor` or `IndexedSlices`.
-
_NumpyWrapperclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IEnumerable<IGraphNodeBase> t, ndarray clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IEnumerable<IGraphNodeBase>t - A `Tensor` or `IndexedSlices`.
-
ndarrayclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IGraphNodeBase t, _ArrayLike clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IGraphNodeBaset - A `Tensor` or `IndexedSlices`.
-
_ArrayLikeclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IEnumerable<IGraphNodeBase> t, ValueTuple<PythonClassContainer, PythonClassContainer> clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IEnumerable<IGraphNodeBase>t - A `Tensor` or `IndexedSlices`.
-
ValueTuple<PythonClassContainer, PythonClassContainer>clip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IndexedSlices t, ValueTuple<PythonClassContainer, PythonClassContainer> clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IndexedSlicest - A `Tensor` or `IndexedSlices`.
-
ValueTuple<PythonClassContainer, PythonClassContainer>clip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IEnumerable<IGraphNodeBase> t, _ArrayLike clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IEnumerable<IGraphNodeBase>t - A `Tensor` or `IndexedSlices`.
-
_ArrayLikeclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IGraphNodeBase t, ndarray clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IGraphNodeBaset - A `Tensor` or `IndexedSlices`.
-
ndarrayclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IndexedSlices t, IGraphNodeBase clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IndexedSlicest - A `Tensor` or `IndexedSlices`.
-
IGraphNodeBaseclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IGraphNodeBase t, double clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IGraphNodeBaset - A `Tensor` or `IndexedSlices`.
-
doubleclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IGraphNodeBase t, ValueTuple<PythonClassContainer, PythonClassContainer> clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IGraphNodeBaset - A `Tensor` or `IndexedSlices`.
-
ValueTuple<PythonClassContainer, PythonClassContainer>clip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(ValueTuple<PythonClassContainer, PythonClassContainer> t, IGraphNodeBase clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>t - A `Tensor` or `IndexedSlices`.
-
IGraphNodeBaseclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IEnumerable<IGraphNodeBase> t, double clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IEnumerable<IGraphNodeBase>t - A `Tensor` or `IndexedSlices`.
-
doubleclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IndexedSlices t, _ArrayLike clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IndexedSlicest - A `Tensor` or `IndexedSlices`.
-
_ArrayLikeclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IGraphNodeBase t, _NumpyWrapper clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IGraphNodeBaset - A `Tensor` or `IndexedSlices`.
-
_NumpyWrapperclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IndexedSlices t, double clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IndexedSlicest - A `Tensor` or `IndexedSlices`.
-
doubleclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IndexedSlices t, ndarray clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IndexedSlicest - A `Tensor` or `IndexedSlices`.
-
ndarrayclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value(IEnumerable<IGraphNodeBase> t, _NumpyWrapper clip_value_min, object clip_value_max, string name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
IEnumerable<IGraphNodeBase>t - A `Tensor` or `IndexedSlices`.
-
_NumpyWrapperclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
stringname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
object clip_by_value_dyn(object t, object clip_value_min, object clip_value_max, object name)
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Parameters
-
objectt - A `Tensor` or `IndexedSlices`.
-
objectclip_value_min - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The minimum value to clip by.
-
objectclip_value_max - A 0-D (scalar) `Tensor`, or a `Tensor` with the same shape as `t`. The maximum value to clip by.
-
objectname - A name for the operation (optional).
Returns
-
object - A clipped `Tensor` or `IndexedSlices`.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
Tensor complex(IGraphNodeBase real, IGraphNodeBase imag, string name)
Converts two real numbers to a complex number. Given a tensor `real` representing the real part of a complex number, and a
tensor `imag` representing the imaginary part of a complex number, this
operation returns complex numbers elementwise of the form \\(a + bj\\), where
*a* represents the `real` part and *b* represents the `imag` part. The input tensors `real` and `imag` must have the same shape.
Parameters
-
IGraphNodeBasereal - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
IGraphNodeBaseimag - A `Tensor`. Must have the same type as `real`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `complex64` or `complex128`. Raises:
Show Example
real = tf.constant([2.25, 3.25])
imag = tf.constant([4.75, 5.75])
tf.complex(real, imag) # [[2.25 + 4.75j], [3.25 + 5.75j]]
object complex_dyn(object real, object imag, object name)
Converts two real numbers to a complex number. Given a tensor `real` representing the real part of a complex number, and a
tensor `imag` representing the imaginary part of a complex number, this
operation returns complex numbers elementwise of the form \\(a + bj\\), where
*a* represents the `real` part and *b* represents the `imag` part. The input tensors `real` and `imag` must have the same shape.
Parameters
-
objectreal - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
objectimag - A `Tensor`. Must have the same type as `real`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `complex64` or `complex128`. Raises:
Show Example
real = tf.constant([2.25, 3.25])
imag = tf.constant([4.75, 5.75])
tf.complex(real, imag) # [[2.25 + 4.75j], [3.25 + 5.75j]]
object complex_struct(object n_a, object n_b, object t_c, string name)
object complex_struct_dyn(object n_a, object n_b, object t_c, object name)
Tensor concat(IEnumerable<IGraphNodeBase> values, int axis, string name)
Concatenates tensors along one dimension. Concatenates the list of tensors `values` along dimension `axis`. If
`values[i].shape = [D0, D1,... Daxis(i),...Dn]`, the concatenated
result has shape [D0, D1,... Raxis,...Dn] where Raxis = sum(Daxis(i)) That is, the data from the input tensors is joined along the `axis`
dimension. The number of dimensions of the input tensors must match, and all dimensions
except `axis` must be equal.
As in Python, the `axis` could also be negative numbers. Negative `axis`
are interpreted as counting from the end of the rank, i.e.,
`axis + rank(values)`-th dimension.
would produce:
Note: If you are concatenating along a new axis consider using stack.
E.g.
can be rewritten as
Parameters
-
IEnumerable<IGraphNodeBase>values - A list of `Tensor` objects or a single `Tensor`.
-
intaxis - 0-D `int32` `Tensor`. Dimension along which to concatenate. Must be in the range `[-rank(values), rank(values))`. As in Python, indexing for axis is 0-based. Positive axis in the rage of `[0, rank(values))` refers to `axis`-th dimension. And negative axis refers to `axis + rank(values)`-th dimension.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` resulting from concatenation of the input tensors.
Show Example
t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0) # [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 1) # [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]] # tensor t3 with shape [2, 3]
# tensor t4 with shape [2, 3]
tf.shape(tf.concat([t3, t4], 0)) # [4, 3]
tf.shape(tf.concat([t3, t4], 1)) # [2, 6]
Tensor concat(object values, int axis, string name)
Concatenates tensors along one dimension. Concatenates the list of tensors `values` along dimension `axis`. If
`values[i].shape = [D0, D1,... Daxis(i),...Dn]`, the concatenated
result has shape [D0, D1,... Raxis,...Dn] where Raxis = sum(Daxis(i)) That is, the data from the input tensors is joined along the `axis`
dimension. The number of dimensions of the input tensors must match, and all dimensions
except `axis` must be equal.
As in Python, the `axis` could also be negative numbers. Negative `axis`
are interpreted as counting from the end of the rank, i.e.,
`axis + rank(values)`-th dimension.
would produce:
Note: If you are concatenating along a new axis consider using stack.
E.g.
can be rewritten as
Parameters
-
objectvalues - A list of `Tensor` objects or a single `Tensor`.
-
intaxis - 0-D `int32` `Tensor`. Dimension along which to concatenate. Must be in the range `[-rank(values), rank(values))`. As in Python, indexing for axis is 0-based. Positive axis in the rage of `[0, rank(values))` refers to `axis`-th dimension. And negative axis refers to `axis + rank(values)`-th dimension.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` resulting from concatenation of the input tensors.
Show Example
t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0) # [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 1) # [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]] # tensor t3 with shape [2, 3]
# tensor t4 with shape [2, 3]
tf.shape(tf.concat([t3, t4], 0)) # [4, 3]
tf.shape(tf.concat([t3, t4], 1)) # [2, 6]
object concat_dyn(object values, object axis, ImplicitContainer<T> name)
Concatenates tensors along one dimension. Concatenates the list of tensors `values` along dimension `axis`. If
`values[i].shape = [D0, D1,... Daxis(i),...Dn]`, the concatenated
result has shape [D0, D1,... Raxis,...Dn] where Raxis = sum(Daxis(i)) That is, the data from the input tensors is joined along the `axis`
dimension. The number of dimensions of the input tensors must match, and all dimensions
except `axis` must be equal.
As in Python, the `axis` could also be negative numbers. Negative `axis`
are interpreted as counting from the end of the rank, i.e.,
`axis + rank(values)`-th dimension.
would produce:
Note: If you are concatenating along a new axis consider using stack.
E.g.
can be rewritten as
Parameters
-
objectvalues - A list of `Tensor` objects or a single `Tensor`.
-
objectaxis - 0-D `int32` `Tensor`. Dimension along which to concatenate. Must be in the range `[-rank(values), rank(values))`. As in Python, indexing for axis is 0-based. Positive axis in the rage of `[0, rank(values))` refers to `axis`-th dimension. And negative axis refers to `axis + rank(values)`-th dimension.
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - A `Tensor` resulting from concatenation of the input tensors.
Show Example
t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0) # [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 1) # [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]] # tensor t3 with shape [2, 3]
# tensor t4 with shape [2, 3]
tf.shape(tf.concat([t3, t4], 0)) # [4, 3]
tf.shape(tf.concat([t3, t4], 1)) # [2, 6]
object cond(object pred, IEnumerable<object> true_fn, PythonFunctionContainer false_fn, IGraphNodeBase strict, string name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
objectpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
IEnumerable<object>true_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
IGraphNodeBasestrict - A boolean that enables/disables 'strict' mode; see above.
-
stringname - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(object pred, PythonFunctionContainer true_fn, PythonFunctionContainer false_fn, bool strict, string name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
objectpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
PythonFunctionContainertrue_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
boolstrict - A boolean that enables/disables 'strict' mode; see above.
-
stringname - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(object pred, IEnumerable<object> true_fn, PythonFunctionContainer false_fn, bool strict, string name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
objectpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
IEnumerable<object>true_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
boolstrict - A boolean that enables/disables 'strict' mode; see above.
-
stringname - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(object pred, IEnumerable<object> true_fn, PythonFunctionContainer false_fn, IGraphNodeBase strict, PythonFunctionContainer name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
objectpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
IEnumerable<object>true_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
IGraphNodeBasestrict - A boolean that enables/disables 'strict' mode; see above.
-
PythonFunctionContainername - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(object pred, PythonFunctionContainer true_fn, PythonFunctionContainer false_fn, IGraphNodeBase strict, string name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
objectpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
PythonFunctionContainertrue_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
IGraphNodeBasestrict - A boolean that enables/disables 'strict' mode; see above.
-
stringname - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(object pred, IEnumerable<object> true_fn, PythonFunctionContainer false_fn, bool strict, PythonFunctionContainer name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
objectpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
IEnumerable<object>true_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
boolstrict - A boolean that enables/disables 'strict' mode; see above.
-
PythonFunctionContainername - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(object pred, PythonFunctionContainer true_fn, PythonFunctionContainer false_fn, IGraphNodeBase strict, PythonFunctionContainer name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
objectpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
PythonFunctionContainertrue_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
IGraphNodeBasestrict - A boolean that enables/disables 'strict' mode; see above.
-
PythonFunctionContainername - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(object pred, PythonFunctionContainer true_fn, PythonFunctionContainer false_fn, bool strict, PythonFunctionContainer name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
objectpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
PythonFunctionContainertrue_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
boolstrict - A boolean that enables/disables 'strict' mode; see above.
-
PythonFunctionContainername - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(PythonClassContainer pred, IEnumerable<object> true_fn, PythonFunctionContainer false_fn, IGraphNodeBase strict, string name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
PythonClassContainerpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
IEnumerable<object>true_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
IGraphNodeBasestrict - A boolean that enables/disables 'strict' mode; see above.
-
stringname - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(PythonClassContainer pred, PythonFunctionContainer true_fn, PythonFunctionContainer false_fn, bool strict, string name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
PythonClassContainerpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
PythonFunctionContainertrue_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
boolstrict - A boolean that enables/disables 'strict' mode; see above.
-
stringname - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(PythonClassContainer pred, IEnumerable<object> true_fn, PythonFunctionContainer false_fn, IGraphNodeBase strict, PythonFunctionContainer name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
PythonClassContainerpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
IEnumerable<object>true_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
IGraphNodeBasestrict - A boolean that enables/disables 'strict' mode; see above.
-
PythonFunctionContainername - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(PythonClassContainer pred, IEnumerable<object> true_fn, PythonFunctionContainer false_fn, bool strict, string name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
PythonClassContainerpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
IEnumerable<object>true_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
boolstrict - A boolean that enables/disables 'strict' mode; see above.
-
stringname - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(PythonClassContainer pred, IEnumerable<object> true_fn, PythonFunctionContainer false_fn, bool strict, PythonFunctionContainer name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
PythonClassContainerpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
IEnumerable<object>true_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
boolstrict - A boolean that enables/disables 'strict' mode; see above.
-
PythonFunctionContainername - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(PythonClassContainer pred, PythonFunctionContainer true_fn, PythonFunctionContainer false_fn, bool strict, PythonFunctionContainer name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
PythonClassContainerpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
PythonFunctionContainertrue_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
boolstrict - A boolean that enables/disables 'strict' mode; see above.
-
PythonFunctionContainername - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(PythonClassContainer pred, PythonFunctionContainer true_fn, PythonFunctionContainer false_fn, IGraphNodeBase strict, string name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
PythonClassContainerpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
PythonFunctionContainertrue_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
IGraphNodeBasestrict - A boolean that enables/disables 'strict' mode; see above.
-
stringname - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond(PythonClassContainer pred, PythonFunctionContainer true_fn, PythonFunctionContainer false_fn, IGraphNodeBase strict, PythonFunctionContainer name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
PythonClassContainerpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
PythonFunctionContainertrue_fn - The callable to be performed if pred is true.
-
PythonFunctionContainerfalse_fn - The callable to be performed if pred is false.
-
IGraphNodeBasestrict - A boolean that enables/disables 'strict' mode; see above.
-
PythonFunctionContainername - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
object cond_dyn(object pred, object true_fn, object false_fn, ImplicitContainer<T> strict, object name, object fn1, object fn2)
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Parameters
-
objectpred - A scalar determining whether to return the result of `true_fn` or `false_fn`.
-
objecttrue_fn - The callable to be performed if pred is true.
-
objectfalse_fn - The callable to be performed if pred is false.
-
ImplicitContainer<T>strict - A boolean that enables/disables 'strict' mode; see above.
-
objectname - Optional name prefix for the returned tensors.
-
objectfn1 -
objectfn2
Returns
-
object - Tensors returned by the call to either `true_fn` or `false_fn`. If the callables return a singleton list, the element is extracted from the list.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
Tensor confusion_matrix(IGraphNodeBase labels, IGraphNodeBase predictions, object num_classes, ImplicitContainer<T> dtype, string name, object weights)
Computes the confusion matrix from predictions and labels. The matrix columns represent the prediction labels and the rows represent the
real labels. The confusion matrix is always a 2-D array of shape `[n, n]`,
where `n` is the number of valid labels for a given classification task. Both
prediction and labels must be 1-D arrays of the same shape in order for this
function to work. If `num_classes` is `None`, then `num_classes` will be set to one plus the
maximum value in either predictions or labels. Class labels are expected to
start at 0. For example, if `num_classes` is 3, then the possible labels
would be `[0, 1, 2]`. If `weights` is not `None`, then each prediction contributes its
corresponding weight to the total value of the confusion matrix cell.
Note that the possible labels are assumed to be `[0, 1, 2, 3, 4]`,
resulting in a 5x5 confusion matrix.
Parameters
-
IGraphNodeBaselabels - 1-D `Tensor` of real labels for the classification task.
-
IGraphNodeBasepredictions - 1-D `Tensor` of predictions for a given classification.
-
objectnum_classes - The possible number of labels the classification task can have. If this value is not provided, it will be calculated using both predictions and labels array.
-
ImplicitContainer<T>dtype - Data type of the confusion matrix.
-
stringname - Scope name.
-
objectweights - An optional `Tensor` whose shape matches `predictions`.
Returns
-
Tensor - A `Tensor` of type `dtype` with shape `[n, n]` representing the confusion matrix, where `n` is the number of possible labels in the classification task.
Show Example
tf.math.confusion_matrix([1, 2, 4], [2, 2, 4]) ==>
[[0 0 0 0 0]
[0 0 1 0 0]
[0 0 1 0 0]
[0 0 0 0 0]
[0 0 0 0 1]]
object confusion_matrix_dyn(object labels, object predictions, object num_classes, ImplicitContainer<T> dtype, object name, object weights)
Computes the confusion matrix from predictions and labels. The matrix columns represent the prediction labels and the rows represent the
real labels. The confusion matrix is always a 2-D array of shape `[n, n]`,
where `n` is the number of valid labels for a given classification task. Both
prediction and labels must be 1-D arrays of the same shape in order for this
function to work. If `num_classes` is `None`, then `num_classes` will be set to one plus the
maximum value in either predictions or labels. Class labels are expected to
start at 0. For example, if `num_classes` is 3, then the possible labels
would be `[0, 1, 2]`. If `weights` is not `None`, then each prediction contributes its
corresponding weight to the total value of the confusion matrix cell.
Note that the possible labels are assumed to be `[0, 1, 2, 3, 4]`,
resulting in a 5x5 confusion matrix.
Parameters
-
objectlabels - 1-D `Tensor` of real labels for the classification task.
-
objectpredictions - 1-D `Tensor` of predictions for a given classification.
-
objectnum_classes - The possible number of labels the classification task can have. If this value is not provided, it will be calculated using both predictions and labels array.
-
ImplicitContainer<T>dtype - Data type of the confusion matrix.
-
objectname - Scope name.
-
objectweights - An optional `Tensor` whose shape matches `predictions`.
Returns
-
object - A `Tensor` of type `dtype` with shape `[n, n]` representing the confusion matrix, where `n` is the number of possible labels in the classification task.
Show Example
tf.math.confusion_matrix([1, 2, 4], [2, 2, 4]) ==>
[[0 0 0 0 0]
[0 0 1 0 0]
[0 0 1 0 0]
[0 0 0 0 0]
[0 0 0 0 1]]
Tensor conj(IEnumerable<IGraphNodeBase> x, string name)
Returns the complex conjugate of a complex number. Given a tensor `input` of complex numbers, this operation returns a tensor of
complex numbers that are the complex conjugate of each element in `input`. The
complex numbers in `input` must be of the form \\(a + bj\\), where *a* is the
real part and *b* is the imaginary part. The complex conjugate returned by this operation is of the form \\(a - bj\\). For example: # tensor 'input' is [-2.25 + 4.75j, 3.25 + 5.75j]
tf.math.conj(input) ==> [-2.25 - 4.75j, 3.25 - 5.75j] If `x` is real, it is returned unchanged.
Parameters
-
IEnumerable<IGraphNodeBase>x - `Tensor` to conjugate. Must have numeric or variant type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` that is the conjugate of `x` (with the same type).
Tensor conj(PythonClassContainer x, string name)
Returns the complex conjugate of a complex number. Given a tensor `input` of complex numbers, this operation returns a tensor of
complex numbers that are the complex conjugate of each element in `input`. The
complex numbers in `input` must be of the form \\(a + bj\\), where *a* is the
real part and *b* is the imaginary part. The complex conjugate returned by this operation is of the form \\(a - bj\\). For example: # tensor 'input' is [-2.25 + 4.75j, 3.25 + 5.75j]
tf.math.conj(input) ==> [-2.25 - 4.75j, 3.25 - 5.75j] If `x` is real, it is returned unchanged.
Parameters
-
PythonClassContainerx - `Tensor` to conjugate. Must have numeric or variant type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` that is the conjugate of `x` (with the same type).
Tensor conj(object x, string name)
Returns the complex conjugate of a complex number. Given a tensor `input` of complex numbers, this operation returns a tensor of
complex numbers that are the complex conjugate of each element in `input`. The
complex numbers in `input` must be of the form \\(a + bj\\), where *a* is the
real part and *b* is the imaginary part. The complex conjugate returned by this operation is of the form \\(a - bj\\). For example: # tensor 'input' is [-2.25 + 4.75j, 3.25 + 5.75j]
tf.math.conj(input) ==> [-2.25 - 4.75j, 3.25 - 5.75j] If `x` is real, it is returned unchanged.
Parameters
-
objectx - `Tensor` to conjugate. Must have numeric or variant type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` that is the conjugate of `x` (with the same type).
object conj_dyn(object x, object name)
Returns the complex conjugate of a complex number. Given a tensor `input` of complex numbers, this operation returns a tensor of
complex numbers that are the complex conjugate of each element in `input`. The
complex numbers in `input` must be of the form \\(a + bj\\), where *a* is the
real part and *b* is the imaginary part. The complex conjugate returned by this operation is of the form \\(a - bj\\). For example: # tensor 'input' is [-2.25 + 4.75j, 3.25 + 5.75j]
tf.math.conj(input) ==> [-2.25 - 4.75j, 3.25 - 5.75j] If `x` is real, it is returned unchanged.
Parameters
-
objectx - `Tensor` to conjugate. Must have numeric or variant type.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` that is the conjugate of `x` (with the same type).
Tensor constant(object value, DType dtype, TensorShape shape, string name, bool verify_shape)
Creates a constant tensor. The resulting tensor is populated with values of type `dtype`, as
specified by arguments `value` and (optionally) `shape` (see examples
below). The argument `value` can be a constant value, or a list of values of type
`dtype`. If `value` is a list, then the length of the list must be less
than or equal to the number of elements implied by the `shape` argument (if
specified). In the case where the list length is less than the number of
elements specified by `shape`, the last element in the list will be used
to fill the remaining entries. The argument `shape` is optional. If present, it specifies the dimensions of
the resulting tensor. If not present, the shape of `value` is used. If the argument `dtype` is not specified, then the type is inferred from
the type of `value`.
tf.constant differs from tf.fill in a few ways: * tf.constant supports arbitrary constants, not just uniform scalar
Tensors like tf.fill.
* tf.constant creates a `Const` node in the computation graph with the
exact value at graph construction time. On the other hand, tf.fill
creates an Op in the graph that is expanded at runtime.
* Because tf.constant only embeds constant values in the graph, it does
not support dynamic shapes based on other runtime Tensors, whereas
tf.fill does.
Parameters
-
objectvalue - A constant value (or list) of output type `dtype`.
-
DTypedtype - The type of the elements of the resulting tensor.
-
TensorShapeshape - Optional dimensions of resulting tensor.
-
stringname - Optional name for the tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
Returns
-
Tensor - A Constant Tensor.
Show Example
# Constant 1-D Tensor populated with value list.
tensor = tf.constant([1, 2, 3, 4, 5, 6, 7]) => [1 2 3 4 5 6 7] # Constant 2-D tensor populated with scalar value -1.
tensor = tf.constant(-1.0, shape=[2, 3]) => [[-1. -1. -1.]
[-1. -1. -1.]]
Tensor constant(object value, DType dtype, IEnumerable<Nullable<int>> shape, string name, bool verify_shape)
Creates a constant tensor. The resulting tensor is populated with values of type `dtype`, as
specified by arguments `value` and (optionally) `shape` (see examples
below). The argument `value` can be a constant value, or a list of values of type
`dtype`. If `value` is a list, then the length of the list must be less
than or equal to the number of elements implied by the `shape` argument (if
specified). In the case where the list length is less than the number of
elements specified by `shape`, the last element in the list will be used
to fill the remaining entries. The argument `shape` is optional. If present, it specifies the dimensions of
the resulting tensor. If not present, the shape of `value` is used. If the argument `dtype` is not specified, then the type is inferred from
the type of `value`.
tf.constant differs from tf.fill in a few ways: * tf.constant supports arbitrary constants, not just uniform scalar
Tensors like tf.fill.
* tf.constant creates a `Const` node in the computation graph with the
exact value at graph construction time. On the other hand, tf.fill
creates an Op in the graph that is expanded at runtime.
* Because tf.constant only embeds constant values in the graph, it does
not support dynamic shapes based on other runtime Tensors, whereas
tf.fill does.
Parameters
-
objectvalue - A constant value (or list) of output type `dtype`.
-
DTypedtype - The type of the elements of the resulting tensor.
-
IEnumerable<Nullable<int>>shape - Optional dimensions of resulting tensor.
-
stringname - Optional name for the tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
Returns
-
Tensor - A Constant Tensor.
Show Example
# Constant 1-D Tensor populated with value list.
tensor = tf.constant([1, 2, 3, 4, 5, 6, 7]) => [1 2 3 4 5 6 7] # Constant 2-D tensor populated with scalar value -1.
tensor = tf.constant(-1.0, shape=[2, 3]) => [[-1. -1. -1.]
[-1. -1. -1.]]
Tensor constant(object value, DType dtype, ValueTuple<int, object> shape, string name, bool verify_shape)
Creates a constant tensor. The resulting tensor is populated with values of type `dtype`, as
specified by arguments `value` and (optionally) `shape` (see examples
below). The argument `value` can be a constant value, or a list of values of type
`dtype`. If `value` is a list, then the length of the list must be less
than or equal to the number of elements implied by the `shape` argument (if
specified). In the case where the list length is less than the number of
elements specified by `shape`, the last element in the list will be used
to fill the remaining entries. The argument `shape` is optional. If present, it specifies the dimensions of
the resulting tensor. If not present, the shape of `value` is used. If the argument `dtype` is not specified, then the type is inferred from
the type of `value`.
tf.constant differs from tf.fill in a few ways: * tf.constant supports arbitrary constants, not just uniform scalar
Tensors like tf.fill.
* tf.constant creates a `Const` node in the computation graph with the
exact value at graph construction time. On the other hand, tf.fill
creates an Op in the graph that is expanded at runtime.
* Because tf.constant only embeds constant values in the graph, it does
not support dynamic shapes based on other runtime Tensors, whereas
tf.fill does.
Parameters
-
objectvalue - A constant value (or list) of output type `dtype`.
-
DTypedtype - The type of the elements of the resulting tensor.
-
ValueTuple<int, object>shape - Optional dimensions of resulting tensor.
-
stringname - Optional name for the tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
Returns
-
Tensor - A Constant Tensor.
Show Example
# Constant 1-D Tensor populated with value list.
tensor = tf.constant([1, 2, 3, 4, 5, 6, 7]) => [1 2 3 4 5 6 7] # Constant 2-D tensor populated with scalar value -1.
tensor = tf.constant(-1.0, shape=[2, 3]) => [[-1. -1. -1.]
[-1. -1. -1.]]
object constant_dyn(object value, object dtype, object shape, ImplicitContainer<T> name, ImplicitContainer<T> verify_shape)
Creates a constant tensor. The resulting tensor is populated with values of type `dtype`, as
specified by arguments `value` and (optionally) `shape` (see examples
below). The argument `value` can be a constant value, or a list of values of type
`dtype`. If `value` is a list, then the length of the list must be less
than or equal to the number of elements implied by the `shape` argument (if
specified). In the case where the list length is less than the number of
elements specified by `shape`, the last element in the list will be used
to fill the remaining entries. The argument `shape` is optional. If present, it specifies the dimensions of
the resulting tensor. If not present, the shape of `value` is used. If the argument `dtype` is not specified, then the type is inferred from
the type of `value`.
tf.constant differs from tf.fill in a few ways: * tf.constant supports arbitrary constants, not just uniform scalar
Tensors like tf.fill.
* tf.constant creates a `Const` node in the computation graph with the
exact value at graph construction time. On the other hand, tf.fill
creates an Op in the graph that is expanded at runtime.
* Because tf.constant only embeds constant values in the graph, it does
not support dynamic shapes based on other runtime Tensors, whereas
tf.fill does.
Parameters
-
objectvalue - A constant value (or list) of output type `dtype`.
-
objectdtype - The type of the elements of the resulting tensor.
-
objectshape - Optional dimensions of resulting tensor.
-
ImplicitContainer<T>name - Optional name for the tensor.
-
ImplicitContainer<T>verify_shape - Boolean that enables verification of a shape of values.
Returns
-
object - A Constant Tensor.
Show Example
# Constant 1-D Tensor populated with value list.
tensor = tf.constant([1, 2, 3, 4, 5, 6, 7]) => [1 2 3 4 5 6 7] # Constant 2-D tensor populated with scalar value -1.
tensor = tf.constant(-1.0, shape=[2, 3]) => [[-1. -1. -1.]
[-1. -1. -1.]]
Tensor<T> constant_scalar<T>(T value, TensorShape shape, string name)
Creates a constant Tensor<T>
Tensor<T> constant<T>(T[] values, string name)
Tensor<T> constant<T>(IArrayLike<T> values, string name)
Creates a constant Tensor<T>
Tensor<T> constant<T>(T[,,,,] values, string name)
Tensor<T> constant<T>(T[,,] values, string name)
Tensor<T> constant<T>(T[,] values, string name)
Tensor<T> constant<T>(T[,,,,,] values, string name)
Tensor<T> constant<T>(T[,,,] values, string name)
IEnumerator<object> container(string container_name)
Returns a context manager that specifies the resource container to use. Stateful operations, such as variables and queues, can maintain their
states on devices so that they can be shared by multiple processes.
A resource container is a string name under which these stateful
operations are tracked. These resources can be released or cleared
with `tf.Session.reset()`.
Parameters
-
stringcontainer_name - container name string.
Returns
-
IEnumerator<object> - A context manager for defining resource containers for stateful ops, yields the container name.
Show Example
with g.container('experiment0'):
# All stateful Operations constructed in this context will be placed
# in resource container "experiment0".
v1 = tf.Variable([1.0])
v2 = tf.Variable([2.0])
with g.container("experiment1"):
# All stateful Operations constructed in this context will be
# placed in resource container "experiment1".
v3 = tf.Variable([3.0])
q1 = tf.queue.FIFOQueue(10, tf.float32)
# All stateful Operations constructed in this context will be
# be created in the "experiment0".
v4 = tf.Variable([4.0])
q1 = tf.queue.FIFOQueue(20, tf.float32)
with g.container(""):
# All stateful Operations constructed in this context will be
# be placed in the default resource container.
v5 = tf.Variable([5.0])
q3 = tf.queue.FIFOQueue(30, tf.float32) # Resets container "experiment0", after which the state of v1, v2, v4, q1
# will become undefined (such as uninitialized).
tf.Session.reset(target, ["experiment0"])
object container_dyn(object container_name)
Returns a context manager that specifies the resource container to use. Stateful operations, such as variables and queues, can maintain their
states on devices so that they can be shared by multiple processes.
A resource container is a string name under which these stateful
operations are tracked. These resources can be released or cleared
with `tf.Session.reset()`.
Parameters
-
objectcontainer_name - container name string.
Returns
-
object - A context manager for defining resource containers for stateful ops, yields the container name.
Show Example
with g.container('experiment0'):
# All stateful Operations constructed in this context will be placed
# in resource container "experiment0".
v1 = tf.Variable([1.0])
v2 = tf.Variable([2.0])
with g.container("experiment1"):
# All stateful Operations constructed in this context will be
# placed in resource container "experiment1".
v3 = tf.Variable([3.0])
q1 = tf.queue.FIFOQueue(10, tf.float32)
# All stateful Operations constructed in this context will be
# be created in the "experiment0".
v4 = tf.Variable([4.0])
q1 = tf.queue.FIFOQueue(20, tf.float32)
with g.container(""):
# All stateful Operations constructed in this context will be
# be placed in the default resource container.
v5 = tf.Variable([5.0])
q3 = tf.queue.FIFOQueue(30, tf.float32) # Resets container "experiment0", after which the state of v1, v2, v4, q1
# will become undefined (such as uninitialized).
tf.Session.reset(target, ["experiment0"])
object control_dependencies(IEnumerable<object> control_inputs)
Returns a context manager that specifies control dependencies. Use with the `with` keyword to specify that all operations constructed
within the context should have control dependencies on
`control_inputs`.
Multiple calls to `control_dependencies()` can be nested, and in
that case a new `Operation` will have control dependencies on the union
of `control_inputs` from all active contexts.
You can pass None to clear the control dependencies:
*N.B.* The control dependencies context applies *only* to ops that
are constructed within the context. Merely using an op or tensor
in the context does not add a control dependency. The following
example illustrates this point:
Also note that though execution of ops created under this scope will trigger
execution of the dependencies, the ops created under this scope might still
be pruned from a normal tensorflow graph. For example, in the following
snippet of code the dependencies are never executed:
This is because evaluating the gradient graph does not require evaluating
the constant(1) op created in the forward pass.
Parameters
-
IEnumerable<object>control_inputs - A list of `Operation` or `Tensor` objects which must be executed or computed before running the operations defined in the context. Can also be `None` to clear the control dependencies.
Returns
-
object - A context manager that specifies control dependencies for all operations constructed within the context.
Show Example
with g.control_dependencies([a, b, c]):
# `d` and `e` will only run after `a`, `b`, and `c` have executed.
d =...
e =...
object control_dependencies(object control_inputs)
Returns a context manager that specifies control dependencies. Use with the `with` keyword to specify that all operations constructed
within the context should have control dependencies on
`control_inputs`.
Multiple calls to `control_dependencies()` can be nested, and in
that case a new `Operation` will have control dependencies on the union
of `control_inputs` from all active contexts.
You can pass None to clear the control dependencies:
*N.B.* The control dependencies context applies *only* to ops that
are constructed within the context. Merely using an op or tensor
in the context does not add a control dependency. The following
example illustrates this point:
Also note that though execution of ops created under this scope will trigger
execution of the dependencies, the ops created under this scope might still
be pruned from a normal tensorflow graph. For example, in the following
snippet of code the dependencies are never executed:
This is because evaluating the gradient graph does not require evaluating
the constant(1) op created in the forward pass.
Parameters
-
objectcontrol_inputs - A list of `Operation` or `Tensor` objects which must be executed or computed before running the operations defined in the context. Can also be `None` to clear the control dependencies.
Returns
-
object - A context manager that specifies control dependencies for all operations constructed within the context.
Show Example
with g.control_dependencies([a, b, c]):
# `d` and `e` will only run after `a`, `b`, and `c` have executed.
d =...
e =...
object control_dependencies_dyn(object control_inputs)
Returns a context manager that specifies control dependencies. Use with the `with` keyword to specify that all operations constructed
within the context should have control dependencies on
`control_inputs`.
Multiple calls to `control_dependencies()` can be nested, and in
that case a new `Operation` will have control dependencies on the union
of `control_inputs` from all active contexts.
You can pass None to clear the control dependencies:
*N.B.* The control dependencies context applies *only* to ops that
are constructed within the context. Merely using an op or tensor
in the context does not add a control dependency. The following
example illustrates this point:
Also note that though execution of ops created under this scope will trigger
execution of the dependencies, the ops created under this scope might still
be pruned from a normal tensorflow graph. For example, in the following
snippet of code the dependencies are never executed:
This is because evaluating the gradient graph does not require evaluating
the constant(1) op created in the forward pass.
Parameters
-
objectcontrol_inputs - A list of `Operation` or `Tensor` objects which must be executed or computed before running the operations defined in the context. Can also be `None` to clear the control dependencies.
Returns
-
object - A context manager that specifies control dependencies for all operations constructed within the context.
Show Example
with g.control_dependencies([a, b, c]):
# `d` and `e` will only run after `a`, `b`, and `c` have executed.
d =...
e =...
bool control_flow_v2_enabled()
Returns `True` if v2 control flow is enabled. Note: v2 control flow is always enabled inside of tf.function.
object control_flow_v2_enabled_dyn()
Returns `True` if v2 control flow is enabled. Note: v2 control flow is always enabled inside of tf.function.
Tensor convert_to_tensor(object value, DType dtype, string name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
objectvalue - An object whose type has a registered `Tensor` conversion function.
-
DTypedtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
stringname - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(object value, PythonFunctionContainer dtype, string name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
objectvalue - An object whose type has a registered `Tensor` conversion function.
-
PythonFunctionContainerdtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
stringname - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(IEnumerable<object> value, DType dtype, string name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
IEnumerable<object>value - An object whose type has a registered `Tensor` conversion function.
-
DTypedtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
stringname - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(IEnumerable<object> value, DType dtype, PythonFunctionContainer name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
IEnumerable<object>value - An object whose type has a registered `Tensor` conversion function.
-
DTypedtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
PythonFunctionContainername - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(PythonFunctionContainer value, PythonFunctionContainer dtype, string name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
PythonFunctionContainervalue - An object whose type has a registered `Tensor` conversion function.
-
PythonFunctionContainerdtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
stringname - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(object value, PythonFunctionContainer dtype, PythonFunctionContainer name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
objectvalue - An object whose type has a registered `Tensor` conversion function.
-
PythonFunctionContainerdtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
PythonFunctionContainername - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(IEnumerator<IGraphNodeBase> value, DType dtype, string name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
IEnumerator<IGraphNodeBase>value - An object whose type has a registered `Tensor` conversion function.
-
DTypedtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
stringname - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(object value, DType dtype, PythonFunctionContainer name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
objectvalue - An object whose type has a registered `Tensor` conversion function.
-
DTypedtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
PythonFunctionContainername - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(IEnumerator<IGraphNodeBase> value, DType dtype, PythonFunctionContainer name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
IEnumerator<IGraphNodeBase>value - An object whose type has a registered `Tensor` conversion function.
-
DTypedtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
PythonFunctionContainername - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(IEnumerator<IGraphNodeBase> value, PythonFunctionContainer dtype, string name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
IEnumerator<IGraphNodeBase>value - An object whose type has a registered `Tensor` conversion function.
-
PythonFunctionContainerdtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
stringname - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(PythonFunctionContainer value, PythonFunctionContainer dtype, PythonFunctionContainer name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
PythonFunctionContainervalue - An object whose type has a registered `Tensor` conversion function.
-
PythonFunctionContainerdtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
PythonFunctionContainername - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(IEnumerable<object> value, PythonFunctionContainer dtype, PythonFunctionContainer name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
IEnumerable<object>value - An object whose type has a registered `Tensor` conversion function.
-
PythonFunctionContainerdtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
PythonFunctionContainername - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(PythonFunctionContainer value, DType dtype, PythonFunctionContainer name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
PythonFunctionContainervalue - An object whose type has a registered `Tensor` conversion function.
-
DTypedtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
PythonFunctionContainername - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(IEnumerable<IGraphNodeBase> value, PythonFunctionContainer dtype, string name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
IEnumerable<IGraphNodeBase>value - An object whose type has a registered `Tensor` conversion function.
-
PythonFunctionContainerdtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
stringname - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(IEnumerator<IGraphNodeBase> value, PythonFunctionContainer dtype, PythonFunctionContainer name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
IEnumerator<IGraphNodeBase>value - An object whose type has a registered `Tensor` conversion function.
-
PythonFunctionContainerdtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
PythonFunctionContainername - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
Tensor convert_to_tensor(PythonFunctionContainer value, DType dtype, string name, object preferred_dtype, DType dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
PythonFunctionContainervalue - An object whose type has a registered `Tensor` conversion function.
-
DTypedtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
stringname - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
DTypedtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
Tensor - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
object convert_to_tensor_dyn(object value, object dtype, object name, object preferred_dtype, object dtype_hint)
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Parameters
-
objectvalue - An object whose type has a registered `Tensor` conversion function.
-
objectdtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
objectname - Optional name to use if a new `Tensor` is created.
-
objectpreferred_dtype - Optional element type for the returned tensor, used when dtype is None. In some cases, a caller may not have a dtype in mind when converting to a tensor, so preferred_dtype can be used as a soft preference. If the conversion to `preferred_dtype` is not possible, this argument has no effect.
-
objectdtype_hint - same meaning as preferred_dtype, and overrides it.
Returns
-
object - A `Tensor` based on `value`.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
_TensorLike convert_to_tensor_or_indexed_slices(IGraphNodeBase value, DType dtype, string name)
Converts the given object to a `Tensor` or an `IndexedSlices`. If `value` is an `IndexedSlices` or `SparseTensor` it is returned
unmodified. Otherwise, it is converted to a `Tensor` using
`convert_to_tensor()`.
Parameters
-
IGraphNodeBasevalue - An `IndexedSlices`, `SparseTensor`, or an object that can be consumed by `convert_to_tensor()`.
-
DTypedtype - (Optional.) The required `DType` of the returned `Tensor` or `IndexedSlices`.
-
stringname - (Optional.) A name to use if a new `Tensor` is created.
Returns
-
_TensorLike - A `Tensor`, `IndexedSlices`, or `SparseTensor` based on `value`.
object convert_to_tensor_or_indexed_slices_dyn(object value, object dtype, object name)
Converts the given object to a `Tensor` or an `IndexedSlices`. If `value` is an `IndexedSlices` or `SparseTensor` it is returned
unmodified. Otherwise, it is converted to a `Tensor` using
`convert_to_tensor()`.
Parameters
-
objectvalue - An `IndexedSlices`, `SparseTensor`, or an object that can be consumed by `convert_to_tensor()`.
-
objectdtype - (Optional.) The required `DType` of the returned `Tensor` or `IndexedSlices`.
-
objectname - (Optional.) A name to use if a new `Tensor` is created.
Returns
-
object - A `Tensor`, `IndexedSlices`, or `SparseTensor` based on `value`.
object convert_to_tensor_or_sparse_tensor(object value, DType dtype, string name)
Converts value to a `SparseTensor` or `Tensor`.
Parameters
-
objectvalue - A `SparseTensor`, `SparseTensorValue`, or an object whose type has a registered `Tensor` conversion function.
-
DTypedtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
stringname - Optional name to use if a new `Tensor` is created.
Returns
-
object - A `SparseTensor` or `Tensor` based on `value`.
object convert_to_tensor_or_sparse_tensor(PythonClassContainer value, DType dtype, string name)
Converts value to a `SparseTensor` or `Tensor`.
Parameters
-
PythonClassContainervalue - A `SparseTensor`, `SparseTensorValue`, or an object whose type has a registered `Tensor` conversion function.
-
DTypedtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
stringname - Optional name to use if a new `Tensor` is created.
Returns
-
object - A `SparseTensor` or `Tensor` based on `value`.
object convert_to_tensor_or_sparse_tensor_dyn(object value, object dtype, object name)
Converts value to a `SparseTensor` or `Tensor`.
Parameters
-
objectvalue - A `SparseTensor`, `SparseTensorValue`, or an object whose type has a registered `Tensor` conversion function.
-
objectdtype - Optional element type for the returned tensor. If missing, the type is inferred from the type of `value`.
-
objectname - Optional name to use if a new `Tensor` is created.
Returns
-
object - A `SparseTensor` or `Tensor` based on `value`.
Tensor copy_op(IGraphNodeBase a, string name)
object copy_op_dyn(object a, object name)
Tensor cos(IGraphNodeBase x, string name)
Computes cos of x element-wise. Given an input tensor, this function computes cosine of every
element in the tensor. Input range is `(-inf, inf)` and
output range is `[-1,1]`. If input lies outside the boundary, `nan`
is returned.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.cos(x) ==> [nan -0.91113025 0.87758255 0.5403023 0.36235774 0.48718765 -0.95215535 nan]
object cos_dyn(object x, object name)
Computes cos of x element-wise. Given an input tensor, this function computes cosine of every
element in the tensor. Input range is `(-inf, inf)` and
output range is `[-1,1]`. If input lies outside the boundary, `nan`
is returned.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.cos(x) ==> [nan -0.91113025 0.87758255 0.5403023 0.36235774 0.48718765 -0.95215535 nan]
Tensor cosh(IGraphNodeBase x, string name)
Computes hyperbolic cosine of x element-wise. Given an input tensor, this function computes hyperbolic cosine of every
element in the tensor. Input range is `[-inf, inf]` and output range
is `[1, inf]`.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 2, 10, float("inf")])
tf.math.cosh(x) ==> [inf 4.0515420e+03 1.1276259e+00 1.5430807e+00 1.8106556e+00 3.7621956e+00 1.1013233e+04 inf]
object cosh_dyn(object x, object name)
Computes hyperbolic cosine of x element-wise. Given an input tensor, this function computes hyperbolic cosine of every
element in the tensor. Input range is `[-inf, inf]` and output range
is `[1, inf]`.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 2, 10, float("inf")])
tf.math.cosh(x) ==> [inf 4.0515420e+03 1.1276259e+00 1.5430807e+00 1.8106556e+00 3.7621956e+00 1.1013233e+04 inf]
object count_nonzero(IEnumerable<IGraphNodeBase> input_tensor, int axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
IEnumerable<IGraphNodeBase>input_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(IGraphNodeBase input_tensor, int axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(IGraphNodeBase input_tensor, IEnumerable<object> axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
IEnumerable<object>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(object input_tensor, int axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
objectinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(RaggedTensor input_tensor, int axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
RaggedTensorinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(RaggedTensor input_tensor, IEnumerable<object> axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
RaggedTensorinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
IEnumerable<object>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(IEnumerable<IGraphNodeBase> input_tensor, IEnumerable<object> axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
IEnumerable<IGraphNodeBase>input_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
IEnumerable<object>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(DType input_tensor, IEnumerable<object> axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
DTypeinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
IEnumerable<object>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(ndarray input_tensor, int axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
ndarrayinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(DType input_tensor, int axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
DTypeinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(ndarray input_tensor, IEnumerable<object> axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
ndarrayinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
IEnumerable<object>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero(object input_tensor, IEnumerable<object> axis, Nullable<bool> keepdims, ImplicitContainer<T> dtype, string name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
objectinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
IEnumerable<object>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
stringname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
object count_nonzero_dyn(object input_tensor, object axis, object keepdims, ImplicitContainer<T> dtype, object name, object reduction_indices, object keep_dims, object input)
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Parameters
-
objectinput_tensor - The tensor to reduce. Should be of numeric type, `bool`, or `string`.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
ImplicitContainer<T>dtype - The output dtype; defaults to
tf.int64. -
objectname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
-
objectinput - Overrides input_tensor. For compatibility.
Returns
-
object - The reduced tensor (number of nonzero values).
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
Tensor count_up_to(ResourceVariable ref, Nullable<int> limit, string name)
Increments 'ref' until it reaches 'limit'. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Prefer Dataset.range instead.
Parameters
-
ResourceVariableref - A Variable. Must be one of the following types: `int32`, `int64`. Should be from a scalar `Variable` node.
-
Nullable<int>limit - An `int`. If incrementing ref would bring it above limit, instead generates an 'OutOfRange' error.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `ref`. A copy of the input before increment. If nothing else modifies the input, the values produced will all be distinct.
Tensor count_up_to(Operation ref, Nullable<int> limit, string name)
Increments 'ref' until it reaches 'limit'. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Prefer Dataset.range instead.
Parameters
-
Operationref - A Variable. Must be one of the following types: `int32`, `int64`. Should be from a scalar `Variable` node.
-
Nullable<int>limit - An `int`. If incrementing ref would bring it above limit, instead generates an 'OutOfRange' error.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `ref`. A copy of the input before increment. If nothing else modifies the input, the values produced will all be distinct.
Tensor count_up_to(IGraphNodeBase ref, Nullable<int> limit, string name)
Increments 'ref' until it reaches 'limit'. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Prefer Dataset.range instead.
Parameters
-
IGraphNodeBaseref - A Variable. Must be one of the following types: `int32`, `int64`. Should be from a scalar `Variable` node.
-
Nullable<int>limit - An `int`. If incrementing ref would bring it above limit, instead generates an 'OutOfRange' error.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `ref`. A copy of the input before increment. If nothing else modifies the input, the values produced will all be distinct.
object count_up_to_dyn(object ref, object limit, object name)
Increments 'ref' until it reaches 'limit'. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Prefer Dataset.range instead.
Parameters
-
objectref - A Variable. Must be one of the following types: `int32`, `int64`. Should be from a scalar `Variable` node.
-
objectlimit - An `int`. If incrementing ref would bring it above limit, instead generates an 'OutOfRange' error.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `ref`. A copy of the input before increment. If nothing else modifies the input, the values produced will all be distinct.
object create_fertile_stats_variable(IGraphNodeBase stats_handle, IGraphNodeBase stats_config, object params, string name)
object create_fertile_stats_variable_dyn(object stats_handle, object stats_config, object params, object name)
IList<object> create_partitioned_variables(IEnumerable<int> shape, IEnumerable<int> slicing, random_uniform_initializer initializer, ImplicitContainer<T> dtype, bool trainable, object collections, string name, object reuse)
Create a list of partitioned variables according to the given `slicing`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.get_variable with a partitioner set. Currently only one dimension of the full variable can be sliced, and the
full variable can be reconstructed by the concatenation of the returned
list along that dimension.
Parameters
-
IEnumerable<int>shape - List of integers. The shape of the full variable.
-
IEnumerable<int>slicing - List of integers. How to partition the variable. Must be of the same length as `shape`. Each value indicate how many slices to create in the corresponding dimension. Presently only one of the values can be more than 1; that is, the variable can only be sliced along one dimension. For convenience, The requested number of partitions does not have to divide the corresponding dimension evenly. If it does not, the shapes of the partitions are incremented by 1 starting from partition 0 until all slack is absorbed. The adjustment rules may change in the future, but as you can save/restore these variables with different slicing specifications this should not be a problem.
-
random_uniform_initializerinitializer - A `Tensor` of shape `shape` or a variable initializer function. If a function, it will be called once for each slice, passing the shape and data type of the slice as parameters. The function must return a tensor with the same shape as the slice.
-
ImplicitContainer<T>dtype - Type of the variables. Ignored if `initializer` is a `Tensor`.
-
booltrainable - If True also add all the variables to the graph collection `GraphKeys.TRAINABLE_VARIABLES`.
-
objectcollections - List of graph collections keys to add the variables to. Defaults to `[GraphKeys.GLOBAL_VARIABLES]`.
-
stringname - Optional name for the full variable. Defaults to `"PartitionedVariable"` and gets uniquified automatically.
-
objectreuse - Boolean or `None`; if `True` and name is set, it would reuse previously created variables. if `False` it will create new variables. if `None`, it would inherit the parent scope reuse.
Returns
-
IList<object> - A list of Variables corresponding to the slicing.
IList<object> create_partitioned_variables(IEnumerable<int> shape, IEnumerable<int> slicing, object initializer, ImplicitContainer<T> dtype, bool trainable, object collections, string name, object reuse)
Create a list of partitioned variables according to the given `slicing`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.get_variable with a partitioner set. Currently only one dimension of the full variable can be sliced, and the
full variable can be reconstructed by the concatenation of the returned
list along that dimension.
Parameters
-
IEnumerable<int>shape - List of integers. The shape of the full variable.
-
IEnumerable<int>slicing - List of integers. How to partition the variable. Must be of the same length as `shape`. Each value indicate how many slices to create in the corresponding dimension. Presently only one of the values can be more than 1; that is, the variable can only be sliced along one dimension. For convenience, The requested number of partitions does not have to divide the corresponding dimension evenly. If it does not, the shapes of the partitions are incremented by 1 starting from partition 0 until all slack is absorbed. The adjustment rules may change in the future, but as you can save/restore these variables with different slicing specifications this should not be a problem.
-
objectinitializer - A `Tensor` of shape `shape` or a variable initializer function. If a function, it will be called once for each slice, passing the shape and data type of the slice as parameters. The function must return a tensor with the same shape as the slice.
-
ImplicitContainer<T>dtype - Type of the variables. Ignored if `initializer` is a `Tensor`.
-
booltrainable - If True also add all the variables to the graph collection `GraphKeys.TRAINABLE_VARIABLES`.
-
objectcollections - List of graph collections keys to add the variables to. Defaults to `[GraphKeys.GLOBAL_VARIABLES]`.
-
stringname - Optional name for the full variable. Defaults to `"PartitionedVariable"` and gets uniquified automatically.
-
objectreuse - Boolean or `None`; if `True` and name is set, it would reuse previously created variables. if `False` it will create new variables. if `None`, it would inherit the parent scope reuse.
Returns
-
IList<object> - A list of Variables corresponding to the slicing.
IList<object> create_partitioned_variables(IEnumerable<int> shape, IEnumerable<int> slicing, IGraphNodeBase initializer, ImplicitContainer<T> dtype, bool trainable, object collections, string name, object reuse)
Create a list of partitioned variables according to the given `slicing`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.get_variable with a partitioner set. Currently only one dimension of the full variable can be sliced, and the
full variable can be reconstructed by the concatenation of the returned
list along that dimension.
Parameters
-
IEnumerable<int>shape - List of integers. The shape of the full variable.
-
IEnumerable<int>slicing - List of integers. How to partition the variable. Must be of the same length as `shape`. Each value indicate how many slices to create in the corresponding dimension. Presently only one of the values can be more than 1; that is, the variable can only be sliced along one dimension. For convenience, The requested number of partitions does not have to divide the corresponding dimension evenly. If it does not, the shapes of the partitions are incremented by 1 starting from partition 0 until all slack is absorbed. The adjustment rules may change in the future, but as you can save/restore these variables with different slicing specifications this should not be a problem.
-
IGraphNodeBaseinitializer - A `Tensor` of shape `shape` or a variable initializer function. If a function, it will be called once for each slice, passing the shape and data type of the slice as parameters. The function must return a tensor with the same shape as the slice.
-
ImplicitContainer<T>dtype - Type of the variables. Ignored if `initializer` is a `Tensor`.
-
booltrainable - If True also add all the variables to the graph collection `GraphKeys.TRAINABLE_VARIABLES`.
-
objectcollections - List of graph collections keys to add the variables to. Defaults to `[GraphKeys.GLOBAL_VARIABLES]`.
-
stringname - Optional name for the full variable. Defaults to `"PartitionedVariable"` and gets uniquified automatically.
-
objectreuse - Boolean or `None`; if `True` and name is set, it would reuse previously created variables. if `False` it will create new variables. if `None`, it would inherit the parent scope reuse.
Returns
-
IList<object> - A list of Variables corresponding to the slicing.
IList<object> create_partitioned_variables(TensorShape shape, IEnumerable<int> slicing, random_uniform_initializer initializer, ImplicitContainer<T> dtype, bool trainable, object collections, string name, object reuse)
Create a list of partitioned variables according to the given `slicing`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.get_variable with a partitioner set. Currently only one dimension of the full variable can be sliced, and the
full variable can be reconstructed by the concatenation of the returned
list along that dimension.
Parameters
-
TensorShapeshape - List of integers. The shape of the full variable.
-
IEnumerable<int>slicing - List of integers. How to partition the variable. Must be of the same length as `shape`. Each value indicate how many slices to create in the corresponding dimension. Presently only one of the values can be more than 1; that is, the variable can only be sliced along one dimension. For convenience, The requested number of partitions does not have to divide the corresponding dimension evenly. If it does not, the shapes of the partitions are incremented by 1 starting from partition 0 until all slack is absorbed. The adjustment rules may change in the future, but as you can save/restore these variables with different slicing specifications this should not be a problem.
-
random_uniform_initializerinitializer - A `Tensor` of shape `shape` or a variable initializer function. If a function, it will be called once for each slice, passing the shape and data type of the slice as parameters. The function must return a tensor with the same shape as the slice.
-
ImplicitContainer<T>dtype - Type of the variables. Ignored if `initializer` is a `Tensor`.
-
booltrainable - If True also add all the variables to the graph collection `GraphKeys.TRAINABLE_VARIABLES`.
-
objectcollections - List of graph collections keys to add the variables to. Defaults to `[GraphKeys.GLOBAL_VARIABLES]`.
-
stringname - Optional name for the full variable. Defaults to `"PartitionedVariable"` and gets uniquified automatically.
-
objectreuse - Boolean or `None`; if `True` and name is set, it would reuse previously created variables. if `False` it will create new variables. if `None`, it would inherit the parent scope reuse.
Returns
-
IList<object> - A list of Variables corresponding to the slicing.
IList<object> create_partitioned_variables(TensorShape shape, IEnumerable<int> slicing, IGraphNodeBase initializer, ImplicitContainer<T> dtype, bool trainable, object collections, string name, object reuse)
Create a list of partitioned variables according to the given `slicing`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.get_variable with a partitioner set. Currently only one dimension of the full variable can be sliced, and the
full variable can be reconstructed by the concatenation of the returned
list along that dimension.
Parameters
-
TensorShapeshape - List of integers. The shape of the full variable.
-
IEnumerable<int>slicing - List of integers. How to partition the variable. Must be of the same length as `shape`. Each value indicate how many slices to create in the corresponding dimension. Presently only one of the values can be more than 1; that is, the variable can only be sliced along one dimension. For convenience, The requested number of partitions does not have to divide the corresponding dimension evenly. If it does not, the shapes of the partitions are incremented by 1 starting from partition 0 until all slack is absorbed. The adjustment rules may change in the future, but as you can save/restore these variables with different slicing specifications this should not be a problem.
-
IGraphNodeBaseinitializer - A `Tensor` of shape `shape` or a variable initializer function. If a function, it will be called once for each slice, passing the shape and data type of the slice as parameters. The function must return a tensor with the same shape as the slice.
-
ImplicitContainer<T>dtype - Type of the variables. Ignored if `initializer` is a `Tensor`.
-
booltrainable - If True also add all the variables to the graph collection `GraphKeys.TRAINABLE_VARIABLES`.
-
objectcollections - List of graph collections keys to add the variables to. Defaults to `[GraphKeys.GLOBAL_VARIABLES]`.
-
stringname - Optional name for the full variable. Defaults to `"PartitionedVariable"` and gets uniquified automatically.
-
objectreuse - Boolean or `None`; if `True` and name is set, it would reuse previously created variables. if `False` it will create new variables. if `None`, it would inherit the parent scope reuse.
Returns
-
IList<object> - A list of Variables corresponding to the slicing.
IList<object> create_partitioned_variables(TensorShape shape, IEnumerable<int> slicing, object initializer, ImplicitContainer<T> dtype, bool trainable, object collections, string name, object reuse)
Create a list of partitioned variables according to the given `slicing`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.get_variable with a partitioner set. Currently only one dimension of the full variable can be sliced, and the
full variable can be reconstructed by the concatenation of the returned
list along that dimension.
Parameters
-
TensorShapeshape - List of integers. The shape of the full variable.
-
IEnumerable<int>slicing - List of integers. How to partition the variable. Must be of the same length as `shape`. Each value indicate how many slices to create in the corresponding dimension. Presently only one of the values can be more than 1; that is, the variable can only be sliced along one dimension. For convenience, The requested number of partitions does not have to divide the corresponding dimension evenly. If it does not, the shapes of the partitions are incremented by 1 starting from partition 0 until all slack is absorbed. The adjustment rules may change in the future, but as you can save/restore these variables with different slicing specifications this should not be a problem.
-
objectinitializer - A `Tensor` of shape `shape` or a variable initializer function. If a function, it will be called once for each slice, passing the shape and data type of the slice as parameters. The function must return a tensor with the same shape as the slice.
-
ImplicitContainer<T>dtype - Type of the variables. Ignored if `initializer` is a `Tensor`.
-
booltrainable - If True also add all the variables to the graph collection `GraphKeys.TRAINABLE_VARIABLES`.
-
objectcollections - List of graph collections keys to add the variables to. Defaults to `[GraphKeys.GLOBAL_VARIABLES]`.
-
stringname - Optional name for the full variable. Defaults to `"PartitionedVariable"` and gets uniquified automatically.
-
objectreuse - Boolean or `None`; if `True` and name is set, it would reuse previously created variables. if `False` it will create new variables. if `None`, it would inherit the parent scope reuse.
Returns
-
IList<object> - A list of Variables corresponding to the slicing.
object create_partitioned_variables_dyn(object shape, object slicing, object initializer, ImplicitContainer<T> dtype, ImplicitContainer<T> trainable, object collections, object name, object reuse)
Create a list of partitioned variables according to the given `slicing`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.get_variable with a partitioner set. Currently only one dimension of the full variable can be sliced, and the
full variable can be reconstructed by the concatenation of the returned
list along that dimension.
Parameters
-
objectshape - List of integers. The shape of the full variable.
-
objectslicing - List of integers. How to partition the variable. Must be of the same length as `shape`. Each value indicate how many slices to create in the corresponding dimension. Presently only one of the values can be more than 1; that is, the variable can only be sliced along one dimension. For convenience, The requested number of partitions does not have to divide the corresponding dimension evenly. If it does not, the shapes of the partitions are incremented by 1 starting from partition 0 until all slack is absorbed. The adjustment rules may change in the future, but as you can save/restore these variables with different slicing specifications this should not be a problem.
-
objectinitializer - A `Tensor` of shape `shape` or a variable initializer function. If a function, it will be called once for each slice, passing the shape and data type of the slice as parameters. The function must return a tensor with the same shape as the slice.
-
ImplicitContainer<T>dtype - Type of the variables. Ignored if `initializer` is a `Tensor`.
-
ImplicitContainer<T>trainable - If True also add all the variables to the graph collection `GraphKeys.TRAINABLE_VARIABLES`.
-
objectcollections - List of graph collections keys to add the variables to. Defaults to `[GraphKeys.GLOBAL_VARIABLES]`.
-
objectname - Optional name for the full variable. Defaults to `"PartitionedVariable"` and gets uniquified automatically.
-
objectreuse - Boolean or `None`; if `True` and name is set, it would reuse previously created variables. if `False` it will create new variables. if `None`, it would inherit the parent scope reuse.
Returns
-
object - A list of Variables corresponding to the slicing.
object create_quantile_accumulator(IGraphNodeBase quantile_accumulator_handle, IGraphNodeBase stamp_token, double epsilon, bool num_quantiles, string container, string shared_name, ImplicitContainer<T> max_elements, bool generate_quantiles, string name)
object create_quantile_accumulator(IGraphNodeBase quantile_accumulator_handle, IGraphNodeBase stamp_token, double epsilon, Nullable<int> num_quantiles, string container, string shared_name, ImplicitContainer<T> max_elements, bool generate_quantiles, string name)
object create_quantile_accumulator_dyn(object quantile_accumulator_handle, object stamp_token, object epsilon, object num_quantiles, ImplicitContainer<T> container, ImplicitContainer<T> shared_name, ImplicitContainer<T> max_elements, ImplicitContainer<T> generate_quantiles, object name)
object create_stats_accumulator_scalar(IGraphNodeBase stats_accumulator_handle, IGraphNodeBase stamp_token, string name)
object create_stats_accumulator_scalar_dyn(object stats_accumulator_handle, object stamp_token, object name)
object create_stats_accumulator_tensor(IGraphNodeBase stats_accumulator_handle, IGraphNodeBase stamp_token, IGraphNodeBase per_slot_gradient_shape, IGraphNodeBase per_slot_hessian_shape, string name)
object create_stats_accumulator_tensor_dyn(object stats_accumulator_handle, object stamp_token, object per_slot_gradient_shape, object per_slot_hessian_shape, object name)
object create_tree_ensemble_variable(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase stamp_token, IGraphNodeBase tree_ensemble_config, string name)
object create_tree_ensemble_variable_dyn(object tree_ensemble_handle, object stamp_token, object tree_ensemble_config, object name)
object create_tree_variable(IGraphNodeBase tree_handle, IGraphNodeBase tree_config, object params, string name)
object create_tree_variable_dyn(object tree_handle, object tree_config, object params, object name)
Tensor cross(IGraphNodeBase a, IGraphNodeBase b, string name)
Compute the pairwise cross product. `a` and `b` must be the same shape; they can either be simple 3-element vectors,
or any shape where the innermost dimension is 3. In the latter case, each pair
of corresponding 3-element vectors is cross-multiplied independently.
Parameters
-
IGraphNodeBasea - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. A tensor containing 3-element vectors.
-
IGraphNodeBaseb - A `Tensor`. Must have the same type as `a`. Another tensor, of same type and shape as `a`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `a`.
object cross_dyn(object a, object b, object name)
Compute the pairwise cross product. `a` and `b` must be the same shape; they can either be simple 3-element vectors,
or any shape where the innermost dimension is 3. In the latter case, each pair
of corresponding 3-element vectors is cross-multiplied independently.
Parameters
-
objecta - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. A tensor containing 3-element vectors.
-
objectb - A `Tensor`. Must have the same type as `a`. Another tensor, of same type and shape as `a`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `a`.
Tensor cumprod(IGraphNodeBase x, ImplicitContainer<T> axis, bool exclusive, bool reverse, string name)
Compute the cumulative product of the tensor `x` along `axis`. By default, this op performs an inclusive cumprod, which means that the
first element of the input is identical to the first element of the output:
By setting the `exclusive` kwarg to `True`, an exclusive cumprod is
performed
instead:
By setting the `reverse` kwarg to `True`, the cumprod is performed in the
opposite direction:
This is more efficient than using separate
tf.reverse ops.
The `reverse` and `exclusive` kwargs can also be combined:
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`.
-
ImplicitContainer<T>axis - A `Tensor` of type `int32` (default: 0). Must be in the range `[-rank(x), rank(x))`.
-
boolexclusive - If `True`, perform exclusive cumprod.
-
boolreverse - A `bool` (default: False).
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Show Example
tf.math.cumprod([a, b, c]) # [a, a * b, a * b * c]
object cumprod_dyn(object x, ImplicitContainer<T> axis, ImplicitContainer<T> exclusive, ImplicitContainer<T> reverse, object name)
Compute the cumulative product of the tensor `x` along `axis`. By default, this op performs an inclusive cumprod, which means that the
first element of the input is identical to the first element of the output:
By setting the `exclusive` kwarg to `True`, an exclusive cumprod is
performed
instead:
By setting the `reverse` kwarg to `True`, the cumprod is performed in the
opposite direction:
This is more efficient than using separate
tf.reverse ops.
The `reverse` and `exclusive` kwargs can also be combined:
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`.
-
ImplicitContainer<T>axis - A `Tensor` of type `int32` (default: 0). Must be in the range `[-rank(x), rank(x))`.
-
ImplicitContainer<T>exclusive - If `True`, perform exclusive cumprod.
-
ImplicitContainer<T>reverse - A `bool` (default: False).
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
tf.math.cumprod([a, b, c]) # [a, a * b, a * b * c]
Tensor cumsum(IGraphNodeBase x, ImplicitContainer<T> axis, bool exclusive, bool reverse, string name)
Compute the cumulative sum of the tensor `x` along `axis`. By default, this op performs an inclusive cumsum, which means that the first
element of the input is identical to the first element of the output:
By setting the `exclusive` kwarg to `True`, an exclusive cumsum is performed
instead:
By setting the `reverse` kwarg to `True`, the cumsum is performed in the
opposite direction:
This is more efficient than using separate
tf.reverse ops. The `reverse` and `exclusive` kwargs can also be combined:
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`.
-
ImplicitContainer<T>axis - A `Tensor` of type `int32` (default: 0). Must be in the range `[-rank(x), rank(x))`.
-
boolexclusive - If `True`, perform exclusive cumsum.
-
boolreverse - A `bool` (default: False).
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Show Example
tf.cumsum([a, b, c]) # [a, a + b, a + b + c]
object cumsum_dyn(object x, ImplicitContainer<T> axis, ImplicitContainer<T> exclusive, ImplicitContainer<T> reverse, object name)
Compute the cumulative sum of the tensor `x` along `axis`. By default, this op performs an inclusive cumsum, which means that the first
element of the input is identical to the first element of the output:
By setting the `exclusive` kwarg to `True`, an exclusive cumsum is performed
instead:
By setting the `reverse` kwarg to `True`, the cumsum is performed in the
opposite direction:
This is more efficient than using separate
tf.reverse ops. The `reverse` and `exclusive` kwargs can also be combined:
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int64`, `int32`, `uint8`, `uint16`, `int16`, `int8`, `complex64`, `complex128`, `qint8`, `quint8`, `qint32`, `half`.
-
ImplicitContainer<T>axis - A `Tensor` of type `int32` (default: 0). Must be in the range `[-rank(x), rank(x))`.
-
ImplicitContainer<T>exclusive - If `True`, perform exclusive cumsum.
-
ImplicitContainer<T>reverse - A `bool` (default: False).
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
tf.cumsum([a, b, c]) # [a, a + b, a + b + c]
object custom_gradient(PythonFunctionContainer f)
Decorator to define a function with a custom gradient. This decorator allows fine grained control over the gradients of a sequence
for operations. This may be useful for multiple reasons, including providing
a more efficient or numerically stable gradient for a sequence of operations. For example, consider the following function that commonly occurs in the
computation of cross entropy and log likelihoods:
Due to numerical instability, the gradient this function evaluated at x=100 is
NaN.
The gradient expression can be analytically simplified to provide numerical
stability:
With this definition, the gradient at x=100 will be correctly evaluated as
1.0. See also
tf.RegisterGradient which registers a gradient function for a
primitive TensorFlow operation. tf.custom_gradient on the other hand allows
for fine grained control over the gradient computation of a sequence of
operations. Note that if the decorated function uses `Variable`s, the enclosing variable
scope must be using `ResourceVariable`s.
Parameters
-
PythonFunctionContainerf - function `f(*x)` that returns a tuple `(y, grad_fn)` where:
- `x` is a sequence of `Tensor` inputs to the function.
- `y` is a `Tensor` or sequence of `Tensor` outputs of applying
TensorFlow operations in `f` to `x`.
- `grad_fn` is a function with the signature `g(*grad_ys)` which returns
a list of `Tensor`s - the derivatives of `Tensor`s in `y` with respect
to the `Tensor`s in `x`. `grad_ys` is a `Tensor` or sequence of
`Tensor`s the same size as `y` holding the initial value gradients for
each `Tensor` in `y`. In a pure mathematical sense, a vector-argument
vector-valued function `f`'s derivatives should be its Jacobian matrix
`J`. Here we are expressing the Jacobian `J` as a function `grad_fn`
which defines how `J` will transform a vector `grad_ys` when
left-multiplied with it (`grad_ys * J`). This functional representation
of a matrix is convenient to use for chain-rule calculation
(in e.g. the back-propagation algorithm). If `f` uses `Variable`s (that are not part of the
inputs), i.e. through `get_variable`, then `grad_fn` should have
signature `g(*grad_ys, variables=None)`, where `variables` is a list of
the `Variable`s, and return a 2-tuple `(grad_xs, grad_vars)`, where
`grad_xs` is the same as above, and `grad_vars` is a `list
` with the derivatives of `Tensor`s in `y` with respect to the variables (that is, grad_vars has one Tensor per variable in variables).
Returns
-
object - A function `h(x)` which returns the same value as `f(x)[0]` and whose
gradient (as calculated by
tf.gradients) is determined by `f(x)[1]`.
Show Example
def log1pexp(x):
return tf.math.log(1 + tf.exp(x))
object custom_gradient_dyn(object f)
Decorator to define a function with a custom gradient. This decorator allows fine grained control over the gradients of a sequence
for operations. This may be useful for multiple reasons, including providing
a more efficient or numerically stable gradient for a sequence of operations. For example, consider the following function that commonly occurs in the
computation of cross entropy and log likelihoods:
Due to numerical instability, the gradient this function evaluated at x=100 is
NaN.
The gradient expression can be analytically simplified to provide numerical
stability:
With this definition, the gradient at x=100 will be correctly evaluated as
1.0. See also
tf.RegisterGradient which registers a gradient function for a
primitive TensorFlow operation. tf.custom_gradient on the other hand allows
for fine grained control over the gradient computation of a sequence of
operations. Note that if the decorated function uses `Variable`s, the enclosing variable
scope must be using `ResourceVariable`s.
Parameters
-
objectf - function `f(*x)` that returns a tuple `(y, grad_fn)` where:
- `x` is a sequence of `Tensor` inputs to the function.
- `y` is a `Tensor` or sequence of `Tensor` outputs of applying
TensorFlow operations in `f` to `x`.
- `grad_fn` is a function with the signature `g(*grad_ys)` which returns
a list of `Tensor`s - the derivatives of `Tensor`s in `y` with respect
to the `Tensor`s in `x`. `grad_ys` is a `Tensor` or sequence of
`Tensor`s the same size as `y` holding the initial value gradients for
each `Tensor` in `y`. In a pure mathematical sense, a vector-argument
vector-valued function `f`'s derivatives should be its Jacobian matrix
`J`. Here we are expressing the Jacobian `J` as a function `grad_fn`
which defines how `J` will transform a vector `grad_ys` when
left-multiplied with it (`grad_ys * J`). This functional representation
of a matrix is convenient to use for chain-rule calculation
(in e.g. the back-propagation algorithm). If `f` uses `Variable`s (that are not part of the
inputs), i.e. through `get_variable`, then `grad_fn` should have
signature `g(*grad_ys, variables=None)`, where `variables` is a list of
the `Variable`s, and return a 2-tuple `(grad_xs, grad_vars)`, where
`grad_xs` is the same as above, and `grad_vars` is a `list
` with the derivatives of `Tensor`s in `y` with respect to the variables (that is, grad_vars has one Tensor per variable in variables).
Returns
-
object - A function `h(x)` which returns the same value as `f(x)[0]` and whose
gradient (as calculated by
tf.gradients) is determined by `f(x)[1]`.
Show Example
def log1pexp(x):
return tf.math.log(1 + tf.exp(x))
Tensor decision_tree_ensemble_resource_handle_op(string container, string shared_name, string name)
object decision_tree_ensemble_resource_handle_op_dyn(ImplicitContainer<T> container, ImplicitContainer<T> shared_name, object name)
Tensor decision_tree_resource_handle_op(string container, string shared_name, string name)
object decision_tree_resource_handle_op_dyn(ImplicitContainer<T> container, ImplicitContainer<T> shared_name, object name)
Tensor decode_base64(IGraphNodeBase input, string name)
Decode web-safe base64-encoded strings. Input may or may not have padding at the end. See EncodeBase64 for padding.
Web-safe means that input must use - and _ instead of + and /.
Parameters
-
IGraphNodeBaseinput - A `Tensor` of type `string`. Base64 strings to decode.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `string`.
object decode_base64_dyn(object input, object name)
Decode web-safe base64-encoded strings. Input may or may not have padding at the end. See EncodeBase64 for padding.
Web-safe means that input must use - and _ instead of + and /.
Parameters
-
objectinput - A `Tensor` of type `string`. Base64 strings to decode.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `string`.
Tensor decode_compressed(IGraphNodeBase bytes, string compression_type, string name)
Decompress strings. This op decompresses each element of the `bytes` input `Tensor`, which
is assumed to be compressed using the given `compression_type`. The `output` is a string `Tensor` of the same shape as `bytes`,
each element containing the decompressed data from the corresponding
element in `bytes`.
Parameters
-
IGraphNodeBasebytes - A `Tensor` of type `string`. A Tensor of string which is compressed.
-
stringcompression_type - An optional `string`. Defaults to `""`. A scalar containing either (i) the empty string (no compression), (ii) "ZLIB", or (iii) "GZIP".
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `string`.
object decode_compressed_dyn(object bytes, ImplicitContainer<T> compression_type, object name)
Decompress strings. This op decompresses each element of the `bytes` input `Tensor`, which
is assumed to be compressed using the given `compression_type`. The `output` is a string `Tensor` of the same shape as `bytes`,
each element containing the decompressed data from the corresponding
element in `bytes`.
Parameters
-
objectbytes - A `Tensor` of type `string`. A Tensor of string which is compressed.
-
ImplicitContainer<T>compression_type - An optional `string`. Defaults to `""`. A scalar containing either (i) the empty string (no compression), (ii) "ZLIB", or (iii) "GZIP".
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `string`.
object decode_csv(IGraphNodeBase records, IEnumerable<IGraphNodeBase> record_defaults, string field_delim, bool use_quote_delim, string name, string na_value, object select_cols)
Convert CSV records to tensors. Each column maps to one tensor. RFC 4180 format is expected for the CSV records.
(https://tools.ietf.org/html/rfc4180)
Note that we allow leading and trailing spaces with int or float field.
Parameters
-
IGraphNodeBaserecords - A `Tensor` of type `string`. Each string is a record/row in the csv and all records should have the same format.
-
IEnumerable<IGraphNodeBase>record_defaults - A list of `Tensor` objects with specific types. Acceptable types are `float32`, `float64`, `int32`, `int64`, `string`. One tensor per column of the input record, with either a scalar default value for that column or an empty vector if the column is required.
-
stringfield_delim - An optional `string`. Defaults to `","`. char delimiter to separate fields in a record.
-
booluse_quote_delim - An optional `bool`. Defaults to `True`. If false, treats double quotation marks as regular characters inside of the string fields (ignoring RFC 4180, Section 2, Bullet 5).
-
stringname - A name for the operation (optional).
-
stringna_value - Additional string to recognize as NA/NaN.
-
objectselect_cols - Optional sorted list of column indices to select. If specified, only this subset of columns will be parsed and returned.
Returns
-
object - A list of `Tensor` objects. Has the same type as `record_defaults`. Each tensor will have the same shape as records.
object decode_csv_dyn(object records, object record_defaults, ImplicitContainer<T> field_delim, ImplicitContainer<T> use_quote_delim, object name, ImplicitContainer<T> na_value, object select_cols)
Convert CSV records to tensors. Each column maps to one tensor. RFC 4180 format is expected for the CSV records.
(https://tools.ietf.org/html/rfc4180)
Note that we allow leading and trailing spaces with int or float field.
Parameters
-
objectrecords - A `Tensor` of type `string`. Each string is a record/row in the csv and all records should have the same format.
-
objectrecord_defaults - A list of `Tensor` objects with specific types. Acceptable types are `float32`, `float64`, `int32`, `int64`, `string`. One tensor per column of the input record, with either a scalar default value for that column or an empty vector if the column is required.
-
ImplicitContainer<T>field_delim - An optional `string`. Defaults to `","`. char delimiter to separate fields in a record.
-
ImplicitContainer<T>use_quote_delim - An optional `bool`. Defaults to `True`. If false, treats double quotation marks as regular characters inside of the string fields (ignoring RFC 4180, Section 2, Bullet 5).
-
objectname - A name for the operation (optional).
-
ImplicitContainer<T>na_value - Additional string to recognize as NA/NaN.
-
objectselect_cols - Optional sorted list of column indices to select. If specified, only this subset of columns will be parsed and returned.
Returns
-
object - A list of `Tensor` objects. Has the same type as `record_defaults`. Each tensor will have the same shape as records.
Tensor decode_json_example(IGraphNodeBase json_examples, string name)
Convert JSON-encoded Example records to binary protocol buffer strings. This op translates a tensor containing Example records, encoded using
the [standard JSON
mapping](https://developers.google.com/protocol-buffers/docs/proto3#json),
into a tensor containing the same records encoded as binary protocol
buffers. The resulting tensor can then be fed to any of the other
Example-parsing ops.
Parameters
-
IGraphNodeBasejson_examples - A `Tensor` of type `string`. Each string is a JSON object serialized according to the JSON mapping of the Example proto.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `string`.
object decode_json_example_dyn(object json_examples, object name)
Convert JSON-encoded Example records to binary protocol buffer strings. This op translates a tensor containing Example records, encoded using
the [standard JSON
mapping](https://developers.google.com/protocol-buffers/docs/proto3#json),
into a tensor containing the same records encoded as binary protocol
buffers. The resulting tensor can then be fed to any of the other
Example-parsing ops.
Parameters
-
objectjson_examples - A `Tensor` of type `string`. Each string is a JSON object serialized according to the JSON mapping of the Example proto.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `string`.
object decode_libsvm(IGraphNodeBase input, int num_features, ImplicitContainer<T> dtype, ImplicitContainer<T> label_dtype, string name)
object decode_libsvm_dyn(object input, object num_features, ImplicitContainer<T> dtype, ImplicitContainer<T> label_dtype, object name)
Tensor decode_raw(double input_bytes, DType out_type, bool little_endian, string name, object bytes)
Convert raw byte strings into tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(bytes)`. They will be removed in a future version.
Instructions for updating:
bytes is deprecated, use input_bytes instead
Parameters
-
doubleinput_bytes - Each element of the input Tensor is converted to an array of bytes.
-
DTypeout_type - `DType` of the output. Acceptable types are `half`, `float`, `double`, `int32`, `uint16`, `uint8`, `int16`, `int8`, `int64`.
-
boollittle_endian - Whether the `input_bytes` data is in little-endian format. Data will be converted into host byte order if necessary.
-
stringname - A name for the operation (optional).
-
objectbytes - Deprecated parameter. Use `input_bytes` instead.
Returns
-
Tensor - A `Tensor` object storing the decoded bytes.
Tensor decode_raw(RaggedTensor input_bytes, DType out_type, bool little_endian, string name, object bytes)
Convert raw byte strings into tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(bytes)`. They will be removed in a future version.
Instructions for updating:
bytes is deprecated, use input_bytes instead
Parameters
-
RaggedTensorinput_bytes - Each element of the input Tensor is converted to an array of bytes.
-
DTypeout_type - `DType` of the output. Acceptable types are `half`, `float`, `double`, `int32`, `uint16`, `uint8`, `int16`, `int8`, `int64`.
-
boollittle_endian - Whether the `input_bytes` data is in little-endian format. Data will be converted into host byte order if necessary.
-
stringname - A name for the operation (optional).
-
objectbytes - Deprecated parameter. Use `input_bytes` instead.
Returns
-
Tensor - A `Tensor` object storing the decoded bytes.
Tensor decode_raw(IGraphNodeBase input_bytes, DType out_type, bool little_endian, string name, object bytes)
Convert raw byte strings into tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(bytes)`. They will be removed in a future version.
Instructions for updating:
bytes is deprecated, use input_bytes instead
Parameters
-
IGraphNodeBaseinput_bytes - Each element of the input Tensor is converted to an array of bytes.
-
DTypeout_type - `DType` of the output. Acceptable types are `half`, `float`, `double`, `int32`, `uint16`, `uint8`, `int16`, `int8`, `int64`.
-
boollittle_endian - Whether the `input_bytes` data is in little-endian format. Data will be converted into host byte order if necessary.
-
stringname - A name for the operation (optional).
-
objectbytes - Deprecated parameter. Use `input_bytes` instead.
Returns
-
Tensor - A `Tensor` object storing the decoded bytes.
Tensor decode_raw(PythonClassContainer input_bytes, DType out_type, bool little_endian, string name, object bytes)
Convert raw byte strings into tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(bytes)`. They will be removed in a future version.
Instructions for updating:
bytes is deprecated, use input_bytes instead
Parameters
-
PythonClassContainerinput_bytes - Each element of the input Tensor is converted to an array of bytes.
-
DTypeout_type - `DType` of the output. Acceptable types are `half`, `float`, `double`, `int32`, `uint16`, `uint8`, `int16`, `int8`, `int64`.
-
boollittle_endian - Whether the `input_bytes` data is in little-endian format. Data will be converted into host byte order if necessary.
-
stringname - A name for the operation (optional).
-
objectbytes - Deprecated parameter. Use `input_bytes` instead.
Returns
-
Tensor - A `Tensor` object storing the decoded bytes.
object decode_raw_dyn(object input_bytes, object out_type, ImplicitContainer<T> little_endian, object name, object bytes)
Convert raw byte strings into tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(bytes)`. They will be removed in a future version.
Instructions for updating:
bytes is deprecated, use input_bytes instead
Parameters
-
objectinput_bytes - Each element of the input Tensor is converted to an array of bytes.
-
objectout_type - `DType` of the output. Acceptable types are `half`, `float`, `double`, `int32`, `uint16`, `uint8`, `int16`, `int8`, `int64`.
-
ImplicitContainer<T>little_endian - Whether the `input_bytes` data is in little-endian format. Data will be converted into host byte order if necessary.
-
objectname - A name for the operation (optional).
-
objectbytes - Deprecated parameter. Use `input_bytes` instead.
Returns
-
object - A `Tensor` object storing the decoded bytes.
object default_attrs(string string_val, ImplicitContainer<T> string_list_val, int int_val, ImplicitContainer<T> int_list_val, int float_val, ImplicitContainer<T> float_list_val, bool bool_val, ImplicitContainer<T> bool_list_val, ImplicitContainer<T> type_val, ImplicitContainer<T> type_list_val, ImplicitContainer<T> shape_val, ImplicitContainer<T> shape_list_val, ImplicitContainer<T> tensor_val, ImplicitContainer<T> tensor_list_val, string name)
object default_attrs_dyn(ImplicitContainer<T> string_val, ImplicitContainer<T> string_list_val, ImplicitContainer<T> int_val, ImplicitContainer<T> int_list_val, ImplicitContainer<T> float_val, ImplicitContainer<T> float_list_val, ImplicitContainer<T> bool_val, ImplicitContainer<T> bool_list_val, ImplicitContainer<T> type_val, ImplicitContainer<T> type_list_val, ImplicitContainer<T> shape_val, ImplicitContainer<T> shape_list_val, ImplicitContainer<T> tensor_val, ImplicitContainer<T> tensor_list_val, object name)
ValueTuple<Tensor, object> delete_session_tensor(object handle, string name)
Delete the tensor for the given tensor handle. This is EXPERIMENTAL and subject to change. Delete the tensor of a given tensor handle. The tensor is produced
in a previous run() and stored in the state of the session.
Parameters
-
objecthandle - The string representation of a persistent tensor handle.
-
stringname - Optional name prefix for the return tensor.
Returns
-
ValueTuple<Tensor, object> - A pair of graph elements. The first is a placeholder for feeding a tensor handle and the second is a deletion operation.
object delete_session_tensor_dyn(object handle, object name)
Delete the tensor for the given tensor handle. This is EXPERIMENTAL and subject to change. Delete the tensor of a given tensor handle. The tensor is produced
in a previous run() and stored in the state of the session.
Parameters
-
objecthandle - The string representation of a persistent tensor handle.
-
objectname - Optional name prefix for the return tensor.
Returns
-
object - A pair of graph elements. The first is a placeholder for feeding a tensor handle and the second is a deletion operation.
Tensor depth_to_space(IEnumerable<object> input, int block_size, string name, string data_format)
DepthToSpace for tensors of type T. Rearranges data from depth into blocks of spatial data.
This is the reverse transformation of SpaceToDepth. More specifically,
this op outputs a copy of the input tensor where values from the `depth`
dimension are moved in spatial blocks to the `height` and `width` dimensions.
The attr `block_size` indicates the input block size and how the data is moved. * Chunks of data of size `block_size * block_size` from depth are rearranged
into non-overlapping blocks of size `block_size x block_size`
* The width the output tensor is `input_depth * block_size`, whereas the
height is `input_height * block_size`.
* The Y, X coordinates within each block of the output image are determined
by the high order component of the input channel index.
* The depth of the input tensor must be divisible by
`block_size * block_size`. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,iY,iX,bY,bX,oC (where n=batch index, iX, iY means X or Y coordinates
within the input image, bX, bY means coordinates
within the output block, oC means output channels).
The output would be the input transposed to the following layout:
n,iY,bY,iX,bX,oC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 1, 1, 4]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1, 2, 3, 4]]]] ``` This operation will output a tensor of shape `[1, 2, 2, 1]`: ```
[[[[1], [2]],
[[3], [4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[1, 1, 4]`,
the corresponding output will have 2x2 elements and will have a depth of
1 channel (1 = `4 / (block_size * block_size)`).
The output element shape is `[2, 2, 1]`. For an input tensor with larger depth, here of shape `[1, 1, 1, 12]`, e.g. ```
x = [[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` This operation, for block size of 2, will return the following tensor of shape
`[1, 2, 2, 3]` ```
[[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]] ``` Similarly, for the following input of shape `[1 2 2 4]`, and a block size of 2: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
``` the operator will return the following tensor of shape `[1 4 4 1]`: ```
x = [[[ [1], [2], [5], [6]],
[ [3], [4], [7], [8]],
[ [9], [10], [13], [14]],
[ [11], [12], [15], [16]]]] ```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
intblock_size - An `int` that is `>= 2`. The size of the spatial block, same as in Space2Depth.
-
stringname - A name for the operation (optional).
-
stringdata_format - An optional `string` from: `"NHWC", "NCHW", "NCHW_VECT_C"`. Defaults to `"NHWC"`.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor depth_to_space(IGraphNodeBase input, int block_size, string name, string data_format)
DepthToSpace for tensors of type T. Rearranges data from depth into blocks of spatial data.
This is the reverse transformation of SpaceToDepth. More specifically,
this op outputs a copy of the input tensor where values from the `depth`
dimension are moved in spatial blocks to the `height` and `width` dimensions.
The attr `block_size` indicates the input block size and how the data is moved. * Chunks of data of size `block_size * block_size` from depth are rearranged
into non-overlapping blocks of size `block_size x block_size`
* The width the output tensor is `input_depth * block_size`, whereas the
height is `input_height * block_size`.
* The Y, X coordinates within each block of the output image are determined
by the high order component of the input channel index.
* The depth of the input tensor must be divisible by
`block_size * block_size`. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,iY,iX,bY,bX,oC (where n=batch index, iX, iY means X or Y coordinates
within the input image, bX, bY means coordinates
within the output block, oC means output channels).
The output would be the input transposed to the following layout:
n,iY,bY,iX,bX,oC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 1, 1, 4]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1, 2, 3, 4]]]] ``` This operation will output a tensor of shape `[1, 2, 2, 1]`: ```
[[[[1], [2]],
[[3], [4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[1, 1, 4]`,
the corresponding output will have 2x2 elements and will have a depth of
1 channel (1 = `4 / (block_size * block_size)`).
The output element shape is `[2, 2, 1]`. For an input tensor with larger depth, here of shape `[1, 1, 1, 12]`, e.g. ```
x = [[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` This operation, for block size of 2, will return the following tensor of shape
`[1, 2, 2, 3]` ```
[[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]] ``` Similarly, for the following input of shape `[1 2 2 4]`, and a block size of 2: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
``` the operator will return the following tensor of shape `[1 4 4 1]`: ```
x = [[[ [1], [2], [5], [6]],
[ [3], [4], [7], [8]],
[ [9], [10], [13], [14]],
[ [11], [12], [15], [16]]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
intblock_size - An `int` that is `>= 2`. The size of the spatial block, same as in Space2Depth.
-
stringname - A name for the operation (optional).
-
stringdata_format - An optional `string` from: `"NHWC", "NCHW", "NCHW_VECT_C"`. Defaults to `"NHWC"`.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor depth_to_space(IndexedSlices input, int block_size, string name, string data_format)
DepthToSpace for tensors of type T. Rearranges data from depth into blocks of spatial data.
This is the reverse transformation of SpaceToDepth. More specifically,
this op outputs a copy of the input tensor where values from the `depth`
dimension are moved in spatial blocks to the `height` and `width` dimensions.
The attr `block_size` indicates the input block size and how the data is moved. * Chunks of data of size `block_size * block_size` from depth are rearranged
into non-overlapping blocks of size `block_size x block_size`
* The width the output tensor is `input_depth * block_size`, whereas the
height is `input_height * block_size`.
* The Y, X coordinates within each block of the output image are determined
by the high order component of the input channel index.
* The depth of the input tensor must be divisible by
`block_size * block_size`. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,iY,iX,bY,bX,oC (where n=batch index, iX, iY means X or Y coordinates
within the input image, bX, bY means coordinates
within the output block, oC means output channels).
The output would be the input transposed to the following layout:
n,iY,bY,iX,bX,oC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 1, 1, 4]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1, 2, 3, 4]]]] ``` This operation will output a tensor of shape `[1, 2, 2, 1]`: ```
[[[[1], [2]],
[[3], [4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[1, 1, 4]`,
the corresponding output will have 2x2 elements and will have a depth of
1 channel (1 = `4 / (block_size * block_size)`).
The output element shape is `[2, 2, 1]`. For an input tensor with larger depth, here of shape `[1, 1, 1, 12]`, e.g. ```
x = [[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` This operation, for block size of 2, will return the following tensor of shape
`[1, 2, 2, 3]` ```
[[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]] ``` Similarly, for the following input of shape `[1 2 2 4]`, and a block size of 2: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
``` the operator will return the following tensor of shape `[1 4 4 1]`: ```
x = [[[ [1], [2], [5], [6]],
[ [3], [4], [7], [8]],
[ [9], [10], [13], [14]],
[ [11], [12], [15], [16]]]] ```
Parameters
-
IndexedSlicesinput - A `Tensor`.
-
intblock_size - An `int` that is `>= 2`. The size of the spatial block, same as in Space2Depth.
-
stringname - A name for the operation (optional).
-
stringdata_format - An optional `string` from: `"NHWC", "NCHW", "NCHW_VECT_C"`. Defaults to `"NHWC"`.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor depth_to_space(ValueTuple<PythonClassContainer, PythonClassContainer> input, int block_size, string name, string data_format)
DepthToSpace for tensors of type T. Rearranges data from depth into blocks of spatial data.
This is the reverse transformation of SpaceToDepth. More specifically,
this op outputs a copy of the input tensor where values from the `depth`
dimension are moved in spatial blocks to the `height` and `width` dimensions.
The attr `block_size` indicates the input block size and how the data is moved. * Chunks of data of size `block_size * block_size` from depth are rearranged
into non-overlapping blocks of size `block_size x block_size`
* The width the output tensor is `input_depth * block_size`, whereas the
height is `input_height * block_size`.
* The Y, X coordinates within each block of the output image are determined
by the high order component of the input channel index.
* The depth of the input tensor must be divisible by
`block_size * block_size`. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,iY,iX,bY,bX,oC (where n=batch index, iX, iY means X or Y coordinates
within the input image, bX, bY means coordinates
within the output block, oC means output channels).
The output would be the input transposed to the following layout:
n,iY,bY,iX,bX,oC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 1, 1, 4]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1, 2, 3, 4]]]] ``` This operation will output a tensor of shape `[1, 2, 2, 1]`: ```
[[[[1], [2]],
[[3], [4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[1, 1, 4]`,
the corresponding output will have 2x2 elements and will have a depth of
1 channel (1 = `4 / (block_size * block_size)`).
The output element shape is `[2, 2, 1]`. For an input tensor with larger depth, here of shape `[1, 1, 1, 12]`, e.g. ```
x = [[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` This operation, for block size of 2, will return the following tensor of shape
`[1, 2, 2, 3]` ```
[[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]] ``` Similarly, for the following input of shape `[1 2 2 4]`, and a block size of 2: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
``` the operator will return the following tensor of shape `[1 4 4 1]`: ```
x = [[[ [1], [2], [5], [6]],
[ [3], [4], [7], [8]],
[ [9], [10], [13], [14]],
[ [11], [12], [15], [16]]]] ```
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>input - A `Tensor`.
-
intblock_size - An `int` that is `>= 2`. The size of the spatial block, same as in Space2Depth.
-
stringname - A name for the operation (optional).
-
stringdata_format - An optional `string` from: `"NHWC", "NCHW", "NCHW_VECT_C"`. Defaults to `"NHWC"`.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object depth_to_space_dyn(object input, object block_size, object name, ImplicitContainer<T> data_format)
DepthToSpace for tensors of type T. Rearranges data from depth into blocks of spatial data.
This is the reverse transformation of SpaceToDepth. More specifically,
this op outputs a copy of the input tensor where values from the `depth`
dimension are moved in spatial blocks to the `height` and `width` dimensions.
The attr `block_size` indicates the input block size and how the data is moved. * Chunks of data of size `block_size * block_size` from depth are rearranged
into non-overlapping blocks of size `block_size x block_size`
* The width the output tensor is `input_depth * block_size`, whereas the
height is `input_height * block_size`.
* The Y, X coordinates within each block of the output image are determined
by the high order component of the input channel index.
* The depth of the input tensor must be divisible by
`block_size * block_size`. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,iY,iX,bY,bX,oC (where n=batch index, iX, iY means X or Y coordinates
within the input image, bX, bY means coordinates
within the output block, oC means output channels).
The output would be the input transposed to the following layout:
n,iY,bY,iX,bX,oC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 1, 1, 4]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1, 2, 3, 4]]]] ``` This operation will output a tensor of shape `[1, 2, 2, 1]`: ```
[[[[1], [2]],
[[3], [4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[1, 1, 4]`,
the corresponding output will have 2x2 elements and will have a depth of
1 channel (1 = `4 / (block_size * block_size)`).
The output element shape is `[2, 2, 1]`. For an input tensor with larger depth, here of shape `[1, 1, 1, 12]`, e.g. ```
x = [[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` This operation, for block size of 2, will return the following tensor of shape
`[1, 2, 2, 3]` ```
[[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]] ``` Similarly, for the following input of shape `[1 2 2 4]`, and a block size of 2: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
``` the operator will return the following tensor of shape `[1 4 4 1]`: ```
x = [[[ [1], [2], [5], [6]],
[ [3], [4], [7], [8]],
[ [9], [10], [13], [14]],
[ [11], [12], [15], [16]]]] ```
Parameters
-
objectinput - A `Tensor`.
-
objectblock_size - An `int` that is `>= 2`. The size of the spatial block, same as in Space2Depth.
-
objectname - A name for the operation (optional).
-
ImplicitContainer<T>data_format - An optional `string` from: `"NHWC", "NCHW", "NCHW_VECT_C"`. Defaults to `"NHWC"`.
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor dequantize(IGraphNodeBase input, IGraphNodeBase min_range, IGraphNodeBase max_range, string mode, string name)
Dequantize the 'input' tensor into a float Tensor. [min_range, max_range] are scalar floats that specify the range for
the 'input' data. The 'mode' attribute controls exactly which calculations are
used to convert the float values to their quantized equivalents. In 'MIN_COMBINED' mode, each value of the tensor will undergo the following: ```
if T == qint8: in[i] += (range(T) + 1)/ 2.0
out[i] = min_range + (in[i]* (max_range - min_range) / range(T))
```
here `range(T) = numeric_limits::max() - numeric_limits::min()` *MIN_COMBINED Mode Example* If the input comes from a QuantizedRelu6, the output type is
quint8 (range of 0-255) but the possible range of QuantizedRelu6 is
0-6. The min_range and max_range values are therefore 0.0 and 6.0.
Dequantize on quint8 will take each value, cast to float, and multiply
by 6 / 255.
Note that if quantizedtype is qint8, the operation will additionally add
each value by 128 prior to casting. If the mode is 'MIN_FIRST', then this approach is used: ```c++
num_discrete_values = 1 << (# of bits in T)
range_adjust = num_discrete_values / (num_discrete_values - 1)
range = (range_max - range_min) * range_adjust
range_scale = range / num_discrete_values
const double offset_input = static_cast(input) - lowest_quantized;
result = range_min + ((input - numeric_limits::min()) * range_scale)
``` *SCALED mode Example* `SCALED` mode matches the quantization approach used in
`QuantizeAndDequantize{V2|V3}`. If the mode is `SCALED`, we do not use the full range of the output type,
choosing to elide the lowest possible value for symmetry (e.g., output range is
-127 to 127, not -128 to 127 for signed 8 bit quantization), so that 0.0 maps to
0. We first find the range of values in our tensor. The
range we use is always centered on 0, so we find m such that
```c++
m = max(abs(input_min), abs(input_max))
``` Our input tensor range is then `[-m, m]`. Next, we choose our fixed-point quantization buckets, `[min_fixed, max_fixed]`.
If T is signed, this is
```
num_bits = sizeof(T) * 8
[min_fixed, max_fixed] =
[-(1 << (num_bits - 1) - 1), (1 << (num_bits - 1)) - 1]
``` Otherwise, if T is unsigned, the fixed-point range is
```
[min_fixed, max_fixed] = [0, (1 << num_bits) - 1]
``` From this we compute our scaling factor, s:
```c++
s = (2 * m) / (max_fixed - min_fixed)
``` Now we can dequantize the elements of our tensor:
```c++
result = input * s
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `qint8`, `quint8`, `qint32`, `qint16`, `quint16`.
-
IGraphNodeBasemin_range - A `Tensor` of type `float32`. The minimum scalar value possibly produced for the input.
-
IGraphNodeBasemax_range - A `Tensor` of type `float32`. The maximum scalar value possibly produced for the input.
-
stringmode - An optional `string` from: `"MIN_COMBINED", "MIN_FIRST", "SCALED"`. Defaults to `"MIN_COMBINED"`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
object dequantize_dyn(object input, object min_range, object max_range, ImplicitContainer<T> mode, object name)
Dequantize the 'input' tensor into a float Tensor. [min_range, max_range] are scalar floats that specify the range for
the 'input' data. The 'mode' attribute controls exactly which calculations are
used to convert the float values to their quantized equivalents. In 'MIN_COMBINED' mode, each value of the tensor will undergo the following: ```
if T == qint8: in[i] += (range(T) + 1)/ 2.0
out[i] = min_range + (in[i]* (max_range - min_range) / range(T))
```
here `range(T) = numeric_limits::max() - numeric_limits::min()` *MIN_COMBINED Mode Example* If the input comes from a QuantizedRelu6, the output type is
quint8 (range of 0-255) but the possible range of QuantizedRelu6 is
0-6. The min_range and max_range values are therefore 0.0 and 6.0.
Dequantize on quint8 will take each value, cast to float, and multiply
by 6 / 255.
Note that if quantizedtype is qint8, the operation will additionally add
each value by 128 prior to casting. If the mode is 'MIN_FIRST', then this approach is used: ```c++
num_discrete_values = 1 << (# of bits in T)
range_adjust = num_discrete_values / (num_discrete_values - 1)
range = (range_max - range_min) * range_adjust
range_scale = range / num_discrete_values
const double offset_input = static_cast(input) - lowest_quantized;
result = range_min + ((input - numeric_limits::min()) * range_scale)
``` *SCALED mode Example* `SCALED` mode matches the quantization approach used in
`QuantizeAndDequantize{V2|V3}`. If the mode is `SCALED`, we do not use the full range of the output type,
choosing to elide the lowest possible value for symmetry (e.g., output range is
-127 to 127, not -128 to 127 for signed 8 bit quantization), so that 0.0 maps to
0. We first find the range of values in our tensor. The
range we use is always centered on 0, so we find m such that
```c++
m = max(abs(input_min), abs(input_max))
``` Our input tensor range is then `[-m, m]`. Next, we choose our fixed-point quantization buckets, `[min_fixed, max_fixed]`.
If T is signed, this is
```
num_bits = sizeof(T) * 8
[min_fixed, max_fixed] =
[-(1 << (num_bits - 1) - 1), (1 << (num_bits - 1)) - 1]
``` Otherwise, if T is unsigned, the fixed-point range is
```
[min_fixed, max_fixed] = [0, (1 << num_bits) - 1]
``` From this we compute our scaling factor, s:
```c++
s = (2 * m) / (max_fixed - min_fixed)
``` Now we can dequantize the elements of our tensor:
```c++
result = input * s
```
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `qint8`, `quint8`, `qint32`, `qint16`, `quint16`.
-
objectmin_range - A `Tensor` of type `float32`. The minimum scalar value possibly produced for the input.
-
objectmax_range - A `Tensor` of type `float32`. The maximum scalar value possibly produced for the input.
-
ImplicitContainer<T>mode - An optional `string` from: `"MIN_COMBINED", "MIN_FIRST", "SCALED"`. Defaults to `"MIN_COMBINED"`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `float32`.
SparseTensor deserialize_many_sparse(IGraphNodeBase serialized_sparse, DType dtype, object rank, string name)
Deserialize and concatenate `SparseTensors` from a serialized minibatch. The input `serialized_sparse` must be a string matrix of shape `[N x 3]` where
`N` is the minibatch size and the rows correspond to packed outputs of
`serialize_sparse`. The ranks of the original `SparseTensor` objects
must all match. When the final `SparseTensor` is created, it has rank one
higher than the ranks of the incoming `SparseTensor` objects (they have been
concatenated along a new row dimension). The output `SparseTensor` object's shape values for all dimensions but the
first are the max across the input `SparseTensor` objects' shape values
for the corresponding dimensions. Its first shape value is `N`, the minibatch
size. The input `SparseTensor` objects' indices are assumed ordered in
standard lexicographic order. If this is not the case, after this
step run `sparse.reorder` to restore index ordering. For example, if the serialized input is a `[2, 3]` matrix representing two
original `SparseTensor` objects: index = [ 0]
[10]
[20]
values = [1, 2, 3]
shape = [50] and index = [ 2]
[10]
values = [4, 5]
shape = [30] then the final deserialized `SparseTensor` will be: index = [0 0]
[0 10]
[0 20]
[1 2]
[1 10]
values = [1, 2, 3, 4, 5]
shape = [2 50]
Parameters
-
IGraphNodeBaseserialized_sparse - 2-D `Tensor` of type `string` of shape `[N, 3]`. The serialized and packed `SparseTensor` objects.
-
DTypedtype - The `dtype` of the serialized `SparseTensor` objects.
-
objectrank - (optional) Python int, the rank of the `SparseTensor` objects.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` representing the deserialized `SparseTensor`s, concatenated along the `SparseTensor`s' first dimension. All of the serialized `SparseTensor`s must have had the same rank and type.
object deserialize_many_sparse_dyn(object serialized_sparse, object dtype, object rank, object name)
Deserialize and concatenate `SparseTensors` from a serialized minibatch. The input `serialized_sparse` must be a string matrix of shape `[N x 3]` where
`N` is the minibatch size and the rows correspond to packed outputs of
`serialize_sparse`. The ranks of the original `SparseTensor` objects
must all match. When the final `SparseTensor` is created, it has rank one
higher than the ranks of the incoming `SparseTensor` objects (they have been
concatenated along a new row dimension). The output `SparseTensor` object's shape values for all dimensions but the
first are the max across the input `SparseTensor` objects' shape values
for the corresponding dimensions. Its first shape value is `N`, the minibatch
size. The input `SparseTensor` objects' indices are assumed ordered in
standard lexicographic order. If this is not the case, after this
step run `sparse.reorder` to restore index ordering. For example, if the serialized input is a `[2, 3]` matrix representing two
original `SparseTensor` objects: index = [ 0]
[10]
[20]
values = [1, 2, 3]
shape = [50] and index = [ 2]
[10]
values = [4, 5]
shape = [30] then the final deserialized `SparseTensor` will be: index = [0 0]
[0 10]
[0 20]
[1 2]
[1 10]
values = [1, 2, 3, 4, 5]
shape = [2 50]
Parameters
-
objectserialized_sparse - 2-D `Tensor` of type `string` of shape `[N, 3]`. The serialized and packed `SparseTensor` objects.
-
objectdtype - The `dtype` of the serialized `SparseTensor` objects.
-
objectrank - (optional) Python int, the rank of the `SparseTensor` objects.
-
objectname - A name prefix for the returned tensors (optional)
Returns
-
object - A `SparseTensor` representing the deserialized `SparseTensor`s, concatenated along the `SparseTensor`s' first dimension. All of the serialized `SparseTensor`s must have had the same rank and type.
object device(object device_name_or_function)
Returns a context manager that specifies the default device to use. The `device_name_or_function` argument may either be a device name
string, a device function, or None: * If it is a device name string, all operations constructed in
this context will be assigned to the device with that name, unless
overridden by a nested `device()` context.
* If it is a function, it will be treated as a function from
Operation objects to device name strings, and invoked each time
a new Operation is created. The Operation will be assigned to
the device with the returned name.
* If it is None, all `device()` invocations from the enclosing context
will be ignored. For information about the valid syntax of device name strings, see
the documentation in
[`DeviceNameUtils`](https://www.tensorflow.org/code/tensorflow/core/util/device_name_utils.h).
**N.B.** The device scope may be overridden by op wrappers or
other library code. For example, a variable assignment op
`v.assign()` must be colocated with the
tf.Variable `v`, and
incompatible device scopes will be ignored.
Parameters
-
objectdevice_name_or_function - The device name or function to use in the context.
Show Example
with g.device('/device:GPU:0'):
# All operations constructed in this context will be placed
# on GPU 0.
with g.device(None):
# All operations constructed in this context will have no
# assigned device. # Defines a function from `Operation` to device string.
def matmul_on_gpu(n):
if n.type == "MatMul":
return "/device:GPU:0"
else:
return "/cpu:0" with g.device(matmul_on_gpu):
# All operations of type "MatMul" constructed in this context
# will be placed on GPU 0; all other operations will be placed
# on CPU 0.
object device(PythonFunctionContainer device_name_or_function)
Returns a context manager that specifies the default device to use. The `device_name_or_function` argument may either be a device name
string, a device function, or None: * If it is a device name string, all operations constructed in
this context will be assigned to the device with that name, unless
overridden by a nested `device()` context.
* If it is a function, it will be treated as a function from
Operation objects to device name strings, and invoked each time
a new Operation is created. The Operation will be assigned to
the device with the returned name.
* If it is None, all `device()` invocations from the enclosing context
will be ignored. For information about the valid syntax of device name strings, see
the documentation in
[`DeviceNameUtils`](https://www.tensorflow.org/code/tensorflow/core/util/device_name_utils.h).
**N.B.** The device scope may be overridden by op wrappers or
other library code. For example, a variable assignment op
`v.assign()` must be colocated with the
tf.Variable `v`, and
incompatible device scopes will be ignored.
Parameters
-
PythonFunctionContainerdevice_name_or_function - The device name or function to use in the context.
Show Example
with g.device('/device:GPU:0'):
# All operations constructed in this context will be placed
# on GPU 0.
with g.device(None):
# All operations constructed in this context will have no
# assigned device. # Defines a function from `Operation` to device string.
def matmul_on_gpu(n):
if n.type == "MatMul":
return "/device:GPU:0"
else:
return "/cpu:0" with g.device(matmul_on_gpu):
# All operations of type "MatMul" constructed in this context
# will be placed on GPU 0; all other operations will be placed
# on CPU 0.
object device_dyn(object device_name_or_function)
Returns a context manager that specifies the default device to use. The `device_name_or_function` argument may either be a device name
string, a device function, or None: * If it is a device name string, all operations constructed in
this context will be assigned to the device with that name, unless
overridden by a nested `device()` context.
* If it is a function, it will be treated as a function from
Operation objects to device name strings, and invoked each time
a new Operation is created. The Operation will be assigned to
the device with the returned name.
* If it is None, all `device()` invocations from the enclosing context
will be ignored. For information about the valid syntax of device name strings, see
the documentation in
[`DeviceNameUtils`](https://www.tensorflow.org/code/tensorflow/core/util/device_name_utils.h).
**N.B.** The device scope may be overridden by op wrappers or
other library code. For example, a variable assignment op
`v.assign()` must be colocated with the
tf.Variable `v`, and
incompatible device scopes will be ignored.
Parameters
-
objectdevice_name_or_function - The device name or function to use in the context.
Show Example
with g.device('/device:GPU:0'):
# All operations constructed in this context will be placed
# on GPU 0.
with g.device(None):
# All operations constructed in this context will have no
# assigned device. # Defines a function from `Operation` to device string.
def matmul_on_gpu(n):
if n.type == "MatMul":
return "/device:GPU:0"
else:
return "/cpu:0" with g.device(matmul_on_gpu):
# All operations of type "MatMul" constructed in this context
# will be placed on GPU 0; all other operations will be placed
# on CPU 0.
Tensor device_placement_op(string name)
object device_placement_op_dyn(object name)
Tensor diag(IGraphNodeBase diagonal, string name)
Returns a diagonal tensor with a given diagonal values. Given a `diagonal`, this operation returns a tensor with the `diagonal` and
everything else padded with zeros. The diagonal is computed as follows: Assume `diagonal` has dimensions [D1,..., Dk], then the output is a tensor of
rank 2k with dimensions [D1,..., Dk, D1,..., Dk] where: `output[i1,..., ik, i1,..., ik] = diagonal[i1,..., ik]` and 0 everywhere else. For example: ```
# 'diagonal' is [1, 2, 3, 4]
tf.diag(diagonal) ==> [[1, 0, 0, 0]
[0, 2, 0, 0]
[0, 0, 3, 0]
[0, 0, 0, 4]]
```
Parameters
-
IGraphNodeBasediagonal - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`. Rank k tensor where k is at most 1.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `diagonal`.
object diag_dyn(object diagonal, object name)
Returns a diagonal tensor with a given diagonal values. Given a `diagonal`, this operation returns a tensor with the `diagonal` and
everything else padded with zeros. The diagonal is computed as follows: Assume `diagonal` has dimensions [D1,..., Dk], then the output is a tensor of
rank 2k with dimensions [D1,..., Dk, D1,..., Dk] where: `output[i1,..., ik, i1,..., ik] = diagonal[i1,..., ik]` and 0 everywhere else. For example: ```
# 'diagonal' is [1, 2, 3, 4]
tf.diag(diagonal) ==> [[1, 0, 0, 0]
[0, 2, 0, 0]
[0, 0, 3, 0]
[0, 0, 0, 4]]
```
Parameters
-
objectdiagonal - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`. Rank k tensor where k is at most 1.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `diagonal`.
Tensor diag_part(IGraphNodeBase input, string name)
Returns the diagonal part of the tensor. This operation returns a tensor with the `diagonal` part
of the `input`. The `diagonal` part is computed as follows: Assume `input` has dimensions `[D1,..., Dk, D1,..., Dk]`, then the output is a
tensor of rank `k` with dimensions `[D1,..., Dk]` where: `diagonal[i1,..., ik] = input[i1,..., ik, i1,..., ik]`. For example: ```
# 'input' is [[1, 0, 0, 0]
[0, 2, 0, 0]
[0, 0, 3, 0]
[0, 0, 0, 4]] tf.diag_part(input) ==> [1, 2, 3, 4]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`. Rank k tensor where k is even and not zero.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object diag_part_dyn(object input, object name)
Returns the diagonal part of the tensor. This operation returns a tensor with the `diagonal` part
of the `input`. The `diagonal` part is computed as follows: Assume `input` has dimensions `[D1,..., Dk, D1,..., Dk]`, then the output is a
tensor of rank `k` with dimensions `[D1,..., Dk]` where: `diagonal[i1,..., ik] = input[i1,..., ik, i1,..., ik]`. For example: ```
# 'input' is [[1, 0, 0, 0]
[0, 2, 0, 0]
[0, 0, 3, 0]
[0, 0, 0, 4]] tf.diag_part(input) ==> [1, 2, 3, 4]
```
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`. Rank k tensor where k is even and not zero.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor digamma(IGraphNodeBase x, string name)
Computes Psi, the derivative of Lgamma (the log of the absolute value of `Gamma(x)`), element-wise.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
object digamma_dyn(object x, object name)
Computes Psi, the derivative of Lgamma (the log of the absolute value of `Gamma(x)`), element-wise.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Dimension dimension_at_index(PythonClassContainer shape, ndarray index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
PythonClassContainershape - A TensorShape instance.
-
ndarrayindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(IEnumerable<object> shape, int index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
IEnumerable<object>shape - A TensorShape instance.
-
intindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(IEnumerable<object> shape, ndarray index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
IEnumerable<object>shape - A TensorShape instance.
-
ndarrayindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(int32 shape, IGraphNodeBase index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
int32shape - A TensorShape instance.
-
IGraphNodeBaseindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(int32 shape, int index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
int32shape - A TensorShape instance.
-
intindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(TensorShape shape, int index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
TensorShapeshape - A TensorShape instance.
-
intindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(TensorShape shape, ndarray index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
TensorShapeshape - A TensorShape instance.
-
ndarrayindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(Dimension shape, ndarray index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(Dimension shape, IGraphNodeBase index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
Dimensionshape - A TensorShape instance.
-
IGraphNodeBaseindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(TensorShape shape, IGraphNodeBase index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
TensorShapeshape - A TensorShape instance.
-
IGraphNodeBaseindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(int32 shape, ndarray index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(IEnumerable<object> shape, IGraphNodeBase index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
IEnumerable<object>shape - A TensorShape instance.
-
IGraphNodeBaseindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(PythonClassContainer shape, IGraphNodeBase index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
PythonClassContainershape - A TensorShape instance.
-
IGraphNodeBaseindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(ValueTuple<int, object> shape, ndarray index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
ValueTuple<int, object>shape - A TensorShape instance.
-
ndarrayindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(ValueTuple<Nullable<int>> shape, IGraphNodeBase index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
ValueTuple<Nullable<int>>shape - A TensorShape instance.
-
IGraphNodeBaseindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(Dimension shape, int index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
Dimensionshape - A TensorShape instance.
-
intindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(ValueTuple<int, object> shape, int index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
ValueTuple<int, object>shape - A TensorShape instance.
-
intindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(ValueTuple<Nullable<int>> shape, int index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
ValueTuple<Nullable<int>>shape - A TensorShape instance.
-
intindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(ValueTuple<Nullable<int>> shape, ndarray index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
ValueTuple<Nullable<int>>shape - A TensorShape instance.
-
ndarrayindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(ValueTuple<int, object> shape, IGraphNodeBase index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
ValueTuple<int, object>shape - A TensorShape instance.
-
IGraphNodeBaseindex - An integer index.
Returns
-
Dimension - A dimension object.
Dimension dimension_at_index(PythonClassContainer shape, int index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
PythonClassContainershape - A TensorShape instance.
-
intindex - An integer index.
Returns
-
Dimension - A dimension object.
object dimension_at_index_dyn(object shape, object index)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
Parameters
-
objectshape - A TensorShape instance.
-
objectindex - An integer index.
Returns
-
object - A dimension object.
object dimension_value(TensorShape dimension)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. When accessing the value of a TensorShape dimension,
use this utility, like this: ```
# If you had this in your V1 code:
value = tensor_shape[i].value # Use `dimension_value` as direct replacement compatible with both V1 & V2:
value = dimension_value(tensor_shape[i]) # This would be the V2 equivalent:
value = tensor_shape[i] # Warning: this will return the dim value in V2!
```
Parameters
-
TensorShapedimension - Either a `Dimension` instance, an integer, or None.
Returns
-
object - A plain value, i.e. an integer or None.
object dimension_value(Dimension dimension)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. When accessing the value of a TensorShape dimension,
use this utility, like this: ```
# If you had this in your V1 code:
value = tensor_shape[i].value # Use `dimension_value` as direct replacement compatible with both V1 & V2:
value = dimension_value(tensor_shape[i]) # This would be the V2 equivalent:
value = tensor_shape[i] # Warning: this will return the dim value in V2!
```
Parameters
-
Dimensiondimension - Either a `Dimension` instance, an integer, or None.
Returns
-
object - A plain value, i.e. an integer or None.
object dimension_value(int dimension)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. When accessing the value of a TensorShape dimension,
use this utility, like this: ```
# If you had this in your V1 code:
value = tensor_shape[i].value # Use `dimension_value` as direct replacement compatible with both V1 & V2:
value = dimension_value(tensor_shape[i]) # This would be the V2 equivalent:
value = tensor_shape[i] # Warning: this will return the dim value in V2!
```
Parameters
-
intdimension - Either a `Dimension` instance, an integer, or None.
Returns
-
object - A plain value, i.e. an integer or None.
object dimension_value_dyn(object dimension)
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. When accessing the value of a TensorShape dimension,
use this utility, like this: ```
# If you had this in your V1 code:
value = tensor_shape[i].value # Use `dimension_value` as direct replacement compatible with both V1 & V2:
value = dimension_value(tensor_shape[i]) # This would be the V2 equivalent:
value = tensor_shape[i] # Warning: this will return the dim value in V2!
```
Parameters
-
objectdimension - Either a `Dimension` instance, an integer, or None.
Returns
-
object - A plain value, i.e. an integer or None.
void disable_control_flow_v2()
Opts out of control flow v2. Note: v2 control flow is always enabled inside of tf.function. Calling this
function has no effect in that case. If your code needs tf.disable_control_flow_v2() to be called to work
properly please file a bug.
object disable_control_flow_v2_dyn()
Opts out of control flow v2. Note: v2 control flow is always enabled inside of tf.function. Calling this
function has no effect in that case. If your code needs tf.disable_control_flow_v2() to be called to work
properly please file a bug.
void disable_eager_execution()
Disables eager execution. This function can only be called before any Graphs, Ops, or Tensors have been
created. It can be used at the beginning of the program for complex migration
projects from TensorFlow 1.x to 2.x.
object disable_eager_execution_dyn()
Disables eager execution. This function can only be called before any Graphs, Ops, or Tensors have been
created. It can be used at the beginning of the program for complex migration
projects from TensorFlow 1.x to 2.x.
void disable_tensor_equality()
Compare Tensors by their id and be hashable. This is a legacy behaviour of TensorFlow and is highly discouraged.
object disable_tensor_equality_dyn()
Compare Tensors by their id and be hashable. This is a legacy behaviour of TensorFlow and is highly discouraged.
void disable_v2_behavior()
Disables TensorFlow 2.x behaviors. This function can be called at the beginning of the program (before `Tensors`,
`Graphs` or other structures have been created, and before devices have been
initialized. It switches all global behaviors that are different between
TensorFlow 1.x and 2.x to behave as intended for 1.x. User can call this function to disable 2.x behavior during complex migrations.
object disable_v2_behavior_dyn()
Disables TensorFlow 2.x behaviors. This function can be called at the beginning of the program (before `Tensors`,
`Graphs` or other structures have been created, and before devices have been
initialized. It switches all global behaviors that are different between
TensorFlow 1.x and 2.x to behave as intended for 1.x. User can call this function to disable 2.x behavior during complex migrations.
void disable_v2_tensorshape()
Disables the V2 TensorShape behavior and reverts to V1 behavior. See docstring for `enable_v2_tensorshape` for details about the new behavior.
object disable_v2_tensorshape_dyn()
Disables the V2 TensorShape behavior and reverts to V1 behavior. See docstring for `enable_v2_tensorshape` for details about the new behavior.
Tensor div(PythonFunctionContainer x, object y, PythonFunctionContainer name)
Divides x / y elementwise (using Python 2 division operator semantics). (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Deprecated in favor of operator or tf.math.divide. NOTE: Prefer using the Tensor division operator or tf.divide which obey Python
3 division operator semantics. This function divides `x` and `y`, forcing Python 2 semantics. That is, if `x`
and `y` are both integers then the result will be an integer. This is in
contrast to Python 3, where division with `/` is always a float while division
with `//` is always an integer.
Parameters
-
PythonFunctionContainerx - `Tensor` numerator of real numeric type.
-
objecty - `Tensor` denominator of real numeric type.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - `x / y` returns the quotient of x and y.
Tensor div(PythonFunctionContainer x, object y, string name)
Divides x / y elementwise (using Python 2 division operator semantics). (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Deprecated in favor of operator or tf.math.divide. NOTE: Prefer using the Tensor division operator or tf.divide which obey Python
3 division operator semantics. This function divides `x` and `y`, forcing Python 2 semantics. That is, if `x`
and `y` are both integers then the result will be an integer. This is in
contrast to Python 3, where division with `/` is always a float while division
with `//` is always an integer.
Parameters
-
PythonFunctionContainerx - `Tensor` numerator of real numeric type.
-
objecty - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` returns the quotient of x and y.
Tensor div(object x, object y, int name)
Divides x / y elementwise (using Python 2 division operator semantics). (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Deprecated in favor of operator or tf.math.divide. NOTE: Prefer using the Tensor division operator or tf.divide which obey Python
3 division operator semantics. This function divides `x` and `y`, forcing Python 2 semantics. That is, if `x`
and `y` are both integers then the result will be an integer. This is in
contrast to Python 3, where division with `/` is always a float while division
with `//` is always an integer.
Parameters
-
objectx - `Tensor` numerator of real numeric type.
-
objecty - `Tensor` denominator of real numeric type.
-
intname - A name for the operation (optional).
Returns
-
Tensor - `x / y` returns the quotient of x and y.
Tensor div(object x, object y, PythonFunctionContainer name)
Divides x / y elementwise (using Python 2 division operator semantics). (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Deprecated in favor of operator or tf.math.divide. NOTE: Prefer using the Tensor division operator or tf.divide which obey Python
3 division operator semantics. This function divides `x` and `y`, forcing Python 2 semantics. That is, if `x`
and `y` are both integers then the result will be an integer. This is in
contrast to Python 3, where division with `/` is always a float while division
with `//` is always an integer.
Parameters
-
objectx - `Tensor` numerator of real numeric type.
-
objecty - `Tensor` denominator of real numeric type.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - `x / y` returns the quotient of x and y.
Tensor div(object x, object y, string name)
Divides x / y elementwise (using Python 2 division operator semantics). (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Deprecated in favor of operator or tf.math.divide. NOTE: Prefer using the Tensor division operator or tf.divide which obey Python
3 division operator semantics. This function divides `x` and `y`, forcing Python 2 semantics. That is, if `x`
and `y` are both integers then the result will be an integer. This is in
contrast to Python 3, where division with `/` is always a float while division
with `//` is always an integer.
Parameters
-
objectx - `Tensor` numerator of real numeric type.
-
objecty - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` returns the quotient of x and y.
Tensor div(PythonFunctionContainer x, object y, int name)
Divides x / y elementwise (using Python 2 division operator semantics). (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Deprecated in favor of operator or tf.math.divide. NOTE: Prefer using the Tensor division operator or tf.divide which obey Python
3 division operator semantics. This function divides `x` and `y`, forcing Python 2 semantics. That is, if `x`
and `y` are both integers then the result will be an integer. This is in
contrast to Python 3, where division with `/` is always a float while division
with `//` is always an integer.
Parameters
-
PythonFunctionContainerx - `Tensor` numerator of real numeric type.
-
objecty - `Tensor` denominator of real numeric type.
-
intname - A name for the operation (optional).
Returns
-
Tensor - `x / y` returns the quotient of x and y.
object div_dyn(object x, object y, object name)
Divides x / y elementwise (using Python 2 division operator semantics). (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Deprecated in favor of operator or tf.math.divide. NOTE: Prefer using the Tensor division operator or tf.divide which obey Python
3 division operator semantics. This function divides `x` and `y`, forcing Python 2 semantics. That is, if `x`
and `y` are both integers then the result will be an integer. This is in
contrast to Python 3, where division with `/` is always a float while division
with `//` is always an integer.
Parameters
-
objectx - `Tensor` numerator of real numeric type.
-
objecty - `Tensor` denominator of real numeric type.
-
objectname - A name for the operation (optional).
Returns
-
object - `x / y` returns the quotient of x and y.
Tensor div_no_nan(IGraphNodeBase x, IGraphNodeBase y, string name)
Computes an unsafe divide which returns 0 if the y is zero.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
IGraphNodeBasey - A `Tensor` whose dtype is compatible with `x`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - The element-wise value of the x divided by y.
object div_no_nan_dyn(object x, object y, object name)
Computes an unsafe divide which returns 0 if the y is zero.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
objecty - A `Tensor` whose dtype is compatible with `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - The element-wise value of the x divided by y.
Tensor divide(object x, object y, string name)
Computes Python style division of `x` by `y`.
Tensor divide(IGraphNodeBase x, object y, string name)
Computes Python style division of `x` by `y`.
Tensor divide(int x, object y, string name)
Computes Python style division of `x` by `y`.
Tensor divide(double x, object y, string name)
Computes Python style division of `x` by `y`.
Tensor divide(IndexedSlices x, object y, string name)
Computes Python style division of `x` by `y`.
object divide_dyn(object x, object y, object name)
Computes Python style division of `x` by `y`.
object dynamic_partition(IGraphNodeBase data, IGraphNodeBase partitions, int num_partitions, string name)
Partitions `data` into `num_partitions` tensors using indices from `partitions`. For each index tuple `js` of size `partitions.ndim`, the slice `data[js,...]`
becomes part of `outputs[partitions[js]]`. The slices with `partitions[js] = i`
are placed in `outputs[i]` in lexicographic order of `js`, and the first
dimension of `outputs[i]` is the number of entries in `partitions` equal to `i`.
In detail,
`data.shape` must start with `partitions.shape`.
See `dynamic_stitch` for an example on how to merge partitions back.
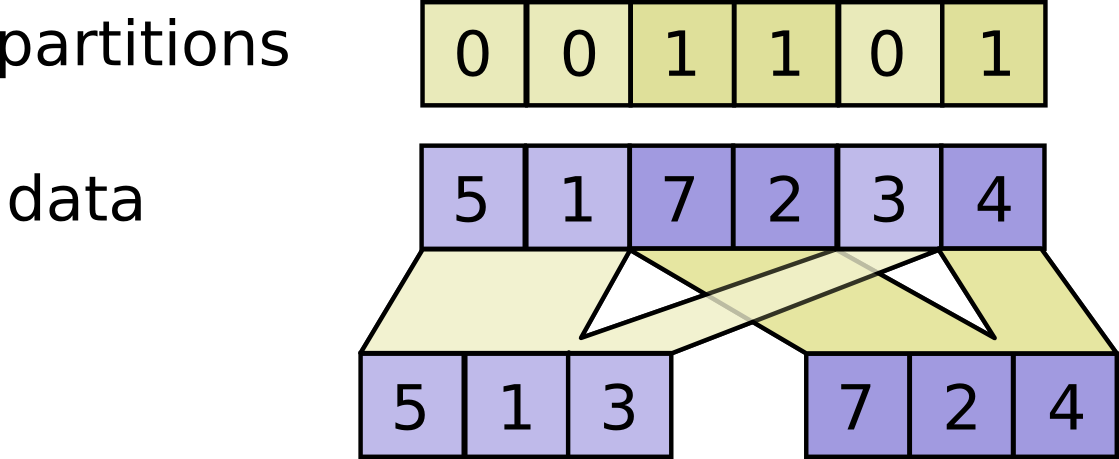

Parameters
-
IGraphNodeBasedata - A `Tensor`.
-
IGraphNodeBasepartitions - A `Tensor` of type `int32`. Any shape. Indices in the range `[0, num_partitions)`.
-
intnum_partitions - An `int` that is `>= 1`. The number of partitions to output.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `num_partitions` `Tensor` objects with the same type as `data`.
Show Example
outputs[i].shape = [sum(partitions == i)] + data.shape[partitions.ndim:] outputs[i] = pack([data[js,...] for js if partitions[js] == i])
object dynamic_partition(IGraphNodeBase data, IGraphNodeBase partitions, ndarray num_partitions, string name)
Partitions `data` into `num_partitions` tensors using indices from `partitions`. For each index tuple `js` of size `partitions.ndim`, the slice `data[js,...]`
becomes part of `outputs[partitions[js]]`. The slices with `partitions[js] = i`
are placed in `outputs[i]` in lexicographic order of `js`, and the first
dimension of `outputs[i]` is the number of entries in `partitions` equal to `i`.
In detail,
`data.shape` must start with `partitions.shape`.
See `dynamic_stitch` for an example on how to merge partitions back.


Parameters
-
IGraphNodeBasedata - A `Tensor`.
-
IGraphNodeBasepartitions - A `Tensor` of type `int32`. Any shape. Indices in the range `[0, num_partitions)`.
-
ndarraynum_partitions - An `int` that is `>= 1`. The number of partitions to output.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `num_partitions` `Tensor` objects with the same type as `data`.
Show Example
outputs[i].shape = [sum(partitions == i)] + data.shape[partitions.ndim:] outputs[i] = pack([data[js,...] for js if partitions[js] == i])
object dynamic_partition_dyn(object data, object partitions, object num_partitions, object name)
Partitions `data` into `num_partitions` tensors using indices from `partitions`. For each index tuple `js` of size `partitions.ndim`, the slice `data[js,...]`
becomes part of `outputs[partitions[js]]`. The slices with `partitions[js] = i`
are placed in `outputs[i]` in lexicographic order of `js`, and the first
dimension of `outputs[i]` is the number of entries in `partitions` equal to `i`.
In detail,
`data.shape` must start with `partitions.shape`.
See `dynamic_stitch` for an example on how to merge partitions back.


Parameters
-
objectdata - A `Tensor`.
-
objectpartitions - A `Tensor` of type `int32`. Any shape. Indices in the range `[0, num_partitions)`.
-
objectnum_partitions - An `int` that is `>= 1`. The number of partitions to output.
-
objectname - A name for the operation (optional).
Returns
-
object - A list of `num_partitions` `Tensor` objects with the same type as `data`.
Show Example
outputs[i].shape = [sum(partitions == i)] + data.shape[partitions.ndim:] outputs[i] = pack([data[js,...] for js if partitions[js] == i])
Tensor dynamic_stitch(IEnumerable<object> indices, IEnumerable<object> data, string name)
Interleave the values from the `data` tensors into a single tensor. Builds a merged tensor such that
For example, if each `indices[m]` is scalar or vector, we have
Each `data[i].shape` must start with the corresponding `indices[i].shape`,
and the rest of `data[i].shape` must be constant w.r.t. `i`. That is, we
must have `data[i].shape = indices[i].shape + constant`. In terms of this
`constant`, the output shape is merged.shape = [max(indices)] + constant Values are merged in order, so if an index appears in both `indices[m][i]` and
`indices[n][j]` for `(m,i) < (n,j)` the slice `data[n][j]` will appear in the
merged result. If you do not need this guarantee, ParallelDynamicStitch might
perform better on some devices.
This method can be used to merge partitions created by `dynamic_partition`
as illustrated on the following example:
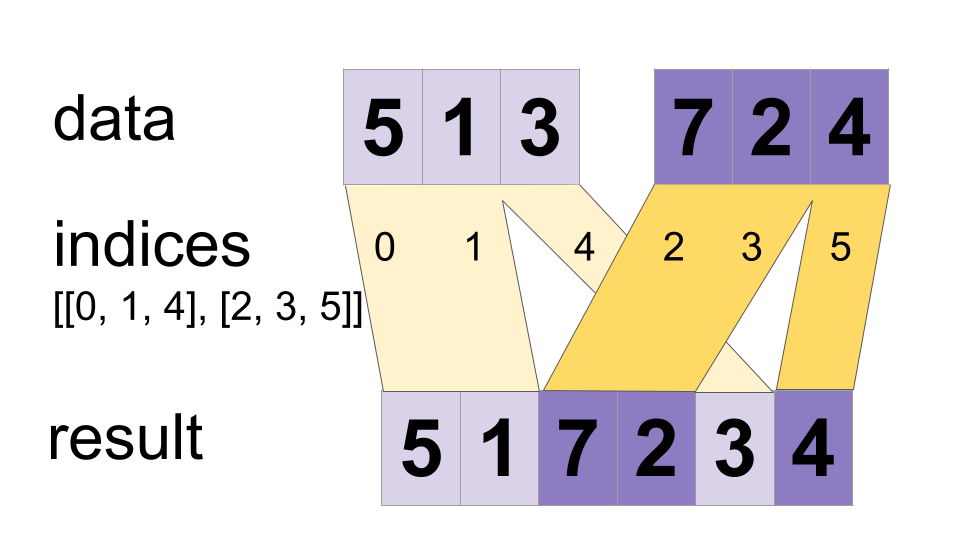

Parameters
-
IEnumerable<object>indices - A list of at least 1 `Tensor` objects with type `int32`.
-
IEnumerable<object>data - A list with the same length as `indices` of `Tensor` objects with the same type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
Show Example
merged[indices[m][i,..., j],...] = data[m][i,..., j,...]
Tensor dynamic_stitch(object indices, IEnumerable<object> data, string name)
Interleave the values from the `data` tensors into a single tensor. Builds a merged tensor such that
For example, if each `indices[m]` is scalar or vector, we have
Each `data[i].shape` must start with the corresponding `indices[i].shape`,
and the rest of `data[i].shape` must be constant w.r.t. `i`. That is, we
must have `data[i].shape = indices[i].shape + constant`. In terms of this
`constant`, the output shape is merged.shape = [max(indices)] + constant Values are merged in order, so if an index appears in both `indices[m][i]` and
`indices[n][j]` for `(m,i) < (n,j)` the slice `data[n][j]` will appear in the
merged result. If you do not need this guarantee, ParallelDynamicStitch might
perform better on some devices.
This method can be used to merge partitions created by `dynamic_partition`
as illustrated on the following example:


Parameters
-
objectindices - A list of at least 1 `Tensor` objects with type `int32`.
-
IEnumerable<object>data - A list with the same length as `indices` of `Tensor` objects with the same type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
Show Example
merged[indices[m][i,..., j],...] = data[m][i,..., j,...]
object dynamic_stitch_dyn(object indices, object data, object name)
Interleave the values from the `data` tensors into a single tensor. Builds a merged tensor such that
For example, if each `indices[m]` is scalar or vector, we have
Each `data[i].shape` must start with the corresponding `indices[i].shape`,
and the rest of `data[i].shape` must be constant w.r.t. `i`. That is, we
must have `data[i].shape = indices[i].shape + constant`. In terms of this
`constant`, the output shape is merged.shape = [max(indices)] + constant Values are merged in order, so if an index appears in both `indices[m][i]` and
`indices[n][j]` for `(m,i) < (n,j)` the slice `data[n][j]` will appear in the
merged result. If you do not need this guarantee, ParallelDynamicStitch might
perform better on some devices.
This method can be used to merge partitions created by `dynamic_partition`
as illustrated on the following example:


Parameters
-
objectindices - A list of at least 1 `Tensor` objects with type `int32`.
-
objectdata - A list with the same length as `indices` of `Tensor` objects with the same type.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `data`.
Show Example
merged[indices[m][i,..., j],...] = data[m][i,..., j,...]
Tensor edit_distance(SparseTensor hypothesis, SparseTensor truth, bool normalize, string name)
Computes the Levenshtein distance between sequences. This operation takes variable-length sequences (`hypothesis` and `truth`),
each provided as a `SparseTensor`, and computes the Levenshtein distance.
You can normalize the edit distance by length of `truth` by setting
`normalize` to true. For example, given the following input:
This operation would return the following:
Parameters
-
SparseTensorhypothesis - A `SparseTensor` containing hypothesis sequences.
-
SparseTensortruth - A `SparseTensor` containing truth sequences.
-
boolnormalize - A `bool`. If `True`, normalizes the Levenshtein distance by length of `truth.`
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A dense `Tensor` with rank `R - 1`, where R is the rank of the `SparseTensor` inputs `hypothesis` and `truth`.
Show Example
# 'hypothesis' is a tensor of shape `[2, 1]` with variable-length values:
# (0,0) = ["a"]
# (1,0) = ["b"]
hypothesis = tf.SparseTensor(
[[0, 0, 0],
[1, 0, 0]],
["a", "b"],
(2, 1, 1)) # 'truth' is a tensor of shape `[2, 2]` with variable-length values:
# (0,0) = []
# (0,1) = ["a"]
# (1,0) = ["b", "c"]
# (1,1) = ["a"]
truth = tf.SparseTensor(
[[0, 1, 0],
[1, 0, 0],
[1, 0, 1],
[1, 1, 0]],
["a", "b", "c", "a"],
(2, 2, 2)) normalize = True
Tensor edit_distance(ValueTuple<object> hypothesis, ValueTuple<object> truth, bool normalize, string name)
Computes the Levenshtein distance between sequences. This operation takes variable-length sequences (`hypothesis` and `truth`),
each provided as a `SparseTensor`, and computes the Levenshtein distance.
You can normalize the edit distance by length of `truth` by setting
`normalize` to true. For example, given the following input:
This operation would return the following:
Parameters
-
ValueTuple<object>hypothesis - A `SparseTensor` containing hypothesis sequences.
-
ValueTuple<object>truth - A `SparseTensor` containing truth sequences.
-
boolnormalize - A `bool`. If `True`, normalizes the Levenshtein distance by length of `truth.`
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A dense `Tensor` with rank `R - 1`, where R is the rank of the `SparseTensor` inputs `hypothesis` and `truth`.
Show Example
# 'hypothesis' is a tensor of shape `[2, 1]` with variable-length values:
# (0,0) = ["a"]
# (1,0) = ["b"]
hypothesis = tf.SparseTensor(
[[0, 0, 0],
[1, 0, 0]],
["a", "b"],
(2, 1, 1)) # 'truth' is a tensor of shape `[2, 2]` with variable-length values:
# (0,0) = []
# (0,1) = ["a"]
# (1,0) = ["b", "c"]
# (1,1) = ["a"]
truth = tf.SparseTensor(
[[0, 1, 0],
[1, 0, 0],
[1, 0, 1],
[1, 1, 0]],
["a", "b", "c", "a"],
(2, 2, 2)) normalize = True
Tensor edit_distance(SparseTensor hypothesis, ValueTuple<object> truth, bool normalize, string name)
Computes the Levenshtein distance between sequences. This operation takes variable-length sequences (`hypothesis` and `truth`),
each provided as a `SparseTensor`, and computes the Levenshtein distance.
You can normalize the edit distance by length of `truth` by setting
`normalize` to true. For example, given the following input:
This operation would return the following:
Parameters
-
SparseTensorhypothesis - A `SparseTensor` containing hypothesis sequences.
-
ValueTuple<object>truth - A `SparseTensor` containing truth sequences.
-
boolnormalize - A `bool`. If `True`, normalizes the Levenshtein distance by length of `truth.`
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A dense `Tensor` with rank `R - 1`, where R is the rank of the `SparseTensor` inputs `hypothesis` and `truth`.
Show Example
# 'hypothesis' is a tensor of shape `[2, 1]` with variable-length values:
# (0,0) = ["a"]
# (1,0) = ["b"]
hypothesis = tf.SparseTensor(
[[0, 0, 0],
[1, 0, 0]],
["a", "b"],
(2, 1, 1)) # 'truth' is a tensor of shape `[2, 2]` with variable-length values:
# (0,0) = []
# (0,1) = ["a"]
# (1,0) = ["b", "c"]
# (1,1) = ["a"]
truth = tf.SparseTensor(
[[0, 1, 0],
[1, 0, 0],
[1, 0, 1],
[1, 1, 0]],
["a", "b", "c", "a"],
(2, 2, 2)) normalize = True
Tensor edit_distance(ValueTuple<object> hypothesis, SparseTensor truth, bool normalize, string name)
Computes the Levenshtein distance between sequences. This operation takes variable-length sequences (`hypothesis` and `truth`),
each provided as a `SparseTensor`, and computes the Levenshtein distance.
You can normalize the edit distance by length of `truth` by setting
`normalize` to true. For example, given the following input:
This operation would return the following:
Parameters
-
ValueTuple<object>hypothesis - A `SparseTensor` containing hypothesis sequences.
-
SparseTensortruth - A `SparseTensor` containing truth sequences.
-
boolnormalize - A `bool`. If `True`, normalizes the Levenshtein distance by length of `truth.`
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A dense `Tensor` with rank `R - 1`, where R is the rank of the `SparseTensor` inputs `hypothesis` and `truth`.
Show Example
# 'hypothesis' is a tensor of shape `[2, 1]` with variable-length values:
# (0,0) = ["a"]
# (1,0) = ["b"]
hypothesis = tf.SparseTensor(
[[0, 0, 0],
[1, 0, 0]],
["a", "b"],
(2, 1, 1)) # 'truth' is a tensor of shape `[2, 2]` with variable-length values:
# (0,0) = []
# (0,1) = ["a"]
# (1,0) = ["b", "c"]
# (1,1) = ["a"]
truth = tf.SparseTensor(
[[0, 1, 0],
[1, 0, 0],
[1, 0, 1],
[1, 1, 0]],
["a", "b", "c", "a"],
(2, 2, 2)) normalize = True
object edit_distance_dyn(object hypothesis, object truth, ImplicitContainer<T> normalize, ImplicitContainer<T> name)
Computes the Levenshtein distance between sequences. This operation takes variable-length sequences (`hypothesis` and `truth`),
each provided as a `SparseTensor`, and computes the Levenshtein distance.
You can normalize the edit distance by length of `truth` by setting
`normalize` to true. For example, given the following input:
This operation would return the following:
Parameters
-
objecthypothesis - A `SparseTensor` containing hypothesis sequences.
-
objecttruth - A `SparseTensor` containing truth sequences.
-
ImplicitContainer<T>normalize - A `bool`. If `True`, normalizes the Levenshtein distance by length of `truth.`
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - A dense `Tensor` with rank `R - 1`, where R is the rank of the `SparseTensor` inputs `hypothesis` and `truth`.
Show Example
# 'hypothesis' is a tensor of shape `[2, 1]` with variable-length values:
# (0,0) = ["a"]
# (1,0) = ["b"]
hypothesis = tf.SparseTensor(
[[0, 0, 0],
[1, 0, 0]],
["a", "b"],
(2, 1, 1)) # 'truth' is a tensor of shape `[2, 2]` with variable-length values:
# (0,0) = []
# (0,1) = ["a"]
# (1,0) = ["b", "c"]
# (1,1) = ["a"]
truth = tf.SparseTensor(
[[0, 1, 0],
[1, 0, 0],
[1, 0, 1],
[1, 1, 0]],
["a", "b", "c", "a"],
(2, 2, 2)) normalize = True
object einsum(string equation, Object[] inputs)
Tensor contraction over specified indices and outer product. This function returns a tensor whose elements are defined by `equation`,
which is written in a shorthand form inspired by the Einstein summation
convention. As an example, consider multiplying two matrices
A and B to form a matrix C. The elements of C are given by: ```
C[i,k] = sum_j A[i,j] * B[j,k]
``` The corresponding `equation` is: ```
ij,jk->ik
``` In general, the `equation` is obtained from the more familiar element-wise
equation by
1. removing variable names, brackets, and commas,
2. replacing "*" with ",",
3. dropping summation signs, and
4. moving the output to the right, and replacing "=" with "->". Many common operations can be expressed in this way.
To enable and control broadcasting, use an ellipsis. For example, to do
batch matrix multiplication, you could use:
This function behaves like `numpy.einsum`, but does not support: * Subscripts where an axis appears more than once for a single input
(e.g. `ijj,k->ik`) unless it is a trace (e.g. `ijji`).
Parameters
-
stringequation - a `str` describing the contraction, in the same format as `numpy.einsum`.
-
Object[]inputs - the inputs to contract (each one a `Tensor`), whose shapes should be consistent with `equation`.
Returns
-
object - The contracted `Tensor`, with shape determined by `equation`.
Show Example
# Matrix multiplication
>>> einsum('ij,jk->ik', m0, m1) # output[i,k] = sum_j m0[i,j] * m1[j, k] # Dot product
>>> einsum('i,i->', u, v) # output = sum_i u[i]*v[i] # Outer product
>>> einsum('i,j->ij', u, v) # output[i,j] = u[i]*v[j] # Transpose
>>> einsum('ij->ji', m) # output[j,i] = m[i,j] # Trace
>>> einsum('ii', m) # output[j,i] = trace(m) = sum_i m[i, i] # Batch matrix multiplication
>>> einsum('aij,ajk->aik', s, t) # out[a,i,k] = sum_j s[a,i,j] * t[a, j, k]
object einsum(string equation, IDictionary<string, object> kwargs, Object[] inputs)
Tensor contraction over specified indices and outer product. This function returns a tensor whose elements are defined by `equation`,
which is written in a shorthand form inspired by the Einstein summation
convention. As an example, consider multiplying two matrices
A and B to form a matrix C. The elements of C are given by: ```
C[i,k] = sum_j A[i,j] * B[j,k]
``` The corresponding `equation` is: ```
ij,jk->ik
``` In general, the `equation` is obtained from the more familiar element-wise
equation by
1. removing variable names, brackets, and commas,
2. replacing "*" with ",",
3. dropping summation signs, and
4. moving the output to the right, and replacing "=" with "->". Many common operations can be expressed in this way.
To enable and control broadcasting, use an ellipsis. For example, to do
batch matrix multiplication, you could use:
This function behaves like `numpy.einsum`, but does not support: * Subscripts where an axis appears more than once for a single input
(e.g. `ijj,k->ik`) unless it is a trace (e.g. `ijji`).
Parameters
-
stringequation - a `str` describing the contraction, in the same format as `numpy.einsum`.
-
IDictionary<string, object>kwargs -
Object[]inputs - the inputs to contract (each one a `Tensor`), whose shapes should be consistent with `equation`.
Returns
-
object - The contracted `Tensor`, with shape determined by `equation`.
Show Example
# Matrix multiplication
>>> einsum('ij,jk->ik', m0, m1) # output[i,k] = sum_j m0[i,j] * m1[j, k] # Dot product
>>> einsum('i,i->', u, v) # output = sum_i u[i]*v[i] # Outer product
>>> einsum('i,j->ij', u, v) # output[i,j] = u[i]*v[j] # Transpose
>>> einsum('ij->ji', m) # output[j,i] = m[i,j] # Trace
>>> einsum('ii', m) # output[j,i] = trace(m) = sum_i m[i, i] # Batch matrix multiplication
>>> einsum('aij,ajk->aik', s, t) # out[a,i,k] = sum_j s[a,i,j] * t[a, j, k]
object einsum_dyn(object equation, IDictionary<string, object> kwargs, Object[] inputs)
Tensor contraction over specified indices and outer product. This function returns a tensor whose elements are defined by `equation`,
which is written in a shorthand form inspired by the Einstein summation
convention. As an example, consider multiplying two matrices
A and B to form a matrix C. The elements of C are given by: ```
C[i,k] = sum_j A[i,j] * B[j,k]
``` The corresponding `equation` is: ```
ij,jk->ik
``` In general, the `equation` is obtained from the more familiar element-wise
equation by
1. removing variable names, brackets, and commas,
2. replacing "*" with ",",
3. dropping summation signs, and
4. moving the output to the right, and replacing "=" with "->". Many common operations can be expressed in this way.
To enable and control broadcasting, use an ellipsis. For example, to do
batch matrix multiplication, you could use:
This function behaves like `numpy.einsum`, but does not support: * Subscripts where an axis appears more than once for a single input
(e.g. `ijj,k->ik`) unless it is a trace (e.g. `ijji`).
Parameters
-
objectequation - a `str` describing the contraction, in the same format as `numpy.einsum`.
-
IDictionary<string, object>kwargs -
Object[]inputs - the inputs to contract (each one a `Tensor`), whose shapes should be consistent with `equation`.
Returns
-
object - The contracted `Tensor`, with shape determined by `equation`.
Show Example
# Matrix multiplication
>>> einsum('ij,jk->ik', m0, m1) # output[i,k] = sum_j m0[i,j] * m1[j, k] # Dot product
>>> einsum('i,i->', u, v) # output = sum_i u[i]*v[i] # Outer product
>>> einsum('i,j->ij', u, v) # output[i,j] = u[i]*v[j] # Transpose
>>> einsum('ij->ji', m) # output[j,i] = m[i,j] # Trace
>>> einsum('ii', m) # output[j,i] = trace(m) = sum_i m[i, i] # Batch matrix multiplication
>>> einsum('aij,ajk->aik', s, t) # out[a,i,k] = sum_j s[a,i,j] * t[a, j, k]
object einsum_dyn(object equation, Object[] inputs)
Tensor contraction over specified indices and outer product. This function returns a tensor whose elements are defined by `equation`,
which is written in a shorthand form inspired by the Einstein summation
convention. As an example, consider multiplying two matrices
A and B to form a matrix C. The elements of C are given by: ```
C[i,k] = sum_j A[i,j] * B[j,k]
``` The corresponding `equation` is: ```
ij,jk->ik
``` In general, the `equation` is obtained from the more familiar element-wise
equation by
1. removing variable names, brackets, and commas,
2. replacing "*" with ",",
3. dropping summation signs, and
4. moving the output to the right, and replacing "=" with "->". Many common operations can be expressed in this way.
To enable and control broadcasting, use an ellipsis. For example, to do
batch matrix multiplication, you could use:
This function behaves like `numpy.einsum`, but does not support: * Subscripts where an axis appears more than once for a single input
(e.g. `ijj,k->ik`) unless it is a trace (e.g. `ijji`).
Parameters
-
objectequation - a `str` describing the contraction, in the same format as `numpy.einsum`.
-
Object[]inputs - the inputs to contract (each one a `Tensor`), whose shapes should be consistent with `equation`.
Returns
-
object - The contracted `Tensor`, with shape determined by `equation`.
Show Example
# Matrix multiplication
>>> einsum('ij,jk->ik', m0, m1) # output[i,k] = sum_j m0[i,j] * m1[j, k] # Dot product
>>> einsum('i,i->', u, v) # output = sum_i u[i]*v[i] # Outer product
>>> einsum('i,j->ij', u, v) # output[i,j] = u[i]*v[j] # Transpose
>>> einsum('ij->ji', m) # output[j,i] = m[i,j] # Trace
>>> einsum('ii', m) # output[j,i] = trace(m) = sum_i m[i, i] # Batch matrix multiplication
>>> einsum('aij,ajk->aik', s, t) # out[a,i,k] = sum_j s[a,i,j] * t[a, j, k]
void enable_control_flow_v2()
Use control flow v2. control flow v2 (cfv2) is an improved version of control flow in TensorFlow
with support for higher order derivatives. Enabling cfv2 will change the
graph/function representation of control flow, e.g.,
tf.while_loop and
tf.cond will generate functional `While` and `If` ops instead of low-level
`Switch`, `Merge` etc. ops. Note: Importing and running graphs exported
with old control flow will still be supported. Calling tf.enable_control_flow_v2() lets you opt-in to this TensorFlow 2.0
feature. Note: v2 control flow is always enabled inside of tf.function. Calling this
function is not required.
object enable_control_flow_v2_dyn()
Use control flow v2. control flow v2 (cfv2) is an improved version of control flow in TensorFlow
with support for higher order derivatives. Enabling cfv2 will change the
graph/function representation of control flow, e.g.,
tf.while_loop and
tf.cond will generate functional `While` and `If` ops instead of low-level
`Switch`, `Merge` etc. ops. Note: Importing and running graphs exported
with old control flow will still be supported. Calling tf.enable_control_flow_v2() lets you opt-in to this TensorFlow 2.0
feature. Note: v2 control flow is always enabled inside of tf.function. Calling this
function is not required.
object enable_eager_execution(object config, object device_policy, object execution_mode)
Enables eager execution for the lifetime of this program. Eager execution provides an imperative interface to TensorFlow. With eager
execution enabled, TensorFlow functions execute operations immediately (as
opposed to adding to a graph to be executed later in a `tf.compat.v1.Session`)
and
return concrete values (as opposed to symbolic references to a node in a
computational graph).
Eager execution cannot be enabled after TensorFlow APIs have been used to
create or execute graphs. It is typically recommended to invoke this function
at program startup and not in a library (as most libraries should be usable
both with and without eager execution).
Parameters
-
objectconfig - (Optional.) A `tf.compat.v1.ConfigProto` to use to configure the environment in which operations are executed. Note that `tf.compat.v1.ConfigProto` is also used to configure graph execution (via `tf.compat.v1.Session`) and many options within `tf.compat.v1.ConfigProto` are not implemented (or are irrelevant) when eager execution is enabled.
-
objectdevice_policy - (Optional.) Policy controlling how operations requiring inputs on a specific device (e.g., a GPU 0) handle inputs on a different device (e.g. GPU 1 or CPU). When set to None, an appropriate value will be picked automatically. The value picked may change between TensorFlow releases. Valid values: - tf.contrib.eager.DEVICE_PLACEMENT_EXPLICIT: raises an error if the placement is not correct. - tf.contrib.eager.DEVICE_PLACEMENT_WARN: copies the tensors which are not on the right device but logs a warning. - tf.contrib.eager.DEVICE_PLACEMENT_SILENT: silently copies the tensors. Note that this may hide performance problems as there is no notification provided when operations are blocked on the tensor being copied between devices. - tf.contrib.eager.DEVICE_PLACEMENT_SILENT_FOR_INT32: silently copies int32 tensors, raising errors on the other ones.
-
objectexecution_mode - (Optional.) Policy controlling how operations dispatched are actually executed. When set to None, an appropriate value will be picked automatically. The value picked may change between TensorFlow releases. Valid values: - tf.contrib.eager.SYNC: executes each operation synchronously. - tf.contrib.eager.ASYNC: executes each operation asynchronously. These operations may return "non-ready" handles.
Show Example
tf.compat.v1.enable_eager_execution() # After eager execution is enabled, operations are executed as they are # defined and Tensor objects hold concrete values, which can be accessed as # numpy.ndarray`s through the numpy() method. assert tf.multiply(6, 7).numpy() == 42
object enable_eager_execution_dyn(object config, object device_policy, object execution_mode)
Enables eager execution for the lifetime of this program. Eager execution provides an imperative interface to TensorFlow. With eager
execution enabled, TensorFlow functions execute operations immediately (as
opposed to adding to a graph to be executed later in a `tf.compat.v1.Session`)
and
return concrete values (as opposed to symbolic references to a node in a
computational graph).
Eager execution cannot be enabled after TensorFlow APIs have been used to
create or execute graphs. It is typically recommended to invoke this function
at program startup and not in a library (as most libraries should be usable
both with and without eager execution).
Parameters
-
objectconfig - (Optional.) A `tf.compat.v1.ConfigProto` to use to configure the environment in which operations are executed. Note that `tf.compat.v1.ConfigProto` is also used to configure graph execution (via `tf.compat.v1.Session`) and many options within `tf.compat.v1.ConfigProto` are not implemented (or are irrelevant) when eager execution is enabled.
-
objectdevice_policy - (Optional.) Policy controlling how operations requiring inputs on a specific device (e.g., a GPU 0) handle inputs on a different device (e.g. GPU 1 or CPU). When set to None, an appropriate value will be picked automatically. The value picked may change between TensorFlow releases. Valid values: - tf.contrib.eager.DEVICE_PLACEMENT_EXPLICIT: raises an error if the placement is not correct. - tf.contrib.eager.DEVICE_PLACEMENT_WARN: copies the tensors which are not on the right device but logs a warning. - tf.contrib.eager.DEVICE_PLACEMENT_SILENT: silently copies the tensors. Note that this may hide performance problems as there is no notification provided when operations are blocked on the tensor being copied between devices. - tf.contrib.eager.DEVICE_PLACEMENT_SILENT_FOR_INT32: silently copies int32 tensors, raising errors on the other ones.
-
objectexecution_mode - (Optional.) Policy controlling how operations dispatched are actually executed. When set to None, an appropriate value will be picked automatically. The value picked may change between TensorFlow releases. Valid values: - tf.contrib.eager.SYNC: executes each operation synchronously. - tf.contrib.eager.ASYNC: executes each operation asynchronously. These operations may return "non-ready" handles.
Show Example
tf.compat.v1.enable_eager_execution() # After eager execution is enabled, operations are executed as they are # defined and Tensor objects hold concrete values, which can be accessed as # numpy.ndarray`s through the numpy() method. assert tf.multiply(6, 7).numpy() == 42
void enable_tensor_equality()
Compare Tensors with element-wise comparison and thus be unhashable. Comparing tensors with element-wise allows comparisons such as
tf.Variable(1.0) == 1.0. Element-wise equality implies that tensors are
unhashable. Thus tensors can no longer be directly used in sets or as a key in
a dictionary.
object enable_tensor_equality_dyn()
Compare Tensors with element-wise comparison and thus be unhashable. Comparing tensors with element-wise allows comparisons such as
tf.Variable(1.0) == 1.0. Element-wise equality implies that tensors are
unhashable. Thus tensors can no longer be directly used in sets or as a key in
a dictionary.
void enable_v2_behavior()
Enables TensorFlow 2.x behaviors. This function can be called at the beginning of the program (before `Tensors`,
`Graphs` or other structures have been created, and before devices have been
initialized. It switches all global behaviors that are different between
TensorFlow 1.x and 2.x to behave as intended for 2.x. This function is called in the main TensorFlow `__init__.py` file, user should
not need to call it, except during complex migrations.
object enable_v2_behavior_dyn()
Enables TensorFlow 2.x behaviors. This function can be called at the beginning of the program (before `Tensors`,
`Graphs` or other structures have been created, and before devices have been
initialized. It switches all global behaviors that are different between
TensorFlow 1.x and 2.x to behave as intended for 2.x. This function is called in the main TensorFlow `__init__.py` file, user should
not need to call it, except during complex migrations.
void enable_v2_tensorshape()
In TensorFlow 2.0, iterating over a TensorShape instance returns values. This enables the new behavior. Concretely, `tensor_shape[i]` returned a Dimension instance in V1, but
it V2 it returns either an integer, or None. Examples: ```
#######################
# If you had this in V1:
value = tensor_shape[i].value # Do this in V2 instead:
value = tensor_shape[i] #######################
# If you had this in V1:
for dim in tensor_shape:
value = dim.value
print(value) # Do this in V2 instead:
for value in tensor_shape:
print(value) #######################
# If you had this in V1:
dim = tensor_shape[i]
dim.assert_is_compatible_with(other_shape) # or using any other shape method # Do this in V2 instead:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i]
dim.assert_is_compatible_with(other_shape) # or using any other shape method # The V2 suggestion above is more explicit, which will save you from
# the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be.
```
object enable_v2_tensorshape_dyn()
In TensorFlow 2.0, iterating over a TensorShape instance returns values. This enables the new behavior. Concretely, `tensor_shape[i]` returned a Dimension instance in V1, but
it V2 it returns either an integer, or None. Examples: ```
#######################
# If you had this in V1:
value = tensor_shape[i].value # Do this in V2 instead:
value = tensor_shape[i] #######################
# If you had this in V1:
for dim in tensor_shape:
value = dim.value
print(value) # Do this in V2 instead:
for value in tensor_shape:
print(value) #######################
# If you had this in V1:
dim = tensor_shape[i]
dim.assert_is_compatible_with(other_shape) # or using any other shape method # Do this in V2 instead:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i]
dim.assert_is_compatible_with(other_shape) # or using any other shape method # The V2 suggestion above is more explicit, which will save you from
# the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be.
```
Tensor encode_base64(IGraphNodeBase input, bool pad, string name)
Encode strings into web-safe base64 format. Refer to the following article for more information on base64 format:
en.wikipedia.org/wiki/Base64. Base64 strings may have padding with '=' at the
end so that the encoded has length multiple of 4. See Padding section of the
link above. Web-safe means that the encoder uses - and _ instead of + and /.
Parameters
-
IGraphNodeBaseinput - A `Tensor` of type `string`. Strings to be encoded.
-
boolpad - An optional `bool`. Defaults to `False`. Bool whether padding is applied at the ends.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `string`.
object encode_base64_dyn(object input, ImplicitContainer<T> pad, object name)
Encode strings into web-safe base64 format. Refer to the following article for more information on base64 format:
en.wikipedia.org/wiki/Base64. Base64 strings may have padding with '=' at the
end so that the encoded has length multiple of 4. See Padding section of the
link above. Web-safe means that the encoder uses - and _ instead of + and /.
Parameters
-
objectinput - A `Tensor` of type `string`. Strings to be encoded.
-
ImplicitContainer<T>pad - An optional `bool`. Defaults to `False`. Bool whether padding is applied at the ends.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `string`.
Tensor equal(PythonClassContainer x, IEnumerable<IGraphNodeBase> y, PythonFunctionContainer name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(IEnumerable<IGraphNodeBase> x, object y, PythonFunctionContainer name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objecty - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(PythonClassContainer x, IEnumerable<IGraphNodeBase> y, string name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(IEnumerable<IGraphNodeBase> x, PythonClassContainer y, string name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonClassContainery - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(IEnumerable<IGraphNodeBase> x, object y, string name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objecty - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(PythonClassContainer x, object y, string name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objecty - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(PythonClassContainer x, object y, PythonFunctionContainer name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objecty - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(object x, IEnumerable<object> y, string name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
IEnumerable<object>y - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(PythonClassContainer x, PythonClassContainer y, string name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonClassContainery - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(IEnumerable<IGraphNodeBase> x, IEnumerable<IGraphNodeBase> y, PythonFunctionContainer name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(PythonClassContainer x, PythonClassContainer y, PythonFunctionContainer name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonClassContainery - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(object x, object y, string name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objecty - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(object x, object y, PythonFunctionContainer name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objecty - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(IEnumerable<IGraphNodeBase> x, IEnumerable<IGraphNodeBase> y, string name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(object x, PythonClassContainer y, PythonFunctionContainer name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonClassContainery - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(object x, IEnumerable<IGraphNodeBase> y, PythonFunctionContainer name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(IEnumerable<IGraphNodeBase> x, PythonClassContainer y, PythonFunctionContainer name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonClassContainery - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
Tensor equal(object x, PythonClassContainer y, string name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonClassContainery - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
object equal_dyn(object x, object y, object name)
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objecty - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
object erf(IGraphNodeBase x, string name)
Computes the Gauss error function of `x` element-wise.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`. If `x` is a `SparseTensor`, returns `SparseTensor(x.indices, tf.math.erf(x.values,...), x.dense_shape)`
object erf_dyn(object x, object name)
Computes the Gauss error function of `x` element-wise.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`. If `x` is a `SparseTensor`, returns `SparseTensor(x.indices, tf.math.erf(x.values,...), x.dense_shape)`
object erfc(IGraphNodeBase x, string name)
Computes the complementary error function of `x` element-wise.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object erfc_dyn(object x, object name)
Computes the complementary error function of `x` element-wise.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
bool executing_eagerly()
Returns True if the current thread has eager execution enabled. Eager execution is typically enabled via
`tf.compat.v1.enable_eager_execution`, but may also be enabled within the
context of a Python function via tf.contrib.eager.py_func.
object executing_eagerly_dyn()
Returns True if the current thread has eager execution enabled. Eager execution is typically enabled via
`tf.compat.v1.enable_eager_execution`, but may also be enabled within the
context of a Python function via tf.contrib.eager.py_func.
object exp(IGraphNodeBase x, string name)
Computes exponential of x element-wise. \\(y = e^x\\). This function computes the exponential of every element in the input tensor.
i.e. `exp(x)` or `e^(x)`, where `x` is the input tensor.
`e` denotes Euler's number and is approximately equal to 2.718281.
Output is positive for any real input.
For complex numbers, the exponential value is calculated as follows: ```
e^(x+iy) = e^x * e^iy = e^x * (cos y + i sin y)
``` Let's consider complex number 1+1j as an example.
e^1 * (cos 1 + i sin 1) = 2.7182818284590 * (0.54030230586+0.8414709848j)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant(2.0)
tf.math.exp(x) ==> 7.389056 x = tf.constant([2.0, 8.0])
tf.math.exp(x) ==> array([7.389056, 2980.958], dtype=float32)
object exp_dyn(object x, object name)
Computes exponential of x element-wise. \\(y = e^x\\). This function computes the exponential of every element in the input tensor.
i.e. `exp(x)` or `e^(x)`, where `x` is the input tensor.
`e` denotes Euler's number and is approximately equal to 2.718281.
Output is positive for any real input.
For complex numbers, the exponential value is calculated as follows: ```
e^(x+iy) = e^x * e^iy = e^x * (cos y + i sin y)
``` Let's consider complex number 1+1j as an example.
e^1 * (cos 1 + i sin 1) = 2.7182818284590 * (0.54030230586+0.8414709848j)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant(2.0)
tf.math.exp(x) ==> 7.389056 x = tf.constant([2.0, 8.0])
tf.math.exp(x) ==> array([7.389056, 2980.958], dtype=float32)
Tensor expand_dims(IGraphNodeBase input, int axis, PythonFunctionContainer name, Nullable<int> dim)
Inserts a dimension of 1 into a tensor's shape. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dim)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation inserts a dimension of 1 at the
dimension index `axis` of `input`'s shape. The dimension index `axis` starts
at zero; if you specify a negative number for `axis` it is counted backward
from the end. This operation is useful if you want to add a batch dimension to a single
element. For example, if you have a single image of shape `[height, width,
channels]`, you can make it a batch of 1 image with `expand_dims(image, 0)`,
which will make the shape `[1, height, width, channels]`. Other examples:
This operation requires that: `-1-input.dims() <= dim <= input.dims()` This operation is related to `squeeze()`, which removes dimensions of
size 1.
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
intaxis - 0-D (scalar). Specifies the dimension index at which to expand the shape of `input`. Must be in the range `[-rank(input) - 1, rank(input)]`.
-
PythonFunctionContainername - The name of the output `Tensor` (optional).
-
Nullable<int>dim - 0-D (scalar). Equivalent to `axis`, to be deprecated.
Returns
-
Tensor - A `Tensor` with the same data as `input`, but its shape has an additional dimension of size 1 added.
Show Example
# 't' is a tensor of shape [2]
tf.shape(tf.expand_dims(t, 0)) # [1, 2]
tf.shape(tf.expand_dims(t, 1)) # [2, 1]
tf.shape(tf.expand_dims(t, -1)) # [2, 1] # 't2' is a tensor of shape [2, 3, 5]
tf.shape(tf.expand_dims(t2, 0)) # [1, 2, 3, 5]
tf.shape(tf.expand_dims(t2, 2)) # [2, 3, 1, 5]
tf.shape(tf.expand_dims(t2, 3)) # [2, 3, 5, 1]
Tensor expand_dims(IGraphNodeBase input, IEnumerable<int> axis, string name, Nullable<int> dim)
Inserts a dimension of 1 into a tensor's shape. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dim)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation inserts a dimension of 1 at the
dimension index `axis` of `input`'s shape. The dimension index `axis` starts
at zero; if you specify a negative number for `axis` it is counted backward
from the end. This operation is useful if you want to add a batch dimension to a single
element. For example, if you have a single image of shape `[height, width,
channels]`, you can make it a batch of 1 image with `expand_dims(image, 0)`,
which will make the shape `[1, height, width, channels]`. Other examples:
This operation requires that: `-1-input.dims() <= dim <= input.dims()` This operation is related to `squeeze()`, which removes dimensions of
size 1.
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
IEnumerable<int>axis - 0-D (scalar). Specifies the dimension index at which to expand the shape of `input`. Must be in the range `[-rank(input) - 1, rank(input)]`.
-
stringname - The name of the output `Tensor` (optional).
-
Nullable<int>dim - 0-D (scalar). Equivalent to `axis`, to be deprecated.
Returns
-
Tensor - A `Tensor` with the same data as `input`, but its shape has an additional dimension of size 1 added.
Show Example
# 't' is a tensor of shape [2]
tf.shape(tf.expand_dims(t, 0)) # [1, 2]
tf.shape(tf.expand_dims(t, 1)) # [2, 1]
tf.shape(tf.expand_dims(t, -1)) # [2, 1] # 't2' is a tensor of shape [2, 3, 5]
tf.shape(tf.expand_dims(t2, 0)) # [1, 2, 3, 5]
tf.shape(tf.expand_dims(t2, 2)) # [2, 3, 1, 5]
tf.shape(tf.expand_dims(t2, 3)) # [2, 3, 5, 1]
Tensor expand_dims(IGraphNodeBase input, IGraphNodeBase axis, string name, Nullable<int> dim)
Inserts a dimension of 1 into a tensor's shape. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dim)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation inserts a dimension of 1 at the
dimension index `axis` of `input`'s shape. The dimension index `axis` starts
at zero; if you specify a negative number for `axis` it is counted backward
from the end. This operation is useful if you want to add a batch dimension to a single
element. For example, if you have a single image of shape `[height, width,
channels]`, you can make it a batch of 1 image with `expand_dims(image, 0)`,
which will make the shape `[1, height, width, channels]`. Other examples:
This operation requires that: `-1-input.dims() <= dim <= input.dims()` This operation is related to `squeeze()`, which removes dimensions of
size 1.
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
IGraphNodeBaseaxis - 0-D (scalar). Specifies the dimension index at which to expand the shape of `input`. Must be in the range `[-rank(input) - 1, rank(input)]`.
-
stringname - The name of the output `Tensor` (optional).
-
Nullable<int>dim - 0-D (scalar). Equivalent to `axis`, to be deprecated.
Returns
-
Tensor - A `Tensor` with the same data as `input`, but its shape has an additional dimension of size 1 added.
Show Example
# 't' is a tensor of shape [2]
tf.shape(tf.expand_dims(t, 0)) # [1, 2]
tf.shape(tf.expand_dims(t, 1)) # [2, 1]
tf.shape(tf.expand_dims(t, -1)) # [2, 1] # 't2' is a tensor of shape [2, 3, 5]
tf.shape(tf.expand_dims(t2, 0)) # [1, 2, 3, 5]
tf.shape(tf.expand_dims(t2, 2)) # [2, 3, 1, 5]
tf.shape(tf.expand_dims(t2, 3)) # [2, 3, 5, 1]
Tensor expand_dims(IGraphNodeBase input, IEnumerable<int> axis, PythonFunctionContainer name, Nullable<int> dim)
Inserts a dimension of 1 into a tensor's shape. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dim)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation inserts a dimension of 1 at the
dimension index `axis` of `input`'s shape. The dimension index `axis` starts
at zero; if you specify a negative number for `axis` it is counted backward
from the end. This operation is useful if you want to add a batch dimension to a single
element. For example, if you have a single image of shape `[height, width,
channels]`, you can make it a batch of 1 image with `expand_dims(image, 0)`,
which will make the shape `[1, height, width, channels]`. Other examples:
This operation requires that: `-1-input.dims() <= dim <= input.dims()` This operation is related to `squeeze()`, which removes dimensions of
size 1.
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
IEnumerable<int>axis - 0-D (scalar). Specifies the dimension index at which to expand the shape of `input`. Must be in the range `[-rank(input) - 1, rank(input)]`.
-
PythonFunctionContainername - The name of the output `Tensor` (optional).
-
Nullable<int>dim - 0-D (scalar). Equivalent to `axis`, to be deprecated.
Returns
-
Tensor - A `Tensor` with the same data as `input`, but its shape has an additional dimension of size 1 added.
Show Example
# 't' is a tensor of shape [2]
tf.shape(tf.expand_dims(t, 0)) # [1, 2]
tf.shape(tf.expand_dims(t, 1)) # [2, 1]
tf.shape(tf.expand_dims(t, -1)) # [2, 1] # 't2' is a tensor of shape [2, 3, 5]
tf.shape(tf.expand_dims(t2, 0)) # [1, 2, 3, 5]
tf.shape(tf.expand_dims(t2, 2)) # [2, 3, 1, 5]
tf.shape(tf.expand_dims(t2, 3)) # [2, 3, 5, 1]
Tensor expand_dims(IGraphNodeBase input, IGraphNodeBase axis, PythonFunctionContainer name, Nullable<int> dim)
Inserts a dimension of 1 into a tensor's shape. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dim)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation inserts a dimension of 1 at the
dimension index `axis` of `input`'s shape. The dimension index `axis` starts
at zero; if you specify a negative number for `axis` it is counted backward
from the end. This operation is useful if you want to add a batch dimension to a single
element. For example, if you have a single image of shape `[height, width,
channels]`, you can make it a batch of 1 image with `expand_dims(image, 0)`,
which will make the shape `[1, height, width, channels]`. Other examples:
This operation requires that: `-1-input.dims() <= dim <= input.dims()` This operation is related to `squeeze()`, which removes dimensions of
size 1.
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
IGraphNodeBaseaxis - 0-D (scalar). Specifies the dimension index at which to expand the shape of `input`. Must be in the range `[-rank(input) - 1, rank(input)]`.
-
PythonFunctionContainername - The name of the output `Tensor` (optional).
-
Nullable<int>dim - 0-D (scalar). Equivalent to `axis`, to be deprecated.
Returns
-
Tensor - A `Tensor` with the same data as `input`, but its shape has an additional dimension of size 1 added.
Show Example
# 't' is a tensor of shape [2]
tf.shape(tf.expand_dims(t, 0)) # [1, 2]
tf.shape(tf.expand_dims(t, 1)) # [2, 1]
tf.shape(tf.expand_dims(t, -1)) # [2, 1] # 't2' is a tensor of shape [2, 3, 5]
tf.shape(tf.expand_dims(t2, 0)) # [1, 2, 3, 5]
tf.shape(tf.expand_dims(t2, 2)) # [2, 3, 1, 5]
tf.shape(tf.expand_dims(t2, 3)) # [2, 3, 5, 1]
Tensor expand_dims(IGraphNodeBase input, int axis, string name, Nullable<int> dim)
Inserts a dimension of 1 into a tensor's shape. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dim)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation inserts a dimension of 1 at the
dimension index `axis` of `input`'s shape. The dimension index `axis` starts
at zero; if you specify a negative number for `axis` it is counted backward
from the end. This operation is useful if you want to add a batch dimension to a single
element. For example, if you have a single image of shape `[height, width,
channels]`, you can make it a batch of 1 image with `expand_dims(image, 0)`,
which will make the shape `[1, height, width, channels]`. Other examples:
This operation requires that: `-1-input.dims() <= dim <= input.dims()` This operation is related to `squeeze()`, which removes dimensions of
size 1.
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
intaxis - 0-D (scalar). Specifies the dimension index at which to expand the shape of `input`. Must be in the range `[-rank(input) - 1, rank(input)]`.
-
stringname - The name of the output `Tensor` (optional).
-
Nullable<int>dim - 0-D (scalar). Equivalent to `axis`, to be deprecated.
Returns
-
Tensor - A `Tensor` with the same data as `input`, but its shape has an additional dimension of size 1 added.
Show Example
# 't' is a tensor of shape [2]
tf.shape(tf.expand_dims(t, 0)) # [1, 2]
tf.shape(tf.expand_dims(t, 1)) # [2, 1]
tf.shape(tf.expand_dims(t, -1)) # [2, 1] # 't2' is a tensor of shape [2, 3, 5]
tf.shape(tf.expand_dims(t2, 0)) # [1, 2, 3, 5]
tf.shape(tf.expand_dims(t2, 2)) # [2, 3, 1, 5]
tf.shape(tf.expand_dims(t2, 3)) # [2, 3, 5, 1]
object expand_dims_dyn(object input, object axis, object name, object dim)
Inserts a dimension of 1 into a tensor's shape. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dim)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation inserts a dimension of 1 at the
dimension index `axis` of `input`'s shape. The dimension index `axis` starts
at zero; if you specify a negative number for `axis` it is counted backward
from the end. This operation is useful if you want to add a batch dimension to a single
element. For example, if you have a single image of shape `[height, width,
channels]`, you can make it a batch of 1 image with `expand_dims(image, 0)`,
which will make the shape `[1, height, width, channels]`. Other examples:
This operation requires that: `-1-input.dims() <= dim <= input.dims()` This operation is related to `squeeze()`, which removes dimensions of
size 1.
Parameters
-
objectinput - A `Tensor`.
-
objectaxis - 0-D (scalar). Specifies the dimension index at which to expand the shape of `input`. Must be in the range `[-rank(input) - 1, rank(input)]`.
-
objectname - The name of the output `Tensor` (optional).
-
objectdim - 0-D (scalar). Equivalent to `axis`, to be deprecated.
Returns
-
object - A `Tensor` with the same data as `input`, but its shape has an additional dimension of size 1 added.
Show Example
# 't' is a tensor of shape [2]
tf.shape(tf.expand_dims(t, 0)) # [1, 2]
tf.shape(tf.expand_dims(t, 1)) # [2, 1]
tf.shape(tf.expand_dims(t, -1)) # [2, 1] # 't2' is a tensor of shape [2, 3, 5]
tf.shape(tf.expand_dims(t2, 0)) # [1, 2, 3, 5]
tf.shape(tf.expand_dims(t2, 2)) # [2, 3, 1, 5]
tf.shape(tf.expand_dims(t2, 3)) # [2, 3, 5, 1]
object expm1(IGraphNodeBase x, string name)
Computes `exp(x) - 1` element-wise. i.e. `exp(x) - 1` or `e^(x) - 1`, where `x` is the input tensor.
`e` denotes Euler's number and is approximately equal to 2.718281.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant(2.0)
tf.math.expm1(x) ==> 6.389056 x = tf.constant([2.0, 8.0])
tf.math.expm1(x) ==> array([6.389056, 2979.958], dtype=float32) x = tf.constant(1 + 1j)
tf.math.expm1(x) ==> (0.46869393991588515+2.2873552871788423j)
object expm1_dyn(object x, object name)
Computes `exp(x) - 1` element-wise. i.e. `exp(x) - 1` or `e^(x) - 1`, where `x` is the input tensor.
`e` denotes Euler's number and is approximately equal to 2.718281.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant(2.0)
tf.math.expm1(x) ==> 6.389056 x = tf.constant([2.0, 8.0])
tf.math.expm1(x) ==> array([6.389056, 2979.958], dtype=float32) x = tf.constant(1 + 1j)
tf.math.expm1(x) ==> (0.46869393991588515+2.2873552871788423j)
Tensor extract_image_patches(IGraphNodeBase images, IEnumerable<int> ksizes, IEnumerable<int> strides, IEnumerable<int> rates, PythonClassContainer padding, string name, object sizes)
Extract `patches` from `images` and put them in the "depth" output dimension.
Parameters
-
IGraphNodeBaseimages - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. 4-D Tensor with shape `[batch, in_rows, in_cols, depth]`.
-
IEnumerable<int>ksizes - A list of `ints` that has length `>= 4`. The size of the sliding window for each dimension of `images`.
-
IEnumerable<int>strides - A list of `ints` that has length `>= 4`. How far the centers of two consecutive patches are in the images. Must be: `[1, stride_rows, stride_cols, 1]`.
-
IEnumerable<int>rates - A list of `ints` that has length `>= 4`. Must be: `[1, rate_rows, rate_cols, 1]`. This is the input stride, specifying how far two consecutive patch samples are in the input. Equivalent to extracting patches with `patch_sizes_eff = patch_sizes + (patch_sizes - 1) * (rates - 1)`, followed by subsampling them spatially by a factor of `rates`. This is equivalent to `rate` in dilated (a.k.a. Atrous) convolutions.
-
PythonClassContainerpadding - A `string` from: `"SAME", "VALID"`. The type of padding algorithm to use.
-
stringname - A name for the operation (optional).
-
objectsizes
Returns
-
Tensor - A `Tensor`. Has the same type as `images`.
Tensor extract_image_patches(IGraphNodeBase images, object ksizes, IEnumerable<int> strides, IEnumerable<int> rates, PythonClassContainer padding, string name, object sizes)
Extract `patches` from `images` and put them in the "depth" output dimension.
Parameters
-
IGraphNodeBaseimages - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. 4-D Tensor with shape `[batch, in_rows, in_cols, depth]`.
-
objectksizes - A list of `ints` that has length `>= 4`. The size of the sliding window for each dimension of `images`.
-
IEnumerable<int>strides - A list of `ints` that has length `>= 4`. How far the centers of two consecutive patches are in the images. Must be: `[1, stride_rows, stride_cols, 1]`.
-
IEnumerable<int>rates - A list of `ints` that has length `>= 4`. Must be: `[1, rate_rows, rate_cols, 1]`. This is the input stride, specifying how far two consecutive patch samples are in the input. Equivalent to extracting patches with `patch_sizes_eff = patch_sizes + (patch_sizes - 1) * (rates - 1)`, followed by subsampling them spatially by a factor of `rates`. This is equivalent to `rate` in dilated (a.k.a. Atrous) convolutions.
-
PythonClassContainerpadding - A `string` from: `"SAME", "VALID"`. The type of padding algorithm to use.
-
stringname - A name for the operation (optional).
-
objectsizes
Returns
-
Tensor - A `Tensor`. Has the same type as `images`.
Tensor extract_image_patches(IGraphNodeBase images, object ksizes, IEnumerable<int> strides, IEnumerable<int> rates, string padding, string name, object sizes)
Extract `patches` from `images` and put them in the "depth" output dimension.
Parameters
-
IGraphNodeBaseimages - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. 4-D Tensor with shape `[batch, in_rows, in_cols, depth]`.
-
objectksizes - A list of `ints` that has length `>= 4`. The size of the sliding window for each dimension of `images`.
-
IEnumerable<int>strides - A list of `ints` that has length `>= 4`. How far the centers of two consecutive patches are in the images. Must be: `[1, stride_rows, stride_cols, 1]`.
-
IEnumerable<int>rates - A list of `ints` that has length `>= 4`. Must be: `[1, rate_rows, rate_cols, 1]`. This is the input stride, specifying how far two consecutive patch samples are in the input. Equivalent to extracting patches with `patch_sizes_eff = patch_sizes + (patch_sizes - 1) * (rates - 1)`, followed by subsampling them spatially by a factor of `rates`. This is equivalent to `rate` in dilated (a.k.a. Atrous) convolutions.
-
stringpadding - A `string` from: `"SAME", "VALID"`. The type of padding algorithm to use.
-
stringname - A name for the operation (optional).
-
objectsizes
Returns
-
Tensor - A `Tensor`. Has the same type as `images`.
Tensor extract_image_patches(IGraphNodeBase images, IEnumerable<int> ksizes, IEnumerable<int> strides, IEnumerable<int> rates, IEnumerable<int> padding, string name, object sizes)
Extract `patches` from `images` and put them in the "depth" output dimension.
Parameters
-
IGraphNodeBaseimages - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. 4-D Tensor with shape `[batch, in_rows, in_cols, depth]`.
-
IEnumerable<int>ksizes - A list of `ints` that has length `>= 4`. The size of the sliding window for each dimension of `images`.
-
IEnumerable<int>strides - A list of `ints` that has length `>= 4`. How far the centers of two consecutive patches are in the images. Must be: `[1, stride_rows, stride_cols, 1]`.
-
IEnumerable<int>rates - A list of `ints` that has length `>= 4`. Must be: `[1, rate_rows, rate_cols, 1]`. This is the input stride, specifying how far two consecutive patch samples are in the input. Equivalent to extracting patches with `patch_sizes_eff = patch_sizes + (patch_sizes - 1) * (rates - 1)`, followed by subsampling them spatially by a factor of `rates`. This is equivalent to `rate` in dilated (a.k.a. Atrous) convolutions.
-
IEnumerable<int>padding - A `string` from: `"SAME", "VALID"`. The type of padding algorithm to use.
-
stringname - A name for the operation (optional).
-
objectsizes
Returns
-
Tensor - A `Tensor`. Has the same type as `images`.
Tensor extract_image_patches(IGraphNodeBase images, IEnumerable<int> ksizes, IEnumerable<int> strides, IEnumerable<int> rates, string padding, string name, object sizes)
Extract `patches` from `images` and put them in the "depth" output dimension.
Parameters
-
IGraphNodeBaseimages - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. 4-D Tensor with shape `[batch, in_rows, in_cols, depth]`.
-
IEnumerable<int>ksizes - A list of `ints` that has length `>= 4`. The size of the sliding window for each dimension of `images`.
-
IEnumerable<int>strides - A list of `ints` that has length `>= 4`. How far the centers of two consecutive patches are in the images. Must be: `[1, stride_rows, stride_cols, 1]`.
-
IEnumerable<int>rates - A list of `ints` that has length `>= 4`. Must be: `[1, rate_rows, rate_cols, 1]`. This is the input stride, specifying how far two consecutive patch samples are in the input. Equivalent to extracting patches with `patch_sizes_eff = patch_sizes + (patch_sizes - 1) * (rates - 1)`, followed by subsampling them spatially by a factor of `rates`. This is equivalent to `rate` in dilated (a.k.a. Atrous) convolutions.
-
stringpadding - A `string` from: `"SAME", "VALID"`. The type of padding algorithm to use.
-
stringname - A name for the operation (optional).
-
objectsizes
Returns
-
Tensor - A `Tensor`. Has the same type as `images`.
Tensor extract_image_patches(IGraphNodeBase images, object ksizes, IEnumerable<int> strides, IEnumerable<int> rates, IEnumerable<int> padding, string name, object sizes)
Extract `patches` from `images` and put them in the "depth" output dimension.
Parameters
-
IGraphNodeBaseimages - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. 4-D Tensor with shape `[batch, in_rows, in_cols, depth]`.
-
objectksizes - A list of `ints` that has length `>= 4`. The size of the sliding window for each dimension of `images`.
-
IEnumerable<int>strides - A list of `ints` that has length `>= 4`. How far the centers of two consecutive patches are in the images. Must be: `[1, stride_rows, stride_cols, 1]`.
-
IEnumerable<int>rates - A list of `ints` that has length `>= 4`. Must be: `[1, rate_rows, rate_cols, 1]`. This is the input stride, specifying how far two consecutive patch samples are in the input. Equivalent to extracting patches with `patch_sizes_eff = patch_sizes + (patch_sizes - 1) * (rates - 1)`, followed by subsampling them spatially by a factor of `rates`. This is equivalent to `rate` in dilated (a.k.a. Atrous) convolutions.
-
IEnumerable<int>padding - A `string` from: `"SAME", "VALID"`. The type of padding algorithm to use.
-
stringname - A name for the operation (optional).
-
objectsizes
Returns
-
Tensor - A `Tensor`. Has the same type as `images`.
object extract_image_patches_dyn(object images, object ksizes, object strides, object rates, object padding, object name, object sizes)
Extract `patches` from `images` and put them in the "depth" output dimension.
Parameters
-
objectimages - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. 4-D Tensor with shape `[batch, in_rows, in_cols, depth]`.
-
objectksizes - A list of `ints` that has length `>= 4`. The size of the sliding window for each dimension of `images`.
-
objectstrides - A list of `ints` that has length `>= 4`. How far the centers of two consecutive patches are in the images. Must be: `[1, stride_rows, stride_cols, 1]`.
-
objectrates - A list of `ints` that has length `>= 4`. Must be: `[1, rate_rows, rate_cols, 1]`. This is the input stride, specifying how far two consecutive patch samples are in the input. Equivalent to extracting patches with `patch_sizes_eff = patch_sizes + (patch_sizes - 1) * (rates - 1)`, followed by subsampling them spatially by a factor of `rates`. This is equivalent to `rate` in dilated (a.k.a. Atrous) convolutions.
-
objectpadding - A `string` from: `"SAME", "VALID"`. The type of padding algorithm to use.
-
objectname - A name for the operation (optional).
-
objectsizes
Returns
-
object - A `Tensor`. Has the same type as `images`.
Tensor extract_volume_patches(IGraphNodeBase input, IEnumerable<int> ksizes, IEnumerable<int> strides, string padding, string name)
Extract `patches` from `input` and put them in the "depth" output dimension. 3D extension of `extract_image_patches`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. 5-D Tensor with shape `[batch, in_planes, in_rows, in_cols, depth]`.
-
IEnumerable<int>ksizes - A list of `ints` that has length `>= 5`. The size of the sliding window for each dimension of `input`.
-
IEnumerable<int>strides - A list of `ints` that has length `>= 5`. 1-D of length 5. How far the centers of two consecutive patches are in `input`. Must be: `[1, stride_planes, stride_rows, stride_cols, 1]`.
-
stringpadding - A `string` from: `"SAME", "VALID"`. The type of padding algorithm to use. We specify the size-related attributes as: ```python ksizes = [1, ksize_planes, ksize_rows, ksize_cols, 1] strides = [1, stride_planes, strides_rows, strides_cols, 1] ```
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object extract_volume_patches_dyn(object input, object ksizes, object strides, object padding, object name)
Extract `patches` from `input` and put them in the "depth" output dimension. 3D extension of `extract_image_patches`.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`. 5-D Tensor with shape `[batch, in_planes, in_rows, in_cols, depth]`.
-
objectksizes - A list of `ints` that has length `>= 5`. The size of the sliding window for each dimension of `input`.
-
objectstrides - A list of `ints` that has length `>= 5`. 1-D of length 5. How far the centers of two consecutive patches are in `input`. Must be: `[1, stride_planes, stride_rows, stride_cols, 1]`.
-
objectpadding - A `string` from: `"SAME", "VALID"`. The type of padding algorithm to use. We specify the size-related attributes as: ```python ksizes = [1, ksize_planes, ksize_rows, ksize_cols, 1] strides = [1, stride_planes, strides_rows, strides_cols, 1] ```
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor eye(IndexedSlices num_rows, IGraphNodeBase num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
IndexedSlicesnum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
IGraphNodeBasenum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(TensorShape num_rows, int num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
TensorShapenum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
intnum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(ValueTuple<PythonClassContainer, PythonClassContainer> num_rows, int num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>num_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
intnum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(object num_rows, IGraphNodeBase num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
objectnum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
IGraphNodeBasenum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(ValueTuple<PythonClassContainer, PythonClassContainer> num_rows, IGraphNodeBase num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>num_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
IGraphNodeBasenum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(object num_rows, int num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
objectnum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
intnum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(Dimension num_rows, int num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
Dimensionnum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
intnum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(IGraphNodeBase num_rows, IGraphNodeBase num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
IGraphNodeBasenum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
IGraphNodeBasenum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(IGraphNodeBase num_rows, int num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
IGraphNodeBasenum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
intnum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(Dimension num_rows, IGraphNodeBase num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
Dimensionnum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
IGraphNodeBasenum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(int num_rows, IGraphNodeBase num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
intnum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
IGraphNodeBasenum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(IndexedSlices num_rows, int num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
IndexedSlicesnum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
intnum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(TensorShape num_rows, IGraphNodeBase num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
TensorShapenum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
IGraphNodeBasenum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor eye(int num_rows, int num_columns, object batch_shape, ImplicitContainer<T> dtype, string name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
intnum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
intnum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
stringname - A name for this `Op`. Defaults to "eye".
Returns
-
Tensor - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
object eye_dyn(object num_rows, object num_columns, object batch_shape, ImplicitContainer<T> dtype, object name)
Construct an identity matrix, or a batch of matrices.
Parameters
-
objectnum_rows - Non-negative `int32` scalar `Tensor` giving the number of rows in each batch matrix.
-
objectnum_columns - Optional non-negative `int32` scalar `Tensor` giving the number of columns in each batch matrix. Defaults to `num_rows`.
-
objectbatch_shape - A list or tuple of Python integers or a 1-D `int32` `Tensor`. If provided, the returned `Tensor` will have leading batch dimensions of this shape.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`
-
objectname - A name for this `Op`. Defaults to "eye".
Returns
-
object - A `Tensor` of shape `batch_shape + [num_rows, num_columns]`
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
Tensor fake_quant_with_min_max_args(IGraphNodeBase inputs, double min, int max, int num_bits, bool narrow_range, string name)
Fake-quantize the 'inputs' tensor, type float to 'outputs' tensor of same type. Attributes `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. Quantization is called fake since the output is still in floating point.
Parameters
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`.
-
doublemin - An optional `float`. Defaults to `-6`.
-
intmax - An optional `float`. Defaults to `6`.
-
intnum_bits - An optional `int`. Defaults to `8`.
-
boolnarrow_range - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
Tensor fake_quant_with_min_max_args(IGraphNodeBase inputs, int min, double max, int num_bits, bool narrow_range, string name)
Fake-quantize the 'inputs' tensor, type float to 'outputs' tensor of same type. Attributes `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. Quantization is called fake since the output is still in floating point.
Parameters
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`.
-
intmin - An optional `float`. Defaults to `-6`.
-
doublemax - An optional `float`. Defaults to `6`.
-
intnum_bits - An optional `int`. Defaults to `8`.
-
boolnarrow_range - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
Tensor fake_quant_with_min_max_args(IGraphNodeBase inputs, int min, int max, int num_bits, bool narrow_range, string name)
Fake-quantize the 'inputs' tensor, type float to 'outputs' tensor of same type. Attributes `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. Quantization is called fake since the output is still in floating point.
Parameters
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`.
-
intmin - An optional `float`. Defaults to `-6`.
-
intmax - An optional `float`. Defaults to `6`.
-
intnum_bits - An optional `int`. Defaults to `8`.
-
boolnarrow_range - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
Tensor fake_quant_with_min_max_args(IGraphNodeBase inputs, double min, double max, int num_bits, bool narrow_range, string name)
Fake-quantize the 'inputs' tensor, type float to 'outputs' tensor of same type. Attributes `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. Quantization is called fake since the output is still in floating point.
Parameters
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`.
-
doublemin - An optional `float`. Defaults to `-6`.
-
doublemax - An optional `float`. Defaults to `6`.
-
intnum_bits - An optional `int`. Defaults to `8`.
-
boolnarrow_range - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
object fake_quant_with_min_max_args_dyn(object inputs, ImplicitContainer<T> min, ImplicitContainer<T> max, ImplicitContainer<T> num_bits, ImplicitContainer<T> narrow_range, object name)
Fake-quantize the 'inputs' tensor, type float to 'outputs' tensor of same type. Attributes `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. Quantization is called fake since the output is still in floating point.
Parameters
-
objectinputs - A `Tensor` of type `float32`.
-
ImplicitContainer<T>min - An optional `float`. Defaults to `-6`.
-
ImplicitContainer<T>max - An optional `float`. Defaults to `6`.
-
ImplicitContainer<T>num_bits - An optional `int`. Defaults to `8`.
-
ImplicitContainer<T>narrow_range - An optional `bool`. Defaults to `False`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `float32`.
Tensor fake_quant_with_min_max_args_gradient(IGraphNodeBase gradients, IGraphNodeBase inputs, double min, double max, int num_bits, bool narrow_range, string name)
Compute gradients for a FakeQuantWithMinMaxArgs operation.
Parameters
-
IGraphNodeBasegradients - A `Tensor` of type `float32`. Backpropagated gradients above the FakeQuantWithMinMaxArgs operation.
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`. Values passed as inputs to the FakeQuantWithMinMaxArgs operation.
-
doublemin - An optional `float`. Defaults to `-6`.
-
doublemax - An optional `float`. Defaults to `6`.
-
intnum_bits - An optional `int`. Defaults to `8`.
-
boolnarrow_range - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
Tensor fake_quant_with_min_max_args_gradient(IGraphNodeBase gradients, IGraphNodeBase inputs, double min, int max, int num_bits, bool narrow_range, string name)
Compute gradients for a FakeQuantWithMinMaxArgs operation.
Parameters
-
IGraphNodeBasegradients - A `Tensor` of type `float32`. Backpropagated gradients above the FakeQuantWithMinMaxArgs operation.
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`. Values passed as inputs to the FakeQuantWithMinMaxArgs operation.
-
doublemin - An optional `float`. Defaults to `-6`.
-
intmax - An optional `float`. Defaults to `6`.
-
intnum_bits - An optional `int`. Defaults to `8`.
-
boolnarrow_range - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
Tensor fake_quant_with_min_max_args_gradient(IGraphNodeBase gradients, IGraphNodeBase inputs, int min, double max, int num_bits, bool narrow_range, string name)
Compute gradients for a FakeQuantWithMinMaxArgs operation.
Parameters
-
IGraphNodeBasegradients - A `Tensor` of type `float32`. Backpropagated gradients above the FakeQuantWithMinMaxArgs operation.
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`. Values passed as inputs to the FakeQuantWithMinMaxArgs operation.
-
intmin - An optional `float`. Defaults to `-6`.
-
doublemax - An optional `float`. Defaults to `6`.
-
intnum_bits - An optional `int`. Defaults to `8`.
-
boolnarrow_range - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
Tensor fake_quant_with_min_max_args_gradient(IGraphNodeBase gradients, IGraphNodeBase inputs, int min, int max, int num_bits, bool narrow_range, string name)
Compute gradients for a FakeQuantWithMinMaxArgs operation.
Parameters
-
IGraphNodeBasegradients - A `Tensor` of type `float32`. Backpropagated gradients above the FakeQuantWithMinMaxArgs operation.
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`. Values passed as inputs to the FakeQuantWithMinMaxArgs operation.
-
intmin - An optional `float`. Defaults to `-6`.
-
intmax - An optional `float`. Defaults to `6`.
-
intnum_bits - An optional `int`. Defaults to `8`.
-
boolnarrow_range - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
object fake_quant_with_min_max_args_gradient_dyn(object gradients, object inputs, ImplicitContainer<T> min, ImplicitContainer<T> max, ImplicitContainer<T> num_bits, ImplicitContainer<T> narrow_range, object name)
Compute gradients for a FakeQuantWithMinMaxArgs operation.
Parameters
-
objectgradients - A `Tensor` of type `float32`. Backpropagated gradients above the FakeQuantWithMinMaxArgs operation.
-
objectinputs - A `Tensor` of type `float32`. Values passed as inputs to the FakeQuantWithMinMaxArgs operation.
-
ImplicitContainer<T>min - An optional `float`. Defaults to `-6`.
-
ImplicitContainer<T>max - An optional `float`. Defaults to `6`.
-
ImplicitContainer<T>num_bits - An optional `int`. Defaults to `8`.
-
ImplicitContainer<T>narrow_range - An optional `bool`. Defaults to `False`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `float32`.
Tensor fake_quant_with_min_max_vars(IGraphNodeBase inputs, IGraphNodeBase min, IGraphNodeBase max, int num_bits, bool narrow_range, string name)
Fake-quantize the 'inputs' tensor of type float via global float scalars `min` and `max` to 'outputs' tensor of same shape as `inputs`. `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. This operation has a gradient and thus allows for training `min` and `max`
values.
Parameters
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`.
-
IGraphNodeBasemin - A `Tensor` of type `float32`.
-
IGraphNodeBasemax - A `Tensor` of type `float32`.
-
intnum_bits - An optional `int`. Defaults to `8`.
-
boolnarrow_range - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
object fake_quant_with_min_max_vars_dyn(object inputs, object min, object max, ImplicitContainer<T> num_bits, ImplicitContainer<T> narrow_range, object name)
Fake-quantize the 'inputs' tensor of type float via global float scalars `min` and `max` to 'outputs' tensor of same shape as `inputs`. `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. This operation has a gradient and thus allows for training `min` and `max`
values.
Parameters
-
objectinputs - A `Tensor` of type `float32`.
-
objectmin - A `Tensor` of type `float32`.
-
objectmax - A `Tensor` of type `float32`.
-
ImplicitContainer<T>num_bits - An optional `int`. Defaults to `8`.
-
ImplicitContainer<T>narrow_range - An optional `bool`. Defaults to `False`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `float32`.
object fake_quant_with_min_max_vars_gradient(IGraphNodeBase gradients, IGraphNodeBase inputs, IGraphNodeBase min, IGraphNodeBase max, int num_bits, bool narrow_range, string name)
Compute gradients for a FakeQuantWithMinMaxVars operation.
Parameters
-
IGraphNodeBasegradients - A `Tensor` of type `float32`. Backpropagated gradients above the FakeQuantWithMinMaxVars operation.
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`. Values passed as inputs to the FakeQuantWithMinMaxVars operation. min, max: Quantization interval, scalar floats.
-
IGraphNodeBasemin - A `Tensor` of type `float32`.
-
IGraphNodeBasemax - A `Tensor` of type `float32`.
-
intnum_bits - An optional `int`. Defaults to `8`. The bitwidth of the quantization; between 2 and 8, inclusive.
-
boolnarrow_range - An optional `bool`. Defaults to `False`. Whether to quantize into 2^num_bits - 1 distinct values.
-
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (backprops_wrt_input, backprop_wrt_min, backprop_wrt_max).
object fake_quant_with_min_max_vars_gradient_dyn(object gradients, object inputs, object min, object max, ImplicitContainer<T> num_bits, ImplicitContainer<T> narrow_range, object name)
Compute gradients for a FakeQuantWithMinMaxVars operation.
Parameters
-
objectgradients - A `Tensor` of type `float32`. Backpropagated gradients above the FakeQuantWithMinMaxVars operation.
-
objectinputs - A `Tensor` of type `float32`. Values passed as inputs to the FakeQuantWithMinMaxVars operation. min, max: Quantization interval, scalar floats.
-
objectmin - A `Tensor` of type `float32`.
-
objectmax - A `Tensor` of type `float32`.
-
ImplicitContainer<T>num_bits - An optional `int`. Defaults to `8`. The bitwidth of the quantization; between 2 and 8, inclusive.
-
ImplicitContainer<T>narrow_range - An optional `bool`. Defaults to `False`. Whether to quantize into 2^num_bits - 1 distinct values.
-
objectname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (backprops_wrt_input, backprop_wrt_min, backprop_wrt_max).
Tensor fake_quant_with_min_max_vars_per_channel(IGraphNodeBase inputs, IGraphNodeBase min, IGraphNodeBase max, int num_bits, bool narrow_range, string name)
Fake-quantize the 'inputs' tensor of type float and one of the shapes: `[d]`, `[b, d]` `[b, h, w, d]` via per-channel floats `min` and `max` of shape `[d]`
to 'outputs' tensor of same shape as `inputs`. `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. This operation has a gradient and thus allows for training `min` and `max`
values.
Parameters
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`.
-
IGraphNodeBasemin - A `Tensor` of type `float32`.
-
IGraphNodeBasemax - A `Tensor` of type `float32`.
-
intnum_bits - An optional `int`. Defaults to `8`.
-
boolnarrow_range - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
object fake_quant_with_min_max_vars_per_channel_dyn(object inputs, object min, object max, ImplicitContainer<T> num_bits, ImplicitContainer<T> narrow_range, object name)
Fake-quantize the 'inputs' tensor of type float and one of the shapes: `[d]`, `[b, d]` `[b, h, w, d]` via per-channel floats `min` and `max` of shape `[d]`
to 'outputs' tensor of same shape as `inputs`. `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. This operation has a gradient and thus allows for training `min` and `max`
values.
Parameters
-
objectinputs - A `Tensor` of type `float32`.
-
objectmin - A `Tensor` of type `float32`.
-
objectmax - A `Tensor` of type `float32`.
-
ImplicitContainer<T>num_bits - An optional `int`. Defaults to `8`.
-
ImplicitContainer<T>narrow_range - An optional `bool`. Defaults to `False`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `float32`.
object fake_quant_with_min_max_vars_per_channel_gradient(IGraphNodeBase gradients, IGraphNodeBase inputs, IGraphNodeBase min, IGraphNodeBase max, int num_bits, bool narrow_range, string name)
Compute gradients for a FakeQuantWithMinMaxVarsPerChannel operation.
Parameters
-
IGraphNodeBasegradients - A `Tensor` of type `float32`. Backpropagated gradients above the FakeQuantWithMinMaxVars operation, shape one of: `[d]`, `[b, d]`, `[b, h, w, d]`.
-
IGraphNodeBaseinputs - A `Tensor` of type `float32`. Values passed as inputs to the FakeQuantWithMinMaxVars operation, shape same as `gradients`. min, max: Quantization interval, floats of shape `[d]`.
-
IGraphNodeBasemin - A `Tensor` of type `float32`.
-
IGraphNodeBasemax - A `Tensor` of type `float32`.
-
intnum_bits - An optional `int`. Defaults to `8`. The bitwidth of the quantization; between 2 and 16, inclusive.
-
boolnarrow_range - An optional `bool`. Defaults to `False`. Whether to quantize into 2^num_bits - 1 distinct values.
-
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (backprops_wrt_input, backprop_wrt_min, backprop_wrt_max).
object fake_quant_with_min_max_vars_per_channel_gradient_dyn(object gradients, object inputs, object min, object max, ImplicitContainer<T> num_bits, ImplicitContainer<T> narrow_range, object name)
Compute gradients for a FakeQuantWithMinMaxVarsPerChannel operation.
Parameters
-
objectgradients - A `Tensor` of type `float32`. Backpropagated gradients above the FakeQuantWithMinMaxVars operation, shape one of: `[d]`, `[b, d]`, `[b, h, w, d]`.
-
objectinputs - A `Tensor` of type `float32`. Values passed as inputs to the FakeQuantWithMinMaxVars operation, shape same as `gradients`. min, max: Quantization interval, floats of shape `[d]`.
-
objectmin - A `Tensor` of type `float32`.
-
objectmax - A `Tensor` of type `float32`.
-
ImplicitContainer<T>num_bits - An optional `int`. Defaults to `8`. The bitwidth of the quantization; between 2 and 16, inclusive.
-
ImplicitContainer<T>narrow_range - An optional `bool`. Defaults to `False`. Whether to quantize into 2^num_bits - 1 distinct values.
-
objectname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (backprops_wrt_input, backprop_wrt_min, backprop_wrt_max).
Tensor feature_usage_counts(IGraphNodeBase tree_handle, object params, string name)
object feature_usage_counts_dyn(object tree_handle, object params, object name)
object fertile_stats_deserialize(IGraphNodeBase stats_handle, IGraphNodeBase stats_config, object params, string name)
object fertile_stats_deserialize_dyn(object stats_handle, object stats_config, object params, object name)
Tensor fertile_stats_is_initialized_op(IGraphNodeBase stats_handle, string name)
object fertile_stats_is_initialized_op_dyn(object stats_handle, object name)
Tensor fertile_stats_resource_handle_op(string container, string shared_name, string name)
object fertile_stats_resource_handle_op_dyn(ImplicitContainer<T> container, ImplicitContainer<T> shared_name, object name)
Tensor fertile_stats_serialize(IGraphNodeBase stats_handle, object params, string name)
object fertile_stats_serialize_dyn(object stats_handle, object params, object name)
Tensor fft(IGraphNodeBase input, Nullable<ValueTuple<int>> name)
Fast Fourier transform. Computes the 1-dimensional discrete Fourier transform over the inner-most
dimension of `input`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex tensor.
-
Nullable<ValueTuple<int>>name - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object fft_dyn(object input, object name)
Fast Fourier transform. Computes the 1-dimensional discrete Fourier transform over the inner-most
dimension of `input`.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex tensor.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor fft2d(IGraphNodeBase input, Nullable<ValueTuple<int>> name)
2D fast Fourier transform. Computes the 2-dimensional discrete Fourier transform over the inner-most
2 dimensions of `input`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex tensor.
-
Nullable<ValueTuple<int>>name - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object fft2d_dyn(object input, object name)
2D fast Fourier transform. Computes the 2-dimensional discrete Fourier transform over the inner-most
2 dimensions of `input`.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex tensor.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor fft3d(IGraphNodeBase input, Nullable<ValueTuple<int>> name)
3D fast Fourier transform. Computes the 3-dimensional discrete Fourier transform over the inner-most 3
dimensions of `input`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex64 tensor.
-
Nullable<ValueTuple<int>>name - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object fft3d_dyn(object input, object name)
3D fast Fourier transform. Computes the 3-dimensional discrete Fourier transform over the inner-most 3
dimensions of `input`.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex64 tensor.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor fill(IGraphNodeBase dims, IGraphNodeBase value, string name)
Creates a tensor filled with a scalar value. This operation creates a tensor of shape `dims` and fills it with `value`. For example: ```
# Output tensor has shape [2, 3].
fill([2, 3], 9) ==> [[9, 9, 9]
[9, 9, 9]]
```
tf.fill differs from tf.constant in a few ways: * tf.fill only supports scalar contents, whereas tf.constant supports
Tensor values.
* tf.fill creates an Op in the computation graph that constructs the
actual
Tensor value at runtime. This is in contrast to tf.constant which embeds
the entire Tensor into the graph with a `Const` node.
* Because tf.fill evaluates at graph runtime, it supports dynamic shapes
based on other runtime Tensors, unlike tf.constant.
Parameters
-
IGraphNodeBasedims - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D. Represents the shape of the output tensor.
-
IGraphNodeBasevalue - A `Tensor`. 0-D (scalar). Value to fill the returned tensor. @compatibility(numpy) Equivalent to np.full @end_compatibility
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `value`.
Tensor fill(IGraphNodeBase dims, IGraphNodeBase value, PythonFunctionContainer name)
Creates a tensor filled with a scalar value. This operation creates a tensor of shape `dims` and fills it with `value`. For example: ```
# Output tensor has shape [2, 3].
fill([2, 3], 9) ==> [[9, 9, 9]
[9, 9, 9]]
```
tf.fill differs from tf.constant in a few ways: * tf.fill only supports scalar contents, whereas tf.constant supports
Tensor values.
* tf.fill creates an Op in the computation graph that constructs the
actual
Tensor value at runtime. This is in contrast to tf.constant which embeds
the entire Tensor into the graph with a `Const` node.
* Because tf.fill evaluates at graph runtime, it supports dynamic shapes
based on other runtime Tensors, unlike tf.constant.
Parameters
-
IGraphNodeBasedims - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D. Represents the shape of the output tensor.
-
IGraphNodeBasevalue - A `Tensor`. 0-D (scalar). Value to fill the returned tensor. @compatibility(numpy) Equivalent to np.full @end_compatibility
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `value`.
object fill_dyn(object dims, object value, object name)
Creates a tensor filled with a scalar value. This operation creates a tensor of shape `dims` and fills it with `value`. For example: ```
# Output tensor has shape [2, 3].
fill([2, 3], 9) ==> [[9, 9, 9]
[9, 9, 9]]
```
tf.fill differs from tf.constant in a few ways: * tf.fill only supports scalar contents, whereas tf.constant supports
Tensor values.
* tf.fill creates an Op in the computation graph that constructs the
actual
Tensor value at runtime. This is in contrast to tf.constant which embeds
the entire Tensor into the graph with a `Const` node.
* Because tf.fill evaluates at graph runtime, it supports dynamic shapes
based on other runtime Tensors, unlike tf.constant.
Parameters
-
objectdims - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D. Represents the shape of the output tensor.
-
objectvalue - A `Tensor`. 0-D (scalar). Value to fill the returned tensor. @compatibility(numpy) Equivalent to np.full @end_compatibility
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `value`.
object finalize_tree(IGraphNodeBase tree_handle, IGraphNodeBase stats_handle, object params, string name)
object finalize_tree_dyn(object tree_handle, object stats_handle, object params, object name)
Tensor fingerprint(IGraphNodeBase data, ImplicitContainer<T> method, string name)
Generates fingerprint values. Generates fingerprint values of `data`. Fingerprint op considers the first dimension of `data` as the batch dimension,
and `output[i]` contains the fingerprint value generated from contents in
`data[i,...]` for all `i`. Fingerprint op writes fingerprint values as byte arrays. For example, the
default method `farmhash64` generates a 64-bit fingerprint value at a time.
This 8-byte value is written out as an
tf.uint8 array of size 8, in
little-endian order. For example, suppose that `data` has data type tf.int32 and shape (2, 3, 4),
and that the fingerprint method is `farmhash64`. In this case, the output
shape is (2, 8), where 2 is the batch dimension size of `data`, and 8 is the
size of each fingerprint value in bytes. `output[0, :]` is generated from
12 integers in `data[0, :, :]` and similarly `output[1, :]` is generated from
other 12 integers in `data[1, :, :]`. Note that this op fingerprints the raw underlying buffer, and it does not
fingerprint Tensor's metadata such as data type and/or shape. For example, the
fingerprint values are invariant under reshapes and bitcasts as long as the
batch dimension remain the same:
For string data, one should expect `tf.fingerprint(data) !=
tf.fingerprint(tf.string.reduce_join(data))` in general.
Parameters
-
IGraphNodeBasedata - A `Tensor`. Must have rank 1 or higher.
-
ImplicitContainer<T>method - A `Tensor` of type
tf.string. Fingerprint method used by this op. Currently available method is `farmhash64`. -
stringname - A name for the operation (optional).
Returns
Show Example
tf.fingerprint(data) == tf.fingerprint(tf.reshape(data,...))
tf.fingerprint(data) == tf.fingerprint(tf.bitcast(data,...))
object fingerprint_dyn(object data, ImplicitContainer<T> method, object name)
Generates fingerprint values. Generates fingerprint values of `data`. Fingerprint op considers the first dimension of `data` as the batch dimension,
and `output[i]` contains the fingerprint value generated from contents in
`data[i,...]` for all `i`. Fingerprint op writes fingerprint values as byte arrays. For example, the
default method `farmhash64` generates a 64-bit fingerprint value at a time.
This 8-byte value is written out as an
tf.uint8 array of size 8, in
little-endian order. For example, suppose that `data` has data type tf.int32 and shape (2, 3, 4),
and that the fingerprint method is `farmhash64`. In this case, the output
shape is (2, 8), where 2 is the batch dimension size of `data`, and 8 is the
size of each fingerprint value in bytes. `output[0, :]` is generated from
12 integers in `data[0, :, :]` and similarly `output[1, :]` is generated from
other 12 integers in `data[1, :, :]`. Note that this op fingerprints the raw underlying buffer, and it does not
fingerprint Tensor's metadata such as data type and/or shape. For example, the
fingerprint values are invariant under reshapes and bitcasts as long as the
batch dimension remain the same:
For string data, one should expect `tf.fingerprint(data) !=
tf.fingerprint(tf.string.reduce_join(data))` in general.
Parameters
-
objectdata - A `Tensor`. Must have rank 1 or higher.
-
ImplicitContainer<T>method - A `Tensor` of type
tf.string. Fingerprint method used by this op. Currently available method is `farmhash64`. -
objectname - A name for the operation (optional).
Returns
-
object - A two-dimensional `Tensor` of type
tf.uint8. The first dimension equals to `data`'s first dimension, and the second dimension size depends on the fingerprint algorithm.
Show Example
tf.fingerprint(data) == tf.fingerprint(tf.reshape(data,...))
tf.fingerprint(data) == tf.fingerprint(tf.bitcast(data,...))
object five_float_outputs(string name)
object five_float_outputs_dyn(object name)
object fixed_size_partitioner(Nullable<int> num_shards, int axis)
Partitioner to specify a fixed number of shards along given axis.
Parameters
-
Nullable<int>num_shards - `int`, number of shards to partition variable.
-
intaxis - `int`, axis to partition on.
Returns
-
object - A partition function usable as the `partitioner` argument to `variable_scope` and `get_variable`.
object fixed_size_partitioner_dyn(object num_shards, ImplicitContainer<T> axis)
Partitioner to specify a fixed number of shards along given axis.
Parameters
-
objectnum_shards - `int`, number of shards to partition variable.
-
ImplicitContainer<T>axis - `int`, axis to partition on.
Returns
-
object - A partition function usable as the `partitioner` argument to `variable_scope` and `get_variable`.
object float_input(IGraphNodeBase a, string name)
object float_input_dyn(object a, object name)
Tensor float_output(string name)
object float_output_dyn(object name)
object float_output_string_output(string name)
object float_output_string_output_dyn(object name)
object floor(IGraphNodeBase x, string name)
Returns element-wise largest integer not greater than x.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Tensor floor_div(IGraphNodeBase x, IGraphNodeBase y, PythonFunctionContainer name)
Returns x // y element-wise. *NOTE*: `floor_div` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Tensor floor_div(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns x // y element-wise. *NOTE*: `floor_div` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
object floor_div_dyn(object x, object y, object name)
Returns x // y element-wise. *NOTE*: `floor_div` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object floor_dyn(object x, object name)
Returns element-wise largest integer not greater than x.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Tensor floordiv(RaggedTensor x, int y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
RaggedTensorx - `Tensor` numerator of real numeric type.
-
inty - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(RaggedTensor x, IGraphNodeBase y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
RaggedTensorx - `Tensor` numerator of real numeric type.
-
IGraphNodeBasey - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(IGraphNodeBase x, RaggedTensor y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
IGraphNodeBasex - `Tensor` numerator of real numeric type.
-
RaggedTensory - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(IGraphNodeBase x, int y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
IGraphNodeBasex - `Tensor` numerator of real numeric type.
-
inty - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(IGraphNodeBase x, IGraphNodeBase y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
IGraphNodeBasex - `Tensor` numerator of real numeric type.
-
IGraphNodeBasey - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(RaggedTensor x, RaggedTensor y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
RaggedTensorx - `Tensor` numerator of real numeric type.
-
RaggedTensory - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(IGraphNodeBase x, double y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
IGraphNodeBasex - `Tensor` numerator of real numeric type.
-
doubley - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(RaggedTensor x, IEnumerable<object> y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
RaggedTensorx - `Tensor` numerator of real numeric type.
-
IEnumerable<object>y - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(IGraphNodeBase x, IEnumerable<object> y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
IGraphNodeBasex - `Tensor` numerator of real numeric type.
-
IEnumerable<object>y - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(ValueTuple<PythonClassContainer, PythonClassContainer> x, IGraphNodeBase y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>x - `Tensor` numerator of real numeric type.
-
IGraphNodeBasey - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(double x, double y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
doublex - `Tensor` numerator of real numeric type.
-
doubley - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(double x, IEnumerable<object> y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
doublex - `Tensor` numerator of real numeric type.
-
IEnumerable<object>y - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(double x, RaggedTensor y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
doublex - `Tensor` numerator of real numeric type.
-
RaggedTensory - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(double x, int y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
doublex - `Tensor` numerator of real numeric type.
-
inty - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(double x, IGraphNodeBase y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
doublex - `Tensor` numerator of real numeric type.
-
IGraphNodeBasey - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(RaggedTensor x, double y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
RaggedTensorx - `Tensor` numerator of real numeric type.
-
doubley - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(ValueTuple<PythonClassContainer, PythonClassContainer> x, IEnumerable<object> y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>x - `Tensor` numerator of real numeric type.
-
IEnumerable<object>y - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(ValueTuple<PythonClassContainer, PythonClassContainer> x, RaggedTensor y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>x - `Tensor` numerator of real numeric type.
-
RaggedTensory - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(ValueTuple<PythonClassContainer, PythonClassContainer> x, int y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>x - `Tensor` numerator of real numeric type.
-
inty - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
Tensor floordiv(ValueTuple<PythonClassContainer, PythonClassContainer> x, double y, string name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>x - `Tensor` numerator of real numeric type.
-
doubley - `Tensor` denominator of real numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` rounded down.
object floordiv_dyn(object x, object y, object name)
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
Parameters
-
objectx - `Tensor` numerator of real numeric type.
-
objecty - `Tensor` denominator of real numeric type.
-
objectname - A name for the operation (optional).
Returns
-
object - `x / y` rounded down.
object foldl(PythonFunctionContainer fn, ndarray elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, IGraphNodeBase elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, IGraphNodeBase elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, IGraphNodeBase elems, IEnumerable<double> initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IEnumerable<double>initializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, IGraphNodeBase elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, ValueTuple<ndarray, object> elems, PythonClassContainer initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
ValueTuple<ndarray, object>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
PythonClassContainerinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, ValueTuple<ndarray, object> elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
ValueTuple<ndarray, object>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, ValueTuple<ndarray, object> elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
ValueTuple<ndarray, object>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, IEnumerable<double> elems, PythonClassContainer initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
IEnumerable<double>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
PythonClassContainerinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, ValueTuple<ndarray, object> elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
ValueTuple<ndarray, object>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, IEnumerable<double> elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
IEnumerable<double>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, IEnumerable<double> elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
IEnumerable<double>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, IEnumerable<double> elems, IEnumerable<double> initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
IEnumerable<double>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IEnumerable<double>initializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, IGraphNodeBase elems, PythonClassContainer initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
PythonClassContainerinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, ndarray elems, PythonClassContainer initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
PythonClassContainerinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, ndarray elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, ValueTuple<ndarray, object> elems, IEnumerable<double> initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
ValueTuple<ndarray, object>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IEnumerable<double>initializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, IEnumerable<double> elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
IEnumerable<double>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, ndarray elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl(PythonFunctionContainer fn, ndarray elems, IEnumerable<double> initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
PythonFunctionContainerfn - The callable to be performed.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IEnumerable<double>initializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldl_dyn(object fn, object elems, object initializer, ImplicitContainer<T> parallel_iterations, ImplicitContainer<T> back_prop, ImplicitContainer<T> swap_memory, object name)
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
objectelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
objectinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
ImplicitContainer<T>parallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
ImplicitContainer<T>back_prop - (optional) True enables support for back propagation.
-
ImplicitContainer<T>swap_memory - (optional) True enables GPU-CPU memory swapping.
-
objectname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from first to last.
object foldr(object fn, IGraphNodeBase elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from last to first.
object foldr(object fn, IGraphNodeBase elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from last to first.
object foldr(object fn, ndarray elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from last to first.
object foldr(object fn, IGraphNodeBase elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from last to first.
object foldr(object fn, ndarray elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from last to first.
object foldr(object fn, ValueTuple<ndarray, object> elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
ValueTuple<ndarray, object>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from last to first.
object foldr(object fn, ValueTuple<ndarray, object> elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
ValueTuple<ndarray, object>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from last to first.
object foldr(object fn, ValueTuple<ndarray, object> elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
ValueTuple<ndarray, object>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from last to first.
object foldr(object fn, ndarray elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, string name)
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from last to first.
object foldr_dyn(object fn, object elems, object initializer, ImplicitContainer<T> parallel_iterations, ImplicitContainer<T> back_prop, ImplicitContainer<T> swap_memory, object name)
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
Parameters
-
objectfn - The callable to be performed.
-
objectelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
objectinitializer - (optional) A tensor or (possibly nested) sequence of tensors, as the initial value for the accumulator.
-
ImplicitContainer<T>parallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
ImplicitContainer<T>back_prop - (optional) True enables support for back propagation.
-
ImplicitContainer<T>swap_memory - (optional) True enables GPU-CPU memory swapping.
-
objectname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors, resulting from applying `fn` consecutively to the list of tensors unpacked from `elems`, from last to first.
object foo1(IGraphNodeBase a, IGraphNodeBase b, IGraphNodeBase c, string name)
object foo1_dyn(object a, object b, object c, object name)
object foo2(IGraphNodeBase a, IGraphNodeBase b, IGraphNodeBase c, string name)
object foo2_dyn(object a, object b, object c, object name)
object foo3(IGraphNodeBase a, IGraphNodeBase b, IGraphNodeBase c, string name)
object foo3_dyn(object a, object b, object c, object name)
object func_attr(_OverloadedFunction f, string name)
object func_attr(object f, string name)
object func_attr(_DefinedFunction f, string name)
object func_attr_dyn(object f, object name)
object func_list_attr(object f, string name)
object func_list_attr_dyn(object f, object name)
object function(PythonFunctionContainer func, IDictionary<string, object> input_signature, bool autograph, object experimental_autograph_options, bool experimental_relax_shapes, Nullable<bool> experimental_compile)
Creates a callable TensorFlow graph from a Python function. `function` constructs a callable that executes a TensorFlow graph
(
tf.Graph) created by tracing the TensorFlow operations in `func`.
This allows the TensorFlow runtime to apply optimizations and exploit
parallelism in the computation defined by `func`. _Example Usage_
Note that unlike other TensorFlow operations, we don't convert python
numerical inputs to tensors. Moreover, a new graph is generated for each
distinct python numerical value, for example calling `g(2)` and `g(3)` will
generate two new graphs (while only one is generated if you call
`g(tf.constant(2))` and `g(tf.constant(3))`). Therefore, python numerical
inputs should be restricted to arguments that will have few distinct values,
such as hyperparameters like the number of layers in a neural network. This
allows TensorFlow to optimize each variant of the neural network. _Referencing tf.Variables_ The Python function `func` may reference stateful objects (such as
tf.Variable).
These are captured as implicit inputs to the callable returned by `function`.
`function` can be applied to methods of an object.
_Usage with tf.keras_ The `call` methods of a tf.keras.Model subclass can be decorated with
`function` in order to apply graph execution optimizations on it.
_Input Signatures_ `function` instantiates a separate graph for every unique set of input
shapes and datatypes. For example, the following code snippet will result
in three distinct graphs being traced, as each input has a different
shape.
An "input signature" can be optionally provided to `function` to control
the graphs traced. The input signature specifies the shape and type of each
`Tensor` argument to the function using a tf.TensorSpec object. For example,
the following code snippet ensures that a single graph is created where the
input `Tensor` is required to be a floating point tensor with no restrictions
on shape.
When an `input_signature` is specified, the callable will convert the inputs
to the specified TensorSpecs. _Tracing and staging_ When `autograph` is `True`, all Python control flow that depends on `Tensor`
values is staged into a TensorFlow graph. When `autograph` is `False`, the
function is traced and control flow is not allowed to depend on data. Note that `function` only stages TensorFlow operations, all Python code that
`func` executes and does not depend on data will shape the _construction_ of
the graph.
For example, consider the following:
`add_noise()` will return a different output every time it is invoked.
However, `traced()` will return the same value every time it is called,
since a particular random value generated by the `np.random.randn` call will
be inserted in the traced/staged TensorFlow graph as a constant. In this
particular example, replacing `np.random.randn(5, 5)` with
`tf.random.normal((5, 5))` will result in the same behavior for `add_noise()`
and `traced()`. _Python Side-Effects_ A corollary of the previous discussion on tracing is the following: If a
Python function `func` has Python side-effects, then executing `func` multiple
times may not be semantically equivalent to executing `F = tf.function(func)`
multiple times; this difference is due to the fact that `function` only
captures the subgraph of TensorFlow operations that is constructed when `func`
is invoked to trace a graph. The same is true if code with Python side effects is used inside control flow,
such as a loop. If your code uses side effects that are not intended to
control graph construction, wrap them inside `tf.compat.v1.py_func`. _Retracing_ A single tf.function object might need to map to multiple computation graphs
under the hood. This should be visible only as performance (tracing graphs has
a nonzero computational and memory cost) but should not affect the correctness
of the program. A traced function should return the same result as it would
when run eagerly, assuming no unintended Python side-effects. Calling a tf.function with tensor arguments of different dtypes should lead
to at least one computational graph per distinct set of dtypes. Alternatively,
always calling a tf.function with tensor arguments of the same shapes and
dtypes and the same non-tensor arguments should not lead to additional
retracings of your function. Other than that, TensorFlow reserves the right to retrace functions as many
times as needed, to ensure that traced functions behave as they would when run
eagerly and to provide the best end-to-end performance. For example, the
behavior of how many traces TensorFlow will do when the function is repeatedly
called with different python scalars as arguments is left undefined to allow
for future optimizations. To control the tracing behavior, use the following tools:
- different tf.function objects are guaranteed to not share traces; and
- specifying a signature or using concrete function objects returned from
get_concrete_function() guarantees that only one function graph will be
built.
Parameters
-
PythonFunctionContainerfunc - function to be compiled. If `func` is None, returns a decorator that can be invoked with a single argument - `func`. The end result is equivalent to providing all the arguments up front. In other words, `tf.function(input_signature=...)(func)` is equivalent to `tf.function(func, input_signature=...)`. The former can be used to decorate Python functions, for example: @tf.function(input_signature=...) def foo(...):...
-
IDictionary<string, object>input_signature - A possibly nested sequence of
tf.TensorSpecobjects specifying the shapes and dtypes of the Tensors that will be supplied to this function. If `None`, a separate function is instantiated for each inferred input signature. If input_signature is specified, every input to `func` must be a `Tensor`, and `func` cannot accept `**kwargs`. -
boolautograph - Whether autograph should be applied on `func` before tracing a graph. This allows for dynamic control flow (Python if's, loops etc.) in the traced graph. See https://www.tensorflow.org/guide/autograph for more information.
-
objectexperimental_autograph_options - Experimental knobs (in the form of a tuple of tensorflow.autograph.Feature values) to control behavior when autograph=True.
-
boolexperimental_relax_shapes - When true, argument shapes may be relaxed to avoid unecessary retracing.
-
Nullable<bool>experimental_compile - If false, execute the function in a regular way. The function is optimized by some graph rewrite passes (some ops might be clustered into a single op) and interpreted by the standard TensorFlow executor, which dispatches op kernels one by one as they become executable. Set it to false when directly running a multi-device function on TPUs (e.g. two TPU cores, one TPU core and its host CPU). If True, the function is compiled directly by XLA (https://www.tensorflow.org/xla). XLA would fuse all the ops and emit more efficient code to run for some devices (e.g. TPU, XLA_GPU) and some use cases (e.g. dense tensor computation). It requires that the whole function is compilable by XLA (e.g. static tensor shape, a subset of operations, no string, compile-time constant input, etc). If None (default), compile the function with XLA when running on TPU and go through the regular function execution path when running on other devices. Note: TensorArrays on TPU don't work with standard TensorFlow executor.
Returns
-
object - If `func` is not None, returns a callable that will execute the compiled
function (and return zero or more
tf.Tensorobjects). If `func` is None, returns a decorator that, when invoked with a single `func` argument, returns a callable equivalent to the case above.
Show Example
def f(x, y):
return tf.reduce_mean(tf.multiply(x ** 2, 3) + y) g = tf.function(f) x = tf.constant([[2.0, 3.0]])
y = tf.constant([[3.0, -2.0]]) # `f` and `g` will return the same value, but `g` will be executed as a
# TensorFlow graph.
assert f(x, y).numpy() == g(x, y).numpy() # Tensors and tf.Variables used by the Python function are captured in the
# graph.
@tf.function
def h():
return f(x, y) assert (h().numpy() == f(x, y).numpy()).all() # Data-dependent control flow is also captured in the graph. Supported
# control flow statements include `if`, `for`, `while`, `break`, `continue`,
# `return`.
@tf.function
def g(x):
if tf.reduce_sum(x) > 0:
return x * x
else:
return -x // 2 # print and TensorFlow side effects are supported, but exercise caution when
# using Python side effects like mutating objects, saving to files, etc.
l = [] @tf.function
def g(x):
for i in x:
print(i) # Works
tf.compat.v1.assign(v, i) # Works
tf.compat.v1.py_func(lambda i: l.append(i))(i) # Works
l.append(i) # Caution! Doesn't work.
object function(PythonFunctionContainer func, IEnumerable<TensorSpec> input_signature, bool autograph, object experimental_autograph_options, bool experimental_relax_shapes, Nullable<bool> experimental_compile)
Creates a callable TensorFlow graph from a Python function. `function` constructs a callable that executes a TensorFlow graph
(
tf.Graph) created by tracing the TensorFlow operations in `func`.
This allows the TensorFlow runtime to apply optimizations and exploit
parallelism in the computation defined by `func`. _Example Usage_
Note that unlike other TensorFlow operations, we don't convert python
numerical inputs to tensors. Moreover, a new graph is generated for each
distinct python numerical value, for example calling `g(2)` and `g(3)` will
generate two new graphs (while only one is generated if you call
`g(tf.constant(2))` and `g(tf.constant(3))`). Therefore, python numerical
inputs should be restricted to arguments that will have few distinct values,
such as hyperparameters like the number of layers in a neural network. This
allows TensorFlow to optimize each variant of the neural network. _Referencing tf.Variables_ The Python function `func` may reference stateful objects (such as
tf.Variable).
These are captured as implicit inputs to the callable returned by `function`.
`function` can be applied to methods of an object.
_Usage with tf.keras_ The `call` methods of a tf.keras.Model subclass can be decorated with
`function` in order to apply graph execution optimizations on it.
_Input Signatures_ `function` instantiates a separate graph for every unique set of input
shapes and datatypes. For example, the following code snippet will result
in three distinct graphs being traced, as each input has a different
shape.
An "input signature" can be optionally provided to `function` to control
the graphs traced. The input signature specifies the shape and type of each
`Tensor` argument to the function using a tf.TensorSpec object. For example,
the following code snippet ensures that a single graph is created where the
input `Tensor` is required to be a floating point tensor with no restrictions
on shape.
When an `input_signature` is specified, the callable will convert the inputs
to the specified TensorSpecs. _Tracing and staging_ When `autograph` is `True`, all Python control flow that depends on `Tensor`
values is staged into a TensorFlow graph. When `autograph` is `False`, the
function is traced and control flow is not allowed to depend on data. Note that `function` only stages TensorFlow operations, all Python code that
`func` executes and does not depend on data will shape the _construction_ of
the graph.
For example, consider the following:
`add_noise()` will return a different output every time it is invoked.
However, `traced()` will return the same value every time it is called,
since a particular random value generated by the `np.random.randn` call will
be inserted in the traced/staged TensorFlow graph as a constant. In this
particular example, replacing `np.random.randn(5, 5)` with
`tf.random.normal((5, 5))` will result in the same behavior for `add_noise()`
and `traced()`. _Python Side-Effects_ A corollary of the previous discussion on tracing is the following: If a
Python function `func` has Python side-effects, then executing `func` multiple
times may not be semantically equivalent to executing `F = tf.function(func)`
multiple times; this difference is due to the fact that `function` only
captures the subgraph of TensorFlow operations that is constructed when `func`
is invoked to trace a graph. The same is true if code with Python side effects is used inside control flow,
such as a loop. If your code uses side effects that are not intended to
control graph construction, wrap them inside `tf.compat.v1.py_func`. _Retracing_ A single tf.function object might need to map to multiple computation graphs
under the hood. This should be visible only as performance (tracing graphs has
a nonzero computational and memory cost) but should not affect the correctness
of the program. A traced function should return the same result as it would
when run eagerly, assuming no unintended Python side-effects. Calling a tf.function with tensor arguments of different dtypes should lead
to at least one computational graph per distinct set of dtypes. Alternatively,
always calling a tf.function with tensor arguments of the same shapes and
dtypes and the same non-tensor arguments should not lead to additional
retracings of your function. Other than that, TensorFlow reserves the right to retrace functions as many
times as needed, to ensure that traced functions behave as they would when run
eagerly and to provide the best end-to-end performance. For example, the
behavior of how many traces TensorFlow will do when the function is repeatedly
called with different python scalars as arguments is left undefined to allow
for future optimizations. To control the tracing behavior, use the following tools:
- different tf.function objects are guaranteed to not share traces; and
- specifying a signature or using concrete function objects returned from
get_concrete_function() guarantees that only one function graph will be
built.
Parameters
-
PythonFunctionContainerfunc - function to be compiled. If `func` is None, returns a decorator that can be invoked with a single argument - `func`. The end result is equivalent to providing all the arguments up front. In other words, `tf.function(input_signature=...)(func)` is equivalent to `tf.function(func, input_signature=...)`. The former can be used to decorate Python functions, for example: @tf.function(input_signature=...) def foo(...):...
-
IEnumerable<TensorSpec>input_signature - A possibly nested sequence of
tf.TensorSpecobjects specifying the shapes and dtypes of the Tensors that will be supplied to this function. If `None`, a separate function is instantiated for each inferred input signature. If input_signature is specified, every input to `func` must be a `Tensor`, and `func` cannot accept `**kwargs`. -
boolautograph - Whether autograph should be applied on `func` before tracing a graph. This allows for dynamic control flow (Python if's, loops etc.) in the traced graph. See https://www.tensorflow.org/guide/autograph for more information.
-
objectexperimental_autograph_options - Experimental knobs (in the form of a tuple of tensorflow.autograph.Feature values) to control behavior when autograph=True.
-
boolexperimental_relax_shapes - When true, argument shapes may be relaxed to avoid unecessary retracing.
-
Nullable<bool>experimental_compile - If false, execute the function in a regular way. The function is optimized by some graph rewrite passes (some ops might be clustered into a single op) and interpreted by the standard TensorFlow executor, which dispatches op kernels one by one as they become executable. Set it to false when directly running a multi-device function on TPUs (e.g. two TPU cores, one TPU core and its host CPU). If True, the function is compiled directly by XLA (https://www.tensorflow.org/xla). XLA would fuse all the ops and emit more efficient code to run for some devices (e.g. TPU, XLA_GPU) and some use cases (e.g. dense tensor computation). It requires that the whole function is compilable by XLA (e.g. static tensor shape, a subset of operations, no string, compile-time constant input, etc). If None (default), compile the function with XLA when running on TPU and go through the regular function execution path when running on other devices. Note: TensorArrays on TPU don't work with standard TensorFlow executor.
Returns
-
object - If `func` is not None, returns a callable that will execute the compiled
function (and return zero or more
tf.Tensorobjects). If `func` is None, returns a decorator that, when invoked with a single `func` argument, returns a callable equivalent to the case above.
Show Example
def f(x, y):
return tf.reduce_mean(tf.multiply(x ** 2, 3) + y) g = tf.function(f) x = tf.constant([[2.0, 3.0]])
y = tf.constant([[3.0, -2.0]]) # `f` and `g` will return the same value, but `g` will be executed as a
# TensorFlow graph.
assert f(x, y).numpy() == g(x, y).numpy() # Tensors and tf.Variables used by the Python function are captured in the
# graph.
@tf.function
def h():
return f(x, y) assert (h().numpy() == f(x, y).numpy()).all() # Data-dependent control flow is also captured in the graph. Supported
# control flow statements include `if`, `for`, `while`, `break`, `continue`,
# `return`.
@tf.function
def g(x):
if tf.reduce_sum(x) > 0:
return x * x
else:
return -x // 2 # print and TensorFlow side effects are supported, but exercise caution when
# using Python side effects like mutating objects, saving to files, etc.
l = [] @tf.function
def g(x):
for i in x:
print(i) # Works
tf.compat.v1.assign(v, i) # Works
tf.compat.v1.py_func(lambda i: l.append(i))(i) # Works
l.append(i) # Caution! Doesn't work.
object function(PythonFunctionContainer func, object input_signature, bool autograph, object experimental_autograph_options, bool experimental_relax_shapes, Nullable<bool> experimental_compile)
Creates a callable TensorFlow graph from a Python function. `function` constructs a callable that executes a TensorFlow graph
(
tf.Graph) created by tracing the TensorFlow operations in `func`.
This allows the TensorFlow runtime to apply optimizations and exploit
parallelism in the computation defined by `func`. _Example Usage_
Note that unlike other TensorFlow operations, we don't convert python
numerical inputs to tensors. Moreover, a new graph is generated for each
distinct python numerical value, for example calling `g(2)` and `g(3)` will
generate two new graphs (while only one is generated if you call
`g(tf.constant(2))` and `g(tf.constant(3))`). Therefore, python numerical
inputs should be restricted to arguments that will have few distinct values,
such as hyperparameters like the number of layers in a neural network. This
allows TensorFlow to optimize each variant of the neural network. _Referencing tf.Variables_ The Python function `func` may reference stateful objects (such as
tf.Variable).
These are captured as implicit inputs to the callable returned by `function`.
`function` can be applied to methods of an object.
_Usage with tf.keras_ The `call` methods of a tf.keras.Model subclass can be decorated with
`function` in order to apply graph execution optimizations on it.
_Input Signatures_ `function` instantiates a separate graph for every unique set of input
shapes and datatypes. For example, the following code snippet will result
in three distinct graphs being traced, as each input has a different
shape.
An "input signature" can be optionally provided to `function` to control
the graphs traced. The input signature specifies the shape and type of each
`Tensor` argument to the function using a tf.TensorSpec object. For example,
the following code snippet ensures that a single graph is created where the
input `Tensor` is required to be a floating point tensor with no restrictions
on shape.
When an `input_signature` is specified, the callable will convert the inputs
to the specified TensorSpecs. _Tracing and staging_ When `autograph` is `True`, all Python control flow that depends on `Tensor`
values is staged into a TensorFlow graph. When `autograph` is `False`, the
function is traced and control flow is not allowed to depend on data. Note that `function` only stages TensorFlow operations, all Python code that
`func` executes and does not depend on data will shape the _construction_ of
the graph.
For example, consider the following:
`add_noise()` will return a different output every time it is invoked.
However, `traced()` will return the same value every time it is called,
since a particular random value generated by the `np.random.randn` call will
be inserted in the traced/staged TensorFlow graph as a constant. In this
particular example, replacing `np.random.randn(5, 5)` with
`tf.random.normal((5, 5))` will result in the same behavior for `add_noise()`
and `traced()`. _Python Side-Effects_ A corollary of the previous discussion on tracing is the following: If a
Python function `func` has Python side-effects, then executing `func` multiple
times may not be semantically equivalent to executing `F = tf.function(func)`
multiple times; this difference is due to the fact that `function` only
captures the subgraph of TensorFlow operations that is constructed when `func`
is invoked to trace a graph. The same is true if code with Python side effects is used inside control flow,
such as a loop. If your code uses side effects that are not intended to
control graph construction, wrap them inside `tf.compat.v1.py_func`. _Retracing_ A single tf.function object might need to map to multiple computation graphs
under the hood. This should be visible only as performance (tracing graphs has
a nonzero computational and memory cost) but should not affect the correctness
of the program. A traced function should return the same result as it would
when run eagerly, assuming no unintended Python side-effects. Calling a tf.function with tensor arguments of different dtypes should lead
to at least one computational graph per distinct set of dtypes. Alternatively,
always calling a tf.function with tensor arguments of the same shapes and
dtypes and the same non-tensor arguments should not lead to additional
retracings of your function. Other than that, TensorFlow reserves the right to retrace functions as many
times as needed, to ensure that traced functions behave as they would when run
eagerly and to provide the best end-to-end performance. For example, the
behavior of how many traces TensorFlow will do when the function is repeatedly
called with different python scalars as arguments is left undefined to allow
for future optimizations. To control the tracing behavior, use the following tools:
- different tf.function objects are guaranteed to not share traces; and
- specifying a signature or using concrete function objects returned from
get_concrete_function() guarantees that only one function graph will be
built.
Parameters
-
PythonFunctionContainerfunc - function to be compiled. If `func` is None, returns a decorator that can be invoked with a single argument - `func`. The end result is equivalent to providing all the arguments up front. In other words, `tf.function(input_signature=...)(func)` is equivalent to `tf.function(func, input_signature=...)`. The former can be used to decorate Python functions, for example: @tf.function(input_signature=...) def foo(...):...
-
objectinput_signature - A possibly nested sequence of
tf.TensorSpecobjects specifying the shapes and dtypes of the Tensors that will be supplied to this function. If `None`, a separate function is instantiated for each inferred input signature. If input_signature is specified, every input to `func` must be a `Tensor`, and `func` cannot accept `**kwargs`. -
boolautograph - Whether autograph should be applied on `func` before tracing a graph. This allows for dynamic control flow (Python if's, loops etc.) in the traced graph. See https://www.tensorflow.org/guide/autograph for more information.
-
objectexperimental_autograph_options - Experimental knobs (in the form of a tuple of tensorflow.autograph.Feature values) to control behavior when autograph=True.
-
boolexperimental_relax_shapes - When true, argument shapes may be relaxed to avoid unecessary retracing.
-
Nullable<bool>experimental_compile - If false, execute the function in a regular way. The function is optimized by some graph rewrite passes (some ops might be clustered into a single op) and interpreted by the standard TensorFlow executor, which dispatches op kernels one by one as they become executable. Set it to false when directly running a multi-device function on TPUs (e.g. two TPU cores, one TPU core and its host CPU). If True, the function is compiled directly by XLA (https://www.tensorflow.org/xla). XLA would fuse all the ops and emit more efficient code to run for some devices (e.g. TPU, XLA_GPU) and some use cases (e.g. dense tensor computation). It requires that the whole function is compilable by XLA (e.g. static tensor shape, a subset of operations, no string, compile-time constant input, etc). If None (default), compile the function with XLA when running on TPU and go through the regular function execution path when running on other devices. Note: TensorArrays on TPU don't work with standard TensorFlow executor.
Returns
-
object - If `func` is not None, returns a callable that will execute the compiled
function (and return zero or more
tf.Tensorobjects). If `func` is None, returns a decorator that, when invoked with a single `func` argument, returns a callable equivalent to the case above.
Show Example
def f(x, y):
return tf.reduce_mean(tf.multiply(x ** 2, 3) + y) g = tf.function(f) x = tf.constant([[2.0, 3.0]])
y = tf.constant([[3.0, -2.0]]) # `f` and `g` will return the same value, but `g` will be executed as a
# TensorFlow graph.
assert f(x, y).numpy() == g(x, y).numpy() # Tensors and tf.Variables used by the Python function are captured in the
# graph.
@tf.function
def h():
return f(x, y) assert (h().numpy() == f(x, y).numpy()).all() # Data-dependent control flow is also captured in the graph. Supported
# control flow statements include `if`, `for`, `while`, `break`, `continue`,
# `return`.
@tf.function
def g(x):
if tf.reduce_sum(x) > 0:
return x * x
else:
return -x // 2 # print and TensorFlow side effects are supported, but exercise caution when
# using Python side effects like mutating objects, saving to files, etc.
l = [] @tf.function
def g(x):
for i in x:
print(i) # Works
tf.compat.v1.assign(v, i) # Works
tf.compat.v1.py_func(lambda i: l.append(i))(i) # Works
l.append(i) # Caution! Doesn't work.
object function(PythonFunctionContainer func, ValueTuple<TensorSpec, object> input_signature, bool autograph, object experimental_autograph_options, bool experimental_relax_shapes, Nullable<bool> experimental_compile)
Creates a callable TensorFlow graph from a Python function. `function` constructs a callable that executes a TensorFlow graph
(
tf.Graph) created by tracing the TensorFlow operations in `func`.
This allows the TensorFlow runtime to apply optimizations and exploit
parallelism in the computation defined by `func`. _Example Usage_
Note that unlike other TensorFlow operations, we don't convert python
numerical inputs to tensors. Moreover, a new graph is generated for each
distinct python numerical value, for example calling `g(2)` and `g(3)` will
generate two new graphs (while only one is generated if you call
`g(tf.constant(2))` and `g(tf.constant(3))`). Therefore, python numerical
inputs should be restricted to arguments that will have few distinct values,
such as hyperparameters like the number of layers in a neural network. This
allows TensorFlow to optimize each variant of the neural network. _Referencing tf.Variables_ The Python function `func` may reference stateful objects (such as
tf.Variable).
These are captured as implicit inputs to the callable returned by `function`.
`function` can be applied to methods of an object.
_Usage with tf.keras_ The `call` methods of a tf.keras.Model subclass can be decorated with
`function` in order to apply graph execution optimizations on it.
_Input Signatures_ `function` instantiates a separate graph for every unique set of input
shapes and datatypes. For example, the following code snippet will result
in three distinct graphs being traced, as each input has a different
shape.
An "input signature" can be optionally provided to `function` to control
the graphs traced. The input signature specifies the shape and type of each
`Tensor` argument to the function using a tf.TensorSpec object. For example,
the following code snippet ensures that a single graph is created where the
input `Tensor` is required to be a floating point tensor with no restrictions
on shape.
When an `input_signature` is specified, the callable will convert the inputs
to the specified TensorSpecs. _Tracing and staging_ When `autograph` is `True`, all Python control flow that depends on `Tensor`
values is staged into a TensorFlow graph. When `autograph` is `False`, the
function is traced and control flow is not allowed to depend on data. Note that `function` only stages TensorFlow operations, all Python code that
`func` executes and does not depend on data will shape the _construction_ of
the graph.
For example, consider the following:
`add_noise()` will return a different output every time it is invoked.
However, `traced()` will return the same value every time it is called,
since a particular random value generated by the `np.random.randn` call will
be inserted in the traced/staged TensorFlow graph as a constant. In this
particular example, replacing `np.random.randn(5, 5)` with
`tf.random.normal((5, 5))` will result in the same behavior for `add_noise()`
and `traced()`. _Python Side-Effects_ A corollary of the previous discussion on tracing is the following: If a
Python function `func` has Python side-effects, then executing `func` multiple
times may not be semantically equivalent to executing `F = tf.function(func)`
multiple times; this difference is due to the fact that `function` only
captures the subgraph of TensorFlow operations that is constructed when `func`
is invoked to trace a graph. The same is true if code with Python side effects is used inside control flow,
such as a loop. If your code uses side effects that are not intended to
control graph construction, wrap them inside `tf.compat.v1.py_func`. _Retracing_ A single tf.function object might need to map to multiple computation graphs
under the hood. This should be visible only as performance (tracing graphs has
a nonzero computational and memory cost) but should not affect the correctness
of the program. A traced function should return the same result as it would
when run eagerly, assuming no unintended Python side-effects. Calling a tf.function with tensor arguments of different dtypes should lead
to at least one computational graph per distinct set of dtypes. Alternatively,
always calling a tf.function with tensor arguments of the same shapes and
dtypes and the same non-tensor arguments should not lead to additional
retracings of your function. Other than that, TensorFlow reserves the right to retrace functions as many
times as needed, to ensure that traced functions behave as they would when run
eagerly and to provide the best end-to-end performance. For example, the
behavior of how many traces TensorFlow will do when the function is repeatedly
called with different python scalars as arguments is left undefined to allow
for future optimizations. To control the tracing behavior, use the following tools:
- different tf.function objects are guaranteed to not share traces; and
- specifying a signature or using concrete function objects returned from
get_concrete_function() guarantees that only one function graph will be
built.
Parameters
-
PythonFunctionContainerfunc - function to be compiled. If `func` is None, returns a decorator that can be invoked with a single argument - `func`. The end result is equivalent to providing all the arguments up front. In other words, `tf.function(input_signature=...)(func)` is equivalent to `tf.function(func, input_signature=...)`. The former can be used to decorate Python functions, for example: @tf.function(input_signature=...) def foo(...):...
-
ValueTuple<TensorSpec, object>input_signature - A possibly nested sequence of
tf.TensorSpecobjects specifying the shapes and dtypes of the Tensors that will be supplied to this function. If `None`, a separate function is instantiated for each inferred input signature. If input_signature is specified, every input to `func` must be a `Tensor`, and `func` cannot accept `**kwargs`. -
boolautograph - Whether autograph should be applied on `func` before tracing a graph. This allows for dynamic control flow (Python if's, loops etc.) in the traced graph. See https://www.tensorflow.org/guide/autograph for more information.
-
objectexperimental_autograph_options - Experimental knobs (in the form of a tuple of tensorflow.autograph.Feature values) to control behavior when autograph=True.
-
boolexperimental_relax_shapes - When true, argument shapes may be relaxed to avoid unecessary retracing.
-
Nullable<bool>experimental_compile - If false, execute the function in a regular way. The function is optimized by some graph rewrite passes (some ops might be clustered into a single op) and interpreted by the standard TensorFlow executor, which dispatches op kernels one by one as they become executable. Set it to false when directly running a multi-device function on TPUs (e.g. two TPU cores, one TPU core and its host CPU). If True, the function is compiled directly by XLA (https://www.tensorflow.org/xla). XLA would fuse all the ops and emit more efficient code to run for some devices (e.g. TPU, XLA_GPU) and some use cases (e.g. dense tensor computation). It requires that the whole function is compilable by XLA (e.g. static tensor shape, a subset of operations, no string, compile-time constant input, etc). If None (default), compile the function with XLA when running on TPU and go through the regular function execution path when running on other devices. Note: TensorArrays on TPU don't work with standard TensorFlow executor.
Returns
-
object - If `func` is not None, returns a callable that will execute the compiled
function (and return zero or more
tf.Tensorobjects). If `func` is None, returns a decorator that, when invoked with a single `func` argument, returns a callable equivalent to the case above.
Show Example
def f(x, y):
return tf.reduce_mean(tf.multiply(x ** 2, 3) + y) g = tf.function(f) x = tf.constant([[2.0, 3.0]])
y = tf.constant([[3.0, -2.0]]) # `f` and `g` will return the same value, but `g` will be executed as a
# TensorFlow graph.
assert f(x, y).numpy() == g(x, y).numpy() # Tensors and tf.Variables used by the Python function are captured in the
# graph.
@tf.function
def h():
return f(x, y) assert (h().numpy() == f(x, y).numpy()).all() # Data-dependent control flow is also captured in the graph. Supported
# control flow statements include `if`, `for`, `while`, `break`, `continue`,
# `return`.
@tf.function
def g(x):
if tf.reduce_sum(x) > 0:
return x * x
else:
return -x // 2 # print and TensorFlow side effects are supported, but exercise caution when
# using Python side effects like mutating objects, saving to files, etc.
l = [] @tf.function
def g(x):
for i in x:
print(i) # Works
tf.compat.v1.assign(v, i) # Works
tf.compat.v1.py_func(lambda i: l.append(i))(i) # Works
l.append(i) # Caution! Doesn't work.
object function(PythonFunctionContainer func, TensorSpec input_signature, bool autograph, object experimental_autograph_options, bool experimental_relax_shapes, Nullable<bool> experimental_compile)
Creates a callable TensorFlow graph from a Python function. `function` constructs a callable that executes a TensorFlow graph
(
tf.Graph) created by tracing the TensorFlow operations in `func`.
This allows the TensorFlow runtime to apply optimizations and exploit
parallelism in the computation defined by `func`. _Example Usage_
Note that unlike other TensorFlow operations, we don't convert python
numerical inputs to tensors. Moreover, a new graph is generated for each
distinct python numerical value, for example calling `g(2)` and `g(3)` will
generate two new graphs (while only one is generated if you call
`g(tf.constant(2))` and `g(tf.constant(3))`). Therefore, python numerical
inputs should be restricted to arguments that will have few distinct values,
such as hyperparameters like the number of layers in a neural network. This
allows TensorFlow to optimize each variant of the neural network. _Referencing tf.Variables_ The Python function `func` may reference stateful objects (such as
tf.Variable).
These are captured as implicit inputs to the callable returned by `function`.
`function` can be applied to methods of an object.
_Usage with tf.keras_ The `call` methods of a tf.keras.Model subclass can be decorated with
`function` in order to apply graph execution optimizations on it.
_Input Signatures_ `function` instantiates a separate graph for every unique set of input
shapes and datatypes. For example, the following code snippet will result
in three distinct graphs being traced, as each input has a different
shape.
An "input signature" can be optionally provided to `function` to control
the graphs traced. The input signature specifies the shape and type of each
`Tensor` argument to the function using a tf.TensorSpec object. For example,
the following code snippet ensures that a single graph is created where the
input `Tensor` is required to be a floating point tensor with no restrictions
on shape.
When an `input_signature` is specified, the callable will convert the inputs
to the specified TensorSpecs. _Tracing and staging_ When `autograph` is `True`, all Python control flow that depends on `Tensor`
values is staged into a TensorFlow graph. When `autograph` is `False`, the
function is traced and control flow is not allowed to depend on data. Note that `function` only stages TensorFlow operations, all Python code that
`func` executes and does not depend on data will shape the _construction_ of
the graph.
For example, consider the following:
`add_noise()` will return a different output every time it is invoked.
However, `traced()` will return the same value every time it is called,
since a particular random value generated by the `np.random.randn` call will
be inserted in the traced/staged TensorFlow graph as a constant. In this
particular example, replacing `np.random.randn(5, 5)` with
`tf.random.normal((5, 5))` will result in the same behavior for `add_noise()`
and `traced()`. _Python Side-Effects_ A corollary of the previous discussion on tracing is the following: If a
Python function `func` has Python side-effects, then executing `func` multiple
times may not be semantically equivalent to executing `F = tf.function(func)`
multiple times; this difference is due to the fact that `function` only
captures the subgraph of TensorFlow operations that is constructed when `func`
is invoked to trace a graph. The same is true if code with Python side effects is used inside control flow,
such as a loop. If your code uses side effects that are not intended to
control graph construction, wrap them inside `tf.compat.v1.py_func`. _Retracing_ A single tf.function object might need to map to multiple computation graphs
under the hood. This should be visible only as performance (tracing graphs has
a nonzero computational and memory cost) but should not affect the correctness
of the program. A traced function should return the same result as it would
when run eagerly, assuming no unintended Python side-effects. Calling a tf.function with tensor arguments of different dtypes should lead
to at least one computational graph per distinct set of dtypes. Alternatively,
always calling a tf.function with tensor arguments of the same shapes and
dtypes and the same non-tensor arguments should not lead to additional
retracings of your function. Other than that, TensorFlow reserves the right to retrace functions as many
times as needed, to ensure that traced functions behave as they would when run
eagerly and to provide the best end-to-end performance. For example, the
behavior of how many traces TensorFlow will do when the function is repeatedly
called with different python scalars as arguments is left undefined to allow
for future optimizations. To control the tracing behavior, use the following tools:
- different tf.function objects are guaranteed to not share traces; and
- specifying a signature or using concrete function objects returned from
get_concrete_function() guarantees that only one function graph will be
built.
Parameters
-
PythonFunctionContainerfunc - function to be compiled. If `func` is None, returns a decorator that can be invoked with a single argument - `func`. The end result is equivalent to providing all the arguments up front. In other words, `tf.function(input_signature=...)(func)` is equivalent to `tf.function(func, input_signature=...)`. The former can be used to decorate Python functions, for example: @tf.function(input_signature=...) def foo(...):...
-
TensorSpecinput_signature - A possibly nested sequence of
tf.TensorSpecobjects specifying the shapes and dtypes of the Tensors that will be supplied to this function. If `None`, a separate function is instantiated for each inferred input signature. If input_signature is specified, every input to `func` must be a `Tensor`, and `func` cannot accept `**kwargs`. -
boolautograph - Whether autograph should be applied on `func` before tracing a graph. This allows for dynamic control flow (Python if's, loops etc.) in the traced graph. See https://www.tensorflow.org/guide/autograph for more information.
-
objectexperimental_autograph_options - Experimental knobs (in the form of a tuple of tensorflow.autograph.Feature values) to control behavior when autograph=True.
-
boolexperimental_relax_shapes - When true, argument shapes may be relaxed to avoid unecessary retracing.
-
Nullable<bool>experimental_compile - If false, execute the function in a regular way. The function is optimized by some graph rewrite passes (some ops might be clustered into a single op) and interpreted by the standard TensorFlow executor, which dispatches op kernels one by one as they become executable. Set it to false when directly running a multi-device function on TPUs (e.g. two TPU cores, one TPU core and its host CPU). If True, the function is compiled directly by XLA (https://www.tensorflow.org/xla). XLA would fuse all the ops and emit more efficient code to run for some devices (e.g. TPU, XLA_GPU) and some use cases (e.g. dense tensor computation). It requires that the whole function is compilable by XLA (e.g. static tensor shape, a subset of operations, no string, compile-time constant input, etc). If None (default), compile the function with XLA when running on TPU and go through the regular function execution path when running on other devices. Note: TensorArrays on TPU don't work with standard TensorFlow executor.
Returns
-
object - If `func` is not None, returns a callable that will execute the compiled
function (and return zero or more
tf.Tensorobjects). If `func` is None, returns a decorator that, when invoked with a single `func` argument, returns a callable equivalent to the case above.
Show Example
def f(x, y):
return tf.reduce_mean(tf.multiply(x ** 2, 3) + y) g = tf.function(f) x = tf.constant([[2.0, 3.0]])
y = tf.constant([[3.0, -2.0]]) # `f` and `g` will return the same value, but `g` will be executed as a
# TensorFlow graph.
assert f(x, y).numpy() == g(x, y).numpy() # Tensors and tf.Variables used by the Python function are captured in the
# graph.
@tf.function
def h():
return f(x, y) assert (h().numpy() == f(x, y).numpy()).all() # Data-dependent control flow is also captured in the graph. Supported
# control flow statements include `if`, `for`, `while`, `break`, `continue`,
# `return`.
@tf.function
def g(x):
if tf.reduce_sum(x) > 0:
return x * x
else:
return -x // 2 # print and TensorFlow side effects are supported, but exercise caution when
# using Python side effects like mutating objects, saving to files, etc.
l = [] @tf.function
def g(x):
for i in x:
print(i) # Works
tf.compat.v1.assign(v, i) # Works
tf.compat.v1.py_func(lambda i: l.append(i))(i) # Works
l.append(i) # Caution! Doesn't work.
object function_dyn(object func, object input_signature, ImplicitContainer<T> autograph, object experimental_autograph_options, ImplicitContainer<T> experimental_relax_shapes, object experimental_compile)
Creates a callable TensorFlow graph from a Python function. `function` constructs a callable that executes a TensorFlow graph
(
tf.Graph) created by tracing the TensorFlow operations in `func`.
This allows the TensorFlow runtime to apply optimizations and exploit
parallelism in the computation defined by `func`. _Example Usage_
Note that unlike other TensorFlow operations, we don't convert python
numerical inputs to tensors. Moreover, a new graph is generated for each
distinct python numerical value, for example calling `g(2)` and `g(3)` will
generate two new graphs (while only one is generated if you call
`g(tf.constant(2))` and `g(tf.constant(3))`). Therefore, python numerical
inputs should be restricted to arguments that will have few distinct values,
such as hyperparameters like the number of layers in a neural network. This
allows TensorFlow to optimize each variant of the neural network. _Referencing tf.Variables_ The Python function `func` may reference stateful objects (such as
tf.Variable).
These are captured as implicit inputs to the callable returned by `function`.
`function` can be applied to methods of an object.
_Usage with tf.keras_ The `call` methods of a tf.keras.Model subclass can be decorated with
`function` in order to apply graph execution optimizations on it.
_Input Signatures_ `function` instantiates a separate graph for every unique set of input
shapes and datatypes. For example, the following code snippet will result
in three distinct graphs being traced, as each input has a different
shape.
An "input signature" can be optionally provided to `function` to control
the graphs traced. The input signature specifies the shape and type of each
`Tensor` argument to the function using a tf.TensorSpec object. For example,
the following code snippet ensures that a single graph is created where the
input `Tensor` is required to be a floating point tensor with no restrictions
on shape.
When an `input_signature` is specified, the callable will convert the inputs
to the specified TensorSpecs. _Tracing and staging_ When `autograph` is `True`, all Python control flow that depends on `Tensor`
values is staged into a TensorFlow graph. When `autograph` is `False`, the
function is traced and control flow is not allowed to depend on data. Note that `function` only stages TensorFlow operations, all Python code that
`func` executes and does not depend on data will shape the _construction_ of
the graph.
For example, consider the following:
`add_noise()` will return a different output every time it is invoked.
However, `traced()` will return the same value every time it is called,
since a particular random value generated by the `np.random.randn` call will
be inserted in the traced/staged TensorFlow graph as a constant. In this
particular example, replacing `np.random.randn(5, 5)` with
`tf.random.normal((5, 5))` will result in the same behavior for `add_noise()`
and `traced()`. _Python Side-Effects_ A corollary of the previous discussion on tracing is the following: If a
Python function `func` has Python side-effects, then executing `func` multiple
times may not be semantically equivalent to executing `F = tf.function(func)`
multiple times; this difference is due to the fact that `function` only
captures the subgraph of TensorFlow operations that is constructed when `func`
is invoked to trace a graph. The same is true if code with Python side effects is used inside control flow,
such as a loop. If your code uses side effects that are not intended to
control graph construction, wrap them inside `tf.compat.v1.py_func`. _Retracing_ A single tf.function object might need to map to multiple computation graphs
under the hood. This should be visible only as performance (tracing graphs has
a nonzero computational and memory cost) but should not affect the correctness
of the program. A traced function should return the same result as it would
when run eagerly, assuming no unintended Python side-effects. Calling a tf.function with tensor arguments of different dtypes should lead
to at least one computational graph per distinct set of dtypes. Alternatively,
always calling a tf.function with tensor arguments of the same shapes and
dtypes and the same non-tensor arguments should not lead to additional
retracings of your function. Other than that, TensorFlow reserves the right to retrace functions as many
times as needed, to ensure that traced functions behave as they would when run
eagerly and to provide the best end-to-end performance. For example, the
behavior of how many traces TensorFlow will do when the function is repeatedly
called with different python scalars as arguments is left undefined to allow
for future optimizations. To control the tracing behavior, use the following tools:
- different tf.function objects are guaranteed to not share traces; and
- specifying a signature or using concrete function objects returned from
get_concrete_function() guarantees that only one function graph will be
built.
Parameters
-
objectfunc - function to be compiled. If `func` is None, returns a decorator that can be invoked with a single argument - `func`. The end result is equivalent to providing all the arguments up front. In other words, `tf.function(input_signature=...)(func)` is equivalent to `tf.function(func, input_signature=...)`. The former can be used to decorate Python functions, for example: @tf.function(input_signature=...) def foo(...):...
-
objectinput_signature - A possibly nested sequence of
tf.TensorSpecobjects specifying the shapes and dtypes of the Tensors that will be supplied to this function. If `None`, a separate function is instantiated for each inferred input signature. If input_signature is specified, every input to `func` must be a `Tensor`, and `func` cannot accept `**kwargs`. -
ImplicitContainer<T>autograph - Whether autograph should be applied on `func` before tracing a graph. This allows for dynamic control flow (Python if's, loops etc.) in the traced graph. See https://www.tensorflow.org/guide/autograph for more information.
-
objectexperimental_autograph_options - Experimental knobs (in the form of a tuple of tensorflow.autograph.Feature values) to control behavior when autograph=True.
-
ImplicitContainer<T>experimental_relax_shapes - When true, argument shapes may be relaxed to avoid unecessary retracing.
-
objectexperimental_compile - If false, execute the function in a regular way. The function is optimized by some graph rewrite passes (some ops might be clustered into a single op) and interpreted by the standard TensorFlow executor, which dispatches op kernels one by one as they become executable. Set it to false when directly running a multi-device function on TPUs (e.g. two TPU cores, one TPU core and its host CPU). If True, the function is compiled directly by XLA (https://www.tensorflow.org/xla). XLA would fuse all the ops and emit more efficient code to run for some devices (e.g. TPU, XLA_GPU) and some use cases (e.g. dense tensor computation). It requires that the whole function is compilable by XLA (e.g. static tensor shape, a subset of operations, no string, compile-time constant input, etc). If None (default), compile the function with XLA when running on TPU and go through the regular function execution path when running on other devices. Note: TensorArrays on TPU don't work with standard TensorFlow executor.
Returns
-
object - If `func` is not None, returns a callable that will execute the compiled
function (and return zero or more
tf.Tensorobjects). If `func` is None, returns a decorator that, when invoked with a single `func` argument, returns a callable equivalent to the case above.
Show Example
def f(x, y):
return tf.reduce_mean(tf.multiply(x ** 2, 3) + y) g = tf.function(f) x = tf.constant([[2.0, 3.0]])
y = tf.constant([[3.0, -2.0]]) # `f` and `g` will return the same value, but `g` will be executed as a
# TensorFlow graph.
assert f(x, y).numpy() == g(x, y).numpy() # Tensors and tf.Variables used by the Python function are captured in the
# graph.
@tf.function
def h():
return f(x, y) assert (h().numpy() == f(x, y).numpy()).all() # Data-dependent control flow is also captured in the graph. Supported
# control flow statements include `if`, `for`, `while`, `break`, `continue`,
# `return`.
@tf.function
def g(x):
if tf.reduce_sum(x) > 0:
return x * x
else:
return -x // 2 # print and TensorFlow side effects are supported, but exercise caution when
# using Python side effects like mutating objects, saving to files, etc.
l = [] @tf.function
def g(x):
for i in x:
print(i) # Works
tf.compat.v1.assign(v, i) # Works
tf.compat.v1.py_func(lambda i: l.append(i))(i) # Works
l.append(i) # Caution! Doesn't work.
Tensor gather(object params, IEnumerable<object> indices, object validate_indices, string name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
objectparams - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
IEnumerable<object>indices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
stringname - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(PythonClassContainer params, object indices, object validate_indices, string name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
PythonClassContainerparams - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
objectindices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
stringname - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(IEnumerable<IGraphNodeBase> params, IEnumerable<object> indices, object validate_indices, PythonFunctionContainer name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
IEnumerable<IGraphNodeBase>params - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
IEnumerable<object>indices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
PythonFunctionContainername - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(IEnumerable<IGraphNodeBase> params, object indices, object validate_indices, string name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
IEnumerable<IGraphNodeBase>params - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
objectindices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
stringname - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(PythonClassContainer params, IEnumerable<object> indices, object validate_indices, PythonFunctionContainer name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
PythonClassContainerparams - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
IEnumerable<object>indices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
PythonFunctionContainername - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(PythonClassContainer params, IEnumerable<object> indices, object validate_indices, string name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
PythonClassContainerparams - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
IEnumerable<object>indices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
stringname - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(PythonClassContainer params, object indices, object validate_indices, PythonFunctionContainer name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
PythonClassContainerparams - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
objectindices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
PythonFunctionContainername - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(object params, object indices, object validate_indices, string name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
objectparams - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
objectindices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
stringname - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(IEnumerable<IGraphNodeBase> params, IEnumerable<object> indices, object validate_indices, string name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
IEnumerable<IGraphNodeBase>params - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
IEnumerable<object>indices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
stringname - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(object params, object indices, object validate_indices, PythonFunctionContainer name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
objectparams - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
objectindices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
PythonFunctionContainername - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(IEnumerable<IGraphNodeBase> params, object indices, object validate_indices, PythonFunctionContainer name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
IEnumerable<IGraphNodeBase>params - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
objectindices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
PythonFunctionContainername - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Tensor gather(object params, IEnumerable<object> indices, object validate_indices, PythonFunctionContainer name, IGraphNodeBase axis, int batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
objectparams - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
IEnumerable<object>indices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
PythonFunctionContainername - A name for the operation (optional).
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
intbatch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
object gather_dyn(object params, object indices, object validate_indices, object name, object axis, ImplicitContainer<T> batch_dims)
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
Parameters
-
objectparams - The `Tensor` from which to gather values. Must be at least rank `axis + 1`.
-
objectindices - The index `Tensor`. Must be one of the following types: `int32`, `int64`. Must be in range `[0, params.shape[axis])`.
-
objectvalidate_indices - Deprecated, does nothing.
-
objectname - A name for the operation (optional).
-
objectaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. The `axis` in `params` to gather `indices` from. Must be greater than or equal to `batch_dims`. Defaults to the first non-batch dimension. Supports negative indexes.
-
ImplicitContainer<T>batch_dims - An `integer`. The number of batch dimensions. Must be less than `rank(indices)`.
Returns
-
object - A `Tensor`. Has the same type as `params`.
Tensor gather_nd(IGraphNodeBase params, IGraphNodeBase indices, string name, IGraphNodeBase batch_dims)
Gather slices from `params` into a Tensor with shape specified by `indices`. `indices` is an K-dimensional integer tensor, best thought of as a
(K-1)-dimensional tensor of indices into `params`, where each element defines
a slice of `params`: output[\\(i_0,..., i_{K-2}\\)] = params[indices[\\(i_0,..., i_{K-2}\\)]] Whereas in
tf.gather `indices` defines slices into the first
dimension of `params`, in tf.gather_nd, `indices` defines slices into the
first `N` dimensions of `params`, where `N = indices.shape[-1]`. The last dimension of `indices` can be at most the rank of
`params`: indices.shape[-1] <= params.rank The last dimension of `indices` corresponds to elements
(if `indices.shape[-1] == params.rank`) or slices
(if `indices.shape[-1] < params.rank`) along dimension `indices.shape[-1]`
of `params`. The output tensor has shape indices.shape[:-1] + params.shape[indices.shape[-1]:] Additionally both 'params' and 'indices' can have M leading batch
dimensions that exactly match. In this case 'batch_dims' must be M. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the
corresponding output value. Some examples below. Simple indexing into a matrix:
Slice indexing into a matrix:
Indexing into a 3-tensor:
The examples below are for the case when only indices have leading extra
dimensions. If both 'params' and 'indices' have leading batch dimensions, use
the 'batch_dims' parameter to run gather_nd in batch mode. Batched indexing into a matrix:
Batched slice indexing into a matrix:
Batched indexing into a 3-tensor:
Examples with batched 'params' and 'indices':
See also tf.gather.
Parameters
-
IGraphNodeBaseparams - A `Tensor`. The tensor from which to gather values.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasebatch_dims - An integer or a scalar 'Tensor'. The number of batch dimensions.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Show Example
indices = [[0, 0], [1, 1]]
params = [['a', 'b'], ['c', 'd']]
output = ['a', 'd']
Tensor gather_nd(IGraphNodeBase params, IGraphNodeBase indices, string name, int batch_dims)
Gather slices from `params` into a Tensor with shape specified by `indices`. `indices` is an K-dimensional integer tensor, best thought of as a
(K-1)-dimensional tensor of indices into `params`, where each element defines
a slice of `params`: output[\\(i_0,..., i_{K-2}\\)] = params[indices[\\(i_0,..., i_{K-2}\\)]] Whereas in
tf.gather `indices` defines slices into the first
dimension of `params`, in tf.gather_nd, `indices` defines slices into the
first `N` dimensions of `params`, where `N = indices.shape[-1]`. The last dimension of `indices` can be at most the rank of
`params`: indices.shape[-1] <= params.rank The last dimension of `indices` corresponds to elements
(if `indices.shape[-1] == params.rank`) or slices
(if `indices.shape[-1] < params.rank`) along dimension `indices.shape[-1]`
of `params`. The output tensor has shape indices.shape[:-1] + params.shape[indices.shape[-1]:] Additionally both 'params' and 'indices' can have M leading batch
dimensions that exactly match. In this case 'batch_dims' must be M. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the
corresponding output value. Some examples below. Simple indexing into a matrix:
Slice indexing into a matrix:
Indexing into a 3-tensor:
The examples below are for the case when only indices have leading extra
dimensions. If both 'params' and 'indices' have leading batch dimensions, use
the 'batch_dims' parameter to run gather_nd in batch mode. Batched indexing into a matrix:
Batched slice indexing into a matrix:
Batched indexing into a 3-tensor:
Examples with batched 'params' and 'indices':
See also tf.gather.
Parameters
-
IGraphNodeBaseparams - A `Tensor`. The tensor from which to gather values.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
stringname - A name for the operation (optional).
-
intbatch_dims - An integer or a scalar 'Tensor'. The number of batch dimensions.
Returns
-
Tensor - A `Tensor`. Has the same type as `params`.
Show Example
indices = [[0, 0], [1, 1]]
params = [['a', 'b'], ['c', 'd']]
output = ['a', 'd']
object gather_nd_dyn(object params, object indices, object name, ImplicitContainer<T> batch_dims)
Gather slices from `params` into a Tensor with shape specified by `indices`. `indices` is an K-dimensional integer tensor, best thought of as a
(K-1)-dimensional tensor of indices into `params`, where each element defines
a slice of `params`: output[\\(i_0,..., i_{K-2}\\)] = params[indices[\\(i_0,..., i_{K-2}\\)]] Whereas in
tf.gather `indices` defines slices into the first
dimension of `params`, in tf.gather_nd, `indices` defines slices into the
first `N` dimensions of `params`, where `N = indices.shape[-1]`. The last dimension of `indices` can be at most the rank of
`params`: indices.shape[-1] <= params.rank The last dimension of `indices` corresponds to elements
(if `indices.shape[-1] == params.rank`) or slices
(if `indices.shape[-1] < params.rank`) along dimension `indices.shape[-1]`
of `params`. The output tensor has shape indices.shape[:-1] + params.shape[indices.shape[-1]:] Additionally both 'params' and 'indices' can have M leading batch
dimensions that exactly match. In this case 'batch_dims' must be M. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the
corresponding output value. Some examples below. Simple indexing into a matrix:
Slice indexing into a matrix:
Indexing into a 3-tensor:
The examples below are for the case when only indices have leading extra
dimensions. If both 'params' and 'indices' have leading batch dimensions, use
the 'batch_dims' parameter to run gather_nd in batch mode. Batched indexing into a matrix:
Batched slice indexing into a matrix:
Batched indexing into a 3-tensor:
Examples with batched 'params' and 'indices':
See also tf.gather.
Parameters
-
objectparams - A `Tensor`. The tensor from which to gather values.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
objectname - A name for the operation (optional).
-
ImplicitContainer<T>batch_dims - An integer or a scalar 'Tensor'. The number of batch dimensions.
Returns
-
object - A `Tensor`. Has the same type as `params`.
Show Example
indices = [[0, 0], [1, 1]]
params = [['a', 'b'], ['c', 'd']]
output = ['a', 'd']
Tensor gather_tree(IGraphNodeBase step_ids, IGraphNodeBase parent_ids, IGraphNodeBase max_sequence_lengths, IGraphNodeBase end_token, string name)
object gather_tree_dyn(object step_ids, object parent_ids, object max_sequence_lengths, object end_token, object name)
IList<object> get_collection(string key, string scope)
Wrapper for `Graph.get_collection()` using the default graph. See
tf.Graph.get_collection
for more details.
Parameters
-
stringkey - The key for the collection. For example, the `GraphKeys` class contains many standard names for collections.
-
stringscope - (Optional.) If supplied, the resulting list is filtered to include only items whose `name` attribute matches using `re.match`. Items without a `name` attribute are never returned if a scope is supplied and the choice or `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
IList<object> - The list of values in the collection with the given `name`, or an empty list if no value has been added to that collection. The list contains the values in the order under which they were collected.
IList<object> get_collection(string key, VariableScope scope)
Wrapper for `Graph.get_collection()` using the default graph. See
tf.Graph.get_collection
for more details.
Parameters
-
stringkey - The key for the collection. For example, the `GraphKeys` class contains many standard names for collections.
-
VariableScopescope - (Optional.) If supplied, the resulting list is filtered to include only items whose `name` attribute matches using `re.match`. Items without a `name` attribute are never returned if a scope is supplied and the choice or `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
IList<object> - The list of values in the collection with the given `name`, or an empty list if no value has been added to that collection. The list contains the values in the order under which they were collected.
IList<object> get_collection(string key, bool scope)
Wrapper for `Graph.get_collection()` using the default graph. See
tf.Graph.get_collection
for more details.
Parameters
-
stringkey - The key for the collection. For example, the `GraphKeys` class contains many standard names for collections.
-
boolscope - (Optional.) If supplied, the resulting list is filtered to include only items whose `name` attribute matches using `re.match`. Items without a `name` attribute are never returned if a scope is supplied and the choice or `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
IList<object> - The list of values in the collection with the given `name`, or an empty list if no value has been added to that collection. The list contains the values in the order under which they were collected.
IList<object> get_collection(IEnumerable<string> key, string scope)
Wrapper for `Graph.get_collection()` using the default graph. See
tf.Graph.get_collection
for more details.
Parameters
-
IEnumerable<string>key - The key for the collection. For example, the `GraphKeys` class contains many standard names for collections.
-
stringscope - (Optional.) If supplied, the resulting list is filtered to include only items whose `name` attribute matches using `re.match`. Items without a `name` attribute are never returned if a scope is supplied and the choice or `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
IList<object> - The list of values in the collection with the given `name`, or an empty list if no value has been added to that collection. The list contains the values in the order under which they were collected.
IList<object> get_collection(IEnumerable<string> key, VariableScope scope)
Wrapper for `Graph.get_collection()` using the default graph. See
tf.Graph.get_collection
for more details.
Parameters
-
IEnumerable<string>key - The key for the collection. For example, the `GraphKeys` class contains many standard names for collections.
-
VariableScopescope - (Optional.) If supplied, the resulting list is filtered to include only items whose `name` attribute matches using `re.match`. Items without a `name` attribute are never returned if a scope is supplied and the choice or `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
IList<object> - The list of values in the collection with the given `name`, or an empty list if no value has been added to that collection. The list contains the values in the order under which they were collected.
IList<object> get_collection(IEnumerable<string> key, bool scope)
Wrapper for `Graph.get_collection()` using the default graph. See
tf.Graph.get_collection
for more details.
Parameters
-
IEnumerable<string>key - The key for the collection. For example, the `GraphKeys` class contains many standard names for collections.
-
boolscope - (Optional.) If supplied, the resulting list is filtered to include only items whose `name` attribute matches using `re.match`. Items without a `name` attribute are never returned if a scope is supplied and the choice or `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
IList<object> - The list of values in the collection with the given `name`, or an empty list if no value has been added to that collection. The list contains the values in the order under which they were collected.
Graph get_default_graph()
Returns the default graph for the current thread. The returned graph will be the innermost graph on which a
`Graph.as_default()` context has been entered, or a global default
graph if none has been explicitly created. NOTE: The default graph is a property of the current thread. If you
create a new thread, and wish to use the default graph in that
thread, you must explicitly add a `with g.as_default():` in that
thread's function.
Returns
-
Graph - The default `Graph` being used in the current thread.
object get_default_graph_dyn()
Returns the default graph for the current thread. The returned graph will be the innermost graph on which a
`Graph.as_default()` context has been entered, or a global default
graph if none has been explicitly created. NOTE: The default graph is a property of the current thread. If you
create a new thread, and wish to use the default graph in that
thread, you must explicitly add a `with g.as_default():` in that
thread's function.
Returns
-
object - The default `Graph` being used in the current thread.
BaseSession get_default_session()
Returns the default session for the current thread. The returned `Session` will be the innermost session on which a
`Session` or `Session.as_default()` context has been entered. NOTE: The default session is a property of the current thread. If you
create a new thread, and wish to use the default session in that
thread, you must explicitly add a `with sess.as_default():` in that
thread's function.
Returns
-
BaseSession - The default `Session` being used in the current thread.
object get_default_session_dyn()
Returns the default session for the current thread. The returned `Session` will be the innermost session on which a
`Session` or `Session.as_default()` context has been entered. NOTE: The default session is a property of the current thread. If you
create a new thread, and wish to use the default session in that
thread, you must explicitly add a `with sess.as_default():` in that
thread's function.
Returns
-
object - The default `Session` being used in the current thread.
object get_local_variable(string name, IEnumerable<int> shape, DType dtype, IndexedSlices initializer, object regularizer, bool trainable, IEnumerable<string> collections, object caching_device, object partitioner, bool validate_shape, object use_resource, object custom_getter, object constraint, VariableSynchronization synchronization, VariableAggregation aggregation)
Gets an existing *local* variable or creates a new one. Behavior is the same as in `get_variable`, except that variables are
added to the `LOCAL_VARIABLES` collection and `trainable` is set to
`False`.
This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
stringname - The name of the new or existing variable.
-
IEnumerable<int>shape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
IndexedSlicesinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
booltrainable -
IEnumerable<string>collections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.LOCAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
objectpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
objectuse_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
objectcustom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
VariableAggregationaggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_local_variable(string name, IEnumerable<int> shape, DType dtype, zeros_initializer initializer, object regularizer, bool trainable, IEnumerable<string> collections, object caching_device, object partitioner, bool validate_shape, object use_resource, object custom_getter, object constraint, VariableSynchronization synchronization, VariableAggregation aggregation)
Gets an existing *local* variable or creates a new one. Behavior is the same as in `get_variable`, except that variables are
added to the `LOCAL_VARIABLES` collection and `trainable` is set to
`False`.
This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
stringname - The name of the new or existing variable.
-
IEnumerable<int>shape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
zeros_initializerinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
booltrainable -
IEnumerable<string>collections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.LOCAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
objectpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
objectuse_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
objectcustom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
VariableAggregationaggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_local_variable(string name, IEnumerable<int> shape, DType dtype, int initializer, object regularizer, bool trainable, IEnumerable<string> collections, object caching_device, object partitioner, bool validate_shape, object use_resource, object custom_getter, object constraint, VariableSynchronization synchronization, VariableAggregation aggregation)
Gets an existing *local* variable or creates a new one. Behavior is the same as in `get_variable`, except that variables are
added to the `LOCAL_VARIABLES` collection and `trainable` is set to
`False`.
This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
stringname - The name of the new or existing variable.
-
IEnumerable<int>shape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
intinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
booltrainable -
IEnumerable<string>collections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.LOCAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
objectpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
objectuse_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
objectcustom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
VariableAggregationaggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_local_variable(string name, IEnumerable<int> shape, DType dtype, ValueTuple<PythonClassContainer, PythonClassContainer> initializer, object regularizer, bool trainable, IEnumerable<string> collections, object caching_device, object partitioner, bool validate_shape, object use_resource, object custom_getter, object constraint, VariableSynchronization synchronization, VariableAggregation aggregation)
Gets an existing *local* variable or creates a new one. Behavior is the same as in `get_variable`, except that variables are
added to the `LOCAL_VARIABLES` collection and `trainable` is set to
`False`.
This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
stringname - The name of the new or existing variable.
-
IEnumerable<int>shape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
ValueTuple<PythonClassContainer, PythonClassContainer>initializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
booltrainable -
IEnumerable<string>collections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.LOCAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
objectpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
objectuse_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
objectcustom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
VariableAggregationaggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_local_variable(string name, IEnumerable<int> shape, DType dtype, IGraphNodeBase initializer, object regularizer, bool trainable, IEnumerable<string> collections, object caching_device, object partitioner, bool validate_shape, object use_resource, object custom_getter, object constraint, VariableSynchronization synchronization, VariableAggregation aggregation)
Gets an existing *local* variable or creates a new one. Behavior is the same as in `get_variable`, except that variables are
added to the `LOCAL_VARIABLES` collection and `trainable` is set to
`False`.
This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
stringname - The name of the new or existing variable.
-
IEnumerable<int>shape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
IGraphNodeBaseinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
booltrainable -
IEnumerable<string>collections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.LOCAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
objectpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
objectuse_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
objectcustom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
VariableAggregationaggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_local_variable_dyn(object name, object shape, object dtype, object initializer, object regularizer, ImplicitContainer<T> trainable, object collections, object caching_device, object partitioner, ImplicitContainer<T> validate_shape, object use_resource, object custom_getter, object constraint, ImplicitContainer<T> synchronization, ImplicitContainer<T> aggregation)
Gets an existing *local* variable or creates a new one. Behavior is the same as in `get_variable`, except that variables are
added to the `LOCAL_VARIABLES` collection and `trainable` is set to
`False`.
This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
objectshape - Shape of the new or existing variable.
-
objectdtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
ImplicitContainer<T>trainable -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.LOCAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
objectpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
ImplicitContainer<T>validate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
objectuse_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
objectcustom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
ImplicitContainer<T>synchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
PythonClassContainer get_logger()
Return TF logger instance.
object get_logger_dyn()
Return TF logger instance.
ValueTuple<int, int> get_seed(int op_seed)
Returns the local seeds an operation should use given an op-specific seed. Given operation-specific seed, `op_seed`, this helper function returns two
seeds derived from graph-level and op-level seeds. Many random operations
internally use the two seeds to allow user to change the seed globally for a
graph, or for only specific operations. For details on how the graph-level seed interacts with op seeds, see
`tf.compat.v1.random.set_random_seed`.
Parameters
-
intop_seed - integer.
Returns
-
ValueTuple<int, int> - A tuple of two integers that should be used for the local seed of this operation.
ValueTuple<int, int> get_seed(IEnumerable<object> op_seed)
Returns the local seeds an operation should use given an op-specific seed. Given operation-specific seed, `op_seed`, this helper function returns two
seeds derived from graph-level and op-level seeds. Many random operations
internally use the two seeds to allow user to change the seed globally for a
graph, or for only specific operations. For details on how the graph-level seed interacts with op seeds, see
`tf.compat.v1.random.set_random_seed`.
Parameters
-
IEnumerable<object>op_seed - integer.
Returns
-
ValueTuple<int, int> - A tuple of two integers that should be used for the local seed of this operation.
ValueTuple<int, int> get_seed(IGraphNodeBase op_seed)
Returns the local seeds an operation should use given an op-specific seed. Given operation-specific seed, `op_seed`, this helper function returns two
seeds derived from graph-level and op-level seeds. Many random operations
internally use the two seeds to allow user to change the seed globally for a
graph, or for only specific operations. For details on how the graph-level seed interacts with op seeds, see
`tf.compat.v1.random.set_random_seed`.
Parameters
-
IGraphNodeBaseop_seed - integer.
Returns
-
ValueTuple<int, int> - A tuple of two integers that should be used for the local seed of this operation.
object get_seed_dyn(object op_seed)
Returns the local seeds an operation should use given an op-specific seed. Given operation-specific seed, `op_seed`, this helper function returns two
seeds derived from graph-level and op-level seeds. Many random operations
internally use the two seeds to allow user to change the seed globally for a
graph, or for only specific operations. For details on how the graph-level seed interacts with op seeds, see
`tf.compat.v1.random.set_random_seed`.
Parameters
-
objectop_seed - integer.
Returns
-
object - A tuple of two integers that should be used for the local seed of this operation.
Tensor get_session_handle(string data, string name)
Return the handle of `data`. This is EXPERIMENTAL and subject to change. Keep `data` "in-place" in the runtime and create a handle that can be
used to retrieve `data` in a subsequent run(). Combined with `get_session_tensor`, we can keep a tensor produced in
one run call in place, and use it as the input in a future run call.
Parameters
-
stringdata - A tensor to be stored in the session.
-
stringname - Optional name prefix for the return tensor.
Returns
-
Tensor - A scalar string tensor representing a unique handle for `data`.
Tensor get_session_handle(IGraphNodeBase data, string name)
Return the handle of `data`. This is EXPERIMENTAL and subject to change. Keep `data` "in-place" in the runtime and create a handle that can be
used to retrieve `data` in a subsequent run(). Combined with `get_session_tensor`, we can keep a tensor produced in
one run call in place, and use it as the input in a future run call.
Parameters
-
IGraphNodeBasedata - A tensor to be stored in the session.
-
stringname - Optional name prefix for the return tensor.
Returns
-
Tensor - A scalar string tensor representing a unique handle for `data`.
object get_session_handle_dyn(object data, object name)
Return the handle of `data`. This is EXPERIMENTAL and subject to change. Keep `data` "in-place" in the runtime and create a handle that can be
used to retrieve `data` in a subsequent run(). Combined with `get_session_tensor`, we can keep a tensor produced in
one run call in place, and use it as the input in a future run call.
Parameters
-
objectdata - A tensor to be stored in the session.
-
objectname - Optional name prefix for the return tensor.
Returns
-
object - A scalar string tensor representing a unique handle for `data`.
ValueTuple<Tensor, object> get_session_tensor(object handle, DType dtype, string name)
Get the tensor of type `dtype` by feeding a tensor handle. This is EXPERIMENTAL and subject to change. Get the value of the tensor from a tensor handle. The tensor
is produced in a previous run() and stored in the state of the
session.
Parameters
-
objecthandle - The string representation of a persistent tensor handle.
-
DTypedtype - The type of the output tensor.
-
stringname - Optional name prefix for the return tensor.
Returns
-
ValueTuple<Tensor, object> - A pair of tensors. The first is a placeholder for feeding a tensor handle and the second is the tensor in the session state keyed by the tensor handle. Example: ```python c = tf.multiply(a, b) h = tf.compat.v1.get_session_handle(c) h = sess.run(h) p, a = tf.compat.v1.get_session_tensor(h.handle, tf.float32) b = tf.multiply(a, 10) c = sess.run(b, feed_dict={p: h.handle}) ```
object get_session_tensor_dyn(object handle, object dtype, object name)
Get the tensor of type `dtype` by feeding a tensor handle. This is EXPERIMENTAL and subject to change. Get the value of the tensor from a tensor handle. The tensor
is produced in a previous run() and stored in the state of the
session.
Parameters
-
objecthandle - The string representation of a persistent tensor handle.
-
objectdtype - The type of the output tensor.
-
objectname - Optional name prefix for the return tensor.
Returns
-
object - A pair of tensors. The first is a placeholder for feeding a tensor handle and the second is the tensor in the session state keyed by the tensor handle. Example: ```python c = tf.multiply(a, b) h = tf.compat.v1.get_session_handle(c) h = sess.run(h) p, a = tf.compat.v1.get_session_tensor(h.handle, tf.float32) b = tf.multiply(a, 10) c = sess.run(b, feed_dict={p: h.handle}) ```
object get_static_value(IEnumerable<IGraphNodeBase> tensor, bool partial)
Returns the constant value of the given tensor, if efficiently calculable. This function attempts to partially evaluate the given tensor, and
returns its value as a numpy ndarray if this succeeds. Compatibility(V1): If `constant_value(tensor)` returns a non-`None` result, it
will no longer be possible to feed a different value for `tensor`. This allows
the result of this function to influence the graph that is constructed, and
permits static shape optimizations.
Parameters
-
IEnumerable<IGraphNodeBase>tensor - The Tensor to be evaluated.
-
boolpartial - If True, the returned numpy array is allowed to have partially evaluated values. Values that can't be evaluated will be None.
Returns
-
object - A numpy ndarray containing the constant value of the given `tensor`, or None if it cannot be calculated.
object get_static_value(PythonClassContainer tensor, bool partial)
Returns the constant value of the given tensor, if efficiently calculable. This function attempts to partially evaluate the given tensor, and
returns its value as a numpy ndarray if this succeeds. Compatibility(V1): If `constant_value(tensor)` returns a non-`None` result, it
will no longer be possible to feed a different value for `tensor`. This allows
the result of this function to influence the graph that is constructed, and
permits static shape optimizations.
Parameters
-
PythonClassContainertensor - The Tensor to be evaluated.
-
boolpartial - If True, the returned numpy array is allowed to have partially evaluated values. Values that can't be evaluated will be None.
Returns
-
object - A numpy ndarray containing the constant value of the given `tensor`, or None if it cannot be calculated.
object get_static_value(object tensor, bool partial)
Returns the constant value of the given tensor, if efficiently calculable. This function attempts to partially evaluate the given tensor, and
returns its value as a numpy ndarray if this succeeds. Compatibility(V1): If `constant_value(tensor)` returns a non-`None` result, it
will no longer be possible to feed a different value for `tensor`. This allows
the result of this function to influence the graph that is constructed, and
permits static shape optimizations.
Parameters
-
objecttensor - The Tensor to be evaluated.
-
boolpartial - If True, the returned numpy array is allowed to have partially evaluated values. Values that can't be evaluated will be None.
Returns
-
object - A numpy ndarray containing the constant value of the given `tensor`, or None if it cannot be calculated.
object get_static_value_dyn(object tensor, ImplicitContainer<T> partial)
Returns the constant value of the given tensor, if efficiently calculable. This function attempts to partially evaluate the given tensor, and
returns its value as a numpy ndarray if this succeeds. Compatibility(V1): If `constant_value(tensor)` returns a non-`None` result, it
will no longer be possible to feed a different value for `tensor`. This allows
the result of this function to influence the graph that is constructed, and
permits static shape optimizations.
Parameters
-
objecttensor - The Tensor to be evaluated.
-
ImplicitContainer<T>partial - If True, the returned numpy array is allowed to have partially evaluated values. Values that can't be evaluated will be None.
Returns
-
object - A numpy ndarray containing the constant value of the given `tensor`, or None if it cannot be calculated.
object get_variable(object name, ValueTuple<int, object> shape, PythonClassContainer dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, object>shape - Shape of the new or existing variable.
-
PythonClassContainerdtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, object, object> shape, PythonClassContainer dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, object, object>shape - Shape of the new or existing variable.
-
PythonClassContainerdtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, int, object, int> shape, PythonClassContainer dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, int, object, int>shape - Shape of the new or existing variable.
-
PythonClassContainerdtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, int, object, int> shape, dtype dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, int, object, int>shape - Shape of the new or existing variable.
-
dtypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, TensorShape shape, PythonClassContainer dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
TensorShapeshape - Shape of the new or existing variable.
-
PythonClassContainerdtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, object, object> shape, DType dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, object, object>shape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, object> shape, dtype dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, object>shape - Shape of the new or existing variable.
-
dtypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple shape, DType dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTupleshape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, object, object> shape, dtype dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, object, object>shape - Shape of the new or existing variable.
-
dtypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, int shape, dtype dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
intshape - Shape of the new or existing variable.
-
dtypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, int shape, DType dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
intshape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, TensorShape shape, DType dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
TensorShapeshape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, int, int, object, int> shape, PythonClassContainer dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, int, int, object, int>shape - Shape of the new or existing variable.
-
PythonClassContainerdtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, int, object, int> shape, DType dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, int, object, int>shape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, int shape, PythonClassContainer dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
intshape - Shape of the new or existing variable.
-
PythonClassContainerdtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple shape, dtype dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTupleshape - Shape of the new or existing variable.
-
dtypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, IEnumerable<Nullable<int>> shape, dtype dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
IEnumerable<Nullable<int>>shape - Shape of the new or existing variable.
-
dtypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, int, int, object, int> shape, dtype dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, int, int, object, int>shape - Shape of the new or existing variable.
-
dtypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, IEnumerable<Nullable<int>> shape, PythonClassContainer dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
IEnumerable<Nullable<int>>shape - Shape of the new or existing variable.
-
PythonClassContainerdtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, int, int, object, int> shape, DType dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, int, int, object, int>shape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, IEnumerable<Nullable<int>> shape, DType dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
IEnumerable<Nullable<int>>shape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple<int, object> shape, DType dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTuple<int, object>shape - Shape of the new or existing variable.
-
DTypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, TensorShape shape, dtype dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
TensorShapeshape - Shape of the new or existing variable.
-
dtypedtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable(object name, ValueTuple shape, PythonClassContainer dtype, object initializer, object regularizer, Nullable<bool> trainable, object collections, object caching_device, PythonFunctionContainer partitioner, bool validate_shape, Nullable<bool> use_resource, Nullable<int> custom_getter, object constraint, VariableSynchronization synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
ValueTupleshape - Shape of the new or existing variable.
-
PythonClassContainerdtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
Nullable<bool>trainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
PythonFunctionContainerpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
boolvalidate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
Nullable<bool>use_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
Nullable<int>custom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
VariableSynchronizationsynchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
object get_variable_dyn(object name, object shape, object dtype, object initializer, object regularizer, object trainable, object collections, object caching_device, object partitioner, ImplicitContainer<T> validate_shape, object use_resource, object custom_getter, object constraint, ImplicitContainer<T> synchronization, ImplicitContainer<T> aggregation)
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Parameters
-
objectname - The name of the new or existing variable.
-
objectshape - Shape of the new or existing variable.
-
objectdtype - Type of the new or existing variable (defaults to `DT_FLOAT`).
-
objectinitializer - Initializer for the variable if one is created. Can either be an initializer object or a Tensor. If it's a Tensor, its shape must be known unless validate_shape is False.
-
objectregularizer - A (Tensor -> Tensor or None) function; the result of
applying it on a newly created variable will be added to the collection
tf.GraphKeys.REGULARIZATION_LOSSESand can be used for regularization. -
objecttrainable - If `True` also add the variable to the graph collection
`GraphKeys.TRAINABLE_VARIABLES` (see
tf.Variable). -
objectcollections - List of graph collections keys to add the Variable to.
Defaults to `[GraphKeys.GLOBAL_VARIABLES]` (see
tf.Variable). -
objectcaching_device - Optional device string or function describing where the Variable should be cached for reading. Defaults to the Variable's device. If not `None`, caches on another device. Typical use is to cache on the device where the Ops using the Variable reside, to deduplicate copying through `Switch` and other conditional statements.
-
objectpartitioner - Optional callable that accepts a fully defined `TensorShape` and `dtype` of the Variable to be created, and returns a list of partitions for each axis (currently only one axis can be partitioned).
-
ImplicitContainer<T>validate_shape - If False, allows the variable to be initialized with a value of unknown shape. If True, the default, the shape of initial_value must be known. For this to be used the initializer must be a Tensor and not an initializer object.
-
objectuse_resource - If False, creates a regular Variable. If true, creates an experimental ResourceVariable instead with well-defined semantics. Defaults to False (will later change to True). When eager execution is enabled this argument is always forced to be True.
-
objectcustom_getter - Callable that takes as a first argument the true getter, and allows overwriting the internal get_variable method. The signature of `custom_getter` should match that of this method, but the most future-proof version will allow for changes: `def custom_getter(getter, *args, **kwargs)`. Direct access to all `get_variable` parameters is also allowed: `def custom_getter(getter, name, *args, **kwargs)`. A simple identity custom getter that simply creates variables with modified names is: ```python def custom_getter(getter, name, *args, **kwargs): return getter(name + '_suffix', *args, **kwargs) ```
-
objectconstraint - An optional projection function to be applied to the variable after being updated by an `Optimizer` (e.g. used to implement norm constraints or value constraints for layer weights). The function must take as input the unprojected Tensor representing the value of the variable and return the Tensor for the projected value (which must have the same shape). Constraints are not safe to use when doing asynchronous distributed training.
-
ImplicitContainer<T>synchronization - Indicates when a distributed a variable will be
aggregated. Accepted values are constants defined in the class
tf.VariableSynchronization. By default the synchronization is set to `AUTO` and the current `DistributionStrategy` chooses when to synchronize. -
ImplicitContainer<T>aggregation - Indicates how a distributed variable will be aggregated.
Accepted values are constants defined in the class
tf.VariableAggregation.
Returns
-
object - The created or existing `Variable` (or `PartitionedVariable`, if a partitioner was used).
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
VariableScope get_variable_scope()
Returns the current variable scope.
object get_variable_scope_dyn()
Returns the current variable scope.
object global_norm(ValueTuple<IGraphNodeBase, object> t_list, string name)
Computes the global norm of multiple tensors. Given a tuple or list of tensors `t_list`, this operation returns the
global norm of the elements in all tensors in `t_list`. The global norm is
computed as: `global_norm = sqrt(sum([l2norm(t)**2 for t in t_list]))` Any entries in `t_list` that are of type None are ignored.
Parameters
-
ValueTuple<IGraphNodeBase, object>t_list - A tuple or list of mixed `Tensors`, `IndexedSlices`, or None.
-
stringname - A name for the operation (optional).
Returns
-
object - A 0-D (scalar) `Tensor` of type `float`.
object global_norm(IEnumerable<object> t_list, string name)
Computes the global norm of multiple tensors. Given a tuple or list of tensors `t_list`, this operation returns the
global norm of the elements in all tensors in `t_list`. The global norm is
computed as: `global_norm = sqrt(sum([l2norm(t)**2 for t in t_list]))` Any entries in `t_list` that are of type None are ignored.
Parameters
-
IEnumerable<object>t_list - A tuple or list of mixed `Tensors`, `IndexedSlices`, or None.
-
stringname - A name for the operation (optional).
Returns
-
object - A 0-D (scalar) `Tensor` of type `float`.
object global_norm_dyn(object t_list, object name)
Computes the global norm of multiple tensors. Given a tuple or list of tensors `t_list`, this operation returns the
global norm of the elements in all tensors in `t_list`. The global norm is
computed as: `global_norm = sqrt(sum([l2norm(t)**2 for t in t_list]))` Any entries in `t_list` that are of type None are ignored.
Parameters
-
objectt_list - A tuple or list of mixed `Tensors`, `IndexedSlices`, or None.
-
objectname - A name for the operation (optional).
Returns
-
object - A 0-D (scalar) `Tensor` of type `float`.
object global_variables(string scope)
Returns global variables. Global variables are variables that are shared across machines in a
distributed environment. The `Variable()` constructor or `get_variable()`
automatically adds new variables to the graph collection
`GraphKeys.GLOBAL_VARIABLES`.
This convenience function returns the contents of that collection. An alternative to global variables are local variables. See
`tf.compat.v1.local_variables`
Parameters
-
stringscope - (Optional.) A string. If supplied, the resulting list is filtered to include only items whose `name` attribute matches `scope` using `re.match`. Items without a `name` attribute are never returned if a scope is supplied. The choice of `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
object - A list of `Variable` objects.
object global_variables_dyn(object scope)
Returns global variables. Global variables are variables that are shared across machines in a
distributed environment. The `Variable()` constructor or `get_variable()`
automatically adds new variables to the graph collection
`GraphKeys.GLOBAL_VARIABLES`.
This convenience function returns the contents of that collection. An alternative to global variables are local variables. See
`tf.compat.v1.local_variables`
Parameters
-
objectscope - (Optional.) A string. If supplied, the resulting list is filtered to include only items whose `name` attribute matches `scope` using `re.match`. Items without a `name` attribute are never returned if a scope is supplied. The choice of `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
object - A list of `Variable` objects.
object global_variables_initializer()
Returns an Op that initializes global variables. This is just a shortcut for `variables_initializer(global_variables())`
Returns
-
object - An Op that initializes global variables in the graph.
object global_variables_initializer_dyn()
Returns an Op that initializes global variables. This is just a shortcut for `variables_initializer(global_variables())`
Returns
-
object - An Op that initializes global variables in the graph.
object grad_pass_through(PythonFunctionContainer f)
Creates a grad-pass-through op with the forward behavior provided in f. Use this function to wrap any op, maintaining its behavior in the forward
pass, but replacing the original op in the backward graph with an identity.
Another example is a 'differentiable' moving average approximation, where
gradients are allowed to flow into the last value fed to the moving average,
but the moving average is still used for the forward pass:
Parameters
-
PythonFunctionContainerf - function `f(*x)` that returns a `Tensor` or nested structure of `Tensor` outputs.
Returns
-
object - A function `h(x)` which returns the same values as `f(x)` and whose gradients are the same as those of an identity function.
Show Example
x = tf.Variable(1.0, name="x")
z = tf.Variable(3.0, name="z") with tf.GradientTape() as tape:
# y will evaluate to 9.0
y = tf.grad_pass_through(x.assign)(z**2)
# grads will evaluate to 6.0
grads = tape.gradient(y, z)
object grad_pass_through(object f)
Creates a grad-pass-through op with the forward behavior provided in f. Use this function to wrap any op, maintaining its behavior in the forward
pass, but replacing the original op in the backward graph with an identity.
Another example is a 'differentiable' moving average approximation, where
gradients are allowed to flow into the last value fed to the moving average,
but the moving average is still used for the forward pass:
Parameters
-
objectf - function `f(*x)` that returns a `Tensor` or nested structure of `Tensor` outputs.
Returns
-
object - A function `h(x)` which returns the same values as `f(x)` and whose gradients are the same as those of an identity function.
Show Example
x = tf.Variable(1.0, name="x")
z = tf.Variable(3.0, name="z") with tf.GradientTape() as tape:
# y will evaluate to 9.0
y = tf.grad_pass_through(x.assign)(z**2)
# grads will evaluate to 6.0
grads = tape.gradient(y, z)
object grad_pass_through_dyn(object f)
Creates a grad-pass-through op with the forward behavior provided in f. Use this function to wrap any op, maintaining its behavior in the forward
pass, but replacing the original op in the backward graph with an identity.
Another example is a 'differentiable' moving average approximation, where
gradients are allowed to flow into the last value fed to the moving average,
but the moving average is still used for the forward pass:
Parameters
-
objectf - function `f(*x)` that returns a `Tensor` or nested structure of `Tensor` outputs.
Returns
-
object - A function `h(x)` which returns the same values as `f(x)` and whose gradients are the same as those of an identity function.
Show Example
x = tf.Variable(1.0, name="x")
z = tf.Variable(3.0, name="z") with tf.GradientTape() as tape:
# y will evaluate to 9.0
y = tf.grad_pass_through(x.assign)(z**2)
# grads will evaluate to 6.0
grads = tape.gradient(y, z)
Tensor gradient_trees_partition_examples(IGraphNodeBase tree_ensemble_handle, IEnumerable<ndarray> dense_float_features, IEnumerable<ndarray> sparse_float_feature_indices, IEnumerable<ndarray> sparse_float_feature_values, IEnumerable<ndarray> sparse_float_feature_shapes, IEnumerable<ndarray> sparse_int_feature_indices, IEnumerable<ndarray> sparse_int_feature_values, IEnumerable<ndarray> sparse_int_feature_shapes, bool use_locking, string name)
object gradient_trees_partition_examples_dyn(object tree_ensemble_handle, object dense_float_features, object sparse_float_feature_indices, object sparse_float_feature_values, object sparse_float_feature_shapes, object sparse_int_feature_indices, object sparse_int_feature_values, object sparse_int_feature_shapes, ImplicitContainer<T> use_locking, object name)
object gradient_trees_prediction(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase seed, IEnumerable<ndarray> dense_float_features, IEnumerable<ndarray> sparse_float_feature_indices, IEnumerable<ndarray> sparse_float_feature_values, IEnumerable<ndarray> sparse_float_feature_shapes, IEnumerable<ndarray> sparse_int_feature_indices, IEnumerable<ndarray> sparse_int_feature_values, IEnumerable<ndarray> sparse_int_feature_shapes, object learner_config, bool apply_dropout, bool apply_averaging, Nullable<int> center_bias, bool reduce_dim, bool use_locking, string name)
object gradient_trees_prediction(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase seed, IEnumerable<ndarray> dense_float_features, IEnumerable<ndarray> sparse_float_feature_indices, IEnumerable<ndarray> sparse_float_feature_values, IEnumerable<ndarray> sparse_float_feature_shapes, IEnumerable<ndarray> sparse_int_feature_indices, IEnumerable<ndarray> sparse_int_feature_values, IEnumerable<ndarray> sparse_int_feature_shapes, object learner_config, bool apply_dropout, bool apply_averaging, bool center_bias, bool reduce_dim, bool use_locking, string name)
object gradient_trees_prediction_dyn(object tree_ensemble_handle, object seed, object dense_float_features, object sparse_float_feature_indices, object sparse_float_feature_values, object sparse_float_feature_shapes, object sparse_int_feature_indices, object sparse_int_feature_values, object sparse_int_feature_shapes, object learner_config, object apply_dropout, object apply_averaging, object center_bias, object reduce_dim, ImplicitContainer<T> use_locking, object name)
object gradient_trees_prediction_verbose(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase seed, IEnumerable<object> dense_float_features, IEnumerable<object> sparse_float_feature_indices, IEnumerable<object> sparse_float_feature_values, IEnumerable<object> sparse_float_feature_shapes, IEnumerable<object> sparse_int_feature_indices, IEnumerable<object> sparse_int_feature_values, IEnumerable<object> sparse_int_feature_shapes, object learner_config, bool apply_dropout, bool apply_averaging, Nullable<int> center_bias, bool reduce_dim, bool use_locking, string name)
object gradient_trees_prediction_verbose(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase seed, IEnumerable<object> dense_float_features, IEnumerable<object> sparse_float_feature_indices, IEnumerable<object> sparse_float_feature_values, IEnumerable<object> sparse_float_feature_shapes, IEnumerable<object> sparse_int_feature_indices, IEnumerable<object> sparse_int_feature_values, IEnumerable<object> sparse_int_feature_shapes, object learner_config, bool apply_dropout, bool apply_averaging, bool center_bias, bool reduce_dim, bool use_locking, string name)
object gradient_trees_prediction_verbose_dyn(object tree_ensemble_handle, object seed, object dense_float_features, object sparse_float_feature_indices, object sparse_float_feature_values, object sparse_float_feature_shapes, object sparse_int_feature_indices, object sparse_int_feature_values, object sparse_int_feature_shapes, object learner_config, object apply_dropout, object apply_averaging, object center_bias, object reduce_dim, ImplicitContainer<T> use_locking, object name)
IList<Tensor> gradients(PythonFunctionContainer ys, object xs, double grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
PythonFunctionContainerys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
doublegrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(IEnumerable<IGraphNodeBase> ys, object xs, bool grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
IEnumerable<IGraphNodeBase>ys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
boolgrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(IEnumerable<IGraphNodeBase> ys, object xs, ValueTuple<object> grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
IEnumerable<IGraphNodeBase>ys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
ValueTuple<object>grad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(PythonFunctionContainer ys, object xs, IGraphNodeBase grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
PythonFunctionContainerys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
IGraphNodeBasegrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(IEnumerable<IGraphNodeBase> ys, object xs, IEnumerable<IGraphNodeBase> grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
IEnumerable<IGraphNodeBase>ys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
IEnumerable<IGraphNodeBase>grad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(object ys, object xs, ValueTuple<object> grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
objectys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
ValueTuple<object>grad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(object ys, object xs, IGraphNodeBase grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
objectys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
IGraphNodeBasegrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(PythonFunctionContainer ys, object xs, bool grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
PythonFunctionContainerys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
boolgrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(object ys, object xs, IEnumerable<IGraphNodeBase> grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
objectys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
IEnumerable<IGraphNodeBase>grad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(IEnumerable<IGraphNodeBase> ys, object xs, double grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
IEnumerable<IGraphNodeBase>ys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
doublegrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(object ys, object xs, double grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
objectys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
doublegrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(PythonFunctionContainer ys, object xs, ValueTuple<object> grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
PythonFunctionContainerys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
ValueTuple<object>grad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(IEnumerable<IGraphNodeBase> ys, object xs, IGraphNodeBase grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
IEnumerable<IGraphNodeBase>ys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
IGraphNodeBasegrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(PythonFunctionContainer ys, object xs, IEnumerable<IGraphNodeBase> grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
PythonFunctionContainerys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
IEnumerable<IGraphNodeBase>grad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(object ys, object xs, bool grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
objectys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
boolgrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(IEnumerable<IGraphNodeBase> ys, object xs, IndexedSlices grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
IEnumerable<IGraphNodeBase>ys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
IndexedSlicesgrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(PythonFunctionContainer ys, object xs, IndexedSlices grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
PythonFunctionContainerys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
IndexedSlicesgrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
IList<Tensor> gradients(object ys, object xs, IndexedSlices grad_ys, string name, bool colocate_gradients_with_ops, int gate_gradients, Nullable<int> aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
objectys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
IndexedSlicesgrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
boolcolocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
intgate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
Nullable<int>aggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
IList<Tensor> - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
object gradients_dyn(object ys, object xs, object grad_ys, ImplicitContainer<T> name, ImplicitContainer<T> colocate_gradients_with_ops, ImplicitContainer<T> gate_gradients, object aggregation_method, object stop_gradients, ImplicitContainer<T> unconnected_gradients)
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Parameters
-
objectys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
objectgrad_ys - Optional. A `Tensor` or list of tensors the same size as `ys` and holding the gradients computed for each y in `ys`.
-
ImplicitContainer<T>name - Optional name to use for grouping all the gradient ops together. defaults to 'gradients'.
-
ImplicitContainer<T>colocate_gradients_with_ops - If True, try colocating gradients with the corresponding op.
-
ImplicitContainer<T>gate_gradients - If True, add a tuple around the gradients returned for an operations. This avoids some race conditions.
-
objectaggregation_method - Specifies the method used to combine gradient terms. Accepted values are constants defined in the class `AggregationMethod`.
-
objectstop_gradients - Optional. A `Tensor` or list of tensors not to differentiate through.
-
ImplicitContainer<T>unconnected_gradients - Optional. Specifies the gradient value returned when
the given input tensors are unconnected. Accepted values are constants
defined in the class
tf.UnconnectedGradientsand the default value is `none`.
Returns
-
object - A list of `sum(dy/dx)` for each x in `xs`.
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
Tensor graph_def_version(string name)
object graph_def_version_dyn(object name)
object greater(IGraphNodeBase x, int y, string name)
object greater(double x, double y, string name)
object greater(IGraphNodeBase x, double y, string name)
object greater(int x, IGraphNodeBase y, string name)
object greater(int x, double y, string name)
object greater(double x, IGraphNodeBase y, string name)
object greater(double x, int y, string name)
object greater(IGraphNodeBase x, IGraphNodeBase y, string name)
object greater(int x, int y, string name)
object greater_dyn(object x, object y, object name)
object greater_equal(IGraphNodeBase x, double y, string name)
object greater_equal(IGraphNodeBase x, int y, string name)
object greater_equal(int x, IGraphNodeBase y, string name)
object greater_equal(double x, IGraphNodeBase y, string name)
object greater_equal(double x, double y, string name)
object greater_equal(int x, double y, string name)
object greater_equal(IGraphNodeBase x, IGraphNodeBase y, string name)
object greater_equal(int x, int y, string name)
object greater_equal(double x, int y, string name)
object greater_equal_dyn(object x, object y, object name)
object group(Object[] inputs)
Create an op that groups multiple operations. When this op finishes, all ops in `inputs` have finished. This op has no
output. See also
tf.tuple and
tf.control_dependencies.
Parameters
-
Object[]inputs - Zero or more tensors to group.
Returns
-
object - An Operation that executes all its inputs.
object group(IDictionary<string, object> kwargs, Object[] inputs)
Create an op that groups multiple operations. When this op finishes, all ops in `inputs` have finished. This op has no
output. See also
tf.tuple and
tf.control_dependencies.
Parameters
-
IDictionary<string, object>kwargs -
Object[]inputs - Zero or more tensors to group.
Returns
-
object - An Operation that executes all its inputs.
object group_dyn(Object[] inputs)
Create an op that groups multiple operations. When this op finishes, all ops in `inputs` have finished. This op has no
output. See also
tf.tuple and
tf.control_dependencies.
Parameters
-
Object[]inputs - Zero or more tensors to group.
Returns
-
object - An Operation that executes all its inputs.
object group_dyn(IDictionary<string, object> kwargs, Object[] inputs)
Create an op that groups multiple operations. When this op finishes, all ops in `inputs` have finished. This op has no
output. See also
tf.tuple and
tf.control_dependencies.
Parameters
-
IDictionary<string, object>kwargs -
Object[]inputs - Zero or more tensors to group.
Returns
-
object - An Operation that executes all its inputs.
object grow_tree_ensemble(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase stamp_token, IGraphNodeBase next_stamp_token, IGraphNodeBase learning_rate, IGraphNodeBase dropout_seed, IGraphNodeBase max_tree_depth, IGraphNodeBase weak_learner_type, IEnumerable<ndarray> partition_ids, IEnumerable<ndarray> gains, IEnumerable<object> splits, object learner_config, bool center_bias, string name)
object grow_tree_ensemble(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase stamp_token, IGraphNodeBase next_stamp_token, IGraphNodeBase learning_rate, IGraphNodeBase dropout_seed, IGraphNodeBase max_tree_depth, IGraphNodeBase weak_learner_type, IEnumerable<ndarray> partition_ids, IEnumerable<ndarray> gains, IEnumerable<object> splits, object learner_config, Nullable<int> center_bias, string name)
object grow_tree_ensemble_dyn(object tree_ensemble_handle, object stamp_token, object next_stamp_token, object learning_rate, object dropout_seed, object max_tree_depth, object weak_learner_type, object partition_ids, object gains, object splits, object learner_config, object center_bias, object name)
object grow_tree_v4(IGraphNodeBase tree_handle, IGraphNodeBase stats_handle, IGraphNodeBase finished_nodes, object params, string name)
object grow_tree_v4_dyn(object tree_handle, object stats_handle, object finished_nodes, object params, object name)
Tensor guarantee_const(IGraphNodeBase input, string name)
Gives a guarantee to the TF runtime that the input tensor is a constant. The runtime is then free to make optimizations based on this. Only accepts value typed tensors as inputs and rejects resource variable handles
as input. Returns the input tensor without modification.
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object guarantee_const_dyn(object input, object name)
Gives a guarantee to the TF runtime that the input tensor is a constant. The runtime is then free to make optimizations based on this. Only accepts value typed tensors as inputs and rejects resource variable handles
as input. Returns the input tensor without modification.
Parameters
-
objectinput - A `Tensor`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
object hard_routing_function(IGraphNodeBase input_data, IGraphNodeBase tree_parameters, IGraphNodeBase tree_biases, object max_nodes, object tree_depth, string name)
object hard_routing_function_dyn(object input_data, object tree_parameters, object tree_biases, object max_nodes, object tree_depth, object name)
IList<Tensor> hessians(IGraphNodeBase ys, IEnumerable<Variable> xs, string name, bool colocate_gradients_with_ops, bool gate_gradients, object aggregation_method)
Constructs the Hessian of sum of `ys` with respect to `x` in `xs`. `hessians()` adds ops to the graph to output the Hessian matrix of `ys`
with respect to `xs`. It returns a list of `Tensor` of length `len(xs)`
where each tensor is the Hessian of `sum(ys)`. The Hessian is a matrix of second-order partial derivatives of a scalar
tensor (see https://en.wikipedia.org/wiki/Hessian_matrix for more details).
Parameters
-
IGraphNodeBaseys - A `Tensor` or list of tensors to be differentiated.
-
IEnumerable<Variable>xs - A `Tensor` or list of tensors to be used for differentiation.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'hessians'.
-
boolcolocate_gradients_with_ops - See `gradients()` documentation for details.
-
boolgate_gradients - See `gradients()` documentation for details.
-
objectaggregation_method - See `gradients()` documentation for details.
Returns
-
IList<Tensor> - A list of Hessian matrices of `sum(ys)` for each `x` in `xs`.
IList<Tensor> hessians(IEnumerable<IGraphNodeBase> ys, IGraphNodeBase xs, string name, bool colocate_gradients_with_ops, bool gate_gradients, object aggregation_method)
Constructs the Hessian of sum of `ys` with respect to `x` in `xs`. `hessians()` adds ops to the graph to output the Hessian matrix of `ys`
with respect to `xs`. It returns a list of `Tensor` of length `len(xs)`
where each tensor is the Hessian of `sum(ys)`. The Hessian is a matrix of second-order partial derivatives of a scalar
tensor (see https://en.wikipedia.org/wiki/Hessian_matrix for more details).
Parameters
-
IEnumerable<IGraphNodeBase>ys - A `Tensor` or list of tensors to be differentiated.
-
IGraphNodeBasexs - A `Tensor` or list of tensors to be used for differentiation.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'hessians'.
-
boolcolocate_gradients_with_ops - See `gradients()` documentation for details.
-
boolgate_gradients - See `gradients()` documentation for details.
-
objectaggregation_method - See `gradients()` documentation for details.
Returns
-
IList<Tensor> - A list of Hessian matrices of `sum(ys)` for each `x` in `xs`.
IList<Tensor> hessians(IEnumerable<IGraphNodeBase> ys, IEnumerable<Variable> xs, string name, bool colocate_gradients_with_ops, bool gate_gradients, object aggregation_method)
Constructs the Hessian of sum of `ys` with respect to `x` in `xs`. `hessians()` adds ops to the graph to output the Hessian matrix of `ys`
with respect to `xs`. It returns a list of `Tensor` of length `len(xs)`
where each tensor is the Hessian of `sum(ys)`. The Hessian is a matrix of second-order partial derivatives of a scalar
tensor (see https://en.wikipedia.org/wiki/Hessian_matrix for more details).
Parameters
-
IEnumerable<IGraphNodeBase>ys - A `Tensor` or list of tensors to be differentiated.
-
IEnumerable<Variable>xs - A `Tensor` or list of tensors to be used for differentiation.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'hessians'.
-
boolcolocate_gradients_with_ops - See `gradients()` documentation for details.
-
boolgate_gradients - See `gradients()` documentation for details.
-
objectaggregation_method - See `gradients()` documentation for details.
Returns
-
IList<Tensor> - A list of Hessian matrices of `sum(ys)` for each `x` in `xs`.
IList<Tensor> hessians(IGraphNodeBase ys, IGraphNodeBase xs, string name, bool colocate_gradients_with_ops, bool gate_gradients, object aggregation_method)
Constructs the Hessian of sum of `ys` with respect to `x` in `xs`. `hessians()` adds ops to the graph to output the Hessian matrix of `ys`
with respect to `xs`. It returns a list of `Tensor` of length `len(xs)`
where each tensor is the Hessian of `sum(ys)`. The Hessian is a matrix of second-order partial derivatives of a scalar
tensor (see https://en.wikipedia.org/wiki/Hessian_matrix for more details).
Parameters
-
IGraphNodeBaseys - A `Tensor` or list of tensors to be differentiated.
-
IGraphNodeBasexs - A `Tensor` or list of tensors to be used for differentiation.
-
stringname - Optional name to use for grouping all the gradient ops together. defaults to 'hessians'.
-
boolcolocate_gradients_with_ops - See `gradients()` documentation for details.
-
boolgate_gradients - See `gradients()` documentation for details.
-
objectaggregation_method - See `gradients()` documentation for details.
Returns
-
IList<Tensor> - A list of Hessian matrices of `sum(ys)` for each `x` in `xs`.
object hessians_dyn(object ys, object xs, ImplicitContainer<T> name, ImplicitContainer<T> colocate_gradients_with_ops, ImplicitContainer<T> gate_gradients, object aggregation_method)
Constructs the Hessian of sum of `ys` with respect to `x` in `xs`. `hessians()` adds ops to the graph to output the Hessian matrix of `ys`
with respect to `xs`. It returns a list of `Tensor` of length `len(xs)`
where each tensor is the Hessian of `sum(ys)`. The Hessian is a matrix of second-order partial derivatives of a scalar
tensor (see https://en.wikipedia.org/wiki/Hessian_matrix for more details).
Parameters
-
objectys - A `Tensor` or list of tensors to be differentiated.
-
objectxs - A `Tensor` or list of tensors to be used for differentiation.
-
ImplicitContainer<T>name - Optional name to use for grouping all the gradient ops together. defaults to 'hessians'.
-
ImplicitContainer<T>colocate_gradients_with_ops - See `gradients()` documentation for details.
-
ImplicitContainer<T>gate_gradients - See `gradients()` documentation for details.
-
objectaggregation_method - See `gradients()` documentation for details.
Returns
-
object - A list of Hessian matrices of `sum(ys)` for each `x` in `xs`.
Tensor histogram_fixed_width(IGraphNodeBase values, IGraphNodeBase value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
IGraphNodeBasevalues - Numeric `Tensor`.
-
IGraphNodeBasevalue_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(float64 values, float64 value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
float64values - Numeric `Tensor`.
-
float64value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(IEnumerable<object> values, IGraphNodeBase value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
IEnumerable<object>values - Numeric `Tensor`.
-
IGraphNodeBasevalue_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(IGraphNodeBase values, double value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
IGraphNodeBasevalues - Numeric `Tensor`.
-
doublevalue_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(float64 values, IGraphNodeBase value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
float64values - Numeric `Tensor`.
-
IGraphNodeBasevalue_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(IEnumerable<object> values, double value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
IEnumerable<object>values - Numeric `Tensor`.
-
doublevalue_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(float64 values, IEnumerable<double> value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
float64values - Numeric `Tensor`.
-
IEnumerable<double>value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(float64 values, double value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
float64values - Numeric `Tensor`.
-
doublevalue_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(IGraphNodeBase values, float64 value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
IGraphNodeBasevalues - Numeric `Tensor`.
-
float64value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(IEnumerable<object> values, IEnumerable<double> value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
IEnumerable<object>values - Numeric `Tensor`.
-
IEnumerable<double>value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(IEnumerable<object> values, float64 value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
IEnumerable<object>values - Numeric `Tensor`.
-
float64value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width(IGraphNodeBase values, IEnumerable<double> value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, string name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
IGraphNodeBasevalues - Numeric `Tensor`.
-
IEnumerable<double>value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A 1-D `Tensor` holding histogram of values.
Tensor histogram_fixed_width_bins(float64 values, float64 value_range, int nbins, ImplicitContainer<T> dtype, string name)
Bins the given values for use in a histogram. Given the tensor `values`, this operation returns a rank 1 `Tensor`
representing the indices of a histogram into which each element
of `values` would be binned. The bins are equal width and
determined by the arguments `value_range` and `nbins`.
Parameters
-
float64values - Numeric `Tensor`.
-
float64value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
intnbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A `Tensor` holding the indices of the binned values whose shape matches `values`.
Tensor histogram_fixed_width_bins(IEnumerable<object> values, float64 value_range, int nbins, ImplicitContainer<T> dtype, string name)
Bins the given values for use in a histogram. Given the tensor `values`, this operation returns a rank 1 `Tensor`
representing the indices of a histogram into which each element
of `values` would be binned. The bins are equal width and
determined by the arguments `value_range` and `nbins`.
Parameters
-
IEnumerable<object>values - Numeric `Tensor`.
-
float64value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
intnbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A `Tensor` holding the indices of the binned values whose shape matches `values`.
Tensor histogram_fixed_width_bins(IGraphNodeBase values, IEnumerable<double> value_range, int nbins, ImplicitContainer<T> dtype, string name)
Bins the given values for use in a histogram. Given the tensor `values`, this operation returns a rank 1 `Tensor`
representing the indices of a histogram into which each element
of `values` would be binned. The bins are equal width and
determined by the arguments `value_range` and `nbins`.
Parameters
-
IGraphNodeBasevalues - Numeric `Tensor`.
-
IEnumerable<double>value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
intnbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A `Tensor` holding the indices of the binned values whose shape matches `values`.
Tensor histogram_fixed_width_bins(float64 values, IEnumerable<double> value_range, int nbins, ImplicitContainer<T> dtype, string name)
Bins the given values for use in a histogram. Given the tensor `values`, this operation returns a rank 1 `Tensor`
representing the indices of a histogram into which each element
of `values` would be binned. The bins are equal width and
determined by the arguments `value_range` and `nbins`.
Parameters
-
float64values - Numeric `Tensor`.
-
IEnumerable<double>value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
intnbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A `Tensor` holding the indices of the binned values whose shape matches `values`.
Tensor histogram_fixed_width_bins(IGraphNodeBase values, float64 value_range, int nbins, ImplicitContainer<T> dtype, string name)
Bins the given values for use in a histogram. Given the tensor `values`, this operation returns a rank 1 `Tensor`
representing the indices of a histogram into which each element
of `values` would be binned. The bins are equal width and
determined by the arguments `value_range` and `nbins`.
Parameters
-
IGraphNodeBasevalues - Numeric `Tensor`.
-
float64value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
intnbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A `Tensor` holding the indices of the binned values whose shape matches `values`.
Tensor histogram_fixed_width_bins(IEnumerable<object> values, IEnumerable<double> value_range, int nbins, ImplicitContainer<T> dtype, string name)
Bins the given values for use in a histogram. Given the tensor `values`, this operation returns a rank 1 `Tensor`
representing the indices of a histogram into which each element
of `values` would be binned. The bins are equal width and
determined by the arguments `value_range` and `nbins`.
Parameters
-
IEnumerable<object>values - Numeric `Tensor`.
-
IEnumerable<double>value_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
intnbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
stringname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
Tensor - A `Tensor` holding the indices of the binned values whose shape matches `values`.
object histogram_fixed_width_bins_dyn(object values, object value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, object name)
Bins the given values for use in a histogram. Given the tensor `values`, this operation returns a rank 1 `Tensor`
representing the indices of a histogram into which each element
of `values` would be binned. The bins are equal width and
determined by the arguments `value_range` and `nbins`.
Parameters
-
objectvalues - Numeric `Tensor`.
-
objectvalue_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
objectname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
object - A `Tensor` holding the indices of the binned values whose shape matches `values`.
object histogram_fixed_width_dyn(object values, object value_range, ImplicitContainer<T> nbins, ImplicitContainer<T> dtype, object name)
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
Parameters
-
objectvalues - Numeric `Tensor`.
-
objectvalue_range - Shape [2] `Tensor` of same `dtype` as `values`. values <= value_range[0] will be mapped to hist[0], values >= value_range[1] will be mapped to hist[-1].
-
ImplicitContainer<T>nbins - Scalar `int32 Tensor`. Number of histogram bins.
-
ImplicitContainer<T>dtype - dtype for returned histogram.
-
objectname - A name for this operation (defaults to 'histogram_fixed_width').
Returns
-
object - A 1-D `Tensor` holding histogram of values.
Tensor identity(IGraphNodeBase input, string name)
Return a tensor with the same shape and contents as input.
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Show Example
import tensorflow as tf
val0 = tf.ones((1,), dtype=tf.float32)
a = tf.atan2(val0, val0)
a_identity = tf.identity(a)
print(a.numpy()) #[0.7853982]
print(a_identity.numpy()) #[0.7853982]
Tensor identity(IGraphNodeBase input, PythonFunctionContainer name)
Return a tensor with the same shape and contents as input.
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Show Example
import tensorflow as tf
val0 = tf.ones((1,), dtype=tf.float32)
a = tf.atan2(val0, val0)
a_identity = tf.identity(a)
print(a.numpy()) #[0.7853982]
print(a_identity.numpy()) #[0.7853982]
object identity_dyn(object input, object name)
Return a tensor with the same shape and contents as input.
Parameters
-
objectinput - A `Tensor`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Show Example
import tensorflow as tf
val0 = tf.ones((1,), dtype=tf.float32)
a = tf.atan2(val0, val0)
a_identity = tf.identity(a)
print(a.numpy()) #[0.7853982]
print(a_identity.numpy()) #[0.7853982]
object identity_n(IEnumerable<object> input, string name)
Returns a list of tensors with the same shapes and contents as the input tensors. This op can be used to override the gradient for complicated functions. For
example, suppose y = f(x) and we wish to apply a custom function g for backprop
such that dx = g(dy). In Python,
Parameters
-
IEnumerable<object>input - A list of `Tensor` objects.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` objects. Has the same type as `input`.
Show Example
with tf.get_default_graph().gradient_override_map(
{'IdentityN': 'OverrideGradientWithG'}):
y, _ = identity_n([f(x), x]) @tf.RegisterGradient('OverrideGradientWithG')
def ApplyG(op, dy, _):
return [None, g(dy)] # Do not backprop to f(x).
object identity_n_dyn(object input, object name)
Returns a list of tensors with the same shapes and contents as the input tensors. This op can be used to override the gradient for complicated functions. For
example, suppose y = f(x) and we wish to apply a custom function g for backprop
such that dx = g(dy). In Python,
Parameters
-
objectinput - A list of `Tensor` objects.
-
objectname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` objects. Has the same type as `input`.
Show Example
with tf.get_default_graph().gradient_override_map(
{'IdentityN': 'OverrideGradientWithG'}):
y, _ = identity_n([f(x), x]) @tf.RegisterGradient('OverrideGradientWithG')
def ApplyG(op, dy, _):
return [None, g(dy)] # Do not backprop to f(x).
Tensor ifft(IGraphNodeBase input, Nullable<ValueTuple<int>> name)
Inverse fast Fourier transform. Computes the inverse 1-dimensional discrete Fourier transform over the
inner-most dimension of `input`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex tensor.
-
Nullable<ValueTuple<int>>name - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object ifft_dyn(object input, object name)
Inverse fast Fourier transform. Computes the inverse 1-dimensional discrete Fourier transform over the
inner-most dimension of `input`.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex tensor.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor ifft2d(IGraphNodeBase input, Nullable<ValueTuple<int>> name)
Inverse 2D fast Fourier transform. Computes the inverse 2-dimensional discrete Fourier transform over the
inner-most 2 dimensions of `input`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex tensor.
-
Nullable<ValueTuple<int>>name - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object ifft2d_dyn(object input, object name)
Inverse 2D fast Fourier transform. Computes the inverse 2-dimensional discrete Fourier transform over the
inner-most 2 dimensions of `input`.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex tensor.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor ifft3d(IGraphNodeBase input, Nullable<ValueTuple<int>> name)
Inverse 3D fast Fourier transform. Computes the inverse 3-dimensional discrete Fourier transform over the
inner-most 3 dimensions of `input`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex64 tensor.
-
Nullable<ValueTuple<int>>name - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object ifft3d_dyn(object input, object name)
Inverse 3D fast Fourier transform. Computes the inverse 3-dimensional discrete Fourier transform over the
inner-most 3 dimensions of `input`.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `complex64`, `complex128`. A complex64 tensor.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor igamma(IGraphNodeBase a, IGraphNodeBase x, string name)
Compute the lower regularized incomplete Gamma function `P(a, x)`. The lower regularized incomplete Gamma function is defined as: \\(P(a, x) = gamma(a, x) / Gamma(a) = 1 - Q(a, x)\\) where \\(gamma(a, x) = \\int_{0}^{x} t^{a-1} exp(-t) dt\\) is the lower incomplete Gamma function. Note, above `Q(a, x)` (`Igammac`) is the upper regularized complete
Gamma function.
Parameters
-
IGraphNodeBasea - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
IGraphNodeBasex - A `Tensor`. Must have the same type as `a`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `a`.
object igamma_dyn(object a, object x, object name)
Compute the lower regularized incomplete Gamma function `P(a, x)`. The lower regularized incomplete Gamma function is defined as: \\(P(a, x) = gamma(a, x) / Gamma(a) = 1 - Q(a, x)\\) where \\(gamma(a, x) = \\int_{0}^{x} t^{a-1} exp(-t) dt\\) is the lower incomplete Gamma function. Note, above `Q(a, x)` (`Igammac`) is the upper regularized complete
Gamma function.
Parameters
-
objecta - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
objectx - A `Tensor`. Must have the same type as `a`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `a`.
Tensor igammac(IGraphNodeBase a, IGraphNodeBase x, string name)
Compute the upper regularized incomplete Gamma function `Q(a, x)`. The upper regularized incomplete Gamma function is defined as: \\(Q(a, x) = Gamma(a, x) / Gamma(a) = 1 - P(a, x)\\) where \\(Gamma(a, x) = int_{x}^{\infty} t^{a-1} exp(-t) dt\\) is the upper incomplete Gama function. Note, above `P(a, x)` (`Igamma`) is the lower regularized complete
Gamma function.
Parameters
-
IGraphNodeBasea - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
IGraphNodeBasex - A `Tensor`. Must have the same type as `a`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `a`.
object igammac_dyn(object a, object x, object name)
Compute the upper regularized incomplete Gamma function `Q(a, x)`. The upper regularized incomplete Gamma function is defined as: \\(Q(a, x) = Gamma(a, x) / Gamma(a) = 1 - P(a, x)\\) where \\(Gamma(a, x) = int_{x}^{\infty} t^{a-1} exp(-t) dt\\) is the upper incomplete Gama function. Note, above `P(a, x)` (`Igamma`) is the lower regularized complete
Gamma function.
Parameters
-
objecta - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
objectx - A `Tensor`. Must have the same type as `a`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `a`.
Tensor imag(IGraphNodeBase input, string name)
Returns the imaginary part of a complex (or real) tensor. Given a tensor `input`, this operation returns a tensor of type `float` that
is the imaginary part of each element in `input` considered as a complex
number. If `input` is real, a tensor of all zeros is returned.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float`, `double`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32` or `float64`.
Show Example
x = tf.constant([-2.25 + 4.75j, 3.25 + 5.75j])
tf.math.imag(x) # [4.75, 5.75]
object imag_dyn(object input, object name)
Returns the imaginary part of a complex (or real) tensor. Given a tensor `input`, this operation returns a tensor of type `float` that
is the imaginary part of each element in `input` considered as a complex
number. If `input` is real, a tensor of all zeros is returned.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float`, `double`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `float32` or `float64`.
Show Example
x = tf.constant([-2.25 + 4.75j, 3.25 + 5.75j])
tf.math.imag(x) # [4.75, 5.75]
Tensor image_connected_components(IGraphNodeBase image, string name)
object image_connected_components_dyn(object image, object name)
Tensor image_projective_transform(IGraphNodeBase images, IGraphNodeBase transforms, string interpolation, string name)
object image_projective_transform_dyn(object images, object transforms, object interpolation, object name)
Tensor image_projective_transform_v2(IGraphNodeBase images, IGraphNodeBase transforms, IGraphNodeBase output_shape, string interpolation, string name)
object image_projective_transform_v2_dyn(object images, object transforms, object output_shape, object interpolation, object name)
IList<object> import_graph_def(string graph_def, IEnumerable<IGraphNodeBase> input_map, IEnumerable<string> return_elements, string name, object op_dict, object producer_op_list)
Imports the graph from `graph_def` into the current default `Graph`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(op_dict)`. They will be removed in a future version.
Instructions for updating:
Please file an issue at https://github.com/tensorflow/tensorflow/issues if you depend on this feature. This function provides a way to import a serialized TensorFlow
[`GraphDef`](https://www.tensorflow.org/code/tensorflow/core/framework/graph.proto)
protocol buffer, and extract individual objects in the `GraphDef` as
tf.Tensor and tf.Operation objects. Once extracted,
these objects are placed into the current default `Graph`. See
tf.Graph.as_graph_def for a way to create a `GraphDef`
proto.
Parameters
-
stringgraph_def - A `GraphDef` proto containing operations to be imported into the default graph.
-
IEnumerable<IGraphNodeBase>input_map - A dictionary mapping input names (as strings) in `graph_def` to `Tensor` objects. The values of the named input tensors in the imported graph will be re-mapped to the respective `Tensor` values.
-
IEnumerable<string>return_elements - A list of strings containing operation names in `graph_def` that will be returned as `Operation` objects; and/or tensor names in `graph_def` that will be returned as `Tensor` objects.
-
stringname - (Optional.) A prefix that will be prepended to the names in `graph_def`. Note that this does not apply to imported function names. Defaults to `"import"`.
-
objectop_dict - (Optional.) Deprecated, do not use.
-
objectproducer_op_list - (Optional.) An `OpList` proto with the (possibly stripped) list of `OpDef`s used by the producer of the graph. If provided, unrecognized attrs for ops in `graph_def` that have their default value according to `producer_op_list` will be removed. This will allow some more `GraphDef`s produced by later binaries to be accepted by earlier binaries.
Returns
-
IList<object> - A list of `Operation` and/or `Tensor` objects from the imported graph, corresponding to the names in `return_elements`, and None if `returns_elements` is None.
IList<object> import_graph_def(object graph_def, IEnumerable<IGraphNodeBase> input_map, IEnumerable<string> return_elements, string name, object op_dict, object producer_op_list)
Imports the graph from `graph_def` into the current default `Graph`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(op_dict)`. They will be removed in a future version.
Instructions for updating:
Please file an issue at https://github.com/tensorflow/tensorflow/issues if you depend on this feature. This function provides a way to import a serialized TensorFlow
[`GraphDef`](https://www.tensorflow.org/code/tensorflow/core/framework/graph.proto)
protocol buffer, and extract individual objects in the `GraphDef` as
tf.Tensor and tf.Operation objects. Once extracted,
these objects are placed into the current default `Graph`. See
tf.Graph.as_graph_def for a way to create a `GraphDef`
proto.
Parameters
-
objectgraph_def - A `GraphDef` proto containing operations to be imported into the default graph.
-
IEnumerable<IGraphNodeBase>input_map - A dictionary mapping input names (as strings) in `graph_def` to `Tensor` objects. The values of the named input tensors in the imported graph will be re-mapped to the respective `Tensor` values.
-
IEnumerable<string>return_elements - A list of strings containing operation names in `graph_def` that will be returned as `Operation` objects; and/or tensor names in `graph_def` that will be returned as `Tensor` objects.
-
stringname - (Optional.) A prefix that will be prepended to the names in `graph_def`. Note that this does not apply to imported function names. Defaults to `"import"`.
-
objectop_dict - (Optional.) Deprecated, do not use.
-
objectproducer_op_list - (Optional.) An `OpList` proto with the (possibly stripped) list of `OpDef`s used by the producer of the graph. If provided, unrecognized attrs for ops in `graph_def` that have their default value according to `producer_op_list` will be removed. This will allow some more `GraphDef`s produced by later binaries to be accepted by earlier binaries.
Returns
-
IList<object> - A list of `Operation` and/or `Tensor` objects from the imported graph, corresponding to the names in `return_elements`, and None if `returns_elements` is None.
IList<object> import_graph_def(string graph_def, IDictionary<object, object> input_map, IEnumerable<string> return_elements, string name, object op_dict, object producer_op_list)
Imports the graph from `graph_def` into the current default `Graph`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(op_dict)`. They will be removed in a future version.
Instructions for updating:
Please file an issue at https://github.com/tensorflow/tensorflow/issues if you depend on this feature. This function provides a way to import a serialized TensorFlow
[`GraphDef`](https://www.tensorflow.org/code/tensorflow/core/framework/graph.proto)
protocol buffer, and extract individual objects in the `GraphDef` as
tf.Tensor and tf.Operation objects. Once extracted,
these objects are placed into the current default `Graph`. See
tf.Graph.as_graph_def for a way to create a `GraphDef`
proto.
Parameters
-
stringgraph_def - A `GraphDef` proto containing operations to be imported into the default graph.
-
IDictionary<object, object>input_map - A dictionary mapping input names (as strings) in `graph_def` to `Tensor` objects. The values of the named input tensors in the imported graph will be re-mapped to the respective `Tensor` values.
-
IEnumerable<string>return_elements - A list of strings containing operation names in `graph_def` that will be returned as `Operation` objects; and/or tensor names in `graph_def` that will be returned as `Tensor` objects.
-
stringname - (Optional.) A prefix that will be prepended to the names in `graph_def`. Note that this does not apply to imported function names. Defaults to `"import"`.
-
objectop_dict - (Optional.) Deprecated, do not use.
-
objectproducer_op_list - (Optional.) An `OpList` proto with the (possibly stripped) list of `OpDef`s used by the producer of the graph. If provided, unrecognized attrs for ops in `graph_def` that have their default value according to `producer_op_list` will be removed. This will allow some more `GraphDef`s produced by later binaries to be accepted by earlier binaries.
Returns
-
IList<object> - A list of `Operation` and/or `Tensor` objects from the imported graph, corresponding to the names in `return_elements`, and None if `returns_elements` is None.
IList<object> import_graph_def(object graph_def, IDictionary<object, object> input_map, IEnumerable<string> return_elements, string name, object op_dict, object producer_op_list)
Imports the graph from `graph_def` into the current default `Graph`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(op_dict)`. They will be removed in a future version.
Instructions for updating:
Please file an issue at https://github.com/tensorflow/tensorflow/issues if you depend on this feature. This function provides a way to import a serialized TensorFlow
[`GraphDef`](https://www.tensorflow.org/code/tensorflow/core/framework/graph.proto)
protocol buffer, and extract individual objects in the `GraphDef` as
tf.Tensor and tf.Operation objects. Once extracted,
these objects are placed into the current default `Graph`. See
tf.Graph.as_graph_def for a way to create a `GraphDef`
proto.
Parameters
-
objectgraph_def - A `GraphDef` proto containing operations to be imported into the default graph.
-
IDictionary<object, object>input_map - A dictionary mapping input names (as strings) in `graph_def` to `Tensor` objects. The values of the named input tensors in the imported graph will be re-mapped to the respective `Tensor` values.
-
IEnumerable<string>return_elements - A list of strings containing operation names in `graph_def` that will be returned as `Operation` objects; and/or tensor names in `graph_def` that will be returned as `Tensor` objects.
-
stringname - (Optional.) A prefix that will be prepended to the names in `graph_def`. Note that this does not apply to imported function names. Defaults to `"import"`.
-
objectop_dict - (Optional.) Deprecated, do not use.
-
objectproducer_op_list - (Optional.) An `OpList` proto with the (possibly stripped) list of `OpDef`s used by the producer of the graph. If provided, unrecognized attrs for ops in `graph_def` that have their default value according to `producer_op_list` will be removed. This will allow some more `GraphDef`s produced by later binaries to be accepted by earlier binaries.
Returns
-
IList<object> - A list of `Operation` and/or `Tensor` objects from the imported graph, corresponding to the names in `return_elements`, and None if `returns_elements` is None.
IList<object> import_graph_def(int graph_def, IEnumerable<IGraphNodeBase> input_map, IEnumerable<string> return_elements, string name, object op_dict, object producer_op_list)
Imports the graph from `graph_def` into the current default `Graph`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(op_dict)`. They will be removed in a future version.
Instructions for updating:
Please file an issue at https://github.com/tensorflow/tensorflow/issues if you depend on this feature. This function provides a way to import a serialized TensorFlow
[`GraphDef`](https://www.tensorflow.org/code/tensorflow/core/framework/graph.proto)
protocol buffer, and extract individual objects in the `GraphDef` as
tf.Tensor and tf.Operation objects. Once extracted,
these objects are placed into the current default `Graph`. See
tf.Graph.as_graph_def for a way to create a `GraphDef`
proto.
Parameters
-
intgraph_def - A `GraphDef` proto containing operations to be imported into the default graph.
-
IEnumerable<IGraphNodeBase>input_map - A dictionary mapping input names (as strings) in `graph_def` to `Tensor` objects. The values of the named input tensors in the imported graph will be re-mapped to the respective `Tensor` values.
-
IEnumerable<string>return_elements - A list of strings containing operation names in `graph_def` that will be returned as `Operation` objects; and/or tensor names in `graph_def` that will be returned as `Tensor` objects.
-
stringname - (Optional.) A prefix that will be prepended to the names in `graph_def`. Note that this does not apply to imported function names. Defaults to `"import"`.
-
objectop_dict - (Optional.) Deprecated, do not use.
-
objectproducer_op_list - (Optional.) An `OpList` proto with the (possibly stripped) list of `OpDef`s used by the producer of the graph. If provided, unrecognized attrs for ops in `graph_def` that have their default value according to `producer_op_list` will be removed. This will allow some more `GraphDef`s produced by later binaries to be accepted by earlier binaries.
Returns
-
IList<object> - A list of `Operation` and/or `Tensor` objects from the imported graph, corresponding to the names in `return_elements`, and None if `returns_elements` is None.
IList<object> import_graph_def(int graph_def, IDictionary<object, object> input_map, IEnumerable<string> return_elements, string name, object op_dict, object producer_op_list)
Imports the graph from `graph_def` into the current default `Graph`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(op_dict)`. They will be removed in a future version.
Instructions for updating:
Please file an issue at https://github.com/tensorflow/tensorflow/issues if you depend on this feature. This function provides a way to import a serialized TensorFlow
[`GraphDef`](https://www.tensorflow.org/code/tensorflow/core/framework/graph.proto)
protocol buffer, and extract individual objects in the `GraphDef` as
tf.Tensor and tf.Operation objects. Once extracted,
these objects are placed into the current default `Graph`. See
tf.Graph.as_graph_def for a way to create a `GraphDef`
proto.
Parameters
-
intgraph_def - A `GraphDef` proto containing operations to be imported into the default graph.
-
IDictionary<object, object>input_map - A dictionary mapping input names (as strings) in `graph_def` to `Tensor` objects. The values of the named input tensors in the imported graph will be re-mapped to the respective `Tensor` values.
-
IEnumerable<string>return_elements - A list of strings containing operation names in `graph_def` that will be returned as `Operation` objects; and/or tensor names in `graph_def` that will be returned as `Tensor` objects.
-
stringname - (Optional.) A prefix that will be prepended to the names in `graph_def`. Note that this does not apply to imported function names. Defaults to `"import"`.
-
objectop_dict - (Optional.) Deprecated, do not use.
-
objectproducer_op_list - (Optional.) An `OpList` proto with the (possibly stripped) list of `OpDef`s used by the producer of the graph. If provided, unrecognized attrs for ops in `graph_def` that have their default value according to `producer_op_list` will be removed. This will allow some more `GraphDef`s produced by later binaries to be accepted by earlier binaries.
Returns
-
IList<object> - A list of `Operation` and/or `Tensor` objects from the imported graph, corresponding to the names in `return_elements`, and None if `returns_elements` is None.
object import_graph_def_dyn(object graph_def, object input_map, object return_elements, object name, object op_dict, object producer_op_list)
Imports the graph from `graph_def` into the current default `Graph`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(op_dict)`. They will be removed in a future version.
Instructions for updating:
Please file an issue at https://github.com/tensorflow/tensorflow/issues if you depend on this feature. This function provides a way to import a serialized TensorFlow
[`GraphDef`](https://www.tensorflow.org/code/tensorflow/core/framework/graph.proto)
protocol buffer, and extract individual objects in the `GraphDef` as
tf.Tensor and tf.Operation objects. Once extracted,
these objects are placed into the current default `Graph`. See
tf.Graph.as_graph_def for a way to create a `GraphDef`
proto.
Parameters
-
objectgraph_def - A `GraphDef` proto containing operations to be imported into the default graph.
-
objectinput_map - A dictionary mapping input names (as strings) in `graph_def` to `Tensor` objects. The values of the named input tensors in the imported graph will be re-mapped to the respective `Tensor` values.
-
objectreturn_elements - A list of strings containing operation names in `graph_def` that will be returned as `Operation` objects; and/or tensor names in `graph_def` that will be returned as `Tensor` objects.
-
objectname - (Optional.) A prefix that will be prepended to the names in `graph_def`. Note that this does not apply to imported function names. Defaults to `"import"`.
-
objectop_dict - (Optional.) Deprecated, do not use.
-
objectproducer_op_list - (Optional.) An `OpList` proto with the (possibly stripped) list of `OpDef`s used by the producer of the graph. If provided, unrecognized attrs for ops in `graph_def` that have their default value according to `producer_op_list` will be removed. This will allow some more `GraphDef`s produced by later binaries to be accepted by earlier binaries.
Returns
-
object - A list of `Operation` and/or `Tensor` objects from the imported graph, corresponding to the names in `return_elements`, and None if `returns_elements` is None.
object in_polymorphic_twice(object a, object b, string name)
object in_polymorphic_twice_dyn(object a, object b, object name)
IContextManager<T> init_scope()
A context manager that lifts ops out of control-flow scopes and function-building graphs. There is often a need to lift variable initialization ops out of control-flow
scopes, function-building graphs, and gradient tapes. Entering an
`init_scope` is a mechanism for satisfying these desiderata. In particular,
entering an `init_scope` has three effects: (1) All control dependencies are cleared the moment the scope is entered;
this is equivalent to entering the context manager returned from
`control_dependencies(None)`, which has the side-effect of exiting
control-flow scopes like
tf.cond and tf.while_loop. (2) All operations that are created while the scope is active are lifted
into the lowest context on the `context_stack` that is not building a
graph function. Here, a context is defined as either a graph or an eager
context. Every context switch, i.e., every installation of a graph as
the default graph and every switch into eager mode, is logged in a
thread-local stack called `context_switches`; the log entry for a
context switch is popped from the stack when the context is exited.
Entering an `init_scope` is equivalent to crawling up
`context_switches`, finding the first context that is not building a
graph function, and entering it. A caveat is that if graph mode is
enabled but the default graph stack is empty, then entering an
`init_scope` will simply install a fresh graph as the default one. (3) The gradient tape is paused while the scope is active. When eager execution is enabled, code inside an init_scope block runs with
eager execution enabled even when defining graph functions via
tf.contrib.eager.defun.
Show Example
tf.compat.v1.enable_eager_execution() @tf.contrib.eager.defun
def func():
# A defun-decorated function constructs TensorFlow graphs,
# it does not execute eagerly.
assert not tf.executing_eagerly()
with tf.init_scope():
# Initialization runs with eager execution enabled
assert tf.executing_eagerly()
object init_scope_dyn()
A context manager that lifts ops out of control-flow scopes and function-building graphs. There is often a need to lift variable initialization ops out of control-flow
scopes, function-building graphs, and gradient tapes. Entering an
`init_scope` is a mechanism for satisfying these desiderata. In particular,
entering an `init_scope` has three effects: (1) All control dependencies are cleared the moment the scope is entered;
this is equivalent to entering the context manager returned from
`control_dependencies(None)`, which has the side-effect of exiting
control-flow scopes like
tf.cond and tf.while_loop. (2) All operations that are created while the scope is active are lifted
into the lowest context on the `context_stack` that is not building a
graph function. Here, a context is defined as either a graph or an eager
context. Every context switch, i.e., every installation of a graph as
the default graph and every switch into eager mode, is logged in a
thread-local stack called `context_switches`; the log entry for a
context switch is popped from the stack when the context is exited.
Entering an `init_scope` is equivalent to crawling up
`context_switches`, finding the first context that is not building a
graph function, and entering it. A caveat is that if graph mode is
enabled but the default graph stack is empty, then entering an
`init_scope` will simply install a fresh graph as the default one. (3) The gradient tape is paused while the scope is active. When eager execution is enabled, code inside an init_scope block runs with
eager execution enabled even when defining graph functions via
tf.contrib.eager.defun.
Show Example
tf.compat.v1.enable_eager_execution() @tf.contrib.eager.defun
def func():
# A defun-decorated function constructs TensorFlow graphs,
# it does not execute eagerly.
assert not tf.executing_eagerly()
with tf.init_scope():
# Initialization runs with eager execution enabled
assert tf.executing_eagerly()
object initialize_all_tables(string name)
Returns an Op that initializes all tables of the default graph. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.tables_initializer instead.
Parameters
-
stringname - Optional name for the initialization op.
Returns
-
object - An Op that initializes all tables. Note that if there are not tables the returned Op is a NoOp.
object initialize_all_tables_dyn(ImplicitContainer<T> name)
Returns an Op that initializes all tables of the default graph. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.tables_initializer instead.
Parameters
-
ImplicitContainer<T>name - Optional name for the initialization op.
Returns
-
object - An Op that initializes all tables. Note that if there are not tables the returned Op is a NoOp.
object initialize_all_variables()
See `tf.compat.v1.global_variables_initializer`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Use
tf.global_variables_initializer instead. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
object initialize_all_variables_dyn()
See `tf.compat.v1.global_variables_initializer`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Use
tf.global_variables_initializer instead. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
object initialize_local_variables()
See `tf.compat.v1.local_variables_initializer`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Use
tf.local_variables_initializer instead. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
object initialize_local_variables_dyn()
See `tf.compat.v1.local_variables_initializer`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Use
tf.local_variables_initializer instead. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
object initialize_variables(object var_list, string name)
See `tf.compat.v1.variables_initializer`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Use
tf.variables_initializer instead. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
object initialize_variables_dyn(object var_list, ImplicitContainer<T> name)
See `tf.compat.v1.variables_initializer`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Use
tf.variables_initializer instead. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
Tensor int_attr(int foo, string name)
object int_attr_dyn(ImplicitContainer<T> foo, object name)
object int_input(IGraphNodeBase a, string name)
object int_input_dyn(object a, object name)
object int_input_float_input(IGraphNodeBase a, IGraphNodeBase b, string name)
object int_input_float_input_dyn(object a, object b, object name)
Tensor int_input_int_output(IGraphNodeBase a, string name)
object int_input_int_output_dyn(object a, object name)
Tensor int_output(string name)
object int_output_dyn(object name)
object int_output_float_output(string name)
object int_output_float_output_dyn(object name)
Tensor int64_output(string name)
object int64_output_dyn(object name)
Tensor invert_permutation(IGraphNodeBase x, string name)
Computes the inverse permutation of a tensor. This operation computes the inverse of an index permutation. It takes a 1-D
integer tensor `x`, which represents the indices of a zero-based array, and
swaps each value with its index position. In other words, for an output tensor
`y` and an input tensor `x`, this operation computes the following: `y[x[i]] = i for i in [0, 1,..., len(x) - 1]` The values must include 0. There can be no duplicate values or negative values. For example: ```
# tensor `x` is [3, 4, 0, 2, 1]
invert_permutation(x) ==> [2, 4, 3, 0, 1]
```
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
object invert_permutation_dyn(object x, object name)
Computes the inverse permutation of a tensor. This operation computes the inverse of an index permutation. It takes a 1-D
integer tensor `x`, which represents the indices of a zero-based array, and
swaps each value with its index position. In other words, for an output tensor
`y` and an input tensor `x`, this operation computes the following: `y[x[i]] = i for i in [0, 1,..., len(x) - 1]` The values must include 0. There can be no duplicate values or negative values. For example: ```
# tensor `x` is [3, 4, 0, 2, 1]
invert_permutation(x) ==> [2, 4, 3, 0, 1]
```
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object is_finite(IGraphNodeBase x, string name)
Returns which elements of x are finite.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object is_finite_dyn(object x, object name)
Returns which elements of x are finite.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object is_inf(IGraphNodeBase x, string name)
Returns which elements of x are Inf.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object is_inf_dyn(object x, object name)
Returns which elements of x are Inf.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object is_nan(IGraphNodeBase x, string name)
Returns which elements of x are NaN.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object is_nan_dyn(object x, object name)
Returns which elements of x are NaN.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
Tensor is_non_decreasing(IEnumerable<int> x, string name)
Returns `True` if `x` is non-decreasing. Elements of `x` are compared in row-major order. The tensor `[x[0],...]`
is non-decreasing if for every adjacent pair we have `x[i] <= x[i+1]`.
If `x` has less than two elements, it is trivially non-decreasing. See also: `is_strictly_increasing`
Parameters
-
IEnumerable<int>x - Numeric `Tensor`.
-
stringname - A name for this operation (optional). Defaults to "is_non_decreasing"
Returns
-
Tensor - Boolean `Tensor`, equal to `True` iff `x` is non-decreasing.
object is_non_decreasing_dyn(object x, object name)
Returns `True` if `x` is non-decreasing. Elements of `x` are compared in row-major order. The tensor `[x[0],...]`
is non-decreasing if for every adjacent pair we have `x[i] <= x[i+1]`.
If `x` has less than two elements, it is trivially non-decreasing. See also: `is_strictly_increasing`
Parameters
-
objectx - Numeric `Tensor`.
-
objectname - A name for this operation (optional). Defaults to "is_non_decreasing"
Returns
-
object - Boolean `Tensor`, equal to `True` iff `x` is non-decreasing.
bool is_numeric_tensor(IEnumerable<int> tensor)
Returns `True` if the elements of `tensor` are numbers. Specifically, returns `True` if the dtype of `tensor` is one of the following: *
tf.float32
* tf.float64
* tf.int8
* tf.int16
* tf.int32
* tf.int64
* tf.uint8
* tf.qint8
* tf.qint32
* tf.quint8
* tf.complex64 Returns `False` if `tensor` is of a non-numeric type or if `tensor` is not
a tf.Tensor object.
bool is_numeric_tensor(IGraphNodeBase tensor)
Returns `True` if the elements of `tensor` are numbers. Specifically, returns `True` if the dtype of `tensor` is one of the following: *
tf.float32
* tf.float64
* tf.int8
* tf.int16
* tf.int32
* tf.int64
* tf.uint8
* tf.qint8
* tf.qint32
* tf.quint8
* tf.complex64 Returns `False` if `tensor` is of a non-numeric type or if `tensor` is not
a tf.Tensor object.
object is_numeric_tensor_dyn(object tensor)
Returns `True` if the elements of `tensor` are numbers. Specifically, returns `True` if the dtype of `tensor` is one of the following: *
tf.float32
* tf.float64
* tf.int8
* tf.int16
* tf.int32
* tf.int64
* tf.uint8
* tf.qint8
* tf.qint32
* tf.quint8
* tf.complex64 Returns `False` if `tensor` is of a non-numeric type or if `tensor` is not
a tf.Tensor object.
Tensor is_strictly_increasing(IEnumerable<int> x, string name)
Returns `True` if `x` is strictly increasing. Elements of `x` are compared in row-major order. The tensor `[x[0],...]`
is strictly increasing if for every adjacent pair we have `x[i] < x[i+1]`.
If `x` has less than two elements, it is trivially strictly increasing. See also: `is_non_decreasing`
Parameters
-
IEnumerable<int>x - Numeric `Tensor`.
-
stringname - A name for this operation (optional). Defaults to "is_strictly_increasing"
Returns
-
Tensor - Boolean `Tensor`, equal to `True` iff `x` is strictly increasing.
object is_strictly_increasing_dyn(object x, object name)
Returns `True` if `x` is strictly increasing. Elements of `x` are compared in row-major order. The tensor `[x[0],...]`
is strictly increasing if for every adjacent pair we have `x[i] < x[i+1]`.
If `x` has less than two elements, it is trivially strictly increasing. See also: `is_non_decreasing`
Parameters
-
objectx - Numeric `Tensor`.
-
objectname - A name for this operation (optional). Defaults to "is_strictly_increasing"
Returns
-
object - Boolean `Tensor`, equal to `True` iff `x` is strictly increasing.
bool is_tensor(PythonFunctionContainer x)
Checks whether `x` is a tensor or "tensor-like". If `is_tensor(x)` returns `True`, it is safe to assume that `x` is a tensor or
can be converted to a tensor using `ops.convert_to_tensor(x)`.
Parameters
-
PythonFunctionContainerx - A python object to check.
Returns
-
bool - `True` if `x` is a tensor or "tensor-like", `False` if not.
bool is_tensor(object x)
Checks whether `x` is a tensor or "tensor-like". If `is_tensor(x)` returns `True`, it is safe to assume that `x` is a tensor or
can be converted to a tensor using `ops.convert_to_tensor(x)`.
Parameters
-
objectx - A python object to check.
Returns
-
bool - `True` if `x` is a tensor or "tensor-like", `False` if not.
bool is_tensor(IEnumerable<IGraphNodeBase> x)
Checks whether `x` is a tensor or "tensor-like". If `is_tensor(x)` returns `True`, it is safe to assume that `x` is a tensor or
can be converted to a tensor using `ops.convert_to_tensor(x)`.
Parameters
-
IEnumerable<IGraphNodeBase>x - A python object to check.
Returns
-
bool - `True` if `x` is a tensor or "tensor-like", `False` if not.
object is_tensor_dyn(object x)
Checks whether `x` is a tensor or "tensor-like". If `is_tensor(x)` returns `True`, it is safe to assume that `x` is a tensor or
can be converted to a tensor using `ops.convert_to_tensor(x)`.
Parameters
-
objectx - A python object to check.
Returns
-
object - `True` if `x` is a tensor or "tensor-like", `False` if not.
Tensor is_variable_initialized(Variable variable)
Tests if a variable has been initialized.
Parameters
-
Variablevariable - A `Variable`.
Returns
-
Tensor - Returns a scalar boolean Tensor, `True` if the variable has been initialized, `False` otherwise. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
object is_variable_initialized_dyn(object variable)
Tests if a variable has been initialized.
Parameters
-
objectvariable - A `Variable`.
Returns
-
object - Returns a scalar boolean Tensor, `True` if the variable has been initialized, `False` otherwise. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
object k_feature_gradient(IGraphNodeBase input_data, IGraphNodeBase tree_parameters, IGraphNodeBase tree_biases, IGraphNodeBase routes, object layer_num, object random_seed, string name)
object k_feature_gradient_dyn(object input_data, object tree_parameters, object tree_biases, object routes, object layer_num, object random_seed, object name)
Tensor k_feature_routing_function(IGraphNodeBase input_data, IGraphNodeBase tree_parameters, IGraphNodeBase tree_biases, int layer_num, object max_nodes, object num_features_per_node, int random_seed, string name)
object k_feature_routing_function_dyn(object input_data, object tree_parameters, object tree_biases, object layer_num, object max_nodes, object num_features_per_node, object random_seed, object name)
Tensor kernel_label(string name)
object kernel_label_dyn(object name)
Tensor kernel_label_required(IGraphNodeBase input, string name)
object kernel_label_required_dyn(object input, object name)
object lbeta(IGraphNodeBase x, string name)
Computes \\(ln(|Beta(x)|)\\), reducing along the last dimension. Given one-dimensional `z = [z_0,...,z_{K-1}]`, we define $$Beta(z) = \prod_j Gamma(z_j) / Gamma(\sum_j z_j)$$ And for `n + 1` dimensional `x` with shape `[N1,..., Nn, K]`, we define
$$lbeta(x)[i1,..., in] = Log(|Beta(x[i1,..., in, :])|)$$. In other words, the last dimension is treated as the `z` vector. Note that if `z = [u, v]`, then
\\(Beta(z) = int_0^1 t^{u-1} (1 - t)^{v-1} dt\\), which defines the
traditional bivariate beta function. If the last dimension is empty, we follow the convention that the sum over
the empty set is zero, and the product is one.
Parameters
-
IGraphNodeBasex - A rank `n + 1` `Tensor`, `n >= 0` with type `float`, or `double`.
-
stringname - A name for the operation (optional).
Returns
-
object - The logarithm of \\(|Beta(x)|\\) reducing along the last dimension.
object lbeta(IEnumerable<object> x, string name)
Computes \\(ln(|Beta(x)|)\\), reducing along the last dimension. Given one-dimensional `z = [z_0,...,z_{K-1}]`, we define $$Beta(z) = \prod_j Gamma(z_j) / Gamma(\sum_j z_j)$$ And for `n + 1` dimensional `x` with shape `[N1,..., Nn, K]`, we define
$$lbeta(x)[i1,..., in] = Log(|Beta(x[i1,..., in, :])|)$$. In other words, the last dimension is treated as the `z` vector. Note that if `z = [u, v]`, then
\\(Beta(z) = int_0^1 t^{u-1} (1 - t)^{v-1} dt\\), which defines the
traditional bivariate beta function. If the last dimension is empty, we follow the convention that the sum over
the empty set is zero, and the product is one.
Parameters
-
IEnumerable<object>x - A rank `n + 1` `Tensor`, `n >= 0` with type `float`, or `double`.
-
stringname - A name for the operation (optional).
Returns
-
object - The logarithm of \\(|Beta(x)|\\) reducing along the last dimension.
object lbeta(CompositeTensor x, string name)
Computes \\(ln(|Beta(x)|)\\), reducing along the last dimension. Given one-dimensional `z = [z_0,...,z_{K-1}]`, we define $$Beta(z) = \prod_j Gamma(z_j) / Gamma(\sum_j z_j)$$ And for `n + 1` dimensional `x` with shape `[N1,..., Nn, K]`, we define
$$lbeta(x)[i1,..., in] = Log(|Beta(x[i1,..., in, :])|)$$. In other words, the last dimension is treated as the `z` vector. Note that if `z = [u, v]`, then
\\(Beta(z) = int_0^1 t^{u-1} (1 - t)^{v-1} dt\\), which defines the
traditional bivariate beta function. If the last dimension is empty, we follow the convention that the sum over
the empty set is zero, and the product is one.
Parameters
-
CompositeTensorx - A rank `n + 1` `Tensor`, `n >= 0` with type `float`, or `double`.
-
stringname - A name for the operation (optional).
Returns
-
object - The logarithm of \\(|Beta(x)|\\) reducing along the last dimension.
object lbeta(PythonClassContainer x, string name)
Computes \\(ln(|Beta(x)|)\\), reducing along the last dimension. Given one-dimensional `z = [z_0,...,z_{K-1}]`, we define $$Beta(z) = \prod_j Gamma(z_j) / Gamma(\sum_j z_j)$$ And for `n + 1` dimensional `x` with shape `[N1,..., Nn, K]`, we define
$$lbeta(x)[i1,..., in] = Log(|Beta(x[i1,..., in, :])|)$$. In other words, the last dimension is treated as the `z` vector. Note that if `z = [u, v]`, then
\\(Beta(z) = int_0^1 t^{u-1} (1 - t)^{v-1} dt\\), which defines the
traditional bivariate beta function. If the last dimension is empty, we follow the convention that the sum over
the empty set is zero, and the product is one.
Parameters
-
PythonClassContainerx - A rank `n + 1` `Tensor`, `n >= 0` with type `float`, or `double`.
-
stringname - A name for the operation (optional).
Returns
-
object - The logarithm of \\(|Beta(x)|\\) reducing along the last dimension.
object lbeta_dyn(object x, object name)
Computes \\(ln(|Beta(x)|)\\), reducing along the last dimension. Given one-dimensional `z = [z_0,...,z_{K-1}]`, we define $$Beta(z) = \prod_j Gamma(z_j) / Gamma(\sum_j z_j)$$ And for `n + 1` dimensional `x` with shape `[N1,..., Nn, K]`, we define
$$lbeta(x)[i1,..., in] = Log(|Beta(x[i1,..., in, :])|)$$. In other words, the last dimension is treated as the `z` vector. Note that if `z = [u, v]`, then
\\(Beta(z) = int_0^1 t^{u-1} (1 - t)^{v-1} dt\\), which defines the
traditional bivariate beta function. If the last dimension is empty, we follow the convention that the sum over
the empty set is zero, and the product is one.
Parameters
-
objectx - A rank `n + 1` `Tensor`, `n >= 0` with type `float`, or `double`.
-
objectname - A name for the operation (optional).
Returns
-
object - The logarithm of \\(|Beta(x)|\\) reducing along the last dimension.
object less(int x, double y, string name)
object less(double x, IGraphNodeBase y, string name)
object less(IGraphNodeBase x, int y, string name)
object less(double x, int y, string name)
object less(int x, IGraphNodeBase y, string name)
object less(double x, double y, string name)
object less(IGraphNodeBase x, IGraphNodeBase y, string name)
object less(IGraphNodeBase x, double y, string name)
object less(int x, int y, string name)
object less_dyn(object x, object y, object name)
object less_equal(IGraphNodeBase x, IGraphNodeBase y, string name)
object less_equal(IGraphNodeBase x, int y, string name)
object less_equal(IGraphNodeBase x, double y, string name)
object less_equal(int x, IGraphNodeBase y, string name)
object less_equal(int x, int y, string name)
object less_equal(int x, double y, string name)
object less_equal(double x, IGraphNodeBase y, string name)
object less_equal(double x, int y, string name)
object less_equal(double x, double y, string name)
object less_equal_dyn(object x, object y, object name)
object lgamma(IGraphNodeBase x, string name)
Computes the log of the absolute value of `Gamma(x)` element-wise.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object lgamma_dyn(object x, object name)
Computes the log of the absolute value of `Gamma(x)` element-wise.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Tensor linspace(IGraphNodeBase start, IGraphNodeBase stop, IGraphNodeBase num, string name)
Generates values in an interval. A sequence of `num` evenly-spaced values are generated beginning at `start`.
If `num > 1`, the values in the sequence increase by `stop - start / num - 1`,
so that the last one is exactly `stop`. For example: ```
tf.linspace(10.0, 12.0, 3, name="linspace") => [ 10.0 11.0 12.0]
```
Parameters
-
IGraphNodeBasestart - A `Tensor`. Must be one of the following types: `bfloat16`, `float32`, `float64`. 0-D tensor. First entry in the range.
-
IGraphNodeBasestop - A `Tensor`. Must have the same type as `start`. 0-D tensor. Last entry in the range.
-
IGraphNodeBasenum - A `Tensor`. Must be one of the following types: `int32`, `int64`. 0-D tensor. Number of values to generate.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `start`.
object linspace_dyn(object start, object stop, object num, object name)
Generates values in an interval. A sequence of `num` evenly-spaced values are generated beginning at `start`.
If `num > 1`, the values in the sequence increase by `stop - start / num - 1`,
so that the last one is exactly `stop`. For example: ```
tf.linspace(10.0, 12.0, 3, name="linspace") => [ 10.0 11.0 12.0]
```
Parameters
-
objectstart - A `Tensor`. Must be one of the following types: `bfloat16`, `float32`, `float64`. 0-D tensor. First entry in the range.
-
objectstop - A `Tensor`. Must have the same type as `start`. 0-D tensor. Last entry in the range.
-
objectnum - A `Tensor`. Must be one of the following types: `int32`, `int64`. 0-D tensor. Number of values to generate.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `start`.
object list_input(object a, string name)
object list_input_dyn(object a, object name)
object list_output(IEnumerable<DType> T, string name)
object list_output_dyn(object T, object name)
void load_file_system_library(object library_filename)
Loads a TensorFlow plugin, containing file system implementation. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.load_library instead. Pass `library_filename` to a platform-specific mechanism for dynamically
loading a library. The rules for determining the exact location of the
library are platform-specific and are not documented here.
Parameters
-
objectlibrary_filename - Path to the plugin. Relative or absolute filesystem path to a dynamic library file.
Returns
-
void - None.
object load_file_system_library_dyn(object library_filename)
Loads a TensorFlow plugin, containing file system implementation. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.load_library instead. Pass `library_filename` to a platform-specific mechanism for dynamically
loading a library. The rules for determining the exact location of the
library are platform-specific and are not documented here.
Parameters
-
objectlibrary_filename - Path to the plugin. Relative or absolute filesystem path to a dynamic library file.
Returns
-
object - None.
void load_library(object library_location)
Loads a TensorFlow plugin. "library_location" can be a path to a specific shared object, or a folder.
If it is a folder, all shared objects that are named "libtfkernel*" will be
loaded. When the library is loaded, kernels registered in the library via the
`REGISTER_*` macros are made available in the TensorFlow process.
Parameters
-
objectlibrary_location - Path to the plugin or the folder of plugins. Relative or absolute filesystem path to a dynamic library file or folder.
Returns
-
void - None
object load_library_dyn(object library_location)
Loads a TensorFlow plugin. "library_location" can be a path to a specific shared object, or a folder.
If it is a folder, all shared objects that are named "libtfkernel*" will be
loaded. When the library is loaded, kernels registered in the library via the
`REGISTER_*` macros are made available in the TensorFlow process.
Parameters
-
objectlibrary_location - Path to the plugin or the folder of plugins. Relative or absolute filesystem path to a dynamic library file or folder.
Returns
-
object - None
object load_op_library(Byte[] library_filename)
Loads a TensorFlow plugin, containing custom ops and kernels. Pass "library_filename" to a platform-specific mechanism for dynamically
loading a library. The rules for determining the exact location of the
library are platform-specific and are not documented here. When the
library is loaded, ops and kernels registered in the library via the
`REGISTER_*` macros are made available in the TensorFlow process. Note
that ops with the same name as an existing op are rejected and not
registered with the process.
Parameters
-
Byte[]library_filename - Path to the plugin. Relative or absolute filesystem path to a dynamic library file.
Returns
-
object - A python module containing the Python wrappers for Ops defined in the plugin.
object load_op_library(string library_filename)
Loads a TensorFlow plugin, containing custom ops and kernels. Pass "library_filename" to a platform-specific mechanism for dynamically
loading a library. The rules for determining the exact location of the
library are platform-specific and are not documented here. When the
library is loaded, ops and kernels registered in the library via the
`REGISTER_*` macros are made available in the TensorFlow process. Note
that ops with the same name as an existing op are rejected and not
registered with the process.
Parameters
-
stringlibrary_filename - Path to the plugin. Relative or absolute filesystem path to a dynamic library file.
Returns
-
object - A python module containing the Python wrappers for Ops defined in the plugin.
object load_op_library_dyn(object library_filename)
Loads a TensorFlow plugin, containing custom ops and kernels. Pass "library_filename" to a platform-specific mechanism for dynamically
loading a library. The rules for determining the exact location of the
library are platform-specific and are not documented here. When the
library is loaded, ops and kernels registered in the library via the
`REGISTER_*` macros are made available in the TensorFlow process. Note
that ops with the same name as an existing op are rejected and not
registered with the process.
Parameters
-
objectlibrary_filename - Path to the plugin. Relative or absolute filesystem path to a dynamic library file.
Returns
-
object - A python module containing the Python wrappers for Ops defined in the plugin.
object local_variables(object scope)
Returns local variables. Local variables - per process variables, usually not saved/restored to
checkpoint and used for temporary or intermediate values.
For example, they can be used as counters for metrics computation or
number of epochs this machine has read data.
The `tf.contrib.framework.local_variable()` function automatically adds the
new variable to `GraphKeys.LOCAL_VARIABLES`.
This convenience function returns the contents of that collection. An alternative to local variables are global variables. See
`tf.compat.v1.global_variables`
Parameters
-
objectscope - (Optional.) A string. If supplied, the resulting list is filtered to include only items whose `name` attribute matches `scope` using `re.match`. Items without a `name` attribute are never returned if a scope is supplied. The choice of `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
object - A list of local `Variable` objects.
object local_variables_dyn(object scope)
Returns local variables. Local variables - per process variables, usually not saved/restored to
checkpoint and used for temporary or intermediate values.
For example, they can be used as counters for metrics computation or
number of epochs this machine has read data.
The `tf.contrib.framework.local_variable()` function automatically adds the
new variable to `GraphKeys.LOCAL_VARIABLES`.
This convenience function returns the contents of that collection. An alternative to local variables are global variables. See
`tf.compat.v1.global_variables`
Parameters
-
objectscope - (Optional.) A string. If supplied, the resulting list is filtered to include only items whose `name` attribute matches `scope` using `re.match`. Items without a `name` attribute are never returned if a scope is supplied. The choice of `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
object - A list of local `Variable` objects.
object local_variables_initializer()
Returns an Op that initializes all local variables. This is just a shortcut for `variables_initializer(local_variables())`
Returns
-
object - An Op that initializes all local variables in the graph.
object local_variables_initializer_dyn()
Returns an Op that initializes all local variables. This is just a shortcut for `variables_initializer(local_variables())`
Returns
-
object - An Op that initializes all local variables in the graph.
object log(object x, string name)
Computes natural logarithm of x element-wise. I.e., \\(y = \log_e x\\).
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object log_dyn(object x, object name)
Computes natural logarithm of x element-wise. I.e., \\(y = \log_e x\\).
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object log_sigmoid(IGraphNodeBase x, string name)
Computes log sigmoid of `x` element-wise. Specifically, `y = log(1 / (1 + exp(-x)))`. For numerical stability,
we use `y = -tf.nn.softplus(-x)`.
Parameters
-
IGraphNodeBasex - A Tensor with type `float32` or `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A Tensor with the same type as `x`.
object log_sigmoid(IEnumerable<double> x, string name)
Computes log sigmoid of `x` element-wise. Specifically, `y = log(1 / (1 + exp(-x)))`. For numerical stability,
we use `y = -tf.nn.softplus(-x)`.
Parameters
-
IEnumerable<double>x - A Tensor with type `float32` or `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A Tensor with the same type as `x`.
object log_sigmoid(float32 x, string name)
Computes log sigmoid of `x` element-wise. Specifically, `y = log(1 / (1 + exp(-x)))`. For numerical stability,
we use `y = -tf.nn.softplus(-x)`.
Parameters
-
float32x - A Tensor with type `float32` or `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A Tensor with the same type as `x`.
object log_sigmoid_dyn(object x, object name)
Computes log sigmoid of `x` element-wise. Specifically, `y = log(1 / (1 + exp(-x)))`. For numerical stability,
we use `y = -tf.nn.softplus(-x)`.
Parameters
-
objectx - A Tensor with type `float32` or `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A Tensor with the same type as `x`.
object log1p(IGraphNodeBase x, string name)
Computes natural logarithm of (1 + x) element-wise. I.e., \\(y = \log_e (1 + x)\\).
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object log1p_dyn(object x, object name)
Computes natural logarithm of (1 + x) element-wise. I.e., \\(y = \log_e (1 + x)\\).
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object logical_and(bool x, IGraphNodeBase y, string name)
Returns the truth value of x AND y element-wise. *NOTE*: `math.logical_and` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
boolx - A `Tensor` of type `bool`.
-
IGraphNodeBasey - A `Tensor` of type `bool`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object logical_and(IGraphNodeBase x, bool y, string name)
Returns the truth value of x AND y element-wise. *NOTE*: `math.logical_and` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor` of type `bool`.
-
booly - A `Tensor` of type `bool`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object logical_and(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns the truth value of x AND y element-wise. *NOTE*: `math.logical_and` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor` of type `bool`.
-
IGraphNodeBasey - A `Tensor` of type `bool`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object logical_and(bool x, bool y, string name)
Returns the truth value of x AND y element-wise. *NOTE*: `math.logical_and` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
boolx - A `Tensor` of type `bool`.
-
booly - A `Tensor` of type `bool`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object logical_and_dyn(object x, object y, object name)
Returns the truth value of x AND y element-wise. *NOTE*: `math.logical_and` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` of type `bool`.
-
objecty - A `Tensor` of type `bool`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object logical_not(IGraphNodeBase x, string name)
object logical_not_dyn(object x, object name)
object logical_or(bool x, IGraphNodeBase y, string name)
Returns the truth value of x OR y element-wise. *NOTE*: `math.logical_or` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
boolx - A `Tensor` of type `bool`.
-
IGraphNodeBasey - A `Tensor` of type `bool`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object logical_or(bool x, bool y, string name)
Returns the truth value of x OR y element-wise. *NOTE*: `math.logical_or` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
boolx - A `Tensor` of type `bool`.
-
booly - A `Tensor` of type `bool`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object logical_or(IGraphNodeBase x, bool y, string name)
Returns the truth value of x OR y element-wise. *NOTE*: `math.logical_or` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor` of type `bool`.
-
booly - A `Tensor` of type `bool`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object logical_or(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns the truth value of x OR y element-wise. *NOTE*: `math.logical_or` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor` of type `bool`.
-
IGraphNodeBasey - A `Tensor` of type `bool`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object logical_or_dyn(object x, object y, object name)
Returns the truth value of x OR y element-wise. *NOTE*: `math.logical_or` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` of type `bool`.
-
objecty - A `Tensor` of type `bool`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `bool`.
object logical_xor(IGraphNodeBase x, IGraphNodeBase y, string name)
Logical XOR function. x ^ y = (x | y) & ~(x & y) Inputs are tensor and if the tensors contains more than one element, an
element-wise logical XOR is computed. Usage:
Parameters
-
IGraphNodeBasex - A `Tensor` type bool.
-
IGraphNodeBasey - A `Tensor` of type bool.
-
stringname
Returns
-
object - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([False, False, True, True], dtype = tf.bool)
y = tf.constant([False, True, False, True], dtype = tf.bool)
z = tf.logical_xor(x, y, name="LogicalXor")
# here z = [False True True False]
object logical_xor(IGraphNodeBase x, IGraphNodeBase y, PythonFunctionContainer name)
Logical XOR function. x ^ y = (x | y) & ~(x & y) Inputs are tensor and if the tensors contains more than one element, an
element-wise logical XOR is computed. Usage:
Parameters
-
IGraphNodeBasex - A `Tensor` type bool.
-
IGraphNodeBasey - A `Tensor` of type bool.
-
PythonFunctionContainername
Returns
-
object - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([False, False, True, True], dtype = tf.bool)
y = tf.constant([False, True, False, True], dtype = tf.bool)
z = tf.logical_xor(x, y, name="LogicalXor")
# here z = [False True True False]
object logical_xor_dyn(object x, object y, ImplicitContainer<T> name)
Logical XOR function. x ^ y = (x | y) & ~(x & y) Inputs are tensor and if the tensors contains more than one element, an
element-wise logical XOR is computed. Usage:
Parameters
-
objectx - A `Tensor` type bool.
-
objecty - A `Tensor` of type bool.
-
ImplicitContainer<T>name
Returns
-
object - A `Tensor` of type bool with the same size as that of x or y.
Show Example
x = tf.constant([False, False, True, True], dtype = tf.bool)
y = tf.constant([False, True, False, True], dtype = tf.bool)
z = tf.logical_xor(x, y, name="LogicalXor")
# here z = [False True True False]
ndarray make_ndarray(object tensor)
Create a numpy ndarray from a tensor. Create a numpy ndarray with the same shape and data as the tensor.
Parameters
-
objecttensor - A TensorProto.
Returns
-
ndarray - A numpy array with the tensor contents.
object make_ndarray_dyn(object tensor)
Create a numpy ndarray from a tensor. Create a numpy ndarray with the same shape and data as the tensor.
Parameters
-
objecttensor - A TensorProto.
Returns
-
object - A numpy array with the tensor contents.
object make_quantile_summaries(IEnumerable<object> dense_float_features, IEnumerable<object> sparse_float_feature_indices, IEnumerable<object> sparse_float_feature_values, IEnumerable<object> sparse_float_feature_shapes, IGraphNodeBase example_weights, double epsilon, string name)
object make_quantile_summaries_dyn(object dense_float_features, object sparse_float_feature_indices, object sparse_float_feature_values, object sparse_float_feature_shapes, object example_weights, object epsilon, object name)
object make_template(string name_, PythonFunctionContainer func_, bool create_scope_now_, string unique_name_, object custom_getter_, IDictionary<string, object> kwargs)
Given an arbitrary function, wrap it so that it does variable sharing. This wraps `func_` in a Template and partially evaluates it. Templates are
functions that create variables the first time they are called and reuse them
thereafter. In order for `func_` to be compatible with a `Template` it must
have the following properties: * The function should create all trainable variables and any variables that
should be reused by calling `tf.compat.v1.get_variable`. If a trainable
variable is
created using
tf.Variable, then a ValueError will be thrown. Variables
that are intended to be locals can be created by specifying
`tf.Variable(..., trainable=false)`.
* The function may use variable scopes and other templates internally to
create and reuse variables, but it shouldn't use
`tf.compat.v1.global_variables` to
capture variables that are defined outside of the scope of the function.
* Internal scopes and variable names should not depend on any arguments that
are not supplied to `make_template`. In general you will get a ValueError
telling you that you are trying to reuse a variable that doesn't exist
if you make a mistake. In the following example, both `z` and `w` will be scaled by the same `y`. It
is important to note that if we didn't assign `scalar_name` and used a
different name for z and w that a `ValueError` would be thrown because it
couldn't reuse the variable.
As a safe-guard, the returned function will raise a `ValueError` after the
first call if trainable variables are created by calling tf.Variable. If all of these are true, then 2 properties are enforced by the template: 1. Calling the same template multiple times will share all non-local
variables.
2. Two different templates are guaranteed to be unique, unless you reenter the
same variable scope as the initial definition of a template and redefine
it. An examples of this exception:
Depending on the value of `create_scope_now_`, the full variable scope may be
captured either at the time of first call or at the time of construction. If
this option is set to True, then all Tensors created by repeated calls to the
template will have an extra trailing _N+1 to their name, as the first time the
scope is entered in the Template constructor no Tensors are created. Note: `name_`, `func_` and `create_scope_now_` have a trailing underscore to
reduce the likelihood of collisions with kwargs.
Parameters
-
stringname_ - A name for the scope created by this template. If necessary, the name will be made unique by appending `_N` to the name.
-
PythonFunctionContainerfunc_ - The function to wrap.
-
boolcreate_scope_now_ - Boolean controlling whether the scope should be created when the template is constructed or when the template is called. Default is False, meaning the scope is created when the template is called.
-
stringunique_name_ - When used, it overrides name_ and is not made unique. If a template of the same scope/unique_name already exists and reuse is false, an error is raised. Defaults to None.
-
objectcustom_getter_ - Optional custom getter for variables used in `func_`. See the `tf.compat.v1.get_variable` `custom_getter` documentation for more information.
-
IDictionary<string, object>kwargs - Keyword arguments to apply to `func_`.
Returns
-
object - A function to encapsulate a set of variables which should be created once and reused. An enclosing scope will be created either when `make_template` is called or when the result is called, depending on the value of `create_scope_now_`. Regardless of the value, the first time the template is called it will enter the scope with no reuse, and call `func_` to create variables, which are guaranteed to be unique. All subsequent calls will re-enter the scope and reuse those variables.
Show Example
def my_op(x, scalar_name):
var1 = tf.compat.v1.get_variable(scalar_name,
shape=[],
initializer=tf.compat.v1.constant_initializer(1))
return x * var1 scale_by_y = tf.compat.v1.make_template('scale_by_y', my_op, scalar_name='y') z = scale_by_y(input1)
w = scale_by_y(input2)
object make_template_dyn(object name_, object func_, ImplicitContainer<T> create_scope_now_, object unique_name_, object custom_getter_, IDictionary<string, object> kwargs)
Given an arbitrary function, wrap it so that it does variable sharing. This wraps `func_` in a Template and partially evaluates it. Templates are
functions that create variables the first time they are called and reuse them
thereafter. In order for `func_` to be compatible with a `Template` it must
have the following properties: * The function should create all trainable variables and any variables that
should be reused by calling `tf.compat.v1.get_variable`. If a trainable
variable is
created using
tf.Variable, then a ValueError will be thrown. Variables
that are intended to be locals can be created by specifying
`tf.Variable(..., trainable=false)`.
* The function may use variable scopes and other templates internally to
create and reuse variables, but it shouldn't use
`tf.compat.v1.global_variables` to
capture variables that are defined outside of the scope of the function.
* Internal scopes and variable names should not depend on any arguments that
are not supplied to `make_template`. In general you will get a ValueError
telling you that you are trying to reuse a variable that doesn't exist
if you make a mistake. In the following example, both `z` and `w` will be scaled by the same `y`. It
is important to note that if we didn't assign `scalar_name` and used a
different name for z and w that a `ValueError` would be thrown because it
couldn't reuse the variable.
As a safe-guard, the returned function will raise a `ValueError` after the
first call if trainable variables are created by calling tf.Variable. If all of these are true, then 2 properties are enforced by the template: 1. Calling the same template multiple times will share all non-local
variables.
2. Two different templates are guaranteed to be unique, unless you reenter the
same variable scope as the initial definition of a template and redefine
it. An examples of this exception:
Depending on the value of `create_scope_now_`, the full variable scope may be
captured either at the time of first call or at the time of construction. If
this option is set to True, then all Tensors created by repeated calls to the
template will have an extra trailing _N+1 to their name, as the first time the
scope is entered in the Template constructor no Tensors are created. Note: `name_`, `func_` and `create_scope_now_` have a trailing underscore to
reduce the likelihood of collisions with kwargs.
Parameters
-
objectname_ - A name for the scope created by this template. If necessary, the name will be made unique by appending `_N` to the name.
-
objectfunc_ - The function to wrap.
-
ImplicitContainer<T>create_scope_now_ - Boolean controlling whether the scope should be created when the template is constructed or when the template is called. Default is False, meaning the scope is created when the template is called.
-
objectunique_name_ - When used, it overrides name_ and is not made unique. If a template of the same scope/unique_name already exists and reuse is false, an error is raised. Defaults to None.
-
objectcustom_getter_ - Optional custom getter for variables used in `func_`. See the `tf.compat.v1.get_variable` `custom_getter` documentation for more information.
-
IDictionary<string, object>kwargs - Keyword arguments to apply to `func_`.
Returns
-
object - A function to encapsulate a set of variables which should be created once and reused. An enclosing scope will be created either when `make_template` is called or when the result is called, depending on the value of `create_scope_now_`. Regardless of the value, the first time the template is called it will enter the scope with no reuse, and call `func_` to create variables, which are guaranteed to be unique. All subsequent calls will re-enter the scope and reuse those variables.
Show Example
def my_op(x, scalar_name):
var1 = tf.compat.v1.get_variable(scalar_name,
shape=[],
initializer=tf.compat.v1.constant_initializer(1))
return x * var1 scale_by_y = tf.compat.v1.make_template('scale_by_y', my_op, scalar_name='y') z = scale_by_y(input1)
w = scale_by_y(input2)
object make_tensor_proto(object values, DType dtype, TensorShape shape, bool verify_shape, bool allow_broadcast)
Create a TensorProto. In TensorFlow 2.0, representing tensors as protos should no longer be a
common workflow. That said, this utility function is still useful for
generating TF Serving request protos: request = tensorflow_serving.apis.predict_pb2.PredictRequest()
request.model_spec.name = "my_model"
request.model_spec.signature_name = "serving_default"
request.inputs["images"].CopyFrom(tf.make_tensor_proto(X_new)) make_tensor_proto accepts "values" of a python scalar, a python list, a
numpy ndarray, or a numpy scalar. If "values" is a python scalar or a python list, make_tensor_proto
first convert it to numpy ndarray. If dtype is None, the
conversion tries its best to infer the right numpy data
type. Otherwise, the resulting numpy array has a compatible data
type with the given dtype. In either case above, the numpy ndarray (either the caller provided
or the auto converted) must have the compatible type with dtype. make_tensor_proto then converts the numpy array to a tensor proto. If "shape" is None, the resulting tensor proto represents the numpy
array precisely. Otherwise, "shape" specifies the tensor's shape and the numpy array
can not have more elements than what "shape" specifies.
Parameters
-
objectvalues - Values to put in the TensorProto.
-
DTypedtype - Optional tensor_pb2 DataType value.
-
TensorShapeshape - List of integers representing the dimensions of tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
-
boolallow_broadcast - Boolean that enables allowing scalars and 1 length vector broadcasting. Cannot be true when verify_shape is true.
Returns
-
object - A `TensorProto`. Depending on the type, it may contain data in the "tensor_content" attribute, which is not directly useful to Python programs. To access the values you should convert the proto back to a numpy ndarray with `tf.make_ndarray(proto)`. If `values` is a `TensorProto`, it is immediately returned; `dtype` and `shape` are ignored.
object make_tensor_proto(object values, PythonClassContainer dtype, IEnumerable<Nullable<int>> shape, bool verify_shape, bool allow_broadcast)
Create a TensorProto. In TensorFlow 2.0, representing tensors as protos should no longer be a
common workflow. That said, this utility function is still useful for
generating TF Serving request protos: request = tensorflow_serving.apis.predict_pb2.PredictRequest()
request.model_spec.name = "my_model"
request.model_spec.signature_name = "serving_default"
request.inputs["images"].CopyFrom(tf.make_tensor_proto(X_new)) make_tensor_proto accepts "values" of a python scalar, a python list, a
numpy ndarray, or a numpy scalar. If "values" is a python scalar or a python list, make_tensor_proto
first convert it to numpy ndarray. If dtype is None, the
conversion tries its best to infer the right numpy data
type. Otherwise, the resulting numpy array has a compatible data
type with the given dtype. In either case above, the numpy ndarray (either the caller provided
or the auto converted) must have the compatible type with dtype. make_tensor_proto then converts the numpy array to a tensor proto. If "shape" is None, the resulting tensor proto represents the numpy
array precisely. Otherwise, "shape" specifies the tensor's shape and the numpy array
can not have more elements than what "shape" specifies.
Parameters
-
objectvalues - Values to put in the TensorProto.
-
PythonClassContainerdtype - Optional tensor_pb2 DataType value.
-
IEnumerable<Nullable<int>>shape - List of integers representing the dimensions of tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
-
boolallow_broadcast - Boolean that enables allowing scalars and 1 length vector broadcasting. Cannot be true when verify_shape is true.
Returns
-
object - A `TensorProto`. Depending on the type, it may contain data in the "tensor_content" attribute, which is not directly useful to Python programs. To access the values you should convert the proto back to a numpy ndarray with `tf.make_ndarray(proto)`. If `values` is a `TensorProto`, it is immediately returned; `dtype` and `shape` are ignored.
object make_tensor_proto(object values, PythonClassContainer dtype, int shape, bool verify_shape, bool allow_broadcast)
Create a TensorProto. In TensorFlow 2.0, representing tensors as protos should no longer be a
common workflow. That said, this utility function is still useful for
generating TF Serving request protos: request = tensorflow_serving.apis.predict_pb2.PredictRequest()
request.model_spec.name = "my_model"
request.model_spec.signature_name = "serving_default"
request.inputs["images"].CopyFrom(tf.make_tensor_proto(X_new)) make_tensor_proto accepts "values" of a python scalar, a python list, a
numpy ndarray, or a numpy scalar. If "values" is a python scalar or a python list, make_tensor_proto
first convert it to numpy ndarray. If dtype is None, the
conversion tries its best to infer the right numpy data
type. Otherwise, the resulting numpy array has a compatible data
type with the given dtype. In either case above, the numpy ndarray (either the caller provided
or the auto converted) must have the compatible type with dtype. make_tensor_proto then converts the numpy array to a tensor proto. If "shape" is None, the resulting tensor proto represents the numpy
array precisely. Otherwise, "shape" specifies the tensor's shape and the numpy array
can not have more elements than what "shape" specifies.
Parameters
-
objectvalues - Values to put in the TensorProto.
-
PythonClassContainerdtype - Optional tensor_pb2 DataType value.
-
intshape - List of integers representing the dimensions of tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
-
boolallow_broadcast - Boolean that enables allowing scalars and 1 length vector broadcasting. Cannot be true when verify_shape is true.
Returns
-
object - A `TensorProto`. Depending on the type, it may contain data in the "tensor_content" attribute, which is not directly useful to Python programs. To access the values you should convert the proto back to a numpy ndarray with `tf.make_ndarray(proto)`. If `values` is a `TensorProto`, it is immediately returned; `dtype` and `shape` are ignored.
object make_tensor_proto(object values, PythonClassContainer dtype, TensorShape shape, bool verify_shape, bool allow_broadcast)
Create a TensorProto. In TensorFlow 2.0, representing tensors as protos should no longer be a
common workflow. That said, this utility function is still useful for
generating TF Serving request protos: request = tensorflow_serving.apis.predict_pb2.PredictRequest()
request.model_spec.name = "my_model"
request.model_spec.signature_name = "serving_default"
request.inputs["images"].CopyFrom(tf.make_tensor_proto(X_new)) make_tensor_proto accepts "values" of a python scalar, a python list, a
numpy ndarray, or a numpy scalar. If "values" is a python scalar or a python list, make_tensor_proto
first convert it to numpy ndarray. If dtype is None, the
conversion tries its best to infer the right numpy data
type. Otherwise, the resulting numpy array has a compatible data
type with the given dtype. In either case above, the numpy ndarray (either the caller provided
or the auto converted) must have the compatible type with dtype. make_tensor_proto then converts the numpy array to a tensor proto. If "shape" is None, the resulting tensor proto represents the numpy
array precisely. Otherwise, "shape" specifies the tensor's shape and the numpy array
can not have more elements than what "shape" specifies.
Parameters
-
objectvalues - Values to put in the TensorProto.
-
PythonClassContainerdtype - Optional tensor_pb2 DataType value.
-
TensorShapeshape - List of integers representing the dimensions of tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
-
boolallow_broadcast - Boolean that enables allowing scalars and 1 length vector broadcasting. Cannot be true when verify_shape is true.
Returns
-
object - A `TensorProto`. Depending on the type, it may contain data in the "tensor_content" attribute, which is not directly useful to Python programs. To access the values you should convert the proto back to a numpy ndarray with `tf.make_ndarray(proto)`. If `values` is a `TensorProto`, it is immediately returned; `dtype` and `shape` are ignored.
object make_tensor_proto(object values, DType dtype, int shape, bool verify_shape, bool allow_broadcast)
Create a TensorProto. In TensorFlow 2.0, representing tensors as protos should no longer be a
common workflow. That said, this utility function is still useful for
generating TF Serving request protos: request = tensorflow_serving.apis.predict_pb2.PredictRequest()
request.model_spec.name = "my_model"
request.model_spec.signature_name = "serving_default"
request.inputs["images"].CopyFrom(tf.make_tensor_proto(X_new)) make_tensor_proto accepts "values" of a python scalar, a python list, a
numpy ndarray, or a numpy scalar. If "values" is a python scalar or a python list, make_tensor_proto
first convert it to numpy ndarray. If dtype is None, the
conversion tries its best to infer the right numpy data
type. Otherwise, the resulting numpy array has a compatible data
type with the given dtype. In either case above, the numpy ndarray (either the caller provided
or the auto converted) must have the compatible type with dtype. make_tensor_proto then converts the numpy array to a tensor proto. If "shape" is None, the resulting tensor proto represents the numpy
array precisely. Otherwise, "shape" specifies the tensor's shape and the numpy array
can not have more elements than what "shape" specifies.
Parameters
-
objectvalues - Values to put in the TensorProto.
-
DTypedtype - Optional tensor_pb2 DataType value.
-
intshape - List of integers representing the dimensions of tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
-
boolallow_broadcast - Boolean that enables allowing scalars and 1 length vector broadcasting. Cannot be true when verify_shape is true.
Returns
-
object - A `TensorProto`. Depending on the type, it may contain data in the "tensor_content" attribute, which is not directly useful to Python programs. To access the values you should convert the proto back to a numpy ndarray with `tf.make_ndarray(proto)`. If `values` is a `TensorProto`, it is immediately returned; `dtype` and `shape` are ignored.
object make_tensor_proto(object values, DType dtype, IEnumerable<Nullable<int>> shape, bool verify_shape, bool allow_broadcast)
Create a TensorProto. In TensorFlow 2.0, representing tensors as protos should no longer be a
common workflow. That said, this utility function is still useful for
generating TF Serving request protos: request = tensorflow_serving.apis.predict_pb2.PredictRequest()
request.model_spec.name = "my_model"
request.model_spec.signature_name = "serving_default"
request.inputs["images"].CopyFrom(tf.make_tensor_proto(X_new)) make_tensor_proto accepts "values" of a python scalar, a python list, a
numpy ndarray, or a numpy scalar. If "values" is a python scalar or a python list, make_tensor_proto
first convert it to numpy ndarray. If dtype is None, the
conversion tries its best to infer the right numpy data
type. Otherwise, the resulting numpy array has a compatible data
type with the given dtype. In either case above, the numpy ndarray (either the caller provided
or the auto converted) must have the compatible type with dtype. make_tensor_proto then converts the numpy array to a tensor proto. If "shape" is None, the resulting tensor proto represents the numpy
array precisely. Otherwise, "shape" specifies the tensor's shape and the numpy array
can not have more elements than what "shape" specifies.
Parameters
-
objectvalues - Values to put in the TensorProto.
-
DTypedtype - Optional tensor_pb2 DataType value.
-
IEnumerable<Nullable<int>>shape - List of integers representing the dimensions of tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
-
boolallow_broadcast - Boolean that enables allowing scalars and 1 length vector broadcasting. Cannot be true when verify_shape is true.
Returns
-
object - A `TensorProto`. Depending on the type, it may contain data in the "tensor_content" attribute, which is not directly useful to Python programs. To access the values you should convert the proto back to a numpy ndarray with `tf.make_ndarray(proto)`. If `values` is a `TensorProto`, it is immediately returned; `dtype` and `shape` are ignored.
object make_tensor_proto(object values, DType dtype, Dimension shape, bool verify_shape, bool allow_broadcast)
Create a TensorProto. In TensorFlow 2.0, representing tensors as protos should no longer be a
common workflow. That said, this utility function is still useful for
generating TF Serving request protos: request = tensorflow_serving.apis.predict_pb2.PredictRequest()
request.model_spec.name = "my_model"
request.model_spec.signature_name = "serving_default"
request.inputs["images"].CopyFrom(tf.make_tensor_proto(X_new)) make_tensor_proto accepts "values" of a python scalar, a python list, a
numpy ndarray, or a numpy scalar. If "values" is a python scalar or a python list, make_tensor_proto
first convert it to numpy ndarray. If dtype is None, the
conversion tries its best to infer the right numpy data
type. Otherwise, the resulting numpy array has a compatible data
type with the given dtype. In either case above, the numpy ndarray (either the caller provided
or the auto converted) must have the compatible type with dtype. make_tensor_proto then converts the numpy array to a tensor proto. If "shape" is None, the resulting tensor proto represents the numpy
array precisely. Otherwise, "shape" specifies the tensor's shape and the numpy array
can not have more elements than what "shape" specifies.
Parameters
-
objectvalues - Values to put in the TensorProto.
-
DTypedtype - Optional tensor_pb2 DataType value.
-
Dimensionshape - List of integers representing the dimensions of tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
-
boolallow_broadcast - Boolean that enables allowing scalars and 1 length vector broadcasting. Cannot be true when verify_shape is true.
Returns
-
object - A `TensorProto`. Depending on the type, it may contain data in the "tensor_content" attribute, which is not directly useful to Python programs. To access the values you should convert the proto back to a numpy ndarray with `tf.make_ndarray(proto)`. If `values` is a `TensorProto`, it is immediately returned; `dtype` and `shape` are ignored.
object make_tensor_proto(object values, PythonClassContainer dtype, Dimension shape, bool verify_shape, bool allow_broadcast)
Create a TensorProto. In TensorFlow 2.0, representing tensors as protos should no longer be a
common workflow. That said, this utility function is still useful for
generating TF Serving request protos: request = tensorflow_serving.apis.predict_pb2.PredictRequest()
request.model_spec.name = "my_model"
request.model_spec.signature_name = "serving_default"
request.inputs["images"].CopyFrom(tf.make_tensor_proto(X_new)) make_tensor_proto accepts "values" of a python scalar, a python list, a
numpy ndarray, or a numpy scalar. If "values" is a python scalar or a python list, make_tensor_proto
first convert it to numpy ndarray. If dtype is None, the
conversion tries its best to infer the right numpy data
type. Otherwise, the resulting numpy array has a compatible data
type with the given dtype. In either case above, the numpy ndarray (either the caller provided
or the auto converted) must have the compatible type with dtype. make_tensor_proto then converts the numpy array to a tensor proto. If "shape" is None, the resulting tensor proto represents the numpy
array precisely. Otherwise, "shape" specifies the tensor's shape and the numpy array
can not have more elements than what "shape" specifies.
Parameters
-
objectvalues - Values to put in the TensorProto.
-
PythonClassContainerdtype - Optional tensor_pb2 DataType value.
-
Dimensionshape - List of integers representing the dimensions of tensor.
-
boolverify_shape - Boolean that enables verification of a shape of values.
-
boolallow_broadcast - Boolean that enables allowing scalars and 1 length vector broadcasting. Cannot be true when verify_shape is true.
Returns
-
object - A `TensorProto`. Depending on the type, it may contain data in the "tensor_content" attribute, which is not directly useful to Python programs. To access the values you should convert the proto back to a numpy ndarray with `tf.make_ndarray(proto)`. If `values` is a `TensorProto`, it is immediately returned; `dtype` and `shape` are ignored.
object make_tensor_proto_dyn(object values, object dtype, object shape, ImplicitContainer<T> verify_shape, ImplicitContainer<T> allow_broadcast)
Create a TensorProto. In TensorFlow 2.0, representing tensors as protos should no longer be a
common workflow. That said, this utility function is still useful for
generating TF Serving request protos: request = tensorflow_serving.apis.predict_pb2.PredictRequest()
request.model_spec.name = "my_model"
request.model_spec.signature_name = "serving_default"
request.inputs["images"].CopyFrom(tf.make_tensor_proto(X_new)) make_tensor_proto accepts "values" of a python scalar, a python list, a
numpy ndarray, or a numpy scalar. If "values" is a python scalar or a python list, make_tensor_proto
first convert it to numpy ndarray. If dtype is None, the
conversion tries its best to infer the right numpy data
type. Otherwise, the resulting numpy array has a compatible data
type with the given dtype. In either case above, the numpy ndarray (either the caller provided
or the auto converted) must have the compatible type with dtype. make_tensor_proto then converts the numpy array to a tensor proto. If "shape" is None, the resulting tensor proto represents the numpy
array precisely. Otherwise, "shape" specifies the tensor's shape and the numpy array
can not have more elements than what "shape" specifies.
Parameters
-
objectvalues - Values to put in the TensorProto.
-
objectdtype - Optional tensor_pb2 DataType value.
-
objectshape - List of integers representing the dimensions of tensor.
-
ImplicitContainer<T>verify_shape - Boolean that enables verification of a shape of values.
-
ImplicitContainer<T>allow_broadcast - Boolean that enables allowing scalars and 1 length vector broadcasting. Cannot be true when verify_shape is true.
Returns
-
object - A `TensorProto`. Depending on the type, it may contain data in the "tensor_content" attribute, which is not directly useful to Python programs. To access the values you should convert the proto back to a numpy ndarray with `tf.make_ndarray(proto)`. If `values` is a `TensorProto`, it is immediately returned; `dtype` and `shape` are ignored.
PythonFunctionContainer map_fn(PythonFunctionContainer fn, IGraphNodeBase elems, IEnumerable<DType> dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
IEnumerable<DType>dtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, int elems, DType dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
intelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
DTypedtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, IndexedSlices elems, DType dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
IndexedSliceselems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
DTypedtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, int elems, ValueTuple<DType, object> dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
intelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
ValueTuple<DType, object>dtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, ndarray elems, IEnumerable<DType> dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
IEnumerable<DType>dtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, int elems, IEnumerable<DType> dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
intelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
IEnumerable<DType>dtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, IEnumerable<int> elems, IEnumerable<DType> dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
IEnumerable<int>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
IEnumerable<DType>dtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, IndexedSlices elems, ValueTuple<DType, object> dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
IndexedSliceselems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
ValueTuple<DType, object>dtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, IndexedSlices elems, IEnumerable<DType> dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
IndexedSliceselems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
IEnumerable<DType>dtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, IGraphNodeBase elems, DType dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
DTypedtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, ndarray elems, ValueTuple<DType, object> dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
ValueTuple<DType, object>dtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, ndarray elems, DType dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
DTypedtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, IEnumerable<int> elems, DType dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
IEnumerable<int>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
DTypedtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, IGraphNodeBase elems, ValueTuple<DType, object> dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
ValueTuple<DType, object>dtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer map_fn(PythonFunctionContainer fn, IEnumerable<int> elems, ValueTuple<DType, object> dtype, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, string name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
IEnumerable<int>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
ValueTuple<DType, object>dtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
Nullable<int>parallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
PythonFunctionContainer - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
object map_fn_dyn(object fn, object elems, object dtype, object parallel_iterations, ImplicitContainer<T> back_prop, ImplicitContainer<T> swap_memory, ImplicitContainer<T> infer_shape, object name)
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Parameters
-
objectfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `dtype` if one is provided, otherwise it must have the same structure as `elems`.
-
objectelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be applied to `fn`.
-
objectdtype - (optional) The output type(s) of `fn`. If `fn` returns a structure of Tensors differing from the structure of `elems`, then `dtype` is not optional and must have the same structure as the output of `fn`.
-
objectparallel_iterations - (optional) The number of iterations allowed to run in parallel. When graph building, the default value is 10. While executing eagerly, the default value is set to 1.
-
ImplicitContainer<T>back_prop - (optional) True enables support for back propagation.
-
ImplicitContainer<T>swap_memory - (optional) True enables GPU-CPU memory swapping.
-
ImplicitContainer<T>infer_shape - (optional) False disables tests for consistent output shapes.
-
objectname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, from first to last.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
Tensor masked_matmul(IGraphNodeBase a, IGraphNodeBase b, IGraphNodeBase mask_indices, IGraphNodeBase transpose_a, IGraphNodeBase transpose_b, string name)
object masked_matmul_dyn(object a, object b, object mask_indices, object transpose_a, object transpose_b, object name)
Tensor matching_files(IGraphNodeBase pattern, string name)
Returns the set of files matching one or more glob patterns. Note that this routine only supports wildcard characters in the
basename portion of the pattern, not in the directory portion.
Note also that the order of filenames returned is deterministic.
Parameters
-
IGraphNodeBasepattern - A `Tensor` of type `string`. Shell wildcard pattern(s). Scalar or vector of type string.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `string`.
object matching_files_dyn(object pattern, object name)
Returns the set of files matching one or more glob patterns. Note that this routine only supports wildcard characters in the
basename portion of the pattern, not in the directory portion.
Note also that the order of filenames returned is deterministic.
Parameters
-
objectpattern - A `Tensor` of type `string`. Shell wildcard pattern(s). Scalar or vector of type string.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `string`.
Tensor matmul(PythonClassContainer a, PythonClassContainer b, bool transpose_a, IGraphNodeBase transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
PythonClassContainera - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
PythonClassContainerb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
IGraphNodeBasetranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(PythonClassContainer a, object b, bool transpose_a, IGraphNodeBase transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
PythonClassContainera - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
objectb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
IGraphNodeBasetranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(object a, PythonClassContainer b, bool transpose_a, bool transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
objecta - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
PythonClassContainerb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
booltranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(IEnumerable<IGraphNodeBase> a, IEnumerable<IGraphNodeBase> b, bool transpose_a, bool transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
IEnumerable<IGraphNodeBase>b - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
booltranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(IEnumerable<IGraphNodeBase> a, PythonClassContainer b, bool transpose_a, IGraphNodeBase transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
PythonClassContainerb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
IGraphNodeBasetranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(object a, PythonClassContainer b, bool transpose_a, IGraphNodeBase transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
objecta - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
PythonClassContainerb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
IGraphNodeBasetranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(object a, object b, bool transpose_a, bool transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
objecta - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
objectb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
booltranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(PythonClassContainer a, IEnumerable<IGraphNodeBase> b, bool transpose_a, bool transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
PythonClassContainera - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
IEnumerable<IGraphNodeBase>b - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
booltranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(PythonClassContainer a, object b, bool transpose_a, bool transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
PythonClassContainera - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
objectb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
booltranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(PythonClassContainer a, PythonClassContainer b, bool transpose_a, bool transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
PythonClassContainera - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
PythonClassContainerb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
booltranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(IEnumerable<IGraphNodeBase> a, object b, bool transpose_a, IGraphNodeBase transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
objectb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
IGraphNodeBasetranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(object a, object b, bool transpose_a, IGraphNodeBase transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
objecta - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
objectb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
IGraphNodeBasetranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(IEnumerable<IGraphNodeBase> a, object b, bool transpose_a, bool transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
objectb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
booltranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(IEnumerable<IGraphNodeBase> a, IEnumerable<IGraphNodeBase> b, bool transpose_a, IGraphNodeBase transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
IEnumerable<IGraphNodeBase>b - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
IGraphNodeBasetranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(object a, IEnumerable<IGraphNodeBase> b, bool transpose_a, bool transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
objecta - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
IEnumerable<IGraphNodeBase>b - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
booltranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(PythonClassContainer a, IEnumerable<IGraphNodeBase> b, bool transpose_a, IGraphNodeBase transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
PythonClassContainera - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
IEnumerable<IGraphNodeBase>b - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
IGraphNodeBasetranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(IEnumerable<IGraphNodeBase> a, PythonClassContainer b, bool transpose_a, bool transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
PythonClassContainerb - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
booltranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matmul(object a, IEnumerable<IGraphNodeBase> b, bool transpose_a, IGraphNodeBase transpose_b, Nullable<bool> adjoint_a, Nullable<bool> adjoint_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
objecta - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
IEnumerable<IGraphNodeBase>b - `Tensor` with same type and rank as `a`.
-
booltranspose_a - If `True`, `a` is transposed before multiplication.
-
IGraphNodeBasetranspose_b - If `True`, `b` is transposed before multiplication.
-
Nullable<bool>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
Nullable<bool>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
boola_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
boolb_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
stringname - Name for the operation (optional).
Returns
-
Tensor - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
object matmul_dyn(object a, object b, ImplicitContainer<T> transpose_a, ImplicitContainer<T> transpose_b, ImplicitContainer<T> adjoint_a, ImplicitContainer<T> adjoint_b, ImplicitContainer<T> a_is_sparse, ImplicitContainer<T> b_is_sparse, object name)
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Parameters
-
objecta - `Tensor` of type `float16`, `float32`, `float64`, `int32`, `complex64`, `complex128` and rank > 1.
-
objectb - `Tensor` with same type and rank as `a`.
-
ImplicitContainer<T>transpose_a - If `True`, `a` is transposed before multiplication.
-
ImplicitContainer<T>transpose_b - If `True`, `b` is transposed before multiplication.
-
ImplicitContainer<T>adjoint_a - If `True`, `a` is conjugated and transposed before multiplication.
-
ImplicitContainer<T>adjoint_b - If `True`, `b` is conjugated and transposed before multiplication.
-
ImplicitContainer<T>a_is_sparse - If `True`, `a` is treated as a sparse matrix.
-
ImplicitContainer<T>b_is_sparse - If `True`, `b` is treated as a sparse matrix.
-
objectname - Name for the operation (optional).
Returns
-
object - A `Tensor` of the same type as `a` and `b` where each inner-most matrix is the product of the corresponding matrices in `a` and `b`, e.g. if all transpose or adjoint attributes are `False`: `output`[..., i, j] = sum_k (`a`[..., i, k] * `b`[..., k, j]), for all indices i, j.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
Tensor matrix_band_part(IGraphNodeBase input, IGraphNodeBase num_lower, IGraphNodeBase num_upper, string name)
Copy a tensor setting everything outside a central band in each innermost matrix to zero. The `band` part is computed as follows:
Assume `input` has `k` dimensions `[I, J, K,..., M, N]`, then the output is a
tensor with the same shape where `band[i, j, k,..., m, n] = in_band(m, n) * input[i, j, k,..., m, n]`. The indicator function `in_band(m, n) = (num_lower < 0 || (m-n) <= num_lower)) &&
(num_upper < 0 || (n-m) <= num_upper)`. For example: ```
# if 'input' is [[ 0, 1, 2, 3]
[-1, 0, 1, 2]
[-2, -1, 0, 1]
[-3, -2, -1, 0]], tf.matrix_band_part(input, 1, -1) ==> [[ 0, 1, 2, 3]
[-1, 0, 1, 2]
[ 0, -1, 0, 1]
[ 0, 0, -1, 0]], tf.matrix_band_part(input, 2, 1) ==> [[ 0, 1, 0, 0]
[-1, 0, 1, 0]
[-2, -1, 0, 1]
[ 0, -2, -1, 0]]
``` Useful special cases: ```
tf.matrix_band_part(input, 0, -1) ==> Upper triangular part.
tf.matrix_band_part(input, -1, 0) ==> Lower triangular part.
tf.matrix_band_part(input, 0, 0) ==> Diagonal.
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Rank `k` tensor.
-
IGraphNodeBasenum_lower - A `Tensor`. Must be one of the following types: `int32`, `int64`. 0-D tensor. Number of subdiagonals to keep. If negative, keep entire lower triangle.
-
IGraphNodeBasenum_upper - A `Tensor`. Must have the same type as `num_lower`. 0-D tensor. Number of superdiagonals to keep. If negative, keep entire upper triangle.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object matrix_band_part_dyn(object input, object num_lower, object num_upper, object name)
Copy a tensor setting everything outside a central band in each innermost matrix to zero. The `band` part is computed as follows:
Assume `input` has `k` dimensions `[I, J, K,..., M, N]`, then the output is a
tensor with the same shape where `band[i, j, k,..., m, n] = in_band(m, n) * input[i, j, k,..., m, n]`. The indicator function `in_band(m, n) = (num_lower < 0 || (m-n) <= num_lower)) &&
(num_upper < 0 || (n-m) <= num_upper)`. For example: ```
# if 'input' is [[ 0, 1, 2, 3]
[-1, 0, 1, 2]
[-2, -1, 0, 1]
[-3, -2, -1, 0]], tf.matrix_band_part(input, 1, -1) ==> [[ 0, 1, 2, 3]
[-1, 0, 1, 2]
[ 0, -1, 0, 1]
[ 0, 0, -1, 0]], tf.matrix_band_part(input, 2, 1) ==> [[ 0, 1, 0, 0]
[-1, 0, 1, 0]
[-2, -1, 0, 1]
[ 0, -2, -1, 0]]
``` Useful special cases: ```
tf.matrix_band_part(input, 0, -1) ==> Upper triangular part.
tf.matrix_band_part(input, -1, 0) ==> Lower triangular part.
tf.matrix_band_part(input, 0, 0) ==> Diagonal.
```
Parameters
-
objectinput - A `Tensor`. Rank `k` tensor.
-
objectnum_lower - A `Tensor`. Must be one of the following types: `int32`, `int64`. 0-D tensor. Number of subdiagonals to keep. If negative, keep entire lower triangle.
-
objectnum_upper - A `Tensor`. Must have the same type as `num_lower`. 0-D tensor. Number of superdiagonals to keep. If negative, keep entire upper triangle.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor matrix_determinant(IGraphNodeBase input, string name)
Computes the determinant of one or more square matrices. The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The output is a tensor containing the determinants
for all input submatrices `[..., :, :]`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `half`, `float32`, `float64`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object matrix_determinant_dyn(object input, object name)
Computes the determinant of one or more square matrices. The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The output is a tensor containing the determinants
for all input submatrices `[..., :, :]`.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `half`, `float32`, `float64`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor matrix_diag(IGraphNodeBase diagonal, string name, IEnumerable<int> k, int num_rows, int num_cols, int padding_value)
Returns a batched diagonal tensor with given batched diagonal values. Returns a tensor with the contents in `diagonal` as `k[0]`-th to `k[1]`-th
diagonals of a matrix, with everything else padded with `padding`. `num_rows`
and `num_cols` specify the dimension of the innermost matrix of the output. If
both are not specified, the op assumes the innermost matrix is square and
infers its size from `k` and the innermost dimension of `diagonal`. If only
one of them is specified, the op assumes the unspecified value is the smallest
possible based on other criteria. Let `diagonal` have `r` dimensions `[I, J,..., L, M, N]`. The output tensor
has rank `r+1` with shape `[I, J,..., L, M, num_rows, num_cols]` when only
one diagonal is given (`k` is an integer or `k[0] == k[1]`). Otherwise, it has
rank `r` with shape `[I, J,..., L, num_rows, num_cols]`. The second innermost dimension of `diagonal` has double meaning. When `k` is
scalar or `k[0] == k[1]`, `M` is part of the batch size [I, J,..., M], and
the output tensor is: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(d_upper, 0)] ; if n - m == d_upper
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, `M` is treated as the number of diagonals for the matrix in the
same batch (`M = k[1]-k[0]+1`), and the output tensor is: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
diagonal = np.array([[1, 2, 3, 4], # Input shape: (2, 4)
[5, 6, 7, 8]])
tf.matrix_diag(diagonal) ==> [[[1, 0, 0, 0], # Output shape: (2, 4, 4)
[0, 2, 0, 0],
[0, 0, 3, 0],
[0, 0, 0, 4]],
[[5, 0, 0, 0],
[0, 6, 0, 0],
[0, 0, 7, 0],
[0, 0, 0, 8]]] # A superdiagonal (per batch).
diagonal = np.array([[1, 2, 3], # Input shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal, k = 1)
==> [[[0, 1, 0, 0], # Output shape: (2, 4, 4)
[0, 0, 2, 0],
[0, 0, 0, 3],
[0, 0, 0, 0]],
[[0, 4, 0, 0],
[0, 0, 5, 0],
[0, 0, 0, 6],
[0, 0, 0, 0]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Input shape: (2, 2, 3)
[4, 5, 0]],
[[6, 7, 9],
[9, 1, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 0, 0], # Output shape: (2, 3, 3)
[4, 2, 0],
[0, 5, 3]],
[[6, 0, 0],
[9, 7, 0],
[0, 1, 9]]] # Rectangular matrix.
diagonal = np.array([1, 2]) # Input shape: (2)
tf.matrix_diag(diagonal, k = -1, num_rows = 3, num_cols = 4)
==> [[0, 0, 0, 0], # Output shape: (3, 4)
[1, 0, 0, 0],
[0, 2, 0, 0]] # Rectangular matrix with inferred num_cols and padding = 9.
tf.matrix_diag(diagonal, k = -1, num_rows = 3, padding = 9)
==> [[9, 9], # Output shape: (3, 2)
[1, 9],
[9, 2]]
```
Parameters
-
IGraphNodeBasediagonal - A `Tensor` with `rank k >= 1`.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
-
intnum_rows - The number of rows of the output matrix. If it is not provided, the op assumes the output matrix is a square matrix and infers the matrix size from `d_lower`, `d_upper`, and the innermost dimension of `diagonal`.
-
intnum_cols - The number of columns of the output matrix. If it is not provided, the op assumes the output matrix is a square matrix and infers the matrix size from `d_lower`, `d_upper`, and the innermost dimension of `diagonal`.
-
intpadding_value - The value to fill the area outside the specified diagonal band with. Default is 0.
Returns
-
Tensor - A Tensor. Has the same type as `diagonal`.
Tensor matrix_diag(IGraphNodeBase diagonal, string name, int k, int num_rows, int num_cols, int padding_value)
Returns a batched diagonal tensor with given batched diagonal values. Returns a tensor with the contents in `diagonal` as `k[0]`-th to `k[1]`-th
diagonals of a matrix, with everything else padded with `padding`. `num_rows`
and `num_cols` specify the dimension of the innermost matrix of the output. If
both are not specified, the op assumes the innermost matrix is square and
infers its size from `k` and the innermost dimension of `diagonal`. If only
one of them is specified, the op assumes the unspecified value is the smallest
possible based on other criteria. Let `diagonal` have `r` dimensions `[I, J,..., L, M, N]`. The output tensor
has rank `r+1` with shape `[I, J,..., L, M, num_rows, num_cols]` when only
one diagonal is given (`k` is an integer or `k[0] == k[1]`). Otherwise, it has
rank `r` with shape `[I, J,..., L, num_rows, num_cols]`. The second innermost dimension of `diagonal` has double meaning. When `k` is
scalar or `k[0] == k[1]`, `M` is part of the batch size [I, J,..., M], and
the output tensor is: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(d_upper, 0)] ; if n - m == d_upper
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, `M` is treated as the number of diagonals for the matrix in the
same batch (`M = k[1]-k[0]+1`), and the output tensor is: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
diagonal = np.array([[1, 2, 3, 4], # Input shape: (2, 4)
[5, 6, 7, 8]])
tf.matrix_diag(diagonal) ==> [[[1, 0, 0, 0], # Output shape: (2, 4, 4)
[0, 2, 0, 0],
[0, 0, 3, 0],
[0, 0, 0, 4]],
[[5, 0, 0, 0],
[0, 6, 0, 0],
[0, 0, 7, 0],
[0, 0, 0, 8]]] # A superdiagonal (per batch).
diagonal = np.array([[1, 2, 3], # Input shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal, k = 1)
==> [[[0, 1, 0, 0], # Output shape: (2, 4, 4)
[0, 0, 2, 0],
[0, 0, 0, 3],
[0, 0, 0, 0]],
[[0, 4, 0, 0],
[0, 0, 5, 0],
[0, 0, 0, 6],
[0, 0, 0, 0]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Input shape: (2, 2, 3)
[4, 5, 0]],
[[6, 7, 9],
[9, 1, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 0, 0], # Output shape: (2, 3, 3)
[4, 2, 0],
[0, 5, 3]],
[[6, 0, 0],
[9, 7, 0],
[0, 1, 9]]] # Rectangular matrix.
diagonal = np.array([1, 2]) # Input shape: (2)
tf.matrix_diag(diagonal, k = -1, num_rows = 3, num_cols = 4)
==> [[0, 0, 0, 0], # Output shape: (3, 4)
[1, 0, 0, 0],
[0, 2, 0, 0]] # Rectangular matrix with inferred num_cols and padding = 9.
tf.matrix_diag(diagonal, k = -1, num_rows = 3, padding = 9)
==> [[9, 9], # Output shape: (3, 2)
[1, 9],
[9, 2]]
```
Parameters
-
IGraphNodeBasediagonal - A `Tensor` with `rank k >= 1`.
-
stringname - A name for the operation (optional).
-
intk - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
-
intnum_rows - The number of rows of the output matrix. If it is not provided, the op assumes the output matrix is a square matrix and infers the matrix size from `d_lower`, `d_upper`, and the innermost dimension of `diagonal`.
-
intnum_cols - The number of columns of the output matrix. If it is not provided, the op assumes the output matrix is a square matrix and infers the matrix size from `d_lower`, `d_upper`, and the innermost dimension of `diagonal`.
-
intpadding_value - The value to fill the area outside the specified diagonal band with. Default is 0.
Returns
-
Tensor - A Tensor. Has the same type as `diagonal`.
object matrix_diag_dyn(object diagonal, ImplicitContainer<T> name, ImplicitContainer<T> k, ImplicitContainer<T> num_rows, ImplicitContainer<T> num_cols, ImplicitContainer<T> padding_value)
Returns a batched diagonal tensor with given batched diagonal values. Returns a tensor with the contents in `diagonal` as `k[0]`-th to `k[1]`-th
diagonals of a matrix, with everything else padded with `padding`. `num_rows`
and `num_cols` specify the dimension of the innermost matrix of the output. If
both are not specified, the op assumes the innermost matrix is square and
infers its size from `k` and the innermost dimension of `diagonal`. If only
one of them is specified, the op assumes the unspecified value is the smallest
possible based on other criteria. Let `diagonal` have `r` dimensions `[I, J,..., L, M, N]`. The output tensor
has rank `r+1` with shape `[I, J,..., L, M, num_rows, num_cols]` when only
one diagonal is given (`k` is an integer or `k[0] == k[1]`). Otherwise, it has
rank `r` with shape `[I, J,..., L, num_rows, num_cols]`. The second innermost dimension of `diagonal` has double meaning. When `k` is
scalar or `k[0] == k[1]`, `M` is part of the batch size [I, J,..., M], and
the output tensor is: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(d_upper, 0)] ; if n - m == d_upper
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, `M` is treated as the number of diagonals for the matrix in the
same batch (`M = k[1]-k[0]+1`), and the output tensor is: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
diagonal = np.array([[1, 2, 3, 4], # Input shape: (2, 4)
[5, 6, 7, 8]])
tf.matrix_diag(diagonal) ==> [[[1, 0, 0, 0], # Output shape: (2, 4, 4)
[0, 2, 0, 0],
[0, 0, 3, 0],
[0, 0, 0, 4]],
[[5, 0, 0, 0],
[0, 6, 0, 0],
[0, 0, 7, 0],
[0, 0, 0, 8]]] # A superdiagonal (per batch).
diagonal = np.array([[1, 2, 3], # Input shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal, k = 1)
==> [[[0, 1, 0, 0], # Output shape: (2, 4, 4)
[0, 0, 2, 0],
[0, 0, 0, 3],
[0, 0, 0, 0]],
[[0, 4, 0, 0],
[0, 0, 5, 0],
[0, 0, 0, 6],
[0, 0, 0, 0]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Input shape: (2, 2, 3)
[4, 5, 0]],
[[6, 7, 9],
[9, 1, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 0, 0], # Output shape: (2, 3, 3)
[4, 2, 0],
[0, 5, 3]],
[[6, 0, 0],
[9, 7, 0],
[0, 1, 9]]] # Rectangular matrix.
diagonal = np.array([1, 2]) # Input shape: (2)
tf.matrix_diag(diagonal, k = -1, num_rows = 3, num_cols = 4)
==> [[0, 0, 0, 0], # Output shape: (3, 4)
[1, 0, 0, 0],
[0, 2, 0, 0]] # Rectangular matrix with inferred num_cols and padding = 9.
tf.matrix_diag(diagonal, k = -1, num_rows = 3, padding = 9)
==> [[9, 9], # Output shape: (3, 2)
[1, 9],
[9, 2]]
```
Parameters
-
objectdiagonal - A `Tensor` with `rank k >= 1`.
-
ImplicitContainer<T>name - A name for the operation (optional).
-
ImplicitContainer<T>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
-
ImplicitContainer<T>num_rows - The number of rows of the output matrix. If it is not provided, the op assumes the output matrix is a square matrix and infers the matrix size from `d_lower`, `d_upper`, and the innermost dimension of `diagonal`.
-
ImplicitContainer<T>num_cols - The number of columns of the output matrix. If it is not provided, the op assumes the output matrix is a square matrix and infers the matrix size from `d_lower`, `d_upper`, and the innermost dimension of `diagonal`.
-
ImplicitContainer<T>padding_value - The value to fill the area outside the specified diagonal band with. Default is 0.
Returns
-
object - A Tensor. Has the same type as `diagonal`.
Tensor matrix_diag_part(IGraphNodeBase input, string name, ValueTuple<int, object> k, int padding_value)
Returns the batched diagonal part of a batched tensor. Returns a tensor with the `k[0]`-th to `k[1]`-th diagonals of the batched
`input`. Assume `input` has `r` dimensions `[I, J,..., L, M, N]`.
Let `max_diag_len` be the maximum length among all diagonals to be extracted,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))`
Let `num_diags` be the number of diagonals to extract,
`num_diags = k[1] - k[0] + 1`. If `num_diags == 1`, the output tensor is of rank `r - 1` with shape
`[I, J,..., L, max_diag_len]` and values: ```
diagonal[i, j,..., l, n]
= input[i, j,..., l, n+y, n+x] ; when 0 <= n-y < M and 0 <= n-x < N,
0 ; otherwise.
```
where `y = max(-k[1], 0)`, `x = max(k[1], 0)`. Otherwise, the output tensor has rank `r` with dimensions
`[I, J,..., L, num_diags, max_diag_len]` with values: ```
diagonal[i, j,..., l, m, n]
= input[i, j,..., l, n+y, n+x] ; when 0 <= n-y < M and 0 <= n-x < N,
0 ; otherwise.
```
where `d = k[1] - m`, `y = max(-d, 0)`, and `x = max(d, 0)`. The input must be at least a matrix. For example: ```
input = np.array([[[1, 2, 3, 4], # Input shape: (2, 3, 4)
[5, 6, 7, 8],
[9, 8, 7, 6]],
[[5, 4, 3, 2],
[1, 2, 3, 4],
[5, 6, 7, 8]]]) # A main diagonal from each batch.
tf.matrix_diag_part(input) ==> [[1, 6, 7], # Output shape: (2, 3)
[5, 2, 7]] # A superdiagonal from each batch.
tf.matrix_diag_part(input, k = 1)
==> [[2, 7, 6], # Output shape: (2, 3)
[4, 3, 8]] # A tridiagonal band from each batch.
tf.matrix_diag_part(input, k = (-1, 1))
==> [[[2, 7, 6], # Output shape: (2, 3, 3)
[1, 6, 7],
[5, 8, 0]],
[[4, 3, 8],
[5, 2, 7],
[1, 6, 0]]] # Padding = 9
tf.matrix_diag_part(input, k = (1, 3), padding = 9)
==> [[[4, 9, 9], # Output shape: (2, 3, 3)
[3, 8, 9],
[2, 7, 6]],
[[2, 9, 9],
[3, 4, 9],
[4, 3, 8]]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with `rank k >= 2`.
-
stringname - A name for the operation (optional).
-
ValueTuple<int, object>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
-
intpadding_value - The value to fill the area outside the specified diagonal band with. Default is 0.
Returns
-
Tensor - A Tensor containing diagonals of `input`. Has the same type as `input`.
Tensor matrix_diag_part(IGraphNodeBase input, string name, int k, int padding_value)
Returns the batched diagonal part of a batched tensor. Returns a tensor with the `k[0]`-th to `k[1]`-th diagonals of the batched
`input`. Assume `input` has `r` dimensions `[I, J,..., L, M, N]`.
Let `max_diag_len` be the maximum length among all diagonals to be extracted,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))`
Let `num_diags` be the number of diagonals to extract,
`num_diags = k[1] - k[0] + 1`. If `num_diags == 1`, the output tensor is of rank `r - 1` with shape
`[I, J,..., L, max_diag_len]` and values: ```
diagonal[i, j,..., l, n]
= input[i, j,..., l, n+y, n+x] ; when 0 <= n-y < M and 0 <= n-x < N,
0 ; otherwise.
```
where `y = max(-k[1], 0)`, `x = max(k[1], 0)`. Otherwise, the output tensor has rank `r` with dimensions
`[I, J,..., L, num_diags, max_diag_len]` with values: ```
diagonal[i, j,..., l, m, n]
= input[i, j,..., l, n+y, n+x] ; when 0 <= n-y < M and 0 <= n-x < N,
0 ; otherwise.
```
where `d = k[1] - m`, `y = max(-d, 0)`, and `x = max(d, 0)`. The input must be at least a matrix. For example: ```
input = np.array([[[1, 2, 3, 4], # Input shape: (2, 3, 4)
[5, 6, 7, 8],
[9, 8, 7, 6]],
[[5, 4, 3, 2],
[1, 2, 3, 4],
[5, 6, 7, 8]]]) # A main diagonal from each batch.
tf.matrix_diag_part(input) ==> [[1, 6, 7], # Output shape: (2, 3)
[5, 2, 7]] # A superdiagonal from each batch.
tf.matrix_diag_part(input, k = 1)
==> [[2, 7, 6], # Output shape: (2, 3)
[4, 3, 8]] # A tridiagonal band from each batch.
tf.matrix_diag_part(input, k = (-1, 1))
==> [[[2, 7, 6], # Output shape: (2, 3, 3)
[1, 6, 7],
[5, 8, 0]],
[[4, 3, 8],
[5, 2, 7],
[1, 6, 0]]] # Padding = 9
tf.matrix_diag_part(input, k = (1, 3), padding = 9)
==> [[[4, 9, 9], # Output shape: (2, 3, 3)
[3, 8, 9],
[2, 7, 6]],
[[2, 9, 9],
[3, 4, 9],
[4, 3, 8]]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with `rank k >= 2`.
-
stringname - A name for the operation (optional).
-
intk - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
-
intpadding_value - The value to fill the area outside the specified diagonal band with. Default is 0.
Returns
-
Tensor - A Tensor containing diagonals of `input`. Has the same type as `input`.
object matrix_diag_part_dyn(object input, ImplicitContainer<T> name, ImplicitContainer<T> k, ImplicitContainer<T> padding_value)
Returns the batched diagonal part of a batched tensor. Returns a tensor with the `k[0]`-th to `k[1]`-th diagonals of the batched
`input`. Assume `input` has `r` dimensions `[I, J,..., L, M, N]`.
Let `max_diag_len` be the maximum length among all diagonals to be extracted,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))`
Let `num_diags` be the number of diagonals to extract,
`num_diags = k[1] - k[0] + 1`. If `num_diags == 1`, the output tensor is of rank `r - 1` with shape
`[I, J,..., L, max_diag_len]` and values: ```
diagonal[i, j,..., l, n]
= input[i, j,..., l, n+y, n+x] ; when 0 <= n-y < M and 0 <= n-x < N,
0 ; otherwise.
```
where `y = max(-k[1], 0)`, `x = max(k[1], 0)`. Otherwise, the output tensor has rank `r` with dimensions
`[I, J,..., L, num_diags, max_diag_len]` with values: ```
diagonal[i, j,..., l, m, n]
= input[i, j,..., l, n+y, n+x] ; when 0 <= n-y < M and 0 <= n-x < N,
0 ; otherwise.
```
where `d = k[1] - m`, `y = max(-d, 0)`, and `x = max(d, 0)`. The input must be at least a matrix. For example: ```
input = np.array([[[1, 2, 3, 4], # Input shape: (2, 3, 4)
[5, 6, 7, 8],
[9, 8, 7, 6]],
[[5, 4, 3, 2],
[1, 2, 3, 4],
[5, 6, 7, 8]]]) # A main diagonal from each batch.
tf.matrix_diag_part(input) ==> [[1, 6, 7], # Output shape: (2, 3)
[5, 2, 7]] # A superdiagonal from each batch.
tf.matrix_diag_part(input, k = 1)
==> [[2, 7, 6], # Output shape: (2, 3)
[4, 3, 8]] # A tridiagonal band from each batch.
tf.matrix_diag_part(input, k = (-1, 1))
==> [[[2, 7, 6], # Output shape: (2, 3, 3)
[1, 6, 7],
[5, 8, 0]],
[[4, 3, 8],
[5, 2, 7],
[1, 6, 0]]] # Padding = 9
tf.matrix_diag_part(input, k = (1, 3), padding = 9)
==> [[[4, 9, 9], # Output shape: (2, 3, 3)
[3, 8, 9],
[2, 7, 6]],
[[2, 9, 9],
[3, 4, 9],
[4, 3, 8]]]
```
Parameters
-
objectinput - A `Tensor` with `rank k >= 2`.
-
ImplicitContainer<T>name - A name for the operation (optional).
-
ImplicitContainer<T>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
-
ImplicitContainer<T>padding_value - The value to fill the area outside the specified diagonal band with. Default is 0.
Returns
-
object - A Tensor containing diagonals of `input`. Has the same type as `input`.
Tensor matrix_inverse(IGraphNodeBase input, bool adjoint, string name)
Computes the inverse of one or more square invertible matrices or their adjoints (conjugate transposes). The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The output is a tensor of the same shape as the input
containing the inverse for all input submatrices `[..., :, :]`. The op uses LU decomposition with partial pivoting to compute the inverses. If a matrix is not invertible there is no guarantee what the op does. It
may detect the condition and raise an exception or it may simply return a
garbage result.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
booladjoint - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object matrix_inverse_dyn(object input, ImplicitContainer<T> adjoint, object name)
Computes the inverse of one or more square invertible matrices or their adjoints (conjugate transposes). The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The output is a tensor of the same shape as the input
containing the inverse for all input submatrices `[..., :, :]`. The op uses LU decomposition with partial pivoting to compute the inverses. If a matrix is not invertible there is no guarantee what the op does. It
may detect the condition and raise an exception or it may simply return a
garbage result.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
ImplicitContainer<T>adjoint - An optional `bool`. Defaults to `False`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor matrix_set_diag(IGraphNodeBase input, IndexedSlices diagonal, string name, ValueTuple<int, object> k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
IndexedSlicesdiagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
ValueTuple<int, object>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, ndarray diagonal, string name, int k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
ndarraydiagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
intk - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, IGraphNodeBase diagonal, string name, int k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
IGraphNodeBasediagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
intk - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, object diagonal, string name, ValueTuple<int, object> k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
objectdiagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
ValueTuple<int, object>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, IGraphNodeBase diagonal, string name, ValueTuple<int, object> k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
IGraphNodeBasediagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
ValueTuple<int, object>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, int diagonal, string name, int k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
intdiagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
intk - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, object diagonal, string name, int k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
objectdiagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
intk - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, IEnumerable<IGraphNodeBase> diagonal, string name, int k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
IEnumerable<IGraphNodeBase>diagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
intk - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, ndarray diagonal, string name, ValueTuple<int, object> k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
ndarraydiagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
ValueTuple<int, object>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, IndexedSlices diagonal, string name, int k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
IndexedSlicesdiagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
intk - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, int diagonal, string name, ValueTuple<int, object> k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
intdiagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
ValueTuple<int, object>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_set_diag(IGraphNodeBase input, IEnumerable<IGraphNodeBase> diagonal, string name, ValueTuple<int, object> k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
IGraphNodeBaseinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
IEnumerable<IGraphNodeBase>diagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
stringname - A name for the operation (optional).
-
ValueTuple<int, object>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
object matrix_set_diag_dyn(object input, object diagonal, ImplicitContainer<T> name, ImplicitContainer<T> k)
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
Parameters
-
objectinput - A `Tensor` with rank `k + 1`, where `k >= 1`.
-
objectdiagonal - A `Tensor` with rank `k`, when `d_lower == d_upper`, or `k + 1`, otherwise. `k >= 1`.
-
ImplicitContainer<T>name - A name for the operation (optional).
-
ImplicitContainer<T>k - Diagonal offset(s). Positive value means superdiagonal, 0 refers to the main diagonal, and negative value means subdiagonals. `k` can be a single integer (for a single diagonal) or a pair of integers specifying the low and high ends of a matrix band. `k[0]` must not be larger than `k[1]`.
Tensor matrix_solve(IGraphNodeBase matrix, IGraphNodeBase rhs, bool adjoint, string name)
Solves systems of linear equations. `Matrix` is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. `Rhs` is a tensor of shape `[..., M, K]`. The `output` is
a tensor shape `[..., M, K]`. If `adjoint` is `False` then each output matrix
satisfies `matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]`.
If `adjoint` is `True` then each output matrix satisfies
`adjoint(matrix[..., :, :]) * output[..., :, :] = rhs[..., :, :]`.
Parameters
-
IGraphNodeBasematrix - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
IGraphNodeBaserhs - A `Tensor`. Must have the same type as `matrix`. Shape is `[..., M, K]`.
-
booladjoint - An optional `bool`. Defaults to `False`. Boolean indicating whether to solve with `matrix` or its (block-wise) adjoint.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `matrix`.
object matrix_solve_dyn(object matrix, object rhs, ImplicitContainer<T> adjoint, object name)
Solves systems of linear equations. `Matrix` is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. `Rhs` is a tensor of shape `[..., M, K]`. The `output` is
a tensor shape `[..., M, K]`. If `adjoint` is `False` then each output matrix
satisfies `matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]`.
If `adjoint` is `True` then each output matrix satisfies
`adjoint(matrix[..., :, :]) * output[..., :, :] = rhs[..., :, :]`.
Parameters
-
objectmatrix - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
objectrhs - A `Tensor`. Must have the same type as `matrix`. Shape is `[..., M, K]`.
-
ImplicitContainer<T>adjoint - An optional `bool`. Defaults to `False`. Boolean indicating whether to solve with `matrix` or its (block-wise) adjoint.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `matrix`.
Tensor matrix_solve_ls(IGraphNodeBase matrix, ndarray rhs, double l2_regularizer, bool fast, string name)
Solves one or more linear least-squares problems. `matrix` is a tensor of shape `[..., M, N]` whose inner-most 2 dimensions
form `M`-by-`N` matrices. Rhs is a tensor of shape `[..., M, K]` whose
inner-most 2 dimensions form `M`-by-`K` matrices. The computed output is a
`Tensor` of shape `[..., N, K]` whose inner-most 2 dimensions form `M`-by-`K`
matrices that solve the equations
`matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]` in the least squares
sense. Below we will use the following notation for each pair of matrix and
right-hand sides in the batch: `matrix`=\\(A \in \Re^{m \times n}\\),
`rhs`=\\(B \in \Re^{m \times k}\\),
`output`=\\(X \in \Re^{n \times k}\\),
`l2_regularizer`=\\(\lambda\\). If `fast` is `True`, then the solution is computed by solving the normal
equations using Cholesky decomposition. Specifically, if \\(m \ge n\\) then
\\(X = (A^T A + \lambda I)^{-1} A^T B\\), which solves the least-squares
problem \\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||A Z - B||_F^2 +
\lambda ||Z||_F^2\\). If \\(m \lt n\\) then `output` is computed as
\\(X = A^T (A A^T + \lambda I)^{-1} B\\), which (for \\(\lambda = 0\\)) is
the minimum-norm solution to the under-determined linear system, i.e.
\\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||Z||_F^2 \\), subject to
\\(A Z = B\\). Notice that the fast path is only numerically stable when
\\(A\\) is numerically full rank and has a condition number
\\(\mathrm{cond}(A) \lt \frac{1}{\sqrt{\epsilon_{mach}}}\\) or\\(\lambda\\)
is sufficiently large. If `fast` is `False` an algorithm based on the numerically robust complete
orthogonal decomposition is used. This computes the minimum-norm
least-squares solution, even when \\(A\\) is rank deficient. This path is
typically 6-7 times slower than the fast path. If `fast` is `False` then
`l2_regularizer` is ignored.
Parameters
-
IGraphNodeBasematrix - `Tensor` of shape `[..., M, N]`.
-
ndarrayrhs - `Tensor` of shape `[..., M, K]`.
-
doublel2_regularizer - 0-D `double` `Tensor`. Ignored if `fast=False`.
-
boolfast - bool. Defaults to `True`.
-
stringname - string, optional name of the operation.
Returns
Tensor matrix_solve_ls(ndarray matrix, ndarray rhs, double l2_regularizer, bool fast, string name)
Solves one or more linear least-squares problems. `matrix` is a tensor of shape `[..., M, N]` whose inner-most 2 dimensions
form `M`-by-`N` matrices. Rhs is a tensor of shape `[..., M, K]` whose
inner-most 2 dimensions form `M`-by-`K` matrices. The computed output is a
`Tensor` of shape `[..., N, K]` whose inner-most 2 dimensions form `M`-by-`K`
matrices that solve the equations
`matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]` in the least squares
sense. Below we will use the following notation for each pair of matrix and
right-hand sides in the batch: `matrix`=\\(A \in \Re^{m \times n}\\),
`rhs`=\\(B \in \Re^{m \times k}\\),
`output`=\\(X \in \Re^{n \times k}\\),
`l2_regularizer`=\\(\lambda\\). If `fast` is `True`, then the solution is computed by solving the normal
equations using Cholesky decomposition. Specifically, if \\(m \ge n\\) then
\\(X = (A^T A + \lambda I)^{-1} A^T B\\), which solves the least-squares
problem \\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||A Z - B||_F^2 +
\lambda ||Z||_F^2\\). If \\(m \lt n\\) then `output` is computed as
\\(X = A^T (A A^T + \lambda I)^{-1} B\\), which (for \\(\lambda = 0\\)) is
the minimum-norm solution to the under-determined linear system, i.e.
\\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||Z||_F^2 \\), subject to
\\(A Z = B\\). Notice that the fast path is only numerically stable when
\\(A\\) is numerically full rank and has a condition number
\\(\mathrm{cond}(A) \lt \frac{1}{\sqrt{\epsilon_{mach}}}\\) or\\(\lambda\\)
is sufficiently large. If `fast` is `False` an algorithm based on the numerically robust complete
orthogonal decomposition is used. This computes the minimum-norm
least-squares solution, even when \\(A\\) is rank deficient. This path is
typically 6-7 times slower than the fast path. If `fast` is `False` then
`l2_regularizer` is ignored.
Parameters
Returns
Tensor matrix_solve_ls(IGraphNodeBase matrix, IGraphNodeBase rhs, double l2_regularizer, bool fast, string name)
Solves one or more linear least-squares problems. `matrix` is a tensor of shape `[..., M, N]` whose inner-most 2 dimensions
form `M`-by-`N` matrices. Rhs is a tensor of shape `[..., M, K]` whose
inner-most 2 dimensions form `M`-by-`K` matrices. The computed output is a
`Tensor` of shape `[..., N, K]` whose inner-most 2 dimensions form `M`-by-`K`
matrices that solve the equations
`matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]` in the least squares
sense. Below we will use the following notation for each pair of matrix and
right-hand sides in the batch: `matrix`=\\(A \in \Re^{m \times n}\\),
`rhs`=\\(B \in \Re^{m \times k}\\),
`output`=\\(X \in \Re^{n \times k}\\),
`l2_regularizer`=\\(\lambda\\). If `fast` is `True`, then the solution is computed by solving the normal
equations using Cholesky decomposition. Specifically, if \\(m \ge n\\) then
\\(X = (A^T A + \lambda I)^{-1} A^T B\\), which solves the least-squares
problem \\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||A Z - B||_F^2 +
\lambda ||Z||_F^2\\). If \\(m \lt n\\) then `output` is computed as
\\(X = A^T (A A^T + \lambda I)^{-1} B\\), which (for \\(\lambda = 0\\)) is
the minimum-norm solution to the under-determined linear system, i.e.
\\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||Z||_F^2 \\), subject to
\\(A Z = B\\). Notice that the fast path is only numerically stable when
\\(A\\) is numerically full rank and has a condition number
\\(\mathrm{cond}(A) \lt \frac{1}{\sqrt{\epsilon_{mach}}}\\) or\\(\lambda\\)
is sufficiently large. If `fast` is `False` an algorithm based on the numerically robust complete
orthogonal decomposition is used. This computes the minimum-norm
least-squares solution, even when \\(A\\) is rank deficient. This path is
typically 6-7 times slower than the fast path. If `fast` is `False` then
`l2_regularizer` is ignored.
Parameters
-
IGraphNodeBasematrix - `Tensor` of shape `[..., M, N]`.
-
IGraphNodeBaserhs - `Tensor` of shape `[..., M, K]`.
-
doublel2_regularizer - 0-D `double` `Tensor`. Ignored if `fast=False`.
-
boolfast - bool. Defaults to `True`.
-
stringname - string, optional name of the operation.
Returns
Tensor matrix_solve_ls(ndarray matrix, IGraphNodeBase rhs, double l2_regularizer, bool fast, string name)
Solves one or more linear least-squares problems. `matrix` is a tensor of shape `[..., M, N]` whose inner-most 2 dimensions
form `M`-by-`N` matrices. Rhs is a tensor of shape `[..., M, K]` whose
inner-most 2 dimensions form `M`-by-`K` matrices. The computed output is a
`Tensor` of shape `[..., N, K]` whose inner-most 2 dimensions form `M`-by-`K`
matrices that solve the equations
`matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]` in the least squares
sense. Below we will use the following notation for each pair of matrix and
right-hand sides in the batch: `matrix`=\\(A \in \Re^{m \times n}\\),
`rhs`=\\(B \in \Re^{m \times k}\\),
`output`=\\(X \in \Re^{n \times k}\\),
`l2_regularizer`=\\(\lambda\\). If `fast` is `True`, then the solution is computed by solving the normal
equations using Cholesky decomposition. Specifically, if \\(m \ge n\\) then
\\(X = (A^T A + \lambda I)^{-1} A^T B\\), which solves the least-squares
problem \\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||A Z - B||_F^2 +
\lambda ||Z||_F^2\\). If \\(m \lt n\\) then `output` is computed as
\\(X = A^T (A A^T + \lambda I)^{-1} B\\), which (for \\(\lambda = 0\\)) is
the minimum-norm solution to the under-determined linear system, i.e.
\\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||Z||_F^2 \\), subject to
\\(A Z = B\\). Notice that the fast path is only numerically stable when
\\(A\\) is numerically full rank and has a condition number
\\(\mathrm{cond}(A) \lt \frac{1}{\sqrt{\epsilon_{mach}}}\\) or\\(\lambda\\)
is sufficiently large. If `fast` is `False` an algorithm based on the numerically robust complete
orthogonal decomposition is used. This computes the minimum-norm
least-squares solution, even when \\(A\\) is rank deficient. This path is
typically 6-7 times slower than the fast path. If `fast` is `False` then
`l2_regularizer` is ignored.
Parameters
-
ndarraymatrix - `Tensor` of shape `[..., M, N]`.
-
IGraphNodeBaserhs - `Tensor` of shape `[..., M, K]`.
-
doublel2_regularizer - 0-D `double` `Tensor`. Ignored if `fast=False`.
-
boolfast - bool. Defaults to `True`.
-
stringname - string, optional name of the operation.
Returns
object matrix_solve_ls_dyn(object matrix, object rhs, ImplicitContainer<T> l2_regularizer, ImplicitContainer<T> fast, object name)
Solves one or more linear least-squares problems. `matrix` is a tensor of shape `[..., M, N]` whose inner-most 2 dimensions
form `M`-by-`N` matrices. Rhs is a tensor of shape `[..., M, K]` whose
inner-most 2 dimensions form `M`-by-`K` matrices. The computed output is a
`Tensor` of shape `[..., N, K]` whose inner-most 2 dimensions form `M`-by-`K`
matrices that solve the equations
`matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]` in the least squares
sense. Below we will use the following notation for each pair of matrix and
right-hand sides in the batch: `matrix`=\\(A \in \Re^{m \times n}\\),
`rhs`=\\(B \in \Re^{m \times k}\\),
`output`=\\(X \in \Re^{n \times k}\\),
`l2_regularizer`=\\(\lambda\\). If `fast` is `True`, then the solution is computed by solving the normal
equations using Cholesky decomposition. Specifically, if \\(m \ge n\\) then
\\(X = (A^T A + \lambda I)^{-1} A^T B\\), which solves the least-squares
problem \\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||A Z - B||_F^2 +
\lambda ||Z||_F^2\\). If \\(m \lt n\\) then `output` is computed as
\\(X = A^T (A A^T + \lambda I)^{-1} B\\), which (for \\(\lambda = 0\\)) is
the minimum-norm solution to the under-determined linear system, i.e.
\\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||Z||_F^2 \\), subject to
\\(A Z = B\\). Notice that the fast path is only numerically stable when
\\(A\\) is numerically full rank and has a condition number
\\(\mathrm{cond}(A) \lt \frac{1}{\sqrt{\epsilon_{mach}}}\\) or\\(\lambda\\)
is sufficiently large. If `fast` is `False` an algorithm based on the numerically robust complete
orthogonal decomposition is used. This computes the minimum-norm
least-squares solution, even when \\(A\\) is rank deficient. This path is
typically 6-7 times slower than the fast path. If `fast` is `False` then
`l2_regularizer` is ignored.
Parameters
-
objectmatrix - `Tensor` of shape `[..., M, N]`.
-
objectrhs - `Tensor` of shape `[..., M, K]`.
-
ImplicitContainer<T>l2_regularizer - 0-D `double` `Tensor`. Ignored if `fast=False`.
-
ImplicitContainer<T>fast - bool. Defaults to `True`.
-
objectname - string, optional name of the operation.
Returns
-
object
Tensor matrix_square_root(IGraphNodeBase input, string name)
Computes the matrix square root of one or more square matrices: matmul(sqrtm(A), sqrtm(A)) = A The input matrix should be invertible. If the input matrix is real, it should
have no eigenvalues which are real and negative (pairs of complex conjugate
eigenvalues are allowed). The matrix square root is computed by first reducing the matrix to
quasi-triangular form with the real Schur decomposition. The square root
of the quasi-triangular matrix is then computed directly. Details of
the algorithm can be found in: Nicholas J. Higham, "Computing real
square roots of a real matrix", Linear Algebra Appl., 1987. The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The output is a tensor of the same shape as the input
containing the matrix square root for all input submatrices `[..., :, :]`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object matrix_square_root_dyn(object input, object name)
Computes the matrix square root of one or more square matrices: matmul(sqrtm(A), sqrtm(A)) = A The input matrix should be invertible. If the input matrix is real, it should
have no eigenvalues which are real and negative (pairs of complex conjugate
eigenvalues are allowed). The matrix square root is computed by first reducing the matrix to
quasi-triangular form with the real Schur decomposition. The square root
of the quasi-triangular matrix is then computed directly. Details of
the algorithm can be found in: Nicholas J. Higham, "Computing real
square roots of a real matrix", Linear Algebra Appl., 1987. The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The output is a tensor of the same shape as the input
containing the matrix square root for all input submatrices `[..., :, :]`.
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor matrix_transpose(IGraphNodeBase a, string name, bool conjugate)
Transposes last two dimensions of tensor `a`.
Note that
tf.matmul provides kwargs allowing for transpose of arguments.
This is done with minimal cost, and is preferable to using this function. E.g.
Parameters
-
IGraphNodeBasea - A `Tensor` with `rank >= 2`.
-
stringname - A name for the operation (optional).
-
boolconjugate - Optional bool. Setting it to `True` is mathematically equivalent to tf.math.conj(tf.linalg.matrix_transpose(input)).
Returns
-
Tensor - A transposed batch matrix `Tensor`.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.linalg.matrix_transpose(x) # [[1, 4],
# [2, 5],
# [3, 6]] x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.linalg.matrix_transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # Matrix with two batch dimensions.
# x.shape is [1, 2, 3, 4]
# tf.linalg.matrix_transpose(x) is shape [1, 2, 4, 3]
object matrix_transpose_dyn(object a, ImplicitContainer<T> name, ImplicitContainer<T> conjugate)
Transposes last two dimensions of tensor `a`.
Note that
tf.matmul provides kwargs allowing for transpose of arguments.
This is done with minimal cost, and is preferable to using this function. E.g.
Parameters
-
objecta - A `Tensor` with `rank >= 2`.
-
ImplicitContainer<T>name - A name for the operation (optional).
-
ImplicitContainer<T>conjugate - Optional bool. Setting it to `True` is mathematically equivalent to tf.math.conj(tf.linalg.matrix_transpose(input)).
Returns
-
object - A transposed batch matrix `Tensor`.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.linalg.matrix_transpose(x) # [[1, 4],
# [2, 5],
# [3, 6]] x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.linalg.matrix_transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # Matrix with two batch dimensions.
# x.shape is [1, 2, 3, 4]
# tf.linalg.matrix_transpose(x) is shape [1, 2, 4, 3]
Tensor matrix_triangular_solve(IGraphNodeBase matrix, IGraphNodeBase rhs, bool lower, bool adjoint, string name)
Solves systems of linear equations with upper or lower triangular matrices by backsubstitution. `matrix` is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions form
square matrices. If `lower` is `True` then the strictly upper triangular part
of each inner-most matrix is assumed to be zero and not accessed.
If `lower` is False then the strictly lower triangular part of each inner-most
matrix is assumed to be zero and not accessed.
`rhs` is a tensor of shape `[..., M, K]`. The output is a tensor of shape `[..., M, K]`. If `adjoint` is
`True` then the innermost matrices in `output` satisfy matrix equations
`matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]`.
If `adjoint` is `False` then the strictly then the innermost matrices in
`output` satisfy matrix equations
`adjoint(matrix[..., i, k]) * output[..., k, j] = rhs[..., i, j]`. Example:
Parameters
-
IGraphNodeBasematrix - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
IGraphNodeBaserhs - A `Tensor`. Must have the same type as `matrix`. Shape is `[..., M, K]`.
-
boollower - An optional `bool`. Defaults to `True`. Boolean indicating whether the innermost matrices in `matrix` are lower or upper triangular.
-
booladjoint - An optional `bool`. Defaults to `False`. Boolean indicating whether to solve with `matrix` or its (block-wise) adjoint.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `matrix`.
Show Example
a = tf.constant([[3, 0, 0, 0],
[2, 1, 0, 0],
[1, 0, 1, 0],
[1, 1, 1, 1]], dtype=tf.float32) b = tf.constant([[4],
[2],
[4],
[2]], dtype=tf.float32) x = tf.linalg.triangular_solve(a, b, lower=True)
x
# # in python3 one can use `a@x`
tf.matmul(a, x)
#
object matrix_triangular_solve_dyn(object matrix, object rhs, ImplicitContainer<T> lower, ImplicitContainer<T> adjoint, object name)
Solves systems of linear equations with upper or lower triangular matrices by backsubstitution. `matrix` is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions form
square matrices. If `lower` is `True` then the strictly upper triangular part
of each inner-most matrix is assumed to be zero and not accessed.
If `lower` is False then the strictly lower triangular part of each inner-most
matrix is assumed to be zero and not accessed.
`rhs` is a tensor of shape `[..., M, K]`. The output is a tensor of shape `[..., M, K]`. If `adjoint` is
`True` then the innermost matrices in `output` satisfy matrix equations
`matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]`.
If `adjoint` is `False` then the strictly then the innermost matrices in
`output` satisfy matrix equations
`adjoint(matrix[..., i, k]) * output[..., k, j] = rhs[..., i, j]`. Example:
Parameters
-
objectmatrix - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. Shape is `[..., M, M]`.
-
objectrhs - A `Tensor`. Must have the same type as `matrix`. Shape is `[..., M, K]`.
-
ImplicitContainer<T>lower - An optional `bool`. Defaults to `True`. Boolean indicating whether the innermost matrices in `matrix` are lower or upper triangular.
-
ImplicitContainer<T>adjoint - An optional `bool`. Defaults to `False`. Boolean indicating whether to solve with `matrix` or its (block-wise) adjoint.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `matrix`.
Show Example
a = tf.constant([[3, 0, 0, 0],
[2, 1, 0, 0],
[1, 0, 1, 0],
[1, 1, 1, 1]], dtype=tf.float32) b = tf.constant([[4],
[2],
[4],
[2]], dtype=tf.float32) x = tf.linalg.triangular_solve(a, b, lower=True)
x
# # in python3 one can use `a@x`
tf.matmul(a, x)
#
Tensor max_bytes_in_use(string name)
object max_bytes_in_use_dyn(object name)
object maximum(IGraphNodeBase x, double y, string name)
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object maximum(int x, IGraphNodeBase y, string name)
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object maximum(int x, int y, string name)
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object maximum(int x, double y, string name)
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object maximum(IGraphNodeBase x, int y, string name)
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object maximum(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object maximum(double x, IGraphNodeBase y, string name)
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object maximum(double x, int y, string name)
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object maximum(double x, double y, string name)
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object maximum_dyn(object x, object y, object name)
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
IList<object> meshgrid(Object[] args)
Broadcasts parameters for evaluation on an N-D grid. Given N one-dimensional coordinate arrays `*args`, returns a list `outputs`
of N-D coordinate arrays for evaluating expressions on an N-D grid. Notes: `meshgrid` supports cartesian ('xy') and matrix ('ij') indexing conventions.
When the `indexing` argument is set to 'xy' (the default), the broadcasting
instructions for the first two dimensions are swapped. Examples: Calling `X, Y = meshgrid(x, y)` with the tensors
Parameters
-
Object[]args - `Tensor`s with rank 1.
Returns
-
IList<object>
Show Example
x = [1, 2, 3]
y = [4, 5, 6]
X, Y = tf.meshgrid(x, y)
# X = [[1, 2, 3],
# [1, 2, 3],
# [1, 2, 3]]
# Y = [[4, 4, 4],
# [5, 5, 5],
# [6, 6, 6]]
IList<object> meshgrid(IDictionary<string, object> kwargs, Object[] args)
Broadcasts parameters for evaluation on an N-D grid. Given N one-dimensional coordinate arrays `*args`, returns a list `outputs`
of N-D coordinate arrays for evaluating expressions on an N-D grid. Notes: `meshgrid` supports cartesian ('xy') and matrix ('ij') indexing conventions.
When the `indexing` argument is set to 'xy' (the default), the broadcasting
instructions for the first two dimensions are swapped. Examples: Calling `X, Y = meshgrid(x, y)` with the tensors
Parameters
-
IDictionary<string, object>kwargs - - indexing: Either 'xy' or 'ij' (optional, default: 'xy'). - name: A name for the operation (optional).
-
Object[]args - `Tensor`s with rank 1.
Returns
-
IList<object>
Show Example
x = [1, 2, 3]
y = [4, 5, 6]
X, Y = tf.meshgrid(x, y)
# X = [[1, 2, 3],
# [1, 2, 3],
# [1, 2, 3]]
# Y = [[4, 4, 4],
# [5, 5, 5],
# [6, 6, 6]]
object meshgrid_dyn(Object[] args)
Broadcasts parameters for evaluation on an N-D grid. Given N one-dimensional coordinate arrays `*args`, returns a list `outputs`
of N-D coordinate arrays for evaluating expressions on an N-D grid. Notes: `meshgrid` supports cartesian ('xy') and matrix ('ij') indexing conventions.
When the `indexing` argument is set to 'xy' (the default), the broadcasting
instructions for the first two dimensions are swapped. Examples: Calling `X, Y = meshgrid(x, y)` with the tensors
Parameters
-
Object[]args - `Tensor`s with rank 1.
Returns
-
object
Show Example
x = [1, 2, 3]
y = [4, 5, 6]
X, Y = tf.meshgrid(x, y)
# X = [[1, 2, 3],
# [1, 2, 3],
# [1, 2, 3]]
# Y = [[4, 4, 4],
# [5, 5, 5],
# [6, 6, 6]]
object meshgrid_dyn(IDictionary<string, object> kwargs, Object[] args)
Broadcasts parameters for evaluation on an N-D grid. Given N one-dimensional coordinate arrays `*args`, returns a list `outputs`
of N-D coordinate arrays for evaluating expressions on an N-D grid. Notes: `meshgrid` supports cartesian ('xy') and matrix ('ij') indexing conventions.
When the `indexing` argument is set to 'xy' (the default), the broadcasting
instructions for the first two dimensions are swapped. Examples: Calling `X, Y = meshgrid(x, y)` with the tensors
Parameters
-
IDictionary<string, object>kwargs - - indexing: Either 'xy' or 'ij' (optional, default: 'xy'). - name: A name for the operation (optional).
-
Object[]args - `Tensor`s with rank 1.
Returns
-
object
Show Example
x = [1, 2, 3]
y = [4, 5, 6]
X, Y = tf.meshgrid(x, y)
# X = [[1, 2, 3],
# [1, 2, 3],
# [1, 2, 3]]
# Y = [[4, 4, 4],
# [5, 5, 5],
# [6, 6, 6]]
object min_max_variable_partitioner(int max_partitions, int axis, string min_slice_size, int bytes_per_string_element)
Partitioner to allocate minimum size per slice. Returns a partitioner that partitions the variable of given shape and dtype
such that each partition has a minimum of `min_slice_size` slice of the
variable. The maximum number of such partitions (upper bound) is given by
`max_partitions`.
Parameters
-
intmax_partitions - Upper bound on the number of partitions. Defaults to 1.
-
intaxis - Axis along which to partition the variable. Defaults to 0.
-
stringmin_slice_size - Minimum size of the variable slice per partition. Defaults to 256K.
-
intbytes_per_string_element - If the `Variable` is of type string, this provides an estimate of how large each scalar in the `Variable` is.
Returns
-
object - A partition function usable as the `partitioner` argument to `variable_scope` and `get_variable`.
object min_max_variable_partitioner(int max_partitions, int axis, IDictionary<object, object> min_slice_size, int bytes_per_string_element)
Partitioner to allocate minimum size per slice. Returns a partitioner that partitions the variable of given shape and dtype
such that each partition has a minimum of `min_slice_size` slice of the
variable. The maximum number of such partitions (upper bound) is given by
`max_partitions`.
Parameters
-
intmax_partitions - Upper bound on the number of partitions. Defaults to 1.
-
intaxis - Axis along which to partition the variable. Defaults to 0.
-
IDictionary<object, object>min_slice_size - Minimum size of the variable slice per partition. Defaults to 256K.
-
intbytes_per_string_element - If the `Variable` is of type string, this provides an estimate of how large each scalar in the `Variable` is.
Returns
-
object - A partition function usable as the `partitioner` argument to `variable_scope` and `get_variable`.
object min_max_variable_partitioner(int max_partitions, int axis, IEnumerable<object> min_slice_size, int bytes_per_string_element)
Partitioner to allocate minimum size per slice. Returns a partitioner that partitions the variable of given shape and dtype
such that each partition has a minimum of `min_slice_size` slice of the
variable. The maximum number of such partitions (upper bound) is given by
`max_partitions`.
Parameters
-
intmax_partitions - Upper bound on the number of partitions. Defaults to 1.
-
intaxis - Axis along which to partition the variable. Defaults to 0.
-
IEnumerable<object>min_slice_size - Minimum size of the variable slice per partition. Defaults to 256K.
-
intbytes_per_string_element - If the `Variable` is of type string, this provides an estimate of how large each scalar in the `Variable` is.
Returns
-
object - A partition function usable as the `partitioner` argument to `variable_scope` and `get_variable`.
object min_max_variable_partitioner(int max_partitions, int axis, ImplicitContainer<T> min_slice_size, int bytes_per_string_element)
Partitioner to allocate minimum size per slice. Returns a partitioner that partitions the variable of given shape and dtype
such that each partition has a minimum of `min_slice_size` slice of the
variable. The maximum number of such partitions (upper bound) is given by
`max_partitions`.
Parameters
-
intmax_partitions - Upper bound on the number of partitions. Defaults to 1.
-
intaxis - Axis along which to partition the variable. Defaults to 0.
-
ImplicitContainer<T>min_slice_size - Minimum size of the variable slice per partition. Defaults to 256K.
-
intbytes_per_string_element - If the `Variable` is of type string, this provides an estimate of how large each scalar in the `Variable` is.
Returns
-
object - A partition function usable as the `partitioner` argument to `variable_scope` and `get_variable`.
object min_max_variable_partitioner_dyn(ImplicitContainer<T> max_partitions, ImplicitContainer<T> axis, ImplicitContainer<T> min_slice_size, ImplicitContainer<T> bytes_per_string_element)
Partitioner to allocate minimum size per slice. Returns a partitioner that partitions the variable of given shape and dtype
such that each partition has a minimum of `min_slice_size` slice of the
variable. The maximum number of such partitions (upper bound) is given by
`max_partitions`.
Parameters
-
ImplicitContainer<T>max_partitions - Upper bound on the number of partitions. Defaults to 1.
-
ImplicitContainer<T>axis - Axis along which to partition the variable. Defaults to 0.
-
ImplicitContainer<T>min_slice_size - Minimum size of the variable slice per partition. Defaults to 256K.
-
ImplicitContainer<T>bytes_per_string_element - If the `Variable` is of type string, this provides an estimate of how large each scalar in the `Variable` is.
Returns
-
object - A partition function usable as the `partitioner` argument to `variable_scope` and `get_variable`.
object minimum(int x, double y, string name)
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object minimum(int x, int y, string name)
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object minimum(int x, IGraphNodeBase y, string name)
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object minimum(double x, IGraphNodeBase y, string name)
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object minimum(double x, int y, string name)
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object minimum(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object minimum(IGraphNodeBase x, int y, string name)
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object minimum(double x, double y, string name)
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object minimum(IGraphNodeBase x, double y, string name)
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object minimum_dyn(object x, object y, object name)
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object mixed_struct(object n_a, string name)
object mixed_struct_dyn(object n_a, object name)
Tensor mod(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns element-wise remainder of division. When `x < 0` xor `y < 0` is true, this follows Python semantics in that the result here is consistent
with a flooring divide. E.g. `floor(x / y) * y + mod(x, y) = x`. *NOTE*: `math.floormod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Tensor mod(IGraphNodeBase x, IGraphNodeBase y, PythonFunctionContainer name)
Returns element-wise remainder of division. When `x < 0` xor `y < 0` is true, this follows Python semantics in that the result here is consistent
with a flooring divide. E.g. `floor(x / y) * y + mod(x, y) = x`. *NOTE*: `math.floormod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
object mod_dyn(object x, object y, object name)
Returns element-wise remainder of division. When `x < 0` xor `y < 0` is true, this follows Python semantics in that the result here is consistent
with a flooring divide. E.g. `floor(x / y) * y + mod(x, y) = x`. *NOTE*: `math.floormod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object model_variables(object scope)
Returns all variables in the MODEL_VARIABLES collection.
Parameters
-
objectscope - (Optional.) A string. If supplied, the resulting list is filtered to include only items whose `name` attribute matches `scope` using `re.match`. Items without a `name` attribute are never returned if a scope is supplied. The choice of `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
object - A list of local Variable objects.
object model_variables_dyn(object scope)
Returns all variables in the MODEL_VARIABLES collection.
Parameters
-
objectscope - (Optional.) A string. If supplied, the resulting list is filtered to include only items whose `name` attribute matches `scope` using `re.match`. Items without a `name` attribute are never returned if a scope is supplied. The choice of `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
object - A list of local Variable objects.
object moving_average_variables(object scope)
Returns all variables that maintain their moving averages. If an `ExponentialMovingAverage` object is created and the `apply()`
method is called on a list of variables, these variables will
be added to the `GraphKeys.MOVING_AVERAGE_VARIABLES` collection.
This convenience function returns the contents of that collection.
Parameters
-
objectscope - (Optional.) A string. If supplied, the resulting list is filtered to include only items whose `name` attribute matches `scope` using `re.match`. Items without a `name` attribute are never returned if a scope is supplied. The choice of `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
object - A list of Variable objects.
object moving_average_variables_dyn(object scope)
Returns all variables that maintain their moving averages. If an `ExponentialMovingAverage` object is created and the `apply()`
method is called on a list of variables, these variables will
be added to the `GraphKeys.MOVING_AVERAGE_VARIABLES` collection.
This convenience function returns the contents of that collection.
Parameters
-
objectscope - (Optional.) A string. If supplied, the resulting list is filtered to include only items whose `name` attribute matches `scope` using `re.match`. Items without a `name` attribute are never returned if a scope is supplied. The choice of `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
object - A list of Variable objects.
Tensor multinomial(IGraphNodeBase logits, IndexedSlices num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IGraphNodeBaselogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IndexedSlicesnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(ndarray logits, IndexedSlices num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
ndarraylogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IndexedSlicesnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(double logits, IGraphNodeBase num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
doublelogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IGraphNodeBasenum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IGraphNodeBase logits, ValueTuple<PythonClassContainer, PythonClassContainer> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IGraphNodeBaselogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
ValueTuple<PythonClassContainer, PythonClassContainer>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(ndarray logits, int num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
ndarraylogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
intnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(float32 logits, ValueTuple<PythonClassContainer, PythonClassContainer> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
float32logits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
ValueTuple<PythonClassContainer, PythonClassContainer>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IGraphNodeBase logits, IEnumerable<object> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IGraphNodeBaselogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IEnumerable<object>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(float32 logits, int num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
float32logits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
intnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IEnumerable<IGraphNodeBase> logits, int num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IEnumerable<IGraphNodeBase>logits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
intnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(double logits, IEnumerable<object> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
doublelogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IEnumerable<object>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(float32 logits, IndexedSlices num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
float32logits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IndexedSlicesnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(float32 logits, IGraphNodeBase num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
float32logits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IGraphNodeBasenum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(double logits, ValueTuple<PythonClassContainer, PythonClassContainer> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
doublelogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
ValueTuple<PythonClassContainer, PythonClassContainer>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IndexedSlices logits, IEnumerable<object> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IndexedSliceslogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IEnumerable<object>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(double logits, int num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
doublelogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
intnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(ndarray logits, IGraphNodeBase num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
ndarraylogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IGraphNodeBasenum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IEnumerable<IGraphNodeBase> logits, IGraphNodeBase num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IEnumerable<IGraphNodeBase>logits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IGraphNodeBasenum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(float32 logits, IEnumerable<object> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
float32logits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IEnumerable<object>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IGraphNodeBase logits, IGraphNodeBase num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IGraphNodeBaselogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IGraphNodeBasenum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IEnumerable<IGraphNodeBase> logits, IndexedSlices num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IEnumerable<IGraphNodeBase>logits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IndexedSlicesnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IEnumerable<IGraphNodeBase> logits, IEnumerable<object> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IEnumerable<IGraphNodeBase>logits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IEnumerable<object>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IEnumerable<IGraphNodeBase> logits, ValueTuple<PythonClassContainer, PythonClassContainer> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IEnumerable<IGraphNodeBase>logits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
ValueTuple<PythonClassContainer, PythonClassContainer>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(ndarray logits, IEnumerable<object> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
ndarraylogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IEnumerable<object>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IndexedSlices logits, IndexedSlices num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IndexedSliceslogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IndexedSlicesnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IndexedSlices logits, int num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IndexedSliceslogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
intnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IGraphNodeBase logits, int num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IGraphNodeBaselogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
intnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IndexedSlices logits, IGraphNodeBase num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IndexedSliceslogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IGraphNodeBasenum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(ndarray logits, ValueTuple<PythonClassContainer, PythonClassContainer> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
ndarraylogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
ValueTuple<PythonClassContainer, PythonClassContainer>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(IndexedSlices logits, ValueTuple<PythonClassContainer, PythonClassContainer> num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
IndexedSliceslogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
ValueTuple<PythonClassContainer, PythonClassContainer>num_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
Tensor multinomial(double logits, IndexedSlices num_samples, Nullable<int> seed, string name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
doublelogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
IndexedSlicesnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
Tensor - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
object multinomial_dyn(object logits, object num_samples, object seed, object name, object output_dtype)
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Parameters
-
objectlogits - 2-D Tensor with shape `[batch_size, num_classes]`. Each slice `[i, :]` represents the unnormalized log-probabilities for all classes.
-
objectnum_samples - 0-D. Number of independent samples to draw for each row slice.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
objectname - Optional name for the operation.
-
objectoutput_dtype - integer type to use for the output. Defaults to int64.
Returns
-
object - The drawn samples of shape `[batch_size, num_samples]`.
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
object multiply(PythonClassContainer x, IEnumerable<IGraphNodeBase> y, string name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(PythonClassContainer x, PythonFunctionContainer y, PythonFunctionContainer name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
PythonFunctionContainery - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(PythonClassContainer x, IEnumerable<IGraphNodeBase> y, PythonFunctionContainer name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(IEnumerable<IGraphNodeBase> x, IEnumerable<IGraphNodeBase> y, string name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(IEnumerable<IGraphNodeBase> x, PythonFunctionContainer y, string name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
PythonFunctionContainery - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(IEnumerable<IGraphNodeBase> x, PythonFunctionContainer y, PythonFunctionContainer name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
PythonFunctionContainery - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(IEnumerable<IGraphNodeBase> x, IEnumerable<IGraphNodeBase> y, PythonFunctionContainer name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(PythonClassContainer x, PythonFunctionContainer y, string name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
PythonFunctionContainery - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(IEnumerable<IGraphNodeBase> x, object y, PythonFunctionContainer name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(PythonClassContainer x, object y, PythonFunctionContainer name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(IEnumerable<IGraphNodeBase> x, object y, string name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(PythonClassContainer x, object y, string name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
PythonClassContainerx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(object x, IEnumerable<IGraphNodeBase> y, PythonFunctionContainer name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(object x, PythonFunctionContainer y, PythonFunctionContainer name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
PythonFunctionContainery - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(object x, object y, string name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(object x, PythonFunctionContainer y, string name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
PythonFunctionContainery - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(object x, IEnumerable<IGraphNodeBase> y, string name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IEnumerable<IGraphNodeBase>y - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply(object x, object y, PythonFunctionContainer name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object multiply_dyn(object x, object y, object name)
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object n_in_polymorphic_twice(object a, object b, string name)
object n_in_polymorphic_twice_dyn(object a, object b, object name)
object n_in_twice(object a, object b, string name)
object n_in_twice_dyn(object a, object b, object name)
object n_in_two_type_variables(object a, object b, string name)
object n_in_two_type_variables_dyn(object a, object b, object name)
object n_ints_in(object a, string name)
object n_ints_in_dyn(object a, object name)
object n_ints_out(object N, string name)
object n_ints_out_default(int N, string name)
object n_ints_out_default_dyn(ImplicitContainer<T> N, object name)
object n_ints_out_dyn(object N, object name)
object n_polymorphic_in(object a, string name)
object n_polymorphic_in_dyn(object a, object name)
object n_polymorphic_out(object T, object N, string name)
object n_polymorphic_out_default(ImplicitContainer<T> T, int N, string name)
object n_polymorphic_out_default_dyn(ImplicitContainer<T> T, ImplicitContainer<T> N, object name)
object n_polymorphic_out_dyn(object T, object N, object name)
object n_polymorphic_restrict_in(object a, string name)
object n_polymorphic_restrict_in_dyn(object a, object name)
object n_polymorphic_restrict_out(object T, object N, string name)
object n_polymorphic_restrict_out_dyn(object T, object N, object name)
object negative(IGraphNodeBase x, string name)
object negative_dyn(object x, object name)
object no_op(PythonFunctionContainer name)
Does nothing. Only useful as a placeholder for control edges.
Parameters
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - The created Operation.
object no_op(string name)
Does nothing. Only useful as a placeholder for control edges.
Parameters
-
stringname - A name for the operation (optional).
Returns
-
object - The created Operation.
object no_op_dyn(object name)
Does nothing. Only useful as a placeholder for control edges.
Parameters
-
objectname - A name for the operation (optional).
Returns
-
object - The created Operation.
object no_regularizer(Variable _)
Use this function to prevent regularization of variables.
object no_regularizer_dyn(object _)
Use this function to prevent regularization of variables.
void NoGradient(string op_type)
Specifies that ops of type `op_type` is not differentiable. This function should *not* be used for operations that have a
well-defined gradient that is not yet implemented. This function is only used when defining a new op type. It may be
used for ops such as `tf.size()` that are not differentiable. For
example:
The gradient computed for 'op_type' will then propagate zeros. For ops that have a well-defined gradient but are not yet implemented,
no declaration should be made, and an error *must* be thrown if
an attempt to request its gradient is made.
Parameters
-
stringop_type - The string type of an operation. This corresponds to the `OpDef.name` field for the proto that defines the operation.
Show Example
tf.no_gradient("Size")
object NoGradient_dyn(object op_type)
Specifies that ops of type `op_type` is not differentiable. This function should *not* be used for operations that have a
well-defined gradient that is not yet implemented. This function is only used when defining a new op type. It may be
used for ops such as `tf.size()` that are not differentiable. For
example:
The gradient computed for 'op_type' will then propagate zeros. For ops that have a well-defined gradient but are not yet implemented,
no declaration should be made, and an error *must* be thrown if
an attempt to request its gradient is made.
Parameters
-
objectop_type - The string type of an operation. This corresponds to the `OpDef.name` field for the proto that defines the operation.
Show Example
tf.no_gradient("Size")
object nondifferentiable_batch_function(int num_batch_threads, int max_batch_size, int batch_timeout_micros, object allowed_batch_sizes, int max_enqueued_batches, bool autograph)
Batches the computation done by the decorated function. So, for example, in the following code
if more than one session.run call is simultaneously trying to compute `b`
the values of `w` will be gathered, non-deterministically concatenated
along the first axis, and only one thread will run the computation. See the
documentation of the `Batch` op for more details. Assumes that all arguments of the decorated function are Tensors which will
be batched along their first dimension. SparseTensor is not supported. The return value of the decorated function
must be a Tensor or a list/tuple of Tensors.
Parameters
-
intnum_batch_threads - Number of scheduling threads for processing batches of work. Determines the number of batches processed in parallel.
-
intmax_batch_size - Batch sizes will never be bigger than this.
-
intbatch_timeout_micros - Maximum number of microseconds to wait before outputting an incomplete batch.
-
objectallowed_batch_sizes - Optional list of allowed batch sizes. If left empty, does nothing. Otherwise, supplies a list of batch sizes, causing the op to pad batches up to one of those sizes. The entries must increase monotonically, and the final entry must equal max_batch_size.
-
intmax_enqueued_batches - The maximum depth of the batch queue. Defaults to 10.
-
boolautograph - Whether to use autograph to compile python and eager style code for efficient graph-mode execution.
Returns
-
object - The decorated function will return the unbatched computation output Tensors.
Show Example
@batch_function(1, 2, 3)
def layer(a):
return tf.matmul(a, a) b = layer(w)
object nondifferentiable_batch_function_dyn(object num_batch_threads, object max_batch_size, object batch_timeout_micros, object allowed_batch_sizes, ImplicitContainer<T> max_enqueued_batches, ImplicitContainer<T> autograph)
Batches the computation done by the decorated function. So, for example, in the following code
if more than one session.run call is simultaneously trying to compute `b`
the values of `w` will be gathered, non-deterministically concatenated
along the first axis, and only one thread will run the computation. See the
documentation of the `Batch` op for more details. Assumes that all arguments of the decorated function are Tensors which will
be batched along their first dimension. SparseTensor is not supported. The return value of the decorated function
must be a Tensor or a list/tuple of Tensors.
Parameters
-
objectnum_batch_threads - Number of scheduling threads for processing batches of work. Determines the number of batches processed in parallel.
-
objectmax_batch_size - Batch sizes will never be bigger than this.
-
objectbatch_timeout_micros - Maximum number of microseconds to wait before outputting an incomplete batch.
-
objectallowed_batch_sizes - Optional list of allowed batch sizes. If left empty, does nothing. Otherwise, supplies a list of batch sizes, causing the op to pad batches up to one of those sizes. The entries must increase monotonically, and the final entry must equal max_batch_size.
-
ImplicitContainer<T>max_enqueued_batches - The maximum depth of the batch queue. Defaults to 10.
-
ImplicitContainer<T>autograph - Whether to use autograph to compile python and eager style code for efficient graph-mode execution.
Returns
-
object - The decorated function will return the unbatched computation output Tensors.
Show Example
@batch_function(1, 2, 3)
def layer(a):
return tf.matmul(a, a) b = layer(w)
object none(string name)
object none_dyn(object name)
object norm(IEnumerable<IGraphNodeBase> tensor, string ord, int axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
IEnumerable<IGraphNodeBase>tensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
stringord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
intaxis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(object tensor, string ord, IEnumerable<int> axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
objecttensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
stringord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
IEnumerable<int>axis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(object tensor, int ord, int axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
objecttensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
intord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
intaxis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(IEnumerable<IGraphNodeBase> tensor, int ord, IEnumerable<int> axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
IEnumerable<IGraphNodeBase>tensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
intord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
IEnumerable<int>axis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(object tensor, int ord, IEnumerable<int> axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
objecttensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
intord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
IEnumerable<int>axis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(IEnumerable<IGraphNodeBase> tensor, double ord, int axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
IEnumerable<IGraphNodeBase>tensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
doubleord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
intaxis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(object tensor, double ord, int axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
objecttensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
doubleord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
intaxis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(IEnumerable<IGraphNodeBase> tensor, int ord, int axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
IEnumerable<IGraphNodeBase>tensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
intord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
intaxis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(object tensor, double ord, IEnumerable<int> axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
objecttensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
doubleord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
IEnumerable<int>axis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(IEnumerable<IGraphNodeBase> tensor, string ord, IEnumerable<int> axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
IEnumerable<IGraphNodeBase>tensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
stringord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
IEnumerable<int>axis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(IEnumerable<IGraphNodeBase> tensor, double ord, IEnumerable<int> axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
IEnumerable<IGraphNodeBase>tensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
doubleord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
IEnumerable<int>axis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm(object tensor, string ord, int axis, Nullable<bool> keepdims, string name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
objecttensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
stringord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
intaxis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
Nullable<bool>keepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
stringname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
object norm_dyn(object tensor, ImplicitContainer<T> ord, object axis, object keepdims, object name, object keep_dims)
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
Parameters
-
objecttensor - `Tensor` of types `float32`, `float64`, `complex64`, `complex128`
-
ImplicitContainer<T>ord - Order of the norm. Supported values are 'fro', 'euclidean', `1`, `2`, `np.inf` and any positive real number yielding the corresponding p-norm. Default is 'euclidean' which is equivalent to Frobenius norm if `tensor` is a matrix and equivalent to 2-norm for vectors. Some restrictions apply: a) The Frobenius norm `fro` is not defined for vectors, b) If axis is a 2-tuple (matrix norm), only 'euclidean', 'fro', `1`, `2`, `np.inf` are supported. See the description of `axis` on how to compute norms for a batch of vectors or matrices stored in a tensor.
-
objectaxis - If `axis` is `None` (the default), the input is considered a vector and a single vector norm is computed over the entire set of values in the tensor, i.e. `norm(tensor, ord=ord)` is equivalent to `norm(reshape(tensor, [-1]), ord=ord)`. If `axis` is a Python integer, the input is considered a batch of vectors, and `axis` determines the axis in `tensor` over which to compute vector norms. If `axis` is a 2-tuple of Python integers it is considered a batch of matrices and `axis` determines the axes in `tensor` over which to compute a matrix norm. Negative indices are supported. Example: If you are passing a tensor that can be either a matrix or a batch of matrices at runtime, pass `axis=[-2,-1]` instead of `axis=None` to make sure that matrix norms are computed.
-
objectkeepdims - If True, the axis indicated in `axis` are kept with size 1. Otherwise, the dimensions in `axis` are removed from the output shape.
-
objectname - The name of the op.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object
Tensor not_equal(IEnumerable<IGraphNodeBase> x, PythonClassContainer y, string name)
Returns the truth value of (x != y) element-wise. **NOTE**: `NotEqual` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonClassContainery - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Tensor not_equal(IEnumerable<IGraphNodeBase> x, object y, string name)
Returns the truth value of (x != y) element-wise. **NOTE**: `NotEqual` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
IEnumerable<IGraphNodeBase>x - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objecty - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Tensor not_equal(object x, PythonClassContainer y, string name)
Returns the truth value of (x != y) element-wise. **NOTE**: `NotEqual` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
PythonClassContainery - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
Tensor not_equal(object x, object y, string name)
Returns the truth value of (x != y) element-wise. **NOTE**: `NotEqual` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objecty - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type bool with the same size as that of x or y.
object not_equal_dyn(object x, object y, object name)
Returns the truth value of (x != y) element-wise. **NOTE**: `NotEqual` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objecty - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type bool with the same size as that of x or y.
object numpy_function(PythonFunctionContainer func, ValueTuple inp, IEnumerable<DType> Tout, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.numpy_function()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.numpy_function()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.numpy_function()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
ValueTupleinp - A list of `Tensor` objects.
-
IEnumerable<DType>Tout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.numpy_function(my_func, [input], tf.float32)
object numpy_function(PythonFunctionContainer func, IEnumerable<object> inp, DType Tout, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.numpy_function()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.numpy_function()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.numpy_function()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
DTypeTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.numpy_function(my_func, [input], tf.float32)
object numpy_function(PythonFunctionContainer func, ValueTuple inp, DType Tout, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.numpy_function()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.numpy_function()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.numpy_function()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
ValueTupleinp - A list of `Tensor` objects.
-
DTypeTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.numpy_function(my_func, [input], tf.float32)
object numpy_function(PythonFunctionContainer func, IEnumerable<object> inp, IEnumerable<DType> Tout, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.numpy_function()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.numpy_function()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.numpy_function()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
IEnumerable<DType>Tout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.numpy_function(my_func, [input], tf.float32)
object numpy_function(object func, IEnumerable<object> inp, DType Tout, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.numpy_function()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.numpy_function()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.numpy_function()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
objectfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
DTypeTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.numpy_function(my_func, [input], tf.float32)
object numpy_function(object func, ValueTuple inp, IEnumerable<DType> Tout, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.numpy_function()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.numpy_function()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.numpy_function()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
objectfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
ValueTupleinp - A list of `Tensor` objects.
-
IEnumerable<DType>Tout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.numpy_function(my_func, [input], tf.float32)
object numpy_function(object func, ValueTuple inp, DType Tout, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.numpy_function()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.numpy_function()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.numpy_function()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
objectfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
ValueTupleinp - A list of `Tensor` objects.
-
DTypeTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.numpy_function(my_func, [input], tf.float32)
object numpy_function(object func, IEnumerable<object> inp, IEnumerable<DType> Tout, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.numpy_function()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.numpy_function()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.numpy_function()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
objectfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
IEnumerable<DType>Tout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.numpy_function(my_func, [input], tf.float32)
object numpy_function_dyn(object func, object inp, object Tout, object name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.numpy_function()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.numpy_function()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.numpy_function()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
objectfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
objectinp - A list of `Tensor` objects.
-
objectTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
objectname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.numpy_function(my_func, [input], tf.float32)
Tensor obtain_next(IGraphNodeBase list, IGraphNodeBase counter, string name)
object obtain_next_dyn(object list, object counter, object name)
object old(string name)
object old_dyn(object name)
Tensor one_hot(IGraphNodeBase indices, ndarray depth, object on_value, object off_value, Nullable<int> axis, DType dtype, string name)
Returns a one-hot tensor. The locations represented by indices in `indices` take value `on_value`,
while all other locations take value `off_value`. `on_value` and `off_value` must have matching data types. If `dtype` is also
provided, they must be the same data type as specified by `dtype`. If `on_value` is not provided, it will default to the value `1` with type
`dtype` If `off_value` is not provided, it will default to the value `0` with type
`dtype` If the input `indices` is rank `N`, the output will have rank `N+1`. The
new axis is created at dimension `axis` (default: the new axis is appended
at the end). If `indices` is a scalar the output shape will be a vector of length `depth` If `indices` is a vector of length `features`, the output shape will be: ```
features x depth if axis == -1
depth x features if axis == 0
``` If `indices` is a matrix (batch) with shape `[batch, features]`, the output
shape will be: ```
batch x features x depth if axis == -1
batch x depth x features if axis == 1
depth x batch x features if axis == 0
``` If `indices` is a RaggedTensor, the 'axis' argument must be positive and refer
to a non-ragged axis. The output will be equivalent to applying 'one_hot' on
the values of the RaggedTensor, and creating a new RaggedTensor from the
result. If `dtype` is not provided, it will attempt to assume the data type of
`on_value` or `off_value`, if one or both are passed in. If none of
`on_value`, `off_value`, or `dtype` are provided, `dtype` will default to the
value
tf.float32. Note: If a non-numeric data type output is desired (tf.string, tf.bool,
etc.), both `on_value` and `off_value` _must_ be provided to `one_hot`.
Parameters
-
IGraphNodeBaseindices - A `Tensor` of indices.
-
ndarraydepth - A scalar defining the depth of the one hot dimension.
-
objecton_value - A scalar defining the value to fill in output when `indices[j] = i`. (default: 1)
-
objectoff_value - A scalar defining the value to fill in output when `indices[j] != i`. (default: 0)
-
Nullable<int>axis - The axis to fill (default: -1, a new inner-most axis).
-
DTypedtype - The data type of the output tensor.
-
stringname - A name for the operation (optional).
Returns
Show Example
indices = [0, 1, 2]
depth = 3
tf.one_hot(indices, depth) # output: [3 x 3]
# [[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]] indices = [0, 2, -1, 1]
depth = 3
tf.one_hot(indices, depth,
on_value=5.0, off_value=0.0,
axis=-1) # output: [4 x 3]
# [[5.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 5.0], # one_hot(2)
# [0.0, 0.0, 0.0], # one_hot(-1)
# [0.0, 5.0, 0.0]] # one_hot(1) indices = [[0, 2], [1, -1]]
depth = 3
tf.one_hot(indices, depth,
on_value=1.0, off_value=0.0,
axis=-1) # output: [2 x 2 x 3]
# [[[1.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 1.0]], # one_hot(2)
# [[0.0, 1.0, 0.0], # one_hot(1)
# [0.0, 0.0, 0.0]]] # one_hot(-1) indices = tf.ragged.constant([[0, 1], [2]])
depth = 3
tf.one_hot(indices, depth) # output: [2 x None x 3]
# [[[1., 0., 0.],
# [0., 1., 0.]],
# [[0., 0., 1.]]]
Tensor one_hot(IGraphNodeBase indices, object depth, object on_value, object off_value, Nullable<int> axis, DType dtype, string name)
Returns a one-hot tensor. The locations represented by indices in `indices` take value `on_value`,
while all other locations take value `off_value`. `on_value` and `off_value` must have matching data types. If `dtype` is also
provided, they must be the same data type as specified by `dtype`. If `on_value` is not provided, it will default to the value `1` with type
`dtype` If `off_value` is not provided, it will default to the value `0` with type
`dtype` If the input `indices` is rank `N`, the output will have rank `N+1`. The
new axis is created at dimension `axis` (default: the new axis is appended
at the end). If `indices` is a scalar the output shape will be a vector of length `depth` If `indices` is a vector of length `features`, the output shape will be: ```
features x depth if axis == -1
depth x features if axis == 0
``` If `indices` is a matrix (batch) with shape `[batch, features]`, the output
shape will be: ```
batch x features x depth if axis == -1
batch x depth x features if axis == 1
depth x batch x features if axis == 0
``` If `indices` is a RaggedTensor, the 'axis' argument must be positive and refer
to a non-ragged axis. The output will be equivalent to applying 'one_hot' on
the values of the RaggedTensor, and creating a new RaggedTensor from the
result. If `dtype` is not provided, it will attempt to assume the data type of
`on_value` or `off_value`, if one or both are passed in. If none of
`on_value`, `off_value`, or `dtype` are provided, `dtype` will default to the
value
tf.float32. Note: If a non-numeric data type output is desired (tf.string, tf.bool,
etc.), both `on_value` and `off_value` _must_ be provided to `one_hot`.
Parameters
-
IGraphNodeBaseindices - A `Tensor` of indices.
-
objectdepth - A scalar defining the depth of the one hot dimension.
-
objecton_value - A scalar defining the value to fill in output when `indices[j] = i`. (default: 1)
-
objectoff_value - A scalar defining the value to fill in output when `indices[j] != i`. (default: 0)
-
Nullable<int>axis - The axis to fill (default: -1, a new inner-most axis).
-
DTypedtype - The data type of the output tensor.
-
stringname - A name for the operation (optional).
Returns
Show Example
indices = [0, 1, 2]
depth = 3
tf.one_hot(indices, depth) # output: [3 x 3]
# [[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]] indices = [0, 2, -1, 1]
depth = 3
tf.one_hot(indices, depth,
on_value=5.0, off_value=0.0,
axis=-1) # output: [4 x 3]
# [[5.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 5.0], # one_hot(2)
# [0.0, 0.0, 0.0], # one_hot(-1)
# [0.0, 5.0, 0.0]] # one_hot(1) indices = [[0, 2], [1, -1]]
depth = 3
tf.one_hot(indices, depth,
on_value=1.0, off_value=0.0,
axis=-1) # output: [2 x 2 x 3]
# [[[1.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 1.0]], # one_hot(2)
# [[0.0, 1.0, 0.0], # one_hot(1)
# [0.0, 0.0, 0.0]]] # one_hot(-1) indices = tf.ragged.constant([[0, 1], [2]])
depth = 3
tf.one_hot(indices, depth) # output: [2 x None x 3]
# [[[1., 0., 0.],
# [0., 1., 0.]],
# [[0., 0., 1.]]]
Tensor one_hot(IGraphNodeBase indices, Dimension depth, object on_value, object off_value, Nullable<int> axis, DType dtype, string name)
Returns a one-hot tensor. The locations represented by indices in `indices` take value `on_value`,
while all other locations take value `off_value`. `on_value` and `off_value` must have matching data types. If `dtype` is also
provided, they must be the same data type as specified by `dtype`. If `on_value` is not provided, it will default to the value `1` with type
`dtype` If `off_value` is not provided, it will default to the value `0` with type
`dtype` If the input `indices` is rank `N`, the output will have rank `N+1`. The
new axis is created at dimension `axis` (default: the new axis is appended
at the end). If `indices` is a scalar the output shape will be a vector of length `depth` If `indices` is a vector of length `features`, the output shape will be: ```
features x depth if axis == -1
depth x features if axis == 0
``` If `indices` is a matrix (batch) with shape `[batch, features]`, the output
shape will be: ```
batch x features x depth if axis == -1
batch x depth x features if axis == 1
depth x batch x features if axis == 0
``` If `indices` is a RaggedTensor, the 'axis' argument must be positive and refer
to a non-ragged axis. The output will be equivalent to applying 'one_hot' on
the values of the RaggedTensor, and creating a new RaggedTensor from the
result. If `dtype` is not provided, it will attempt to assume the data type of
`on_value` or `off_value`, if one or both are passed in. If none of
`on_value`, `off_value`, or `dtype` are provided, `dtype` will default to the
value
tf.float32. Note: If a non-numeric data type output is desired (tf.string, tf.bool,
etc.), both `on_value` and `off_value` _must_ be provided to `one_hot`.
Parameters
-
IGraphNodeBaseindices - A `Tensor` of indices.
-
Dimensiondepth - A scalar defining the depth of the one hot dimension.
-
objecton_value - A scalar defining the value to fill in output when `indices[j] = i`. (default: 1)
-
objectoff_value - A scalar defining the value to fill in output when `indices[j] != i`. (default: 0)
-
Nullable<int>axis - The axis to fill (default: -1, a new inner-most axis).
-
DTypedtype - The data type of the output tensor.
-
stringname - A name for the operation (optional).
Returns
Show Example
indices = [0, 1, 2]
depth = 3
tf.one_hot(indices, depth) # output: [3 x 3]
# [[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]] indices = [0, 2, -1, 1]
depth = 3
tf.one_hot(indices, depth,
on_value=5.0, off_value=0.0,
axis=-1) # output: [4 x 3]
# [[5.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 5.0], # one_hot(2)
# [0.0, 0.0, 0.0], # one_hot(-1)
# [0.0, 5.0, 0.0]] # one_hot(1) indices = [[0, 2], [1, -1]]
depth = 3
tf.one_hot(indices, depth,
on_value=1.0, off_value=0.0,
axis=-1) # output: [2 x 2 x 3]
# [[[1.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 1.0]], # one_hot(2)
# [[0.0, 1.0, 0.0], # one_hot(1)
# [0.0, 0.0, 0.0]]] # one_hot(-1) indices = tf.ragged.constant([[0, 1], [2]])
depth = 3
tf.one_hot(indices, depth) # output: [2 x None x 3]
# [[[1., 0., 0.],
# [0., 1., 0.]],
# [[0., 0., 1.]]]
Tensor one_hot(IGraphNodeBase indices, TensorShape depth, object on_value, object off_value, Nullable<int> axis, DType dtype, string name)
Returns a one-hot tensor. The locations represented by indices in `indices` take value `on_value`,
while all other locations take value `off_value`. `on_value` and `off_value` must have matching data types. If `dtype` is also
provided, they must be the same data type as specified by `dtype`. If `on_value` is not provided, it will default to the value `1` with type
`dtype` If `off_value` is not provided, it will default to the value `0` with type
`dtype` If the input `indices` is rank `N`, the output will have rank `N+1`. The
new axis is created at dimension `axis` (default: the new axis is appended
at the end). If `indices` is a scalar the output shape will be a vector of length `depth` If `indices` is a vector of length `features`, the output shape will be: ```
features x depth if axis == -1
depth x features if axis == 0
``` If `indices` is a matrix (batch) with shape `[batch, features]`, the output
shape will be: ```
batch x features x depth if axis == -1
batch x depth x features if axis == 1
depth x batch x features if axis == 0
``` If `indices` is a RaggedTensor, the 'axis' argument must be positive and refer
to a non-ragged axis. The output will be equivalent to applying 'one_hot' on
the values of the RaggedTensor, and creating a new RaggedTensor from the
result. If `dtype` is not provided, it will attempt to assume the data type of
`on_value` or `off_value`, if one or both are passed in. If none of
`on_value`, `off_value`, or `dtype` are provided, `dtype` will default to the
value
tf.float32. Note: If a non-numeric data type output is desired (tf.string, tf.bool,
etc.), both `on_value` and `off_value` _must_ be provided to `one_hot`.
Parameters
-
IGraphNodeBaseindices - A `Tensor` of indices.
-
TensorShapedepth - A scalar defining the depth of the one hot dimension.
-
objecton_value - A scalar defining the value to fill in output when `indices[j] = i`. (default: 1)
-
objectoff_value - A scalar defining the value to fill in output when `indices[j] != i`. (default: 0)
-
Nullable<int>axis - The axis to fill (default: -1, a new inner-most axis).
-
DTypedtype - The data type of the output tensor.
-
stringname - A name for the operation (optional).
Returns
Show Example
indices = [0, 1, 2]
depth = 3
tf.one_hot(indices, depth) # output: [3 x 3]
# [[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]] indices = [0, 2, -1, 1]
depth = 3
tf.one_hot(indices, depth,
on_value=5.0, off_value=0.0,
axis=-1) # output: [4 x 3]
# [[5.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 5.0], # one_hot(2)
# [0.0, 0.0, 0.0], # one_hot(-1)
# [0.0, 5.0, 0.0]] # one_hot(1) indices = [[0, 2], [1, -1]]
depth = 3
tf.one_hot(indices, depth,
on_value=1.0, off_value=0.0,
axis=-1) # output: [2 x 2 x 3]
# [[[1.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 1.0]], # one_hot(2)
# [[0.0, 1.0, 0.0], # one_hot(1)
# [0.0, 0.0, 0.0]]] # one_hot(-1) indices = tf.ragged.constant([[0, 1], [2]])
depth = 3
tf.one_hot(indices, depth) # output: [2 x None x 3]
# [[[1., 0., 0.],
# [0., 1., 0.]],
# [[0., 0., 1.]]]
Tensor one_hot(IGraphNodeBase indices, int32 depth, object on_value, object off_value, Nullable<int> axis, DType dtype, string name)
Returns a one-hot tensor. The locations represented by indices in `indices` take value `on_value`,
while all other locations take value `off_value`. `on_value` and `off_value` must have matching data types. If `dtype` is also
provided, they must be the same data type as specified by `dtype`. If `on_value` is not provided, it will default to the value `1` with type
`dtype` If `off_value` is not provided, it will default to the value `0` with type
`dtype` If the input `indices` is rank `N`, the output will have rank `N+1`. The
new axis is created at dimension `axis` (default: the new axis is appended
at the end). If `indices` is a scalar the output shape will be a vector of length `depth` If `indices` is a vector of length `features`, the output shape will be: ```
features x depth if axis == -1
depth x features if axis == 0
``` If `indices` is a matrix (batch) with shape `[batch, features]`, the output
shape will be: ```
batch x features x depth if axis == -1
batch x depth x features if axis == 1
depth x batch x features if axis == 0
``` If `indices` is a RaggedTensor, the 'axis' argument must be positive and refer
to a non-ragged axis. The output will be equivalent to applying 'one_hot' on
the values of the RaggedTensor, and creating a new RaggedTensor from the
result. If `dtype` is not provided, it will attempt to assume the data type of
`on_value` or `off_value`, if one or both are passed in. If none of
`on_value`, `off_value`, or `dtype` are provided, `dtype` will default to the
value
tf.float32. Note: If a non-numeric data type output is desired (tf.string, tf.bool,
etc.), both `on_value` and `off_value` _must_ be provided to `one_hot`.
Parameters
-
IGraphNodeBaseindices - A `Tensor` of indices.
-
int32depth - A scalar defining the depth of the one hot dimension.
-
objecton_value - A scalar defining the value to fill in output when `indices[j] = i`. (default: 1)
-
objectoff_value - A scalar defining the value to fill in output when `indices[j] != i`. (default: 0)
-
Nullable<int>axis - The axis to fill (default: -1, a new inner-most axis).
-
DTypedtype - The data type of the output tensor.
-
stringname - A name for the operation (optional).
Returns
Show Example
indices = [0, 1, 2]
depth = 3
tf.one_hot(indices, depth) # output: [3 x 3]
# [[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]] indices = [0, 2, -1, 1]
depth = 3
tf.one_hot(indices, depth,
on_value=5.0, off_value=0.0,
axis=-1) # output: [4 x 3]
# [[5.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 5.0], # one_hot(2)
# [0.0, 0.0, 0.0], # one_hot(-1)
# [0.0, 5.0, 0.0]] # one_hot(1) indices = [[0, 2], [1, -1]]
depth = 3
tf.one_hot(indices, depth,
on_value=1.0, off_value=0.0,
axis=-1) # output: [2 x 2 x 3]
# [[[1.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 1.0]], # one_hot(2)
# [[0.0, 1.0, 0.0], # one_hot(1)
# [0.0, 0.0, 0.0]]] # one_hot(-1) indices = tf.ragged.constant([[0, 1], [2]])
depth = 3
tf.one_hot(indices, depth) # output: [2 x None x 3]
# [[[1., 0., 0.],
# [0., 1., 0.]],
# [[0., 0., 1.]]]
Tensor one_hot(IGraphNodeBase indices, int depth, object on_value, object off_value, Nullable<int> axis, DType dtype, string name)
Returns a one-hot tensor. The locations represented by indices in `indices` take value `on_value`,
while all other locations take value `off_value`. `on_value` and `off_value` must have matching data types. If `dtype` is also
provided, they must be the same data type as specified by `dtype`. If `on_value` is not provided, it will default to the value `1` with type
`dtype` If `off_value` is not provided, it will default to the value `0` with type
`dtype` If the input `indices` is rank `N`, the output will have rank `N+1`. The
new axis is created at dimension `axis` (default: the new axis is appended
at the end). If `indices` is a scalar the output shape will be a vector of length `depth` If `indices` is a vector of length `features`, the output shape will be: ```
features x depth if axis == -1
depth x features if axis == 0
``` If `indices` is a matrix (batch) with shape `[batch, features]`, the output
shape will be: ```
batch x features x depth if axis == -1
batch x depth x features if axis == 1
depth x batch x features if axis == 0
``` If `indices` is a RaggedTensor, the 'axis' argument must be positive and refer
to a non-ragged axis. The output will be equivalent to applying 'one_hot' on
the values of the RaggedTensor, and creating a new RaggedTensor from the
result. If `dtype` is not provided, it will attempt to assume the data type of
`on_value` or `off_value`, if one or both are passed in. If none of
`on_value`, `off_value`, or `dtype` are provided, `dtype` will default to the
value
tf.float32. Note: If a non-numeric data type output is desired (tf.string, tf.bool,
etc.), both `on_value` and `off_value` _must_ be provided to `one_hot`.
Parameters
-
IGraphNodeBaseindices - A `Tensor` of indices.
-
intdepth - A scalar defining the depth of the one hot dimension.
-
objecton_value - A scalar defining the value to fill in output when `indices[j] = i`. (default: 1)
-
objectoff_value - A scalar defining the value to fill in output when `indices[j] != i`. (default: 0)
-
Nullable<int>axis - The axis to fill (default: -1, a new inner-most axis).
-
DTypedtype - The data type of the output tensor.
-
stringname - A name for the operation (optional).
Returns
Show Example
indices = [0, 1, 2]
depth = 3
tf.one_hot(indices, depth) # output: [3 x 3]
# [[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]] indices = [0, 2, -1, 1]
depth = 3
tf.one_hot(indices, depth,
on_value=5.0, off_value=0.0,
axis=-1) # output: [4 x 3]
# [[5.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 5.0], # one_hot(2)
# [0.0, 0.0, 0.0], # one_hot(-1)
# [0.0, 5.0, 0.0]] # one_hot(1) indices = [[0, 2], [1, -1]]
depth = 3
tf.one_hot(indices, depth,
on_value=1.0, off_value=0.0,
axis=-1) # output: [2 x 2 x 3]
# [[[1.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 1.0]], # one_hot(2)
# [[0.0, 1.0, 0.0], # one_hot(1)
# [0.0, 0.0, 0.0]]] # one_hot(-1) indices = tf.ragged.constant([[0, 1], [2]])
depth = 3
tf.one_hot(indices, depth) # output: [2 x None x 3]
# [[[1., 0., 0.],
# [0., 1., 0.]],
# [[0., 0., 1.]]]
Tensor one_hot(IGraphNodeBase indices, IGraphNodeBase depth, object on_value, object off_value, Nullable<int> axis, DType dtype, string name)
Returns a one-hot tensor. The locations represented by indices in `indices` take value `on_value`,
while all other locations take value `off_value`. `on_value` and `off_value` must have matching data types. If `dtype` is also
provided, they must be the same data type as specified by `dtype`. If `on_value` is not provided, it will default to the value `1` with type
`dtype` If `off_value` is not provided, it will default to the value `0` with type
`dtype` If the input `indices` is rank `N`, the output will have rank `N+1`. The
new axis is created at dimension `axis` (default: the new axis is appended
at the end). If `indices` is a scalar the output shape will be a vector of length `depth` If `indices` is a vector of length `features`, the output shape will be: ```
features x depth if axis == -1
depth x features if axis == 0
``` If `indices` is a matrix (batch) with shape `[batch, features]`, the output
shape will be: ```
batch x features x depth if axis == -1
batch x depth x features if axis == 1
depth x batch x features if axis == 0
``` If `indices` is a RaggedTensor, the 'axis' argument must be positive and refer
to a non-ragged axis. The output will be equivalent to applying 'one_hot' on
the values of the RaggedTensor, and creating a new RaggedTensor from the
result. If `dtype` is not provided, it will attempt to assume the data type of
`on_value` or `off_value`, if one or both are passed in. If none of
`on_value`, `off_value`, or `dtype` are provided, `dtype` will default to the
value
tf.float32. Note: If a non-numeric data type output is desired (tf.string, tf.bool,
etc.), both `on_value` and `off_value` _must_ be provided to `one_hot`.
Parameters
-
IGraphNodeBaseindices - A `Tensor` of indices.
-
IGraphNodeBasedepth - A scalar defining the depth of the one hot dimension.
-
objecton_value - A scalar defining the value to fill in output when `indices[j] = i`. (default: 1)
-
objectoff_value - A scalar defining the value to fill in output when `indices[j] != i`. (default: 0)
-
Nullable<int>axis - The axis to fill (default: -1, a new inner-most axis).
-
DTypedtype - The data type of the output tensor.
-
stringname - A name for the operation (optional).
Returns
Show Example
indices = [0, 1, 2]
depth = 3
tf.one_hot(indices, depth) # output: [3 x 3]
# [[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]] indices = [0, 2, -1, 1]
depth = 3
tf.one_hot(indices, depth,
on_value=5.0, off_value=0.0,
axis=-1) # output: [4 x 3]
# [[5.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 5.0], # one_hot(2)
# [0.0, 0.0, 0.0], # one_hot(-1)
# [0.0, 5.0, 0.0]] # one_hot(1) indices = [[0, 2], [1, -1]]
depth = 3
tf.one_hot(indices, depth,
on_value=1.0, off_value=0.0,
axis=-1) # output: [2 x 2 x 3]
# [[[1.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 1.0]], # one_hot(2)
# [[0.0, 1.0, 0.0], # one_hot(1)
# [0.0, 0.0, 0.0]]] # one_hot(-1) indices = tf.ragged.constant([[0, 1], [2]])
depth = 3
tf.one_hot(indices, depth) # output: [2 x None x 3]
# [[[1., 0., 0.],
# [0., 1., 0.]],
# [[0., 0., 1.]]]
object one_hot_dyn(object indices, object depth, object on_value, object off_value, object axis, object dtype, object name)
Returns a one-hot tensor. The locations represented by indices in `indices` take value `on_value`,
while all other locations take value `off_value`. `on_value` and `off_value` must have matching data types. If `dtype` is also
provided, they must be the same data type as specified by `dtype`. If `on_value` is not provided, it will default to the value `1` with type
`dtype` If `off_value` is not provided, it will default to the value `0` with type
`dtype` If the input `indices` is rank `N`, the output will have rank `N+1`. The
new axis is created at dimension `axis` (default: the new axis is appended
at the end). If `indices` is a scalar the output shape will be a vector of length `depth` If `indices` is a vector of length `features`, the output shape will be: ```
features x depth if axis == -1
depth x features if axis == 0
``` If `indices` is a matrix (batch) with shape `[batch, features]`, the output
shape will be: ```
batch x features x depth if axis == -1
batch x depth x features if axis == 1
depth x batch x features if axis == 0
``` If `indices` is a RaggedTensor, the 'axis' argument must be positive and refer
to a non-ragged axis. The output will be equivalent to applying 'one_hot' on
the values of the RaggedTensor, and creating a new RaggedTensor from the
result. If `dtype` is not provided, it will attempt to assume the data type of
`on_value` or `off_value`, if one or both are passed in. If none of
`on_value`, `off_value`, or `dtype` are provided, `dtype` will default to the
value
tf.float32. Note: If a non-numeric data type output is desired (tf.string, tf.bool,
etc.), both `on_value` and `off_value` _must_ be provided to `one_hot`.
Parameters
-
objectindices - A `Tensor` of indices.
-
objectdepth - A scalar defining the depth of the one hot dimension.
-
objecton_value - A scalar defining the value to fill in output when `indices[j] = i`. (default: 1)
-
objectoff_value - A scalar defining the value to fill in output when `indices[j] != i`. (default: 0)
-
objectaxis - The axis to fill (default: -1, a new inner-most axis).
-
objectdtype - The data type of the output tensor.
-
objectname - A name for the operation (optional).
Returns
-
object
Show Example
indices = [0, 1, 2]
depth = 3
tf.one_hot(indices, depth) # output: [3 x 3]
# [[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]] indices = [0, 2, -1, 1]
depth = 3
tf.one_hot(indices, depth,
on_value=5.0, off_value=0.0,
axis=-1) # output: [4 x 3]
# [[5.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 5.0], # one_hot(2)
# [0.0, 0.0, 0.0], # one_hot(-1)
# [0.0, 5.0, 0.0]] # one_hot(1) indices = [[0, 2], [1, -1]]
depth = 3
tf.one_hot(indices, depth,
on_value=1.0, off_value=0.0,
axis=-1) # output: [2 x 2 x 3]
# [[[1.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 1.0]], # one_hot(2)
# [[0.0, 1.0, 0.0], # one_hot(1)
# [0.0, 0.0, 0.0]]] # one_hot(-1) indices = tf.ragged.constant([[0, 1], [2]])
depth = 3
tf.one_hot(indices, depth) # output: [2 x None x 3]
# [[[1., 0., 0.],
# [0., 1., 0.]],
# [[0., 0., 1.]]]
Tensor ones(object shape, ImplicitContainer<T> dtype, string name)
Creates a tensor with all elements set to 1. This operation returns a tensor of type `dtype` with shape `shape` and all
elements set to 1.
Parameters
-
objectshape - A list of integers, a tuple of integers, or a 1-D `Tensor` of type `int32`.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with all elements set to 1.
Show Example
tf.ones([2, 3], tf.int32) # [[1, 1, 1], [1, 1, 1]]
Tensor ones(object shape, PythonClassContainer dtype, PythonFunctionContainer name)
Creates a tensor with all elements set to 1. This operation returns a tensor of type `dtype` with shape `shape` and all
elements set to 1.
Parameters
-
objectshape - A list of integers, a tuple of integers, or a 1-D `Tensor` of type `int32`.
-
PythonClassContainerdtype - The type of an element in the resulting `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with all elements set to 1.
Show Example
tf.ones([2, 3], tf.int32) # [[1, 1, 1], [1, 1, 1]]
Tensor ones(object shape, PythonClassContainer dtype, string name)
Creates a tensor with all elements set to 1. This operation returns a tensor of type `dtype` with shape `shape` and all
elements set to 1.
Parameters
-
objectshape - A list of integers, a tuple of integers, or a 1-D `Tensor` of type `int32`.
-
PythonClassContainerdtype - The type of an element in the resulting `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with all elements set to 1.
Show Example
tf.ones([2, 3], tf.int32) # [[1, 1, 1], [1, 1, 1]]
Tensor ones(object shape, ImplicitContainer<T> dtype, PythonFunctionContainer name)
Creates a tensor with all elements set to 1. This operation returns a tensor of type `dtype` with shape `shape` and all
elements set to 1.
Parameters
-
objectshape - A list of integers, a tuple of integers, or a 1-D `Tensor` of type `int32`.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with all elements set to 1.
Show Example
tf.ones([2, 3], tf.int32) # [[1, 1, 1], [1, 1, 1]]
object ones_dyn(object shape, ImplicitContainer<T> dtype, object name)
Creates a tensor with all elements set to 1. This operation returns a tensor of type `dtype` with shape `shape` and all
elements set to 1.
Parameters
-
objectshape - A list of integers, a tuple of integers, or a 1-D `Tensor` of type `int32`.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` with all elements set to 1.
Show Example
tf.ones([2, 3], tf.int32) # [[1, 1, 1], [1, 1, 1]]
Tensor ones_like(IGraphNodeBase tensor, DType dtype, string name, bool optimize)
Creates a tensor with all elements set to 1. Given a single tensor (`tensor`), this operation returns a tensor of the same
type and shape as `tensor` with all elements set to 1. Optionally, you can
specify a new type (`dtype`) for the returned tensor.
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
DTypedtype - A type for the returned `Tensor`. Must be `float32`, `float64`, `int8`, `uint8`, `int16`, `uint16`, `int32`, `int64`, `complex64`, `complex128` or `bool`.
-
stringname - A name for the operation (optional).
-
booloptimize - if true, attempt to statically determine the shape of 'tensor' and encode it as a constant.
Returns
-
Tensor - A `Tensor` with all elements set to 1.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.ones_like(tensor) # [[1, 1, 1], [1, 1, 1]]
Tensor ones_like(IGraphNodeBase tensor, PythonClassContainer dtype, string name, bool optimize)
Creates a tensor with all elements set to 1. Given a single tensor (`tensor`), this operation returns a tensor of the same
type and shape as `tensor` with all elements set to 1. Optionally, you can
specify a new type (`dtype`) for the returned tensor.
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
PythonClassContainerdtype - A type for the returned `Tensor`. Must be `float32`, `float64`, `int8`, `uint8`, `int16`, `uint16`, `int32`, `int64`, `complex64`, `complex128` or `bool`.
-
stringname - A name for the operation (optional).
-
booloptimize - if true, attempt to statically determine the shape of 'tensor' and encode it as a constant.
Returns
-
Tensor - A `Tensor` with all elements set to 1.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.ones_like(tensor) # [[1, 1, 1], [1, 1, 1]]
Tensor ones_like(IGraphNodeBase tensor, dtype dtype, string name, bool optimize)
Creates a tensor with all elements set to 1. Given a single tensor (`tensor`), this operation returns a tensor of the same
type and shape as `tensor` with all elements set to 1. Optionally, you can
specify a new type (`dtype`) for the returned tensor.
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
dtypedtype - A type for the returned `Tensor`. Must be `float32`, `float64`, `int8`, `uint8`, `int16`, `uint16`, `int32`, `int64`, `complex64`, `complex128` or `bool`.
-
stringname - A name for the operation (optional).
-
booloptimize - if true, attempt to statically determine the shape of 'tensor' and encode it as a constant.
Returns
-
Tensor - A `Tensor` with all elements set to 1.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.ones_like(tensor) # [[1, 1, 1], [1, 1, 1]]
object ones_like_dyn(object tensor, object dtype, object name, ImplicitContainer<T> optimize)
Creates a tensor with all elements set to 1. Given a single tensor (`tensor`), this operation returns a tensor of the same
type and shape as `tensor` with all elements set to 1. Optionally, you can
specify a new type (`dtype`) for the returned tensor.
Parameters
-
objecttensor - A `Tensor`.
-
objectdtype - A type for the returned `Tensor`. Must be `float32`, `float64`, `int8`, `uint8`, `int16`, `uint16`, `int32`, `int64`, `complex64`, `complex128` or `bool`.
-
objectname - A name for the operation (optional).
-
ImplicitContainer<T>optimize - if true, attempt to statically determine the shape of 'tensor' and encode it as a constant.
Returns
-
object - A `Tensor` with all elements set to 1.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.ones_like(tensor) # [[1, 1, 1], [1, 1, 1]]
IContextManager<T> op_scope(object values, string name, object default_name)
DEPRECATED. Same as name_scope above, just different argument order.
object op_scope_dyn(object values, object name, object default_name)
DEPRECATED. Same as name_scope above, just different argument order.
Tensor op_with_default_attr(int default_float, string name)
object op_with_default_attr_dyn(ImplicitContainer<T> default_float, object name)
object op_with_future_default_attr(string name)
object op_with_future_default_attr_dyn(object name)
Tensor out_t(object T, string name)
object out_t_dyn(object T, object name)
object out_type_list(object T, string name)
object out_type_list_dyn(object T, object name)
object out_type_list_restrict(object t, string name)
object out_type_list_restrict_dyn(object t, object name)
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, PythonFunctionContainer name, string constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
PythonFunctionContainername - A name for the operation (optional).
-
stringconstant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, string name, IEnumerable<int> constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
stringname - A name for the operation (optional).
-
IEnumerable<int>constant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, PythonFunctionContainer name, Complex constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
PythonFunctionContainername - A name for the operation (optional).
-
Complexconstant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, PythonFunctionContainer name, int constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
PythonFunctionContainername - A name for the operation (optional).
-
intconstant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, PythonFunctionContainer name, double constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
PythonFunctionContainername - A name for the operation (optional).
-
doubleconstant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, string name, int constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
stringname - A name for the operation (optional).
-
intconstant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, string name, IGraphNodeBase constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
stringname - A name for the operation (optional).
-
IGraphNodeBaseconstant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, string name, Complex constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
stringname - A name for the operation (optional).
-
Complexconstant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, PythonFunctionContainer name, IEnumerable<int> constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
PythonFunctionContainername - A name for the operation (optional).
-
IEnumerable<int>constant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, PythonFunctionContainer name, IGraphNodeBase constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
PythonFunctionContainername - A name for the operation (optional).
-
IGraphNodeBaseconstant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, string name, double constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
stringname - A name for the operation (optional).
-
doubleconstant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor pad(IGraphNodeBase tensor, IGraphNodeBase paddings, string mode, string name, string constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBasepaddings - A `Tensor` of type `int32`.
-
stringmode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
stringname - A name for the operation (optional).
-
stringconstant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
object pad_dyn(object tensor, object paddings, ImplicitContainer<T> mode, object name, ImplicitContainer<T> constant_values)
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Parameters
-
objecttensor - A `Tensor`.
-
objectpaddings - A `Tensor` of type `int32`.
-
ImplicitContainer<T>mode - One of "CONSTANT", "REFLECT", or "SYMMETRIC" (case-insensitive)
-
objectname - A name for the operation (optional).
-
ImplicitContainer<T>constant_values - In "CONSTANT" mode, the scalar pad value to use. Must be same type as `tensor`.
Returns
-
object - A `Tensor`. Has the same type as `tensor`.
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
Tensor parallel_stack(IEnumerable<object> values, string name)
Stacks a list of rank-`R` tensors into one rank-`(R+1)` tensor in parallel. Requires that the shape of inputs be known at graph construction time. Packs the list of tensors in `values` into a tensor with rank one higher than
each tensor in `values`, by packing them along the first dimension.
Given a list of length `N` of tensors of shape `(A, B, C)`; the `output`
tensor will have the shape `(N, A, B, C)`.
The difference between `stack` and `parallel_stack` is that `stack` requires
all the inputs be computed before the operation will begin but doesn't require
that the input shapes be known during graph construction. `parallel_stack` will copy pieces of the input into the output as they become
available, in some situations this can provide a performance benefit. Unlike `stack`, `parallel_stack` does NOT support backpropagation. This is the opposite of unstack. The numpy equivalent is tf.parallel_stack([x, y, z]) = np.asarray([x, y, z])
Parameters
-
IEnumerable<object>values - A list of `Tensor` objects with the same shape and type.
-
stringname - A name for this operation (optional).
Returns
Show Example
x = tf.constant([1, 4])
y = tf.constant([2, 5])
z = tf.constant([3, 6])
tf.parallel_stack([x, y, z]) # [[1, 4], [2, 5], [3, 6]]
object parallel_stack_dyn(object values, ImplicitContainer<T> name)
Stacks a list of rank-`R` tensors into one rank-`(R+1)` tensor in parallel. Requires that the shape of inputs be known at graph construction time. Packs the list of tensors in `values` into a tensor with rank one higher than
each tensor in `values`, by packing them along the first dimension.
Given a list of length `N` of tensors of shape `(A, B, C)`; the `output`
tensor will have the shape `(N, A, B, C)`.
The difference between `stack` and `parallel_stack` is that `stack` requires
all the inputs be computed before the operation will begin but doesn't require
that the input shapes be known during graph construction. `parallel_stack` will copy pieces of the input into the output as they become
available, in some situations this can provide a performance benefit. Unlike `stack`, `parallel_stack` does NOT support backpropagation. This is the opposite of unstack. The numpy equivalent is tf.parallel_stack([x, y, z]) = np.asarray([x, y, z])
Parameters
-
objectvalues - A list of `Tensor` objects with the same shape and type.
-
ImplicitContainer<T>name - A name for this operation (optional).
Returns
-
object
Show Example
x = tf.constant([1, 4])
y = tf.constant([2, 5])
z = tf.constant([3, 6])
tf.parallel_stack([x, y, z]) # [[1, 4], [2, 5], [3, 6]]
IDictionary<object, object> parse_example(IDictionary<object, object> serialized, IDictionary<string, object> features, string name, object example_names)
Parses `Example` protos into a `dict` of tensors. Parses a number of serialized [`Example`](https://www.tensorflow.org/code/tensorflow/core/example/example.proto)
protos given in `serialized`. We refer to `serialized` as a batch with
`batch_size` many entries of individual `Example` protos. `example_names` may contain descriptive names for the corresponding serialized
protos. These may be useful for debugging purposes, but they have no effect on
the output. If not `None`, `example_names` must be the same length as
`serialized`. This op parses serialized examples into a dictionary mapping keys to `Tensor`
and `SparseTensor` objects. `features` is a dict from keys to `VarLenFeature`,
`SparseFeature`, and `FixedLenFeature` objects. Each `VarLenFeature`
and `SparseFeature` is mapped to a `SparseTensor`, and each
`FixedLenFeature` is mapped to a `Tensor`. Each `VarLenFeature` maps to a `SparseTensor` of the specified type
representing a ragged matrix. Its indices are `[batch, index]` where `batch`
identifies the example in `serialized`, and `index` is the value's index in
the list of values associated with that feature and example. Each `SparseFeature` maps to a `SparseTensor` of the specified type
representing a Tensor of `dense_shape` `[batch_size] + SparseFeature.size`.
Its `values` come from the feature in the examples with key `value_key`.
A `values[i]` comes from a position `k` in the feature of an example at batch
entry `batch`. This positional information is recorded in `indices[i]` as
`[batch, index_0, index_1,...]` where `index_j` is the `k-th` value of
the feature in the example at with key `SparseFeature.index_key[j]`.
In other words, we split the indices (except the first index indicating the
batch entry) of a `SparseTensor` by dimension into different features of the
`Example`. Due to its complexity a `VarLenFeature` should be preferred over a
`SparseFeature` whenever possible. Each `FixedLenFeature` `df` maps to a `Tensor` of the specified type (or
tf.float32 if not specified) and shape `(serialized.size(),) + df.shape`. `FixedLenFeature` entries with a `default_value` are optional. With no default
value, we will fail if that `Feature` is missing from any example in
`serialized`. Each `FixedLenSequenceFeature` `df` maps to a `Tensor` of the specified type
(or tf.float32 if not specified) and shape
`(serialized.size(), None) + df.shape`.
All examples in `serialized` will be padded with `default_value` along the
second dimension. Examples: For example, if one expects a tf.float32 `VarLenFeature` `ft` and three
serialized `Example`s are provided: ```
serialized = [
features
{ feature { key: "ft" value { float_list { value: [1.0, 2.0] } } } },
features
{ feature []},
features
{ feature { key: "ft" value { float_list { value: [3.0] } } }
]
``` then the output will look like:
If instead a `FixedLenSequenceFeature` with `default_value = -1.0` and
`shape=[]` is used then the output will look like:
Given two `Example` input protos in `serialized`: ```
[
features {
feature { key: "kw" value { bytes_list { value: [ "knit", "big" ] } } }
feature { key: "gps" value { float_list { value: [] } } }
},
features {
feature { key: "kw" value { bytes_list { value: [ "emmy" ] } } }
feature { key: "dank" value { int64_list { value: [ 42 ] } } }
feature { key: "gps" value { } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"kw": VarLenFeature(tf.string),
"dank": VarLenFeature(tf.int64),
"gps": VarLenFeature(tf.float32),
}
``` Then the output is a dictionary:
For dense results in two serialized `Example`s: ```
[
features {
feature { key: "age" value { int64_list { value: [ 0 ] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
},
features {
feature { key: "age" value { int64_list { value: [] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
}
]
``` We can use arguments: ```
example_names: ["input0", "input1"],
features: {
"age": FixedLenFeature([], dtype=tf.int64, default_value=-1),
"gender": FixedLenFeature([], dtype=tf.string),
}
``` And the expected output is:
An alternative to `VarLenFeature` to obtain a `SparseTensor` is
`SparseFeature`. For example, given two `Example` input protos in
`serialized`: ```
[
features {
feature { key: "val" value { float_list { value: [ 0.5, -1.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 3, 20 ] } } }
},
features {
feature { key: "val" value { float_list { value: [ 0.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 42 ] } } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"sparse": SparseFeature(
index_key="ix", value_key="val", dtype=tf.float32, size=100),
}
``` Then the output is a dictionary:
Parameters
-
IDictionary<object, object>serialized - A vector (1-D Tensor) of strings, a batch of binary serialized `Example` protos.
-
IDictionary<string, object>features - A `dict` mapping feature keys to `FixedLenFeature`, `VarLenFeature`, and `SparseFeature` values.
-
stringname - A name for this operation (optional).
-
objectexample_names - A vector (1-D Tensor) of strings (optional), the names of the serialized protos in the batch.
Returns
-
IDictionary<object, object> - A `dict` mapping feature keys to `Tensor` and `SparseTensor` values.
Show Example
{"ft": SparseTensor(indices=[[0, 0], [0, 1], [2, 0]],
values=[1.0, 2.0, 3.0],
dense_shape=(3, 2)) }
IDictionary<object, object> parse_example(ValueTuple<PythonClassContainer, PythonClassContainer> serialized, IDictionary<string, object> features, string name, object example_names)
Parses `Example` protos into a `dict` of tensors. Parses a number of serialized [`Example`](https://www.tensorflow.org/code/tensorflow/core/example/example.proto)
protos given in `serialized`. We refer to `serialized` as a batch with
`batch_size` many entries of individual `Example` protos. `example_names` may contain descriptive names for the corresponding serialized
protos. These may be useful for debugging purposes, but they have no effect on
the output. If not `None`, `example_names` must be the same length as
`serialized`. This op parses serialized examples into a dictionary mapping keys to `Tensor`
and `SparseTensor` objects. `features` is a dict from keys to `VarLenFeature`,
`SparseFeature`, and `FixedLenFeature` objects. Each `VarLenFeature`
and `SparseFeature` is mapped to a `SparseTensor`, and each
`FixedLenFeature` is mapped to a `Tensor`. Each `VarLenFeature` maps to a `SparseTensor` of the specified type
representing a ragged matrix. Its indices are `[batch, index]` where `batch`
identifies the example in `serialized`, and `index` is the value's index in
the list of values associated with that feature and example. Each `SparseFeature` maps to a `SparseTensor` of the specified type
representing a Tensor of `dense_shape` `[batch_size] + SparseFeature.size`.
Its `values` come from the feature in the examples with key `value_key`.
A `values[i]` comes from a position `k` in the feature of an example at batch
entry `batch`. This positional information is recorded in `indices[i]` as
`[batch, index_0, index_1,...]` where `index_j` is the `k-th` value of
the feature in the example at with key `SparseFeature.index_key[j]`.
In other words, we split the indices (except the first index indicating the
batch entry) of a `SparseTensor` by dimension into different features of the
`Example`. Due to its complexity a `VarLenFeature` should be preferred over a
`SparseFeature` whenever possible. Each `FixedLenFeature` `df` maps to a `Tensor` of the specified type (or
tf.float32 if not specified) and shape `(serialized.size(),) + df.shape`. `FixedLenFeature` entries with a `default_value` are optional. With no default
value, we will fail if that `Feature` is missing from any example in
`serialized`. Each `FixedLenSequenceFeature` `df` maps to a `Tensor` of the specified type
(or tf.float32 if not specified) and shape
`(serialized.size(), None) + df.shape`.
All examples in `serialized` will be padded with `default_value` along the
second dimension. Examples: For example, if one expects a tf.float32 `VarLenFeature` `ft` and three
serialized `Example`s are provided: ```
serialized = [
features
{ feature { key: "ft" value { float_list { value: [1.0, 2.0] } } } },
features
{ feature []},
features
{ feature { key: "ft" value { float_list { value: [3.0] } } }
]
``` then the output will look like:
If instead a `FixedLenSequenceFeature` with `default_value = -1.0` and
`shape=[]` is used then the output will look like:
Given two `Example` input protos in `serialized`: ```
[
features {
feature { key: "kw" value { bytes_list { value: [ "knit", "big" ] } } }
feature { key: "gps" value { float_list { value: [] } } }
},
features {
feature { key: "kw" value { bytes_list { value: [ "emmy" ] } } }
feature { key: "dank" value { int64_list { value: [ 42 ] } } }
feature { key: "gps" value { } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"kw": VarLenFeature(tf.string),
"dank": VarLenFeature(tf.int64),
"gps": VarLenFeature(tf.float32),
}
``` Then the output is a dictionary:
For dense results in two serialized `Example`s: ```
[
features {
feature { key: "age" value { int64_list { value: [ 0 ] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
},
features {
feature { key: "age" value { int64_list { value: [] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
}
]
``` We can use arguments: ```
example_names: ["input0", "input1"],
features: {
"age": FixedLenFeature([], dtype=tf.int64, default_value=-1),
"gender": FixedLenFeature([], dtype=tf.string),
}
``` And the expected output is:
An alternative to `VarLenFeature` to obtain a `SparseTensor` is
`SparseFeature`. For example, given two `Example` input protos in
`serialized`: ```
[
features {
feature { key: "val" value { float_list { value: [ 0.5, -1.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 3, 20 ] } } }
},
features {
feature { key: "val" value { float_list { value: [ 0.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 42 ] } } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"sparse": SparseFeature(
index_key="ix", value_key="val", dtype=tf.float32, size=100),
}
``` Then the output is a dictionary:
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>serialized - A vector (1-D Tensor) of strings, a batch of binary serialized `Example` protos.
-
IDictionary<string, object>features - A `dict` mapping feature keys to `FixedLenFeature`, `VarLenFeature`, and `SparseFeature` values.
-
stringname - A name for this operation (optional).
-
objectexample_names - A vector (1-D Tensor) of strings (optional), the names of the serialized protos in the batch.
Returns
-
IDictionary<object, object> - A `dict` mapping feature keys to `Tensor` and `SparseTensor` values.
Show Example
{"ft": SparseTensor(indices=[[0, 0], [0, 1], [2, 0]],
values=[1.0, 2.0, 3.0],
dense_shape=(3, 2)) }
IDictionary<object, object> parse_example(IEnumerable<object> serialized, IDictionary<string, object> features, string name, object example_names)
Parses `Example` protos into a `dict` of tensors. Parses a number of serialized [`Example`](https://www.tensorflow.org/code/tensorflow/core/example/example.proto)
protos given in `serialized`. We refer to `serialized` as a batch with
`batch_size` many entries of individual `Example` protos. `example_names` may contain descriptive names for the corresponding serialized
protos. These may be useful for debugging purposes, but they have no effect on
the output. If not `None`, `example_names` must be the same length as
`serialized`. This op parses serialized examples into a dictionary mapping keys to `Tensor`
and `SparseTensor` objects. `features` is a dict from keys to `VarLenFeature`,
`SparseFeature`, and `FixedLenFeature` objects. Each `VarLenFeature`
and `SparseFeature` is mapped to a `SparseTensor`, and each
`FixedLenFeature` is mapped to a `Tensor`. Each `VarLenFeature` maps to a `SparseTensor` of the specified type
representing a ragged matrix. Its indices are `[batch, index]` where `batch`
identifies the example in `serialized`, and `index` is the value's index in
the list of values associated with that feature and example. Each `SparseFeature` maps to a `SparseTensor` of the specified type
representing a Tensor of `dense_shape` `[batch_size] + SparseFeature.size`.
Its `values` come from the feature in the examples with key `value_key`.
A `values[i]` comes from a position `k` in the feature of an example at batch
entry `batch`. This positional information is recorded in `indices[i]` as
`[batch, index_0, index_1,...]` where `index_j` is the `k-th` value of
the feature in the example at with key `SparseFeature.index_key[j]`.
In other words, we split the indices (except the first index indicating the
batch entry) of a `SparseTensor` by dimension into different features of the
`Example`. Due to its complexity a `VarLenFeature` should be preferred over a
`SparseFeature` whenever possible. Each `FixedLenFeature` `df` maps to a `Tensor` of the specified type (or
tf.float32 if not specified) and shape `(serialized.size(),) + df.shape`. `FixedLenFeature` entries with a `default_value` are optional. With no default
value, we will fail if that `Feature` is missing from any example in
`serialized`. Each `FixedLenSequenceFeature` `df` maps to a `Tensor` of the specified type
(or tf.float32 if not specified) and shape
`(serialized.size(), None) + df.shape`.
All examples in `serialized` will be padded with `default_value` along the
second dimension. Examples: For example, if one expects a tf.float32 `VarLenFeature` `ft` and three
serialized `Example`s are provided: ```
serialized = [
features
{ feature { key: "ft" value { float_list { value: [1.0, 2.0] } } } },
features
{ feature []},
features
{ feature { key: "ft" value { float_list { value: [3.0] } } }
]
``` then the output will look like:
If instead a `FixedLenSequenceFeature` with `default_value = -1.0` and
`shape=[]` is used then the output will look like:
Given two `Example` input protos in `serialized`: ```
[
features {
feature { key: "kw" value { bytes_list { value: [ "knit", "big" ] } } }
feature { key: "gps" value { float_list { value: [] } } }
},
features {
feature { key: "kw" value { bytes_list { value: [ "emmy" ] } } }
feature { key: "dank" value { int64_list { value: [ 42 ] } } }
feature { key: "gps" value { } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"kw": VarLenFeature(tf.string),
"dank": VarLenFeature(tf.int64),
"gps": VarLenFeature(tf.float32),
}
``` Then the output is a dictionary:
For dense results in two serialized `Example`s: ```
[
features {
feature { key: "age" value { int64_list { value: [ 0 ] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
},
features {
feature { key: "age" value { int64_list { value: [] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
}
]
``` We can use arguments: ```
example_names: ["input0", "input1"],
features: {
"age": FixedLenFeature([], dtype=tf.int64, default_value=-1),
"gender": FixedLenFeature([], dtype=tf.string),
}
``` And the expected output is:
An alternative to `VarLenFeature` to obtain a `SparseTensor` is
`SparseFeature`. For example, given two `Example` input protos in
`serialized`: ```
[
features {
feature { key: "val" value { float_list { value: [ 0.5, -1.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 3, 20 ] } } }
},
features {
feature { key: "val" value { float_list { value: [ 0.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 42 ] } } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"sparse": SparseFeature(
index_key="ix", value_key="val", dtype=tf.float32, size=100),
}
``` Then the output is a dictionary:
Parameters
-
IEnumerable<object>serialized - A vector (1-D Tensor) of strings, a batch of binary serialized `Example` protos.
-
IDictionary<string, object>features - A `dict` mapping feature keys to `FixedLenFeature`, `VarLenFeature`, and `SparseFeature` values.
-
stringname - A name for this operation (optional).
-
objectexample_names - A vector (1-D Tensor) of strings (optional), the names of the serialized protos in the batch.
Returns
-
IDictionary<object, object> - A `dict` mapping feature keys to `Tensor` and `SparseTensor` values.
Show Example
{"ft": SparseTensor(indices=[[0, 0], [0, 1], [2, 0]],
values=[1.0, 2.0, 3.0],
dense_shape=(3, 2)) }
IDictionary<object, object> parse_example(IGraphNodeBase serialized, IDictionary<string, object> features, string name, object example_names)
Parses `Example` protos into a `dict` of tensors. Parses a number of serialized [`Example`](https://www.tensorflow.org/code/tensorflow/core/example/example.proto)
protos given in `serialized`. We refer to `serialized` as a batch with
`batch_size` many entries of individual `Example` protos. `example_names` may contain descriptive names for the corresponding serialized
protos. These may be useful for debugging purposes, but they have no effect on
the output. If not `None`, `example_names` must be the same length as
`serialized`. This op parses serialized examples into a dictionary mapping keys to `Tensor`
and `SparseTensor` objects. `features` is a dict from keys to `VarLenFeature`,
`SparseFeature`, and `FixedLenFeature` objects. Each `VarLenFeature`
and `SparseFeature` is mapped to a `SparseTensor`, and each
`FixedLenFeature` is mapped to a `Tensor`. Each `VarLenFeature` maps to a `SparseTensor` of the specified type
representing a ragged matrix. Its indices are `[batch, index]` where `batch`
identifies the example in `serialized`, and `index` is the value's index in
the list of values associated with that feature and example. Each `SparseFeature` maps to a `SparseTensor` of the specified type
representing a Tensor of `dense_shape` `[batch_size] + SparseFeature.size`.
Its `values` come from the feature in the examples with key `value_key`.
A `values[i]` comes from a position `k` in the feature of an example at batch
entry `batch`. This positional information is recorded in `indices[i]` as
`[batch, index_0, index_1,...]` where `index_j` is the `k-th` value of
the feature in the example at with key `SparseFeature.index_key[j]`.
In other words, we split the indices (except the first index indicating the
batch entry) of a `SparseTensor` by dimension into different features of the
`Example`. Due to its complexity a `VarLenFeature` should be preferred over a
`SparseFeature` whenever possible. Each `FixedLenFeature` `df` maps to a `Tensor` of the specified type (or
tf.float32 if not specified) and shape `(serialized.size(),) + df.shape`. `FixedLenFeature` entries with a `default_value` are optional. With no default
value, we will fail if that `Feature` is missing from any example in
`serialized`. Each `FixedLenSequenceFeature` `df` maps to a `Tensor` of the specified type
(or tf.float32 if not specified) and shape
`(serialized.size(), None) + df.shape`.
All examples in `serialized` will be padded with `default_value` along the
second dimension. Examples: For example, if one expects a tf.float32 `VarLenFeature` `ft` and three
serialized `Example`s are provided: ```
serialized = [
features
{ feature { key: "ft" value { float_list { value: [1.0, 2.0] } } } },
features
{ feature []},
features
{ feature { key: "ft" value { float_list { value: [3.0] } } }
]
``` then the output will look like:
If instead a `FixedLenSequenceFeature` with `default_value = -1.0` and
`shape=[]` is used then the output will look like:
Given two `Example` input protos in `serialized`: ```
[
features {
feature { key: "kw" value { bytes_list { value: [ "knit", "big" ] } } }
feature { key: "gps" value { float_list { value: [] } } }
},
features {
feature { key: "kw" value { bytes_list { value: [ "emmy" ] } } }
feature { key: "dank" value { int64_list { value: [ 42 ] } } }
feature { key: "gps" value { } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"kw": VarLenFeature(tf.string),
"dank": VarLenFeature(tf.int64),
"gps": VarLenFeature(tf.float32),
}
``` Then the output is a dictionary:
For dense results in two serialized `Example`s: ```
[
features {
feature { key: "age" value { int64_list { value: [ 0 ] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
},
features {
feature { key: "age" value { int64_list { value: [] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
}
]
``` We can use arguments: ```
example_names: ["input0", "input1"],
features: {
"age": FixedLenFeature([], dtype=tf.int64, default_value=-1),
"gender": FixedLenFeature([], dtype=tf.string),
}
``` And the expected output is:
An alternative to `VarLenFeature` to obtain a `SparseTensor` is
`SparseFeature`. For example, given two `Example` input protos in
`serialized`: ```
[
features {
feature { key: "val" value { float_list { value: [ 0.5, -1.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 3, 20 ] } } }
},
features {
feature { key: "val" value { float_list { value: [ 0.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 42 ] } } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"sparse": SparseFeature(
index_key="ix", value_key="val", dtype=tf.float32, size=100),
}
``` Then the output is a dictionary:
Parameters
-
IGraphNodeBaseserialized - A vector (1-D Tensor) of strings, a batch of binary serialized `Example` protos.
-
IDictionary<string, object>features - A `dict` mapping feature keys to `FixedLenFeature`, `VarLenFeature`, and `SparseFeature` values.
-
stringname - A name for this operation (optional).
-
objectexample_names - A vector (1-D Tensor) of strings (optional), the names of the serialized protos in the batch.
Returns
-
IDictionary<object, object> - A `dict` mapping feature keys to `Tensor` and `SparseTensor` values.
Show Example
{"ft": SparseTensor(indices=[[0, 0], [0, 1], [2, 0]],
values=[1.0, 2.0, 3.0],
dense_shape=(3, 2)) }
object parse_example_dyn(object serialized, object features, object name, object example_names)
Parses `Example` protos into a `dict` of tensors. Parses a number of serialized [`Example`](https://www.tensorflow.org/code/tensorflow/core/example/example.proto)
protos given in `serialized`. We refer to `serialized` as a batch with
`batch_size` many entries of individual `Example` protos. `example_names` may contain descriptive names for the corresponding serialized
protos. These may be useful for debugging purposes, but they have no effect on
the output. If not `None`, `example_names` must be the same length as
`serialized`. This op parses serialized examples into a dictionary mapping keys to `Tensor`
and `SparseTensor` objects. `features` is a dict from keys to `VarLenFeature`,
`SparseFeature`, and `FixedLenFeature` objects. Each `VarLenFeature`
and `SparseFeature` is mapped to a `SparseTensor`, and each
`FixedLenFeature` is mapped to a `Tensor`. Each `VarLenFeature` maps to a `SparseTensor` of the specified type
representing a ragged matrix. Its indices are `[batch, index]` where `batch`
identifies the example in `serialized`, and `index` is the value's index in
the list of values associated with that feature and example. Each `SparseFeature` maps to a `SparseTensor` of the specified type
representing a Tensor of `dense_shape` `[batch_size] + SparseFeature.size`.
Its `values` come from the feature in the examples with key `value_key`.
A `values[i]` comes from a position `k` in the feature of an example at batch
entry `batch`. This positional information is recorded in `indices[i]` as
`[batch, index_0, index_1,...]` where `index_j` is the `k-th` value of
the feature in the example at with key `SparseFeature.index_key[j]`.
In other words, we split the indices (except the first index indicating the
batch entry) of a `SparseTensor` by dimension into different features of the
`Example`. Due to its complexity a `VarLenFeature` should be preferred over a
`SparseFeature` whenever possible. Each `FixedLenFeature` `df` maps to a `Tensor` of the specified type (or
tf.float32 if not specified) and shape `(serialized.size(),) + df.shape`. `FixedLenFeature` entries with a `default_value` are optional. With no default
value, we will fail if that `Feature` is missing from any example in
`serialized`. Each `FixedLenSequenceFeature` `df` maps to a `Tensor` of the specified type
(or tf.float32 if not specified) and shape
`(serialized.size(), None) + df.shape`.
All examples in `serialized` will be padded with `default_value` along the
second dimension. Examples: For example, if one expects a tf.float32 `VarLenFeature` `ft` and three
serialized `Example`s are provided: ```
serialized = [
features
{ feature { key: "ft" value { float_list { value: [1.0, 2.0] } } } },
features
{ feature []},
features
{ feature { key: "ft" value { float_list { value: [3.0] } } }
]
``` then the output will look like:
If instead a `FixedLenSequenceFeature` with `default_value = -1.0` and
`shape=[]` is used then the output will look like:
Given two `Example` input protos in `serialized`: ```
[
features {
feature { key: "kw" value { bytes_list { value: [ "knit", "big" ] } } }
feature { key: "gps" value { float_list { value: [] } } }
},
features {
feature { key: "kw" value { bytes_list { value: [ "emmy" ] } } }
feature { key: "dank" value { int64_list { value: [ 42 ] } } }
feature { key: "gps" value { } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"kw": VarLenFeature(tf.string),
"dank": VarLenFeature(tf.int64),
"gps": VarLenFeature(tf.float32),
}
``` Then the output is a dictionary:
For dense results in two serialized `Example`s: ```
[
features {
feature { key: "age" value { int64_list { value: [ 0 ] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
},
features {
feature { key: "age" value { int64_list { value: [] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
}
]
``` We can use arguments: ```
example_names: ["input0", "input1"],
features: {
"age": FixedLenFeature([], dtype=tf.int64, default_value=-1),
"gender": FixedLenFeature([], dtype=tf.string),
}
``` And the expected output is:
An alternative to `VarLenFeature` to obtain a `SparseTensor` is
`SparseFeature`. For example, given two `Example` input protos in
`serialized`: ```
[
features {
feature { key: "val" value { float_list { value: [ 0.5, -1.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 3, 20 ] } } }
},
features {
feature { key: "val" value { float_list { value: [ 0.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 42 ] } } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"sparse": SparseFeature(
index_key="ix", value_key="val", dtype=tf.float32, size=100),
}
``` Then the output is a dictionary:
Parameters
-
objectserialized - A vector (1-D Tensor) of strings, a batch of binary serialized `Example` protos.
-
objectfeatures - A `dict` mapping feature keys to `FixedLenFeature`, `VarLenFeature`, and `SparseFeature` values.
-
objectname - A name for this operation (optional).
-
objectexample_names - A vector (1-D Tensor) of strings (optional), the names of the serialized protos in the batch.
Returns
-
object - A `dict` mapping feature keys to `Tensor` and `SparseTensor` values.
Show Example
{"ft": SparseTensor(indices=[[0, 0], [0, 1], [2, 0]],
values=[1.0, 2.0, 3.0],
dense_shape=(3, 2)) }
IDictionary<object, object> parse_single_example(IGraphNodeBase serialized, IDictionary<string, object> features, string name, string example_names)
Parses a single `Example` proto. Similar to `parse_example`, except: For dense tensors, the returned `Tensor` is identical to the output of
`parse_example`, except there is no batch dimension, the output shape is the
same as the shape given in `dense_shape`. For `SparseTensor`s, the first (batch) column of the indices matrix is removed
(the indices matrix is a column vector), the values vector is unchanged, and
the first (`batch_size`) entry of the shape vector is removed (it is now a
single element vector). One might see performance advantages by batching `Example` protos with
`parse_example` instead of using this function directly.
Parameters
-
IGraphNodeBaseserialized - A scalar string Tensor, a single serialized Example. See `_parse_single_example_raw` documentation for more details.
-
IDictionary<string, object>features - A `dict` mapping feature keys to `FixedLenFeature` or `VarLenFeature` values.
-
stringname - A name for this operation (optional).
-
stringexample_names - (Optional) A scalar string Tensor, the associated name. See `_parse_single_example_raw` documentation for more details.
Returns
-
IDictionary<object, object> - A `dict` mapping feature keys to `Tensor` and `SparseTensor` values.
IDictionary<object, object> parse_single_example(IEnumerable<double> serialized, IDictionary<string, object> features, string name, string example_names)
Parses a single `Example` proto. Similar to `parse_example`, except: For dense tensors, the returned `Tensor` is identical to the output of
`parse_example`, except there is no batch dimension, the output shape is the
same as the shape given in `dense_shape`. For `SparseTensor`s, the first (batch) column of the indices matrix is removed
(the indices matrix is a column vector), the values vector is unchanged, and
the first (`batch_size`) entry of the shape vector is removed (it is now a
single element vector). One might see performance advantages by batching `Example` protos with
`parse_example` instead of using this function directly.
Parameters
-
IEnumerable<double>serialized - A scalar string Tensor, a single serialized Example. See `_parse_single_example_raw` documentation for more details.
-
IDictionary<string, object>features - A `dict` mapping feature keys to `FixedLenFeature` or `VarLenFeature` values.
-
stringname - A name for this operation (optional).
-
stringexample_names - (Optional) A scalar string Tensor, the associated name. See `_parse_single_example_raw` documentation for more details.
Returns
-
IDictionary<object, object> - A `dict` mapping feature keys to `Tensor` and `SparseTensor` values.
IDictionary<object, object> parse_single_example(ValueTuple<PythonClassContainer, PythonClassContainer> serialized, IDictionary<string, object> features, string name, string example_names)
Parses a single `Example` proto. Similar to `parse_example`, except: For dense tensors, the returned `Tensor` is identical to the output of
`parse_example`, except there is no batch dimension, the output shape is the
same as the shape given in `dense_shape`. For `SparseTensor`s, the first (batch) column of the indices matrix is removed
(the indices matrix is a column vector), the values vector is unchanged, and
the first (`batch_size`) entry of the shape vector is removed (it is now a
single element vector). One might see performance advantages by batching `Example` protos with
`parse_example` instead of using this function directly.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>serialized - A scalar string Tensor, a single serialized Example. See `_parse_single_example_raw` documentation for more details.
-
IDictionary<string, object>features - A `dict` mapping feature keys to `FixedLenFeature` or `VarLenFeature` values.
-
stringname - A name for this operation (optional).
-
stringexample_names - (Optional) A scalar string Tensor, the associated name. See `_parse_single_example_raw` documentation for more details.
Returns
-
IDictionary<object, object> - A `dict` mapping feature keys to `Tensor` and `SparseTensor` values.
object parse_single_example_dyn(object serialized, object features, object name, object example_names)
Parses a single `Example` proto. Similar to `parse_example`, except: For dense tensors, the returned `Tensor` is identical to the output of
`parse_example`, except there is no batch dimension, the output shape is the
same as the shape given in `dense_shape`. For `SparseTensor`s, the first (batch) column of the indices matrix is removed
(the indices matrix is a column vector), the values vector is unchanged, and
the first (`batch_size`) entry of the shape vector is removed (it is now a
single element vector). One might see performance advantages by batching `Example` protos with
`parse_example` instead of using this function directly.
Parameters
-
objectserialized - A scalar string Tensor, a single serialized Example. See `_parse_single_example_raw` documentation for more details.
-
objectfeatures - A `dict` mapping feature keys to `FixedLenFeature` or `VarLenFeature` values.
-
objectname - A name for this operation (optional).
-
objectexample_names - (Optional) A scalar string Tensor, the associated name. See `_parse_single_example_raw` documentation for more details.
Returns
-
object - A `dict` mapping feature keys to `Tensor` and `SparseTensor` values.
ValueTuple<IDictionary<object, object>, object> parse_single_sequence_example(IGraphNodeBase serialized, IDictionary<object, object> context_features, IDictionary<object, object> sequence_features, object example_name, string name)
Parses a single `SequenceExample` proto. Parses a single serialized [`SequenceExample`](https://www.tensorflow.org/code/tensorflow/core/example/example.proto)
proto given in `serialized`. This op parses a serialized sequence example into a tuple of dictionaries,
each mapping keys to `Tensor` and `SparseTensor` objects.
The first dictionary contains mappings for keys appearing in
`context_features`, and the second dictionary contains mappings for keys
appearing in `sequence_features`. At least one of `context_features` and `sequence_features` must be provided
and non-empty. The `context_features` keys are associated with a `SequenceExample` as a
whole, independent of time / frame. In contrast, the `sequence_features` keys
provide a way to access variable-length data within the `FeatureList` section
of the `SequenceExample` proto. While the shapes of `context_features` values
are fixed with respect to frame, the frame dimension (the first dimension)
of `sequence_features` values may vary between `SequenceExample` protos,
and even between `feature_list` keys within the same `SequenceExample`. `context_features` contains `VarLenFeature` and `FixedLenFeature` objects.
Each `VarLenFeature` is mapped to a `SparseTensor`, and each `FixedLenFeature`
is mapped to a `Tensor`, of the specified type, shape, and default value. `sequence_features` contains `VarLenFeature` and `FixedLenSequenceFeature`
objects. Each `VarLenFeature` is mapped to a `SparseTensor`, and each
`FixedLenSequenceFeature` is mapped to a `Tensor`, each of the specified type.
The shape will be `(T,) + df.dense_shape` for `FixedLenSequenceFeature` `df`, where
`T` is the length of the associated `FeatureList` in the `SequenceExample`.
For instance, `FixedLenSequenceFeature([])` yields a scalar 1-D `Tensor` of
static shape `[None]` and dynamic shape `[T]`, while
`FixedLenSequenceFeature([k])` (for `int k >= 1`) yields a 2-D matrix `Tensor`
of static shape `[None, k]` and dynamic shape `[T, k]`. Each `SparseTensor` corresponding to `sequence_features` represents a ragged
vector. Its indices are `[time, index]`, where `time` is the `FeatureList`
entry and `index` is the value's index in the list of values associated with
that time. `FixedLenFeature` entries with a `default_value` and `FixedLenSequenceFeature`
entries with `allow_missing=True` are optional; otherwise, we will fail if
that `Feature` or `FeatureList` is missing from any example in `serialized`. `example_name` may contain a descriptive name for the corresponding serialized
proto. This may be useful for debugging purposes, but it has no effect on the
output. If not `None`, `example_name` must be a scalar. Note that the batch version of this function, `tf.parse_sequence_example`,
is written for better memory efficiency and will be faster on large
`SequenceExample`s.
Parameters
-
IGraphNodeBaseserialized - A scalar (0-D Tensor) of type string, a single binary serialized `SequenceExample` proto.
-
IDictionary<object, object>context_features - A `dict` mapping feature keys to `FixedLenFeature` or `VarLenFeature` values. These features are associated with a `SequenceExample` as a whole.
-
IDictionary<object, object>sequence_features - A `dict` mapping feature keys to `FixedLenSequenceFeature` or `VarLenFeature` values. These features are associated with data within the `FeatureList` section of the `SequenceExample` proto.
-
objectexample_name - A scalar (0-D Tensor) of strings (optional), the name of the serialized proto.
-
stringname - A name for this operation (optional).
Returns
-
ValueTuple<IDictionary<object, object>, object> - A tuple of two `dict`s, each mapping keys to `Tensor`s and `SparseTensor`s. The first dict contains the context key/values. The second dict contains the feature_list key/values.
object parse_single_sequence_example_dyn(object serialized, object context_features, object sequence_features, object example_name, object name)
Parses a single `SequenceExample` proto. Parses a single serialized [`SequenceExample`](https://www.tensorflow.org/code/tensorflow/core/example/example.proto)
proto given in `serialized`. This op parses a serialized sequence example into a tuple of dictionaries,
each mapping keys to `Tensor` and `SparseTensor` objects.
The first dictionary contains mappings for keys appearing in
`context_features`, and the second dictionary contains mappings for keys
appearing in `sequence_features`. At least one of `context_features` and `sequence_features` must be provided
and non-empty. The `context_features` keys are associated with a `SequenceExample` as a
whole, independent of time / frame. In contrast, the `sequence_features` keys
provide a way to access variable-length data within the `FeatureList` section
of the `SequenceExample` proto. While the shapes of `context_features` values
are fixed with respect to frame, the frame dimension (the first dimension)
of `sequence_features` values may vary between `SequenceExample` protos,
and even between `feature_list` keys within the same `SequenceExample`. `context_features` contains `VarLenFeature` and `FixedLenFeature` objects.
Each `VarLenFeature` is mapped to a `SparseTensor`, and each `FixedLenFeature`
is mapped to a `Tensor`, of the specified type, shape, and default value. `sequence_features` contains `VarLenFeature` and `FixedLenSequenceFeature`
objects. Each `VarLenFeature` is mapped to a `SparseTensor`, and each
`FixedLenSequenceFeature` is mapped to a `Tensor`, each of the specified type.
The shape will be `(T,) + df.dense_shape` for `FixedLenSequenceFeature` `df`, where
`T` is the length of the associated `FeatureList` in the `SequenceExample`.
For instance, `FixedLenSequenceFeature([])` yields a scalar 1-D `Tensor` of
static shape `[None]` and dynamic shape `[T]`, while
`FixedLenSequenceFeature([k])` (for `int k >= 1`) yields a 2-D matrix `Tensor`
of static shape `[None, k]` and dynamic shape `[T, k]`. Each `SparseTensor` corresponding to `sequence_features` represents a ragged
vector. Its indices are `[time, index]`, where `time` is the `FeatureList`
entry and `index` is the value's index in the list of values associated with
that time. `FixedLenFeature` entries with a `default_value` and `FixedLenSequenceFeature`
entries with `allow_missing=True` are optional; otherwise, we will fail if
that `Feature` or `FeatureList` is missing from any example in `serialized`. `example_name` may contain a descriptive name for the corresponding serialized
proto. This may be useful for debugging purposes, but it has no effect on the
output. If not `None`, `example_name` must be a scalar. Note that the batch version of this function, `tf.parse_sequence_example`,
is written for better memory efficiency and will be faster on large
`SequenceExample`s.
Parameters
-
objectserialized - A scalar (0-D Tensor) of type string, a single binary serialized `SequenceExample` proto.
-
objectcontext_features - A `dict` mapping feature keys to `FixedLenFeature` or `VarLenFeature` values. These features are associated with a `SequenceExample` as a whole.
-
objectsequence_features - A `dict` mapping feature keys to `FixedLenSequenceFeature` or `VarLenFeature` values. These features are associated with data within the `FeatureList` section of the `SequenceExample` proto.
-
objectexample_name - A scalar (0-D Tensor) of strings (optional), the name of the serialized proto.
-
objectname - A name for this operation (optional).
Returns
-
object - A tuple of two `dict`s, each mapping keys to `Tensor`s and `SparseTensor`s. The first dict contains the context key/values. The second dict contains the feature_list key/values.
Tensor parse_tensor(IGraphNodeBase serialized, DType out_type, string name)
Transforms a serialized tensorflow.TensorProto proto into a Tensor.
Parameters
-
IGraphNodeBaseserialized - A `Tensor` of type `string`. A scalar string containing a serialized TensorProto proto.
-
DTypeout_type - A
tf.DType. The type of the serialized tensor. The provided type must match the type of the serialized tensor and no implicit conversion will take place. -
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `out_type`.
object parse_tensor_dyn(object serialized, object out_type, object name)
Transforms a serialized tensorflow.TensorProto proto into a Tensor.
Parameters
-
objectserialized - A `Tensor` of type `string`. A scalar string containing a serialized TensorProto proto.
-
objectout_type - A
tf.DType. The type of the serialized tensor. The provided type must match the type of the serialized tensor and no implicit conversion will take place. -
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `out_type`.
Tensor periodic_resample(IGraphNodeBase values, TensorShape shape, string name)
object periodic_resample_dyn(object values, object shape, object name)
Tensor periodic_resample_op_grad(IGraphNodeBase grad, object original_shape, object desired_shape, string name)
object periodic_resample_op_grad_dyn(object grad, object original_shape, object desired_shape, object name)
Tensor placeholder(PythonClassContainer dtype, TensorShape shape, string name)
Inserts a placeholder for a tensor that will be always fed. **Important**: This tensor will produce an error if evaluated. Its value must
be fed using the `feed_dict` optional argument to `Session.run()`,
`Tensor.eval()`, or `Operation.run()`.
Parameters
-
PythonClassContainerdtype - The type of elements in the tensor to be fed.
-
TensorShapeshape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a tensor of any shape.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.placeholder(tf.float32, shape=(1024, 1024))
y = tf.matmul(x, x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. rand_array = np.random.rand(1024, 1024)
print(sess.run(y, feed_dict={x: rand_array})) # Will succeed.
Tensor placeholder(DType dtype, PythonFunctionContainer shape, string name)
Inserts a placeholder for a tensor that will be always fed. **Important**: This tensor will produce an error if evaluated. Its value must
be fed using the `feed_dict` optional argument to `Session.run()`,
`Tensor.eval()`, or `Operation.run()`.
Parameters
-
DTypedtype - The type of elements in the tensor to be fed.
-
PythonFunctionContainershape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a tensor of any shape.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.placeholder(tf.float32, shape=(1024, 1024))
y = tf.matmul(x, x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. rand_array = np.random.rand(1024, 1024)
print(sess.run(y, feed_dict={x: rand_array})) # Will succeed.
Tensor placeholder(PythonClassContainer dtype, PythonFunctionContainer shape, string name)
Inserts a placeholder for a tensor that will be always fed. **Important**: This tensor will produce an error if evaluated. Its value must
be fed using the `feed_dict` optional argument to `Session.run()`,
`Tensor.eval()`, or `Operation.run()`.
Parameters
-
PythonClassContainerdtype - The type of elements in the tensor to be fed.
-
PythonFunctionContainershape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a tensor of any shape.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.placeholder(tf.float32, shape=(1024, 1024))
y = tf.matmul(x, x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. rand_array = np.random.rand(1024, 1024)
print(sess.run(y, feed_dict={x: rand_array})) # Will succeed.
Tensor placeholder(DType dtype, TensorShape shape, string name)
Inserts a placeholder for a tensor that will be always fed. **Important**: This tensor will produce an error if evaluated. Its value must
be fed using the `feed_dict` optional argument to `Session.run()`,
`Tensor.eval()`, or `Operation.run()`.
Parameters
-
DTypedtype - The type of elements in the tensor to be fed.
-
TensorShapeshape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a tensor of any shape.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.placeholder(tf.float32, shape=(1024, 1024))
y = tf.matmul(x, x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. rand_array = np.random.rand(1024, 1024)
print(sess.run(y, feed_dict={x: rand_array})) # Will succeed.
object placeholder_dyn(object dtype, object shape, object name)
Inserts a placeholder for a tensor that will be always fed. **Important**: This tensor will produce an error if evaluated. Its value must
be fed using the `feed_dict` optional argument to `Session.run()`,
`Tensor.eval()`, or `Operation.run()`.
Parameters
-
objectdtype - The type of elements in the tensor to be fed.
-
objectshape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a tensor of any shape.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.placeholder(tf.float32, shape=(1024, 1024))
y = tf.matmul(x, x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. rand_array = np.random.rand(1024, 1024)
print(sess.run(y, feed_dict={x: rand_array})) # Will succeed.
Tensor placeholder_with_default(IGraphNodeBase input, IEnumerable<int> shape, string name)
A placeholder op that passes through `input` when its output is not fed.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. The default value to produce when output is not fed.
-
IEnumerable<int>shape - A
tf.TensorShapeor list of `int`s. The (possibly partial) shape of the tensor. -
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor placeholder_with_default(IGraphNodeBase input, TensorShape shape, string name)
A placeholder op that passes through `input` when its output is not fed.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. The default value to produce when output is not fed.
-
TensorShapeshape - A
tf.TensorShapeor list of `int`s. The (possibly partial) shape of the tensor. -
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object placeholder_with_default_dyn(object input, object shape, object name)
A placeholder op that passes through `input` when its output is not fed.
Parameters
-
objectinput - A `Tensor`. The default value to produce when output is not fed.
-
objectshape - A
tf.TensorShapeor list of `int`s. The (possibly partial) shape of the tensor. -
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor polygamma(IGraphNodeBase a, IGraphNodeBase x, string name)
Compute the polygamma function \\(\psi^{(n)}(x)\\). The polygamma function is defined as: \\(\psi^{(a)}(x) = \frac{d^a}{dx^a} \psi(x)\\) where \\(\psi(x)\\) is the digamma function.
The polygamma function is defined only for non-negative integer orders \\a\\.
Parameters
-
IGraphNodeBasea - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
IGraphNodeBasex - A `Tensor`. Must have the same type as `a`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `a`.
object polygamma_dyn(object a, object x, object name)
Compute the polygamma function \\(\psi^{(n)}(x)\\). The polygamma function is defined as: \\(\psi^{(a)}(x) = \frac{d^a}{dx^a} \psi(x)\\) where \\(\psi(x)\\) is the digamma function.
The polygamma function is defined only for non-negative integer orders \\a\\.
Parameters
-
objecta - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
objectx - A `Tensor`. Must have the same type as `a`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `a`.
Tensor polymorphic(IGraphNodeBase a, string name)
Tensor polymorphic_default_out(ImplicitContainer<T> T, string name)
object polymorphic_default_out_dyn(ImplicitContainer<T> T, object name)
object polymorphic_dyn(object a, object name)
Tensor polymorphic_out(object T, string name)
object polymorphic_out_dyn(object T, object name)
object pow(int x, double y, string name)
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Parameters
-
intx - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
doubley - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
object pow(int x, int y, string name)
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Parameters
-
intx - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
inty - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
object pow(int x, IGraphNodeBase y, string name)
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Parameters
-
intx - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
IGraphNodeBasey - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
object pow(IGraphNodeBase x, IGraphNodeBase y, string name)
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Parameters
-
IGraphNodeBasex - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
IGraphNodeBasey - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
object pow(IGraphNodeBase x, int y, string name)
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Parameters
-
IGraphNodeBasex - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
inty - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
object pow(double x, IGraphNodeBase y, string name)
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Parameters
-
doublex - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
IGraphNodeBasey - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
object pow(double x, double y, string name)
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Parameters
-
doublex - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
doubley - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
object pow(IGraphNodeBase x, double y, string name)
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Parameters
-
IGraphNodeBasex - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
doubley - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
object pow(double x, int y, string name)
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Parameters
-
doublex - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
inty - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
object pow_dyn(object x, object y, object name)
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Parameters
-
objectx - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
objecty - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, `int64`, `complex64`, or `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
object print(Object[] inputs)
Print the specified inputs. A TensorFlow operator that prints the specified inputs to a desired
output stream or logging level. The inputs may be dense or sparse Tensors,
primitive python objects, data structures that contain tensors, and printable
Python objects. Printed tensors will recursively show the first and last
elements of each dimension to summarize. Example:
Single-input usage:
(This prints "[0 1 2... 7 8 9]" to sys.stderr) Multi-input usage:
(This prints "tensors: [0 1 2... 7 8 9] {2: [0 2 4... 14 16 18]}" to
sys.stdout) Changing the input separator:
(This prints "[0 1],[0 2]" to sys.stderr) Usage in a
tf.function:
(This prints "[0 1 2... 7 8 9]" to sys.stderr) @compatibility(TF 1.x Graphs and Sessions)
In graphs manually created outside of tf.function, this method returns
the created TF operator that prints the data. To make sure the
operator runs, users need to pass the produced op to
`tf.compat.v1.Session`'s run method, or to use the op as a control
dependency for executed ops by specifying
`with tf.compat.v1.control_dependencies([print_op])`.
@end_compatibility Compatibility usage in TF 1.x graphs:
(This prints "tensors: [0 1 2... 7 8 9] {2: [0 2 4... 14 16 18]}" to
sys.stdout) Note: In Jupyter notebooks and colabs, tf.print prints to the notebook
cell outputs. It will not write to the notebook kernel's console logs.
Parameters
-
Object[]inputs - Positional arguments that are the inputs to print. Inputs in the printed output will be separated by spaces. Inputs may be python primitives, tensors, data structures such as dicts and lists that may contain tensors (with the data structures possibly nested in arbitrary ways), and printable python objects.
Returns
-
object - None when executing eagerly. During graph tracing this returns a TF operator that prints the specified inputs in the specified output stream or logging level. This operator will be automatically executed except inside of `tf.compat.v1` graphs and sessions.
Show Example
tensor = tf.range(10)
tf.print(tensor, output_stream=sys.stderr)
object print(IDictionary<string, object> kwargs, Object[] inputs)
Print the specified inputs. A TensorFlow operator that prints the specified inputs to a desired
output stream or logging level. The inputs may be dense or sparse Tensors,
primitive python objects, data structures that contain tensors, and printable
Python objects. Printed tensors will recursively show the first and last
elements of each dimension to summarize. Example:
Single-input usage:
(This prints "[0 1 2... 7 8 9]" to sys.stderr) Multi-input usage:
(This prints "tensors: [0 1 2... 7 8 9] {2: [0 2 4... 14 16 18]}" to
sys.stdout) Changing the input separator:
(This prints "[0 1],[0 2]" to sys.stderr) Usage in a
tf.function:
(This prints "[0 1 2... 7 8 9]" to sys.stderr) @compatibility(TF 1.x Graphs and Sessions)
In graphs manually created outside of tf.function, this method returns
the created TF operator that prints the data. To make sure the
operator runs, users need to pass the produced op to
`tf.compat.v1.Session`'s run method, or to use the op as a control
dependency for executed ops by specifying
`with tf.compat.v1.control_dependencies([print_op])`.
@end_compatibility Compatibility usage in TF 1.x graphs:
(This prints "tensors: [0 1 2... 7 8 9] {2: [0 2 4... 14 16 18]}" to
sys.stdout) Note: In Jupyter notebooks and colabs, tf.print prints to the notebook
cell outputs. It will not write to the notebook kernel's console logs.
Parameters
-
IDictionary<string, object>kwargs -
Object[]inputs - Positional arguments that are the inputs to print. Inputs in the printed output will be separated by spaces. Inputs may be python primitives, tensors, data structures such as dicts and lists that may contain tensors (with the data structures possibly nested in arbitrary ways), and printable python objects.
Returns
-
object - None when executing eagerly. During graph tracing this returns a TF operator that prints the specified inputs in the specified output stream or logging level. This operator will be automatically executed except inside of `tf.compat.v1` graphs and sessions.
Show Example
tensor = tf.range(10)
tf.print(tensor, output_stream=sys.stderr)
Tensor Print(ValueTuple<IEnumerable<object>, object> input_, IEnumerable<IGraphNodeBase> data, string message, Nullable<int> first_n, Nullable<int> summarize, string name)
Prints a list of tensors. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-08-20.
Instructions for updating:
Use tf.print instead of tf.Print. Note that tf.print returns a no-output operator that directly prints the output. Outside of defuns or eager mode, this operator will not be executed unless it is directly specified in session.run or used as a control dependency for other operators. This is only a concern in graph mode. Below is an example of how to ensure tf.print executes in graph mode: This is an identity op (behaves like
tf.identity) with the side effect
of printing `data` when evaluating. Note: This op prints to the standard error. It is not currently compatible
with jupyter notebook (printing to the notebook *server's* output, not into
the notebook).
Parameters
-
ValueTuple<IEnumerable<object>, object>input_ - A tensor passed through this op.
-
IEnumerable<IGraphNodeBase>data - A list of tensors to print out when op is evaluated.
-
stringmessage - A string, prefix of the error message.
-
Nullable<int>first_n - Only log `first_n` number of times. Negative numbers log always; this is the default.
-
Nullable<int>summarize - Only print this many entries of each tensor. If None, then a maximum of 3 elements are printed per input tensor.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type and contents as `input_`. ```python sess = tf.compat.v1.Session() with sess.as_default(): tensor = tf.range(10) print_op = tf.print(tensor) with tf.control_dependencies([print_op]): out = tf.add(tensor, tensor) sess.run(out) ``` Additionally, to use tf.print in python 2.7, users must make sure to import the following: `from __future__ import print_function`
Tensor Print(IGraphNodeBase input_, IEnumerable<IGraphNodeBase> data, string message, Nullable<int> first_n, Nullable<int> summarize, string name)
Prints a list of tensors. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-08-20.
Instructions for updating:
Use tf.print instead of tf.Print. Note that tf.print returns a no-output operator that directly prints the output. Outside of defuns or eager mode, this operator will not be executed unless it is directly specified in session.run or used as a control dependency for other operators. This is only a concern in graph mode. Below is an example of how to ensure tf.print executes in graph mode: This is an identity op (behaves like
tf.identity) with the side effect
of printing `data` when evaluating. Note: This op prints to the standard error. It is not currently compatible
with jupyter notebook (printing to the notebook *server's* output, not into
the notebook).
Parameters
-
IGraphNodeBaseinput_ - A tensor passed through this op.
-
IEnumerable<IGraphNodeBase>data - A list of tensors to print out when op is evaluated.
-
stringmessage - A string, prefix of the error message.
-
Nullable<int>first_n - Only log `first_n` number of times. Negative numbers log always; this is the default.
-
Nullable<int>summarize - Only print this many entries of each tensor. If None, then a maximum of 3 elements are printed per input tensor.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type and contents as `input_`. ```python sess = tf.compat.v1.Session() with sess.as_default(): tensor = tf.range(10) print_op = tf.print(tensor) with tf.control_dependencies([print_op]): out = tf.add(tensor, tensor) sess.run(out) ``` Additionally, to use tf.print in python 2.7, users must make sure to import the following: `from __future__ import print_function`
Tensor Print(int input_, IEnumerable<IGraphNodeBase> data, string message, Nullable<int> first_n, Nullable<int> summarize, string name)
Prints a list of tensors. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-08-20.
Instructions for updating:
Use tf.print instead of tf.Print. Note that tf.print returns a no-output operator that directly prints the output. Outside of defuns or eager mode, this operator will not be executed unless it is directly specified in session.run or used as a control dependency for other operators. This is only a concern in graph mode. Below is an example of how to ensure tf.print executes in graph mode: This is an identity op (behaves like
tf.identity) with the side effect
of printing `data` when evaluating. Note: This op prints to the standard error. It is not currently compatible
with jupyter notebook (printing to the notebook *server's* output, not into
the notebook).
Parameters
-
intinput_ - A tensor passed through this op.
-
IEnumerable<IGraphNodeBase>data - A list of tensors to print out when op is evaluated.
-
stringmessage - A string, prefix of the error message.
-
Nullable<int>first_n - Only log `first_n` number of times. Negative numbers log always; this is the default.
-
Nullable<int>summarize - Only print this many entries of each tensor. If None, then a maximum of 3 elements are printed per input tensor.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type and contents as `input_`. ```python sess = tf.compat.v1.Session() with sess.as_default(): tensor = tf.range(10) print_op = tf.print(tensor) with tf.control_dependencies([print_op]): out = tf.add(tensor, tensor) sess.run(out) ``` Additionally, to use tf.print in python 2.7, users must make sure to import the following: `from __future__ import print_function`
Tensor Print(IEnumerable<object> input_, IEnumerable<IGraphNodeBase> data, string message, Nullable<int> first_n, Nullable<int> summarize, string name)
Prints a list of tensors. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-08-20.
Instructions for updating:
Use tf.print instead of tf.Print. Note that tf.print returns a no-output operator that directly prints the output. Outside of defuns or eager mode, this operator will not be executed unless it is directly specified in session.run or used as a control dependency for other operators. This is only a concern in graph mode. Below is an example of how to ensure tf.print executes in graph mode: This is an identity op (behaves like
tf.identity) with the side effect
of printing `data` when evaluating. Note: This op prints to the standard error. It is not currently compatible
with jupyter notebook (printing to the notebook *server's* output, not into
the notebook).
Parameters
-
IEnumerable<object>input_ - A tensor passed through this op.
-
IEnumerable<IGraphNodeBase>data - A list of tensors to print out when op is evaluated.
-
stringmessage - A string, prefix of the error message.
-
Nullable<int>first_n - Only log `first_n` number of times. Negative numbers log always; this is the default.
-
Nullable<int>summarize - Only print this many entries of each tensor. If None, then a maximum of 3 elements are printed per input tensor.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type and contents as `input_`. ```python sess = tf.compat.v1.Session() with sess.as_default(): tensor = tf.range(10) print_op = tf.print(tensor) with tf.control_dependencies([print_op]): out = tf.add(tensor, tensor) sess.run(out) ``` Additionally, to use tf.print in python 2.7, users must make sure to import the following: `from __future__ import print_function`
object print_dyn(IDictionary<string, object> kwargs, Object[] inputs)
Print the specified inputs. A TensorFlow operator that prints the specified inputs to a desired
output stream or logging level. The inputs may be dense or sparse Tensors,
primitive python objects, data structures that contain tensors, and printable
Python objects. Printed tensors will recursively show the first and last
elements of each dimension to summarize. Example:
Single-input usage:
(This prints "[0 1 2... 7 8 9]" to sys.stderr) Multi-input usage:
(This prints "tensors: [0 1 2... 7 8 9] {2: [0 2 4... 14 16 18]}" to
sys.stdout) Changing the input separator:
(This prints "[0 1],[0 2]" to sys.stderr) Usage in a
tf.function:
(This prints "[0 1 2... 7 8 9]" to sys.stderr) @compatibility(TF 1.x Graphs and Sessions)
In graphs manually created outside of tf.function, this method returns
the created TF operator that prints the data. To make sure the
operator runs, users need to pass the produced op to
`tf.compat.v1.Session`'s run method, or to use the op as a control
dependency for executed ops by specifying
`with tf.compat.v1.control_dependencies([print_op])`.
@end_compatibility Compatibility usage in TF 1.x graphs:
(This prints "tensors: [0 1 2... 7 8 9] {2: [0 2 4... 14 16 18]}" to
sys.stdout) Note: In Jupyter notebooks and colabs, tf.print prints to the notebook
cell outputs. It will not write to the notebook kernel's console logs.
Parameters
-
IDictionary<string, object>kwargs -
Object[]inputs - Positional arguments that are the inputs to print. Inputs in the printed output will be separated by spaces. Inputs may be python primitives, tensors, data structures such as dicts and lists that may contain tensors (with the data structures possibly nested in arbitrary ways), and printable python objects.
Returns
-
object - None when executing eagerly. During graph tracing this returns a TF operator that prints the specified inputs in the specified output stream or logging level. This operator will be automatically executed except inside of `tf.compat.v1` graphs and sessions.
Show Example
tensor = tf.range(10)
tf.print(tensor, output_stream=sys.stderr)
object print_dyn(Object[] inputs)
Print the specified inputs. A TensorFlow operator that prints the specified inputs to a desired
output stream or logging level. The inputs may be dense or sparse Tensors,
primitive python objects, data structures that contain tensors, and printable
Python objects. Printed tensors will recursively show the first and last
elements of each dimension to summarize. Example:
Single-input usage:
(This prints "[0 1 2... 7 8 9]" to sys.stderr) Multi-input usage:
(This prints "tensors: [0 1 2... 7 8 9] {2: [0 2 4... 14 16 18]}" to
sys.stdout) Changing the input separator:
(This prints "[0 1],[0 2]" to sys.stderr) Usage in a
tf.function:
(This prints "[0 1 2... 7 8 9]" to sys.stderr) @compatibility(TF 1.x Graphs and Sessions)
In graphs manually created outside of tf.function, this method returns
the created TF operator that prints the data. To make sure the
operator runs, users need to pass the produced op to
`tf.compat.v1.Session`'s run method, or to use the op as a control
dependency for executed ops by specifying
`with tf.compat.v1.control_dependencies([print_op])`.
@end_compatibility Compatibility usage in TF 1.x graphs:
(This prints "tensors: [0 1 2... 7 8 9] {2: [0 2 4... 14 16 18]}" to
sys.stdout) Note: In Jupyter notebooks and colabs, tf.print prints to the notebook
cell outputs. It will not write to the notebook kernel's console logs.
Parameters
-
Object[]inputs - Positional arguments that are the inputs to print. Inputs in the printed output will be separated by spaces. Inputs may be python primitives, tensors, data structures such as dicts and lists that may contain tensors (with the data structures possibly nested in arbitrary ways), and printable python objects.
Returns
-
object - None when executing eagerly. During graph tracing this returns a TF operator that prints the specified inputs in the specified output stream or logging level. This operator will be automatically executed except inside of `tf.compat.v1` graphs and sessions.
Show Example
tensor = tf.range(10)
tf.print(tensor, output_stream=sys.stderr)
object Print_dyn(object input_, object data, object message, object first_n, object summarize, object name)
Prints a list of tensors. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-08-20.
Instructions for updating:
Use tf.print instead of tf.Print. Note that tf.print returns a no-output operator that directly prints the output. Outside of defuns or eager mode, this operator will not be executed unless it is directly specified in session.run or used as a control dependency for other operators. This is only a concern in graph mode. Below is an example of how to ensure tf.print executes in graph mode: This is an identity op (behaves like
tf.identity) with the side effect
of printing `data` when evaluating. Note: This op prints to the standard error. It is not currently compatible
with jupyter notebook (printing to the notebook *server's* output, not into
the notebook).
Parameters
-
objectinput_ - A tensor passed through this op.
-
objectdata - A list of tensors to print out when op is evaluated.
-
objectmessage - A string, prefix of the error message.
-
objectfirst_n - Only log `first_n` number of times. Negative numbers log always; this is the default.
-
objectsummarize - Only print this many entries of each tensor. If None, then a maximum of 3 elements are printed per input tensor.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type and contents as `input_`. ```python sess = tf.compat.v1.Session() with sess.as_default(): tensor = tf.range(10) print_op = tf.print(tensor) with tf.control_dependencies([print_op]): out = tf.add(tensor, tensor) sess.run(out) ``` Additionally, to use tf.print in python 2.7, users must make sure to import the following: `from __future__ import print_function`
Tensor process_input_v4(IGraphNodeBase tree_handle, IGraphNodeBase stats_handle, IGraphNodeBase input_data, IGraphNodeBase sparse_input_indices, IGraphNodeBase sparse_input_values, IGraphNodeBase sparse_input_shape, IGraphNodeBase input_labels, IGraphNodeBase input_weights, IGraphNodeBase leaf_ids, int random_seed, string input_spec, object params, string name)
object process_input_v4_dyn(object tree_handle, object stats_handle, object input_data, object sparse_input_indices, object sparse_input_values, object sparse_input_shape, object input_labels, object input_weights, object leaf_ids, object random_seed, object input_spec, object params, object name)
object py_func(PythonFunctionContainer func, IEnumerable<IGraphNodeBase> inp, IEnumerable<DType> Tout, bool stateful, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.py_func()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.py_func()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.py_func()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
IEnumerable<IGraphNodeBase>inp - A list of `Tensor` objects.
-
IEnumerable<DType>Tout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
boolstateful - (Boolean.) If True, the function should be considered stateful. If a function is stateless, when given the same input it will return the same output and have no observable side effects. Optimizations such as common subexpression elimination are only performed on stateless operations.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.py_func(my_func, [input], tf.float32)
object py_func(PythonFunctionContainer func, IEnumerable<IGraphNodeBase> inp, DType Tout, bool stateful, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.py_func()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.py_func()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.py_func()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
IEnumerable<IGraphNodeBase>inp - A list of `Tensor` objects.
-
DTypeTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
boolstateful - (Boolean.) If True, the function should be considered stateful. If a function is stateless, when given the same input it will return the same output and have no observable side effects. Optimizations such as common subexpression elimination are only performed on stateless operations.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.py_func(my_func, [input], tf.float32)
object py_func(PythonFunctionContainer func, IEnumerable<IGraphNodeBase> inp, ValueTuple<DType, object> Tout, bool stateful, string name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.py_func()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.py_func()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.py_func()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
IEnumerable<IGraphNodeBase>inp - A list of `Tensor` objects.
-
ValueTuple<DType, object>Tout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
boolstateful - (Boolean.) If True, the function should be considered stateful. If a function is stateless, when given the same input it will return the same output and have no observable side effects. Optimizations such as common subexpression elimination are only performed on stateless operations.
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.py_func(my_func, [input], tf.float32)
object py_func_dyn(object func, object inp, object Tout, ImplicitContainer<T> stateful, object name)
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.py_func()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.py_func()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.py_func()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Parameters
-
objectfunc - A Python function, which accepts `ndarray` objects as arguments and
returns a list of `ndarray` objects (or a single `ndarray`). This function
must accept as many arguments as there are tensors in `inp`, and these
argument types will match the corresponding
tf.Tensorobjects in `inp`. The returns `ndarray`s must match the number and types defined `Tout`. Important Note: Input and output numpy `ndarray`s of `func` are not guaranteed to be copies. In some cases their underlying memory will be shared with the corresponding TensorFlow tensors. In-place modification or storing `func` input or return values in python datastructures without explicit (np.)copy can have non-deterministic consequences. -
objectinp - A list of `Tensor` objects.
-
objectTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns.
-
ImplicitContainer<T>stateful - (Boolean.) If True, the function should be considered stateful. If a function is stateless, when given the same input it will return the same output and have no observable side effects. Optimizations such as common subexpression elimination are only performed on stateless operations.
-
objectname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes.
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.py_func(my_func, [input], tf.float32)
object py_function(IGraphNodeBase func, IEnumerable<object> inp, MatchDType Tout, string name)
Wraps a python function into a TensorFlow op that executes it eagerly. This function allows expressing computations in a TensorFlow graph as
Python functions. In particular, it wraps a Python function `func`
in a once-differentiable TensorFlow operation that executes it with eager
execution enabled. As a consequence,
tf.py_function makes it
possible to express control flow using Python constructs (`if`, `while`,
`for`, etc.), instead of TensorFlow control flow constructs (tf.cond,
tf.while_loop). For example, you might use tf.py_function to
implement the log huber function:
You can also use tf.py_function to debug your models at runtime
using Python tools, i.e., you can isolate portions of your code that
you want to debug, wrap them in Python functions and insert `pdb` tracepoints
or print statements as desired, and wrap those functions in
tf.py_function. For more information on eager execution, see the
[Eager guide](https://tensorflow.org/guide/eager). tf.py_function is similar in spirit to `tf.compat.v1.py_func`, but unlike
the latter, the former lets you use TensorFlow operations in the wrapped
Python function. In particular, while `tf.compat.v1.py_func` only runs on CPUs
and
wraps functions that take NumPy arrays as inputs and return NumPy arrays as
outputs, tf.py_function can be placed on GPUs and wraps functions
that take Tensors as inputs, execute TensorFlow operations in their bodies,
and return Tensors as outputs. Like `tf.compat.v1.py_func`, tf.py_function has the following limitations
with respect to serialization and distribution: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.py_function()`. If you are using distributed
TensorFlow, you must run a tf.distribute.Server in the same process as the
program that calls `tf.py_function()` and you must pin the created
operation to a device in that server (e.g. using `with tf.device():`).
Parameters
-
IGraphNodeBasefunc - A Python function which accepts a list of `Tensor` objects having
element types that match the corresponding
tf.Tensorobjects in `inp` and returns a list of `Tensor` objects (or a single `Tensor`, or `None`) having element types that match the corresponding values in `Tout`. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
MatchDTypeTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns; an empty list if no value is returned (i.e., if the return value is `None`).
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes; an empty list if `func` returns None.
Show Example
def log_huber(x, m):
if tf.abs(x) <= m:
return x**2
else:
return m**2 * (1 - 2 * tf.math.log(m) + tf.math.log(x**2)) x = tf.compat.v1.placeholder(tf.float32)
m = tf.compat.v1.placeholder(tf.float32) y = tf.py_function(func=log_huber, inp=[x, m], Tout=tf.float32)
dy_dx = tf.gradients(y, x)[0] with tf.compat.v1.Session() as sess:
# The session executes `log_huber` eagerly. Given the feed values below,
# it will take the first branch, so `y` evaluates to 1.0 and
# `dy_dx` evaluates to 2.0.
y, dy_dx = sess.run([y, dy_dx], feed_dict={x: 1.0, m: 2.0})
object py_function(PythonFunctionContainer func, IEnumerable<object> inp, IEnumerable<object> Tout, string name)
Wraps a python function into a TensorFlow op that executes it eagerly. This function allows expressing computations in a TensorFlow graph as
Python functions. In particular, it wraps a Python function `func`
in a once-differentiable TensorFlow operation that executes it with eager
execution enabled. As a consequence,
tf.py_function makes it
possible to express control flow using Python constructs (`if`, `while`,
`for`, etc.), instead of TensorFlow control flow constructs (tf.cond,
tf.while_loop). For example, you might use tf.py_function to
implement the log huber function:
You can also use tf.py_function to debug your models at runtime
using Python tools, i.e., you can isolate portions of your code that
you want to debug, wrap them in Python functions and insert `pdb` tracepoints
or print statements as desired, and wrap those functions in
tf.py_function. For more information on eager execution, see the
[Eager guide](https://tensorflow.org/guide/eager). tf.py_function is similar in spirit to `tf.compat.v1.py_func`, but unlike
the latter, the former lets you use TensorFlow operations in the wrapped
Python function. In particular, while `tf.compat.v1.py_func` only runs on CPUs
and
wraps functions that take NumPy arrays as inputs and return NumPy arrays as
outputs, tf.py_function can be placed on GPUs and wraps functions
that take Tensors as inputs, execute TensorFlow operations in their bodies,
and return Tensors as outputs. Like `tf.compat.v1.py_func`, tf.py_function has the following limitations
with respect to serialization and distribution: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.py_function()`. If you are using distributed
TensorFlow, you must run a tf.distribute.Server in the same process as the
program that calls `tf.py_function()` and you must pin the created
operation to a device in that server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function which accepts a list of `Tensor` objects having
element types that match the corresponding
tf.Tensorobjects in `inp` and returns a list of `Tensor` objects (or a single `Tensor`, or `None`) having element types that match the corresponding values in `Tout`. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
IEnumerable<object>Tout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns; an empty list if no value is returned (i.e., if the return value is `None`).
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes; an empty list if `func` returns None.
Show Example
def log_huber(x, m):
if tf.abs(x) <= m:
return x**2
else:
return m**2 * (1 - 2 * tf.math.log(m) + tf.math.log(x**2)) x = tf.compat.v1.placeholder(tf.float32)
m = tf.compat.v1.placeholder(tf.float32) y = tf.py_function(func=log_huber, inp=[x, m], Tout=tf.float32)
dy_dx = tf.gradients(y, x)[0] with tf.compat.v1.Session() as sess:
# The session executes `log_huber` eagerly. Given the feed values below,
# it will take the first branch, so `y` evaluates to 1.0 and
# `dy_dx` evaluates to 2.0.
y, dy_dx = sess.run([y, dy_dx], feed_dict={x: 1.0, m: 2.0})
object py_function(IGraphNodeBase func, IEnumerable<object> inp, IEnumerable<object> Tout, string name)
Wraps a python function into a TensorFlow op that executes it eagerly. This function allows expressing computations in a TensorFlow graph as
Python functions. In particular, it wraps a Python function `func`
in a once-differentiable TensorFlow operation that executes it with eager
execution enabled. As a consequence,
tf.py_function makes it
possible to express control flow using Python constructs (`if`, `while`,
`for`, etc.), instead of TensorFlow control flow constructs (tf.cond,
tf.while_loop). For example, you might use tf.py_function to
implement the log huber function:
You can also use tf.py_function to debug your models at runtime
using Python tools, i.e., you can isolate portions of your code that
you want to debug, wrap them in Python functions and insert `pdb` tracepoints
or print statements as desired, and wrap those functions in
tf.py_function. For more information on eager execution, see the
[Eager guide](https://tensorflow.org/guide/eager). tf.py_function is similar in spirit to `tf.compat.v1.py_func`, but unlike
the latter, the former lets you use TensorFlow operations in the wrapped
Python function. In particular, while `tf.compat.v1.py_func` only runs on CPUs
and
wraps functions that take NumPy arrays as inputs and return NumPy arrays as
outputs, tf.py_function can be placed on GPUs and wraps functions
that take Tensors as inputs, execute TensorFlow operations in their bodies,
and return Tensors as outputs. Like `tf.compat.v1.py_func`, tf.py_function has the following limitations
with respect to serialization and distribution: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.py_function()`. If you are using distributed
TensorFlow, you must run a tf.distribute.Server in the same process as the
program that calls `tf.py_function()` and you must pin the created
operation to a device in that server (e.g. using `with tf.device():`).
Parameters
-
IGraphNodeBasefunc - A Python function which accepts a list of `Tensor` objects having
element types that match the corresponding
tf.Tensorobjects in `inp` and returns a list of `Tensor` objects (or a single `Tensor`, or `None`) having element types that match the corresponding values in `Tout`. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
IEnumerable<object>Tout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns; an empty list if no value is returned (i.e., if the return value is `None`).
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes; an empty list if `func` returns None.
Show Example
def log_huber(x, m):
if tf.abs(x) <= m:
return x**2
else:
return m**2 * (1 - 2 * tf.math.log(m) + tf.math.log(x**2)) x = tf.compat.v1.placeholder(tf.float32)
m = tf.compat.v1.placeholder(tf.float32) y = tf.py_function(func=log_huber, inp=[x, m], Tout=tf.float32)
dy_dx = tf.gradients(y, x)[0] with tf.compat.v1.Session() as sess:
# The session executes `log_huber` eagerly. Given the feed values below,
# it will take the first branch, so `y` evaluates to 1.0 and
# `dy_dx` evaluates to 2.0.
y, dy_dx = sess.run([y, dy_dx], feed_dict={x: 1.0, m: 2.0})
object py_function(PythonFunctionContainer func, IEnumerable<object> inp, MatchDType Tout, string name)
Wraps a python function into a TensorFlow op that executes it eagerly. This function allows expressing computations in a TensorFlow graph as
Python functions. In particular, it wraps a Python function `func`
in a once-differentiable TensorFlow operation that executes it with eager
execution enabled. As a consequence,
tf.py_function makes it
possible to express control flow using Python constructs (`if`, `while`,
`for`, etc.), instead of TensorFlow control flow constructs (tf.cond,
tf.while_loop). For example, you might use tf.py_function to
implement the log huber function:
You can also use tf.py_function to debug your models at runtime
using Python tools, i.e., you can isolate portions of your code that
you want to debug, wrap them in Python functions and insert `pdb` tracepoints
or print statements as desired, and wrap those functions in
tf.py_function. For more information on eager execution, see the
[Eager guide](https://tensorflow.org/guide/eager). tf.py_function is similar in spirit to `tf.compat.v1.py_func`, but unlike
the latter, the former lets you use TensorFlow operations in the wrapped
Python function. In particular, while `tf.compat.v1.py_func` only runs on CPUs
and
wraps functions that take NumPy arrays as inputs and return NumPy arrays as
outputs, tf.py_function can be placed on GPUs and wraps functions
that take Tensors as inputs, execute TensorFlow operations in their bodies,
and return Tensors as outputs. Like `tf.compat.v1.py_func`, tf.py_function has the following limitations
with respect to serialization and distribution: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.py_function()`. If you are using distributed
TensorFlow, you must run a tf.distribute.Server in the same process as the
program that calls `tf.py_function()` and you must pin the created
operation to a device in that server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function which accepts a list of `Tensor` objects having
element types that match the corresponding
tf.Tensorobjects in `inp` and returns a list of `Tensor` objects (or a single `Tensor`, or `None`) having element types that match the corresponding values in `Tout`. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
MatchDTypeTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns; an empty list if no value is returned (i.e., if the return value is `None`).
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes; an empty list if `func` returns None.
Show Example
def log_huber(x, m):
if tf.abs(x) <= m:
return x**2
else:
return m**2 * (1 - 2 * tf.math.log(m) + tf.math.log(x**2)) x = tf.compat.v1.placeholder(tf.float32)
m = tf.compat.v1.placeholder(tf.float32) y = tf.py_function(func=log_huber, inp=[x, m], Tout=tf.float32)
dy_dx = tf.gradients(y, x)[0] with tf.compat.v1.Session() as sess:
# The session executes `log_huber` eagerly. Given the feed values below,
# it will take the first branch, so `y` evaluates to 1.0 and
# `dy_dx` evaluates to 2.0.
y, dy_dx = sess.run([y, dy_dx], feed_dict={x: 1.0, m: 2.0})
object py_function(PythonFunctionContainer func, IEnumerable<object> inp, ValueTuple<IEnumerable<object>, object> Tout, string name)
Wraps a python function into a TensorFlow op that executes it eagerly. This function allows expressing computations in a TensorFlow graph as
Python functions. In particular, it wraps a Python function `func`
in a once-differentiable TensorFlow operation that executes it with eager
execution enabled. As a consequence,
tf.py_function makes it
possible to express control flow using Python constructs (`if`, `while`,
`for`, etc.), instead of TensorFlow control flow constructs (tf.cond,
tf.while_loop). For example, you might use tf.py_function to
implement the log huber function:
You can also use tf.py_function to debug your models at runtime
using Python tools, i.e., you can isolate portions of your code that
you want to debug, wrap them in Python functions and insert `pdb` tracepoints
or print statements as desired, and wrap those functions in
tf.py_function. For more information on eager execution, see the
[Eager guide](https://tensorflow.org/guide/eager). tf.py_function is similar in spirit to `tf.compat.v1.py_func`, but unlike
the latter, the former lets you use TensorFlow operations in the wrapped
Python function. In particular, while `tf.compat.v1.py_func` only runs on CPUs
and
wraps functions that take NumPy arrays as inputs and return NumPy arrays as
outputs, tf.py_function can be placed on GPUs and wraps functions
that take Tensors as inputs, execute TensorFlow operations in their bodies,
and return Tensors as outputs. Like `tf.compat.v1.py_func`, tf.py_function has the following limitations
with respect to serialization and distribution: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.py_function()`. If you are using distributed
TensorFlow, you must run a tf.distribute.Server in the same process as the
program that calls `tf.py_function()` and you must pin the created
operation to a device in that server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function which accepts a list of `Tensor` objects having
element types that match the corresponding
tf.Tensorobjects in `inp` and returns a list of `Tensor` objects (or a single `Tensor`, or `None`) having element types that match the corresponding values in `Tout`. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
ValueTuple<IEnumerable<object>, object>Tout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns; an empty list if no value is returned (i.e., if the return value is `None`).
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes; an empty list if `func` returns None.
Show Example
def log_huber(x, m):
if tf.abs(x) <= m:
return x**2
else:
return m**2 * (1 - 2 * tf.math.log(m) + tf.math.log(x**2)) x = tf.compat.v1.placeholder(tf.float32)
m = tf.compat.v1.placeholder(tf.float32) y = tf.py_function(func=log_huber, inp=[x, m], Tout=tf.float32)
dy_dx = tf.gradients(y, x)[0] with tf.compat.v1.Session() as sess:
# The session executes `log_huber` eagerly. Given the feed values below,
# it will take the first branch, so `y` evaluates to 1.0 and
# `dy_dx` evaluates to 2.0.
y, dy_dx = sess.run([y, dy_dx], feed_dict={x: 1.0, m: 2.0})
object py_function(IGraphNodeBase func, IEnumerable<object> inp, ValueTuple<IEnumerable<object>, object> Tout, string name)
Wraps a python function into a TensorFlow op that executes it eagerly. This function allows expressing computations in a TensorFlow graph as
Python functions. In particular, it wraps a Python function `func`
in a once-differentiable TensorFlow operation that executes it with eager
execution enabled. As a consequence,
tf.py_function makes it
possible to express control flow using Python constructs (`if`, `while`,
`for`, etc.), instead of TensorFlow control flow constructs (tf.cond,
tf.while_loop). For example, you might use tf.py_function to
implement the log huber function:
You can also use tf.py_function to debug your models at runtime
using Python tools, i.e., you can isolate portions of your code that
you want to debug, wrap them in Python functions and insert `pdb` tracepoints
or print statements as desired, and wrap those functions in
tf.py_function. For more information on eager execution, see the
[Eager guide](https://tensorflow.org/guide/eager). tf.py_function is similar in spirit to `tf.compat.v1.py_func`, but unlike
the latter, the former lets you use TensorFlow operations in the wrapped
Python function. In particular, while `tf.compat.v1.py_func` only runs on CPUs
and
wraps functions that take NumPy arrays as inputs and return NumPy arrays as
outputs, tf.py_function can be placed on GPUs and wraps functions
that take Tensors as inputs, execute TensorFlow operations in their bodies,
and return Tensors as outputs. Like `tf.compat.v1.py_func`, tf.py_function has the following limitations
with respect to serialization and distribution: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.py_function()`. If you are using distributed
TensorFlow, you must run a tf.distribute.Server in the same process as the
program that calls `tf.py_function()` and you must pin the created
operation to a device in that server (e.g. using `with tf.device():`).
Parameters
-
IGraphNodeBasefunc - A Python function which accepts a list of `Tensor` objects having
element types that match the corresponding
tf.Tensorobjects in `inp` and returns a list of `Tensor` objects (or a single `Tensor`, or `None`) having element types that match the corresponding values in `Tout`. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
ValueTuple<IEnumerable<object>, object>Tout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns; an empty list if no value is returned (i.e., if the return value is `None`).
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes; an empty list if `func` returns None.
Show Example
def log_huber(x, m):
if tf.abs(x) <= m:
return x**2
else:
return m**2 * (1 - 2 * tf.math.log(m) + tf.math.log(x**2)) x = tf.compat.v1.placeholder(tf.float32)
m = tf.compat.v1.placeholder(tf.float32) y = tf.py_function(func=log_huber, inp=[x, m], Tout=tf.float32)
dy_dx = tf.gradients(y, x)[0] with tf.compat.v1.Session() as sess:
# The session executes `log_huber` eagerly. Given the feed values below,
# it will take the first branch, so `y` evaluates to 1.0 and
# `dy_dx` evaluates to 2.0.
y, dy_dx = sess.run([y, dy_dx], feed_dict={x: 1.0, m: 2.0})
object py_function(IGraphNodeBase func, IEnumerable<object> inp, DType Tout, string name)
Wraps a python function into a TensorFlow op that executes it eagerly. This function allows expressing computations in a TensorFlow graph as
Python functions. In particular, it wraps a Python function `func`
in a once-differentiable TensorFlow operation that executes it with eager
execution enabled. As a consequence,
tf.py_function makes it
possible to express control flow using Python constructs (`if`, `while`,
`for`, etc.), instead of TensorFlow control flow constructs (tf.cond,
tf.while_loop). For example, you might use tf.py_function to
implement the log huber function:
You can also use tf.py_function to debug your models at runtime
using Python tools, i.e., you can isolate portions of your code that
you want to debug, wrap them in Python functions and insert `pdb` tracepoints
or print statements as desired, and wrap those functions in
tf.py_function. For more information on eager execution, see the
[Eager guide](https://tensorflow.org/guide/eager). tf.py_function is similar in spirit to `tf.compat.v1.py_func`, but unlike
the latter, the former lets you use TensorFlow operations in the wrapped
Python function. In particular, while `tf.compat.v1.py_func` only runs on CPUs
and
wraps functions that take NumPy arrays as inputs and return NumPy arrays as
outputs, tf.py_function can be placed on GPUs and wraps functions
that take Tensors as inputs, execute TensorFlow operations in their bodies,
and return Tensors as outputs. Like `tf.compat.v1.py_func`, tf.py_function has the following limitations
with respect to serialization and distribution: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.py_function()`. If you are using distributed
TensorFlow, you must run a tf.distribute.Server in the same process as the
program that calls `tf.py_function()` and you must pin the created
operation to a device in that server (e.g. using `with tf.device():`).
Parameters
-
IGraphNodeBasefunc - A Python function which accepts a list of `Tensor` objects having
element types that match the corresponding
tf.Tensorobjects in `inp` and returns a list of `Tensor` objects (or a single `Tensor`, or `None`) having element types that match the corresponding values in `Tout`. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
DTypeTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns; an empty list if no value is returned (i.e., if the return value is `None`).
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes; an empty list if `func` returns None.
Show Example
def log_huber(x, m):
if tf.abs(x) <= m:
return x**2
else:
return m**2 * (1 - 2 * tf.math.log(m) + tf.math.log(x**2)) x = tf.compat.v1.placeholder(tf.float32)
m = tf.compat.v1.placeholder(tf.float32) y = tf.py_function(func=log_huber, inp=[x, m], Tout=tf.float32)
dy_dx = tf.gradients(y, x)[0] with tf.compat.v1.Session() as sess:
# The session executes `log_huber` eagerly. Given the feed values below,
# it will take the first branch, so `y` evaluates to 1.0 and
# `dy_dx` evaluates to 2.0.
y, dy_dx = sess.run([y, dy_dx], feed_dict={x: 1.0, m: 2.0})
object py_function(PythonFunctionContainer func, IEnumerable<object> inp, DType Tout, string name)
Wraps a python function into a TensorFlow op that executes it eagerly. This function allows expressing computations in a TensorFlow graph as
Python functions. In particular, it wraps a Python function `func`
in a once-differentiable TensorFlow operation that executes it with eager
execution enabled. As a consequence,
tf.py_function makes it
possible to express control flow using Python constructs (`if`, `while`,
`for`, etc.), instead of TensorFlow control flow constructs (tf.cond,
tf.while_loop). For example, you might use tf.py_function to
implement the log huber function:
You can also use tf.py_function to debug your models at runtime
using Python tools, i.e., you can isolate portions of your code that
you want to debug, wrap them in Python functions and insert `pdb` tracepoints
or print statements as desired, and wrap those functions in
tf.py_function. For more information on eager execution, see the
[Eager guide](https://tensorflow.org/guide/eager). tf.py_function is similar in spirit to `tf.compat.v1.py_func`, but unlike
the latter, the former lets you use TensorFlow operations in the wrapped
Python function. In particular, while `tf.compat.v1.py_func` only runs on CPUs
and
wraps functions that take NumPy arrays as inputs and return NumPy arrays as
outputs, tf.py_function can be placed on GPUs and wraps functions
that take Tensors as inputs, execute TensorFlow operations in their bodies,
and return Tensors as outputs. Like `tf.compat.v1.py_func`, tf.py_function has the following limitations
with respect to serialization and distribution: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.py_function()`. If you are using distributed
TensorFlow, you must run a tf.distribute.Server in the same process as the
program that calls `tf.py_function()` and you must pin the created
operation to a device in that server (e.g. using `with tf.device():`).
Parameters
-
PythonFunctionContainerfunc - A Python function which accepts a list of `Tensor` objects having
element types that match the corresponding
tf.Tensorobjects in `inp` and returns a list of `Tensor` objects (or a single `Tensor`, or `None`) having element types that match the corresponding values in `Tout`. -
IEnumerable<object>inp - A list of `Tensor` objects.
-
DTypeTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns; an empty list if no value is returned (i.e., if the return value is `None`).
-
stringname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes; an empty list if `func` returns None.
Show Example
def log_huber(x, m):
if tf.abs(x) <= m:
return x**2
else:
return m**2 * (1 - 2 * tf.math.log(m) + tf.math.log(x**2)) x = tf.compat.v1.placeholder(tf.float32)
m = tf.compat.v1.placeholder(tf.float32) y = tf.py_function(func=log_huber, inp=[x, m], Tout=tf.float32)
dy_dx = tf.gradients(y, x)[0] with tf.compat.v1.Session() as sess:
# The session executes `log_huber` eagerly. Given the feed values below,
# it will take the first branch, so `y` evaluates to 1.0 and
# `dy_dx` evaluates to 2.0.
y, dy_dx = sess.run([y, dy_dx], feed_dict={x: 1.0, m: 2.0})
object py_function_dyn(object func, object inp, object Tout, object name)
Wraps a python function into a TensorFlow op that executes it eagerly. This function allows expressing computations in a TensorFlow graph as
Python functions. In particular, it wraps a Python function `func`
in a once-differentiable TensorFlow operation that executes it with eager
execution enabled. As a consequence,
tf.py_function makes it
possible to express control flow using Python constructs (`if`, `while`,
`for`, etc.), instead of TensorFlow control flow constructs (tf.cond,
tf.while_loop). For example, you might use tf.py_function to
implement the log huber function:
You can also use tf.py_function to debug your models at runtime
using Python tools, i.e., you can isolate portions of your code that
you want to debug, wrap them in Python functions and insert `pdb` tracepoints
or print statements as desired, and wrap those functions in
tf.py_function. For more information on eager execution, see the
[Eager guide](https://tensorflow.org/guide/eager). tf.py_function is similar in spirit to `tf.compat.v1.py_func`, but unlike
the latter, the former lets you use TensorFlow operations in the wrapped
Python function. In particular, while `tf.compat.v1.py_func` only runs on CPUs
and
wraps functions that take NumPy arrays as inputs and return NumPy arrays as
outputs, tf.py_function can be placed on GPUs and wraps functions
that take Tensors as inputs, execute TensorFlow operations in their bodies,
and return Tensors as outputs. Like `tf.compat.v1.py_func`, tf.py_function has the following limitations
with respect to serialization and distribution: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.py_function()`. If you are using distributed
TensorFlow, you must run a tf.distribute.Server in the same process as the
program that calls `tf.py_function()` and you must pin the created
operation to a device in that server (e.g. using `with tf.device():`).
Parameters
-
objectfunc - A Python function which accepts a list of `Tensor` objects having
element types that match the corresponding
tf.Tensorobjects in `inp` and returns a list of `Tensor` objects (or a single `Tensor`, or `None`) having element types that match the corresponding values in `Tout`. -
objectinp - A list of `Tensor` objects.
-
objectTout - A list or tuple of tensorflow data types or a single tensorflow data type if there is only one, indicating what `func` returns; an empty list if no value is returned (i.e., if the return value is `None`).
-
objectname - A name for the operation (optional).
Returns
-
object - A list of `Tensor` or a single `Tensor` which `func` computes; an empty list if `func` returns None.
Show Example
def log_huber(x, m):
if tf.abs(x) <= m:
return x**2
else:
return m**2 * (1 - 2 * tf.math.log(m) + tf.math.log(x**2)) x = tf.compat.v1.placeholder(tf.float32)
m = tf.compat.v1.placeholder(tf.float32) y = tf.py_function(func=log_huber, inp=[x, m], Tout=tf.float32)
dy_dx = tf.gradients(y, x)[0] with tf.compat.v1.Session() as sess:
# The session executes `log_huber` eagerly. Given the feed values below,
# it will take the first branch, so `y` evaluates to 1.0 and
# `dy_dx` evaluates to 2.0.
y, dy_dx = sess.run([y, dy_dx], feed_dict={x: 1.0, m: 2.0})
object qr(IGraphNodeBase input, bool full_matrices, string name)
Computes the QR decompositions of one or more matrices. Computes the QR decomposition of each inner matrix in `tensor` such that
`tensor[..., :, :] = q[..., :, :] * r[..., :,:])`
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. A tensor of shape `[..., M, N]` whose inner-most 2 dimensions form matrices of size `[M, N]`. Let `P` be the minimum of `M` and `N`.
-
boolfull_matrices - An optional `bool`. Defaults to `False`. If true, compute full-sized `q` and `r`. If false (the default), compute only the leading `P` columns of `q`.
-
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (q, r).
Show Example
# a is a tensor.
# q is a tensor of orthonormal matrices.
# r is a tensor of upper triangular matrices.
q, r = qr(a)
q_full, r_full = qr(a, full_matrices=True)
object qr_dyn(object input, ImplicitContainer<T> full_matrices, object name)
Computes the QR decompositions of one or more matrices. Computes the QR decomposition of each inner matrix in `tensor` such that
`tensor[..., :, :] = q[..., :, :] * r[..., :,:])`
Parameters
-
objectinput - A `Tensor`. Must be one of the following types: `float64`, `float32`, `half`, `complex64`, `complex128`. A tensor of shape `[..., M, N]` whose inner-most 2 dimensions form matrices of size `[M, N]`. Let `P` be the minimum of `M` and `N`.
-
ImplicitContainer<T>full_matrices - An optional `bool`. Defaults to `False`. If true, compute full-sized `q` and `r`. If false (the default), compute only the leading `P` columns of `q`.
-
objectname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (q, r).
Show Example
# a is a tensor.
# q is a tensor of orthonormal matrices.
# r is a tensor of upper triangular matrices.
q, r = qr(a)
q_full, r_full = qr(a, full_matrices=True)
object quantile_accumulator_add_summaries(IEnumerable<IGraphNodeBase> quantile_accumulator_handles, IGraphNodeBase stamp_token, IEnumerable<object> summaries, string name)
object quantile_accumulator_add_summaries_dyn(object quantile_accumulator_handles, object stamp_token, object summaries, object name)
object quantile_accumulator_deserialize(IGraphNodeBase quantile_accumulator_handle, IGraphNodeBase stamp_token, IGraphNodeBase stream_state, IGraphNodeBase are_buckets_ready, IGraphNodeBase buckets, string name)
object quantile_accumulator_deserialize_dyn(object quantile_accumulator_handle, object stamp_token, object stream_state, object are_buckets_ready, object buckets, object name)
object quantile_accumulator_flush(IGraphNodeBase quantile_accumulator_handle, IGraphNodeBase stamp_token, IGraphNodeBase next_stamp_token, string name)
object quantile_accumulator_flush_dyn(object quantile_accumulator_handle, object stamp_token, object next_stamp_token, object name)
Tensor quantile_accumulator_flush_summary(IGraphNodeBase quantile_accumulator_handle, IGraphNodeBase stamp_token, IGraphNodeBase next_stamp_token, string name)
object quantile_accumulator_flush_summary_dyn(object quantile_accumulator_handle, object stamp_token, object next_stamp_token, object name)
object quantile_accumulator_get_buckets(IEnumerable<object> quantile_accumulator_handles, IGraphNodeBase stamp_token, string name)
object quantile_accumulator_get_buckets_dyn(object quantile_accumulator_handles, object stamp_token, object name)
Tensor quantile_accumulator_is_initialized(IGraphNodeBase quantile_accumulator_handle, string name)
object quantile_accumulator_is_initialized_dyn(object quantile_accumulator_handle, object name)
object quantile_accumulator_serialize(IGraphNodeBase quantile_accumulator_handle, string name)
object quantile_accumulator_serialize_dyn(object quantile_accumulator_handle, object name)
object quantile_buckets(IEnumerable<IGraphNodeBase> dense_float_features, IEnumerable<object> sparse_float_feature_indices, IEnumerable<object> sparse_float_feature_values, IEnumerable<object> sparse_float_feature_shapes, IGraphNodeBase example_weights, IEnumerable<object> dense_config, IEnumerable<object> sparse_config, string name)
object quantile_buckets_dyn(object dense_float_features, object sparse_float_feature_indices, object sparse_float_feature_values, object sparse_float_feature_shapes, object example_weights, object dense_config, object sparse_config, object name)
Tensor quantile_stream_resource_handle_op(string container, object shared_name, string name)
Tensor quantile_stream_resource_handle_op(string container, Byte[] shared_name, string name)
Tensor quantile_stream_resource_handle_op(string container, string shared_name, string name)
object quantile_stream_resource_handle_op_dyn(ImplicitContainer<T> container, ImplicitContainer<T> shared_name, object name)
object quantiles(IEnumerable<object> dense_values, IEnumerable<object> sparse_values, IEnumerable<object> dense_buckets, IEnumerable<object> sparse_buckets, IEnumerable<object> sparse_indices, string name)
object quantiles_dyn(object dense_values, object sparse_values, object dense_buckets, object sparse_buckets, object sparse_indices, object name)
object quantize(IGraphNodeBase input, double min_range, double max_range, DType T, string mode, string round_mode, string name)
Quantize the 'input' tensor of type float to 'output' tensor of type 'T'. [min_range, max_range] are scalar floats that specify the range for
the 'input' data. The 'mode' attribute controls exactly which calculations are
used to convert the float values to their quantized equivalents. The
'round_mode' attribute controls which rounding tie-breaking algorithm is used
when rounding float values to their quantized equivalents. In 'MIN_COMBINED' mode, each value of the tensor will undergo the following: ```
out[i] = (in[i] - min_range) * range(T) / (max_range - min_range)
if T == qint8: out[i] -= (range(T) + 1) / 2.0
``` here `range(T) = numeric_limits::max() - numeric_limits::min()` *MIN_COMBINED Mode Example* Assume the input is type float and has a possible range of [0.0, 6.0] and the
output type is quint8 ([0, 255]). The min_range and max_range values should be
specified as 0.0 and 6.0. Quantizing from float to quint8 will multiply each
value of the input by 255/6 and cast to quint8. If the output type was qint8 ([-128, 127]), the operation will additionally
subtract each value by 128 prior to casting, so that the range of values aligns
with the range of qint8. If the mode is 'MIN_FIRST', then this approach is used: ```
num_discrete_values = 1 << (# of bits in T)
range_adjust = num_discrete_values / (num_discrete_values - 1)
range = (range_max - range_min) * range_adjust
range_scale = num_discrete_values / range
quantized = round(input * range_scale) - round(range_min * range_scale) +
numeric_limits::min()
quantized = max(quantized, numeric_limits::min())
quantized = min(quantized, numeric_limits::max())
``` The biggest difference between this and MIN_COMBINED is that the minimum range
is rounded first, before it's subtracted from the rounded value. With
MIN_COMBINED, a small bias is introduced where repeated iterations of quantizing
and dequantizing will introduce a larger and larger error. *SCALED mode Example* `SCALED` mode matches the quantization approach used in
`QuantizeAndDequantize{V2|V3}`. If the mode is `SCALED`, we do not use the full range of the output type,
choosing to elide the lowest possible value for symmetry (e.g., output range is
-127 to 127, not -128 to 127 for signed 8 bit quantization), so that 0.0 maps to
0. We first find the range of values in our tensor. The
range we use is always centered on 0, so we find m such that ```c++
m = max(abs(input_min), abs(input_max))
``` Our input tensor range is then `[-m, m]`. Next, we choose our fixed-point quantization buckets, `[min_fixed, max_fixed]`.
If T is signed, this is ```
num_bits = sizeof(T) * 8
[min_fixed, max_fixed] =
[-(1 << (num_bits - 1) - 1), (1 << (num_bits - 1)) - 1]
``` Otherwise, if T is unsigned, the fixed-point range is ```
[min_fixed, max_fixed] = [0, (1 << num_bits) - 1]
``` From this we compute our scaling factor, s: ```c++
s = (max_fixed - min_fixed) / (2 * m)
``` Now we can quantize the elements of our tensor: ```c++
result = round(input * s)
``` One thing to watch out for is that the operator may choose to adjust the
requested minimum and maximum values slightly during the quantization process,
so you should always use the output ports as the range for further calculations.
For example, if the requested minimum and maximum values are close to equal,
they will be separated by a small epsilon value to prevent ill-formed quantized
buffers from being created. Otherwise, you can end up with buffers where all the
quantized values map to the same float value, which causes problems for
operations that have to perform further calculations on them.
Parameters
-
IGraphNodeBaseinput - A `Tensor` of type `float32`.
-
doublemin_range - A `Tensor` of type `float32`. The minimum scalar value possibly produced for the input.
-
doublemax_range - A `Tensor` of type `float32`. The maximum scalar value possibly produced for the input.
-
DTypeT - A
tf.DTypefrom: `tf.qint8, tf.quint8, tf.qint32, tf.qint16, tf.quint16`. -
stringmode - An optional `string` from: `"MIN_COMBINED", "MIN_FIRST", "SCALED"`. Defaults to `"MIN_COMBINED"`.
-
stringround_mode - An optional `string` from: `"HALF_AWAY_FROM_ZERO", "HALF_TO_EVEN"`. Defaults to `"HALF_AWAY_FROM_ZERO"`.
-
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (output, output_min, output_max).
object quantize_dyn(object input, object min_range, object max_range, object T, ImplicitContainer<T> mode, ImplicitContainer<T> round_mode, object name)
Quantize the 'input' tensor of type float to 'output' tensor of type 'T'. [min_range, max_range] are scalar floats that specify the range for
the 'input' data. The 'mode' attribute controls exactly which calculations are
used to convert the float values to their quantized equivalents. The
'round_mode' attribute controls which rounding tie-breaking algorithm is used
when rounding float values to their quantized equivalents. In 'MIN_COMBINED' mode, each value of the tensor will undergo the following: ```
out[i] = (in[i] - min_range) * range(T) / (max_range - min_range)
if T == qint8: out[i] -= (range(T) + 1) / 2.0
``` here `range(T) = numeric_limits::max() - numeric_limits::min()` *MIN_COMBINED Mode Example* Assume the input is type float and has a possible range of [0.0, 6.0] and the
output type is quint8 ([0, 255]). The min_range and max_range values should be
specified as 0.0 and 6.0. Quantizing from float to quint8 will multiply each
value of the input by 255/6 and cast to quint8. If the output type was qint8 ([-128, 127]), the operation will additionally
subtract each value by 128 prior to casting, so that the range of values aligns
with the range of qint8. If the mode is 'MIN_FIRST', then this approach is used: ```
num_discrete_values = 1 << (# of bits in T)
range_adjust = num_discrete_values / (num_discrete_values - 1)
range = (range_max - range_min) * range_adjust
range_scale = num_discrete_values / range
quantized = round(input * range_scale) - round(range_min * range_scale) +
numeric_limits::min()
quantized = max(quantized, numeric_limits::min())
quantized = min(quantized, numeric_limits::max())
``` The biggest difference between this and MIN_COMBINED is that the minimum range
is rounded first, before it's subtracted from the rounded value. With
MIN_COMBINED, a small bias is introduced where repeated iterations of quantizing
and dequantizing will introduce a larger and larger error. *SCALED mode Example* `SCALED` mode matches the quantization approach used in
`QuantizeAndDequantize{V2|V3}`. If the mode is `SCALED`, we do not use the full range of the output type,
choosing to elide the lowest possible value for symmetry (e.g., output range is
-127 to 127, not -128 to 127 for signed 8 bit quantization), so that 0.0 maps to
0. We first find the range of values in our tensor. The
range we use is always centered on 0, so we find m such that ```c++
m = max(abs(input_min), abs(input_max))
``` Our input tensor range is then `[-m, m]`. Next, we choose our fixed-point quantization buckets, `[min_fixed, max_fixed]`.
If T is signed, this is ```
num_bits = sizeof(T) * 8
[min_fixed, max_fixed] =
[-(1 << (num_bits - 1) - 1), (1 << (num_bits - 1)) - 1]
``` Otherwise, if T is unsigned, the fixed-point range is ```
[min_fixed, max_fixed] = [0, (1 << num_bits) - 1]
``` From this we compute our scaling factor, s: ```c++
s = (max_fixed - min_fixed) / (2 * m)
``` Now we can quantize the elements of our tensor: ```c++
result = round(input * s)
``` One thing to watch out for is that the operator may choose to adjust the
requested minimum and maximum values slightly during the quantization process,
so you should always use the output ports as the range for further calculations.
For example, if the requested minimum and maximum values are close to equal,
they will be separated by a small epsilon value to prevent ill-formed quantized
buffers from being created. Otherwise, you can end up with buffers where all the
quantized values map to the same float value, which causes problems for
operations that have to perform further calculations on them.
Parameters
-
objectinput - A `Tensor` of type `float32`.
-
objectmin_range - A `Tensor` of type `float32`. The minimum scalar value possibly produced for the input.
-
objectmax_range - A `Tensor` of type `float32`. The maximum scalar value possibly produced for the input.
-
objectT - A
tf.DTypefrom: `tf.qint8, tf.quint8, tf.qint32, tf.qint16, tf.quint16`. -
ImplicitContainer<T>mode - An optional `string` from: `"MIN_COMBINED", "MIN_FIRST", "SCALED"`. Defaults to `"MIN_COMBINED"`.
-
ImplicitContainer<T>round_mode - An optional `string` from: `"HALF_AWAY_FROM_ZERO", "HALF_TO_EVEN"`. Defaults to `"HALF_AWAY_FROM_ZERO"`.
-
objectname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (output, output_min, output_max).
object quantize_v2(object input, object min_range, object max_range, object T, string mode, string name, string round_mode)
Please use
tf.quantization.quantize instead.
object quantize_v2_dyn(object input, object min_range, object max_range, object T, ImplicitContainer<T> mode, object name, ImplicitContainer<T> round_mode)
Please use
tf.quantization.quantize instead.
object quantized_concat(IGraphNodeBase concat_dim, object values, object input_mins, object input_maxes, string name)
Concatenates quantized tensors along one dimension.
Parameters
-
IGraphNodeBaseconcat_dim - A `Tensor` of type `int32`. 0-D. The dimension along which to concatenate. Must be in the range [0, rank(values)).
-
objectvalues - A list of at least 2 `Tensor` objects with the same type. The `N` Tensors to concatenate. Their ranks and types must match, and their sizes must match in all dimensions except `concat_dim`.
-
objectinput_mins - A list with the same length as `values` of `Tensor` objects with type `float32`. The minimum scalar values for each of the input tensors.
-
objectinput_maxes - A list with the same length as `values` of `Tensor` objects with type `float32`. The maximum scalar values for each of the input tensors.
-
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (output, output_min, output_max).
object quantized_concat_dyn(object concat_dim, object values, object input_mins, object input_maxes, object name)
Concatenates quantized tensors along one dimension.
Parameters
-
objectconcat_dim - A `Tensor` of type `int32`. 0-D. The dimension along which to concatenate. Must be in the range [0, rank(values)).
-
objectvalues - A list of at least 2 `Tensor` objects with the same type. The `N` Tensors to concatenate. Their ranks and types must match, and their sizes must match in all dimensions except `concat_dim`.
-
objectinput_mins - A list with the same length as `values` of `Tensor` objects with type `float32`. The minimum scalar values for each of the input tensors.
-
objectinput_maxes - A list with the same length as `values` of `Tensor` objects with type `float32`. The maximum scalar values for each of the input tensors.
-
objectname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (output, output_min, output_max).
Tensor random_crop(IGraphNodeBase value, IEnumerable<int> size, Nullable<int> seed, string name)
Randomly crops a tensor to a given size. Slices a shape `size` portion out of `value` at a uniformly chosen offset.
Requires `value.shape >= size`. If a dimension should not be cropped, pass the full size of that dimension.
For example, RGB images can be cropped with
`size = [crop_height, crop_width, 3]`.
Parameters
-
IGraphNodeBasevalue - Input tensor to crop.
-
IEnumerable<int>size - 1-D tensor with size the rank of `value`.
-
Nullable<int>seed - Python integer. Used to create a random seed. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for this operation (optional).
Returns
-
Tensor - A cropped tensor of the same rank as `value` and shape `size`.
Tensor random_crop(IEnumerable<double> value, IEnumerable<int> size, Nullable<int> seed, string name)
Randomly crops a tensor to a given size. Slices a shape `size` portion out of `value` at a uniformly chosen offset.
Requires `value.shape >= size`. If a dimension should not be cropped, pass the full size of that dimension.
For example, RGB images can be cropped with
`size = [crop_height, crop_width, 3]`.
Parameters
-
IEnumerable<double>value - Input tensor to crop.
-
IEnumerable<int>size - 1-D tensor with size the rank of `value`.
-
Nullable<int>seed - Python integer. Used to create a random seed. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for this operation (optional).
Returns
-
Tensor - A cropped tensor of the same rank as `value` and shape `size`.
Tensor random_crop(ValueTuple<PythonClassContainer, PythonClassContainer> value, IEnumerable<int> size, Nullable<int> seed, string name)
Randomly crops a tensor to a given size. Slices a shape `size` portion out of `value` at a uniformly chosen offset.
Requires `value.shape >= size`. If a dimension should not be cropped, pass the full size of that dimension.
For example, RGB images can be cropped with
`size = [crop_height, crop_width, 3]`.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>value - Input tensor to crop.
-
IEnumerable<int>size - 1-D tensor with size the rank of `value`.
-
Nullable<int>seed - Python integer. Used to create a random seed. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for this operation (optional).
Returns
-
Tensor - A cropped tensor of the same rank as `value` and shape `size`.
Tensor random_crop(IndexedSlices value, IEnumerable<int> size, Nullable<int> seed, string name)
Randomly crops a tensor to a given size. Slices a shape `size` portion out of `value` at a uniformly chosen offset.
Requires `value.shape >= size`. If a dimension should not be cropped, pass the full size of that dimension.
For example, RGB images can be cropped with
`size = [crop_height, crop_width, 3]`.
Parameters
-
IndexedSlicesvalue - Input tensor to crop.
-
IEnumerable<int>size - 1-D tensor with size the rank of `value`.
-
Nullable<int>seed - Python integer. Used to create a random seed. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for this operation (optional).
Returns
-
Tensor - A cropped tensor of the same rank as `value` and shape `size`.
object random_crop_dyn(object value, object size, object seed, object name)
Randomly crops a tensor to a given size. Slices a shape `size` portion out of `value` at a uniformly chosen offset.
Requires `value.shape >= size`. If a dimension should not be cropped, pass the full size of that dimension.
For example, RGB images can be cropped with
`size = [crop_height, crop_width, 3]`.
Parameters
-
objectvalue - Input tensor to crop.
-
objectsize - 1-D tensor with size the rank of `value`.
-
objectseed - Python integer. Used to create a random seed. See `tf.compat.v1.set_random_seed` for behavior.
-
objectname - A name for this operation (optional).
Returns
-
object - A cropped tensor of the same rank as `value` and shape `size`.
object random_gamma(IEnumerable<int> shape, IGraphNodeBase alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
IGraphNodeBasealpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, IEnumerable<object> alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
IEnumerable<object>alpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, double alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
doublealpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, CompositeTensor alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
CompositeTensoralpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, IGraphNodeBase alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
IGraphNodeBasealpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, IGraphNodeBase alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
IGraphNodeBasealpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, ndarray alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
ndarrayalpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, PythonClassContainer alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
PythonClassContaineralpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, CompositeTensor alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
CompositeTensoralpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, PythonClassContainer alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
PythonClassContaineralpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, PythonClassContainer alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
PythonClassContaineralpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, double alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
doublealpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, ndarray alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
ndarrayalpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, ndarray alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
ndarrayalpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, double alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
doublealpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, CompositeTensor alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
CompositeTensoralpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, PythonClassContainer alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
PythonClassContaineralpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, IEnumerable<object> alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
IEnumerable<object>alpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, IEnumerable<object> alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
IEnumerable<object>alpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, CompositeTensor alpha, object beta, PythonClassContainer dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
CompositeTensoralpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
PythonClassContainerdtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, IEnumerable<object> alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
IEnumerable<object>alpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, double alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
doublealpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IGraphNodeBase shape, ndarray alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
ndarrayalpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma(IEnumerable<int> shape, IGraphNodeBase alpha, object beta, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
IGraphNodeBasealpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
object random_gamma_dyn(object shape, object alpha, object beta, ImplicitContainer<T> dtype, object seed, object name)
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Parameters
-
objectshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per alpha/beta-parameterized distribution.
-
objectalpha - A Tensor or Python value or N-D array of type `dtype`. `alpha` provides the shape parameter(s) describing the gamma distribution(s) to sample. Must be broadcastable with `beta`.
-
objectbeta - A Tensor or Python value or N-D array of type `dtype`. Defaults to 1. `beta` provides the inverse scale parameter(s) of the gamma distribution(s) to sample. Must be broadcastable with `alpha`.
-
ImplicitContainer<T>dtype - The type of alpha, beta, and the output: `float16`, `float32`, or `float64`.
-
objectseed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
objectname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
Tensor random_normal(TensorShape shape, double mean, IGraphNodeBase stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
IGraphNodeBasestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IEnumerable<int> shape, int mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(TensorShape shape, double mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IEnumerable<int> shape, int mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IGraphNodeBase shape, int mean, IGraphNodeBase stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
IGraphNodeBasestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IGraphNodeBase shape, IGraphNodeBase mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBasemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IEnumerable<int> shape, double mean, IGraphNodeBase stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
IGraphNodeBasestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IGraphNodeBase shape, IGraphNodeBase mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBasemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IEnumerable<int> shape, double mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IEnumerable<int> shape, int mean, IGraphNodeBase stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
IGraphNodeBasestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IEnumerable<int> shape, IGraphNodeBase mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBasemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IGraphNodeBase shape, IGraphNodeBase mean, IGraphNodeBase stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBasemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
IGraphNodeBasestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IGraphNodeBase shape, double mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IGraphNodeBase shape, double mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IGraphNodeBase shape, double mean, IGraphNodeBase stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
IGraphNodeBasestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(TensorShape shape, IGraphNodeBase mean, IGraphNodeBase stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBasemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
IGraphNodeBasestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(TensorShape shape, IGraphNodeBase mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBasemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(TensorShape shape, IGraphNodeBase mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBasemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(TensorShape shape, int mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(TensorShape shape, int mean, IGraphNodeBase stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
IGraphNodeBasestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IGraphNodeBase shape, int mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IGraphNodeBase shape, int mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IEnumerable<int> shape, IGraphNodeBase mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBasemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IEnumerable<int> shape, IGraphNodeBase mean, IGraphNodeBase stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBasemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
IGraphNodeBasestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(TensorShape shape, double mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(TensorShape shape, int mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
Tensor random_normal(IEnumerable<int> shape, double mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a normal distribution.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random normal values.
object random_normal_dyn(object shape, ImplicitContainer<T> mean, ImplicitContainer<T> stddev, ImplicitContainer<T> dtype, object seed, object name)
Outputs random values from a normal distribution.
Parameters
-
objectshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
ImplicitContainer<T>mean - A 0-D Tensor or Python value of type `dtype`. The mean of the normal distribution.
-
ImplicitContainer<T>stddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
objectname - A name for the operation (optional).
Returns
-
object - A tensor of the specified shape filled with random normal values.
Tensor random_poisson(IndexedSlices lam, ValueTuple shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
IndexedSliceslam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
ValueTupleshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(int lam, ValueTuple shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
intlam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
ValueTupleshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(IGraphNodeBase lam, IEnumerable<int> shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
IGraphNodeBaselam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(int lam, IEnumerable<int> shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
intlam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(int lam, IGraphNodeBase shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
intlam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(IGraphNodeBase lam, ValueTuple shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
IGraphNodeBaselam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
ValueTupleshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(IGraphNodeBase lam, IGraphNodeBase shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
IGraphNodeBaselam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(double lam, IEnumerable<int> shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
doublelam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(IndexedSlices lam, IGraphNodeBase shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
IndexedSliceslam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(ValueTuple<PythonClassContainer, PythonClassContainer> lam, IEnumerable<int> shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>lam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(IEnumerable<object> lam, IGraphNodeBase shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
IEnumerable<object>lam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(IEnumerable<object> lam, IEnumerable<int> shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
IEnumerable<object>lam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(double lam, ValueTuple shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
doublelam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
ValueTupleshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(IndexedSlices lam, IEnumerable<int> shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
IndexedSliceslam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(ValueTuple<PythonClassContainer, PythonClassContainer> lam, IGraphNodeBase shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>lam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(ValueTuple<PythonClassContainer, PythonClassContainer> lam, ValueTuple shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>lam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
ValueTupleshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(double lam, IGraphNodeBase shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
doublelam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_poisson(IEnumerable<object> lam, ValueTuple shape, ImplicitContainer<T> dtype, Nullable<int> seed, string name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
IEnumerable<object>lam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
ValueTupleshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - Optional name for the operation.
Returns
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
object random_poisson_dyn(object lam, object shape, ImplicitContainer<T> dtype, object seed, object name)
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Parameters
-
objectlam - A Tensor or Python value or N-D array of type `dtype`. `lam` provides the rate parameter(s) describing the poisson distribution(s) to sample.
-
objectshape - A 1-D integer Tensor or Python array. The shape of the output samples to be drawn per "rate"-parameterized distribution.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32` or `int64`.
-
objectseed - A Python integer. Used to create a random seed for the distributions. See `tf.compat.v1.set_random_seed` for behavior.
-
objectname - Optional name for the operation.
Returns
-
object
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
Tensor random_shuffle(IEnumerable<object> value, Nullable<int> seed, string name)
Randomly shuffles a tensor along its first dimension. The tensor is shuffled along dimension 0, such that each `value[j]` is mapped
to one and only one `output[i]`. For example, a mapping that might occur for a
3x2 tensor is:
Parameters
-
IEnumerable<object>value - A Tensor to be shuffled.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of same shape and type as `value`, shuffled along its first dimension.
Show Example
[[1, 2], [[5, 6],
[3, 4], ==> [1, 2],
[5, 6]] [3, 4]]
Tensor random_shuffle(IGraphNodeBase value, Nullable<int> seed, string name)
Randomly shuffles a tensor along its first dimension. The tensor is shuffled along dimension 0, such that each `value[j]` is mapped
to one and only one `output[i]`. For example, a mapping that might occur for a
3x2 tensor is:
Parameters
-
IGraphNodeBasevalue - A Tensor to be shuffled.
-
Nullable<int>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of same shape and type as `value`, shuffled along its first dimension.
Show Example
[[1, 2], [[5, 6],
[3, 4], ==> [1, 2],
[5, 6]] [3, 4]]
object random_shuffle_dyn(object value, object seed, object name)
Randomly shuffles a tensor along its first dimension. The tensor is shuffled along dimension 0, such that each `value[j]` is mapped
to one and only one `output[i]`. For example, a mapping that might occur for a
3x2 tensor is:
Parameters
-
objectvalue - A Tensor to be shuffled.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
objectname - A name for the operation (optional).
Returns
-
object - A tensor of same shape and type as `value`, shuffled along its first dimension.
Show Example
[[1, 2], [[5, 6],
[3, 4], ==> [1, 2],
[5, 6]] [3, 4]]
Tensor random_uniform(TensorShape shape, IEnumerable<int> minval, object maxval, PythonClassContainer dtype, int seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IEnumerable<int>minval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
PythonClassContainerdtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
intseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, double minval, object maxval, PythonClassContainer dtype, int seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doubleminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
PythonClassContainerdtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
intseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, IEnumerable<int> minval, object maxval, ImplicitContainer<T> dtype, int seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IEnumerable<int>minval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
intseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, IGraphNodeBase minval, object maxval, PythonClassContainer dtype, int seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBaseminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
PythonClassContainerdtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
intseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, int minval, object maxval, PythonClassContainer dtype, int seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
PythonClassContainerdtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
intseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, int minval, object maxval, PythonClassContainer dtype, IEnumerable<object> seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
PythonClassContainerdtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
IEnumerable<object>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, string minval, object maxval, PythonClassContainer dtype, int seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
stringminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
PythonClassContainerdtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
intseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, IGraphNodeBase minval, object maxval, ImplicitContainer<T> dtype, IEnumerable<object> seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBaseminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
IEnumerable<object>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, IEnumerable<int> minval, object maxval, PythonClassContainer dtype, IEnumerable<object> seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IEnumerable<int>minval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
PythonClassContainerdtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
IEnumerable<object>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, int minval, object maxval, ImplicitContainer<T> dtype, int seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
intseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, int minval, object maxval, ImplicitContainer<T> dtype, IEnumerable<object> seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
IEnumerable<object>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, IEnumerable<int> minval, object maxval, ImplicitContainer<T> dtype, IEnumerable<object> seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IEnumerable<int>minval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
IEnumerable<object>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, string minval, object maxval, ImplicitContainer<T> dtype, IEnumerable<object> seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
stringminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
IEnumerable<object>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, double minval, object maxval, PythonClassContainer dtype, IEnumerable<object> seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doubleminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
PythonClassContainerdtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
IEnumerable<object>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, double minval, object maxval, ImplicitContainer<T> dtype, IEnumerable<object> seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doubleminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
IEnumerable<object>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, string minval, object maxval, ImplicitContainer<T> dtype, int seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
stringminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
intseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, IGraphNodeBase minval, object maxval, PythonClassContainer dtype, IEnumerable<object> seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBaseminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
PythonClassContainerdtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
IEnumerable<object>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, string minval, object maxval, PythonClassContainer dtype, IEnumerable<object> seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
stringminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
PythonClassContainerdtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
IEnumerable<object>seed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, IGraphNodeBase minval, object maxval, ImplicitContainer<T> dtype, int seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
IGraphNodeBaseminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
intseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
Tensor random_uniform(TensorShape shape, double minval, object maxval, ImplicitContainer<T> dtype, int seed, string name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doubleminval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
intseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random uniform values.
object random_uniform_dyn(object shape, ImplicitContainer<T> minval, object maxval, ImplicitContainer<T> dtype, object seed, object name)
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
Parameters
-
objectshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
ImplicitContainer<T>minval - A 0-D Tensor or Python value of type `dtype`. The lower bound on the range of random values to generate. Defaults to 0.
-
objectmaxval - A 0-D Tensor or Python value of type `dtype`. The upper bound on the range of random values to generate. Defaults to 1 if `dtype` is floating point.
-
ImplicitContainer<T>dtype - The type of the output: `float16`, `float32`, `float64`, `int32`, or `int64`.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
objectname - A name for the operation (optional).
Returns
-
object - A tensor of the specified shape filled with random uniform values.
Tensor range(IEnumerable<object> start, PythonClassContainer limit, IGraphNodeBase delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerable<object>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
IGraphNodeBasedelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerable<object> start, PythonClassContainer limit, object delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerable<object>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
objectdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerable<object> start, object limit, IGraphNodeBase delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerable<object>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
IGraphNodeBasedelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerator<IGraphNodeBase> start, object limit, object delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerator<IGraphNodeBase>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
objectdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerator<IGraphNodeBase> start, PythonClassContainer limit, object delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerator<IGraphNodeBase>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
objectdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(object start, PythonClassContainer limit, double delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
objectstart - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
doubledelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerator<IGraphNodeBase> start, object limit, double delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerator<IGraphNodeBase>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
doubledelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerator<IGraphNodeBase> start, object limit, IGraphNodeBase delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerator<IGraphNodeBase>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
IGraphNodeBasedelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerable<object> start, object limit, double delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerable<object>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
doubledelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerator<IGraphNodeBase> start, PythonClassContainer limit, IGraphNodeBase delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerator<IGraphNodeBase>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
IGraphNodeBasedelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(object start, PythonClassContainer limit, IGraphNodeBase delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
objectstart - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
IGraphNodeBasedelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerable<object> start, PythonClassContainer limit, double delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerable<object>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
doubledelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(object start, object limit, int delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
objectstart - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
intdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(object start, object limit, IGraphNodeBase delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
objectstart - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
IGraphNodeBasedelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerator<IGraphNodeBase> start, PythonClassContainer limit, double delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerator<IGraphNodeBase>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
doubledelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(object start, PythonClassContainer limit, object delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
objectstart - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
objectdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(object start, PythonClassContainer limit, int delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
objectstart - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
intdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(object start, object limit, double delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
objectstart - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
doubledelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerator<IGraphNodeBase> start, object limit, int delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerator<IGraphNodeBase>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
intdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerable<object> start, object limit, int delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerable<object>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
intdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(object start, object limit, object delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
objectstart - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
objectdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerator<IGraphNodeBase> start, PythonClassContainer limit, int delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerator<IGraphNodeBase>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
intdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerable<object> start, object limit, object delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerable<object>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
objectdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor range(IEnumerable<object> start, PythonClassContainer limit, int delta, DType dtype, string name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
IEnumerable<object>start - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
PythonClassContainerlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
intdelta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
DTypedtype - The type of the elements of the resulting tensor.
-
stringname - A name for the operation. Defaults to "range".
Returns
-
Tensor - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
object range_dyn(object start, object limit, ImplicitContainer<T> delta, object dtype, ImplicitContainer<T> name)
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Parameters
-
objectstart - A 0-D `Tensor` (scalar). Acts as first entry in the range if `limit` is not None; otherwise, acts as range limit and first entry defaults to 0.
-
objectlimit - A 0-D `Tensor` (scalar). Upper limit of sequence, exclusive. If None, defaults to the value of `start` while the first entry of the range defaults to 0.
-
ImplicitContainer<T>delta - A 0-D `Tensor` (scalar). Number that increments `start`. Defaults to 1.
-
objectdtype - The type of the elements of the resulting tensor.
-
ImplicitContainer<T>name - A name for the operation. Defaults to "range".
Returns
-
object - An 1-D `Tensor` of type `dtype`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
Tensor rank(object input, PythonFunctionContainer name)
Returns the rank of a tensor. Returns a 0-D `int32` `Tensor` representing the rank of `input`.
**Note**: The rank of a tensor is not the same as the rank of a matrix. The
rank of a tensor is the number of indices required to uniquely select each
element of the tensor. Rank is also known as "order", "degree", or "ndims."
Parameters
-
objectinput - A `Tensor` or `SparseTensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `int32`.
Show Example
# shape of tensor 't' is [2, 2, 3]
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.rank(t) # 3
Tensor rank(object input, string name)
Returns the rank of a tensor. Returns a 0-D `int32` `Tensor` representing the rank of `input`.
**Note**: The rank of a tensor is not the same as the rank of a matrix. The
rank of a tensor is the number of indices required to uniquely select each
element of the tensor. Rank is also known as "order", "degree", or "ndims."
Parameters
-
objectinput - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `int32`.
Show Example
# shape of tensor 't' is [2, 2, 3]
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.rank(t) # 3
Tensor rank(PythonClassContainer input, PythonFunctionContainer name)
Returns the rank of a tensor. Returns a 0-D `int32` `Tensor` representing the rank of `input`.
**Note**: The rank of a tensor is not the same as the rank of a matrix. The
rank of a tensor is the number of indices required to uniquely select each
element of the tensor. Rank is also known as "order", "degree", or "ndims."
Parameters
-
PythonClassContainerinput - A `Tensor` or `SparseTensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `int32`.
Show Example
# shape of tensor 't' is [2, 2, 3]
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.rank(t) # 3
Tensor rank(IEnumerable<IGraphNodeBase> input, string name)
Returns the rank of a tensor. Returns a 0-D `int32` `Tensor` representing the rank of `input`.
**Note**: The rank of a tensor is not the same as the rank of a matrix. The
rank of a tensor is the number of indices required to uniquely select each
element of the tensor. Rank is also known as "order", "degree", or "ndims."
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `int32`.
Show Example
# shape of tensor 't' is [2, 2, 3]
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.rank(t) # 3
Tensor rank(IEnumerable<IGraphNodeBase> input, PythonFunctionContainer name)
Returns the rank of a tensor. Returns a 0-D `int32` `Tensor` representing the rank of `input`.
**Note**: The rank of a tensor is not the same as the rank of a matrix. The
rank of a tensor is the number of indices required to uniquely select each
element of the tensor. Rank is also known as "order", "degree", or "ndims."
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor` or `SparseTensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `int32`.
Show Example
# shape of tensor 't' is [2, 2, 3]
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.rank(t) # 3
Tensor rank(PythonClassContainer input, string name)
Returns the rank of a tensor. Returns a 0-D `int32` `Tensor` representing the rank of `input`.
**Note**: The rank of a tensor is not the same as the rank of a matrix. The
rank of a tensor is the number of indices required to uniquely select each
element of the tensor. Rank is also known as "order", "degree", or "ndims."
Parameters
-
PythonClassContainerinput - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `int32`.
Show Example
# shape of tensor 't' is [2, 2, 3]
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.rank(t) # 3
object rank_dyn(object input, object name)
Returns the rank of a tensor. Returns a 0-D `int32` `Tensor` representing the rank of `input`.
**Note**: The rank of a tensor is not the same as the rank of a matrix. The
rank of a tensor is the number of indices required to uniquely select each
element of the tensor. Rank is also known as "order", "degree", or "ndims."
Parameters
-
objectinput - A `Tensor` or `SparseTensor`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `int32`.
Show Example
# shape of tensor 't' is [2, 2, 3]
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.rank(t) # 3
Tensor read_file(IGraphNodeBase filename, string name)
Reads and outputs the entire contents of the input filename.
Parameters
-
IGraphNodeBasefilename - A `Tensor` of type `string`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `string`.
object read_file_dyn(object filename, object name)
Reads and outputs the entire contents of the input filename.
Parameters
-
objectfilename - A `Tensor` of type `string`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `string`.
Tensor real(IGraphNodeBase input, string name)
Returns the real part of a complex (or real) tensor. Given a tensor `input`, this operation returns a tensor of type `float` that
is the real part of each element in `input` considered as a complex number.
If `input` is already real, it is returned unchanged.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. Must have numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32` or `float64`.
Show Example
x = tf.constant([-2.25 + 4.75j, 3.25 + 5.75j])
tf.math.real(x) # [-2.25, 3.25]
object real_dyn(object input, object name)
Returns the real part of a complex (or real) tensor. Given a tensor `input`, this operation returns a tensor of type `float` that
is the real part of each element in `input` considered as a complex number.
If `input` is already real, it is returned unchanged.
Parameters
-
objectinput - A `Tensor`. Must have numeric type.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `float32` or `float64`.
Show Example
x = tf.constant([-2.25 + 4.75j, 3.25 + 5.75j])
tf.math.real(x) # [-2.25, 3.25]
Tensor realdiv(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns x / y element-wise for real types. If `x` and `y` are reals, this will return the floating-point division. *NOTE*: `Div` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
Tensor realdiv(IGraphNodeBase x, IGraphNodeBase y, PythonFunctionContainer name)
Returns x / y element-wise for real types. If `x` and `y` are reals, this will return the floating-point division. *NOTE*: `Div` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
object realdiv_dyn(object x, object y, object name)
Returns x / y element-wise for real types. If `x` and `y` are reals, this will return the floating-point division. *NOTE*: `Div` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object reciprocal(IGraphNodeBase x, string name)
Computes the reciprocal of x element-wise. I.e., \\(y = 1 / x\\).
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object reciprocal_dyn(object x, object name)
Computes the reciprocal of x element-wise. I.e., \\(y = 1 / x\\).
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object recompute_grad(object f)
An eager-compatible version of recompute_grad. For f(*args, **kwargs), this supports gradients with respect to args, or to
gradients with respect to any variables residing in the kwarg 'variables'.
Note that for keras layer and model objects, this is handled automatically. Warning: If `f` was originally a tf.keras Model or Layer object, `g` will not
be able to access the member variables of that object, because `g` returns
through the wrapper function `inner`. When recomputing gradients through
objects that inherit from keras, we suggest keeping a reference to the
underlying object around for the purpose of accessing these variables.
Parameters
-
objectf - function `f(*x)` that returns a `Tensor` or sequence of `Tensor` outputs.
Returns
-
object - A function `g` that wraps `f`, but which recomputes `f` on the backwards pass of a gradient call.
object recompute_grad(Model f)
An eager-compatible version of recompute_grad. For f(*args, **kwargs), this supports gradients with respect to args, or to
gradients with respect to any variables residing in the kwarg 'variables'.
Note that for keras layer and model objects, this is handled automatically. Warning: If `f` was originally a tf.keras Model or Layer object, `g` will not
be able to access the member variables of that object, because `g` returns
through the wrapper function `inner`. When recomputing gradients through
objects that inherit from keras, we suggest keeping a reference to the
underlying object around for the purpose of accessing these variables.
Parameters
-
Modelf - function `f(*x)` that returns a `Tensor` or sequence of `Tensor` outputs.
Returns
-
object - A function `g` that wraps `f`, but which recomputes `f` on the backwards pass of a gradient call.
object recompute_grad_dyn(object f)
An eager-compatible version of recompute_grad. For f(*args, **kwargs), this supports gradients with respect to args, or to
gradients with respect to any variables residing in the kwarg 'variables'.
Note that for keras layer and model objects, this is handled automatically. Warning: If `f` was originally a tf.keras Model or Layer object, `g` will not
be able to access the member variables of that object, because `g` returns
through the wrapper function `inner`. When recomputing gradients through
objects that inherit from keras, we suggest keeping a reference to the
underlying object around for the purpose of accessing these variables.
Parameters
-
objectf - function `f(*x)` that returns a `Tensor` or sequence of `Tensor` outputs.
Returns
-
object - A function `g` that wraps `f`, but which recomputes `f` on the backwards pass of a gradient call.
Tensor reduce_all(IGraphNodeBase input_tensor, object axis, object keepdims, string name, IEnumerable<int> reduction_indices, object keep_dims)
Computes the "logical and" of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The boolean tensor to reduce.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[True, True], [False, False]])
tf.reduce_all(x) # False
tf.reduce_all(x, 0) # [False, False]
tf.reduce_all(x, 1) # [True, False]
Tensor reduce_all(IEnumerable<object> input_tensor, object axis, object keepdims, string name, IEnumerable<int> reduction_indices, object keep_dims)
Computes the "logical and" of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The boolean tensor to reduce.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[True, True], [False, False]])
tf.reduce_all(x) # False
tf.reduce_all(x, 0) # [False, False]
tf.reduce_all(x, 1) # [True, False]
object reduce_all_dyn(object input_tensor, object axis, object keepdims, object name, object reduction_indices, object keep_dims)
Computes the "logical and" of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
objectinput_tensor - The boolean tensor to reduce.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
objectname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced tensor.
Show Example
x = tf.constant([[True, True], [False, False]])
tf.reduce_all(x) # False
tf.reduce_all(x, 0) # [False, False]
tf.reduce_all(x, 1) # [True, False]
Tensor reduce_any(IGraphNodeBase input_tensor, Nullable<int> axis, object keepdims, string name, IEnumerable<int> reduction_indices, object keep_dims)
Computes the "logical or" of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The boolean tensor to reduce.
-
Nullable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[True, True], [False, False]])
tf.reduce_any(x) # True
tf.reduce_any(x, 0) # [True, True]
tf.reduce_any(x, 1) # [True, False]
Tensor reduce_any(IEnumerable<object> input_tensor, Nullable<int> axis, object keepdims, string name, IEnumerable<int> reduction_indices, object keep_dims)
Computes the "logical or" of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The boolean tensor to reduce.
-
Nullable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[True, True], [False, False]])
tf.reduce_any(x) # True
tf.reduce_any(x, 0) # [True, True]
tf.reduce_any(x, 1) # [True, False]
object reduce_any_dyn(object input_tensor, object axis, object keepdims, object name, object reduction_indices, object keep_dims)
Computes the "logical or" of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
objectinput_tensor - The boolean tensor to reduce.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
objectname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced tensor.
Show Example
x = tf.constant([[True, True], [False, False]])
tf.reduce_any(x) # True
tf.reduce_any(x, 0) # [True, True]
tf.reduce_any(x, 1) # [True, False]
Tensor reduce_join(object inputs, object axis, Nullable<bool> keep_dims, string separator, string name, Nullable<int> reduction_indices, Nullable<bool> keepdims)
Joins a string Tensor across the given dimensions. Computes the string join across dimensions in the given string Tensor of shape
`[\\(d_0, d_1,..., d_{n-1}\\)]`. Returns a new Tensor created by joining the input
strings with the given separator (default: empty string). Negative indices are
counted backwards from the end, with `-1` being equivalent to `n - 1`. If
indices are not specified, joins across all dimensions beginning from `n - 1`
through `0`.
Parameters
-
objectinputs - A `Tensor` of type `string`. The input to be joined. All reduced indices must have non-zero size.
-
objectaxis - A `Tensor` of type `int32`. The dimensions to reduce over. Dimensions are reduced in the order specified. Omitting `axis` is equivalent to passing `[n-1, n-2,..., 0]`. Negative indices from `-n` to `-1` are supported.
-
Nullable<bool>keep_dims - An optional `bool`. Defaults to `False`. If `True`, retain reduced dimensions with length `1`.
-
stringseparator - An optional `string`. Defaults to `""`. The separator to use when joining.
-
stringname - A name for the operation (optional).
-
Nullable<int>reduction_indices -
Nullable<bool>keepdims
Returns
-
Tensor - A `Tensor` of type `string`.
Show Example
# tensor `a` is [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, -2) = tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, -1) = tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, 0, keep_dims=True) ==> [["ac", "bd"]]
tf.strings.reduce_join(a, 1, keep_dims=True) ==> [["ab"], ["cd"]]
tf.strings.reduce_join(a, 0, separator=".") ==> ["a.c", "b.d"]
tf.strings.reduce_join(a, [0, 1]) ==> "acbd"
tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
tf.strings.reduce_join(a, []) ==> [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a) = tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
Tensor reduce_join(object inputs, IGraphNodeBase axis, Nullable<bool> keep_dims, string separator, string name, Nullable<int> reduction_indices, Nullable<bool> keepdims)
Joins a string Tensor across the given dimensions. Computes the string join across dimensions in the given string Tensor of shape
`[\\(d_0, d_1,..., d_{n-1}\\)]`. Returns a new Tensor created by joining the input
strings with the given separator (default: empty string). Negative indices are
counted backwards from the end, with `-1` being equivalent to `n - 1`. If
indices are not specified, joins across all dimensions beginning from `n - 1`
through `0`.
Parameters
-
objectinputs - A `Tensor` of type `string`. The input to be joined. All reduced indices must have non-zero size.
-
IGraphNodeBaseaxis - A `Tensor` of type `int32`. The dimensions to reduce over. Dimensions are reduced in the order specified. Omitting `axis` is equivalent to passing `[n-1, n-2,..., 0]`. Negative indices from `-n` to `-1` are supported.
-
Nullable<bool>keep_dims - An optional `bool`. Defaults to `False`. If `True`, retain reduced dimensions with length `1`.
-
stringseparator - An optional `string`. Defaults to `""`. The separator to use when joining.
-
stringname - A name for the operation (optional).
-
Nullable<int>reduction_indices -
Nullable<bool>keepdims
Returns
-
Tensor - A `Tensor` of type `string`.
Show Example
# tensor `a` is [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, -2) = tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, -1) = tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, 0, keep_dims=True) ==> [["ac", "bd"]]
tf.strings.reduce_join(a, 1, keep_dims=True) ==> [["ab"], ["cd"]]
tf.strings.reduce_join(a, 0, separator=".") ==> ["a.c", "b.d"]
tf.strings.reduce_join(a, [0, 1]) ==> "acbd"
tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
tf.strings.reduce_join(a, []) ==> [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a) = tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
Tensor reduce_join(object inputs, ndarray axis, Nullable<bool> keep_dims, string separator, string name, Nullable<int> reduction_indices, Nullable<bool> keepdims)
Joins a string Tensor across the given dimensions. Computes the string join across dimensions in the given string Tensor of shape
`[\\(d_0, d_1,..., d_{n-1}\\)]`. Returns a new Tensor created by joining the input
strings with the given separator (default: empty string). Negative indices are
counted backwards from the end, with `-1` being equivalent to `n - 1`. If
indices are not specified, joins across all dimensions beginning from `n - 1`
through `0`.
Parameters
-
objectinputs - A `Tensor` of type `string`. The input to be joined. All reduced indices must have non-zero size.
-
ndarrayaxis - A `Tensor` of type `int32`. The dimensions to reduce over. Dimensions are reduced in the order specified. Omitting `axis` is equivalent to passing `[n-1, n-2,..., 0]`. Negative indices from `-n` to `-1` are supported.
-
Nullable<bool>keep_dims - An optional `bool`. Defaults to `False`. If `True`, retain reduced dimensions with length `1`.
-
stringseparator - An optional `string`. Defaults to `""`. The separator to use when joining.
-
stringname - A name for the operation (optional).
-
Nullable<int>reduction_indices -
Nullable<bool>keepdims
Returns
-
Tensor - A `Tensor` of type `string`.
Show Example
# tensor `a` is [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, -2) = tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, -1) = tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, 0, keep_dims=True) ==> [["ac", "bd"]]
tf.strings.reduce_join(a, 1, keep_dims=True) ==> [["ab"], ["cd"]]
tf.strings.reduce_join(a, 0, separator=".") ==> ["a.c", "b.d"]
tf.strings.reduce_join(a, [0, 1]) ==> "acbd"
tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
tf.strings.reduce_join(a, []) ==> [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a) = tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
Tensor reduce_join(object inputs, int axis, Nullable<bool> keep_dims, string separator, string name, Nullable<int> reduction_indices, Nullable<bool> keepdims)
Joins a string Tensor across the given dimensions. Computes the string join across dimensions in the given string Tensor of shape
`[\\(d_0, d_1,..., d_{n-1}\\)]`. Returns a new Tensor created by joining the input
strings with the given separator (default: empty string). Negative indices are
counted backwards from the end, with `-1` being equivalent to `n - 1`. If
indices are not specified, joins across all dimensions beginning from `n - 1`
through `0`.
Parameters
-
objectinputs - A `Tensor` of type `string`. The input to be joined. All reduced indices must have non-zero size.
-
intaxis - A `Tensor` of type `int32`. The dimensions to reduce over. Dimensions are reduced in the order specified. Omitting `axis` is equivalent to passing `[n-1, n-2,..., 0]`. Negative indices from `-n` to `-1` are supported.
-
Nullable<bool>keep_dims - An optional `bool`. Defaults to `False`. If `True`, retain reduced dimensions with length `1`.
-
stringseparator - An optional `string`. Defaults to `""`. The separator to use when joining.
-
stringname - A name for the operation (optional).
-
Nullable<int>reduction_indices -
Nullable<bool>keepdims
Returns
-
Tensor - A `Tensor` of type `string`.
Show Example
# tensor `a` is [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, -2) = tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, -1) = tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, 0, keep_dims=True) ==> [["ac", "bd"]]
tf.strings.reduce_join(a, 1, keep_dims=True) ==> [["ab"], ["cd"]]
tf.strings.reduce_join(a, 0, separator=".") ==> ["a.c", "b.d"]
tf.strings.reduce_join(a, [0, 1]) ==> "acbd"
tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
tf.strings.reduce_join(a, []) ==> [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a) = tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
Tensor reduce_join(object inputs, ValueTuple<object, IEnumerable<object>> axis, Nullable<bool> keep_dims, string separator, string name, Nullable<int> reduction_indices, Nullable<bool> keepdims)
Joins a string Tensor across the given dimensions. Computes the string join across dimensions in the given string Tensor of shape
`[\\(d_0, d_1,..., d_{n-1}\\)]`. Returns a new Tensor created by joining the input
strings with the given separator (default: empty string). Negative indices are
counted backwards from the end, with `-1` being equivalent to `n - 1`. If
indices are not specified, joins across all dimensions beginning from `n - 1`
through `0`.
Parameters
-
objectinputs - A `Tensor` of type `string`. The input to be joined. All reduced indices must have non-zero size.
-
ValueTuple<object, IEnumerable<object>>axis - A `Tensor` of type `int32`. The dimensions to reduce over. Dimensions are reduced in the order specified. Omitting `axis` is equivalent to passing `[n-1, n-2,..., 0]`. Negative indices from `-n` to `-1` are supported.
-
Nullable<bool>keep_dims - An optional `bool`. Defaults to `False`. If `True`, retain reduced dimensions with length `1`.
-
stringseparator - An optional `string`. Defaults to `""`. The separator to use when joining.
-
stringname - A name for the operation (optional).
-
Nullable<int>reduction_indices -
Nullable<bool>keepdims
Returns
-
Tensor - A `Tensor` of type `string`.
Show Example
# tensor `a` is [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, -2) = tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, -1) = tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, 0, keep_dims=True) ==> [["ac", "bd"]]
tf.strings.reduce_join(a, 1, keep_dims=True) ==> [["ab"], ["cd"]]
tf.strings.reduce_join(a, 0, separator=".") ==> ["a.c", "b.d"]
tf.strings.reduce_join(a, [0, 1]) ==> "acbd"
tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
tf.strings.reduce_join(a, []) ==> [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a) = tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
Tensor reduce_join(object inputs, IEnumerable<object> axis, Nullable<bool> keep_dims, string separator, string name, Nullable<int> reduction_indices, Nullable<bool> keepdims)
Joins a string Tensor across the given dimensions. Computes the string join across dimensions in the given string Tensor of shape
`[\\(d_0, d_1,..., d_{n-1}\\)]`. Returns a new Tensor created by joining the input
strings with the given separator (default: empty string). Negative indices are
counted backwards from the end, with `-1` being equivalent to `n - 1`. If
indices are not specified, joins across all dimensions beginning from `n - 1`
through `0`.
Parameters
-
objectinputs - A `Tensor` of type `string`. The input to be joined. All reduced indices must have non-zero size.
-
IEnumerable<object>axis - A `Tensor` of type `int32`. The dimensions to reduce over. Dimensions are reduced in the order specified. Omitting `axis` is equivalent to passing `[n-1, n-2,..., 0]`. Negative indices from `-n` to `-1` are supported.
-
Nullable<bool>keep_dims - An optional `bool`. Defaults to `False`. If `True`, retain reduced dimensions with length `1`.
-
stringseparator - An optional `string`. Defaults to `""`. The separator to use when joining.
-
stringname - A name for the operation (optional).
-
Nullable<int>reduction_indices -
Nullable<bool>keepdims
Returns
-
Tensor - A `Tensor` of type `string`.
Show Example
# tensor `a` is [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, -2) = tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, -1) = tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, 0, keep_dims=True) ==> [["ac", "bd"]]
tf.strings.reduce_join(a, 1, keep_dims=True) ==> [["ab"], ["cd"]]
tf.strings.reduce_join(a, 0, separator=".") ==> ["a.c", "b.d"]
tf.strings.reduce_join(a, [0, 1]) ==> "acbd"
tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
tf.strings.reduce_join(a, []) ==> [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a) = tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
object reduce_join_dyn(object inputs, object axis, object keep_dims, ImplicitContainer<T> separator, object name, object reduction_indices, object keepdims)
Joins a string Tensor across the given dimensions. Computes the string join across dimensions in the given string Tensor of shape
`[\\(d_0, d_1,..., d_{n-1}\\)]`. Returns a new Tensor created by joining the input
strings with the given separator (default: empty string). Negative indices are
counted backwards from the end, with `-1` being equivalent to `n - 1`. If
indices are not specified, joins across all dimensions beginning from `n - 1`
through `0`.
Parameters
-
objectinputs - A `Tensor` of type `string`. The input to be joined. All reduced indices must have non-zero size.
-
objectaxis - A `Tensor` of type `int32`. The dimensions to reduce over. Dimensions are reduced in the order specified. Omitting `axis` is equivalent to passing `[n-1, n-2,..., 0]`. Negative indices from `-n` to `-1` are supported.
-
objectkeep_dims - An optional `bool`. Defaults to `False`. If `True`, retain reduced dimensions with length `1`.
-
ImplicitContainer<T>separator - An optional `string`. Defaults to `""`. The separator to use when joining.
-
objectname - A name for the operation (optional).
-
objectreduction_indices -
objectkeepdims
Returns
-
object - A `Tensor` of type `string`.
Show Example
# tensor `a` is [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, -2) = tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, -1) = tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, 0, keep_dims=True) ==> [["ac", "bd"]]
tf.strings.reduce_join(a, 1, keep_dims=True) ==> [["ab"], ["cd"]]
tf.strings.reduce_join(a, 0, separator=".") ==> ["a.c", "b.d"]
tf.strings.reduce_join(a, [0, 1]) ==> "acbd"
tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
tf.strings.reduce_join(a, []) ==> [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a) = tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
object reduce_logsumexp(IEnumerable<object> input_tensor, IEnumerable<int> axis, object keepdims, string name, IEnumerable<int> reduction_indices, object keep_dims)
Computes log(sum(exp(elements across dimensions of a tensor))). (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. This function is more numerically stable than log(sum(exp(input))). It avoids
overflows caused by taking the exp of large inputs and underflows caused by
taking the log of small inputs.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced tensor.
Show Example
x = tf.constant([[0., 0., 0.], [0., 0., 0.]])
tf.reduce_logsumexp(x) # log(6)
tf.reduce_logsumexp(x, 0) # [log(2), log(2), log(2)]
tf.reduce_logsumexp(x, 1) # [log(3), log(3)]
tf.reduce_logsumexp(x, 1, keepdims=True) # [[log(3)], [log(3)]]
tf.reduce_logsumexp(x, [0, 1]) # log(6)
object reduce_logsumexp_dyn(object input_tensor, object axis, object keepdims, object name, object reduction_indices, object keep_dims)
Computes log(sum(exp(elements across dimensions of a tensor))). (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. This function is more numerically stable than log(sum(exp(input))). It avoids
overflows caused by taking the exp of large inputs and underflows caused by
taking the log of small inputs.
Parameters
-
objectinput_tensor - The tensor to reduce. Should have numeric type.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
objectname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced tensor.
Show Example
x = tf.constant([[0., 0., 0.], [0., 0., 0.]])
tf.reduce_logsumexp(x) # log(6)
tf.reduce_logsumexp(x, 0) # [log(2), log(2), log(2)]
tf.reduce_logsumexp(x, 1) # [log(3), log(3)]
tf.reduce_logsumexp(x, 1, keepdims=True) # [[log(3)], [log(3)]]
tf.reduce_logsumexp(x, [0, 1]) # log(6)
Tensor reduce_max(IEnumerable<object> input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, IGraphNodeBase reduction_indices, Nullable<bool> keep_dims)
Computes the maximum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have real numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasereduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Tensor reduce_max(IGraphNodeBase input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, IGraphNodeBase reduction_indices, Nullable<bool> keep_dims)
Computes the maximum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should have real numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasereduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Tensor reduce_max(IEnumerable<object> input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the maximum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have real numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Tensor reduce_max(IGraphNodeBase input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the maximum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should have real numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
object reduce_max_dyn(object input_tensor, object axis, object keepdims, object name, object reduction_indices, object keep_dims)
Computes the maximum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
objectinput_tensor - The tensor to reduce. Should have real numeric type.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
objectname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced tensor.
Tensor reduce_mean(IEnumerable<object> input_tensor, IEnumerable<int> axis, object keepdims, string name, IGraphNodeBase reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasereduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IGraphNodeBase input_tensor, int axis, object keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IndexedSlices input_tensor, int axis, object keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IndexedSlicesinput_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IGraphNodeBase input_tensor, IEnumerable<int> axis, object keepdims, string name, IGraphNodeBase reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasereduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IndexedSlices input_tensor, IEnumerable<int> axis, object keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IndexedSlicesinput_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IGraphNodeBase input_tensor, int axis, object keepdims, string name, IGraphNodeBase reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasereduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(ValueTuple<PythonClassContainer, PythonClassContainer> input_tensor, int axis, object keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>input_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IEnumerable<object> input_tensor, int axis, object keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(ValueTuple<PythonClassContainer, PythonClassContainer> input_tensor, int axis, object keepdims, string name, IGraphNodeBase reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>input_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasereduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(ValueTuple<PythonClassContainer, PythonClassContainer> input_tensor, IEnumerable<int> axis, object keepdims, string name, IGraphNodeBase reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>input_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasereduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(ValueTuple<PythonClassContainer, PythonClassContainer> input_tensor, IEnumerable<int> axis, object keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>input_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IGraphNodeBase input_tensor, IEnumerable<int> axis, object keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IEnumerable<object> input_tensor, IEnumerable<int> axis, object keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IndexedSlices input_tensor, IEnumerable<int> axis, object keepdims, string name, IGraphNodeBase reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IndexedSlicesinput_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasereduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IndexedSlices input_tensor, int axis, object keepdims, string name, IGraphNodeBase reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IndexedSlicesinput_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasereduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_mean(IEnumerable<object> input_tensor, int axis, object keepdims, string name, IGraphNodeBase reduction_indices, Nullable<bool> keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IGraphNodeBasereduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
object reduce_mean_dyn(object input_tensor, object axis, object keepdims, object name, object reduction_indices, object keep_dims)
Computes the mean of elements across dimensions of a tensor. Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
objectinput_tensor - The tensor to reduce. Should have numeric type.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
objectname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced tensor.
Show Example
x = tf.constant([[1., 1.], [2., 2.]])
tf.reduce_mean(x) # 1.5
tf.reduce_mean(x, 0) # [1.5, 1.5]
tf.reduce_mean(x, 1) # [1., 2.]
Tensor reduce_min(IEnumerable<object> input_tensor, IEnumerable<int> axis, object keepdims, string name, IEnumerable<int> reduction_indices, object keep_dims)
Computes the minimum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have real numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
object reduce_min_dyn(object input_tensor, object axis, object keepdims, object name, object reduction_indices, object keep_dims)
Computes the minimum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
objectinput_tensor - The tensor to reduce. Should have real numeric type.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
objectname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced tensor.
Tensor reduce_prod(IEnumerable<object> input_tensor, IEnumerable<int> axis, object keepdims, string name, IEnumerable<int> reduction_indices, object keep_dims)
Computes the product of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor.
object reduce_prod_dyn(object input_tensor, object axis, object keepdims, object name, object reduction_indices, object keep_dims)
Computes the product of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
objectinput_tensor - The tensor to reduce. Should have numeric type.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
objectname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced tensor.
Tensor reduce_slice_max(IGraphNodeBase data, IGraphNodeBase indices, IGraphNodeBase axis, string name)
object reduce_slice_max_dyn(object data, object indices, object axis, object name)
Tensor reduce_slice_min(IGraphNodeBase data, IGraphNodeBase indices, IGraphNodeBase axis, string name)
object reduce_slice_min_dyn(object data, object indices, object axis, object name)
Tensor reduce_slice_prod(IGraphNodeBase data, IGraphNodeBase indices, IGraphNodeBase axis, string name)
object reduce_slice_prod_dyn(object data, object indices, object axis, object name)
Tensor reduce_slice_sum(IGraphNodeBase data, IGraphNodeBase indices, IGraphNodeBase axis, string name)
object reduce_slice_sum_dyn(object data, object indices, object axis, object name)
Tensor reduce_sum(IGraphNodeBase input_tensor, int axis, Nullable<bool> keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IEnumerable<object> input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(ValueTuple<PythonClassContainer, PythonClassContainer> input_tensor, int axis, Nullable<bool> keepdims, string name, int reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>input_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
intreduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(ValueTuple<PythonClassContainer, PythonClassContainer> input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, int reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>input_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
intreduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IndexedSlices input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IndexedSlicesinput_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IEnumerable<object> input_tensor, int axis, Nullable<bool> keepdims, string name, int reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
intreduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IEnumerable<object> input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, int reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
intreduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(ValueTuple<PythonClassContainer, PythonClassContainer> input_tensor, int axis, Nullable<bool> keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>input_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IEnumerable<object> input_tensor, int axis, Nullable<bool> keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IEnumerable<object>input_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IGraphNodeBase input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IGraphNodeBase input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, int reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
intreduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IndexedSlices input_tensor, int axis, Nullable<bool> keepdims, string name, int reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IndexedSlicesinput_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
intreduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IGraphNodeBase input_tensor, int axis, Nullable<bool> keepdims, string name, int reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IGraphNodeBaseinput_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
intreduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(ValueTuple<PythonClassContainer, PythonClassContainer> input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>input_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IndexedSlices input_tensor, IEnumerable<int> axis, Nullable<bool> keepdims, string name, int reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IndexedSlicesinput_tensor - The tensor to reduce. Should have numeric type.
-
IEnumerable<int>axis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
intreduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
Tensor reduce_sum(IndexedSlices input_tensor, int axis, Nullable<bool> keepdims, string name, IEnumerable<int> reduction_indices, Nullable<bool> keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
IndexedSlicesinput_tensor - The tensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
Nullable<bool>keepdims - If true, retains reduced dimensions with length 1.
-
stringname - A name for the operation (optional).
-
IEnumerable<int>reduction_indices - The old (deprecated) name for axis.
-
Nullable<bool>keep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
object reduce_sum_dyn(object input_tensor, object axis, object keepdims, object name, object reduction_indices, object keep_dims)
Computes the sum of elements across dimensions of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` is None, all dimensions are reduced, and a
tensor with a single element is returned.
Parameters
-
objectinput_tensor - The tensor to reduce. Should have numeric type.
-
objectaxis - The dimensions to reduce. If `None` (the default), reduces all dimensions. Must be in the range `[-rank(input_tensor), rank(input_tensor))`.
-
objectkeepdims - If true, retains reduced dimensions with length 1.
-
objectname - A name for the operation (optional).
-
objectreduction_indices - The old (deprecated) name for axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced tensor, of the same dtype as the input_tensor.
Show Example
x = tf.constant([[1, 1, 1], [1, 1, 1]])
tf.reduce_sum(x) # 6
tf.reduce_sum(x, 0) # [2, 2, 2]
tf.reduce_sum(x, 1) # [3, 3]
tf.reduce_sum(x, 1, keepdims=True) # [[3], [3]]
tf.reduce_sum(x, [0, 1]) # 6
object ref_in(object a, string name)
object ref_in_dyn(object a, object name)
object ref_input_float_input(IGraphNodeBase a, IGraphNodeBase b, string name)
object ref_input_float_input_dyn(object a, object b, object name)
Tensor ref_input_float_input_int_output(IGraphNodeBase a, IGraphNodeBase b, string name)
object ref_input_float_input_int_output_dyn(object a, object b, object name)
object ref_input_int_input(IGraphNodeBase a, IGraphNodeBase b, string name)
object ref_input_int_input_dyn(object a, object b, object name)
object ref_out(object T, string name)
object ref_out_dyn(object T, object name)
Tensor ref_output(string name)
object ref_output_dyn(object name)
object ref_output_float_output(string name)
object ref_output_float_output_dyn(object name)
Tensor regex_replace(IGraphNodeBase input, string pattern, string rewrite, bool replace_global, string name)
Replace elements of `input` matching regex `pattern` with `rewrite`.
Parameters
-
IGraphNodeBaseinput - string `Tensor`, the source strings to process.
-
stringpattern - string or scalar string `Tensor`, regular expression to use, see more details at https://github.com/google/re2/wiki/Syntax
-
stringrewrite - string or scalar string `Tensor`, value to use in match replacement, supports backslash-escaped digits (\1 to \9) can be to insert text matching corresponding parenthesized group.
-
boolreplace_global - `bool`, if `True` replace all non-overlapping matches, else replace only the first match.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - string `Tensor` of the same shape as `input` with specified replacements.
object regex_replace_dyn(object input, object pattern, object rewrite, ImplicitContainer<T> replace_global, object name)
Replace elements of `input` matching regex `pattern` with `rewrite`.
Parameters
-
objectinput - string `Tensor`, the source strings to process.
-
objectpattern - string or scalar string `Tensor`, regular expression to use, see more details at https://github.com/google/re2/wiki/Syntax
-
objectrewrite - string or scalar string `Tensor`, value to use in match replacement, supports backslash-escaped digits (\1 to \9) can be to insert text matching corresponding parenthesized group.
-
ImplicitContainer<T>replace_global - `bool`, if `True` replace all non-overlapping matches, else replace only the first match.
-
objectname - A name for the operation (optional).
Returns
-
object - string `Tensor` of the same shape as `input` with specified replacements.
void register_tensor_conversion_function(object base_type, PythonFunctionContainer conversion_func, int priority)
Registers a function for converting objects of `base_type` to `Tensor`. The conversion function must have the following signature:
It must return a `Tensor` with the given `dtype` if specified. If the
conversion function creates a new `Tensor`, it should use the given
`name` if specified. All exceptions will be propagated to the caller. The conversion function may return `NotImplemented` for some
inputs. In this case, the conversion process will continue to try
subsequent conversion functions. If `as_ref` is true, the function must return a `Tensor` reference,
such as a `Variable`. NOTE: The conversion functions will execute in order of priority,
followed by order of registration. To ensure that a conversion function
`F` runs before another conversion function `G`, ensure that `F` is
registered with a smaller priority than `G`.
Parameters
-
objectbase_type - The base type or tuple of base types for all objects that `conversion_func` accepts.
-
PythonFunctionContainerconversion_func - A function that converts instances of `base_type` to `Tensor`.
-
intpriority - Optional integer that indicates the priority for applying this conversion function. Conversion functions with smaller priority values run earlier than conversion functions with larger priority values. Defaults to 100.
Show Example
def conversion_func(value, dtype=None, name=None, as_ref=False):
#...
void register_tensor_conversion_function(PythonClassContainer base_type, PythonFunctionContainer conversion_func, int priority)
Registers a function for converting objects of `base_type` to `Tensor`. The conversion function must have the following signature:
It must return a `Tensor` with the given `dtype` if specified. If the
conversion function creates a new `Tensor`, it should use the given
`name` if specified. All exceptions will be propagated to the caller. The conversion function may return `NotImplemented` for some
inputs. In this case, the conversion process will continue to try
subsequent conversion functions. If `as_ref` is true, the function must return a `Tensor` reference,
such as a `Variable`. NOTE: The conversion functions will execute in order of priority,
followed by order of registration. To ensure that a conversion function
`F` runs before another conversion function `G`, ensure that `F` is
registered with a smaller priority than `G`.
Parameters
-
PythonClassContainerbase_type - The base type or tuple of base types for all objects that `conversion_func` accepts.
-
PythonFunctionContainerconversion_func - A function that converts instances of `base_type` to `Tensor`.
-
intpriority - Optional integer that indicates the priority for applying this conversion function. Conversion functions with smaller priority values run earlier than conversion functions with larger priority values. Defaults to 100.
Show Example
def conversion_func(value, dtype=None, name=None, as_ref=False):
#...
object register_tensor_conversion_function_dyn(object base_type, object conversion_func, ImplicitContainer<T> priority)
Registers a function for converting objects of `base_type` to `Tensor`. The conversion function must have the following signature:
It must return a `Tensor` with the given `dtype` if specified. If the
conversion function creates a new `Tensor`, it should use the given
`name` if specified. All exceptions will be propagated to the caller. The conversion function may return `NotImplemented` for some
inputs. In this case, the conversion process will continue to try
subsequent conversion functions. If `as_ref` is true, the function must return a `Tensor` reference,
such as a `Variable`. NOTE: The conversion functions will execute in order of priority,
followed by order of registration. To ensure that a conversion function
`F` runs before another conversion function `G`, ensure that `F` is
registered with a smaller priority than `G`.
Parameters
-
objectbase_type - The base type or tuple of base types for all objects that `conversion_func` accepts.
-
objectconversion_func - A function that converts instances of `base_type` to `Tensor`.
-
ImplicitContainer<T>priority - Optional integer that indicates the priority for applying this conversion function. Conversion functions with smaller priority values run earlier than conversion functions with larger priority values. Defaults to 100.
Show Example
def conversion_func(value, dtype=None, name=None, as_ref=False):
#...
Tensor reinterpret_string_to_float(IGraphNodeBase input_data, string name)
object reinterpret_string_to_float_dyn(object input_data, object name)
object remote_fused_graph_execute(IEnumerable<object> inputs, IEnumerable<PythonClassContainer> Toutputs, object serialized_remote_fused_graph_execute_info, string name)
object remote_fused_graph_execute_dyn(object inputs, object Toutputs, object serialized_remote_fused_graph_execute_info, object name)
Tensor repeat(IGraphNodeBase input, IGraphNodeBase repeats, Nullable<int> axis, string name)
Repeat elements of `input`
Parameters
-
IGraphNodeBaseinput - An `N`-dimensional Tensor.
-
IGraphNodeBaserepeats - An 1-D `int` Tensor. The number of repetitions for each element. repeats is broadcasted to fit the shape of the given axis. `len(repeats)` must equal `input.shape[axis]` if axis is not None.
-
Nullable<int>axis - An int. The axis along which to repeat values. By default (axis=None), use the flattened input array, and return a flat output array.
-
stringname - A name for the operation.
Returns
-
Tensor - A Tensor which has the same shape as `input`, except along the given axis. If axis is None then the output array is flattened to match the flattened input array. #### Examples: ```python >>> repeat(['a', 'b', 'c'], repeats=[3, 0, 2], axis=0) ['a', 'a', 'a', 'c', 'c'] >>> repeat([[1, 2], [3, 4]], repeats=[2, 3], axis=0) [[1, 2], [1, 2], [3, 4], [3, 4], [3, 4]] >>> repeat([[1, 2], [3, 4]], repeats=[2, 3], axis=1) [[1, 1, 2, 2, 2], [3, 3, 4, 4, 4]] >>> repeat(3, repeats=4) [3, 3, 3, 3] >>> repeat([[1,2], [3,4]], repeats=2) [1, 1, 2, 2, 3, 3, 4, 4] ```
Tensor repeat(IGraphNodeBase input, IEnumerable<int> repeats, Nullable<int> axis, string name)
Repeat elements of `input`
Parameters
-
IGraphNodeBaseinput - An `N`-dimensional Tensor.
-
IEnumerable<int>repeats - An 1-D `int` Tensor. The number of repetitions for each element. repeats is broadcasted to fit the shape of the given axis. `len(repeats)` must equal `input.shape[axis]` if axis is not None.
-
Nullable<int>axis - An int. The axis along which to repeat values. By default (axis=None), use the flattened input array, and return a flat output array.
-
stringname - A name for the operation.
Returns
-
Tensor - A Tensor which has the same shape as `input`, except along the given axis. If axis is None then the output array is flattened to match the flattened input array. #### Examples: ```python >>> repeat(['a', 'b', 'c'], repeats=[3, 0, 2], axis=0) ['a', 'a', 'a', 'c', 'c'] >>> repeat([[1, 2], [3, 4]], repeats=[2, 3], axis=0) [[1, 2], [1, 2], [3, 4], [3, 4], [3, 4]] >>> repeat([[1, 2], [3, 4]], repeats=[2, 3], axis=1) [[1, 1, 2, 2, 2], [3, 3, 4, 4, 4]] >>> repeat(3, repeats=4) [3, 3, 3, 3] >>> repeat([[1,2], [3,4]], repeats=2) [1, 1, 2, 2, 3, 3, 4, 4] ```
Tensor repeat(IGraphNodeBase input, int repeats, Nullable<int> axis, string name)
Repeat elements of `input`
Parameters
-
IGraphNodeBaseinput - An `N`-dimensional Tensor.
-
intrepeats - An 1-D `int` Tensor. The number of repetitions for each element. repeats is broadcasted to fit the shape of the given axis. `len(repeats)` must equal `input.shape[axis]` if axis is not None.
-
Nullable<int>axis - An int. The axis along which to repeat values. By default (axis=None), use the flattened input array, and return a flat output array.
-
stringname - A name for the operation.
Returns
-
Tensor - A Tensor which has the same shape as `input`, except along the given axis. If axis is None then the output array is flattened to match the flattened input array. #### Examples: ```python >>> repeat(['a', 'b', 'c'], repeats=[3, 0, 2], axis=0) ['a', 'a', 'a', 'c', 'c'] >>> repeat([[1, 2], [3, 4]], repeats=[2, 3], axis=0) [[1, 2], [1, 2], [3, 4], [3, 4], [3, 4]] >>> repeat([[1, 2], [3, 4]], repeats=[2, 3], axis=1) [[1, 1, 2, 2, 2], [3, 3, 4, 4, 4]] >>> repeat(3, repeats=4) [3, 3, 3, 3] >>> repeat([[1,2], [3,4]], repeats=2) [1, 1, 2, 2, 3, 3, 4, 4] ```
object repeat_dyn(object input, object repeats, object axis, object name)
Repeat elements of `input`
Parameters
-
objectinput - An `N`-dimensional Tensor.
-
objectrepeats - An 1-D `int` Tensor. The number of repetitions for each element. repeats is broadcasted to fit the shape of the given axis. `len(repeats)` must equal `input.shape[axis]` if axis is not None.
-
objectaxis - An int. The axis along which to repeat values. By default (axis=None), use the flattened input array, and return a flat output array.
-
objectname - A name for the operation.
Returns
-
object - A Tensor which has the same shape as `input`, except along the given axis. If axis is None then the output array is flattened to match the flattened input array. #### Examples: ```python >>> repeat(['a', 'b', 'c'], repeats=[3, 0, 2], axis=0) ['a', 'a', 'a', 'c', 'c'] >>> repeat([[1, 2], [3, 4]], repeats=[2, 3], axis=0) [[1, 2], [1, 2], [3, 4], [3, 4], [3, 4]] >>> repeat([[1, 2], [3, 4]], repeats=[2, 3], axis=1) [[1, 1, 2, 2, 2], [3, 3, 4, 4, 4]] >>> repeat(3, repeats=4) [3, 3, 3, 3] >>> repeat([[1,2], [3,4]], repeats=2) [1, 1, 2, 2, 3, 3, 4, 4] ```
Tensor report_uninitialized_variables(object var_list, string name)
Adds ops to list the names of uninitialized variables. When run, it returns a 1-D tensor containing the names of uninitialized
variables if there are any, or an empty array if there are none.
Parameters
-
objectvar_list - List of `Variable` objects to check. Defaults to the value of `global_variables() + local_variables()`
-
stringname - Optional name of the `Operation`.
Returns
-
Tensor - A 1-D tensor containing names of the uninitialized variables, or an empty 1-D tensor if there are no variables or no uninitialized variables. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
object report_uninitialized_variables_dyn(object var_list, ImplicitContainer<T> name)
Adds ops to list the names of uninitialized variables. When run, it returns a 1-D tensor containing the names of uninitialized
variables if there are any, or an empty array if there are none.
Parameters
-
objectvar_list - List of `Variable` objects to check. Defaults to the value of `global_variables() + local_variables()`
-
ImplicitContainer<T>name - Optional name of the `Operation`.
Returns
-
object - A 1-D tensor containing names of the uninitialized variables, or an empty 1-D tensor if there are no variables or no uninitialized variables. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
ValueTuple<Tensor, object> required_space_to_batch_paddings(IEnumerable<int> input_shape, ValueTuple<int, object> block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IEnumerable<int>input_shape - int32 Tensor of shape [N].
-
ValueTuple<int, object>block_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IEnumerable<int> input_shape, IEnumerable<double> block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IEnumerable<int>input_shape - int32 Tensor of shape [N].
-
IEnumerable<double>block_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(ndarray input_shape, int block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
ndarrayinput_shape - int32 Tensor of shape [N].
-
intblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IEnumerable<int> input_shape, int block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IEnumerable<int>input_shape - int32 Tensor of shape [N].
-
intblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IEnumerable<int> input_shape, IGraphNodeBase block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IEnumerable<int>input_shape - int32 Tensor of shape [N].
-
IGraphNodeBaseblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IEnumerable<int> input_shape, object block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IEnumerable<int>input_shape - int32 Tensor of shape [N].
-
objectblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IGraphNodeBase input_shape, ndarray block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IGraphNodeBaseinput_shape - int32 Tensor of shape [N].
-
ndarrayblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IGraphNodeBase input_shape, IEnumerable<double> block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IGraphNodeBaseinput_shape - int32 Tensor of shape [N].
-
IEnumerable<double>block_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IEnumerable<int> input_shape, ndarray block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IEnumerable<int>input_shape - int32 Tensor of shape [N].
-
ndarrayblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(ndarray input_shape, ndarray block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
ndarrayinput_shape - int32 Tensor of shape [N].
-
ndarrayblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IGraphNodeBase input_shape, int block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IGraphNodeBaseinput_shape - int32 Tensor of shape [N].
-
intblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IGraphNodeBase input_shape, IGraphNodeBase block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IGraphNodeBaseinput_shape - int32 Tensor of shape [N].
-
IGraphNodeBaseblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(ndarray input_shape, IEnumerable<double> block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
ndarrayinput_shape - int32 Tensor of shape [N].
-
IEnumerable<double>block_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IGraphNodeBase input_shape, object block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IGraphNodeBaseinput_shape - int32 Tensor of shape [N].
-
objectblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(ndarray input_shape, ValueTuple<int, object> block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
ndarrayinput_shape - int32 Tensor of shape [N].
-
ValueTuple<int, object>block_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(ndarray input_shape, object block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
ndarrayinput_shape - int32 Tensor of shape [N].
-
objectblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(ndarray input_shape, IGraphNodeBase block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
ndarrayinput_shape - int32 Tensor of shape [N].
-
IGraphNodeBaseblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
ValueTuple<Tensor, object> required_space_to_batch_paddings(IGraphNodeBase input_shape, ValueTuple<int, object> block_shape, object base_paddings, string name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
IGraphNodeBaseinput_shape - int32 Tensor of shape [N].
-
ValueTuple<int, object>block_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
stringname - string. Optional name prefix.
Returns
-
ValueTuple<Tensor, object> - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
object required_space_to_batch_paddings_dyn(object input_shape, object block_shape, object base_paddings, object name)
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
Parameters
-
objectinput_shape - int32 Tensor of shape [N].
-
objectblock_shape - int32 Tensor of shape [N].
-
objectbase_paddings - Optional int32 Tensor of shape [N, 2]. Specifies the minimum amount of padding to use. All elements must be >= 0. If not specified, defaults to 0.
-
objectname - string. Optional name prefix.
Returns
-
object - (paddings, crops), where: `paddings` and `crops` are int32 Tensors of rank 2 and shape [N, 2]
Tensor requires_older_graph_version(string name)
object requires_older_graph_version_dyn(object name)
Tensor resampler(IGraphNodeBase data, IGraphNodeBase warp, string name)
object resampler_dyn(object data, object warp, object name)
object resampler_grad(IGraphNodeBase data, IGraphNodeBase warp, IGraphNodeBase grad_output, string name)
object resampler_grad_dyn(object data, object warp, object grad_output, object name)
object reserved_attr(object range, string name)
object reserved_attr_dyn(object range, object name)
object reserved_input(IGraphNodeBase input, string name)
object reserved_input_dyn(object input, object name)
void reset_default_graph()
Clears the default graph stack and resets the global default graph. NOTE: The default graph is a property of the current thread. This
function applies only to the current thread. Calling this function while
a `tf.compat.v1.Session` or `tf.compat.v1.InteractiveSession` is active will
result in undefined
behavior. Using any previously created
tf.Operation or tf.Tensor objects
after calling this function will result in undefined behavior.
object reset_default_graph_dyn()
Clears the default graph stack and resets the global default graph. NOTE: The default graph is a property of the current thread. This
function applies only to the current thread. Calling this function while
a `tf.compat.v1.Session` or `tf.compat.v1.InteractiveSession` is active will
result in undefined
behavior. Using any previously created
tf.Operation or tf.Tensor objects
after calling this function will result in undefined behavior.
Tensor reshape(IGraphNodeBase tensor, IGraphNodeBase shape, PythonFunctionContainer name)
Reshapes a tensor. Given `tensor`, this operation returns a tensor that has the same values
as `tensor` with shape `shape`. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total size remains constant. In particular,
a `shape` of `[-1]` flattens into 1-D. At most one component of `shape` can
be -1. If `shape` is 1-D or higher, then the operation returns a tensor with shape
`shape` filled with the values of `tensor`. In this case, the number of
elements implied by `shape` must be the same as the number of elements in
`tensor`. For example: ```
# tensor 't' is [1, 2, 3, 4, 5, 6, 7, 8, 9]
# tensor 't' has shape [9]
reshape(t, [3, 3]) ==> [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]] # tensor 't' is [[[1, 1], [2, 2]],
# [[3, 3], [4, 4]]]
# tensor 't' has shape [2, 2, 2]
reshape(t, [2, 4]) ==> [[1, 1, 2, 2],
[3, 3, 4, 4]] # tensor 't' is [[[1, 1, 1],
# [2, 2, 2]],
# [[3, 3, 3],
# [4, 4, 4]],
# [[5, 5, 5],
# [6, 6, 6]]]
# tensor 't' has shape [3, 2, 3]
# pass '[-1]' to flatten 't'
reshape(t, [-1]) ==> [1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6] # -1 can also be used to infer the shape # -1 is inferred to be 9:
reshape(t, [2, -1]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3],
[4, 4, 4, 5, 5, 5, 6, 6, 6]]
# -1 is inferred to be 2:
reshape(t, [-1, 9]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3],
[4, 4, 4, 5, 5, 5, 6, 6, 6]]
# -1 is inferred to be 3:
reshape(t, [ 2, -1, 3]) ==> [[[1, 1, 1],
[2, 2, 2],
[3, 3, 3]],
[[4, 4, 4],
[5, 5, 5],
[6, 6, 6]]] # tensor 't' is [7]
# shape `[]` reshapes to a scalar
reshape(t, []) ==> 7
```
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBaseshape - A `Tensor`. Must be one of the following types: `int32`, `int64`. Defines the shape of the output tensor.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Tensor reshape(IGraphNodeBase tensor, IGraphNodeBase shape, string name)
Reshapes a tensor. Given `tensor`, this operation returns a tensor that has the same values
as `tensor` with shape `shape`. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total size remains constant. In particular,
a `shape` of `[-1]` flattens into 1-D. At most one component of `shape` can
be -1. If `shape` is 1-D or higher, then the operation returns a tensor with shape
`shape` filled with the values of `tensor`. In this case, the number of
elements implied by `shape` must be the same as the number of elements in
`tensor`. For example: ```
# tensor 't' is [1, 2, 3, 4, 5, 6, 7, 8, 9]
# tensor 't' has shape [9]
reshape(t, [3, 3]) ==> [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]] # tensor 't' is [[[1, 1], [2, 2]],
# [[3, 3], [4, 4]]]
# tensor 't' has shape [2, 2, 2]
reshape(t, [2, 4]) ==> [[1, 1, 2, 2],
[3, 3, 4, 4]] # tensor 't' is [[[1, 1, 1],
# [2, 2, 2]],
# [[3, 3, 3],
# [4, 4, 4]],
# [[5, 5, 5],
# [6, 6, 6]]]
# tensor 't' has shape [3, 2, 3]
# pass '[-1]' to flatten 't'
reshape(t, [-1]) ==> [1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6] # -1 can also be used to infer the shape # -1 is inferred to be 9:
reshape(t, [2, -1]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3],
[4, 4, 4, 5, 5, 5, 6, 6, 6]]
# -1 is inferred to be 2:
reshape(t, [-1, 9]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3],
[4, 4, 4, 5, 5, 5, 6, 6, 6]]
# -1 is inferred to be 3:
reshape(t, [ 2, -1, 3]) ==> [[[1, 1, 1],
[2, 2, 2],
[3, 3, 3]],
[[4, 4, 4],
[5, 5, 5],
[6, 6, 6]]] # tensor 't' is [7]
# shape `[]` reshapes to a scalar
reshape(t, []) ==> 7
```
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
IGraphNodeBaseshape - A `Tensor`. Must be one of the following types: `int32`, `int64`. Defines the shape of the output tensor.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Tensor reshape(IGraphNodeBase tensor, string name, TensorDimension[] shape)
Given a tensor , this operation returns a new Tensor that has the same values as tensor in the same order,
except with a new shape given by shape.
object reshape(object tensor, IEnumerable<int> shape, string name)
Tensor reshape(IGraphNodeBase tensor, TensorDimension[] shape)
Given a tensor , this operation returns a new Tensor that has the same values as tensor in the same order,
except with a new shape given by shape.
object reshape_dyn(object tensor, object shape, object name)
Reshapes a tensor. Given `tensor`, this operation returns a tensor that has the same values
as `tensor` with shape `shape`. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total size remains constant. In particular,
a `shape` of `[-1]` flattens into 1-D. At most one component of `shape` can
be -1. If `shape` is 1-D or higher, then the operation returns a tensor with shape
`shape` filled with the values of `tensor`. In this case, the number of
elements implied by `shape` must be the same as the number of elements in
`tensor`. For example: ```
# tensor 't' is [1, 2, 3, 4, 5, 6, 7, 8, 9]
# tensor 't' has shape [9]
reshape(t, [3, 3]) ==> [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]] # tensor 't' is [[[1, 1], [2, 2]],
# [[3, 3], [4, 4]]]
# tensor 't' has shape [2, 2, 2]
reshape(t, [2, 4]) ==> [[1, 1, 2, 2],
[3, 3, 4, 4]] # tensor 't' is [[[1, 1, 1],
# [2, 2, 2]],
# [[3, 3, 3],
# [4, 4, 4]],
# [[5, 5, 5],
# [6, 6, 6]]]
# tensor 't' has shape [3, 2, 3]
# pass '[-1]' to flatten 't'
reshape(t, [-1]) ==> [1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6] # -1 can also be used to infer the shape # -1 is inferred to be 9:
reshape(t, [2, -1]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3],
[4, 4, 4, 5, 5, 5, 6, 6, 6]]
# -1 is inferred to be 2:
reshape(t, [-1, 9]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3],
[4, 4, 4, 5, 5, 5, 6, 6, 6]]
# -1 is inferred to be 3:
reshape(t, [ 2, -1, 3]) ==> [[[1, 1, 1],
[2, 2, 2],
[3, 3, 3]],
[[4, 4, 4],
[5, 5, 5],
[6, 6, 6]]] # tensor 't' is [7]
# shape `[]` reshapes to a scalar
reshape(t, []) ==> 7
```
Parameters
-
objecttensor - A `Tensor`.
-
objectshape - A `Tensor`. Must be one of the following types: `int32`, `int64`. Defines the shape of the output tensor.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `tensor`.
Tensor<T> reshape<T>(Tensor<T> tensor, TensorDimension[] shape)
Given a tensor , this operation returns a new Tensor<T> that has the same values as tensor in the same order,
except with a new shape given by shape.
Tensor<T> reshape<T>(Tensor<T> tensor, string name, TensorDimension[] shape)
Given a tensor , this operation returns a new Tensor<T> that has the same values as tensor in the same order,
except with a new shape given by shape.
object resource_create_op(IGraphNodeBase resource, string name)
object resource_create_op_dyn(object resource, object name)
Tensor resource_initialized_op(IGraphNodeBase resource, string name)
object resource_initialized_op_dyn(object resource, object name)
object resource_using_op(IGraphNodeBase resource, string name)
object resource_using_op_dyn(object resource, object name)
Tensor restrict(IGraphNodeBase a, string name)
object restrict_dyn(object a, object name)
Tensor reverse(IGraphNodeBase tensor, IGraphNodeBase axis, string name)
Reverses specific dimensions of a tensor. NOTE
tf.reverse has now changed behavior in preparation for 1.0.
tf.reverse_v2 is currently an alias that will be deprecated before TF 1.0. Given a `tensor`, and a `int32` tensor `axis` representing the set of
dimensions of `tensor` to reverse. This operation reverses each dimension
`i` for which there exists `j` s.t. `axis[j] == i`. `tensor` can have up to 8 dimensions. The number of dimensions specified
in `axis` may be 0 or more entries. If an index is specified more than
once, a InvalidArgument error is raised. For example: ```
# tensor 't' is [[[[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]],
# [[12, 13, 14, 15],
# [16, 17, 18, 19],
# [20, 21, 22, 23]]]]
# tensor 't' shape is [1, 2, 3, 4] # 'dims' is [3] or 'dims' is [-1]
reverse(t, dims) ==> [[[[ 3, 2, 1, 0],
[ 7, 6, 5, 4],
[ 11, 10, 9, 8]],
[[15, 14, 13, 12],
[19, 18, 17, 16],
[23, 22, 21, 20]]]] # 'dims' is '[1]' (or 'dims' is '[-3]')
reverse(t, dims) ==> [[[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]]]] # 'dims' is '[2]' (or 'dims' is '[-2]')
reverse(t, dims) ==> [[[[8, 9, 10, 11],
[4, 5, 6, 7],
[0, 1, 2, 3]]
[[20, 21, 22, 23],
[16, 17, 18, 19],
[12, 13, 14, 15]]]]
```
Parameters
-
IGraphNodeBasetensor - A `Tensor`. Must be one of the following types: `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `bool`, `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`, `string`. Up to 8-D.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D. The indices of the dimensions to reverse. Must be in the range `[-rank(tensor), rank(tensor))`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
object reverse_dyn(object tensor, object axis, object name)
Reverses specific dimensions of a tensor. NOTE
tf.reverse has now changed behavior in preparation for 1.0.
tf.reverse_v2 is currently an alias that will be deprecated before TF 1.0. Given a `tensor`, and a `int32` tensor `axis` representing the set of
dimensions of `tensor` to reverse. This operation reverses each dimension
`i` for which there exists `j` s.t. `axis[j] == i`. `tensor` can have up to 8 dimensions. The number of dimensions specified
in `axis` may be 0 or more entries. If an index is specified more than
once, a InvalidArgument error is raised. For example: ```
# tensor 't' is [[[[ 0, 1, 2, 3],
# [ 4, 5, 6, 7],
# [ 8, 9, 10, 11]],
# [[12, 13, 14, 15],
# [16, 17, 18, 19],
# [20, 21, 22, 23]]]]
# tensor 't' shape is [1, 2, 3, 4] # 'dims' is [3] or 'dims' is [-1]
reverse(t, dims) ==> [[[[ 3, 2, 1, 0],
[ 7, 6, 5, 4],
[ 11, 10, 9, 8]],
[[15, 14, 13, 12],
[19, 18, 17, 16],
[23, 22, 21, 20]]]] # 'dims' is '[1]' (or 'dims' is '[-3]')
reverse(t, dims) ==> [[[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]
[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]]]] # 'dims' is '[2]' (or 'dims' is '[-2]')
reverse(t, dims) ==> [[[[8, 9, 10, 11],
[4, 5, 6, 7],
[0, 1, 2, 3]]
[[20, 21, 22, 23],
[16, 17, 18, 19],
[12, 13, 14, 15]]]]
```
Parameters
-
objecttensor - A `Tensor`. Must be one of the following types: `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `bool`, `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`, `string`. Up to 8-D.
-
objectaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D. The indices of the dimensions to reverse. Must be in the range `[-rank(tensor), rank(tensor))`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `tensor`.
Tensor reverse_sequence(object input, IEnumerable<int> seq_lengths, Nullable<int> seq_axis, Nullable<int> batch_axis, string name, Nullable<int> seq_dim, Nullable<int> batch_dim)
Reverses variable length slices. This op first slices `input` along the dimension `batch_axis`, and for each
slice `i`, reverses the first `seq_lengths[i]` elements along
the dimension `seq_axis`. The elements of `seq_lengths` must obey `seq_lengths[i] <= input.dims[seq_dim]`,
and `seq_lengths` must be a vector of length `input.dims[batch_dim]`. The output slice `i` along dimension `batch_axis` is then given by input
slice `i`, with the first `seq_lengths[i]` slices along dimension
`seq_axis` reversed. For example: ```
# Given this:
batch_dim = 0
seq_dim = 1
input.dims = (4, 8,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0, 0:7, :,...] = input[0, 7:0:-1, :,...]
output[1, 0:2, :,...] = input[1, 2:0:-1, :,...]
output[2, 0:3, :,...] = input[2, 3:0:-1, :,...]
output[3, 0:5, :,...] = input[3, 5:0:-1, :,...] # while entries past seq_lens are copied through:
output[0, 7:, :,...] = input[0, 7:, :,...]
output[1, 2:, :,...] = input[1, 2:, :,...]
output[2, 3:, :,...] = input[2, 3:, :,...]
output[3, 2:, :,...] = input[3, 2:, :,...]
``` In contrast, if: ```
# Given this:
batch_dim = 2
seq_dim = 0
input.dims = (8, ?, 4,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0:7, :, 0, :,...] = input[7:0:-1, :, 0, :,...]
output[0:2, :, 1, :,...] = input[2:0:-1, :, 1, :,...]
output[0:3, :, 2, :,...] = input[3:0:-1, :, 2, :,...]
output[0:5, :, 3, :,...] = input[5:0:-1, :, 3, :,...] # while entries past seq_lens are copied through:
output[7:, :, 0, :,...] = input[7:, :, 0, :,...]
output[2:, :, 1, :,...] = input[2:, :, 1, :,...]
output[3:, :, 2, :,...] = input[3:, :, 2, :,...]
output[2:, :, 3, :,...] = input[2:, :, 3, :,...]
```
Parameters
-
objectinput - A `Tensor`. The input to reverse.
-
IEnumerable<int>seq_lengths - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with length `input.dims(batch_dim)` and `max(seq_lengths) <= input.dims(seq_dim)`
-
Nullable<int>seq_axis - An `int`. The dimension which is partially reversed.
-
Nullable<int>batch_axis - An optional `int`. Defaults to `0`. The dimension along which reversal is performed.
-
stringname - A name for the operation (optional).
-
Nullable<int>seq_dim -
Nullable<int>batch_dim
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor reverse_sequence(IEnumerable<object> input, IGraphNodeBase seq_lengths, Nullable<int> seq_axis, Nullable<int> batch_axis, string name, Nullable<int> seq_dim, Nullable<int> batch_dim)
Reverses variable length slices. This op first slices `input` along the dimension `batch_axis`, and for each
slice `i`, reverses the first `seq_lengths[i]` elements along
the dimension `seq_axis`. The elements of `seq_lengths` must obey `seq_lengths[i] <= input.dims[seq_dim]`,
and `seq_lengths` must be a vector of length `input.dims[batch_dim]`. The output slice `i` along dimension `batch_axis` is then given by input
slice `i`, with the first `seq_lengths[i]` slices along dimension
`seq_axis` reversed. For example: ```
# Given this:
batch_dim = 0
seq_dim = 1
input.dims = (4, 8,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0, 0:7, :,...] = input[0, 7:0:-1, :,...]
output[1, 0:2, :,...] = input[1, 2:0:-1, :,...]
output[2, 0:3, :,...] = input[2, 3:0:-1, :,...]
output[3, 0:5, :,...] = input[3, 5:0:-1, :,...] # while entries past seq_lens are copied through:
output[0, 7:, :,...] = input[0, 7:, :,...]
output[1, 2:, :,...] = input[1, 2:, :,...]
output[2, 3:, :,...] = input[2, 3:, :,...]
output[3, 2:, :,...] = input[3, 2:, :,...]
``` In contrast, if: ```
# Given this:
batch_dim = 2
seq_dim = 0
input.dims = (8, ?, 4,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0:7, :, 0, :,...] = input[7:0:-1, :, 0, :,...]
output[0:2, :, 1, :,...] = input[2:0:-1, :, 1, :,...]
output[0:3, :, 2, :,...] = input[3:0:-1, :, 2, :,...]
output[0:5, :, 3, :,...] = input[5:0:-1, :, 3, :,...] # while entries past seq_lens are copied through:
output[7:, :, 0, :,...] = input[7:, :, 0, :,...]
output[2:, :, 1, :,...] = input[2:, :, 1, :,...]
output[3:, :, 2, :,...] = input[3:, :, 2, :,...]
output[2:, :, 3, :,...] = input[2:, :, 3, :,...]
```
Parameters
-
IEnumerable<object>input - A `Tensor`. The input to reverse.
-
IGraphNodeBaseseq_lengths - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with length `input.dims(batch_dim)` and `max(seq_lengths) <= input.dims(seq_dim)`
-
Nullable<int>seq_axis - An `int`. The dimension which is partially reversed.
-
Nullable<int>batch_axis - An optional `int`. Defaults to `0`. The dimension along which reversal is performed.
-
stringname - A name for the operation (optional).
-
Nullable<int>seq_dim -
Nullable<int>batch_dim
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor reverse_sequence(object input, IGraphNodeBase seq_lengths, Nullable<int> seq_axis, Nullable<int> batch_axis, string name, Nullable<int> seq_dim, Nullable<int> batch_dim)
Reverses variable length slices. This op first slices `input` along the dimension `batch_axis`, and for each
slice `i`, reverses the first `seq_lengths[i]` elements along
the dimension `seq_axis`. The elements of `seq_lengths` must obey `seq_lengths[i] <= input.dims[seq_dim]`,
and `seq_lengths` must be a vector of length `input.dims[batch_dim]`. The output slice `i` along dimension `batch_axis` is then given by input
slice `i`, with the first `seq_lengths[i]` slices along dimension
`seq_axis` reversed. For example: ```
# Given this:
batch_dim = 0
seq_dim = 1
input.dims = (4, 8,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0, 0:7, :,...] = input[0, 7:0:-1, :,...]
output[1, 0:2, :,...] = input[1, 2:0:-1, :,...]
output[2, 0:3, :,...] = input[2, 3:0:-1, :,...]
output[3, 0:5, :,...] = input[3, 5:0:-1, :,...] # while entries past seq_lens are copied through:
output[0, 7:, :,...] = input[0, 7:, :,...]
output[1, 2:, :,...] = input[1, 2:, :,...]
output[2, 3:, :,...] = input[2, 3:, :,...]
output[3, 2:, :,...] = input[3, 2:, :,...]
``` In contrast, if: ```
# Given this:
batch_dim = 2
seq_dim = 0
input.dims = (8, ?, 4,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0:7, :, 0, :,...] = input[7:0:-1, :, 0, :,...]
output[0:2, :, 1, :,...] = input[2:0:-1, :, 1, :,...]
output[0:3, :, 2, :,...] = input[3:0:-1, :, 2, :,...]
output[0:5, :, 3, :,...] = input[5:0:-1, :, 3, :,...] # while entries past seq_lens are copied through:
output[7:, :, 0, :,...] = input[7:, :, 0, :,...]
output[2:, :, 1, :,...] = input[2:, :, 1, :,...]
output[3:, :, 2, :,...] = input[3:, :, 2, :,...]
output[2:, :, 3, :,...] = input[2:, :, 3, :,...]
```
Parameters
-
objectinput - A `Tensor`. The input to reverse.
-
IGraphNodeBaseseq_lengths - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with length `input.dims(batch_dim)` and `max(seq_lengths) <= input.dims(seq_dim)`
-
Nullable<int>seq_axis - An `int`. The dimension which is partially reversed.
-
Nullable<int>batch_axis - An optional `int`. Defaults to `0`. The dimension along which reversal is performed.
-
stringname - A name for the operation (optional).
-
Nullable<int>seq_dim -
Nullable<int>batch_dim
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor reverse_sequence(IGraphNodeBase input, IEnumerable<int> seq_lengths, Nullable<int> seq_axis, Nullable<int> batch_axis, string name, Nullable<int> seq_dim, Nullable<int> batch_dim)
Reverses variable length slices. This op first slices `input` along the dimension `batch_axis`, and for each
slice `i`, reverses the first `seq_lengths[i]` elements along
the dimension `seq_axis`. The elements of `seq_lengths` must obey `seq_lengths[i] <= input.dims[seq_dim]`,
and `seq_lengths` must be a vector of length `input.dims[batch_dim]`. The output slice `i` along dimension `batch_axis` is then given by input
slice `i`, with the first `seq_lengths[i]` slices along dimension
`seq_axis` reversed. For example: ```
# Given this:
batch_dim = 0
seq_dim = 1
input.dims = (4, 8,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0, 0:7, :,...] = input[0, 7:0:-1, :,...]
output[1, 0:2, :,...] = input[1, 2:0:-1, :,...]
output[2, 0:3, :,...] = input[2, 3:0:-1, :,...]
output[3, 0:5, :,...] = input[3, 5:0:-1, :,...] # while entries past seq_lens are copied through:
output[0, 7:, :,...] = input[0, 7:, :,...]
output[1, 2:, :,...] = input[1, 2:, :,...]
output[2, 3:, :,...] = input[2, 3:, :,...]
output[3, 2:, :,...] = input[3, 2:, :,...]
``` In contrast, if: ```
# Given this:
batch_dim = 2
seq_dim = 0
input.dims = (8, ?, 4,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0:7, :, 0, :,...] = input[7:0:-1, :, 0, :,...]
output[0:2, :, 1, :,...] = input[2:0:-1, :, 1, :,...]
output[0:3, :, 2, :,...] = input[3:0:-1, :, 2, :,...]
output[0:5, :, 3, :,...] = input[5:0:-1, :, 3, :,...] # while entries past seq_lens are copied through:
output[7:, :, 0, :,...] = input[7:, :, 0, :,...]
output[2:, :, 1, :,...] = input[2:, :, 1, :,...]
output[3:, :, 2, :,...] = input[3:, :, 2, :,...]
output[2:, :, 3, :,...] = input[2:, :, 3, :,...]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`. The input to reverse.
-
IEnumerable<int>seq_lengths - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with length `input.dims(batch_dim)` and `max(seq_lengths) <= input.dims(seq_dim)`
-
Nullable<int>seq_axis - An `int`. The dimension which is partially reversed.
-
Nullable<int>batch_axis - An optional `int`. Defaults to `0`. The dimension along which reversal is performed.
-
stringname - A name for the operation (optional).
-
Nullable<int>seq_dim -
Nullable<int>batch_dim
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor reverse_sequence(IGraphNodeBase input, IGraphNodeBase seq_lengths, Nullable<int> seq_axis, Nullable<int> batch_axis, string name, Nullable<int> seq_dim, Nullable<int> batch_dim)
Reverses variable length slices. This op first slices `input` along the dimension `batch_axis`, and for each
slice `i`, reverses the first `seq_lengths[i]` elements along
the dimension `seq_axis`. The elements of `seq_lengths` must obey `seq_lengths[i] <= input.dims[seq_dim]`,
and `seq_lengths` must be a vector of length `input.dims[batch_dim]`. The output slice `i` along dimension `batch_axis` is then given by input
slice `i`, with the first `seq_lengths[i]` slices along dimension
`seq_axis` reversed. For example: ```
# Given this:
batch_dim = 0
seq_dim = 1
input.dims = (4, 8,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0, 0:7, :,...] = input[0, 7:0:-1, :,...]
output[1, 0:2, :,...] = input[1, 2:0:-1, :,...]
output[2, 0:3, :,...] = input[2, 3:0:-1, :,...]
output[3, 0:5, :,...] = input[3, 5:0:-1, :,...] # while entries past seq_lens are copied through:
output[0, 7:, :,...] = input[0, 7:, :,...]
output[1, 2:, :,...] = input[1, 2:, :,...]
output[2, 3:, :,...] = input[2, 3:, :,...]
output[3, 2:, :,...] = input[3, 2:, :,...]
``` In contrast, if: ```
# Given this:
batch_dim = 2
seq_dim = 0
input.dims = (8, ?, 4,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0:7, :, 0, :,...] = input[7:0:-1, :, 0, :,...]
output[0:2, :, 1, :,...] = input[2:0:-1, :, 1, :,...]
output[0:3, :, 2, :,...] = input[3:0:-1, :, 2, :,...]
output[0:5, :, 3, :,...] = input[5:0:-1, :, 3, :,...] # while entries past seq_lens are copied through:
output[7:, :, 0, :,...] = input[7:, :, 0, :,...]
output[2:, :, 1, :,...] = input[2:, :, 1, :,...]
output[3:, :, 2, :,...] = input[3:, :, 2, :,...]
output[2:, :, 3, :,...] = input[2:, :, 3, :,...]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`. The input to reverse.
-
IGraphNodeBaseseq_lengths - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with length `input.dims(batch_dim)` and `max(seq_lengths) <= input.dims(seq_dim)`
-
Nullable<int>seq_axis - An `int`. The dimension which is partially reversed.
-
Nullable<int>batch_axis - An optional `int`. Defaults to `0`. The dimension along which reversal is performed.
-
stringname - A name for the operation (optional).
-
Nullable<int>seq_dim -
Nullable<int>batch_dim
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor reverse_sequence(IEnumerable<object> input, IEnumerable<int> seq_lengths, Nullable<int> seq_axis, Nullable<int> batch_axis, string name, Nullable<int> seq_dim, Nullable<int> batch_dim)
Reverses variable length slices. This op first slices `input` along the dimension `batch_axis`, and for each
slice `i`, reverses the first `seq_lengths[i]` elements along
the dimension `seq_axis`. The elements of `seq_lengths` must obey `seq_lengths[i] <= input.dims[seq_dim]`,
and `seq_lengths` must be a vector of length `input.dims[batch_dim]`. The output slice `i` along dimension `batch_axis` is then given by input
slice `i`, with the first `seq_lengths[i]` slices along dimension
`seq_axis` reversed. For example: ```
# Given this:
batch_dim = 0
seq_dim = 1
input.dims = (4, 8,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0, 0:7, :,...] = input[0, 7:0:-1, :,...]
output[1, 0:2, :,...] = input[1, 2:0:-1, :,...]
output[2, 0:3, :,...] = input[2, 3:0:-1, :,...]
output[3, 0:5, :,...] = input[3, 5:0:-1, :,...] # while entries past seq_lens are copied through:
output[0, 7:, :,...] = input[0, 7:, :,...]
output[1, 2:, :,...] = input[1, 2:, :,...]
output[2, 3:, :,...] = input[2, 3:, :,...]
output[3, 2:, :,...] = input[3, 2:, :,...]
``` In contrast, if: ```
# Given this:
batch_dim = 2
seq_dim = 0
input.dims = (8, ?, 4,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0:7, :, 0, :,...] = input[7:0:-1, :, 0, :,...]
output[0:2, :, 1, :,...] = input[2:0:-1, :, 1, :,...]
output[0:3, :, 2, :,...] = input[3:0:-1, :, 2, :,...]
output[0:5, :, 3, :,...] = input[5:0:-1, :, 3, :,...] # while entries past seq_lens are copied through:
output[7:, :, 0, :,...] = input[7:, :, 0, :,...]
output[2:, :, 1, :,...] = input[2:, :, 1, :,...]
output[3:, :, 2, :,...] = input[3:, :, 2, :,...]
output[2:, :, 3, :,...] = input[2:, :, 3, :,...]
```
Parameters
-
IEnumerable<object>input - A `Tensor`. The input to reverse.
-
IEnumerable<int>seq_lengths - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with length `input.dims(batch_dim)` and `max(seq_lengths) <= input.dims(seq_dim)`
-
Nullable<int>seq_axis - An `int`. The dimension which is partially reversed.
-
Nullable<int>batch_axis - An optional `int`. Defaults to `0`. The dimension along which reversal is performed.
-
stringname - A name for the operation (optional).
-
Nullable<int>seq_dim -
Nullable<int>batch_dim
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object reverse_sequence_dyn(object input, object seq_lengths, object seq_axis, object batch_axis, object name, object seq_dim, object batch_dim)
Reverses variable length slices. This op first slices `input` along the dimension `batch_axis`, and for each
slice `i`, reverses the first `seq_lengths[i]` elements along
the dimension `seq_axis`. The elements of `seq_lengths` must obey `seq_lengths[i] <= input.dims[seq_dim]`,
and `seq_lengths` must be a vector of length `input.dims[batch_dim]`. The output slice `i` along dimension `batch_axis` is then given by input
slice `i`, with the first `seq_lengths[i]` slices along dimension
`seq_axis` reversed. For example: ```
# Given this:
batch_dim = 0
seq_dim = 1
input.dims = (4, 8,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0, 0:7, :,...] = input[0, 7:0:-1, :,...]
output[1, 0:2, :,...] = input[1, 2:0:-1, :,...]
output[2, 0:3, :,...] = input[2, 3:0:-1, :,...]
output[3, 0:5, :,...] = input[3, 5:0:-1, :,...] # while entries past seq_lens are copied through:
output[0, 7:, :,...] = input[0, 7:, :,...]
output[1, 2:, :,...] = input[1, 2:, :,...]
output[2, 3:, :,...] = input[2, 3:, :,...]
output[3, 2:, :,...] = input[3, 2:, :,...]
``` In contrast, if: ```
# Given this:
batch_dim = 2
seq_dim = 0
input.dims = (8, ?, 4,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0:7, :, 0, :,...] = input[7:0:-1, :, 0, :,...]
output[0:2, :, 1, :,...] = input[2:0:-1, :, 1, :,...]
output[0:3, :, 2, :,...] = input[3:0:-1, :, 2, :,...]
output[0:5, :, 3, :,...] = input[5:0:-1, :, 3, :,...] # while entries past seq_lens are copied through:
output[7:, :, 0, :,...] = input[7:, :, 0, :,...]
output[2:, :, 1, :,...] = input[2:, :, 1, :,...]
output[3:, :, 2, :,...] = input[3:, :, 2, :,...]
output[2:, :, 3, :,...] = input[2:, :, 3, :,...]
```
Parameters
-
objectinput - A `Tensor`. The input to reverse.
-
objectseq_lengths - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with length `input.dims(batch_dim)` and `max(seq_lengths) <= input.dims(seq_dim)`
-
objectseq_axis - An `int`. The dimension which is partially reversed.
-
objectbatch_axis - An optional `int`. Defaults to `0`. The dimension along which reversal is performed.
-
objectname - A name for the operation (optional).
-
objectseq_dim -
objectbatch_dim
Returns
-
object - A `Tensor`. Has the same type as `input`.
object rint(IGraphNodeBase x, string name)
Returns element-wise integer closest to x. If the result is midway between two representable values,
the even representable is chosen.
For example: ```
rint(-1.5) ==> -2.0
rint(0.5000001) ==> 1.0
rint([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0]) ==> [-2., -2., -0., 0., 2., 2., 2.]
```
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object rint_dyn(object x, object name)
Returns element-wise integer closest to x. If the result is midway between two representable values,
the even representable is chosen.
For example: ```
rint(-1.5) ==> -2.0
rint(0.5000001) ==> 1.0
rint([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0]) ==> [-2., -2., -0., 0., 2., 2., 2.]
```
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Tensor roll(IGraphNodeBase input, int shift, IGraphNodeBase axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
intshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IEnumerable<object> input, IEnumerable<int> shift, int axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
IEnumerable<int>shift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IEnumerable<object> input, IEnumerable<int> shift, IGraphNodeBase axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
IEnumerable<int>shift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IEnumerable<object> input, int shift, IEnumerable<int> axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
intshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IEnumerable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IEnumerable<object> input, int shift, int axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
intshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IEnumerable<object> input, int shift, IGraphNodeBase axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
intshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IEnumerable<object> input, IGraphNodeBase shift, IEnumerable<int> axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
IGraphNodeBaseshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IEnumerable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IEnumerable<object> input, IGraphNodeBase shift, int axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
IGraphNodeBaseshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IGraphNodeBase input, IGraphNodeBase shift, int axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
IGraphNodeBaseshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IGraphNodeBase input, IGraphNodeBase shift, IEnumerable<int> axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
IGraphNodeBaseshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IEnumerable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IEnumerable<object> input, IEnumerable<int> shift, IEnumerable<int> axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
IEnumerable<int>shift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IEnumerable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IGraphNodeBase input, int shift, int axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
intshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IGraphNodeBase input, int shift, IEnumerable<int> axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
intshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IEnumerable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IGraphNodeBase input, IEnumerable<int> shift, IGraphNodeBase axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
IEnumerable<int>shift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IGraphNodeBase input, IGraphNodeBase shift, IGraphNodeBase axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
IGraphNodeBaseshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IGraphNodeBase input, IEnumerable<int> shift, IEnumerable<int> axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
IEnumerable<int>shift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IEnumerable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(int input, IGraphNodeBase shift, IGraphNodeBase axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
intinput - A `Tensor`.
-
IGraphNodeBaseshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(int input, IGraphNodeBase shift, int axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
intinput - A `Tensor`.
-
IGraphNodeBaseshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(int input, IGraphNodeBase shift, IEnumerable<int> axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
intinput - A `Tensor`.
-
IGraphNodeBaseshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IEnumerable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(int input, int shift, IGraphNodeBase axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
intinput - A `Tensor`.
-
intshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(int input, int shift, int axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
intinput - A `Tensor`.
-
intshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(int input, int shift, IEnumerable<int> axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
intinput - A `Tensor`.
-
intshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IEnumerable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IEnumerable<object> input, IGraphNodeBase shift, IGraphNodeBase axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
IGraphNodeBaseshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(int input, IEnumerable<int> shift, IEnumerable<int> axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
intinput - A `Tensor`.
-
IEnumerable<int>shift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IEnumerable<int>axis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(IGraphNodeBase input, IEnumerable<int> shift, int axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
IEnumerable<int>shift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(int input, IEnumerable<int> shift, int axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
intinput - A `Tensor`.
-
IEnumerable<int>shift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
intaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor roll(int input, IEnumerable<int> shift, IGraphNodeBase axis, string name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
intinput - A `Tensor`.
-
IEnumerable<int>shift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
IGraphNodeBaseaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object roll_dyn(object input, object shift, object axis, object name)
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
Parameters
-
objectinput - A `Tensor`.
-
objectshift - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `shift[i]` specifies the number of places by which elements are shifted positively (towards larger indices) along the dimension specified by `axis[i]`. Negative shifts will roll the elements in the opposite direction.
-
objectaxis - A `Tensor`. Must be one of the following types: `int32`, `int64`. Dimension must be 0-D or 1-D. `axis[i]` specifies the dimension that the shift `shift[i]` should occur. If the same axis is referenced more than once, the total shift for that axis will be the sum of all the shifts that belong to that axis.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
object round(IGraphNodeBase x, string name)
Rounds the values of a tensor to the nearest integer, element-wise. Rounds half to even. Also known as bankers rounding. If you want to round
according to the current system rounding mode use tf::cint.
Parameters
-
IGraphNodeBasex - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, or `int64`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` of same shape and type as `x`.
Show Example
x = tf.constant([0.9, 2.5, 2.3, 1.5, -4.5])
tf.round(x) # [ 1.0, 2.0, 2.0, 2.0, -4.0 ]
object round_dyn(object x, object name)
Rounds the values of a tensor to the nearest integer, element-wise. Rounds half to even. Also known as bankers rounding. If you want to round
according to the current system rounding mode use tf::cint.
Parameters
-
objectx - A `Tensor` of type `float16`, `float32`, `float64`, `int32`, or `int64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of same shape and type as `x`.
Show Example
x = tf.constant([0.9, 2.5, 2.3, 1.5, -4.5])
tf.round(x) # [ 1.0, 2.0, 2.0, 2.0, -4.0 ]
Tensor routing_function(IGraphNodeBase input_data, IGraphNodeBase tree_parameters, IGraphNodeBase tree_biases, int max_nodes, string name)
object routing_function_dyn(object input_data, object tree_parameters, object tree_biases, object max_nodes, object name)
Tensor routing_gradient(IGraphNodeBase input_data, IGraphNodeBase tree_parameters, IGraphNodeBase tree_biases, IGraphNodeBase routes, object max_nodes, string name)
object routing_gradient_dyn(object input_data, object tree_parameters, object tree_biases, object routes, object max_nodes, object name)
Tensor rpc(IGraphNodeBase address, IGraphNodeBase method, IGraphNodeBase request, string protocol, bool fail_fast, int timeout_in_ms, string name)
object rpc_dyn(object address, object method, object request, ImplicitContainer<T> protocol, ImplicitContainer<T> fail_fast, ImplicitContainer<T> timeout_in_ms, object name)
object rsqrt(IGraphNodeBase x, string name)
Computes reciprocal of square root of x element-wise. I.e., \\(y = 1 / \sqrt{x}\\).
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object rsqrt_dyn(object x, object name)
Computes reciprocal of square root of x element-wise. I.e., \\(y = 1 / \sqrt{x}\\).
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object saturate_cast(IGraphNodeBase value, DType dtype, string name)
Performs a safe saturating cast of `value` to `dtype`. This function casts the input to `dtype` without applying any scaling. If
there is a danger that values would over or underflow in the cast, this op
applies the appropriate clamping before the cast.
Parameters
-
IGraphNodeBasevalue - A `Tensor`.
-
DTypedtype - The desired output `DType`.
-
stringname - A name for the operation (optional).
Returns
-
object - `value` safely cast to `dtype`.
object saturate_cast(IGraphNodeBase value, DType dtype, PythonFunctionContainer name)
Performs a safe saturating cast of `value` to `dtype`. This function casts the input to `dtype` without applying any scaling. If
there is a danger that values would over or underflow in the cast, this op
applies the appropriate clamping before the cast.
Parameters
-
IGraphNodeBasevalue - A `Tensor`.
-
DTypedtype - The desired output `DType`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - `value` safely cast to `dtype`.
object saturate_cast_dyn(object value, object dtype, object name)
Performs a safe saturating cast of `value` to `dtype`. This function casts the input to `dtype` without applying any scaling. If
there is a danger that values would over or underflow in the cast, this op
applies the appropriate clamping before the cast.
Parameters
-
objectvalue - A `Tensor`.
-
objectdtype - The desired output `DType`.
-
objectname - A name for the operation (optional).
Returns
-
object - `value` safely cast to `dtype`.
object scalar_mul(double scalar, IGraphNodeBase x, PythonFunctionContainer name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
doublescalar - A 0-D scalar `Tensor`. Must have known shape.
-
IGraphNodeBasex - A `Tensor` or `IndexedSlices` to be scaled.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(int scalar, IndexedSlices x, string name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
intscalar - A 0-D scalar `Tensor`. Must have known shape.
-
IndexedSlicesx - A `Tensor` or `IndexedSlices` to be scaled.
-
stringname - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(int scalar, ResourceVariable x, PythonFunctionContainer name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
intscalar - A 0-D scalar `Tensor`. Must have known shape.
-
ResourceVariablex - A `Tensor` or `IndexedSlices` to be scaled.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(double scalar, IndexedSlices x, string name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
doublescalar - A 0-D scalar `Tensor`. Must have known shape.
-
IndexedSlicesx - A `Tensor` or `IndexedSlices` to be scaled.
-
stringname - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(double scalar, ResourceVariable x, PythonFunctionContainer name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
doublescalar - A 0-D scalar `Tensor`. Must have known shape.
-
ResourceVariablex - A `Tensor` or `IndexedSlices` to be scaled.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(double scalar, ResourceVariable x, string name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
doublescalar - A 0-D scalar `Tensor`. Must have known shape.
-
ResourceVariablex - A `Tensor` or `IndexedSlices` to be scaled.
-
stringname - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(double scalar, IndexedSlices x, PythonFunctionContainer name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
doublescalar - A 0-D scalar `Tensor`. Must have known shape.
-
IndexedSlicesx - A `Tensor` or `IndexedSlices` to be scaled.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(double scalar, IGraphNodeBase x, string name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
doublescalar - A 0-D scalar `Tensor`. Must have known shape.
-
IGraphNodeBasex - A `Tensor` or `IndexedSlices` to be scaled.
-
stringname - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(int scalar, IGraphNodeBase x, string name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
intscalar - A 0-D scalar `Tensor`. Must have known shape.
-
IGraphNodeBasex - A `Tensor` or `IndexedSlices` to be scaled.
-
stringname - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(int scalar, IndexedSlices x, PythonFunctionContainer name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
intscalar - A 0-D scalar `Tensor`. Must have known shape.
-
IndexedSlicesx - A `Tensor` or `IndexedSlices` to be scaled.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(int scalar, IGraphNodeBase x, PythonFunctionContainer name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
intscalar - A 0-D scalar `Tensor`. Must have known shape.
-
IGraphNodeBasex - A `Tensor` or `IndexedSlices` to be scaled.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul(int scalar, ResourceVariable x, string name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
intscalar - A 0-D scalar `Tensor`. Must have known shape.
-
ResourceVariablex - A `Tensor` or `IndexedSlices` to be scaled.
-
stringname - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scalar_mul_dyn(object scalar, object x, object name)
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
Parameters
-
objectscalar - A 0-D scalar `Tensor`. Must have known shape.
-
objectx - A `Tensor` or `IndexedSlices` to be scaled.
-
objectname - A name for the operation (optional).
Returns
-
object - `scalar * x` of the same type (`Tensor` or `IndexedSlices`) as `x`.
object scan(PythonFunctionContainer fn, ndarray elems, ValueTuple<ndarray, object> initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ValueTuple<ndarray, object>initializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, ndarray elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IEnumerable<ndarray> elems, IndexedSlices initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IEnumerable<ndarray>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IndexedSlicesinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IEnumerable<ndarray> elems, ValueTuple<ndarray, object> initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IEnumerable<ndarray>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ValueTuple<ndarray, object>initializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IEnumerable<ndarray> elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IEnumerable<ndarray>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, ndarray elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, ndarray elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, ndarray elems, IndexedSlices initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
ndarrayelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IndexedSlicesinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IEnumerable<IGraphNodeBase> elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IEnumerable<IGraphNodeBase>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IndexedSlices elems, ValueTuple<ndarray, object> initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IndexedSliceselems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ValueTuple<ndarray, object>initializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IndexedSlices elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IndexedSliceselems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IGraphNodeBase elems, IndexedSlices initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IndexedSlicesinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IndexedSlices elems, IndexedSlices initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IndexedSliceselems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IndexedSlicesinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IndexedSlices elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IndexedSliceselems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IndexedSlices elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IndexedSliceselems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IGraphNodeBase elems, ValueTuple<ndarray, object> initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ValueTuple<ndarray, object>initializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IGraphNodeBase elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IGraphNodeBase elems, ndarray initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
ndarrayinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IEnumerable<ndarray> elems, int initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IEnumerable<ndarray>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
intinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan(PythonFunctionContainer fn, IGraphNodeBase elems, IGraphNodeBase initializer, int parallel_iterations, bool back_prop, bool swap_memory, bool infer_shape, bool reverse, string name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
PythonFunctionContainerfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
IGraphNodeBaseinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
intparallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
boolback_prop - (optional) True enables support for back propagation.
-
boolswap_memory - (optional) True enables GPU-CPU memory swapping.
-
boolinfer_shape - (optional) False disables tests for consistent output shapes.
-
boolreverse - (optional) True scans the tensor last to first (instead of first to last).
-
stringname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scan_dyn(object fn, object elems, object initializer, ImplicitContainer<T> parallel_iterations, ImplicitContainer<T> back_prop, ImplicitContainer<T> swap_memory, ImplicitContainer<T> infer_shape, ImplicitContainer<T> reverse, object name)
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
Parameters
-
objectfn - The callable to be performed. It accepts two arguments. The first will have the same structure as `initializer` if one is provided, otherwise it will have the same structure as `elems`. The second will have the same (possibly nested) structure as `elems`. Its output must have the same structure as `initializer` if one is provided, otherwise it must have the same structure as `elems`.
-
objectelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be the first argument to `fn`.
-
objectinitializer - (optional) A tensor or (possibly nested) sequence of tensors, initial value for the accumulator, and the expected output type of `fn`.
-
ImplicitContainer<T>parallel_iterations - (optional) The number of iterations allowed to run in parallel.
-
ImplicitContainer<T>back_prop - (optional) True enables support for back propagation.
-
ImplicitContainer<T>swap_memory - (optional) True enables GPU-CPU memory swapping.
-
ImplicitContainer<T>infer_shape - (optional) False disables tests for consistent output shapes.
-
ImplicitContainer<T>reverse - (optional) True scans the tensor last to first (instead of first to last).
-
objectname - (optional) Name prefix for the returned tensors.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying `fn` to tensors unpacked from `elems` along the first dimension, and the previous accumulator value(s), from first to last (or last to first, if `reverse=True`).
object scatter_add(PartitionedVariable ref, IGraphNodeBase indices, IGraphNodeBase updates, Nullable<bool> use_locking, string name)
Adds sparse updates to the variable referenced by `resource`. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the updated value.
Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions add. Requires `updates.shape = indices.shape + ref.shape[1:]`.


Parameters
-
PartitionedVariableref - A `Variable`.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to store in `ref`.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - Same as `ref`. Returned as a convenience for operations that want to use the updated values after the update is done.
Show Example
# Scalar indices
ref[indices,...] += updates[...] # Vector indices (for each i)
ref[indices[i],...] += updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] += updates[i,..., j,...]
object scatter_add(Variable ref, IGraphNodeBase indices, IGraphNodeBase updates, Nullable<bool> use_locking, string name)
Adds sparse updates to the variable referenced by `resource`. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the updated value.
Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions add. Requires `updates.shape = indices.shape + ref.shape[1:]`.


Parameters
-
Variableref - A `Variable`.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to store in `ref`.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - Same as `ref`. Returned as a convenience for operations that want to use the updated values after the update is done.
Show Example
# Scalar indices
ref[indices,...] += updates[...] # Vector indices (for each i)
ref[indices[i],...] += updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] += updates[i,..., j,...]
object scatter_add(IEnumerable<object> ref, IGraphNodeBase indices, IGraphNodeBase updates, Nullable<bool> use_locking, string name)
Adds sparse updates to the variable referenced by `resource`. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the updated value.
Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions add. Requires `updates.shape = indices.shape + ref.shape[1:]`.


Parameters
-
IEnumerable<object>ref - A `Variable`.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to store in `ref`.
-
Nullable<bool>use_locking - An optional `bool`. Defaults to `False`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - Same as `ref`. Returned as a convenience for operations that want to use the updated values after the update is done.
Show Example
# Scalar indices
ref[indices,...] += updates[...] # Vector indices (for each i)
ref[indices[i],...] += updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] += updates[i,..., j,...]
object scatter_add_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Adds sparse updates to the variable referenced by `resource`. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the updated value.
Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions add. Requires `updates.shape = indices.shape + ref.shape[1:]`.


Parameters
-
objectref - A `Variable`.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
objectupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to store in `ref`.
-
ImplicitContainer<T>use_locking - An optional `bool`. Defaults to `False`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - Same as `ref`. Returned as a convenience for operations that want to use the updated values after the update is done.
Show Example
# Scalar indices
ref[indices,...] += updates[...] # Vector indices (for each i)
ref[indices[i],...] += updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] += updates[i,..., j,...]
object scatter_add_ndim(IGraphNodeBase input, IGraphNodeBase indices, IGraphNodeBase deltas, string name)
object scatter_add_ndim_dyn(object input, object indices, object deltas, object name)
Tensor scatter_div(object ref, IGraphNodeBase indices, IGraphNodeBase updates, bool use_locking, string name)
Divides a variable reference by sparse updates. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions divide. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`. Should be from a `Variable` node.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of values that `ref` is divided by.
-
booluse_locking - An optional `bool`. Defaults to `False`. If True, the operation will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A mutable `Tensor`. Has the same type as `ref`.
Show Example
# Scalar indices
ref[indices,...] /= updates[...] # Vector indices (for each i)
ref[indices[i],...] /= updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] /= updates[i,..., j,...]
object scatter_div_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Divides a variable reference by sparse updates. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions divide. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`. Should be from a `Variable` node.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
objectupdates - A `Tensor`. Must have the same type as `ref`. A tensor of values that `ref` is divided by.
-
ImplicitContainer<T>use_locking - An optional `bool`. Defaults to `False`. If True, the operation will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - A mutable `Tensor`. Has the same type as `ref`.
Show Example
# Scalar indices
ref[indices,...] /= updates[...] # Vector indices (for each i)
ref[indices[i],...] /= updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] /= updates[i,..., j,...]
Tensor scatter_max(object ref, IGraphNodeBase indices, IGraphNodeBase updates, bool use_locking, string name)
Reduces sparse updates into a variable reference using the `max` operation. This operation computes # Scalar indices
ref[indices,...] = max(ref[indices,...], updates[...]) # Vector indices (for each i)
ref[indices[i],...] = max(ref[indices[i],...], updates[i,...]) # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] = max(ref[indices[i,..., j],...],
updates[i,..., j,...]) This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions combine. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.


Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `half`, `bfloat16`, `float32`, `float64`, `int32`, `int64`. Should be from a `Variable` node.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to reduce into `ref`.
-
booluse_locking - An optional `bool`. Defaults to `False`. If True, the update will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A mutable `Tensor`. Has the same type as `ref`.
object scatter_max_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Reduces sparse updates into a variable reference using the `max` operation. This operation computes # Scalar indices
ref[indices,...] = max(ref[indices,...], updates[...]) # Vector indices (for each i)
ref[indices[i],...] = max(ref[indices[i],...], updates[i,...]) # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] = max(ref[indices[i,..., j],...],
updates[i,..., j,...]) This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions combine. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.


Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `half`, `bfloat16`, `float32`, `float64`, `int32`, `int64`. Should be from a `Variable` node.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
objectupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to reduce into `ref`.
-
ImplicitContainer<T>use_locking - An optional `bool`. Defaults to `False`. If True, the update will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - A mutable `Tensor`. Has the same type as `ref`.
Tensor scatter_min(object ref, IGraphNodeBase indices, IGraphNodeBase updates, bool use_locking, string name)
Reduces sparse updates into a variable reference using the `min` operation. This operation computes # Scalar indices
ref[indices,...] = min(ref[indices,...], updates[...]) # Vector indices (for each i)
ref[indices[i],...] = min(ref[indices[i],...], updates[i,...]) # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] = min(ref[indices[i,..., j],...],
updates[i,..., j,...]) This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions combine. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.


Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `half`, `bfloat16`, `float32`, `float64`, `int32`, `int64`. Should be from a `Variable` node.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to reduce into `ref`.
-
booluse_locking - An optional `bool`. Defaults to `False`. If True, the update will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A mutable `Tensor`. Has the same type as `ref`.
object scatter_min_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Reduces sparse updates into a variable reference using the `min` operation. This operation computes # Scalar indices
ref[indices,...] = min(ref[indices,...], updates[...]) # Vector indices (for each i)
ref[indices[i],...] = min(ref[indices[i],...], updates[i,...]) # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] = min(ref[indices[i,..., j],...],
updates[i,..., j,...]) This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions combine. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.


Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `half`, `bfloat16`, `float32`, `float64`, `int32`, `int64`. Should be from a `Variable` node.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
objectupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to reduce into `ref`.
-
ImplicitContainer<T>use_locking - An optional `bool`. Defaults to `False`. If True, the update will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - A mutable `Tensor`. Has the same type as `ref`.
Tensor scatter_mul(object ref, IGraphNodeBase indices, IGraphNodeBase updates, bool use_locking, string name)
Multiplies sparse updates into a variable reference. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions multiply. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`. Should be from a `Variable` node.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to multiply to `ref`.
-
booluse_locking - An optional `bool`. Defaults to `False`. If True, the operation will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A mutable `Tensor`. Has the same type as `ref`.
Show Example
# Scalar indices
ref[indices,...] *= updates[...] # Vector indices (for each i)
ref[indices[i],...] *= updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] *= updates[i,..., j,...]
object scatter_mul_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Multiplies sparse updates into a variable reference. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions multiply. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`. Should be from a `Variable` node.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
objectupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to multiply to `ref`.
-
ImplicitContainer<T>use_locking - An optional `bool`. Defaults to `False`. If True, the operation will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - A mutable `Tensor`. Has the same type as `ref`.
Show Example
# Scalar indices
ref[indices,...] *= updates[...] # Vector indices (for each i)
ref[indices[i],...] *= updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] *= updates[i,..., j,...]
Tensor scatter_nd(IGraphNodeBase indices, IGraphNodeBase updates, IGraphNodeBase shape, string name)
Scatter `updates` into a new tensor according to `indices`. Creates a new tensor by applying sparse `updates` to individual values or
slices within a tensor (initially zero for numeric, empty for string) of
the given `shape` according to indices. This operator is the inverse of the
 In Python, this scatter operation would look like this:
The resulting tensor would look like this: [0, 11, 0, 10, 9, 0, 0, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values.
In Python, this scatter operation would look like this:
The resulting tensor would look like this: [0, 11, 0, 10, 9, 0, 0, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values.
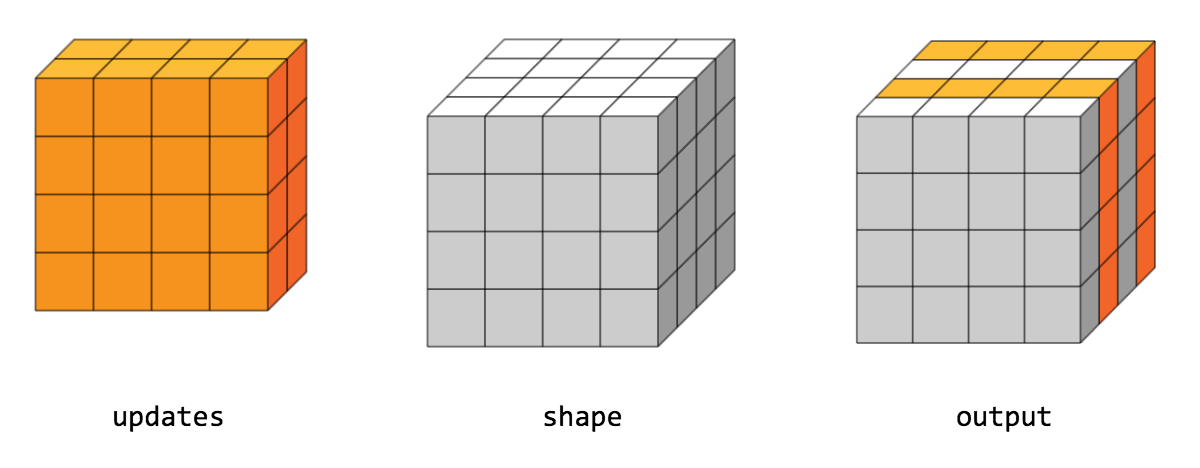 In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
tf.gather_nd operator which extracts values or slices from a given tensor. This operation is similar to tensor_scatter_add, except that the tensor is
zero-initialized. Calling `tf.scatter_nd(indices, values, shape)` is identical
to `tensor_scatter_add(tf.zeros(shape, values.dtype), indices, values)` If `indices` contains duplicates, then their updates are accumulated (summed). **WARNING**: The order in which updates are applied is nondeterministic, so the
output will be nondeterministic if `indices` contains duplicates -- because
of some numerical approximation issues, numbers summed in different order
may yield different results. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of scatter is to insert individual elements in a tensor by
index. For example, say we want to insert 4 scattered elements in a rank-1
tensor with 8 elements. 

Parameters
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
IGraphNodeBaseupdates - A `Tensor`. Updates to scatter into output.
-
IGraphNodeBaseshape - A `Tensor`. Must have the same type as `indices`. 1-D. The shape of the resulting tensor.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `updates`.
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
shape = tf.constant([8])
scatter = tf.scatter_nd(indices, updates, shape)
with tf.Session() as sess:
print(sess.run(scatter))
object scatter_nd_add(Variable ref, IGraphNodeBase indices, IGraphNodeBase updates, bool use_locking, string name)
Applies sparse addition to individual values or slices in a Variable. `ref` is a `Tensor` with rank `P` and `indices` is a `Tensor` of rank `Q`. `indices` must be integer tensor, containing indices into `ref`.
It must be shape `[d_0,..., d_{Q-2}, K]` where `0 < K <= P`. The innermost dimension of `indices` (with length `K`) corresponds to
indices into elements (if `K = P`) or slices (if `K < P`) along the `K`th
dimension of `ref`. `updates` is `Tensor` of rank `Q-1+P-K` with shape: ```
[d_0,..., d_{Q-2}, ref.shape[K],..., ref.shape[P-1]]
``` For example, say we want to add 4 scattered elements to a rank-1 tensor to
8 elements. In Python, that addition would look like this:
The resulting update to ref would look like this: [1, 13, 3, 14, 14, 6, 7, 20] See
tf.scatter_nd for more details about how to make updates to
slices.
Parameters
-
Variableref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`. A mutable Tensor. Should be from a Variable node.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into ref.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to add to ref.
-
booluse_locking - An optional `bool`. Defaults to `False`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - A mutable `Tensor`. Has the same type as `ref`.
Show Example
ref = tf.Variable([1, 2, 3, 4, 5, 6, 7, 8])
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
add = tf.compat.v1.scatter_nd_add(ref, indices, updates)
with tf.compat.v1.Session() as sess:
print sess.run(add)
object scatter_nd_add_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Applies sparse addition to individual values or slices in a Variable. `ref` is a `Tensor` with rank `P` and `indices` is a `Tensor` of rank `Q`. `indices` must be integer tensor, containing indices into `ref`.
It must be shape `[d_0,..., d_{Q-2}, K]` where `0 < K <= P`. The innermost dimension of `indices` (with length `K`) corresponds to
indices into elements (if `K = P`) or slices (if `K < P`) along the `K`th
dimension of `ref`. `updates` is `Tensor` of rank `Q-1+P-K` with shape: ```
[d_0,..., d_{Q-2}, ref.shape[K],..., ref.shape[P-1]]
``` For example, say we want to add 4 scattered elements to a rank-1 tensor to
8 elements. In Python, that addition would look like this:
The resulting update to ref would look like this: [1, 13, 3, 14, 14, 6, 7, 20] See
tf.scatter_nd for more details about how to make updates to
slices.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`. A mutable Tensor. Should be from a Variable node.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into ref.
-
objectupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to add to ref.
-
ImplicitContainer<T>use_locking - An optional `bool`. Defaults to `False`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - A mutable `Tensor`. Has the same type as `ref`.
Show Example
ref = tf.Variable([1, 2, 3, 4, 5, 6, 7, 8])
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
add = tf.compat.v1.scatter_nd_add(ref, indices, updates)
with tf.compat.v1.Session() as sess:
print sess.run(add)
object scatter_nd_dyn(object indices, object updates, object shape, object name)
Scatter `updates` into a new tensor according to `indices`. Creates a new tensor by applying sparse `updates` to individual values or
slices within a tensor (initially zero for numeric, empty for string) of
the given `shape` according to indices. This operator is the inverse of the
 In Python, this scatter operation would look like this:
The resulting tensor would look like this: [0, 11, 0, 10, 9, 0, 0, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values.
In Python, this scatter operation would look like this:
The resulting tensor would look like this: [0, 11, 0, 10, 9, 0, 0, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values.
 In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
tf.gather_nd operator which extracts values or slices from a given tensor. This operation is similar to tensor_scatter_add, except that the tensor is
zero-initialized. Calling `tf.scatter_nd(indices, values, shape)` is identical
to `tensor_scatter_add(tf.zeros(shape, values.dtype), indices, values)` If `indices` contains duplicates, then their updates are accumulated (summed). **WARNING**: The order in which updates are applied is nondeterministic, so the
output will be nondeterministic if `indices` contains duplicates -- because
of some numerical approximation issues, numbers summed in different order
may yield different results. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of scatter is to insert individual elements in a tensor by
index. For example, say we want to insert 4 scattered elements in a rank-1
tensor with 8 elements. 

Parameters
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
objectupdates - A `Tensor`. Updates to scatter into output.
-
objectshape - A `Tensor`. Must have the same type as `indices`. 1-D. The shape of the resulting tensor.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `updates`.
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
shape = tf.constant([8])
scatter = tf.scatter_nd(indices, updates, shape)
with tf.Session() as sess:
print(sess.run(scatter))
object scatter_nd_sub(Variable ref, IGraphNodeBase indices, IGraphNodeBase updates, bool use_locking, string name)
Applies sparse subtraction to individual values or slices in a Variable. `ref` is a `Tensor` with rank `P` and `indices` is a `Tensor` of rank `Q`. `indices` must be integer tensor, containing indices into `ref`.
It must be shape `[d_0,..., d_{Q-2}, K]` where `0 < K <= P`. The innermost dimension of `indices` (with length `K`) corresponds to
indices into elements (if `K = P`) or slices (if `K < P`) along the `K`th
dimension of `ref`. `updates` is `Tensor` of rank `Q-1+P-K` with shape: ```
[d_0,..., d_{Q-2}, ref.shape[K],..., ref.shape[P-1]]
``` For example, say we want to subtract 4 scattered elements from a rank-1 tensor
with 8 elements. In Python, that update would look like this:
The resulting update to ref would look like this: [1, -9, 3, -6, -6, 6, 7, -4] See
tf.scatter_nd for more details about how to make updates to
slices.
Parameters
-
Variableref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`. A mutable Tensor. Should be from a Variable node.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into ref.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to add to ref.
-
booluse_locking - An optional `bool`. Defaults to `False`. An optional bool. Defaults to True. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - A mutable `Tensor`. Has the same type as `ref`.
Show Example
ref = tf.Variable([1, 2, 3, 4, 5, 6, 7, 8])
indices = tf.constant([[4], [3], [1] ,[7]])
updates = tf.constant([9, 10, 11, 12])
op = tf.compat.v1.scatter_nd_sub(ref, indices, updates)
with tf.compat.v1.Session() as sess:
print sess.run(op)
object scatter_nd_sub_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Applies sparse subtraction to individual values or slices in a Variable. `ref` is a `Tensor` with rank `P` and `indices` is a `Tensor` of rank `Q`. `indices` must be integer tensor, containing indices into `ref`.
It must be shape `[d_0,..., d_{Q-2}, K]` where `0 < K <= P`. The innermost dimension of `indices` (with length `K`) corresponds to
indices into elements (if `K = P`) or slices (if `K < P`) along the `K`th
dimension of `ref`. `updates` is `Tensor` of rank `Q-1+P-K` with shape: ```
[d_0,..., d_{Q-2}, ref.shape[K],..., ref.shape[P-1]]
``` For example, say we want to subtract 4 scattered elements from a rank-1 tensor
with 8 elements. In Python, that update would look like this:
The resulting update to ref would look like this: [1, -9, 3, -6, -6, 6, 7, -4] See
tf.scatter_nd for more details about how to make updates to
slices.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`. A mutable Tensor. Should be from a Variable node.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into ref.
-
objectupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to add to ref.
-
ImplicitContainer<T>use_locking - An optional `bool`. Defaults to `False`. An optional bool. Defaults to True. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - A mutable `Tensor`. Has the same type as `ref`.
Show Example
ref = tf.Variable([1, 2, 3, 4, 5, 6, 7, 8])
indices = tf.constant([[4], [3], [1] ,[7]])
updates = tf.constant([9, 10, 11, 12])
op = tf.compat.v1.scatter_nd_sub(ref, indices, updates)
with tf.compat.v1.Session() as sess:
print sess.run(op)
object scatter_nd_update(Variable ref, IGraphNodeBase indices, IGraphNodeBase updates, bool use_locking, string name)
Applies sparse `updates` to individual values or slices in a Variable. `ref` is a `Tensor` with rank `P` and `indices` is a `Tensor` of rank `Q`. `indices` must be integer tensor, containing indices into `ref`.
It must be shape `[d_0,..., d_{Q-2}, K]` where `0 < K <= P`. The innermost dimension of `indices` (with length `K`) corresponds to
indices into elements (if `K = P`) or slices (if `K < P`) along the `K`th
dimension of `ref`. `updates` is `Tensor` of rank `Q-1+P-K` with shape: ```
[d_0,..., d_{Q-2}, ref.shape[K],..., ref.shape[P-1]].
``` For example, say we want to update 4 scattered elements to a rank-1 tensor to
8 elements. In Python, that update would look like this:
The resulting update to ref would look like this: [1, 11, 3, 10, 9, 6, 7, 12] See
tf.scatter_nd for more details about how to make updates to
slices.
Parameters
-
Variableref - A Variable.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into ref.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A Tensor. Must have the same type as ref. A tensor of updated values to add to ref.
-
booluse_locking - An optional `bool`. Defaults to `True`. An optional bool. Defaults to True. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - The value of the variable after the update.
Show Example
ref = tf.Variable([1, 2, 3, 4, 5, 6, 7, 8])
indices = tf.constant([[4], [3], [1] ,[7]])
updates = tf.constant([9, 10, 11, 12])
update = tf.compat.v1.scatter_nd_update(ref, indices, updates)
with tf.compat.v1.Session() as sess:
print sess.run(update)
object scatter_nd_update_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Applies sparse `updates` to individual values or slices in a Variable. `ref` is a `Tensor` with rank `P` and `indices` is a `Tensor` of rank `Q`. `indices` must be integer tensor, containing indices into `ref`.
It must be shape `[d_0,..., d_{Q-2}, K]` where `0 < K <= P`. The innermost dimension of `indices` (with length `K`) corresponds to
indices into elements (if `K = P`) or slices (if `K < P`) along the `K`th
dimension of `ref`. `updates` is `Tensor` of rank `Q-1+P-K` with shape: ```
[d_0,..., d_{Q-2}, ref.shape[K],..., ref.shape[P-1]].
``` For example, say we want to update 4 scattered elements to a rank-1 tensor to
8 elements. In Python, that update would look like this:
The resulting update to ref would look like this: [1, 11, 3, 10, 9, 6, 7, 12] See
tf.scatter_nd for more details about how to make updates to
slices.
Parameters
-
objectref - A Variable.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into ref.
-
objectupdates - A `Tensor`. Must have the same type as `ref`. A Tensor. Must have the same type as ref. A tensor of updated values to add to ref.
-
ImplicitContainer<T>use_locking - An optional `bool`. Defaults to `True`. An optional bool. Defaults to True. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - The value of the variable after the update.
Show Example
ref = tf.Variable([1, 2, 3, 4, 5, 6, 7, 8])
indices = tf.constant([[4], [3], [1] ,[7]])
updates = tf.constant([9, 10, 11, 12])
update = tf.compat.v1.scatter_nd_update(ref, indices, updates)
with tf.compat.v1.Session() as sess:
print sess.run(update)
object scatter_sub(Variable ref, IGraphNodeBase indices, IGraphNodeBase updates, bool use_locking, string name)
Subtracts sparse updates to a variable reference.
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their (negated) contributions add. Requires `updates.shape = indices.shape + ref.shape[1:]` or
`updates.shape = []`.
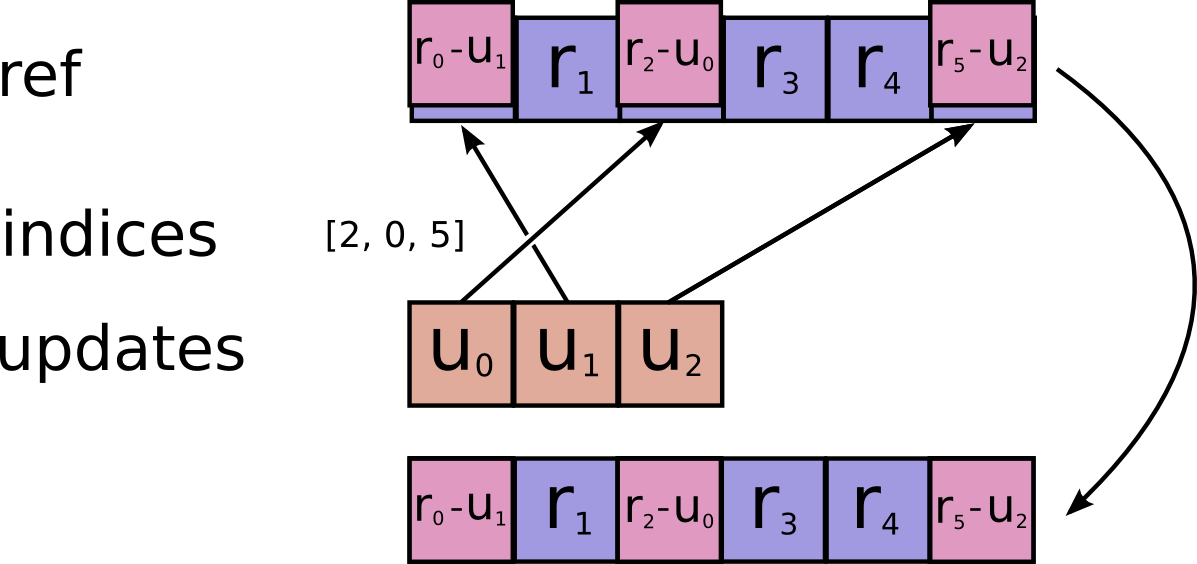
Parameters
-
Variableref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`. Should be from a `Variable` node.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to subtract from `ref`.
-
booluse_locking - An optional `bool`. Defaults to `False`. If True, the subtraction will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - A mutable `Tensor`. Has the same type as `ref`.
Show Example
# Scalar indices
ref[indices,...] -= updates[...] # Vector indices (for each i)
ref[indices[i],...] -= updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] -= updates[i,..., j,...]
object scatter_sub_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Subtracts sparse updates to a variable reference.
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their (negated) contributions add. Requires `updates.shape = indices.shape + ref.shape[1:]` or
`updates.shape = []`.
Parameters
-
objectref - A mutable `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`. Should be from a `Variable` node.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
objectupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to subtract from `ref`.
-
ImplicitContainer<T>use_locking - An optional `bool`. Defaults to `False`. If True, the subtraction will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - A mutable `Tensor`. Has the same type as `ref`.
Show Example
# Scalar indices
ref[indices,...] -= updates[...] # Vector indices (for each i)
ref[indices[i],...] -= updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] -= updates[i,..., j,...]
object scatter_update(Variable ref, IGraphNodeBase indices, IGraphNodeBase updates, bool use_locking, string name)
Applies sparse updates to a variable reference. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. If values in `ref` is to be updated more than once, because there are
duplicate entries in `indices`, the order at which the updates happen
for each value is undefined. Requires `updates.shape = indices.shape + ref.shape[1:]`.

Parameters
-
Variableref - A `Variable`.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to store in `ref`.
-
booluse_locking - An optional `bool`. Defaults to `True`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - Same as `ref`. Returned as a convenience for operations that want to use the updated values after the update is done.
Show Example
# Scalar indices
ref[indices,...] = updates[...] # Vector indices (for each i)
ref[indices[i],...] = updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] = updates[i,..., j,...]
object scatter_update(PartitionedVariable ref, IGraphNodeBase indices, IGraphNodeBase updates, bool use_locking, string name)
Applies sparse updates to a variable reference. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. If values in `ref` is to be updated more than once, because there are
duplicate entries in `indices`, the order at which the updates happen
for each value is undefined. Requires `updates.shape = indices.shape + ref.shape[1:]`.


Parameters
-
PartitionedVariableref - A `Variable`.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to store in `ref`.
-
booluse_locking - An optional `bool`. Defaults to `True`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
stringname - A name for the operation (optional).
Returns
-
object - Same as `ref`. Returned as a convenience for operations that want to use the updated values after the update is done.
Show Example
# Scalar indices
ref[indices,...] = updates[...] # Vector indices (for each i)
ref[indices[i],...] = updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] = updates[i,..., j,...]
object scatter_update_dyn(object ref, object indices, object updates, ImplicitContainer<T> use_locking, object name)
Applies sparse updates to a variable reference. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. If values in `ref` is to be updated more than once, because there are
duplicate entries in `indices`, the order at which the updates happen
for each value is undefined. Requires `updates.shape = indices.shape + ref.shape[1:]`.


Parameters
-
objectref - A `Variable`.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor of indices into the first dimension of `ref`.
-
objectupdates - A `Tensor`. Must have the same type as `ref`. A tensor of updated values to store in `ref`.
-
ImplicitContainer<T>use_locking - An optional `bool`. Defaults to `True`. If True, the assignment will be protected by a lock; otherwise the behavior is undefined, but may exhibit less contention.
-
objectname - A name for the operation (optional).
Returns
-
object - Same as `ref`. Returned as a convenience for operations that want to use the updated values after the update is done.
Show Example
# Scalar indices
ref[indices,...] = updates[...] # Vector indices (for each i)
ref[indices[i],...] = updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] = updates[i,..., j,...]
Tensor searchsorted(IGraphNodeBase sorted_sequence, IGraphNodeBase values, string side, ImplicitContainer<T> out_type, string name)
Searches input tensor for values on the innermost dimension. A 2-D example: ```
sorted_sequence = [[0, 3, 9, 9, 10],
[1, 2, 3, 4, 5]]
values = [[2, 4, 9],
[0, 2, 6]] result = searchsorted(sorted_sequence, values, side="left") result == [[1, 2, 2],
[0, 1, 5]] result = searchsorted(sorted_sequence, values, side="right") result == [[1, 2, 4],
[0, 2, 5]]
```
Parameters
-
IGraphNodeBasesorted_sequence - N-D `Tensor` containing a sorted sequence.
-
IGraphNodeBasevalues - N-D `Tensor` containing the search values.
-
stringside - 'left' or 'right'; 'left' corresponds to lower_bound and 'right' to upper_bound.
-
ImplicitContainer<T>out_type - The output type (`int32` or `int64`). Default is
tf.int32. -
stringname - Optional name for the operation.
Returns
-
Tensor - An N-D `Tensor` the size of values containing the result of applying either lower_bound or upper_bound (depending on side) to each value. The result is not a global index to the entire `Tensor`, but the index in the last dimension.
Tensor searchsorted(IGraphNodeBase sorted_sequence, ndarray values, string side, ImplicitContainer<T> out_type, string name)
Searches input tensor for values on the innermost dimension. A 2-D example: ```
sorted_sequence = [[0, 3, 9, 9, 10],
[1, 2, 3, 4, 5]]
values = [[2, 4, 9],
[0, 2, 6]] result = searchsorted(sorted_sequence, values, side="left") result == [[1, 2, 2],
[0, 1, 5]] result = searchsorted(sorted_sequence, values, side="right") result == [[1, 2, 4],
[0, 2, 5]]
```
Parameters
-
IGraphNodeBasesorted_sequence - N-D `Tensor` containing a sorted sequence.
-
ndarrayvalues - N-D `Tensor` containing the search values.
-
stringside - 'left' or 'right'; 'left' corresponds to lower_bound and 'right' to upper_bound.
-
ImplicitContainer<T>out_type - The output type (`int32` or `int64`). Default is
tf.int32. -
stringname - Optional name for the operation.
Returns
-
Tensor - An N-D `Tensor` the size of values containing the result of applying either lower_bound or upper_bound (depending on side) to each value. The result is not a global index to the entire `Tensor`, but the index in the last dimension.
Tensor searchsorted(ndarray sorted_sequence, ndarray values, string side, ImplicitContainer<T> out_type, string name)
Searches input tensor for values on the innermost dimension. A 2-D example: ```
sorted_sequence = [[0, 3, 9, 9, 10],
[1, 2, 3, 4, 5]]
values = [[2, 4, 9],
[0, 2, 6]] result = searchsorted(sorted_sequence, values, side="left") result == [[1, 2, 2],
[0, 1, 5]] result = searchsorted(sorted_sequence, values, side="right") result == [[1, 2, 4],
[0, 2, 5]]
```
Parameters
-
ndarraysorted_sequence - N-D `Tensor` containing a sorted sequence.
-
ndarrayvalues - N-D `Tensor` containing the search values.
-
stringside - 'left' or 'right'; 'left' corresponds to lower_bound and 'right' to upper_bound.
-
ImplicitContainer<T>out_type - The output type (`int32` or `int64`). Default is
tf.int32. -
stringname - Optional name for the operation.
Returns
-
Tensor - An N-D `Tensor` the size of values containing the result of applying either lower_bound or upper_bound (depending on side) to each value. The result is not a global index to the entire `Tensor`, but the index in the last dimension.
Tensor searchsorted(ndarray sorted_sequence, IGraphNodeBase values, string side, ImplicitContainer<T> out_type, string name)
Searches input tensor for values on the innermost dimension. A 2-D example: ```
sorted_sequence = [[0, 3, 9, 9, 10],
[1, 2, 3, 4, 5]]
values = [[2, 4, 9],
[0, 2, 6]] result = searchsorted(sorted_sequence, values, side="left") result == [[1, 2, 2],
[0, 1, 5]] result = searchsorted(sorted_sequence, values, side="right") result == [[1, 2, 4],
[0, 2, 5]]
```
Parameters
-
ndarraysorted_sequence - N-D `Tensor` containing a sorted sequence.
-
IGraphNodeBasevalues - N-D `Tensor` containing the search values.
-
stringside - 'left' or 'right'; 'left' corresponds to lower_bound and 'right' to upper_bound.
-
ImplicitContainer<T>out_type - The output type (`int32` or `int64`). Default is
tf.int32. -
stringname - Optional name for the operation.
Returns
-
Tensor - An N-D `Tensor` the size of values containing the result of applying either lower_bound or upper_bound (depending on side) to each value. The result is not a global index to the entire `Tensor`, but the index in the last dimension.
object searchsorted_dyn(object sorted_sequence, object values, ImplicitContainer<T> side, ImplicitContainer<T> out_type, object name)
Searches input tensor for values on the innermost dimension. A 2-D example: ```
sorted_sequence = [[0, 3, 9, 9, 10],
[1, 2, 3, 4, 5]]
values = [[2, 4, 9],
[0, 2, 6]] result = searchsorted(sorted_sequence, values, side="left") result == [[1, 2, 2],
[0, 1, 5]] result = searchsorted(sorted_sequence, values, side="right") result == [[1, 2, 4],
[0, 2, 5]]
```
Parameters
-
objectsorted_sequence - N-D `Tensor` containing a sorted sequence.
-
objectvalues - N-D `Tensor` containing the search values.
-
ImplicitContainer<T>side - 'left' or 'right'; 'left' corresponds to lower_bound and 'right' to upper_bound.
-
ImplicitContainer<T>out_type - The output type (`int32` or `int64`). Default is
tf.int32. -
objectname - Optional name for the operation.
Returns
-
object - An N-D `Tensor` the size of values containing the result of applying either lower_bound or upper_bound (depending on side) to each value. The result is not a global index to the entire `Tensor`, but the index in the last dimension.
Tensor segment_max(IGraphNodeBase data, IGraphNodeBase segment_ids, string name)
Computes the maximum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \max_j(data_j)\\) where `max` is over `j` such
that `segment_ids[j] == i`. If the max is empty for a given segment ID `i`, `output[i] = 0`.
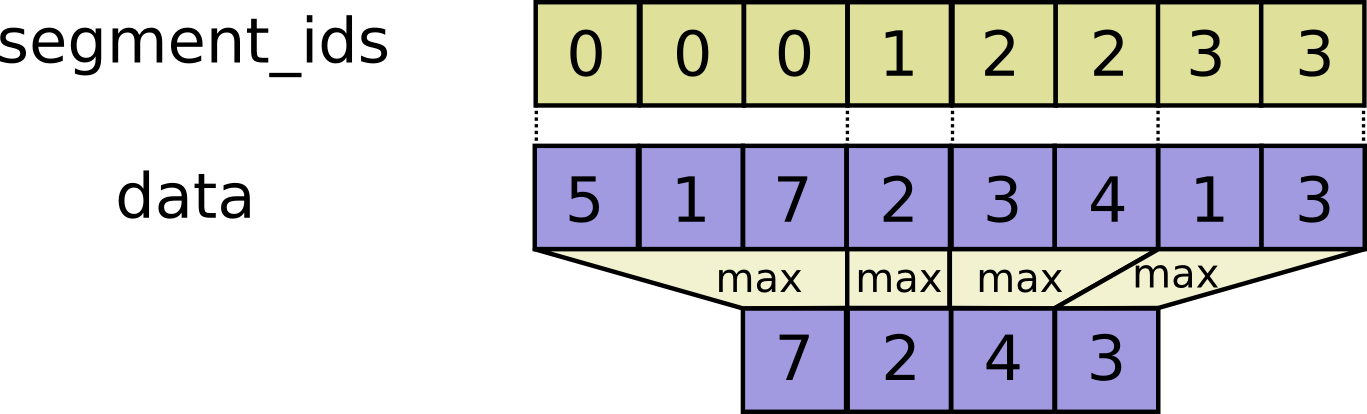 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_max(c, tf.constant([0, 0, 1]))
# ==> [[4, 3, 3, 4],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_max(c, tf.constant([0, 0, 1]))
# ==> [[4, 3, 3, 4],
# [5, 6, 7, 8]]
```

Parameters
-
IGraphNodeBasedata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasesegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
object segment_max_dyn(object data, object segment_ids, object name)
Computes the maximum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \max_j(data_j)\\) where `max` is over `j` such
that `segment_ids[j] == i`. If the max is empty for a given segment ID `i`, `output[i] = 0`.
 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_max(c, tf.constant([0, 0, 1]))
# ==> [[4, 3, 3, 4],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_max(c, tf.constant([0, 0, 1]))
# ==> [[4, 3, 3, 4],
# [5, 6, 7, 8]]
```

Parameters
-
objectdata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`.
-
objectsegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `data`.
Tensor segment_mean(IGraphNodeBase data, IGraphNodeBase segment_ids, string name)
Computes the mean along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \frac{\sum_j data_j}{N}\\) where `mean` is
over `j` such that `segment_ids[j] == i` and `N` is the total number of
values summed. If the mean is empty for a given segment ID `i`, `output[i] = 0`.
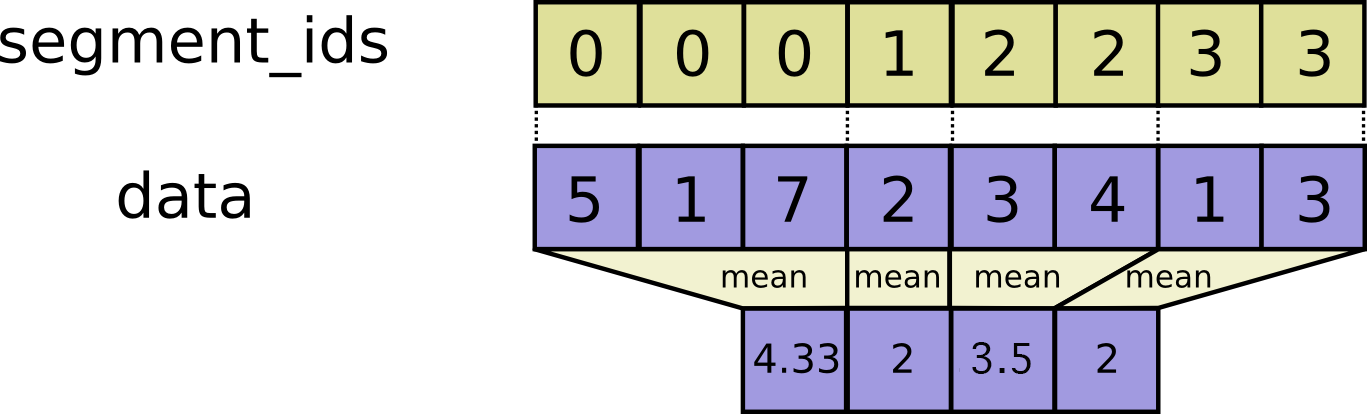 For example: ```
c = tf.constant([[1.0,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_mean(c, tf.constant([0, 0, 1]))
# ==> [[2.5, 2.5, 2.5, 2.5],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1.0,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_mean(c, tf.constant([0, 0, 1]))
# ==> [[2.5, 2.5, 2.5, 2.5],
# [5, 6, 7, 8]]
```

Parameters
-
IGraphNodeBasedata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasesegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
object segment_mean_dyn(object data, object segment_ids, object name)
Computes the mean along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \frac{\sum_j data_j}{N}\\) where `mean` is
over `j` such that `segment_ids[j] == i` and `N` is the total number of
values summed. If the mean is empty for a given segment ID `i`, `output[i] = 0`.
 For example: ```
c = tf.constant([[1.0,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_mean(c, tf.constant([0, 0, 1]))
# ==> [[2.5, 2.5, 2.5, 2.5],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1.0,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_mean(c, tf.constant([0, 0, 1]))
# ==> [[2.5, 2.5, 2.5, 2.5],
# [5, 6, 7, 8]]
```

Parameters
-
objectdata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
objectsegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `data`.
Tensor segment_min(IGraphNodeBase data, IGraphNodeBase segment_ids, string name)
Computes the minimum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \min_j(data_j)\\) where `min` is over `j` such
that `segment_ids[j] == i`. If the min is empty for a given segment ID `i`, `output[i] = 0`.
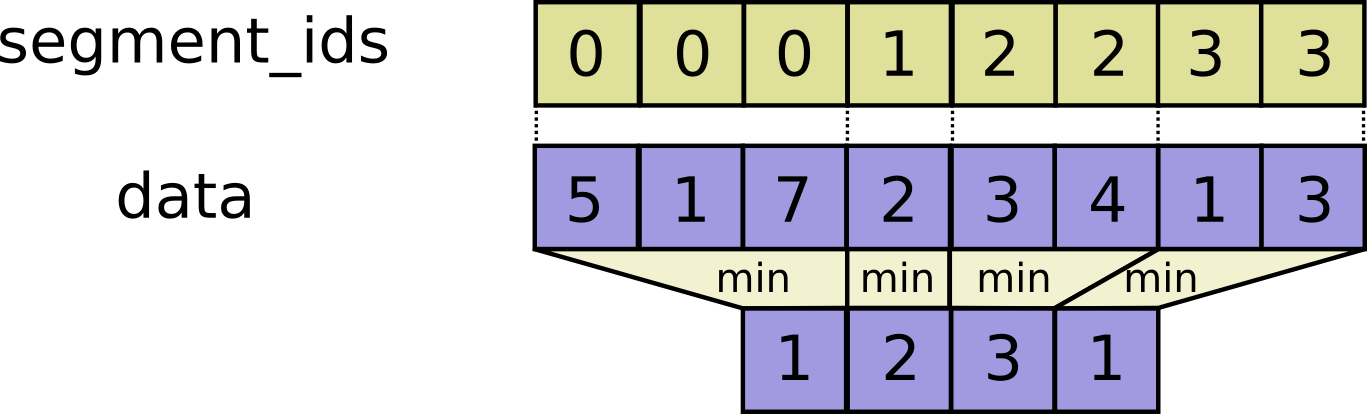 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_min(c, tf.constant([0, 0, 1]))
# ==> [[1, 2, 2, 1],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_min(c, tf.constant([0, 0, 1]))
# ==> [[1, 2, 2, 1],
# [5, 6, 7, 8]]
```

Parameters
-
IGraphNodeBasedata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasesegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
object segment_min_dyn(object data, object segment_ids, object name)
Computes the minimum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \min_j(data_j)\\) where `min` is over `j` such
that `segment_ids[j] == i`. If the min is empty for a given segment ID `i`, `output[i] = 0`.
 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_min(c, tf.constant([0, 0, 1]))
# ==> [[1, 2, 2, 1],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_min(c, tf.constant([0, 0, 1]))
# ==> [[1, 2, 2, 1],
# [5, 6, 7, 8]]
```

Parameters
-
objectdata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`.
-
objectsegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `data`.
Tensor segment_prod(IGraphNodeBase data, IGraphNodeBase segment_ids, string name)
Computes the product along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \prod_j data_j\\) where the product is over `j` such
that `segment_ids[j] == i`. If the product is empty for a given segment ID `i`, `output[i] = 1`.
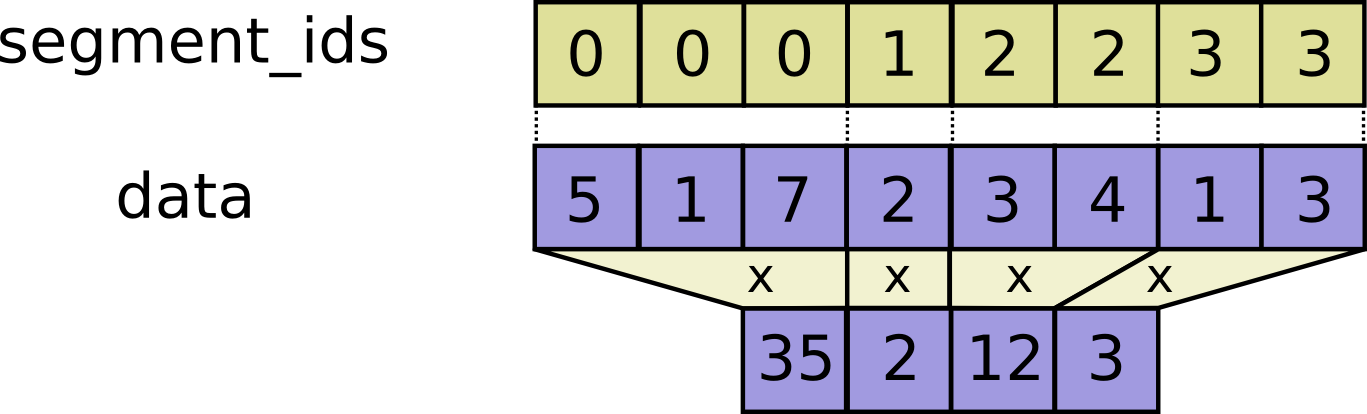 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_prod(c, tf.constant([0, 0, 1]))
# ==> [[4, 6, 6, 4],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_prod(c, tf.constant([0, 0, 1]))
# ==> [[4, 6, 6, 4],
# [5, 6, 7, 8]]
```

Parameters
-
IGraphNodeBasedata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasesegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
object segment_prod_dyn(object data, object segment_ids, object name)
Computes the product along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \prod_j data_j\\) where the product is over `j` such
that `segment_ids[j] == i`. If the product is empty for a given segment ID `i`, `output[i] = 1`.
 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_prod(c, tf.constant([0, 0, 1]))
# ==> [[4, 6, 6, 4],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_prod(c, tf.constant([0, 0, 1]))
# ==> [[4, 6, 6, 4],
# [5, 6, 7, 8]]
```

Parameters
-
objectdata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
objectsegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `data`.
Tensor segment_sum(IGraphNodeBase data, IGraphNodeBase segment_ids, string name)
Computes the sum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \sum_j data_j\\) where sum is over `j` such
that `segment_ids[j] == i`. If the sum is empty for a given segment ID `i`, `output[i] = 0`.
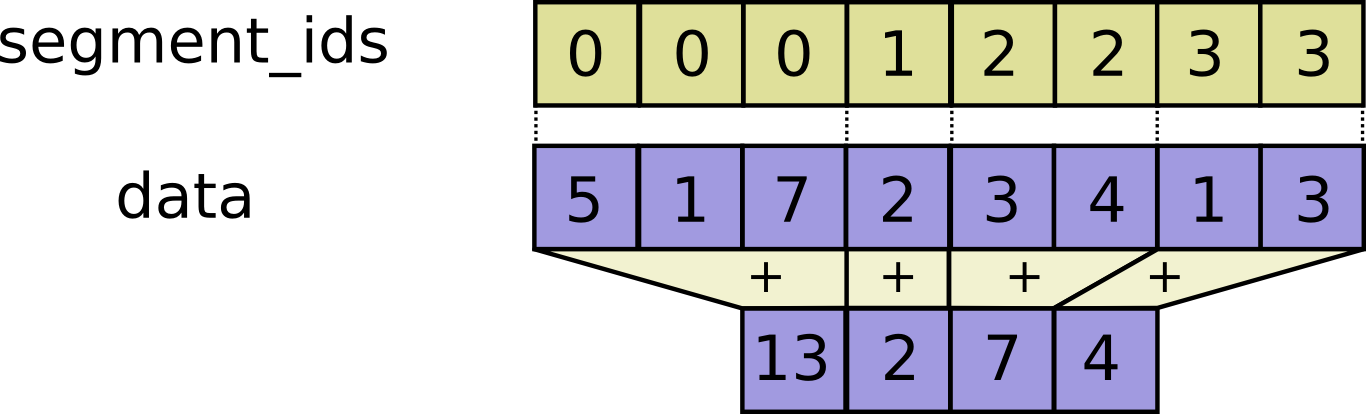 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_sum(c, tf.constant([0, 0, 1]))
# ==> [[5, 5, 5, 5],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_sum(c, tf.constant([0, 0, 1]))
# ==> [[5, 5, 5, 5],
# [5, 6, 7, 8]]
```

Parameters
-
IGraphNodeBasedata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasesegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
Tensor segment_sum(IGraphNodeBase data, IGraphNodeBase segment_ids, PythonFunctionContainer name)
Computes the sum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \sum_j data_j\\) where sum is over `j` such
that `segment_ids[j] == i`. If the sum is empty for a given segment ID `i`, `output[i] = 0`.
 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_sum(c, tf.constant([0, 0, 1]))
# ==> [[5, 5, 5, 5],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_sum(c, tf.constant([0, 0, 1]))
# ==> [[5, 5, 5, 5],
# [5, 6, 7, 8]]
```

Parameters
-
IGraphNodeBasedata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasesegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
object segment_sum_dyn(object data, object segment_ids, object name)
Computes the sum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \sum_j data_j\\) where sum is over `j` such
that `segment_ids[j] == i`. If the sum is empty for a given segment ID `i`, `output[i] = 0`.
 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_sum(c, tf.constant([0, 0, 1]))
# ==> [[5, 5, 5, 5],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_sum(c, tf.constant([0, 0, 1]))
# ==> [[5, 5, 5, 5],
# [5, 6, 7, 8]]
```

Parameters
-
objectdata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
objectsegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A 1-D tensor whose size is equal to the size of `data`'s first dimension. Values should be sorted and can be repeated.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `data`.
ValueTuple<object, object> self_adjoint_eig(IGraphNodeBase tensor, string name)
Computes the eigen decomposition of a batch of self-adjoint matrices. Computes the eigenvalues and eigenvectors of the innermost N-by-N matrices
in `tensor` such that
`tensor[...,:,:] * v[..., :,i] = e[..., i] * v[...,:,i]`, for i=0...N-1.
Parameters
-
IGraphNodeBasetensor - `Tensor` of shape `[..., N, N]`. Only the lower triangular part of each inner inner matrix is referenced.
-
stringname - string, optional name of the operation.
Returns
-
ValueTuple<object, object>
object self_adjoint_eig_dyn(object tensor, object name)
Computes the eigen decomposition of a batch of self-adjoint matrices. Computes the eigenvalues and eigenvectors of the innermost N-by-N matrices
in `tensor` such that
`tensor[...,:,:] * v[..., :,i] = e[..., i] * v[...,:,i]`, for i=0...N-1.
Parameters
-
objecttensor - `Tensor` of shape `[..., N, N]`. Only the lower triangular part of each inner inner matrix is referenced.
-
objectname - string, optional name of the operation.
Returns
-
object
object self_adjoint_eigvals(IGraphNodeBase tensor, string name)
Computes the eigenvalues of one or more self-adjoint matrices. Note: If your program backpropagates through this function, you should replace
it with a call to tf.linalg.eigh (possibly ignoring the second output) to
avoid computing the eigen decomposition twice. This is because the
eigenvectors are used to compute the gradient w.r.t. the eigenvalues. See
_SelfAdjointEigV2Grad in linalg_grad.py.
Parameters
-
IGraphNodeBasetensor - `Tensor` of shape `[..., N, N]`.
-
stringname - string, optional name of the operation.
Returns
-
object
object self_adjoint_eigvals_dyn(object tensor, object name)
Computes the eigenvalues of one or more self-adjoint matrices. Note: If your program backpropagates through this function, you should replace
it with a call to tf.linalg.eigh (possibly ignoring the second output) to
avoid computing the eigen decomposition twice. This is because the
eigenvectors are used to compute the gradient w.r.t. the eigenvalues. See
_SelfAdjointEigV2Grad in linalg_grad.py.
Parameters
-
objecttensor - `Tensor` of shape `[..., N, N]`.
-
objectname - string, optional name of the operation.
Returns
-
object
Tensor sequence_file_dataset(IGraphNodeBase filenames, IEnumerable<object> output_types, string name)
object sequence_file_dataset_dyn(object filenames, object output_types, object name)
Tensor sequence_mask(IEnumerable<int> lengths, IGraphNodeBase maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
IEnumerable<int>lengths - integer tensor, all its values <= maxlen.
-
IGraphNodeBasemaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(IEnumerable<int> lengths, TensorShape maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
IEnumerable<int>lengths - integer tensor, all its values <= maxlen.
-
TensorShapemaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(IEnumerable<int> lengths, IEnumerable<int> maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
IEnumerable<int>lengths - integer tensor, all its values <= maxlen.
-
IEnumerable<int>maxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(ValueTuple<IEnumerable<object>, object> lengths, TensorShape maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
ValueTuple<IEnumerable<object>, object>lengths - integer tensor, all its values <= maxlen.
-
TensorShapemaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(IEnumerable<int> lengths, Dimension maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
IEnumerable<int>lengths - integer tensor, all its values <= maxlen.
-
Dimensionmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(IGraphNodeBase lengths, Dimension maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
IGraphNodeBaselengths - integer tensor, all its values <= maxlen.
-
Dimensionmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(object lengths, int maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
objectlengths - integer tensor, all its values <= maxlen.
-
intmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(ValueTuple<IEnumerable<object>, object> lengths, IEnumerable<int> maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
ValueTuple<IEnumerable<object>, object>lengths - integer tensor, all its values <= maxlen.
-
IEnumerable<int>maxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(object lengths, IGraphNodeBase maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
objectlengths - integer tensor, all its values <= maxlen.
-
IGraphNodeBasemaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(ValueTuple<IEnumerable<object>, object> lengths, Dimension maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
ValueTuple<IEnumerable<object>, object>lengths - integer tensor, all its values <= maxlen.
-
Dimensionmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(IGraphNodeBase lengths, IEnumerable<int> maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
IGraphNodeBaselengths - integer tensor, all its values <= maxlen.
-
IEnumerable<int>maxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(object lengths, TensorShape maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
objectlengths - integer tensor, all its values <= maxlen.
-
TensorShapemaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(IEnumerable<int> lengths, int maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
IEnumerable<int>lengths - integer tensor, all its values <= maxlen.
-
intmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(int lengths, int maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
intlengths - integer tensor, all its values <= maxlen.
-
intmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(ValueTuple<IEnumerable<object>, object> lengths, IGraphNodeBase maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
ValueTuple<IEnumerable<object>, object>lengths - integer tensor, all its values <= maxlen.
-
IGraphNodeBasemaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(int lengths, TensorShape maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
intlengths - integer tensor, all its values <= maxlen.
-
TensorShapemaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(object lengths, Dimension maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
objectlengths - integer tensor, all its values <= maxlen.
-
Dimensionmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(IGraphNodeBase lengths, int maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
IGraphNodeBaselengths - integer tensor, all its values <= maxlen.
-
intmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(object lengths, IEnumerable<int> maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
objectlengths - integer tensor, all its values <= maxlen.
-
IEnumerable<int>maxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(int lengths, IEnumerable<int> maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
intlengths - integer tensor, all its values <= maxlen.
-
IEnumerable<int>maxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(IGraphNodeBase lengths, TensorShape maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
IGraphNodeBaselengths - integer tensor, all its values <= maxlen.
-
TensorShapemaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(int lengths, Dimension maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
intlengths - integer tensor, all its values <= maxlen.
-
Dimensionmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(int lengths, IGraphNodeBase maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
intlengths - integer tensor, all its values <= maxlen.
-
IGraphNodeBasemaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(ValueTuple<IEnumerable<object>, object> lengths, int maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
ValueTuple<IEnumerable<object>, object>lengths - integer tensor, all its values <= maxlen.
-
intmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor sequence_mask(IGraphNodeBase lengths, IGraphNodeBase maxlen, ImplicitContainer<T> dtype, string name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
IGraphNodeBaselengths - integer tensor, all its values <= maxlen.
-
IGraphNodeBasemaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
stringname - name of the op.
Returns
-
Tensor - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
object sequence_mask_dyn(object lengths, object maxlen, ImplicitContainer<T> dtype, object name)
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Parameters
-
objectlengths - integer tensor, all its values <= maxlen.
-
objectmaxlen - scalar integer tensor, size of last dimension of returned tensor. Default is the maximum value in `lengths`.
-
ImplicitContainer<T>dtype - output type of the resulting tensor.
-
objectname - name of the op.
Returns
-
object - A mask tensor of shape `lengths.shape + (maxlen,)`, cast to specified dtype.
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
Tensor serialize_many_sparse(SparseTensor sp_input, string name, ImplicitContainer<T> out_type)
Serialize `N`-minibatch `SparseTensor` into an `[N, 3]` `Tensor`. The `SparseTensor` must have rank `R` greater than 1, and the first dimension
is treated as the minibatch dimension. Elements of the `SparseTensor`
must be sorted in increasing order of this first dimension. The serialized
`SparseTensor` objects going into each row of the output `Tensor` will have
rank `R-1`. The minibatch size `N` is extracted from `sparse_shape[0]`.
Parameters
-
SparseTensorsp_input - The input rank `R` `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional).
-
ImplicitContainer<T>out_type - The `dtype` to use for serialization.
Returns
-
Tensor - A matrix (2-D `Tensor`) with `N` rows and `3` columns. Each column represents serialized `SparseTensor`'s indices, values, and shape (respectively).
object serialize_many_sparse_dyn(object sp_input, object name, ImplicitContainer<T> out_type)
Serialize `N`-minibatch `SparseTensor` into an `[N, 3]` `Tensor`. The `SparseTensor` must have rank `R` greater than 1, and the first dimension
is treated as the minibatch dimension. Elements of the `SparseTensor`
must be sorted in increasing order of this first dimension. The serialized
`SparseTensor` objects going into each row of the output `Tensor` will have
rank `R-1`. The minibatch size `N` is extracted from `sparse_shape[0]`.
Parameters
-
objectsp_input - The input rank `R` `SparseTensor`.
-
objectname - A name prefix for the returned tensors (optional).
-
ImplicitContainer<T>out_type - The `dtype` to use for serialization.
Returns
-
object - A matrix (2-D `Tensor`) with `N` rows and `3` columns. Each column represents serialized `SparseTensor`'s indices, values, and shape (respectively).
Tensor serialize_sparse(object sp_input, string name, ImplicitContainer<T> out_type)
Serialize a `SparseTensor` into a 3-vector (1-D `Tensor`) object.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional).
-
ImplicitContainer<T>out_type - The `dtype` to use for serialization.
Returns
-
Tensor - A 3-vector (1-D `Tensor`), with each column representing the serialized `SparseTensor`'s indices, values, and shape (respectively).
Tensor serialize_sparse(SparseTensor sp_input, string name, ImplicitContainer<T> out_type)
Serialize a `SparseTensor` into a 3-vector (1-D `Tensor`) object.
Parameters
-
SparseTensorsp_input - The input `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional).
-
ImplicitContainer<T>out_type - The `dtype` to use for serialization.
Returns
-
Tensor - A 3-vector (1-D `Tensor`), with each column representing the serialized `SparseTensor`'s indices, values, and shape (respectively).
object serialize_sparse_dyn(object sp_input, object name, ImplicitContainer<T> out_type)
Serialize a `SparseTensor` into a 3-vector (1-D `Tensor`) object.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
objectname - A name prefix for the returned tensors (optional).
-
ImplicitContainer<T>out_type - The `dtype` to use for serialization.
Returns
-
object - A 3-vector (1-D `Tensor`), with each column representing the serialized `SparseTensor`'s indices, values, and shape (respectively).
Tensor serialize_tensor(IGraphNodeBase tensor, string name)
Transforms a Tensor into a serialized TensorProto proto.
Parameters
-
IGraphNodeBasetensor - A `Tensor`. A Tensor of type `T`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `string`.
object serialize_tensor_dyn(object tensor, object name)
Transforms a Tensor into a serialized TensorProto proto.
Parameters
-
objecttensor - A `Tensor`. A Tensor of type `T`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `string`.
void set_random_seed(Nullable<int> seed)
Sets the graph-level random seed for the default graph. Operations that rely on a random seed actually derive it from two seeds:
the graph-level and operation-level seeds. This sets the graph-level seed. Its interactions with operation-level seeds is as follows: 1. If neither the graph-level nor the operation seed is set:
A random seed is used for this op.
2. If the graph-level seed is set, but the operation seed is not:
The system deterministically picks an operation seed in conjunction
with the graph-level seed so that it gets a unique random sequence.
3. If the graph-level seed is not set, but the operation seed is set:
A default graph-level seed and the specified operation seed are used to
determine the random sequence.
4. If both the graph-level and the operation seed are set:
Both seeds are used in conjunction to determine the random sequence. To illustrate the user-visible effects, consider these examples: To generate different sequences across sessions, set neither
graph-level nor op-level seeds:
To generate the same repeatable sequence for an op across sessions, set the
seed for the op:
To make the random sequences generated by all ops be repeatable across
sessions, set a graph-level seed:
Parameters
-
Nullable<int>seed - integer.
Show Example
a = tf.random.uniform([1])
b = tf.random.normal([1]) print("Session 1")
with tf.compat.v1.Session() as sess1:
print(sess1.run(a)) # generates 'A1'
print(sess1.run(a)) # generates 'A2'
print(sess1.run(b)) # generates 'B1'
print(sess1.run(b)) # generates 'B2' print("Session 2")
with tf.compat.v1.Session() as sess2:
print(sess2.run(a)) # generates 'A3'
print(sess2.run(a)) # generates 'A4'
print(sess2.run(b)) # generates 'B3'
print(sess2.run(b)) # generates 'B4'
object set_random_seed_dyn(object seed)
Sets the graph-level random seed for the default graph. Operations that rely on a random seed actually derive it from two seeds:
the graph-level and operation-level seeds. This sets the graph-level seed. Its interactions with operation-level seeds is as follows: 1. If neither the graph-level nor the operation seed is set:
A random seed is used for this op.
2. If the graph-level seed is set, but the operation seed is not:
The system deterministically picks an operation seed in conjunction
with the graph-level seed so that it gets a unique random sequence.
3. If the graph-level seed is not set, but the operation seed is set:
A default graph-level seed and the specified operation seed are used to
determine the random sequence.
4. If both the graph-level and the operation seed are set:
Both seeds are used in conjunction to determine the random sequence. To illustrate the user-visible effects, consider these examples: To generate different sequences across sessions, set neither
graph-level nor op-level seeds:
To generate the same repeatable sequence for an op across sessions, set the
seed for the op:
To make the random sequences generated by all ops be repeatable across
sessions, set a graph-level seed:
Parameters
-
objectseed - integer.
Show Example
a = tf.random.uniform([1])
b = tf.random.normal([1]) print("Session 1")
with tf.compat.v1.Session() as sess1:
print(sess1.run(a)) # generates 'A1'
print(sess1.run(a)) # generates 'A2'
print(sess1.run(b)) # generates 'B1'
print(sess1.run(b)) # generates 'B2' print("Session 2")
with tf.compat.v1.Session() as sess2:
print(sess2.run(a)) # generates 'A3'
print(sess2.run(a)) # generates 'A4'
print(sess2.run(b)) # generates 'B3'
print(sess2.run(b)) # generates 'B4'
object setdiff1d(IGraphNodeBase x, ValueTuple<PythonClassContainer, PythonClassContainer> y, ImplicitContainer<T> index_dtype, string name)
Computes the difference between two lists of numbers or strings. Given a list `x` and a list `y`, this operation returns a list `out` that
represents all values that are in `x` but not in `y`. The returned list `out`
is sorted in the same order that the numbers appear in `x` (duplicates are
preserved). This operation also returns a list `idx` that represents the
position of each `out` element in `x`. In other words: `out[i] = x[idx[i]] for i in [0, 1,..., len(out) - 1]` For example, given this input: ```
x = [1, 2, 3, 4, 5, 6]
y = [1, 3, 5]
``` This operation would return: ```
out ==> [2, 4, 6]
idx ==> [1, 3, 5]
```
Parameters
-
IGraphNodeBasex - A `Tensor`. 1-D. Values to keep.
-
ValueTuple<PythonClassContainer, PythonClassContainer>y - A `Tensor`. Must have the same type as `x`. 1-D. Values to remove.
-
ImplicitContainer<T>index_dtype -
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (out, idx).
object setdiff1d(IGraphNodeBase x, IndexedSlices y, ImplicitContainer<T> index_dtype, string name)
Computes the difference between two lists of numbers or strings. Given a list `x` and a list `y`, this operation returns a list `out` that
represents all values that are in `x` but not in `y`. The returned list `out`
is sorted in the same order that the numbers appear in `x` (duplicates are
preserved). This operation also returns a list `idx` that represents the
position of each `out` element in `x`. In other words: `out[i] = x[idx[i]] for i in [0, 1,..., len(out) - 1]` For example, given this input: ```
x = [1, 2, 3, 4, 5, 6]
y = [1, 3, 5]
``` This operation would return: ```
out ==> [2, 4, 6]
idx ==> [1, 3, 5]
```
Parameters
-
IGraphNodeBasex - A `Tensor`. 1-D. Values to keep.
-
IndexedSlicesy - A `Tensor`. Must have the same type as `x`. 1-D. Values to remove.
-
ImplicitContainer<T>index_dtype -
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (out, idx).
object setdiff1d(IGraphNodeBase x, IGraphNodeBase y, ImplicitContainer<T> index_dtype, string name)
Computes the difference between two lists of numbers or strings. Given a list `x` and a list `y`, this operation returns a list `out` that
represents all values that are in `x` but not in `y`. The returned list `out`
is sorted in the same order that the numbers appear in `x` (duplicates are
preserved). This operation also returns a list `idx` that represents the
position of each `out` element in `x`. In other words: `out[i] = x[idx[i]] for i in [0, 1,..., len(out) - 1]` For example, given this input: ```
x = [1, 2, 3, 4, 5, 6]
y = [1, 3, 5]
``` This operation would return: ```
out ==> [2, 4, 6]
idx ==> [1, 3, 5]
```
Parameters
-
IGraphNodeBasex - A `Tensor`. 1-D. Values to keep.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`. 1-D. Values to remove.
-
ImplicitContainer<T>index_dtype -
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (out, idx).
object setdiff1d(IGraphNodeBase x, IEnumerable<object> y, ImplicitContainer<T> index_dtype, string name)
Computes the difference between two lists of numbers or strings. Given a list `x` and a list `y`, this operation returns a list `out` that
represents all values that are in `x` but not in `y`. The returned list `out`
is sorted in the same order that the numbers appear in `x` (duplicates are
preserved). This operation also returns a list `idx` that represents the
position of each `out` element in `x`. In other words: `out[i] = x[idx[i]] for i in [0, 1,..., len(out) - 1]` For example, given this input: ```
x = [1, 2, 3, 4, 5, 6]
y = [1, 3, 5]
``` This operation would return: ```
out ==> [2, 4, 6]
idx ==> [1, 3, 5]
```
Parameters
-
IGraphNodeBasex - A `Tensor`. 1-D. Values to keep.
-
IEnumerable<object>y - A `Tensor`. Must have the same type as `x`. 1-D. Values to remove.
-
ImplicitContainer<T>index_dtype -
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (out, idx).
object setdiff1d_dyn(object x, object y, ImplicitContainer<T> index_dtype, object name)
Computes the difference between two lists of numbers or strings. Given a list `x` and a list `y`, this operation returns a list `out` that
represents all values that are in `x` but not in `y`. The returned list `out`
is sorted in the same order that the numbers appear in `x` (duplicates are
preserved). This operation also returns a list `idx` that represents the
position of each `out` element in `x`. In other words: `out[i] = x[idx[i]] for i in [0, 1,..., len(out) - 1]` For example, given this input: ```
x = [1, 2, 3, 4, 5, 6]
y = [1, 3, 5]
``` This operation would return: ```
out ==> [2, 4, 6]
idx ==> [1, 3, 5]
```
Parameters
-
objectx - A `Tensor`. 1-D. Values to keep.
-
objecty - A `Tensor`. Must have the same type as `x`. 1-D. Values to remove.
-
ImplicitContainer<T>index_dtype -
objectname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (out, idx).
Tensor shape(object input, string name, ImplicitContainer<T> out_type)
Returns the shape of a tensor. This operation returns a 1-D integer tensor representing the shape of `input`.
Parameters
-
objectinput - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified output type of the operation (`int32` or
`int64`). Defaults to
tf.int32.
Returns
-
Tensor - A `Tensor` of type `out_type`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.shape(t) # [2, 2, 3]
Tensor shape(IEnumerable<IGraphNodeBase> input, string name, ImplicitContainer<T> out_type)
Returns the shape of a tensor. This operation returns a 1-D integer tensor representing the shape of `input`.
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified output type of the operation (`int32` or
`int64`). Defaults to
tf.int32.
Returns
-
Tensor - A `Tensor` of type `out_type`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.shape(t) # [2, 2, 3]
Tensor shape(object input, string name, PythonFunctionContainer out_type)
Returns the shape of a tensor. This operation returns a 1-D integer tensor representing the shape of `input`.
Parameters
-
objectinput - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
-
PythonFunctionContainerout_type - (Optional) The specified output type of the operation (`int32` or
`int64`). Defaults to
tf.int32.
Returns
-
Tensor - A `Tensor` of type `out_type`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.shape(t) # [2, 2, 3]
Tensor shape(PythonFunctionContainer input, string name, PythonFunctionContainer out_type)
Returns the shape of a tensor. This operation returns a 1-D integer tensor representing the shape of `input`.
Parameters
-
PythonFunctionContainerinput - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
-
PythonFunctionContainerout_type - (Optional) The specified output type of the operation (`int32` or
`int64`). Defaults to
tf.int32.
Returns
-
Tensor - A `Tensor` of type `out_type`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.shape(t) # [2, 2, 3]
Tensor shape(PythonFunctionContainer input, string name, ImplicitContainer<T> out_type)
Returns the shape of a tensor. This operation returns a 1-D integer tensor representing the shape of `input`.
Parameters
-
PythonFunctionContainerinput - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified output type of the operation (`int32` or
`int64`). Defaults to
tf.int32.
Returns
-
Tensor - A `Tensor` of type `out_type`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.shape(t) # [2, 2, 3]
Tensor shape(IEnumerable<IGraphNodeBase> input, string name, PythonFunctionContainer out_type)
Returns the shape of a tensor. This operation returns a 1-D integer tensor representing the shape of `input`.
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
-
PythonFunctionContainerout_type - (Optional) The specified output type of the operation (`int32` or
`int64`). Defaults to
tf.int32.
Returns
-
Tensor - A `Tensor` of type `out_type`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.shape(t) # [2, 2, 3]
object shape_dyn(object input, object name, ImplicitContainer<T> out_type)
Returns the shape of a tensor. This operation returns a 1-D integer tensor representing the shape of `input`.
Parameters
-
objectinput - A `Tensor` or `SparseTensor`.
-
objectname - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified output type of the operation (`int32` or
`int64`). Defaults to
tf.int32.
Returns
-
object - A `Tensor` of type `out_type`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.shape(t) # [2, 2, 3]
object shape_n(IEnumerable<IGraphNodeBase> input, ImplicitContainer<T> out_type, string name)
Returns shape of tensors.
Parameters
-
IEnumerable<IGraphNodeBase>input - A list of at least 1 `Tensor` object with the same type.
-
ImplicitContainer<T>out_type - The specified output type of the operation (`int32` or `int64`).
Defaults to
tf.int32(optional). -
stringname - A name for the operation (optional).
Returns
-
object - A list with the same length as `input` of `Tensor` objects with type `out_type`.
object shape_n_dyn(object input, ImplicitContainer<T> out_type, object name)
Returns shape of tensors.
Parameters
-
objectinput - A list of at least 1 `Tensor` object with the same type.
-
ImplicitContainer<T>out_type - The specified output type of the operation (`int32` or `int64`).
Defaults to
tf.int32(optional). -
objectname - A name for the operation (optional).
Returns
-
object - A list with the same length as `input` of `Tensor` objects with type `out_type`.
object sigmoid(IGraphNodeBase x, string name)
Computes sigmoid of `x` element-wise. Specifically, `y = 1 / (1 + exp(-x))`.
Parameters
-
IGraphNodeBasex - A Tensor with type `float16`, `float32`, `float64`, `complex64`, or `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A Tensor with the same type as `x`.
object sigmoid_dyn(object x, object name)
Computes sigmoid of `x` element-wise. Specifically, `y = 1 / (1 + exp(-x))`.
Parameters
-
objectx - A Tensor with type `float16`, `float32`, `float64`, `complex64`, or `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A Tensor with the same type as `x`.
object sign(IGraphNodeBase x, string name)
Returns an element-wise indication of the sign of a number. `y = sign(x) = -1` if `x < 0`; 0 if `x == 0`; 1 if `x > 0`. For complex numbers, `y = sign(x) = x / |x|` if `x != 0`, otherwise `y = 0`.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`. If `x` is a `SparseTensor`, returns `SparseTensor(x.indices, tf.math.sign(x.values,...), x.dense_shape)`
object sign_dyn(object x, object name)
Returns an element-wise indication of the sign of a number. `y = sign(x) = -1` if `x < 0`; 0 if `x == 0`; 1 if `x > 0`. For complex numbers, `y = sign(x) = x / |x|` if `x != 0`, otherwise `y = 0`.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`. If `x` is a `SparseTensor`, returns `SparseTensor(x.indices, tf.math.sign(x.values,...), x.dense_shape)`
Tensor simple(IGraphNodeBase a, string name)
object simple_dyn(object a, object name)
object simple_struct(object n_a, string name)
object simple_struct_dyn(object n_a, object name)
object sin(IGraphNodeBase x, string name)
Computes sine of x element-wise. Given an input tensor, this function computes sine of every
element in the tensor. Input range is `(-inf, inf)` and
output range is `[-1,1]`.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 200, 10, float("inf")])
tf.math.sin(x) ==> [nan -0.4121185 -0.47942555 0.84147096 0.9320391 -0.87329733 -0.54402107 nan]
object sin_dyn(object x, object name)
Computes sine of x element-wise. Given an input tensor, this function computes sine of every
element in the tensor. Input range is `(-inf, inf)` and
output range is `[-1,1]`.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 200, 10, float("inf")])
tf.math.sin(x) ==> [nan -0.4121185 -0.47942555 0.84147096 0.9320391 -0.87329733 -0.54402107 nan]
object single_image_random_dot_stereograms(IGraphNodeBase depth_values, Nullable<bool> hidden_surface_removal, Nullable<int> convergence_dots_size, Nullable<int> dots_per_inch, Nullable<double> eye_separation, Nullable<double> mu, Nullable<bool> normalize, Nullable<int> normalize_max, Nullable<int> normalize_min, Nullable<int> border_level, Nullable<int> number_colors, ImplicitContainer<T> output_image_shape, ImplicitContainer<T> output_data_window, string name)
object single_image_random_dot_stereograms_dyn(object depth_values, ImplicitContainer<T> hidden_surface_removal, ImplicitContainer<T> convergence_dots_size, ImplicitContainer<T> dots_per_inch, ImplicitContainer<T> eye_separation, ImplicitContainer<T> mu, ImplicitContainer<T> normalize, ImplicitContainer<T> normalize_max, ImplicitContainer<T> normalize_min, ImplicitContainer<T> border_level, ImplicitContainer<T> number_colors, ImplicitContainer<T> output_image_shape, ImplicitContainer<T> output_data_window, object name)
object sinh(IGraphNodeBase x, string name)
Computes hyperbolic sine of x element-wise. Given an input tensor, this function computes hyperbolic sine of every
element in the tensor. Input range is `[-inf,inf]` and output range
is `[-inf,inf]`.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 2, 10, float("inf")])
tf.math.sinh(x) ==> [-inf -4.0515420e+03 -5.2109528e-01 1.1752012e+00 1.5094614e+00 3.6268604e+00 1.1013232e+04 inf]
object sinh_dyn(object x, object name)
Computes hyperbolic sine of x element-wise. Given an input tensor, this function computes hyperbolic sine of every
element in the tensor. Input range is `[-inf,inf]` and output range
is `[-inf,inf]`.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 2, 10, float("inf")])
tf.math.sinh(x) ==> [-inf -4.0515420e+03 -5.2109528e-01 1.1752012e+00 1.5094614e+00 3.6268604e+00 1.1013232e+04 inf]
Tensor size(object input, string name, ImplicitContainer<T> out_type)
Returns the size of a tensor. Returns a 0-D `Tensor` representing the number of elements in `input`
of type `out_type`. Defaults to tf.int32.
Parameters
-
objectinput - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified non-quantized numeric output type of the
operation. Defaults to
tf.int32.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.size(t) # 12
Tensor size(IEnumerable<object> input, PythonFunctionContainer name, ImplicitContainer<T> out_type)
Returns the size of a tensor. Returns a 0-D `Tensor` representing the number of elements in `input`
of type `out_type`. Defaults to tf.int32.
Parameters
-
IEnumerable<object>input - A `Tensor` or `SparseTensor`.
-
PythonFunctionContainername - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified non-quantized numeric output type of the
operation. Defaults to
tf.int32.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.size(t) # 12
Tensor size(PythonClassContainer input, string name, ImplicitContainer<T> out_type)
Returns the size of a tensor. Returns a 0-D `Tensor` representing the number of elements in `input`
of type `out_type`. Defaults to tf.int32.
Parameters
-
PythonClassContainerinput - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified non-quantized numeric output type of the
operation. Defaults to
tf.int32.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.size(t) # 12
Tensor size(PythonClassContainer input, PythonFunctionContainer name, ImplicitContainer<T> out_type)
Returns the size of a tensor. Returns a 0-D `Tensor` representing the number of elements in `input`
of type `out_type`. Defaults to tf.int32.
Parameters
-
PythonClassContainerinput - A `Tensor` or `SparseTensor`.
-
PythonFunctionContainername - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified non-quantized numeric output type of the
operation. Defaults to
tf.int32.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.size(t) # 12
Tensor size(object input, PythonFunctionContainer name, ImplicitContainer<T> out_type)
Returns the size of a tensor. Returns a 0-D `Tensor` representing the number of elements in `input`
of type `out_type`. Defaults to tf.int32.
Parameters
-
objectinput - A `Tensor` or `SparseTensor`.
-
PythonFunctionContainername - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified non-quantized numeric output type of the
operation. Defaults to
tf.int32.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.size(t) # 12
Tensor size(IEnumerable<IGraphNodeBase> input, string name, ImplicitContainer<T> out_type)
Returns the size of a tensor. Returns a 0-D `Tensor` representing the number of elements in `input`
of type `out_type`. Defaults to tf.int32.
Parameters
-
IEnumerable<IGraphNodeBase>input - A `Tensor` or `SparseTensor`.
-
stringname - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified non-quantized numeric output type of the
operation. Defaults to
tf.int32.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.size(t) # 12
object size_dyn(object input, object name, ImplicitContainer<T> out_type)
Returns the size of a tensor. Returns a 0-D `Tensor` representing the number of elements in `input`
of type `out_type`. Defaults to tf.int32.
Parameters
-
objectinput - A `Tensor` or `SparseTensor`.
-
objectname - A name for the operation (optional).
-
ImplicitContainer<T>out_type - (Optional) The specified non-quantized numeric output type of the
operation. Defaults to
tf.int32.
Returns
-
object - A `Tensor` of type `out_type`. Defaults to
tf.int32.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.size(t) # 12
object skip_gram_generate_candidates(IGraphNodeBase input_tensor, IGraphNodeBase min_skips, IGraphNodeBase max_skips, IGraphNodeBase start, IGraphNodeBase limit, IGraphNodeBase emit_self_as_target, int seed, int seed2, string name)
object skip_gram_generate_candidates_dyn(object input_tensor, object min_skips, object max_skips, object start, object limit, object emit_self_as_target, ImplicitContainer<T> seed, ImplicitContainer<T> seed2, object name)
Tensor slice(IGraphNodeBase input_, IGraphNodeBase begin, IGraphNodeBase size, string name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasesize - An `int32` or `int64` `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IEnumerable<int> begin, TensorShape size, PythonFunctionContainer name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
TensorShapesize - An `int32` or `int64` `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IEnumerable<int> begin, IEnumerable<int> size, PythonFunctionContainer name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>size - An `int32` or `int64` `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IEnumerable<int> begin, IEnumerable<int> size, string name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>size - An `int32` or `int64` `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IEnumerable<int> begin, TensorShape size, string name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
TensorShapesize - An `int32` or `int64` `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IGraphNodeBase begin, TensorShape size, string name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
TensorShapesize - An `int32` or `int64` `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IGraphNodeBase begin, IEnumerable<int> size, PythonFunctionContainer name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>size - An `int32` or `int64` `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IEnumerable<int> begin, IGraphNodeBase size, string name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasesize - An `int32` or `int64` `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IGraphNodeBase begin, TensorShape size, PythonFunctionContainer name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
TensorShapesize - An `int32` or `int64` `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IGraphNodeBase begin, IGraphNodeBase size, PythonFunctionContainer name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasesize - An `int32` or `int64` `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IEnumerable<int> begin, IGraphNodeBase size, PythonFunctionContainer name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasesize - An `int32` or `int64` `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor slice(IGraphNodeBase input_, IGraphNodeBase begin, IEnumerable<int> size, string name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>size - An `int32` or `int64` `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
object slice_dyn(object input_, object begin, object size, object name)
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Parameters
-
objectinput_ - A `Tensor`.
-
objectbegin - An `int32` or `int64` `Tensor`.
-
objectsize - An `int32` or `int64` `Tensor`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` the same type as `input_`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
Tensor sort(IGraphNodeBase values, int axis, string direction, string name)
Sorts a tensor. Usage:
Parameters
-
IGraphNodeBasevalues - 1-D or higher numeric `Tensor`.
-
intaxis - The axis along which to sort. The default is -1, which sorts the last axis.
-
stringdirection - The direction in which to sort the values (`'ASCENDING'` or `'DESCENDING'`).
-
stringname - Optional name for the operation.
Returns
-
Tensor - A `Tensor` with the same dtype and shape as `values`, with the elements sorted along the given `axis`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.sort(a,axis=-1,direction='ASCENDING',name=None)
c = tf.keras.backend.eval(b)
# Here, c = [ 1. 2.8 10. 26.9 62.3 166.32]
object sort_dyn(object values, ImplicitContainer<T> axis, ImplicitContainer<T> direction, object name)
Sorts a tensor. Usage:
Parameters
-
objectvalues - 1-D or higher numeric `Tensor`.
-
ImplicitContainer<T>axis - The axis along which to sort. The default is -1, which sorts the last axis.
-
ImplicitContainer<T>direction - The direction in which to sort the values (`'ASCENDING'` or `'DESCENDING'`).
-
objectname - Optional name for the operation.
Returns
-
object - A `Tensor` with the same dtype and shape as `values`, with the elements sorted along the given `axis`.
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.sort(a,axis=-1,direction='ASCENDING',name=None)
c = tf.keras.backend.eval(b)
# Here, c = [ 1. 2.8 10. 26.9 62.3 166.32]
Tensor space_to_batch(IGraphNodeBase input, IEnumerable<object> paddings, Nullable<int> block_size, string name, object block_shape)
SpaceToBatch for 4-D tensors of type T. This is a legacy version of the more general SpaceToBatchND. Zero-pads and then rearranges (permutes) blocks of spatial data into batch.
More specifically, this op outputs a copy of the input tensor where values from
the `height` and `width` dimensions are moved to the `batch` dimension. After
the zero-padding, both `height` and `width` of the input must be divisible by the
block size.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. 4-D with shape `[batch, height, width, depth]`.
-
IEnumerable<object>paddings - A `Tensor`. Must be one of the following types: `int32`, `int64`. 2-D tensor of non-negative integers with shape `[2, 2]`. It specifies the padding of the input with zeros across the spatial dimensions as follows: paddings = [[pad_top, pad_bottom], [pad_left, pad_right]] The effective spatial dimensions of the zero-padded input tensor will be: height_pad = pad_top + height + pad_bottom width_pad = pad_left + width + pad_right The attr `block_size` must be greater than one. It indicates the block size. * Non-overlapping blocks of size `block_size x block size` in the height and width dimensions are rearranged into the batch dimension at each location. * The batch of the output tensor is `batch * block_size * block_size`. * Both height_pad and width_pad must be divisible by block_size. The shape of the output will be: [batch*block_size*block_size, height_pad/block_size, width_pad/block_size, depth] Some examples: (1) For the following input of shape `[1, 2, 2, 1]` and block_size of 2: ``` x = [[[[1], [2]], [[3], [4]]]] ``` The output tensor has shape `[4, 1, 1, 1]` and value: ``` [[[[1]]], [[[2]]], [[[3]]], [[[4]]]] ``` (2) For the following input of shape `[1, 2, 2, 3]` and block_size of 2: ``` x = [[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]]] ``` The output tensor has shape `[4, 1, 1, 3]` and value: ``` [[[[1, 2, 3]]], [[[4, 5, 6]]], [[[7, 8, 9]]], [[[10, 11, 12]]]] ``` (3) For the following input of shape `[1, 4, 4, 1]` and block_size of 2: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]], [[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ``` The output tensor has shape `[4, 2, 2, 1]` and value: ``` x = [[[[1], [3]], [[9], [11]]], [[[2], [4]], [[10], [12]]], [[[5], [7]], [[13], [15]]], [[[6], [8]], [[14], [16]]]] ``` (4) For the following input of shape `[2, 2, 4, 1]` and block_size of 2: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]]], [[[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ``` The output tensor has shape `[8, 1, 2, 1]` and value: ``` x = [[[[1], [3]]], [[[9], [11]]], [[[2], [4]]], [[[10], [12]]], [[[5], [7]]], [[[13], [15]]], [[[6], [8]]], [[[14], [16]]]] ``` Among others, this operation is useful for reducing atrous convolution into regular convolution.
-
Nullable<int>block_size - An `int` that is `>= 2`.
-
stringname - A name for the operation (optional).
-
objectblock_shape
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object space_to_batch_dyn(object input, object paddings, object block_size, object name, object block_shape)
SpaceToBatch for 4-D tensors of type T. This is a legacy version of the more general SpaceToBatchND. Zero-pads and then rearranges (permutes) blocks of spatial data into batch.
More specifically, this op outputs a copy of the input tensor where values from
the `height` and `width` dimensions are moved to the `batch` dimension. After
the zero-padding, both `height` and `width` of the input must be divisible by the
block size.
Parameters
-
objectinput - A `Tensor`. 4-D with shape `[batch, height, width, depth]`.
-
objectpaddings - A `Tensor`. Must be one of the following types: `int32`, `int64`. 2-D tensor of non-negative integers with shape `[2, 2]`. It specifies the padding of the input with zeros across the spatial dimensions as follows: paddings = [[pad_top, pad_bottom], [pad_left, pad_right]] The effective spatial dimensions of the zero-padded input tensor will be: height_pad = pad_top + height + pad_bottom width_pad = pad_left + width + pad_right The attr `block_size` must be greater than one. It indicates the block size. * Non-overlapping blocks of size `block_size x block size` in the height and width dimensions are rearranged into the batch dimension at each location. * The batch of the output tensor is `batch * block_size * block_size`. * Both height_pad and width_pad must be divisible by block_size. The shape of the output will be: [batch*block_size*block_size, height_pad/block_size, width_pad/block_size, depth] Some examples: (1) For the following input of shape `[1, 2, 2, 1]` and block_size of 2: ``` x = [[[[1], [2]], [[3], [4]]]] ``` The output tensor has shape `[4, 1, 1, 1]` and value: ``` [[[[1]]], [[[2]]], [[[3]]], [[[4]]]] ``` (2) For the following input of shape `[1, 2, 2, 3]` and block_size of 2: ``` x = [[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]]] ``` The output tensor has shape `[4, 1, 1, 3]` and value: ``` [[[[1, 2, 3]]], [[[4, 5, 6]]], [[[7, 8, 9]]], [[[10, 11, 12]]]] ``` (3) For the following input of shape `[1, 4, 4, 1]` and block_size of 2: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]], [[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ``` The output tensor has shape `[4, 2, 2, 1]` and value: ``` x = [[[[1], [3]], [[9], [11]]], [[[2], [4]], [[10], [12]]], [[[5], [7]], [[13], [15]]], [[[6], [8]], [[14], [16]]]] ``` (4) For the following input of shape `[2, 2, 4, 1]` and block_size of 2: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]]], [[[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ``` The output tensor has shape `[8, 1, 2, 1]` and value: ``` x = [[[[1], [3]]], [[[9], [11]]], [[[2], [4]]], [[[10], [12]]], [[[5], [7]]], [[[13], [15]]], [[[6], [8]]], [[[14], [16]]]] ``` Among others, this operation is useful for reducing atrous convolution into regular convolution.
-
objectblock_size - An `int` that is `>= 2`.
-
objectname - A name for the operation (optional).
-
objectblock_shape
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor space_to_batch_nd(IGraphNodeBase input, IGraphNodeBase block_shape, IGraphNodeBase paddings, string name)
SpaceToBatch for N-D tensors of type T. This operation divides "spatial" dimensions `[1,..., M]` of the input into a
grid of blocks of shape `block_shape`, and interleaves these blocks with the
"batch" dimension (0) such that in the output, the spatial dimensions
`[1,..., M]` correspond to the position within the grid, and the batch
dimension combines both the position within a spatial block and the original
batch position. Prior to division into blocks, the spatial dimensions of the
input are optionally zero padded according to `paddings`. See below for a
precise description.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. N-D with shape `input_shape = [batch] + spatial_shape + remaining_shape`, where spatial_shape has `M` dimensions.
-
IGraphNodeBaseblock_shape - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with shape `[M]`, all values must be >= 1.
-
IGraphNodeBasepaddings - A `Tensor`. Must be one of the following types: `int32`, `int64`. 2-D with shape `[M, 2]`, all values must be >= 0. `paddings[i] = [pad_start, pad_end]` specifies the padding for input dimension `i + 1`, which corresponds to spatial dimension `i`. It is required that `block_shape[i]` divides `input_shape[i + 1] + pad_start + pad_end`. This operation is equivalent to the following steps: 1. Zero-pad the start and end of dimensions `[1,..., M]` of the input according to `paddings` to produce `padded` of shape `padded_shape`. 2. Reshape `padded` to `reshaped_padded` of shape: [batch] + [padded_shape[1] / block_shape[0], block_shape[0], ..., padded_shape[M] / block_shape[M-1], block_shape[M-1]] + remaining_shape 3. Permute dimensions of `reshaped_padded` to produce `permuted_reshaped_padded` of shape: block_shape + [batch] + [padded_shape[1] / block_shape[0], ..., padded_shape[M] / block_shape[M-1]] + remaining_shape 4. Reshape `permuted_reshaped_padded` to flatten `block_shape` into the batch dimension, producing an output tensor of shape: [batch * prod(block_shape)] + [padded_shape[1] / block_shape[0], ..., padded_shape[M] / block_shape[M-1]] + remaining_shape Some examples: (1) For the following input of shape `[1, 2, 2, 1]`, `block_shape = [2, 2]`, and `paddings = [[0, 0], [0, 0]]`: ``` x = [[[[1], [2]], [[3], [4]]]] ``` The output tensor has shape `[4, 1, 1, 1]` and value: ``` [[[[1]]], [[[2]]], [[[3]]], [[[4]]]] ``` (2) For the following input of shape `[1, 2, 2, 3]`, `block_shape = [2, 2]`, and `paddings = [[0, 0], [0, 0]]`: ``` x = [[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]]] ``` The output tensor has shape `[4, 1, 1, 3]` and value: ``` [[[[1, 2, 3]]], [[[4, 5, 6]]], [[[7, 8, 9]]], [[[10, 11, 12]]]] ``` (3) For the following input of shape `[1, 4, 4, 1]`, `block_shape = [2, 2]`, and `paddings = [[0, 0], [0, 0]]`: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]], [[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ``` The output tensor has shape `[4, 2, 2, 1]` and value: ``` x = [[[[1], [3]], [[9], [11]]], [[[2], [4]], [[10], [12]]], [[[5], [7]], [[13], [15]]], [[[6], [8]], [[14], [16]]]] ``` (4) For the following input of shape `[2, 2, 4, 1]`, block_shape = `[2, 2]`, and paddings = `[[0, 0], [2, 0]]`: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]]], [[[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ``` The output tensor has shape `[8, 1, 3, 1]` and value: ``` x = [[[[0], [1], [3]]], [[[0], [9], [11]]], [[[0], [2], [4]]], [[[0], [10], [12]]], [[[0], [5], [7]]], [[[0], [13], [15]]], [[[0], [6], [8]]], [[[0], [14], [16]]]] ``` Among others, this operation is useful for reducing atrous convolution into regular convolution.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object space_to_batch_nd_dyn(object input, object block_shape, object paddings, object name)
SpaceToBatch for N-D tensors of type T. This operation divides "spatial" dimensions `[1,..., M]` of the input into a
grid of blocks of shape `block_shape`, and interleaves these blocks with the
"batch" dimension (0) such that in the output, the spatial dimensions
`[1,..., M]` correspond to the position within the grid, and the batch
dimension combines both the position within a spatial block and the original
batch position. Prior to division into blocks, the spatial dimensions of the
input are optionally zero padded according to `paddings`. See below for a
precise description.
Parameters
-
objectinput - A `Tensor`. N-D with shape `input_shape = [batch] + spatial_shape + remaining_shape`, where spatial_shape has `M` dimensions.
-
objectblock_shape - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D with shape `[M]`, all values must be >= 1.
-
objectpaddings - A `Tensor`. Must be one of the following types: `int32`, `int64`. 2-D with shape `[M, 2]`, all values must be >= 0. `paddings[i] = [pad_start, pad_end]` specifies the padding for input dimension `i + 1`, which corresponds to spatial dimension `i`. It is required that `block_shape[i]` divides `input_shape[i + 1] + pad_start + pad_end`. This operation is equivalent to the following steps: 1. Zero-pad the start and end of dimensions `[1,..., M]` of the input according to `paddings` to produce `padded` of shape `padded_shape`. 2. Reshape `padded` to `reshaped_padded` of shape: [batch] + [padded_shape[1] / block_shape[0], block_shape[0], ..., padded_shape[M] / block_shape[M-1], block_shape[M-1]] + remaining_shape 3. Permute dimensions of `reshaped_padded` to produce `permuted_reshaped_padded` of shape: block_shape + [batch] + [padded_shape[1] / block_shape[0], ..., padded_shape[M] / block_shape[M-1]] + remaining_shape 4. Reshape `permuted_reshaped_padded` to flatten `block_shape` into the batch dimension, producing an output tensor of shape: [batch * prod(block_shape)] + [padded_shape[1] / block_shape[0], ..., padded_shape[M] / block_shape[M-1]] + remaining_shape Some examples: (1) For the following input of shape `[1, 2, 2, 1]`, `block_shape = [2, 2]`, and `paddings = [[0, 0], [0, 0]]`: ``` x = [[[[1], [2]], [[3], [4]]]] ``` The output tensor has shape `[4, 1, 1, 1]` and value: ``` [[[[1]]], [[[2]]], [[[3]]], [[[4]]]] ``` (2) For the following input of shape `[1, 2, 2, 3]`, `block_shape = [2, 2]`, and `paddings = [[0, 0], [0, 0]]`: ``` x = [[[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]]] ``` The output tensor has shape `[4, 1, 1, 3]` and value: ``` [[[[1, 2, 3]]], [[[4, 5, 6]]], [[[7, 8, 9]]], [[[10, 11, 12]]]] ``` (3) For the following input of shape `[1, 4, 4, 1]`, `block_shape = [2, 2]`, and `paddings = [[0, 0], [0, 0]]`: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]], [[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ``` The output tensor has shape `[4, 2, 2, 1]` and value: ``` x = [[[[1], [3]], [[9], [11]]], [[[2], [4]], [[10], [12]]], [[[5], [7]], [[13], [15]]], [[[6], [8]], [[14], [16]]]] ``` (4) For the following input of shape `[2, 2, 4, 1]`, block_shape = `[2, 2]`, and paddings = `[[0, 0], [2, 0]]`: ``` x = [[[[1], [2], [3], [4]], [[5], [6], [7], [8]]], [[[9], [10], [11], [12]], [[13], [14], [15], [16]]]] ``` The output tensor has shape `[8, 1, 3, 1]` and value: ``` x = [[[[0], [1], [3]]], [[[0], [9], [11]]], [[[0], [2], [4]]], [[[0], [10], [12]]], [[[0], [5], [7]]], [[[0], [13], [15]]], [[[0], [6], [8]]], [[[0], [14], [16]]]] ``` Among others, this operation is useful for reducing atrous convolution into regular convolution.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor space_to_depth(ValueTuple<PythonClassContainer, PythonClassContainer> input, int block_size, string name, string data_format)
SpaceToDepth for tensors of type T. Rearranges blocks of spatial data, into depth. More specifically,
this op outputs a copy of the input tensor where values from the `height`
and `width` dimensions are moved to the `depth` dimension.
The attr `block_size` indicates the input block size. * Non-overlapping blocks of size `block_size x block size` are rearranged
into depth at each location.
* The depth of the output tensor is `block_size * block_size * input_depth`.
* The Y, X coordinates within each block of the input become the high order
component of the output channel index.
* The input tensor's height and width must be divisible by block_size. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,oY,bY,oX,bX,iC (where n=batch index, oX, oY means X or Y coordinates
within the output image, bX, bY means coordinates
within the input block, iC means input channels).
The output would be a transpose to the following layout:
n,oY,oX,bY,bX,iC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 2, 2, 1]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1], [2]],
[[3], [4]]]]
``` This operation will output a tensor of shape `[1, 1, 1, 4]`: ```
[[[[1, 2, 3, 4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[2, 2, 1]`,
the corresponding output will have a single element (i.e. width and height are
both 1) and will have a depth of 4 channels (1 * block_size * block_size).
The output element shape is `[1, 1, 4]`. For an input tensor with larger depth, here of shape `[1, 2, 2, 3]`, e.g. ```
x = [[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]]
``` This operation, for block_size of 2, will return the following tensor of shape
`[1, 1, 1, 12]` ```
[[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` Similarly, for the following input of shape `[1 4 4 1]`, and a block size of 2: ```
x = [[[[1], [2], [5], [6]],
[[3], [4], [7], [8]],
[[9], [10], [13], [14]],
[[11], [12], [15], [16]]]]
``` the operator will return the following tensor of shape `[1 2 2 4]`: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
```
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>input - A `Tensor`.
-
intblock_size - An `int` that is `>= 2`. The size of the spatial block.
-
stringname - A name for the operation (optional).
-
stringdata_format - An optional `string` from: `"NHWC", "NCHW", "NCHW_VECT_C"`. Defaults to `"NHWC"`.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor space_to_depth(IndexedSlices input, int block_size, string name, string data_format)
SpaceToDepth for tensors of type T. Rearranges blocks of spatial data, into depth. More specifically,
this op outputs a copy of the input tensor where values from the `height`
and `width` dimensions are moved to the `depth` dimension.
The attr `block_size` indicates the input block size. * Non-overlapping blocks of size `block_size x block size` are rearranged
into depth at each location.
* The depth of the output tensor is `block_size * block_size * input_depth`.
* The Y, X coordinates within each block of the input become the high order
component of the output channel index.
* The input tensor's height and width must be divisible by block_size. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,oY,bY,oX,bX,iC (where n=batch index, oX, oY means X or Y coordinates
within the output image, bX, bY means coordinates
within the input block, iC means input channels).
The output would be a transpose to the following layout:
n,oY,oX,bY,bX,iC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 2, 2, 1]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1], [2]],
[[3], [4]]]]
``` This operation will output a tensor of shape `[1, 1, 1, 4]`: ```
[[[[1, 2, 3, 4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[2, 2, 1]`,
the corresponding output will have a single element (i.e. width and height are
both 1) and will have a depth of 4 channels (1 * block_size * block_size).
The output element shape is `[1, 1, 4]`. For an input tensor with larger depth, here of shape `[1, 2, 2, 3]`, e.g. ```
x = [[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]]
``` This operation, for block_size of 2, will return the following tensor of shape
`[1, 1, 1, 12]` ```
[[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` Similarly, for the following input of shape `[1 4 4 1]`, and a block size of 2: ```
x = [[[[1], [2], [5], [6]],
[[3], [4], [7], [8]],
[[9], [10], [13], [14]],
[[11], [12], [15], [16]]]]
``` the operator will return the following tensor of shape `[1 2 2 4]`: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
```
Parameters
-
IndexedSlicesinput - A `Tensor`.
-
intblock_size - An `int` that is `>= 2`. The size of the spatial block.
-
stringname - A name for the operation (optional).
-
stringdata_format - An optional `string` from: `"NHWC", "NCHW", "NCHW_VECT_C"`. Defaults to `"NHWC"`.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor space_to_depth(IEnumerable<object> input, int block_size, string name, string data_format)
SpaceToDepth for tensors of type T. Rearranges blocks of spatial data, into depth. More specifically,
this op outputs a copy of the input tensor where values from the `height`
and `width` dimensions are moved to the `depth` dimension.
The attr `block_size` indicates the input block size. * Non-overlapping blocks of size `block_size x block size` are rearranged
into depth at each location.
* The depth of the output tensor is `block_size * block_size * input_depth`.
* The Y, X coordinates within each block of the input become the high order
component of the output channel index.
* The input tensor's height and width must be divisible by block_size. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,oY,bY,oX,bX,iC (where n=batch index, oX, oY means X or Y coordinates
within the output image, bX, bY means coordinates
within the input block, iC means input channels).
The output would be a transpose to the following layout:
n,oY,oX,bY,bX,iC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 2, 2, 1]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1], [2]],
[[3], [4]]]]
``` This operation will output a tensor of shape `[1, 1, 1, 4]`: ```
[[[[1, 2, 3, 4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[2, 2, 1]`,
the corresponding output will have a single element (i.e. width and height are
both 1) and will have a depth of 4 channels (1 * block_size * block_size).
The output element shape is `[1, 1, 4]`. For an input tensor with larger depth, here of shape `[1, 2, 2, 3]`, e.g. ```
x = [[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]]
``` This operation, for block_size of 2, will return the following tensor of shape
`[1, 1, 1, 12]` ```
[[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` Similarly, for the following input of shape `[1 4 4 1]`, and a block size of 2: ```
x = [[[[1], [2], [5], [6]],
[[3], [4], [7], [8]],
[[9], [10], [13], [14]],
[[11], [12], [15], [16]]]]
``` the operator will return the following tensor of shape `[1 2 2 4]`: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
```
Parameters
-
IEnumerable<object>input - A `Tensor`.
-
intblock_size - An `int` that is `>= 2`. The size of the spatial block.
-
stringname - A name for the operation (optional).
-
stringdata_format - An optional `string` from: `"NHWC", "NCHW", "NCHW_VECT_C"`. Defaults to `"NHWC"`.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor space_to_depth(IGraphNodeBase input, int block_size, string name, string data_format)
SpaceToDepth for tensors of type T. Rearranges blocks of spatial data, into depth. More specifically,
this op outputs a copy of the input tensor where values from the `height`
and `width` dimensions are moved to the `depth` dimension.
The attr `block_size` indicates the input block size. * Non-overlapping blocks of size `block_size x block size` are rearranged
into depth at each location.
* The depth of the output tensor is `block_size * block_size * input_depth`.
* The Y, X coordinates within each block of the input become the high order
component of the output channel index.
* The input tensor's height and width must be divisible by block_size. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,oY,bY,oX,bX,iC (where n=batch index, oX, oY means X or Y coordinates
within the output image, bX, bY means coordinates
within the input block, iC means input channels).
The output would be a transpose to the following layout:
n,oY,oX,bY,bX,iC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 2, 2, 1]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1], [2]],
[[3], [4]]]]
``` This operation will output a tensor of shape `[1, 1, 1, 4]`: ```
[[[[1, 2, 3, 4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[2, 2, 1]`,
the corresponding output will have a single element (i.e. width and height are
both 1) and will have a depth of 4 channels (1 * block_size * block_size).
The output element shape is `[1, 1, 4]`. For an input tensor with larger depth, here of shape `[1, 2, 2, 3]`, e.g. ```
x = [[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]]
``` This operation, for block_size of 2, will return the following tensor of shape
`[1, 1, 1, 12]` ```
[[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` Similarly, for the following input of shape `[1 4 4 1]`, and a block size of 2: ```
x = [[[[1], [2], [5], [6]],
[[3], [4], [7], [8]],
[[9], [10], [13], [14]],
[[11], [12], [15], [16]]]]
``` the operator will return the following tensor of shape `[1 2 2 4]`: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
```
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
intblock_size - An `int` that is `>= 2`. The size of the spatial block.
-
stringname - A name for the operation (optional).
-
stringdata_format - An optional `string` from: `"NHWC", "NCHW", "NCHW_VECT_C"`. Defaults to `"NHWC"`.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object space_to_depth_dyn(object input, object block_size, object name, ImplicitContainer<T> data_format)
SpaceToDepth for tensors of type T. Rearranges blocks of spatial data, into depth. More specifically,
this op outputs a copy of the input tensor where values from the `height`
and `width` dimensions are moved to the `depth` dimension.
The attr `block_size` indicates the input block size. * Non-overlapping blocks of size `block_size x block size` are rearranged
into depth at each location.
* The depth of the output tensor is `block_size * block_size * input_depth`.
* The Y, X coordinates within each block of the input become the high order
component of the output channel index.
* The input tensor's height and width must be divisible by block_size. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,oY,bY,oX,bX,iC (where n=batch index, oX, oY means X or Y coordinates
within the output image, bX, bY means coordinates
within the input block, iC means input channels).
The output would be a transpose to the following layout:
n,oY,oX,bY,bX,iC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 2, 2, 1]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1], [2]],
[[3], [4]]]]
``` This operation will output a tensor of shape `[1, 1, 1, 4]`: ```
[[[[1, 2, 3, 4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[2, 2, 1]`,
the corresponding output will have a single element (i.e. width and height are
both 1) and will have a depth of 4 channels (1 * block_size * block_size).
The output element shape is `[1, 1, 4]`. For an input tensor with larger depth, here of shape `[1, 2, 2, 3]`, e.g. ```
x = [[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]]
``` This operation, for block_size of 2, will return the following tensor of shape
`[1, 1, 1, 12]` ```
[[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` Similarly, for the following input of shape `[1 4 4 1]`, and a block size of 2: ```
x = [[[[1], [2], [5], [6]],
[[3], [4], [7], [8]],
[[9], [10], [13], [14]],
[[11], [12], [15], [16]]]]
``` the operator will return the following tensor of shape `[1 2 2 4]`: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
```
Parameters
-
objectinput - A `Tensor`.
-
objectblock_size - An `int` that is `>= 2`. The size of the spatial block.
-
objectname - A name for the operation (optional).
-
ImplicitContainer<T>data_format - An optional `string` from: `"NHWC", "NCHW", "NCHW_VECT_C"`. Defaults to `"NHWC"`.
Returns
-
object - A `Tensor`. Has the same type as `input`.
object sparse_add(IGraphNodeBase a, IGraphNodeBase b, Nullable<double> threshold, Nullable<double> thresh)
Adds two tensors, at least one of each is a `SparseTensor`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(thresh)`. They will be removed in a future version.
Instructions for updating:
thresh is deprecated, use threshold instead If one `SparseTensor` and one `Tensor` are passed in, returns a `Tensor`. If
both arguments are `SparseTensor`s, this returns a `SparseTensor`. The order
of arguments does not matter. Use vanilla `tf.add()` for adding two dense
`Tensor`s. The shapes of the two operands must match: broadcasting is not supported. The indices of any input `SparseTensor` are assumed ordered in standard
lexicographic order. If this is not the case, before this step run
`SparseReorder` to restore index ordering. If both arguments are sparse, we perform "clipping" as follows. By default,
if two values sum to zero at some index, the output `SparseTensor` would still
include that particular location in its index, storing a zero in the
corresponding value slot. To override this, callers can specify `thresh`,
indicating that if the sum has a magnitude strictly smaller than `thresh`, its
corresponding value and index would then not be included. In particular,
`thresh == 0.0` (default) means everything is kept and actual thresholding
happens only for a positive value. For example, suppose the logical sum of two sparse operands is (densified): [ 2]
[.1 0]
[ 6 -.2] Then, * `thresh == 0` (the default): all 5 index/value pairs will be returned.
* `thresh == 0.11`: only.1 and 0 will vanish, and the remaining three
index/value pairs will be returned.
* `thresh == 0.21`:.1, 0, and -.2 will vanish.
Parameters
-
IGraphNodeBasea - The first operand; `SparseTensor` or `Tensor`.
-
IGraphNodeBaseb - The second operand; `SparseTensor` or `Tensor`. At least one operand must be sparse.
-
Nullable<double>threshold - An optional 0-D `Tensor` (defaults to `0`). The magnitude threshold that determines if an output value/index pair takes space. Its dtype should match that of the values if they are real; if the latter are complex64/complex128, then the dtype should be float32/float64, correspondingly.
-
Nullable<double>thresh - Deprecated alias for `threshold`.
Returns
-
object - A `SparseTensor` or a `Tensor`, representing the sum.
object sparse_add(object a, object b, Nullable<double> threshold, Nullable<double> thresh)
Adds two tensors, at least one of each is a `SparseTensor`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(thresh)`. They will be removed in a future version.
Instructions for updating:
thresh is deprecated, use threshold instead If one `SparseTensor` and one `Tensor` are passed in, returns a `Tensor`. If
both arguments are `SparseTensor`s, this returns a `SparseTensor`. The order
of arguments does not matter. Use vanilla `tf.add()` for adding two dense
`Tensor`s. The shapes of the two operands must match: broadcasting is not supported. The indices of any input `SparseTensor` are assumed ordered in standard
lexicographic order. If this is not the case, before this step run
`SparseReorder` to restore index ordering. If both arguments are sparse, we perform "clipping" as follows. By default,
if two values sum to zero at some index, the output `SparseTensor` would still
include that particular location in its index, storing a zero in the
corresponding value slot. To override this, callers can specify `thresh`,
indicating that if the sum has a magnitude strictly smaller than `thresh`, its
corresponding value and index would then not be included. In particular,
`thresh == 0.0` (default) means everything is kept and actual thresholding
happens only for a positive value. For example, suppose the logical sum of two sparse operands is (densified): [ 2]
[.1 0]
[ 6 -.2] Then, * `thresh == 0` (the default): all 5 index/value pairs will be returned.
* `thresh == 0.11`: only.1 and 0 will vanish, and the remaining three
index/value pairs will be returned.
* `thresh == 0.21`:.1, 0, and -.2 will vanish.
Parameters
-
objecta - The first operand; `SparseTensor` or `Tensor`.
-
objectb - The second operand; `SparseTensor` or `Tensor`. At least one operand must be sparse.
-
Nullable<double>threshold - An optional 0-D `Tensor` (defaults to `0`). The magnitude threshold that determines if an output value/index pair takes space. Its dtype should match that of the values if they are real; if the latter are complex64/complex128, then the dtype should be float32/float64, correspondingly.
-
Nullable<double>thresh - Deprecated alias for `threshold`.
Returns
-
object - A `SparseTensor` or a `Tensor`, representing the sum.
object sparse_add(object a, IGraphNodeBase b, Nullable<double> threshold, Nullable<double> thresh)
Adds two tensors, at least one of each is a `SparseTensor`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(thresh)`. They will be removed in a future version.
Instructions for updating:
thresh is deprecated, use threshold instead If one `SparseTensor` and one `Tensor` are passed in, returns a `Tensor`. If
both arguments are `SparseTensor`s, this returns a `SparseTensor`. The order
of arguments does not matter. Use vanilla `tf.add()` for adding two dense
`Tensor`s. The shapes of the two operands must match: broadcasting is not supported. The indices of any input `SparseTensor` are assumed ordered in standard
lexicographic order. If this is not the case, before this step run
`SparseReorder` to restore index ordering. If both arguments are sparse, we perform "clipping" as follows. By default,
if two values sum to zero at some index, the output `SparseTensor` would still
include that particular location in its index, storing a zero in the
corresponding value slot. To override this, callers can specify `thresh`,
indicating that if the sum has a magnitude strictly smaller than `thresh`, its
corresponding value and index would then not be included. In particular,
`thresh == 0.0` (default) means everything is kept and actual thresholding
happens only for a positive value. For example, suppose the logical sum of two sparse operands is (densified): [ 2]
[.1 0]
[ 6 -.2] Then, * `thresh == 0` (the default): all 5 index/value pairs will be returned.
* `thresh == 0.11`: only.1 and 0 will vanish, and the remaining three
index/value pairs will be returned.
* `thresh == 0.21`:.1, 0, and -.2 will vanish.
Parameters
-
objecta - The first operand; `SparseTensor` or `Tensor`.
-
IGraphNodeBaseb - The second operand; `SparseTensor` or `Tensor`. At least one operand must be sparse.
-
Nullable<double>threshold - An optional 0-D `Tensor` (defaults to `0`). The magnitude threshold that determines if an output value/index pair takes space. Its dtype should match that of the values if they are real; if the latter are complex64/complex128, then the dtype should be float32/float64, correspondingly.
-
Nullable<double>thresh - Deprecated alias for `threshold`.
Returns
-
object - A `SparseTensor` or a `Tensor`, representing the sum.
object sparse_add(IGraphNodeBase a, object b, Nullable<double> threshold, Nullable<double> thresh)
Adds two tensors, at least one of each is a `SparseTensor`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(thresh)`. They will be removed in a future version.
Instructions for updating:
thresh is deprecated, use threshold instead If one `SparseTensor` and one `Tensor` are passed in, returns a `Tensor`. If
both arguments are `SparseTensor`s, this returns a `SparseTensor`. The order
of arguments does not matter. Use vanilla `tf.add()` for adding two dense
`Tensor`s. The shapes of the two operands must match: broadcasting is not supported. The indices of any input `SparseTensor` are assumed ordered in standard
lexicographic order. If this is not the case, before this step run
`SparseReorder` to restore index ordering. If both arguments are sparse, we perform "clipping" as follows. By default,
if two values sum to zero at some index, the output `SparseTensor` would still
include that particular location in its index, storing a zero in the
corresponding value slot. To override this, callers can specify `thresh`,
indicating that if the sum has a magnitude strictly smaller than `thresh`, its
corresponding value and index would then not be included. In particular,
`thresh == 0.0` (default) means everything is kept and actual thresholding
happens only for a positive value. For example, suppose the logical sum of two sparse operands is (densified): [ 2]
[.1 0]
[ 6 -.2] Then, * `thresh == 0` (the default): all 5 index/value pairs will be returned.
* `thresh == 0.11`: only.1 and 0 will vanish, and the remaining three
index/value pairs will be returned.
* `thresh == 0.21`:.1, 0, and -.2 will vanish.
Parameters
-
IGraphNodeBasea - The first operand; `SparseTensor` or `Tensor`.
-
objectb - The second operand; `SparseTensor` or `Tensor`. At least one operand must be sparse.
-
Nullable<double>threshold - An optional 0-D `Tensor` (defaults to `0`). The magnitude threshold that determines if an output value/index pair takes space. Its dtype should match that of the values if they are real; if the latter are complex64/complex128, then the dtype should be float32/float64, correspondingly.
-
Nullable<double>thresh - Deprecated alias for `threshold`.
Returns
-
object - A `SparseTensor` or a `Tensor`, representing the sum.
object sparse_add_dyn(object a, object b, object threshold, object thresh)
Adds two tensors, at least one of each is a `SparseTensor`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(thresh)`. They will be removed in a future version.
Instructions for updating:
thresh is deprecated, use threshold instead If one `SparseTensor` and one `Tensor` are passed in, returns a `Tensor`. If
both arguments are `SparseTensor`s, this returns a `SparseTensor`. The order
of arguments does not matter. Use vanilla `tf.add()` for adding two dense
`Tensor`s. The shapes of the two operands must match: broadcasting is not supported. The indices of any input `SparseTensor` are assumed ordered in standard
lexicographic order. If this is not the case, before this step run
`SparseReorder` to restore index ordering. If both arguments are sparse, we perform "clipping" as follows. By default,
if two values sum to zero at some index, the output `SparseTensor` would still
include that particular location in its index, storing a zero in the
corresponding value slot. To override this, callers can specify `thresh`,
indicating that if the sum has a magnitude strictly smaller than `thresh`, its
corresponding value and index would then not be included. In particular,
`thresh == 0.0` (default) means everything is kept and actual thresholding
happens only for a positive value. For example, suppose the logical sum of two sparse operands is (densified): [ 2]
[.1 0]
[ 6 -.2] Then, * `thresh == 0` (the default): all 5 index/value pairs will be returned.
* `thresh == 0.11`: only.1 and 0 will vanish, and the remaining three
index/value pairs will be returned.
* `thresh == 0.21`:.1, 0, and -.2 will vanish.
Parameters
-
objecta - The first operand; `SparseTensor` or `Tensor`.
-
objectb - The second operand; `SparseTensor` or `Tensor`. At least one operand must be sparse.
-
objectthreshold - An optional 0-D `Tensor` (defaults to `0`). The magnitude threshold that determines if an output value/index pair takes space. Its dtype should match that of the values if they are real; if the latter are complex64/complex128, then the dtype should be float32/float64, correspondingly.
-
objectthresh - Deprecated alias for `threshold`.
Returns
-
object - A `SparseTensor` or a `Tensor`, representing the sum.
SparseTensor sparse_concat(int axis, IEnumerable<object> sp_inputs, PythonFunctionContainer name, bool expand_nonconcat_dim, object concat_dim, object expand_nonconcat_dims)
Concatenates a list of `SparseTensor` along the specified dimension. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(concat_dim)`. They will be removed in a future version.
Instructions for updating:
concat_dim is deprecated, use axis instead Concatenation is with respect to the dense versions of each sparse input.
It is assumed that each inputs is a `SparseTensor` whose elements are ordered
along increasing dimension number. If expand_nonconcat_dim is False, all inputs' shapes must match, except for
the concat dimension. If expand_nonconcat_dim is True, then inputs' shapes are
allowed to vary among all inputs. The `indices`, `values`, and `shapes` lists must have the same length. If expand_nonconcat_dim is False, then the output shape is identical to the
inputs', except along the concat dimension, where it is the sum of the inputs'
sizes along that dimension. If expand_nonconcat_dim is True, then the output shape along the non-concat
dimensions will be expand to be the largest among all inputs, and it is the
sum of the inputs sizes along the concat dimension. The output elements will be resorted to preserve the sort order along
increasing dimension number. This op runs in `O(M log M)` time, where `M` is the total number of non-empty
values across all inputs. This is due to the need for an internal sort in
order to concatenate efficiently across an arbitrary dimension. For example, if `axis = 1` and the inputs are sp_inputs[0]: shape = [2, 3]
[0, 2]: "a"
[1, 0]: "b"
[1, 1]: "c" sp_inputs[1]: shape = [2, 4]
[0, 1]: "d"
[0, 2]: "e" then the output will be shape = [2, 7]
[0, 2]: "a"
[0, 4]: "d"
[0, 5]: "e"
[1, 0]: "b"
[1, 1]: "c" Graphically this is equivalent to doing [ a] concat [ d e ] = [ a d e ]
[b c ] [ ] [b c ] Another example, if 'axis = 1' and the inputs are sp_inputs[0]: shape = [3, 3]
[0, 2]: "a"
[1, 0]: "b"
[2, 1]: "c" sp_inputs[1]: shape = [2, 4]
[0, 1]: "d"
[0, 2]: "e" if expand_nonconcat_dim = False, this will result in an error. But if
expand_nonconcat_dim = True, this will result in: shape = [3, 7]
[0, 2]: "a"
[0, 4]: "d"
[0, 5]: "e"
[1, 0]: "b"
[2, 1]: "c" Graphically this is equivalent to doing [ a] concat [ d e ] = [ a d e ]
[b ] [ ] [b ]
[ c ] [ c ]
Parameters
-
intaxis - Dimension to concatenate along. Must be in range [-rank, rank), where rank is the number of dimensions in each input `SparseTensor`.
-
IEnumerable<object>sp_inputs - List of `SparseTensor` to concatenate.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional).
-
boolexpand_nonconcat_dim - Whether to allow the expansion in the non-concat dimensions. Defaulted to False.
-
objectconcat_dim - The old (deprecated) name for axis.
-
objectexpand_nonconcat_dims - alias for expand_nonconcat_dim
Returns
-
SparseTensor - A `SparseTensor` with the concatenated output.
SparseTensor sparse_concat(int axis, IEnumerable<object> sp_inputs, string name, bool expand_nonconcat_dim, object concat_dim, object expand_nonconcat_dims)
Concatenates a list of `SparseTensor` along the specified dimension. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(concat_dim)`. They will be removed in a future version.
Instructions for updating:
concat_dim is deprecated, use axis instead Concatenation is with respect to the dense versions of each sparse input.
It is assumed that each inputs is a `SparseTensor` whose elements are ordered
along increasing dimension number. If expand_nonconcat_dim is False, all inputs' shapes must match, except for
the concat dimension. If expand_nonconcat_dim is True, then inputs' shapes are
allowed to vary among all inputs. The `indices`, `values`, and `shapes` lists must have the same length. If expand_nonconcat_dim is False, then the output shape is identical to the
inputs', except along the concat dimension, where it is the sum of the inputs'
sizes along that dimension. If expand_nonconcat_dim is True, then the output shape along the non-concat
dimensions will be expand to be the largest among all inputs, and it is the
sum of the inputs sizes along the concat dimension. The output elements will be resorted to preserve the sort order along
increasing dimension number. This op runs in `O(M log M)` time, where `M` is the total number of non-empty
values across all inputs. This is due to the need for an internal sort in
order to concatenate efficiently across an arbitrary dimension. For example, if `axis = 1` and the inputs are sp_inputs[0]: shape = [2, 3]
[0, 2]: "a"
[1, 0]: "b"
[1, 1]: "c" sp_inputs[1]: shape = [2, 4]
[0, 1]: "d"
[0, 2]: "e" then the output will be shape = [2, 7]
[0, 2]: "a"
[0, 4]: "d"
[0, 5]: "e"
[1, 0]: "b"
[1, 1]: "c" Graphically this is equivalent to doing [ a] concat [ d e ] = [ a d e ]
[b c ] [ ] [b c ] Another example, if 'axis = 1' and the inputs are sp_inputs[0]: shape = [3, 3]
[0, 2]: "a"
[1, 0]: "b"
[2, 1]: "c" sp_inputs[1]: shape = [2, 4]
[0, 1]: "d"
[0, 2]: "e" if expand_nonconcat_dim = False, this will result in an error. But if
expand_nonconcat_dim = True, this will result in: shape = [3, 7]
[0, 2]: "a"
[0, 4]: "d"
[0, 5]: "e"
[1, 0]: "b"
[2, 1]: "c" Graphically this is equivalent to doing [ a] concat [ d e ] = [ a d e ]
[b ] [ ] [b ]
[ c ] [ c ]
Parameters
-
intaxis - Dimension to concatenate along. Must be in range [-rank, rank), where rank is the number of dimensions in each input `SparseTensor`.
-
IEnumerable<object>sp_inputs - List of `SparseTensor` to concatenate.
-
stringname - A name prefix for the returned tensors (optional).
-
boolexpand_nonconcat_dim - Whether to allow the expansion in the non-concat dimensions. Defaulted to False.
-
objectconcat_dim - The old (deprecated) name for axis.
-
objectexpand_nonconcat_dims - alias for expand_nonconcat_dim
Returns
-
SparseTensor - A `SparseTensor` with the concatenated output.
object sparse_concat_dyn(object axis, object sp_inputs, object name, ImplicitContainer<T> expand_nonconcat_dim, object concat_dim, object expand_nonconcat_dims)
Concatenates a list of `SparseTensor` along the specified dimension. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(concat_dim)`. They will be removed in a future version.
Instructions for updating:
concat_dim is deprecated, use axis instead Concatenation is with respect to the dense versions of each sparse input.
It is assumed that each inputs is a `SparseTensor` whose elements are ordered
along increasing dimension number. If expand_nonconcat_dim is False, all inputs' shapes must match, except for
the concat dimension. If expand_nonconcat_dim is True, then inputs' shapes are
allowed to vary among all inputs. The `indices`, `values`, and `shapes` lists must have the same length. If expand_nonconcat_dim is False, then the output shape is identical to the
inputs', except along the concat dimension, where it is the sum of the inputs'
sizes along that dimension. If expand_nonconcat_dim is True, then the output shape along the non-concat
dimensions will be expand to be the largest among all inputs, and it is the
sum of the inputs sizes along the concat dimension. The output elements will be resorted to preserve the sort order along
increasing dimension number. This op runs in `O(M log M)` time, where `M` is the total number of non-empty
values across all inputs. This is due to the need for an internal sort in
order to concatenate efficiently across an arbitrary dimension. For example, if `axis = 1` and the inputs are sp_inputs[0]: shape = [2, 3]
[0, 2]: "a"
[1, 0]: "b"
[1, 1]: "c" sp_inputs[1]: shape = [2, 4]
[0, 1]: "d"
[0, 2]: "e" then the output will be shape = [2, 7]
[0, 2]: "a"
[0, 4]: "d"
[0, 5]: "e"
[1, 0]: "b"
[1, 1]: "c" Graphically this is equivalent to doing [ a] concat [ d e ] = [ a d e ]
[b c ] [ ] [b c ] Another example, if 'axis = 1' and the inputs are sp_inputs[0]: shape = [3, 3]
[0, 2]: "a"
[1, 0]: "b"
[2, 1]: "c" sp_inputs[1]: shape = [2, 4]
[0, 1]: "d"
[0, 2]: "e" if expand_nonconcat_dim = False, this will result in an error. But if
expand_nonconcat_dim = True, this will result in: shape = [3, 7]
[0, 2]: "a"
[0, 4]: "d"
[0, 5]: "e"
[1, 0]: "b"
[2, 1]: "c" Graphically this is equivalent to doing [ a] concat [ d e ] = [ a d e ]
[b ] [ ] [b ]
[ c ] [ c ]
Parameters
-
objectaxis - Dimension to concatenate along. Must be in range [-rank, rank), where rank is the number of dimensions in each input `SparseTensor`.
-
objectsp_inputs - List of `SparseTensor` to concatenate.
-
objectname - A name prefix for the returned tensors (optional).
-
ImplicitContainer<T>expand_nonconcat_dim - Whether to allow the expansion in the non-concat dimensions. Defaulted to False.
-
objectconcat_dim - The old (deprecated) name for axis.
-
objectexpand_nonconcat_dims - alias for expand_nonconcat_dim
Returns
-
object - A `SparseTensor` with the concatenated output.
object sparse_feature_cross(IEnumerable<object> indices, IEnumerable<object> values, IEnumerable<object> shapes, IEnumerable<object> dense, bool hashed_output, int num_buckets, DType out_type, DType internal_type, string name)
object sparse_feature_cross(IEnumerable<object> indices, IEnumerable<object> values, IEnumerable<object> shapes, IEnumerable<object> dense, bool hashed_output, IEnumerable<object> num_buckets, DType out_type, DType internal_type, string name)
object sparse_feature_cross_dyn(object indices, object values, object shapes, object dense, object hashed_output, object num_buckets, object out_type, object internal_type, object name)
object sparse_feature_cross_v2(IEnumerable<object> indices, IEnumerable<object> values, IEnumerable<object> shapes, IEnumerable<object> dense, bool hashed_output, int num_buckets, Nullable<int> hash_key, DType out_type, DType internal_type, string name)
object sparse_feature_cross_v2(IEnumerable<object> indices, IEnumerable<object> values, IEnumerable<object> shapes, IEnumerable<object> dense, bool hashed_output, IEnumerable<object> num_buckets, Nullable<int> hash_key, DType out_type, DType internal_type, string name)
object sparse_feature_cross_v2_dyn(object indices, object values, object shapes, object dense, object hashed_output, object num_buckets, object hash_key, object out_type, object internal_type, object name)
ValueTuple<SparseTensor, object> sparse_fill_empty_rows(object sp_input, int default_value, string name)
Fills empty rows in the input 2-D `SparseTensor` with a default value. This op adds entries with the specified `default_value` at index
`[row, 0]` for any row in the input that does not already have a value. For example, suppose `sp_input` has shape `[5, 6]` and non-empty values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d Rows 1 and 4 are empty, so the output will be of shape `[5, 6]` with values: [0, 1]: a
[0, 3]: b
[1, 0]: default_value
[2, 0]: c
[3, 1]: d
[4, 0]: default_value Note that the input may have empty columns at the end, with no effect on
this op. The output `SparseTensor` will be in row-major order and will have the
same shape as the input. This op also returns an indicator vector such that empty_row_indicator[i] = True iff row i was an empty row.
Parameters
-
objectsp_input - A `SparseTensor` with shape `[N, M]`.
-
intdefault_value - The value to fill for empty rows, with the same type as `sp_input.`
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
ValueTuple<SparseTensor, object>
ValueTuple<SparseTensor, object> sparse_fill_empty_rows(object sp_input, double default_value, string name)
Fills empty rows in the input 2-D `SparseTensor` with a default value. This op adds entries with the specified `default_value` at index
`[row, 0]` for any row in the input that does not already have a value. For example, suppose `sp_input` has shape `[5, 6]` and non-empty values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d Rows 1 and 4 are empty, so the output will be of shape `[5, 6]` with values: [0, 1]: a
[0, 3]: b
[1, 0]: default_value
[2, 0]: c
[3, 1]: d
[4, 0]: default_value Note that the input may have empty columns at the end, with no effect on
this op. The output `SparseTensor` will be in row-major order and will have the
same shape as the input. This op also returns an indicator vector such that empty_row_indicator[i] = True iff row i was an empty row.
Parameters
-
objectsp_input - A `SparseTensor` with shape `[N, M]`.
-
doubledefault_value - The value to fill for empty rows, with the same type as `sp_input.`
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
ValueTuple<SparseTensor, object>
ValueTuple<SparseTensor, object> sparse_fill_empty_rows(object sp_input, string default_value, string name)
Fills empty rows in the input 2-D `SparseTensor` with a default value. This op adds entries with the specified `default_value` at index
`[row, 0]` for any row in the input that does not already have a value. For example, suppose `sp_input` has shape `[5, 6]` and non-empty values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d Rows 1 and 4 are empty, so the output will be of shape `[5, 6]` with values: [0, 1]: a
[0, 3]: b
[1, 0]: default_value
[2, 0]: c
[3, 1]: d
[4, 0]: default_value Note that the input may have empty columns at the end, with no effect on
this op. The output `SparseTensor` will be in row-major order and will have the
same shape as the input. This op also returns an indicator vector such that empty_row_indicator[i] = True iff row i was an empty row.
Parameters
-
objectsp_input - A `SparseTensor` with shape `[N, M]`.
-
stringdefault_value - The value to fill for empty rows, with the same type as `sp_input.`
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
ValueTuple<SparseTensor, object>
ValueTuple<SparseTensor, object> sparse_fill_empty_rows(IGraphNodeBase sp_input, string default_value, string name)
Fills empty rows in the input 2-D `SparseTensor` with a default value. This op adds entries with the specified `default_value` at index
`[row, 0]` for any row in the input that does not already have a value. For example, suppose `sp_input` has shape `[5, 6]` and non-empty values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d Rows 1 and 4 are empty, so the output will be of shape `[5, 6]` with values: [0, 1]: a
[0, 3]: b
[1, 0]: default_value
[2, 0]: c
[3, 1]: d
[4, 0]: default_value Note that the input may have empty columns at the end, with no effect on
this op. The output `SparseTensor` will be in row-major order and will have the
same shape as the input. This op also returns an indicator vector such that empty_row_indicator[i] = True iff row i was an empty row.
Parameters
-
IGraphNodeBasesp_input - A `SparseTensor` with shape `[N, M]`.
-
stringdefault_value - The value to fill for empty rows, with the same type as `sp_input.`
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
ValueTuple<SparseTensor, object>
ValueTuple<SparseTensor, object> sparse_fill_empty_rows(IGraphNodeBase sp_input, IGraphNodeBase default_value, string name)
Fills empty rows in the input 2-D `SparseTensor` with a default value. This op adds entries with the specified `default_value` at index
`[row, 0]` for any row in the input that does not already have a value. For example, suppose `sp_input` has shape `[5, 6]` and non-empty values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d Rows 1 and 4 are empty, so the output will be of shape `[5, 6]` with values: [0, 1]: a
[0, 3]: b
[1, 0]: default_value
[2, 0]: c
[3, 1]: d
[4, 0]: default_value Note that the input may have empty columns at the end, with no effect on
this op. The output `SparseTensor` will be in row-major order and will have the
same shape as the input. This op also returns an indicator vector such that empty_row_indicator[i] = True iff row i was an empty row.
Parameters
-
IGraphNodeBasesp_input - A `SparseTensor` with shape `[N, M]`.
-
IGraphNodeBasedefault_value - The value to fill for empty rows, with the same type as `sp_input.`
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
ValueTuple<SparseTensor, object>
ValueTuple<SparseTensor, object> sparse_fill_empty_rows(IGraphNodeBase sp_input, int default_value, string name)
Fills empty rows in the input 2-D `SparseTensor` with a default value. This op adds entries with the specified `default_value` at index
`[row, 0]` for any row in the input that does not already have a value. For example, suppose `sp_input` has shape `[5, 6]` and non-empty values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d Rows 1 and 4 are empty, so the output will be of shape `[5, 6]` with values: [0, 1]: a
[0, 3]: b
[1, 0]: default_value
[2, 0]: c
[3, 1]: d
[4, 0]: default_value Note that the input may have empty columns at the end, with no effect on
this op. The output `SparseTensor` will be in row-major order and will have the
same shape as the input. This op also returns an indicator vector such that empty_row_indicator[i] = True iff row i was an empty row.
Parameters
-
IGraphNodeBasesp_input - A `SparseTensor` with shape `[N, M]`.
-
intdefault_value - The value to fill for empty rows, with the same type as `sp_input.`
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
ValueTuple<SparseTensor, object>
ValueTuple<SparseTensor, object> sparse_fill_empty_rows(IGraphNodeBase sp_input, double default_value, string name)
Fills empty rows in the input 2-D `SparseTensor` with a default value. This op adds entries with the specified `default_value` at index
`[row, 0]` for any row in the input that does not already have a value. For example, suppose `sp_input` has shape `[5, 6]` and non-empty values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d Rows 1 and 4 are empty, so the output will be of shape `[5, 6]` with values: [0, 1]: a
[0, 3]: b
[1, 0]: default_value
[2, 0]: c
[3, 1]: d
[4, 0]: default_value Note that the input may have empty columns at the end, with no effect on
this op. The output `SparseTensor` will be in row-major order and will have the
same shape as the input. This op also returns an indicator vector such that empty_row_indicator[i] = True iff row i was an empty row.
Parameters
-
IGraphNodeBasesp_input - A `SparseTensor` with shape `[N, M]`.
-
doubledefault_value - The value to fill for empty rows, with the same type as `sp_input.`
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
ValueTuple<SparseTensor, object>
ValueTuple<SparseTensor, object> sparse_fill_empty_rows(object sp_input, IGraphNodeBase default_value, string name)
Fills empty rows in the input 2-D `SparseTensor` with a default value. This op adds entries with the specified `default_value` at index
`[row, 0]` for any row in the input that does not already have a value. For example, suppose `sp_input` has shape `[5, 6]` and non-empty values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d Rows 1 and 4 are empty, so the output will be of shape `[5, 6]` with values: [0, 1]: a
[0, 3]: b
[1, 0]: default_value
[2, 0]: c
[3, 1]: d
[4, 0]: default_value Note that the input may have empty columns at the end, with no effect on
this op. The output `SparseTensor` will be in row-major order and will have the
same shape as the input. This op also returns an indicator vector such that empty_row_indicator[i] = True iff row i was an empty row.
Parameters
-
objectsp_input - A `SparseTensor` with shape `[N, M]`.
-
IGraphNodeBasedefault_value - The value to fill for empty rows, with the same type as `sp_input.`
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
ValueTuple<SparseTensor, object>
object sparse_fill_empty_rows_dyn(object sp_input, object default_value, object name)
Fills empty rows in the input 2-D `SparseTensor` with a default value. This op adds entries with the specified `default_value` at index
`[row, 0]` for any row in the input that does not already have a value. For example, suppose `sp_input` has shape `[5, 6]` and non-empty values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d Rows 1 and 4 are empty, so the output will be of shape `[5, 6]` with values: [0, 1]: a
[0, 3]: b
[1, 0]: default_value
[2, 0]: c
[3, 1]: d
[4, 0]: default_value Note that the input may have empty columns at the end, with no effect on
this op. The output `SparseTensor` will be in row-major order and will have the
same shape as the input. This op also returns an indicator vector such that empty_row_indicator[i] = True iff row i was an empty row.
Parameters
-
objectsp_input - A `SparseTensor` with shape `[N, M]`.
-
objectdefault_value - The value to fill for empty rows, with the same type as `sp_input.`
-
objectname - A name prefix for the returned tensors (optional)
Returns
-
object
IndexedSlices sparse_mask(IndexedSlices a, IGraphNodeBase mask_indices, string name)
Masks elements of `IndexedSlices`. Given an `IndexedSlices` instance `a`, returns another `IndexedSlices` that
contains a subset of the slices of `a`. Only the slices at indices not
specified in `mask_indices` are returned. This is useful when you need to extract a subset of slices in an
`IndexedSlices` object.
Parameters
-
IndexedSlicesa - An `IndexedSlices` instance.
-
IGraphNodeBasemask_indices - Indices of elements to mask.
-
stringname - A name for the operation (optional).
Returns
-
IndexedSlices - The masked `IndexedSlices` instance.
Show Example
# `a` contains slices at indices [12, 26, 37, 45] from a large tensor
# with shape [1000, 10]
a.indices # [12, 26, 37, 45]
tf.shape(a.values) # [4, 10] # `b` will be the subset of `a` slices at its second and third indices, so
# we want to mask its first and last indices (which are at absolute
# indices 12, 45)
b = tf.sparse.mask(a, [12, 45]) b.indices # [26, 37]
tf.shape(b.values) # [2, 10]
object sparse_mask_dyn(object a, object mask_indices, object name)
Masks elements of `IndexedSlices`. Given an `IndexedSlices` instance `a`, returns another `IndexedSlices` that
contains a subset of the slices of `a`. Only the slices at indices not
specified in `mask_indices` are returned. This is useful when you need to extract a subset of slices in an
`IndexedSlices` object.
Parameters
-
objecta - An `IndexedSlices` instance.
-
objectmask_indices - Indices of elements to mask.
-
objectname - A name for the operation (optional).
Returns
-
object - The masked `IndexedSlices` instance.
Show Example
# `a` contains slices at indices [12, 26, 37, 45] from a large tensor
# with shape [1000, 10]
a.indices # [12, 26, 37, 45]
tf.shape(a.values) # [4, 10] # `b` will be the subset of `a` slices at its second and third indices, so
# we want to mask its first and last indices (which are at absolute
# indices 12, 45)
b = tf.sparse.mask(a, [12, 45]) b.indices # [26, 37]
tf.shape(b.values) # [2, 10]
Tensor sparse_matmul(IGraphNodeBase a, IGraphNodeBase b, bool transpose_a, bool transpose_b, bool a_is_sparse, bool b_is_sparse, string name)
Multiply matrix "a" by matrix "b". The inputs must be two-dimensional matrices and the inner dimension of "a" must
match the outer dimension of "b". Both "a" and "b" must be `Tensor`s not
`SparseTensor`s. This op is optimized for the case where at least one of "a" or
"b" is sparse, in the sense that they have a large proportion of zero values.
The breakeven for using this versus a dense matrix multiply on one platform was
30% zero values in the sparse matrix. The gradient computation of this operation will only take advantage of sparsity
in the input gradient when that gradient comes from a Relu.
Parameters
-
IGraphNodeBasea - A `Tensor`. Must be one of the following types: `float32`, `bfloat16`.
-
IGraphNodeBaseb - A `Tensor`. Must be one of the following types: `float32`, `bfloat16`.
-
booltranspose_a - An optional `bool`. Defaults to `False`.
-
booltranspose_b - An optional `bool`. Defaults to `False`.
-
boola_is_sparse - An optional `bool`. Defaults to `False`.
-
boolb_is_sparse - An optional `bool`. Defaults to `False`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float32`.
object sparse_matmul_dyn(object a, object b, ImplicitContainer<T> transpose_a, ImplicitContainer<T> transpose_b, ImplicitContainer<T> a_is_sparse, ImplicitContainer<T> b_is_sparse, object name)
Multiply matrix "a" by matrix "b". The inputs must be two-dimensional matrices and the inner dimension of "a" must
match the outer dimension of "b". Both "a" and "b" must be `Tensor`s not
`SparseTensor`s. This op is optimized for the case where at least one of "a" or
"b" is sparse, in the sense that they have a large proportion of zero values.
The breakeven for using this versus a dense matrix multiply on one platform was
30% zero values in the sparse matrix. The gradient computation of this operation will only take advantage of sparsity
in the input gradient when that gradient comes from a Relu.
Parameters
-
objecta - A `Tensor`. Must be one of the following types: `float32`, `bfloat16`.
-
objectb - A `Tensor`. Must be one of the following types: `float32`, `bfloat16`.
-
ImplicitContainer<T>transpose_a - An optional `bool`. Defaults to `False`.
-
ImplicitContainer<T>transpose_b - An optional `bool`. Defaults to `False`.
-
ImplicitContainer<T>a_is_sparse - An optional `bool`. Defaults to `False`.
-
ImplicitContainer<T>b_is_sparse - An optional `bool`. Defaults to `False`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `float32`.
SparseTensor sparse_maximum(SparseTensor sp_a, SparseTensor sp_b, string name)
Returns the element-wise max of two SparseTensors. Assumes the two SparseTensors have the same shape, i.e., no broadcasting.
Example:
Parameters
-
SparseTensorsp_a - a `SparseTensor` operand whose dtype is real, and indices lexicographically ordered.
-
SparseTensorsp_b - the other `SparseTensor` operand with the same requirements (and the same shape).
-
stringname - optional name of the operation.
Returns
Show Example
sp_zero = sparse_tensor.SparseTensor([[0]], [0], [7])
sp_one = sparse_tensor.SparseTensor([[1]], [1], [7])
res = tf.sparse.maximum(sp_zero, sp_one).eval()
# "res" should be equal to SparseTensor([[0], [1]], [0, 1], [7]).
object sparse_maximum_dyn(object sp_a, object sp_b, object name)
Returns the element-wise max of two SparseTensors. Assumes the two SparseTensors have the same shape, i.e., no broadcasting.
Example:
Parameters
-
objectsp_a - a `SparseTensor` operand whose dtype is real, and indices lexicographically ordered.
-
objectsp_b - the other `SparseTensor` operand with the same requirements (and the same shape).
-
objectname - optional name of the operation.
Returns
-
object
Show Example
sp_zero = sparse_tensor.SparseTensor([[0]], [0], [7])
sp_one = sparse_tensor.SparseTensor([[1]], [1], [7])
res = tf.sparse.maximum(sp_zero, sp_one).eval()
# "res" should be equal to SparseTensor([[0], [1]], [0, 1], [7]).
SparseTensor sparse_merge(IGraphNodeBase sp_ids, object sp_values, int vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
IGraphNodeBasesp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
intvocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(IEnumerable<SparseTensor> sp_ids, object sp_values, int vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
IEnumerable<SparseTensor>sp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
intvocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(IndexedSlices sp_ids, object sp_values, IGraphNodeBase vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
IndexedSlicessp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IGraphNodeBasevocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(IGraphNodeBase sp_ids, object sp_values, IEnumerable<int> vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
IGraphNodeBasesp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IEnumerable<int>vocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(object sp_ids, object sp_values, IGraphNodeBase vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
objectsp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IGraphNodeBasevocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(IndexedSlices sp_ids, object sp_values, int vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
IndexedSlicessp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
intvocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(ndarray sp_ids, object sp_values, int vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
ndarraysp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
intvocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(IEnumerable<SparseTensor> sp_ids, object sp_values, IEnumerable<int> vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
IEnumerable<SparseTensor>sp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IEnumerable<int>vocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(IndexedSlices sp_ids, object sp_values, IEnumerable<int> vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
IndexedSlicessp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IEnumerable<int>vocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(ndarray sp_ids, object sp_values, IEnumerable<int> vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
ndarraysp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IEnumerable<int>vocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(ndarray sp_ids, object sp_values, IGraphNodeBase vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
ndarraysp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IGraphNodeBasevocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(IEnumerable<SparseTensor> sp_ids, object sp_values, IGraphNodeBase vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
IEnumerable<SparseTensor>sp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IGraphNodeBasevocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(PythonClassContainer sp_ids, object sp_values, IGraphNodeBase vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
PythonClassContainersp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IGraphNodeBasevocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(object sp_ids, object sp_values, IEnumerable<int> vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
objectsp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IEnumerable<int>vocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(IGraphNodeBase sp_ids, object sp_values, IGraphNodeBase vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
IGraphNodeBasesp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IGraphNodeBasevocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(object sp_ids, object sp_values, int vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
objectsp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
intvocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(PythonClassContainer sp_ids, object sp_values, int vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
PythonClassContainersp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
intvocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_merge(PythonClassContainer sp_ids, object sp_values, IEnumerable<int> vocab_size, string name, bool already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
PythonClassContainersp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
IEnumerable<int>vocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
stringname - A name prefix for the returned tensors (optional)
-
boolalready_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
SparseTensor - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
object sparse_merge_dyn(object sp_ids, object sp_values, object vocab_size, object name, ImplicitContainer<T> already_sorted)
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Parameters
-
objectsp_ids - A single `SparseTensor` with `values` property of type `int32` or `int64` or a Python list of such `SparseTensor`s or a list thereof.
-
objectsp_values - A `SparseTensor` of any type.
-
objectvocab_size - A scalar `int64` Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_ids.values < vocab_size)`. Or a list thereof with `all(0 <= sp_ids[i].values < vocab_size[i])` for all `i`.
-
objectname - A name prefix for the returned tensors (optional)
-
ImplicitContainer<T>already_sorted - A boolean to specify whether the per-batch values in `sp_values` are already sorted. If so skip sorting, False by default (optional).
Returns
-
object - A `SparseTensor` compactly representing a batch of feature ids and values, useful for passing to functions that expect such a `SparseTensor`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
SparseTensor sparse_minimum(SparseTensor sp_a, SparseTensor sp_b, string name)
Returns the element-wise min of two SparseTensors. Assumes the two SparseTensors have the same shape, i.e., no broadcasting.
Example:
Parameters
-
SparseTensorsp_a - a `SparseTensor` operand whose dtype is real, and indices lexicographically ordered.
-
SparseTensorsp_b - the other `SparseTensor` operand with the same requirements (and the same shape).
-
stringname - optional name of the operation.
Returns
Show Example
sp_zero = sparse_tensor.SparseTensor([[0]], [0], [7])
sp_one = sparse_tensor.SparseTensor([[1]], [1], [7])
res = tf.sparse.minimum(sp_zero, sp_one).eval()
# "res" should be equal to SparseTensor([[0], [1]], [0, 0], [7]).
object sparse_minimum_dyn(object sp_a, object sp_b, object name)
Returns the element-wise min of two SparseTensors. Assumes the two SparseTensors have the same shape, i.e., no broadcasting.
Example:
Parameters
-
objectsp_a - a `SparseTensor` operand whose dtype is real, and indices lexicographically ordered.
-
objectsp_b - the other `SparseTensor` operand with the same requirements (and the same shape).
-
objectname - optional name of the operation.
Returns
-
object
Show Example
sp_zero = sparse_tensor.SparseTensor([[0]], [0], [7])
sp_one = sparse_tensor.SparseTensor([[1]], [1], [7])
res = tf.sparse.minimum(sp_zero, sp_one).eval()
# "res" should be equal to SparseTensor([[0], [1]], [0, 0], [7]).
SparseTensor sparse_placeholder(dtype dtype, IEnumerable<object> shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
dtypedtype - The type of `values` elements in the tensor to be fed.
-
IEnumerable<object>shape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(PythonClassContainer dtype, ValueTuple<int, int> shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
PythonClassContainerdtype - The type of `values` elements in the tensor to be fed.
-
ValueTuple<int, int>shape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(DType dtype, TensorShape shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
DTypedtype - The type of `values` elements in the tensor to be fed.
-
TensorShapeshape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(DType dtype, IEnumerable<object> shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
DTypedtype - The type of `values` elements in the tensor to be fed.
-
IEnumerable<object>shape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(DType dtype, PythonClassContainer shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
DTypedtype - The type of `values` elements in the tensor to be fed.
-
PythonClassContainershape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(PythonClassContainer dtype, IEnumerable<object> shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
PythonClassContainerdtype - The type of `values` elements in the tensor to be fed.
-
IEnumerable<object>shape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(DType dtype, ValueTuple<int, int> shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
DTypedtype - The type of `values` elements in the tensor to be fed.
-
ValueTuple<int, int>shape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(PythonClassContainer dtype, PythonClassContainer shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
PythonClassContainerdtype - The type of `values` elements in the tensor to be fed.
-
PythonClassContainershape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(dtype dtype, TensorShape shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
dtypedtype - The type of `values` elements in the tensor to be fed.
-
TensorShapeshape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(PythonClassContainer dtype, TensorShape shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
PythonClassContainerdtype - The type of `values` elements in the tensor to be fed.
-
TensorShapeshape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(dtype dtype, ValueTuple<int, int> shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
dtypedtype - The type of `values` elements in the tensor to be fed.
-
ValueTuple<int, int>shape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
SparseTensor sparse_placeholder(dtype dtype, PythonClassContainer shape, string name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
dtypedtype - The type of `values` elements in the tensor to be fed.
-
PythonClassContainershape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
stringname - A name for prefixing the operations (optional).
Returns
-
SparseTensor - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
object sparse_placeholder_dyn(object dtype, object shape, object name)
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Parameters
-
objectdtype - The type of `values` elements in the tensor to be fed.
-
objectshape - The shape of the tensor to be fed (optional). If the shape is not specified, you can feed a sparse tensor of any shape.
-
objectname - A name for prefixing the operations (optional).
Returns
-
object - A `SparseTensor` that may be used as a handle for feeding a value, but not evaluated directly.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
Tensor sparse_reduce_max(SparseTensor sp_input, int axis, Nullable<bool> keepdims, object reduction_axes, object keep_dims)
Computes the max of elements across dimensions of a SparseTensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(reduction_axes)`. They will be removed in a future version.
Instructions for updating:
reduction_axes is deprecated, use axis instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_max()`. In particular, this Op also returns a dense `Tensor`
instead of a sparse one. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
similar to the indexing rules in Python. The values not defined in `sp_input` don't participate in the reduce max,
as opposed to be implicitly assumed 0 -- hence it can return negative values
for sparse `reduction_axes`. But, in case there are no values in
`reduction_axes`, it will reduce to 0. See second example below.
Parameters
-
SparseTensorsp_input - The SparseTensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
Nullable<bool>keepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of `axis`.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced Tensor.
Show Example
# 'x' represents [[1, ?, 2]
# [?, 3, ?]]
# where ? is implicitly-zero.
tf.sparse.reduce_max(x) ==> 3
tf.sparse.reduce_max(x, 0) ==> [1, 3, 2]
tf.sparse.reduce_max(x, 1) ==> [2, 3] # Can also use -1 as the axis.
tf.sparse.reduce_max(x, 1, keepdims=True) ==> [[2], [3]]
tf.sparse.reduce_max(x, [0, 1]) ==> 3 # 'y' represents [[-7, ?]
# [ 4, 3]
# [ ?, ?]
tf.sparse.reduce_max(x, 1) ==> [-7, 4, 0]
Tensor sparse_reduce_max(SparseTensor sp_input, IEnumerable<object> axis, Nullable<bool> keepdims, object reduction_axes, object keep_dims)
Computes the max of elements across dimensions of a SparseTensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(reduction_axes)`. They will be removed in a future version.
Instructions for updating:
reduction_axes is deprecated, use axis instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_max()`. In particular, this Op also returns a dense `Tensor`
instead of a sparse one. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
similar to the indexing rules in Python. The values not defined in `sp_input` don't participate in the reduce max,
as opposed to be implicitly assumed 0 -- hence it can return negative values
for sparse `reduction_axes`. But, in case there are no values in
`reduction_axes`, it will reduce to 0. See second example below.
Parameters
-
SparseTensorsp_input - The SparseTensor to reduce. Should have numeric type.
-
IEnumerable<object>axis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
Nullable<bool>keepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of `axis`.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced Tensor.
Show Example
# 'x' represents [[1, ?, 2]
# [?, 3, ?]]
# where ? is implicitly-zero.
tf.sparse.reduce_max(x) ==> 3
tf.sparse.reduce_max(x, 0) ==> [1, 3, 2]
tf.sparse.reduce_max(x, 1) ==> [2, 3] # Can also use -1 as the axis.
tf.sparse.reduce_max(x, 1, keepdims=True) ==> [[2], [3]]
tf.sparse.reduce_max(x, [0, 1]) ==> 3 # 'y' represents [[-7, ?]
# [ 4, 3]
# [ ?, ?]
tf.sparse.reduce_max(x, 1) ==> [-7, 4, 0]
object sparse_reduce_max_dyn(object sp_input, object axis, object keepdims, object reduction_axes, object keep_dims)
Computes the max of elements across dimensions of a SparseTensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(reduction_axes)`. They will be removed in a future version.
Instructions for updating:
reduction_axes is deprecated, use axis instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_max()`. In particular, this Op also returns a dense `Tensor`
instead of a sparse one. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
similar to the indexing rules in Python. The values not defined in `sp_input` don't participate in the reduce max,
as opposed to be implicitly assumed 0 -- hence it can return negative values
for sparse `reduction_axes`. But, in case there are no values in
`reduction_axes`, it will reduce to 0. See second example below.
Parameters
-
objectsp_input - The SparseTensor to reduce. Should have numeric type.
-
objectaxis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
objectkeepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of `axis`.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced Tensor.
Show Example
# 'x' represents [[1, ?, 2]
# [?, 3, ?]]
# where ? is implicitly-zero.
tf.sparse.reduce_max(x) ==> 3
tf.sparse.reduce_max(x, 0) ==> [1, 3, 2]
tf.sparse.reduce_max(x, 1) ==> [2, 3] # Can also use -1 as the axis.
tf.sparse.reduce_max(x, 1, keepdims=True) ==> [[2], [3]]
tf.sparse.reduce_max(x, [0, 1]) ==> 3 # 'y' represents [[-7, ?]
# [ 4, 3]
# [ ?, ?]
tf.sparse.reduce_max(x, 1) ==> [-7, 4, 0]
SparseTensor sparse_reduce_max_sparse(object sp_input, IEnumerable<object> axis, Nullable<bool> keepdims, object reduction_axes, object keep_dims)
Computes the max of elements across dimensions of a SparseTensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_max()`. In contrast to SparseReduceSum, this Op returns a
SparseTensor. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
which are interpreted according to the indexing rules in Python.
Parameters
-
objectsp_input - The SparseTensor to reduce. Should have numeric type.
-
IEnumerable<object>axis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
Nullable<bool>keepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
SparseTensor - The reduced SparseTensor.
SparseTensor sparse_reduce_max_sparse(object sp_input, int axis, Nullable<bool> keepdims, object reduction_axes, object keep_dims)
Computes the max of elements across dimensions of a SparseTensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_max()`. In contrast to SparseReduceSum, this Op returns a
SparseTensor. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
which are interpreted according to the indexing rules in Python.
Parameters
-
objectsp_input - The SparseTensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
Nullable<bool>keepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
SparseTensor - The reduced SparseTensor.
object sparse_reduce_max_sparse_dyn(object sp_input, object axis, object keepdims, object reduction_axes, object keep_dims)
Computes the max of elements across dimensions of a SparseTensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_max()`. In contrast to SparseReduceSum, this Op returns a
SparseTensor. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
which are interpreted according to the indexing rules in Python.
Parameters
-
objectsp_input - The SparseTensor to reduce. Should have numeric type.
-
objectaxis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
objectkeepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced SparseTensor.
Tensor sparse_reduce_sum(IGraphNodeBase sp_input, IEnumerable<object> axis, Nullable<bool> keepdims, object reduction_axes, object keep_dims)
Computes the sum of elements across dimensions of a SparseTensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(reduction_axes)`. They will be removed in a future version.
Instructions for updating:
reduction_axes is deprecated, use axis instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_sum()`. In particular, this Op also returns a dense `Tensor`
instead of a sparse one. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
similar to the indexing rules in Python.
Parameters
-
IGraphNodeBasesp_input - The SparseTensor to reduce. Should have numeric type.
-
IEnumerable<object>axis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
Nullable<bool>keepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of `axis`.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced Tensor.
Show Example
# 'x' represents [[1, ?, 1]
# [?, 1, ?]]
# where ? is implicitly-zero.
tf.sparse.reduce_sum(x) ==> 3
tf.sparse.reduce_sum(x, 0) ==> [1, 1, 1]
tf.sparse.reduce_sum(x, 1) ==> [2, 1] # Can also use -1 as the axis.
tf.sparse.reduce_sum(x, 1, keepdims=True) ==> [[2], [1]]
tf.sparse.reduce_sum(x, [0, 1]) ==> 3
Tensor sparse_reduce_sum(IGraphNodeBase sp_input, int axis, Nullable<bool> keepdims, object reduction_axes, object keep_dims)
Computes the sum of elements across dimensions of a SparseTensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(reduction_axes)`. They will be removed in a future version.
Instructions for updating:
reduction_axes is deprecated, use axis instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_sum()`. In particular, this Op also returns a dense `Tensor`
instead of a sparse one. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
similar to the indexing rules in Python.
Parameters
-
IGraphNodeBasesp_input - The SparseTensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
Nullable<bool>keepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of `axis`.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
Tensor - The reduced Tensor.
Show Example
# 'x' represents [[1, ?, 1]
# [?, 1, ?]]
# where ? is implicitly-zero.
tf.sparse.reduce_sum(x) ==> 3
tf.sparse.reduce_sum(x, 0) ==> [1, 1, 1]
tf.sparse.reduce_sum(x, 1) ==> [2, 1] # Can also use -1 as the axis.
tf.sparse.reduce_sum(x, 1, keepdims=True) ==> [[2], [1]]
tf.sparse.reduce_sum(x, [0, 1]) ==> 3
object sparse_reduce_sum_dyn(object sp_input, object axis, object keepdims, object reduction_axes, object keep_dims)
Computes the sum of elements across dimensions of a SparseTensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(reduction_axes)`. They will be removed in a future version.
Instructions for updating:
reduction_axes is deprecated, use axis instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_sum()`. In particular, this Op also returns a dense `Tensor`
instead of a sparse one. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
similar to the indexing rules in Python.
Parameters
-
objectsp_input - The SparseTensor to reduce. Should have numeric type.
-
objectaxis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
objectkeepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of `axis`.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced Tensor.
Show Example
# 'x' represents [[1, ?, 1]
# [?, 1, ?]]
# where ? is implicitly-zero.
tf.sparse.reduce_sum(x) ==> 3
tf.sparse.reduce_sum(x, 0) ==> [1, 1, 1]
tf.sparse.reduce_sum(x, 1) ==> [2, 1] # Can also use -1 as the axis.
tf.sparse.reduce_sum(x, 1, keepdims=True) ==> [[2], [1]]
tf.sparse.reduce_sum(x, [0, 1]) ==> 3
SparseTensor sparse_reduce_sum_sparse(object sp_input, int axis, Nullable<bool> keepdims, object reduction_axes, object keep_dims)
Computes the sum of elements across dimensions of a SparseTensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_sum()`. In contrast to SparseReduceSum, this Op returns a
SparseTensor. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
which are interpreted according to the indexing rules in Python.
Parameters
-
objectsp_input - The SparseTensor to reduce. Should have numeric type.
-
intaxis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
Nullable<bool>keepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
SparseTensor - The reduced SparseTensor.
SparseTensor sparse_reduce_sum_sparse(object sp_input, IEnumerable<object> axis, Nullable<bool> keepdims, object reduction_axes, object keep_dims)
Computes the sum of elements across dimensions of a SparseTensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_sum()`. In contrast to SparseReduceSum, this Op returns a
SparseTensor. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
which are interpreted according to the indexing rules in Python.
Parameters
-
objectsp_input - The SparseTensor to reduce. Should have numeric type.
-
IEnumerable<object>axis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
Nullable<bool>keepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
SparseTensor - The reduced SparseTensor.
object sparse_reduce_sum_sparse_dyn(object sp_input, object axis, object keepdims, object reduction_axes, object keep_dims)
Computes the sum of elements across dimensions of a SparseTensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_sum()`. In contrast to SparseReduceSum, this Op returns a
SparseTensor. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
which are interpreted according to the indexing rules in Python.
Parameters
-
objectsp_input - The SparseTensor to reduce. Should have numeric type.
-
objectaxis - The dimensions to reduce; list or scalar. If `None` (the default), reduces all dimensions.
-
objectkeepdims - If true, retain reduced dimensions with length 1.
-
objectreduction_axes - Deprecated name of axis.
-
objectkeep_dims - Deprecated alias for `keepdims`.
Returns
-
object - The reduced SparseTensor.
SparseTensor sparse_reorder(object sp_input, string name)
Reorders a `SparseTensor` into the canonical, row-major ordering. Note that by convention, all sparse ops preserve the canonical ordering
along increasing dimension number. The only time ordering can be violated
is during manual manipulation of the indices and values to add entries. Reordering does not affect the shape of the `SparseTensor`. For example, if `sp_input` has shape `[4, 5]` and `indices` / `values`: [0, 3]: b
[0, 1]: a
[3, 1]: d
[2, 0]: c then the output will be a `SparseTensor` of shape `[4, 5]` and
`indices` / `values`: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d
Parameters
-
objectsp_input - The input `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same shape and non-empty values, but in canonical ordering.
SparseTensor sparse_reorder(SparseTensor sp_input, string name)
Reorders a `SparseTensor` into the canonical, row-major ordering. Note that by convention, all sparse ops preserve the canonical ordering
along increasing dimension number. The only time ordering can be violated
is during manual manipulation of the indices and values to add entries. Reordering does not affect the shape of the `SparseTensor`. For example, if `sp_input` has shape `[4, 5]` and `indices` / `values`: [0, 3]: b
[0, 1]: a
[3, 1]: d
[2, 0]: c then the output will be a `SparseTensor` of shape `[4, 5]` and
`indices` / `values`: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d
Parameters
-
SparseTensorsp_input - The input `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same shape and non-empty values, but in canonical ordering.
object sparse_reorder_dyn(object sp_input, object name)
Reorders a `SparseTensor` into the canonical, row-major ordering. Note that by convention, all sparse ops preserve the canonical ordering
along increasing dimension number. The only time ordering can be violated
is during manual manipulation of the indices and values to add entries. Reordering does not affect the shape of the `SparseTensor`. For example, if `sp_input` has shape `[4, 5]` and `indices` / `values`: [0, 3]: b
[0, 1]: a
[3, 1]: d
[2, 0]: c then the output will be a `SparseTensor` of shape `[4, 5]` and
`indices` / `values`: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d
Parameters
-
objectsp_input - The input `SparseTensor`.
-
objectname - A name prefix for the returned tensors (optional)
Returns
-
object - A `SparseTensor` with the same shape and non-empty values, but in canonical ordering.
SparseTensor sparse_reset_shape(SparseTensor sp_input, ndarray new_shape)
Resets the shape of a `SparseTensor` with indices and values unchanged. If `new_shape` is None, returns a copy of `sp_input` with its shape reset
to the tight bounding box of `sp_input`. This will be a shape consisting of
all zeros if sp_input has no values. If `new_shape` is provided, then it must be larger or equal in all dimensions
compared to the shape of `sp_input`. When this condition is met, the returned
SparseTensor will have its shape reset to `new_shape` and its indices and
values unchanged from that of `sp_input.` For example: Consider a `sp_input` with shape [2, 3, 5]: [0, 0, 1]: a
[0, 1, 0]: b
[0, 2, 2]: c
[1, 0, 3]: d - It is an error to set `new_shape` as [3, 7] since this represents a
rank-2 tensor while `sp_input` is rank-3. This is either a ValueError
during graph construction (if both shapes are known) or an OpError during
run time. - Setting `new_shape` as [2, 3, 6] will be fine as this shape is larger or
equal in every dimension compared to the original shape [2, 3, 5]. - On the other hand, setting new_shape as [2, 3, 4] is also an error: The
third dimension is smaller than the original shape [2, 3, 5] (and an
`InvalidArgumentError` will be raised). - If `new_shape` is None, the returned SparseTensor will have a shape
[2, 3, 4], which is the tight bounding box of `sp_input`.
Parameters
-
SparseTensorsp_input - The input `SparseTensor`.
-
ndarraynew_shape - None or a vector representing the new shape for the returned `SparseTensor`.
Returns
-
SparseTensor - A `SparseTensor` indices and values unchanged from `input_sp`. Its shape is `new_shape` if that is set. Otherwise it is the tight bounding box of `input_sp`
SparseTensor sparse_reset_shape(object sp_input, IGraphNodeBase new_shape)
Resets the shape of a `SparseTensor` with indices and values unchanged. If `new_shape` is None, returns a copy of `sp_input` with its shape reset
to the tight bounding box of `sp_input`. This will be a shape consisting of
all zeros if sp_input has no values. If `new_shape` is provided, then it must be larger or equal in all dimensions
compared to the shape of `sp_input`. When this condition is met, the returned
SparseTensor will have its shape reset to `new_shape` and its indices and
values unchanged from that of `sp_input.` For example: Consider a `sp_input` with shape [2, 3, 5]: [0, 0, 1]: a
[0, 1, 0]: b
[0, 2, 2]: c
[1, 0, 3]: d - It is an error to set `new_shape` as [3, 7] since this represents a
rank-2 tensor while `sp_input` is rank-3. This is either a ValueError
during graph construction (if both shapes are known) or an OpError during
run time. - Setting `new_shape` as [2, 3, 6] will be fine as this shape is larger or
equal in every dimension compared to the original shape [2, 3, 5]. - On the other hand, setting new_shape as [2, 3, 4] is also an error: The
third dimension is smaller than the original shape [2, 3, 5] (and an
`InvalidArgumentError` will be raised). - If `new_shape` is None, the returned SparseTensor will have a shape
[2, 3, 4], which is the tight bounding box of `sp_input`.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
IGraphNodeBasenew_shape - None or a vector representing the new shape for the returned `SparseTensor`.
Returns
-
SparseTensor - A `SparseTensor` indices and values unchanged from `input_sp`. Its shape is `new_shape` if that is set. Otherwise it is the tight bounding box of `input_sp`
SparseTensor sparse_reset_shape(SparseTensor sp_input, IGraphNodeBase new_shape)
Resets the shape of a `SparseTensor` with indices and values unchanged. If `new_shape` is None, returns a copy of `sp_input` with its shape reset
to the tight bounding box of `sp_input`. This will be a shape consisting of
all zeros if sp_input has no values. If `new_shape` is provided, then it must be larger or equal in all dimensions
compared to the shape of `sp_input`. When this condition is met, the returned
SparseTensor will have its shape reset to `new_shape` and its indices and
values unchanged from that of `sp_input.` For example: Consider a `sp_input` with shape [2, 3, 5]: [0, 0, 1]: a
[0, 1, 0]: b
[0, 2, 2]: c
[1, 0, 3]: d - It is an error to set `new_shape` as [3, 7] since this represents a
rank-2 tensor while `sp_input` is rank-3. This is either a ValueError
during graph construction (if both shapes are known) or an OpError during
run time. - Setting `new_shape` as [2, 3, 6] will be fine as this shape is larger or
equal in every dimension compared to the original shape [2, 3, 5]. - On the other hand, setting new_shape as [2, 3, 4] is also an error: The
third dimension is smaller than the original shape [2, 3, 5] (and an
`InvalidArgumentError` will be raised). - If `new_shape` is None, the returned SparseTensor will have a shape
[2, 3, 4], which is the tight bounding box of `sp_input`.
Parameters
-
SparseTensorsp_input - The input `SparseTensor`.
-
IGraphNodeBasenew_shape - None or a vector representing the new shape for the returned `SparseTensor`.
Returns
-
SparseTensor - A `SparseTensor` indices and values unchanged from `input_sp`. Its shape is `new_shape` if that is set. Otherwise it is the tight bounding box of `input_sp`
SparseTensor sparse_reset_shape(object sp_input, ndarray new_shape)
Resets the shape of a `SparseTensor` with indices and values unchanged. If `new_shape` is None, returns a copy of `sp_input` with its shape reset
to the tight bounding box of `sp_input`. This will be a shape consisting of
all zeros if sp_input has no values. If `new_shape` is provided, then it must be larger or equal in all dimensions
compared to the shape of `sp_input`. When this condition is met, the returned
SparseTensor will have its shape reset to `new_shape` and its indices and
values unchanged from that of `sp_input.` For example: Consider a `sp_input` with shape [2, 3, 5]: [0, 0, 1]: a
[0, 1, 0]: b
[0, 2, 2]: c
[1, 0, 3]: d - It is an error to set `new_shape` as [3, 7] since this represents a
rank-2 tensor while `sp_input` is rank-3. This is either a ValueError
during graph construction (if both shapes are known) or an OpError during
run time. - Setting `new_shape` as [2, 3, 6] will be fine as this shape is larger or
equal in every dimension compared to the original shape [2, 3, 5]. - On the other hand, setting new_shape as [2, 3, 4] is also an error: The
third dimension is smaller than the original shape [2, 3, 5] (and an
`InvalidArgumentError` will be raised). - If `new_shape` is None, the returned SparseTensor will have a shape
[2, 3, 4], which is the tight bounding box of `sp_input`.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
ndarraynew_shape - None or a vector representing the new shape for the returned `SparseTensor`.
Returns
-
SparseTensor - A `SparseTensor` indices and values unchanged from `input_sp`. Its shape is `new_shape` if that is set. Otherwise it is the tight bounding box of `input_sp`
object sparse_reset_shape_dyn(object sp_input, object new_shape)
Resets the shape of a `SparseTensor` with indices and values unchanged. If `new_shape` is None, returns a copy of `sp_input` with its shape reset
to the tight bounding box of `sp_input`. This will be a shape consisting of
all zeros if sp_input has no values. If `new_shape` is provided, then it must be larger or equal in all dimensions
compared to the shape of `sp_input`. When this condition is met, the returned
SparseTensor will have its shape reset to `new_shape` and its indices and
values unchanged from that of `sp_input.` For example: Consider a `sp_input` with shape [2, 3, 5]: [0, 0, 1]: a
[0, 1, 0]: b
[0, 2, 2]: c
[1, 0, 3]: d - It is an error to set `new_shape` as [3, 7] since this represents a
rank-2 tensor while `sp_input` is rank-3. This is either a ValueError
during graph construction (if both shapes are known) or an OpError during
run time. - Setting `new_shape` as [2, 3, 6] will be fine as this shape is larger or
equal in every dimension compared to the original shape [2, 3, 5]. - On the other hand, setting new_shape as [2, 3, 4] is also an error: The
third dimension is smaller than the original shape [2, 3, 5] (and an
`InvalidArgumentError` will be raised). - If `new_shape` is None, the returned SparseTensor will have a shape
[2, 3, 4], which is the tight bounding box of `sp_input`.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
objectnew_shape - None or a vector representing the new shape for the returned `SparseTensor`.
Returns
-
object - A `SparseTensor` indices and values unchanged from `input_sp`. Its shape is `new_shape` if that is set. Otherwise it is the tight bounding box of `input_sp`
SparseTensor sparse_reshape(IGraphNodeBase sp_input, IGraphNodeBase shape, PythonFunctionContainer name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
IGraphNodeBasesp_input - The input `SparseTensor`.
-
IGraphNodeBaseshape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(object sp_input, IGraphNodeBase shape, PythonFunctionContainer name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
objectsp_input - The input `SparseTensor`.
-
IGraphNodeBaseshape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(object sp_input, IEnumerable<int> shape, string name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
objectsp_input - The input `SparseTensor`.
-
IEnumerable<int>shape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(IGraphNodeBase sp_input, IGraphNodeBase shape, string name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
IGraphNodeBasesp_input - The input `SparseTensor`.
-
IGraphNodeBaseshape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(ValueTuple<PythonClassContainer, PythonClassContainer> sp_input, IGraphNodeBase shape, PythonFunctionContainer name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>sp_input - The input `SparseTensor`.
-
IGraphNodeBaseshape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(ValueTuple<PythonClassContainer, PythonClassContainer> sp_input, IGraphNodeBase shape, string name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>sp_input - The input `SparseTensor`.
-
IGraphNodeBaseshape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(ValueTuple<PythonClassContainer, PythonClassContainer> sp_input, IEnumerable<int> shape, PythonFunctionContainer name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>sp_input - The input `SparseTensor`.
-
IEnumerable<int>shape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(ValueTuple<PythonClassContainer, PythonClassContainer> sp_input, IEnumerable<int> shape, string name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>sp_input - The input `SparseTensor`.
-
IEnumerable<int>shape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(object sp_input, IEnumerable<int> shape, PythonFunctionContainer name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
objectsp_input - The input `SparseTensor`.
-
IEnumerable<int>shape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(IGraphNodeBase sp_input, IEnumerable<int> shape, string name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
IGraphNodeBasesp_input - The input `SparseTensor`.
-
IEnumerable<int>shape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(IGraphNodeBase sp_input, IEnumerable<int> shape, PythonFunctionContainer name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
IGraphNodeBasesp_input - The input `SparseTensor`.
-
IEnumerable<int>shape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(IndexedSlices sp_input, IEnumerable<int> shape, string name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
IndexedSlicessp_input - The input `SparseTensor`.
-
IEnumerable<int>shape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(IndexedSlices sp_input, IGraphNodeBase shape, string name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
IndexedSlicessp_input - The input `SparseTensor`.
-
IGraphNodeBaseshape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(IndexedSlices sp_input, IGraphNodeBase shape, PythonFunctionContainer name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
IndexedSlicessp_input - The input `SparseTensor`.
-
IGraphNodeBaseshape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(IndexedSlices sp_input, IEnumerable<int> shape, PythonFunctionContainer name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
IndexedSlicessp_input - The input `SparseTensor`.
-
IEnumerable<int>shape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_reshape(object sp_input, IGraphNodeBase shape, string name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
objectsp_input - The input `SparseTensor`.
-
IGraphNodeBaseshape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
object sparse_reshape_dyn(object sp_input, object shape, object name)
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
Parameters
-
objectsp_input - The input `SparseTensor`.
-
objectshape - A 1-D (vector) int64 `Tensor` specifying the new dense shape of the represented `SparseTensor`.
-
objectname - A name prefix for the returned tensors (optional)
Returns
-
object - A `SparseTensor` with the same non-empty values but with indices calculated by the new dense shape.
SparseTensor sparse_retain(object sp_input, ndarray to_retain)
Retains specified non-empty values within a `SparseTensor`. For example, if `sp_input` has shape `[4, 5]` and 4 non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d and `to_retain = [True, False, False, True]`, then the output will
be a `SparseTensor` of shape `[4, 5]` with 2 non-empty values: [0, 1]: a
[3, 1]: d
Parameters
-
objectsp_input - The input `SparseTensor` with `N` non-empty elements.
-
ndarrayto_retain - A bool vector of length `N` with `M` true values.
Returns
-
SparseTensor - A `SparseTensor` with the same shape as the input and `M` non-empty elements corresponding to the true positions in `to_retain`.
SparseTensor sparse_retain(IGraphNodeBase sp_input, IGraphNodeBase to_retain)
Retains specified non-empty values within a `SparseTensor`. For example, if `sp_input` has shape `[4, 5]` and 4 non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d and `to_retain = [True, False, False, True]`, then the output will
be a `SparseTensor` of shape `[4, 5]` with 2 non-empty values: [0, 1]: a
[3, 1]: d
Parameters
-
IGraphNodeBasesp_input - The input `SparseTensor` with `N` non-empty elements.
-
IGraphNodeBaseto_retain - A bool vector of length `N` with `M` true values.
Returns
-
SparseTensor - A `SparseTensor` with the same shape as the input and `M` non-empty elements corresponding to the true positions in `to_retain`.
SparseTensor sparse_retain(object sp_input, IGraphNodeBase to_retain)
Retains specified non-empty values within a `SparseTensor`. For example, if `sp_input` has shape `[4, 5]` and 4 non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d and `to_retain = [True, False, False, True]`, then the output will
be a `SparseTensor` of shape `[4, 5]` with 2 non-empty values: [0, 1]: a
[3, 1]: d
Parameters
-
objectsp_input - The input `SparseTensor` with `N` non-empty elements.
-
IGraphNodeBaseto_retain - A bool vector of length `N` with `M` true values.
Returns
-
SparseTensor - A `SparseTensor` with the same shape as the input and `M` non-empty elements corresponding to the true positions in `to_retain`.
SparseTensor sparse_retain(IGraphNodeBase sp_input, ndarray to_retain)
Retains specified non-empty values within a `SparseTensor`. For example, if `sp_input` has shape `[4, 5]` and 4 non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d and `to_retain = [True, False, False, True]`, then the output will
be a `SparseTensor` of shape `[4, 5]` with 2 non-empty values: [0, 1]: a
[3, 1]: d
Parameters
-
IGraphNodeBasesp_input - The input `SparseTensor` with `N` non-empty elements.
-
ndarrayto_retain - A bool vector of length `N` with `M` true values.
Returns
-
SparseTensor - A `SparseTensor` with the same shape as the input and `M` non-empty elements corresponding to the true positions in `to_retain`.
object sparse_retain_dyn(object sp_input, object to_retain)
Retains specified non-empty values within a `SparseTensor`. For example, if `sp_input` has shape `[4, 5]` and 4 non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d and `to_retain = [True, False, False, True]`, then the output will
be a `SparseTensor` of shape `[4, 5]` with 2 non-empty values: [0, 1]: a
[3, 1]: d
Parameters
-
objectsp_input - The input `SparseTensor` with `N` non-empty elements.
-
objectto_retain - A bool vector of length `N` with `M` true values.
Returns
-
object - A `SparseTensor` with the same shape as the input and `M` non-empty elements corresponding to the true positions in `to_retain`.
Tensor sparse_segment_mean(IGraphNodeBase data, IEnumerable<int> indices, PythonClassContainer segment_ids, PythonFunctionContainer name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
PythonClassContainersegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_mean(IGraphNodeBase data, IEnumerable<int> indices, IGraphNodeBase segment_ids, PythonFunctionContainer name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IGraphNodeBasesegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_mean(IGraphNodeBase data, IEnumerable<int> indices, IGraphNodeBase segment_ids, string name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IGraphNodeBasesegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_mean(IGraphNodeBase data, IEnumerable<int> indices, IndexedSlices segment_ids, PythonFunctionContainer name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IndexedSlicessegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_mean(IGraphNodeBase data, IEnumerable<int> indices, int segment_ids, string name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
intsegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_mean(IGraphNodeBase data, IEnumerable<int> indices, int segment_ids, PythonFunctionContainer name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
intsegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_mean(IGraphNodeBase data, IEnumerable<int> indices, IEnumerable<int> segment_ids, PythonFunctionContainer name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IEnumerable<int>segment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_mean(IGraphNodeBase data, IEnumerable<int> indices, PythonClassContainer segment_ids, string name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
PythonClassContainersegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_mean(IGraphNodeBase data, IEnumerable<int> indices, IndexedSlices segment_ids, string name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IndexedSlicessegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_mean(IGraphNodeBase data, IEnumerable<int> indices, IEnumerable<int> segment_ids, string name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IEnumerable<int>segment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
object sparse_segment_mean_dyn(object data, object indices, object segment_ids, object name, object num_segments)
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
objectdata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
objectsegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
objectname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
object - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sqrt_n(IGraphNodeBase data, object indices, IGraphNodeBase segment_ids, string name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IGraphNodeBasesegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sqrt_n(IGraphNodeBase data, object indices, PythonClassContainer segment_ids, string name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
PythonClassContainersegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sqrt_n(IGraphNodeBase data, object indices, int segment_ids, PythonFunctionContainer name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
intsegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sqrt_n(IGraphNodeBase data, object indices, IEnumerable<PythonClassContainer> segment_ids, string name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IEnumerable<PythonClassContainer>segment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sqrt_n(IGraphNodeBase data, object indices, IndexedSlices segment_ids, string name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IndexedSlicessegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sqrt_n(IGraphNodeBase data, object indices, IndexedSlices segment_ids, PythonFunctionContainer name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IndexedSlicessegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sqrt_n(IGraphNodeBase data, object indices, PythonClassContainer segment_ids, PythonFunctionContainer name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
PythonClassContainersegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sqrt_n(IGraphNodeBase data, object indices, int segment_ids, string name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
intsegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sqrt_n(IGraphNodeBase data, object indices, IEnumerable<PythonClassContainer> segment_ids, PythonFunctionContainer name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IEnumerable<PythonClassContainer>segment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sqrt_n(IGraphNodeBase data, object indices, IGraphNodeBase segment_ids, PythonFunctionContainer name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IGraphNodeBasesegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
object sparse_segment_sqrt_n_dyn(object data, object indices, object segment_ids, object name, object num_segments)
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
Parameters
-
objectdata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
objectsegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
objectname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
object - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Tensor sparse_segment_sum(IGraphNodeBase data, IEnumerable<int> indices, IEnumerable<int> segment_ids, PythonFunctionContainer name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IEnumerable<int>segment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
Tensor sparse_segment_sum(IGraphNodeBase data, IEnumerable<int> indices, IEnumerable<int> segment_ids, string name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IEnumerable<int>segment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
Tensor sparse_segment_sum(IGraphNodeBase data, IEnumerable<int> indices, PythonClassContainer segment_ids, string name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
PythonClassContainersegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
Tensor sparse_segment_sum(IGraphNodeBase data, IEnumerable<int> indices, IndexedSlices segment_ids, string name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IndexedSlicessegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
Tensor sparse_segment_sum(IGraphNodeBase data, IEnumerable<int> indices, PythonClassContainer segment_ids, PythonFunctionContainer name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
PythonClassContainersegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
Tensor sparse_segment_sum(IGraphNodeBase data, IEnumerable<int> indices, IndexedSlices segment_ids, PythonFunctionContainer name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IndexedSlicessegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
Tensor sparse_segment_sum(IGraphNodeBase data, IEnumerable<int> indices, int segment_ids, string name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
intsegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
Tensor sparse_segment_sum(IGraphNodeBase data, IEnumerable<int> indices, IGraphNodeBase segment_ids, PythonFunctionContainer name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IGraphNodeBasesegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
Tensor sparse_segment_sum(IGraphNodeBase data, IEnumerable<int> indices, IGraphNodeBase segment_ids, string name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
IGraphNodeBasesegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
stringname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
Tensor sparse_segment_sum(IGraphNodeBase data, IEnumerable<int> indices, int segment_ids, PythonFunctionContainer name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
IGraphNodeBasedata - A `Tensor` with data that will be assembled in the output.
-
IEnumerable<int>indices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
intsegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
PythonFunctionContainername - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
Tensor - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
object sparse_segment_sum_dyn(object data, object indices, object segment_ids, object name, object num_segments)
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Parameters
-
objectdata - A `Tensor` with data that will be assembled in the output.
-
objectindices - A 1-D `Tensor` with indices into `data`. Has same rank as `segment_ids`.
-
objectsegment_ids - A 1-D `Tensor` with indices into the output `Tensor`. Values should be sorted and can be repeated.
-
objectname - A name for the operation (optional).
-
objectnum_segments - An optional int32 scalar. Indicates the size of the output `Tensor`.
Returns
-
object - A `tensor` of the shape as data, except for dimension 0 which has size `k`, the number of segments specified via `num_segments` or inferred for the last element in `segments_ids`.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
SparseTensor sparse_slice(SparseTensor sp_input, IGraphNodeBase start, IEnumerable<int> size, string name)
Slice a `SparseTensor` based on the `start` and `size. For example, if the input is input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: sparse.slice([0, 0], [2, 4]) = shape = [2, 4]
[ a ]
[b c ] sparse.slice([0, 4], [2, 3]) = shape = [2, 3]
[ d e ]
[ ]
Parameters
-
SparseTensorsp_input - The `SparseTensor` to split.
-
IGraphNodeBasestart - 1-D. tensor represents the start of the slice.
-
IEnumerable<int>size - 1-D. tensor represents the size of the slice.
-
stringname - A name for the operation (optional).
Returns
-
SparseTensor - A `SparseTensor` objects resulting from splicing.
SparseTensor sparse_slice(SparseTensor sp_input, IEnumerable<int> start, IEnumerable<int> size, string name)
Slice a `SparseTensor` based on the `start` and `size. For example, if the input is input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: sparse.slice([0, 0], [2, 4]) = shape = [2, 4]
[ a ]
[b c ] sparse.slice([0, 4], [2, 3]) = shape = [2, 3]
[ d e ]
[ ]
Parameters
-
SparseTensorsp_input - The `SparseTensor` to split.
-
IEnumerable<int>start - 1-D. tensor represents the start of the slice.
-
IEnumerable<int>size - 1-D. tensor represents the size of the slice.
-
stringname - A name for the operation (optional).
Returns
-
SparseTensor - A `SparseTensor` objects resulting from splicing.
object sparse_slice_dyn(object sp_input, object start, object size, object name)
Slice a `SparseTensor` based on the `start` and `size. For example, if the input is input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: sparse.slice([0, 0], [2, 4]) = shape = [2, 4]
[ a ]
[b c ] sparse.slice([0, 4], [2, 3]) = shape = [2, 3]
[ d e ]
[ ]
Parameters
-
objectsp_input - The `SparseTensor` to split.
-
objectstart - 1-D. tensor represents the start of the slice.
-
objectsize - 1-D. tensor represents the size of the slice.
-
objectname - A name for the operation (optional).
Returns
-
object - A `SparseTensor` objects resulting from splicing.
SparseTensor sparse_softmax(SparseTensor sp_input, string name)
Applies softmax to a batched N-D `SparseTensor`. The inputs represent an N-D SparseTensor with logical shape `[..., B, C]`
(where `N >= 2`), and with indices sorted in the canonical lexicographic
order. This op is equivalent to applying the normal `tf.nn.softmax()` to each
innermost logical submatrix with shape `[B, C]`, but with the catch that *the
implicitly zero elements do not participate*. Specifically, the algorithm is
equivalent to: (1) Applies `tf.nn.softmax()` to a densified view of each innermost
submatrix with shape `[B, C]`, along the size-C dimension;
(2) Masks out the original implicitly-zero locations;
(3) Renormalizes the remaining elements. Hence, the `SparseTensor` result has exactly the same non-zero indices and
shape. Example:
Parameters
-
SparseTensorsp_input - N-D `SparseTensor`, where `N >= 2`.
-
stringname - optional name of the operation.
Returns
Show Example
# First batch:
# [? e.]
# [1. ? ]
# Second batch:
# [e ? ]
# [e e ]
shape = [2, 2, 2] # 3-D SparseTensor
values = np.asarray([[[0., np.e], [1., 0.]], [[np.e, 0.], [np.e, np.e]]])
indices = np.vstack(np.where(values)).astype(np.int64).T result = tf.sparse.softmax(tf.SparseTensor(indices, values, shape))
#...returning a 3-D SparseTensor, equivalent to:
# [? 1.] [1 ?]
# [1. ? ] and [.5 .5]
# where ? means implicitly zero.
object sparse_softmax_dyn(object sp_input, object name)
Applies softmax to a batched N-D `SparseTensor`. The inputs represent an N-D SparseTensor with logical shape `[..., B, C]`
(where `N >= 2`), and with indices sorted in the canonical lexicographic
order. This op is equivalent to applying the normal `tf.nn.softmax()` to each
innermost logical submatrix with shape `[B, C]`, but with the catch that *the
implicitly zero elements do not participate*. Specifically, the algorithm is
equivalent to: (1) Applies `tf.nn.softmax()` to a densified view of each innermost
submatrix with shape `[B, C]`, along the size-C dimension;
(2) Masks out the original implicitly-zero locations;
(3) Renormalizes the remaining elements. Hence, the `SparseTensor` result has exactly the same non-zero indices and
shape. Example:
Parameters
-
objectsp_input - N-D `SparseTensor`, where `N >= 2`.
-
objectname - optional name of the operation.
Returns
-
object
Show Example
# First batch:
# [? e.]
# [1. ? ]
# Second batch:
# [e ? ]
# [e e ]
shape = [2, 2, 2] # 3-D SparseTensor
values = np.asarray([[[0., np.e], [1., 0.]], [[np.e, 0.], [np.e, np.e]]])
indices = np.vstack(np.where(values)).astype(np.int64).T result = tf.sparse.softmax(tf.SparseTensor(indices, values, shape))
#...returning a 3-D SparseTensor, equivalent to:
# [? 1.] [1 ?]
# [1. ? ] and [.5 .5]
# where ? means implicitly zero.
IList<SparseTensor> sparse_split(int keyword_required, object sp_input, Nullable<int> num_split, Nullable<int> axis, string name, object split_dim)
Split a `SparseTensor` into `num_split` tensors along `axis`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(split_dim)`. They will be removed in a future version.
Instructions for updating:
split_dim is deprecated, use axis instead If the `sp_input.dense_shape[axis]` is not an integer multiple of `num_split`
each slice starting from 0:`shape[axis] % num_split` gets extra one
dimension. For example, if `axis = 1` and `num_split = 2` and the
input is: input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: output_tensor[0] =
[ a ]
[b c ] output_tensor[1] =
[ d e ]
[ ]
Parameters
-
intkeyword_required - Python 2 standin for * (temporary for argument reorder)
-
objectsp_input - The `SparseTensor` to split.
-
Nullable<int>num_split - A Python integer. The number of ways to split.
-
Nullable<int>axis - A 0-D `int32` `Tensor`. The dimension along which to split.
-
stringname - A name for the operation (optional).
-
objectsplit_dim - Deprecated old name for axis.
Returns
-
IList<SparseTensor> - `num_split` `SparseTensor` objects resulting from splitting `value`.
IList<SparseTensor> sparse_split(ImplicitContainer<T> keyword_required, SparseTensor sp_input, Nullable<int> num_split, Nullable<int> axis, string name, object split_dim)
Split a `SparseTensor` into `num_split` tensors along `axis`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(split_dim)`. They will be removed in a future version.
Instructions for updating:
split_dim is deprecated, use axis instead If the `sp_input.dense_shape[axis]` is not an integer multiple of `num_split`
each slice starting from 0:`shape[axis] % num_split` gets extra one
dimension. For example, if `axis = 1` and `num_split = 2` and the
input is: input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: output_tensor[0] =
[ a ]
[b c ] output_tensor[1] =
[ d e ]
[ ]
Parameters
-
ImplicitContainer<T>keyword_required - Python 2 standin for * (temporary for argument reorder)
-
SparseTensorsp_input - The `SparseTensor` to split.
-
Nullable<int>num_split - A Python integer. The number of ways to split.
-
Nullable<int>axis - A 0-D `int32` `Tensor`. The dimension along which to split.
-
stringname - A name for the operation (optional).
-
objectsplit_dim - Deprecated old name for axis.
Returns
-
IList<SparseTensor> - `num_split` `SparseTensor` objects resulting from splitting `value`.
IList<SparseTensor> sparse_split(int keyword_required, int sp_input, Nullable<int> num_split, Nullable<int> axis, string name, object split_dim)
Split a `SparseTensor` into `num_split` tensors along `axis`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(split_dim)`. They will be removed in a future version.
Instructions for updating:
split_dim is deprecated, use axis instead If the `sp_input.dense_shape[axis]` is not an integer multiple of `num_split`
each slice starting from 0:`shape[axis] % num_split` gets extra one
dimension. For example, if `axis = 1` and `num_split = 2` and the
input is: input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: output_tensor[0] =
[ a ]
[b c ] output_tensor[1] =
[ d e ]
[ ]
Parameters
-
intkeyword_required - Python 2 standin for * (temporary for argument reorder)
-
intsp_input - The `SparseTensor` to split.
-
Nullable<int>num_split - A Python integer. The number of ways to split.
-
Nullable<int>axis - A 0-D `int32` `Tensor`. The dimension along which to split.
-
stringname - A name for the operation (optional).
-
objectsplit_dim - Deprecated old name for axis.
Returns
-
IList<SparseTensor> - `num_split` `SparseTensor` objects resulting from splitting `value`.
IList<SparseTensor> sparse_split(int keyword_required, SparseTensor sp_input, Nullable<int> num_split, Nullable<int> axis, string name, object split_dim)
Split a `SparseTensor` into `num_split` tensors along `axis`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(split_dim)`. They will be removed in a future version.
Instructions for updating:
split_dim is deprecated, use axis instead If the `sp_input.dense_shape[axis]` is not an integer multiple of `num_split`
each slice starting from 0:`shape[axis] % num_split` gets extra one
dimension. For example, if `axis = 1` and `num_split = 2` and the
input is: input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: output_tensor[0] =
[ a ]
[b c ] output_tensor[1] =
[ d e ]
[ ]
Parameters
-
intkeyword_required - Python 2 standin for * (temporary for argument reorder)
-
SparseTensorsp_input - The `SparseTensor` to split.
-
Nullable<int>num_split - A Python integer. The number of ways to split.
-
Nullable<int>axis - A 0-D `int32` `Tensor`. The dimension along which to split.
-
stringname - A name for the operation (optional).
-
objectsplit_dim - Deprecated old name for axis.
Returns
-
IList<SparseTensor> - `num_split` `SparseTensor` objects resulting from splitting `value`.
IList<SparseTensor> sparse_split(ImplicitContainer<T> keyword_required, int sp_input, Nullable<int> num_split, Nullable<int> axis, string name, object split_dim)
Split a `SparseTensor` into `num_split` tensors along `axis`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(split_dim)`. They will be removed in a future version.
Instructions for updating:
split_dim is deprecated, use axis instead If the `sp_input.dense_shape[axis]` is not an integer multiple of `num_split`
each slice starting from 0:`shape[axis] % num_split` gets extra one
dimension. For example, if `axis = 1` and `num_split = 2` and the
input is: input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: output_tensor[0] =
[ a ]
[b c ] output_tensor[1] =
[ d e ]
[ ]
Parameters
-
ImplicitContainer<T>keyword_required - Python 2 standin for * (temporary for argument reorder)
-
intsp_input - The `SparseTensor` to split.
-
Nullable<int>num_split - A Python integer. The number of ways to split.
-
Nullable<int>axis - A 0-D `int32` `Tensor`. The dimension along which to split.
-
stringname - A name for the operation (optional).
-
objectsplit_dim - Deprecated old name for axis.
Returns
-
IList<SparseTensor> - `num_split` `SparseTensor` objects resulting from splitting `value`.
IList<SparseTensor> sparse_split(ImplicitContainer<T> keyword_required, object sp_input, Nullable<int> num_split, Nullable<int> axis, string name, object split_dim)
Split a `SparseTensor` into `num_split` tensors along `axis`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(split_dim)`. They will be removed in a future version.
Instructions for updating:
split_dim is deprecated, use axis instead If the `sp_input.dense_shape[axis]` is not an integer multiple of `num_split`
each slice starting from 0:`shape[axis] % num_split` gets extra one
dimension. For example, if `axis = 1` and `num_split = 2` and the
input is: input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: output_tensor[0] =
[ a ]
[b c ] output_tensor[1] =
[ d e ]
[ ]
Parameters
-
ImplicitContainer<T>keyword_required - Python 2 standin for * (temporary for argument reorder)
-
objectsp_input - The `SparseTensor` to split.
-
Nullable<int>num_split - A Python integer. The number of ways to split.
-
Nullable<int>axis - A 0-D `int32` `Tensor`. The dimension along which to split.
-
stringname - A name for the operation (optional).
-
objectsplit_dim - Deprecated old name for axis.
Returns
-
IList<SparseTensor> - `num_split` `SparseTensor` objects resulting from splitting `value`.
object sparse_split_dyn(ImplicitContainer<T> keyword_required, object sp_input, object num_split, object axis, object name, object split_dim)
Split a `SparseTensor` into `num_split` tensors along `axis`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(split_dim)`. They will be removed in a future version.
Instructions for updating:
split_dim is deprecated, use axis instead If the `sp_input.dense_shape[axis]` is not an integer multiple of `num_split`
each slice starting from 0:`shape[axis] % num_split` gets extra one
dimension. For example, if `axis = 1` and `num_split = 2` and the
input is: input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: output_tensor[0] =
[ a ]
[b c ] output_tensor[1] =
[ d e ]
[ ]
Parameters
-
ImplicitContainer<T>keyword_required - Python 2 standin for * (temporary for argument reorder)
-
objectsp_input - The `SparseTensor` to split.
-
objectnum_split - A Python integer. The number of ways to split.
-
objectaxis - A 0-D `int32` `Tensor`. The dimension along which to split.
-
objectname - A name for the operation (optional).
-
objectsplit_dim - Deprecated old name for axis.
Returns
-
object - `num_split` `SparseTensor` objects resulting from splitting `value`.
Tensor sparse_tensor_dense_matmul(IGraphNodeBase sp_a, ResourceVariable b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
IGraphNodeBasesp_a - SparseTensor A, of rank 2.
-
ResourceVariableb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(PythonClassContainer sp_a, ResourceVariable b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
PythonClassContainersp_a - SparseTensor A, of rank 2.
-
ResourceVariableb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(IEnumerable<IGraphNodeBase> sp_a, ValueTuple<SparseTensor, int> b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
IEnumerable<IGraphNodeBase>sp_a - SparseTensor A, of rank 2.
-
ValueTuple<SparseTensor, int>b - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(PythonClassContainer sp_a, ReplicatedVariable b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
PythonClassContainersp_a - SparseTensor A, of rank 2.
-
ReplicatedVariableb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(IEnumerable<IGraphNodeBase> sp_a, ReplicatedVariable b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
IEnumerable<IGraphNodeBase>sp_a - SparseTensor A, of rank 2.
-
ReplicatedVariableb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(PythonClassContainer sp_a, ValueTuple<SparseTensor, int> b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
PythonClassContainersp_a - SparseTensor A, of rank 2.
-
ValueTuple<SparseTensor, int>b - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(object sp_a, ValueTuple<SparseTensor, int> b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
objectsp_a - SparseTensor A, of rank 2.
-
ValueTuple<SparseTensor, int>b - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(object sp_a, ReplicatedVariable b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
objectsp_a - SparseTensor A, of rank 2.
-
ReplicatedVariableb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(object sp_a, ResourceVariable b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
objectsp_a - SparseTensor A, of rank 2.
-
ResourceVariableb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(PythonClassContainer sp_a, IGraphNodeBase b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
PythonClassContainersp_a - SparseTensor A, of rank 2.
-
IGraphNodeBaseb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(object sp_a, IGraphNodeBase b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
objectsp_a - SparseTensor A, of rank 2.
-
IGraphNodeBaseb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(IEnumerable<object> sp_a, IGraphNodeBase b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
IEnumerable<object>sp_a - SparseTensor A, of rank 2.
-
IGraphNodeBaseb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(IGraphNodeBase sp_a, ValueTuple<SparseTensor, int> b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
IGraphNodeBasesp_a - SparseTensor A, of rank 2.
-
ValueTuple<SparseTensor, int>b - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(IGraphNodeBase sp_a, ReplicatedVariable b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
IGraphNodeBasesp_a - SparseTensor A, of rank 2.
-
ReplicatedVariableb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(IGraphNodeBase sp_a, IGraphNodeBase b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
IGraphNodeBasesp_a - SparseTensor A, of rank 2.
-
IGraphNodeBaseb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_dense_matmul(IEnumerable<IGraphNodeBase> sp_a, ResourceVariable b, bool adjoint_a, bool adjoint_b, string name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
IEnumerable<IGraphNodeBase>sp_a - SparseTensor A, of rank 2.
-
ResourceVariableb - A dense Matrix with the same dtype as sp_a.
-
booladjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
booladjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
object sparse_tensor_dense_matmul_dyn(object sp_a, object b, ImplicitContainer<T> adjoint_a, ImplicitContainer<T> adjoint_b, object name)
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
Parameters
-
objectsp_a - SparseTensor A, of rank 2.
-
objectb - A dense Matrix with the same dtype as sp_a.
-
ImplicitContainer<T>adjoint_a - Use the adjoint of A in the matrix multiply. If A is complex, this is transpose(conj(A)). Otherwise it's transpose(A).
-
ImplicitContainer<T>adjoint_b - Use the adjoint of B in the matrix multiply. If B is complex, this is transpose(conj(B)). Otherwise it's transpose(B).
-
objectname - A name prefix for the returned tensors (optional)
Returns
-
object - A dense matrix (pseudo-code in dense np.matrix notation): `A = A.H if adjoint_a else A` `B = B.H if adjoint_b else B` `return A*B`
Tensor sparse_tensor_to_dense(PythonClassContainer sp_input, string default_value, bool validate_indices, PythonFunctionContainer name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
PythonClassContainersp_input - The input `SparseTensor`.
-
stringdefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(object sp_input, int default_value, bool validate_indices, PythonFunctionContainer name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
intdefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(PythonClassContainer sp_input, int default_value, bool validate_indices, string name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
PythonClassContainersp_input - The input `SparseTensor`.
-
intdefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(PythonClassContainer sp_input, int default_value, bool validate_indices, PythonFunctionContainer name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
PythonClassContainersp_input - The input `SparseTensor`.
-
intdefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(PythonClassContainer sp_input, bool default_value, bool validate_indices, string name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
PythonClassContainersp_input - The input `SparseTensor`.
-
booldefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(PythonClassContainer sp_input, bool default_value, bool validate_indices, PythonFunctionContainer name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
PythonClassContainersp_input - The input `SparseTensor`.
-
booldefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(object sp_input, bool default_value, bool validate_indices, PythonFunctionContainer name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
booldefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(object sp_input, bool default_value, bool validate_indices, string name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
booldefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(object sp_input, int default_value, bool validate_indices, string name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
intdefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(PythonClassContainer sp_input, string default_value, bool validate_indices, string name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
PythonClassContainersp_input - The input `SparseTensor`.
-
stringdefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(object sp_input, string default_value, bool validate_indices, PythonFunctionContainer name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
stringdefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
PythonFunctionContainername - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_tensor_to_dense(object sp_input, string default_value, bool validate_indices, string name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
stringdefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name prefix for the returned tensors (optional).
Returns
-
Tensor - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
object sparse_tensor_to_dense_dyn(object sp_input, object default_value, ImplicitContainer<T> validate_indices, object name)
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
Parameters
-
objectsp_input - The input `SparseTensor`.
-
objectdefault_value - Scalar value to set for indices not specified in `sp_input`. Defaults to zero.
-
ImplicitContainer<T>validate_indices - A boolean value. If `True`, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
objectname - A name prefix for the returned tensors (optional).
Returns
-
object - A dense tensor with shape `sp_input.dense_shape` and values specified by the non-empty values in `sp_input`. Indices not in `sp_input` are assigned `default_value`.
Tensor sparse_to_dense(int sparse_indices, IEnumerable<int> output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
intsparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IEnumerable<int>output_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(IGraphNodeBase sparse_indices, IDictionary<object, object> output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
IGraphNodeBasesparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IDictionary<object, object>output_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(IEnumerable<IGraphNodeBase> sparse_indices, IGraphNodeBase output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
IEnumerable<IGraphNodeBase>sparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IGraphNodeBaseoutput_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(int sparse_indices, IGraphNodeBase output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
intsparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IGraphNodeBaseoutput_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(int sparse_indices, IDictionary<object, object> output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
intsparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IDictionary<object, object>output_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(object sparse_indices, ndarray output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
objectsparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
ndarrayoutput_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(int sparse_indices, ndarray output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
intsparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
ndarrayoutput_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(IGraphNodeBase sparse_indices, ndarray output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
IGraphNodeBasesparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
ndarrayoutput_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(IEnumerable<IGraphNodeBase> sparse_indices, IDictionary<object, object> output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
IEnumerable<IGraphNodeBase>sparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IDictionary<object, object>output_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(IGraphNodeBase sparse_indices, IEnumerable<int> output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
IGraphNodeBasesparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IEnumerable<int>output_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(IGraphNodeBase sparse_indices, IGraphNodeBase output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
IGraphNodeBasesparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IGraphNodeBaseoutput_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(object sparse_indices, IEnumerable<int> output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
objectsparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IEnumerable<int>output_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(IEnumerable<IGraphNodeBase> sparse_indices, ndarray output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
IEnumerable<IGraphNodeBase>sparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
ndarrayoutput_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(object sparse_indices, IGraphNodeBase output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
objectsparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IGraphNodeBaseoutput_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(IEnumerable<IGraphNodeBase> sparse_indices, IEnumerable<int> output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
IEnumerable<IGraphNodeBase>sparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IEnumerable<int>output_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_dense(object sparse_indices, IDictionary<object, object> output_shape, object sparse_values, ImplicitContainer<T> default_value, bool validate_indices, string name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
objectsparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
IDictionary<object, object>output_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
boolvalidate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
object sparse_to_dense_dyn(object sparse_indices, object output_shape, object sparse_values, ImplicitContainer<T> default_value, ImplicitContainer<T> validate_indices, object name)
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Parameters
-
objectsparse_indices - A 0-D, 1-D, or 2-D `Tensor` of type `int32` or `int64`. `sparse_indices[i]` contains the complete index where `sparse_values[i]` will be placed.
-
objectoutput_shape - A 1-D `Tensor` of the same type as `sparse_indices`. Shape of the dense output tensor.
-
objectsparse_values - A 0-D or 1-D `Tensor`. Values corresponding to each row of `sparse_indices`, or a scalar value to be used for all sparse indices.
-
ImplicitContainer<T>default_value - A 0-D `Tensor` of the same type as `sparse_values`. Value to set for indices not specified in `sparse_indices`. Defaults to zero.
-
ImplicitContainer<T>validate_indices - A boolean value. If True, indices are checked to make sure they are sorted in lexicographic order and that there are no repeats.
-
objectname - A name for the operation (optional).
Returns
-
object - Dense `Tensor` of shape `output_shape`. Has the same type as `sparse_values`.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
Tensor sparse_to_indicator(SparseTensor sp_input, Nullable<int> vocab_size, string name)
Converts a `SparseTensor` of ids into a dense bool indicator tensor. The last dimension of `sp_input.indices` is discarded and replaced with
the values of `sp_input`. If `sp_input.dense_shape = [D0, D1,..., Dn, K]`,
then `output.shape = [D0, D1,..., Dn, vocab_size]`, where output[d_0, d_1,..., d_n, sp_input[d_0, d_1,..., d_n, k]] = True and False elsewhere in `output`. For example, if `sp_input.dense_shape = [2, 3, 4]` with non-empty values: [0, 0, 0]: 0
[0, 1, 0]: 10
[1, 0, 3]: 103
[1, 1, 1]: 150
[1, 1, 2]: 149
[1, 1, 3]: 150
[1, 2, 1]: 121 and `vocab_size = 200`, then the output will be a `[2, 3, 200]` dense bool
tensor with False everywhere except at positions (0, 0, 0), (0, 1, 10), (1, 0, 103), (1, 1, 149), (1, 1, 150),
(1, 2, 121). Note that repeats are allowed in the input SparseTensor.
This op is useful for converting `SparseTensor`s into dense formats for
compatibility with ops that expect dense tensors. The input `SparseTensor` must be in row-major order.
Parameters
-
SparseTensorsp_input - A `SparseTensor` with `values` property of type `int32` or `int64`.
-
Nullable<int>vocab_size - A scalar int64 Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_input.values < vocab_size)`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
Tensor - A dense bool indicator tensor representing the indices with specified value.
object sparse_to_indicator_dyn(object sp_input, object vocab_size, object name)
Converts a `SparseTensor` of ids into a dense bool indicator tensor. The last dimension of `sp_input.indices` is discarded and replaced with
the values of `sp_input`. If `sp_input.dense_shape = [D0, D1,..., Dn, K]`,
then `output.shape = [D0, D1,..., Dn, vocab_size]`, where output[d_0, d_1,..., d_n, sp_input[d_0, d_1,..., d_n, k]] = True and False elsewhere in `output`. For example, if `sp_input.dense_shape = [2, 3, 4]` with non-empty values: [0, 0, 0]: 0
[0, 1, 0]: 10
[1, 0, 3]: 103
[1, 1, 1]: 150
[1, 1, 2]: 149
[1, 1, 3]: 150
[1, 2, 1]: 121 and `vocab_size = 200`, then the output will be a `[2, 3, 200]` dense bool
tensor with False everywhere except at positions (0, 0, 0), (0, 1, 10), (1, 0, 103), (1, 1, 149), (1, 1, 150),
(1, 2, 121). Note that repeats are allowed in the input SparseTensor.
This op is useful for converting `SparseTensor`s into dense formats for
compatibility with ops that expect dense tensors. The input `SparseTensor` must be in row-major order.
Parameters
-
objectsp_input - A `SparseTensor` with `values` property of type `int32` or `int64`.
-
objectvocab_size - A scalar int64 Tensor (or Python int) containing the new size of the last dimension, `all(0 <= sp_input.values < vocab_size)`.
-
objectname - A name prefix for the returned tensors (optional)
Returns
-
object - A dense bool indicator tensor representing the indices with specified value.
SparseTensor sparse_transpose(SparseTensor sp_input, object perm, string name)
Transposes a `SparseTensor` The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. For example, if `sp_input` has shape `[4, 5]` and `indices` / `values`: [0, 3]: b
[0, 1]: a
[3, 1]: d
[2, 0]: c then the output will be a `SparseTensor` of shape `[5, 4]` and
`indices` / `values`: [0, 2]: c
[1, 0]: a
[1, 3]: d
[3, 0]: b
Parameters
-
SparseTensorsp_input - The input `SparseTensor`.
-
objectperm - A permutation of the dimensions of `sp_input`.
-
stringname - A name prefix for the returned tensors (optional)
Returns
-
SparseTensor - A transposed `SparseTensor`.
object sparse_transpose_dyn(object sp_input, object perm, object name)
Transposes a `SparseTensor` The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. For example, if `sp_input` has shape `[4, 5]` and `indices` / `values`: [0, 3]: b
[0, 1]: a
[3, 1]: d
[2, 0]: c then the output will be a `SparseTensor` of shape `[5, 4]` and
`indices` / `values`: [0, 2]: c
[1, 0]: a
[1, 3]: d
[3, 0]: b
Parameters
-
objectsp_input - The input `SparseTensor`.
-
objectperm - A permutation of the dimensions of `sp_input`.
-
objectname - A name prefix for the returned tensors (optional)
Returns
-
object - A transposed `SparseTensor`.
object split(object value, IGraphNodeBase num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
objectvalue - The `Tensor` to split.
-
IGraphNodeBasenum_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(IEnumerable<IGraphNodeBase> value, int num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
IEnumerable<IGraphNodeBase>value - The `Tensor` to split.
-
intnum_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(object value, ValueTuple<int, object> num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
objectvalue - The `Tensor` to split.
-
ValueTuple<int, object>num_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(PythonClassContainer value, IEnumerable<int> num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
PythonClassContainervalue - The `Tensor` to split.
-
IEnumerable<int>num_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(PythonClassContainer value, IGraphNodeBase num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
PythonClassContainervalue - The `Tensor` to split.
-
IGraphNodeBasenum_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(IEnumerable<IGraphNodeBase> value, IGraphNodeBase num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
IEnumerable<IGraphNodeBase>value - The `Tensor` to split.
-
IGraphNodeBasenum_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(IEnumerable<IGraphNodeBase> value, IEnumerable<int> num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
IEnumerable<IGraphNodeBase>value - The `Tensor` to split.
-
IEnumerable<int>num_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(PythonClassContainer value, ValueTuple<int, object> num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
PythonClassContainervalue - The `Tensor` to split.
-
ValueTuple<int, object>num_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(IEnumerable<IGraphNodeBase> value, ValueTuple<int, object> num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
IEnumerable<IGraphNodeBase>value - The `Tensor` to split.
-
ValueTuple<int, object>num_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(object value, IEnumerable<int> num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
objectvalue - The `Tensor` to split.
-
IEnumerable<int>num_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(PythonClassContainer value, int num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
PythonClassContainervalue - The `Tensor` to split.
-
intnum_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split(object value, int num_or_size_splits, ImplicitContainer<T> axis, Nullable<int> num, string name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
objectvalue - The `Tensor` to split.
-
intnum_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
Nullable<int>num - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
stringname - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object split_dyn(object value, object num_or_size_splits, ImplicitContainer<T> axis, object num, ImplicitContainer<T> name)
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Parameters
-
objectvalue - The `Tensor` to split.
-
objectnum_or_size_splits - Either an integer indicating the number of splits along split_dim or a 1-D integer `Tensor` or Python list containing the sizes of each output tensor along split_dim. If a scalar then it must evenly divide `value.shape[axis]`; otherwise the sum of sizes along the split dimension must match that of the `value`.
-
ImplicitContainer<T>axis - An integer or scalar `int32` `Tensor`. The dimension along which to split. Must be in the range `[-rank(value), rank(value))`. Defaults to 0.
-
objectnum - Optional, used to specify the number of outputs when it cannot be inferred from the shape of `size_splits`.
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - if `num_or_size_splits` is a scalar returns `num_or_size_splits` `Tensor` objects; if `num_or_size_splits` is a 1-D Tensor returns `num_or_size_splits.get_shape[0]` `Tensor` objects resulting from splitting `value`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
object sqrt(IGraphNodeBase x, string name)
Computes square root of x element-wise. I.e., \\(y = \sqrt{x} = x^{1/2}\\).
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`. If `x` is a `SparseTensor`, returns `SparseTensor(x.indices, tf.math.sqrt(x.values,...), x.dense_shape)`
object sqrt_dyn(object x, object name)
Computes square root of x element-wise. I.e., \\(y = \sqrt{x} = x^{1/2}\\).
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`. If `x` is a `SparseTensor`, returns `SparseTensor(x.indices, tf.math.sqrt(x.values,...), x.dense_shape)`
object square(IGraphNodeBase x, string name)
Computes square of x element-wise. I.e., \\(y = x * x = x^2\\).
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`. If `x` is a `SparseTensor`, returns `SparseTensor(x.indices, tf.math.square(x.values,...), x.dense_shape)`
object square_dyn(object x, object name)
Computes square of x element-wise. I.e., \\(y = x * x = x^2\\).
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`. If `x` is a `SparseTensor`, returns `SparseTensor(x.indices, tf.math.square(x.values,...), x.dense_shape)`
object squared_difference(double x, double y, string name)
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object squared_difference(int x, double y, string name)
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object squared_difference(double x, IGraphNodeBase y, string name)
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object squared_difference(int x, int y, string name)
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object squared_difference(int x, IGraphNodeBase y, string name)
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object squared_difference(IGraphNodeBase x, double y, string name)
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object squared_difference(IGraphNodeBase x, int y, string name)
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object squared_difference(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object squared_difference(double x, int y, string name)
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object squared_difference_dyn(object x, object y, object name)
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Tensor squeeze(IGraphNodeBase input, int axis, string name, object squeeze_dims)
Removes dimensions of size 1 from the shape of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(squeeze_dims)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation returns a tensor of the same type with
all dimensions of size 1 removed. If you don't want to remove all size 1
dimensions, you can remove specific size 1 dimensions by specifying
`axis`.
Or, to remove specific size 1 dimensions:
Note: if `input` is a
tf.RaggedTensor, then this operation takes `O(N)`
time, where `N` is the number of elements in the squeezed dimensions.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. The `input` to squeeze.
-
intaxis - An optional list of `ints`. Defaults to `[]`. If specified, only squeezes the dimensions listed. The dimension index starts at 0. It is an error to squeeze a dimension that is not 1. Must be in the range `[-rank(input), rank(input))`. Must be specified if `input` is a `RaggedTensor`.
-
stringname - A name for the operation (optional).
-
objectsqueeze_dims - Deprecated keyword argument that is now axis.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`. Contains the same data as `input`, but has one or more dimensions of size 1 removed.
Show Example
# 't' is a tensor of shape [1, 2, 1, 3, 1, 1]
tf.shape(tf.squeeze(t)) # [2, 3]
Tensor squeeze(IGraphNodeBase input, IEnumerable<int> axis, string name, object squeeze_dims)
Removes dimensions of size 1 from the shape of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(squeeze_dims)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation returns a tensor of the same type with
all dimensions of size 1 removed. If you don't want to remove all size 1
dimensions, you can remove specific size 1 dimensions by specifying
`axis`.
Or, to remove specific size 1 dimensions:
Note: if `input` is a
tf.RaggedTensor, then this operation takes `O(N)`
time, where `N` is the number of elements in the squeezed dimensions.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. The `input` to squeeze.
-
IEnumerable<int>axis - An optional list of `ints`. Defaults to `[]`. If specified, only squeezes the dimensions listed. The dimension index starts at 0. It is an error to squeeze a dimension that is not 1. Must be in the range `[-rank(input), rank(input))`. Must be specified if `input` is a `RaggedTensor`.
-
stringname - A name for the operation (optional).
-
objectsqueeze_dims - Deprecated keyword argument that is now axis.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`. Contains the same data as `input`, but has one or more dimensions of size 1 removed.
Show Example
# 't' is a tensor of shape [1, 2, 1, 3, 1, 1]
tf.shape(tf.squeeze(t)) # [2, 3]
Tensor squeeze(IGraphNodeBase input, IGraphNodeBase axis, string name, object squeeze_dims)
Removes dimensions of size 1 from the shape of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(squeeze_dims)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation returns a tensor of the same type with
all dimensions of size 1 removed. If you don't want to remove all size 1
dimensions, you can remove specific size 1 dimensions by specifying
`axis`.
Or, to remove specific size 1 dimensions:
Note: if `input` is a
tf.RaggedTensor, then this operation takes `O(N)`
time, where `N` is the number of elements in the squeezed dimensions.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. The `input` to squeeze.
-
IGraphNodeBaseaxis - An optional list of `ints`. Defaults to `[]`. If specified, only squeezes the dimensions listed. The dimension index starts at 0. It is an error to squeeze a dimension that is not 1. Must be in the range `[-rank(input), rank(input))`. Must be specified if `input` is a `RaggedTensor`.
-
stringname - A name for the operation (optional).
-
objectsqueeze_dims - Deprecated keyword argument that is now axis.
Returns
-
Tensor - A `Tensor`. Has the same type as `input`. Contains the same data as `input`, but has one or more dimensions of size 1 removed.
Show Example
# 't' is a tensor of shape [1, 2, 1, 3, 1, 1]
tf.shape(tf.squeeze(t)) # [2, 3]
object squeeze_dyn(object input, object axis, object name, object squeeze_dims)
Removes dimensions of size 1 from the shape of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(squeeze_dims)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation returns a tensor of the same type with
all dimensions of size 1 removed. If you don't want to remove all size 1
dimensions, you can remove specific size 1 dimensions by specifying
`axis`.
Or, to remove specific size 1 dimensions:
Note: if `input` is a
tf.RaggedTensor, then this operation takes `O(N)`
time, where `N` is the number of elements in the squeezed dimensions.
Parameters
-
objectinput - A `Tensor`. The `input` to squeeze.
-
objectaxis - An optional list of `ints`. Defaults to `[]`. If specified, only squeezes the dimensions listed. The dimension index starts at 0. It is an error to squeeze a dimension that is not 1. Must be in the range `[-rank(input), rank(input))`. Must be specified if `input` is a `RaggedTensor`.
-
objectname - A name for the operation (optional).
-
objectsqueeze_dims - Deprecated keyword argument that is now axis.
Returns
-
object - A `Tensor`. Has the same type as `input`. Contains the same data as `input`, but has one or more dimensions of size 1 removed.
Show Example
# 't' is a tensor of shape [1, 2, 1, 3, 1, 1]
tf.shape(tf.squeeze(t)) # [2, 3]
Tensor stack(object values, int axis, string name)
Stacks a list of rank-`R` tensors into one rank-`(R+1)` `RaggedTensor`. Given a list of tensors or ragged tensors with the same rank `R`
(`R >= axis`), returns a rank-`R+1` `RaggedTensor` `result` such that
`result[i0...iaxis]` is `[value[i0...iaxis] for value in values]`. #### Example:
Parameters
-
objectvalues - A list of
tf.Tensorortf.RaggedTensor. May not be empty. All `values` must have the same rank and the same dtype; but unliketf.stack, they can have arbitrary dimension sizes. -
intaxis - A python integer, indicating the dimension along which to stack.
(Note: Unlike
tf.stack, the `axis` parameter must be statically known.) Negative values are supported only if the rank of at least one `values` value is statically known. -
stringname - A name prefix for the returned tensor (optional).
Returns
-
Tensor - A `RaggedTensor` with rank `R+1`. `result.ragged_rank=1+max(axis, max(rt.ragged_rank for rt in values]))`.
Show Example
>>> t1 = tf.ragged.constant([[1, 2], [3, 4, 5]])
>>> t2 = tf.ragged.constant([[6], [7, 8, 9]])
>>> tf.ragged.stack([t1, t2], axis=0)
[[[1, 2], [3, 4, 5]], [[6], [7, 9, 0]]]
>>> tf.ragged.stack([t1, t2], axis=1)
[[[1, 2], [6]], [[3, 4, 5], [7, 8, 9]]]
Tensor stack(IEnumerable<IGraphNodeBase> values, int axis, string name)
Stacks a list of rank-`R` tensors into one rank-`(R+1)` `RaggedTensor`. Given a list of tensors or ragged tensors with the same rank `R`
(`R >= axis`), returns a rank-`R+1` `RaggedTensor` `result` such that
`result[i0...iaxis]` is `[value[i0...iaxis] for value in values]`. #### Example:
Parameters
-
IEnumerable<IGraphNodeBase>values - A list of
tf.Tensorortf.RaggedTensor. May not be empty. All `values` must have the same rank and the same dtype; but unliketf.stack, they can have arbitrary dimension sizes. -
intaxis - A python integer, indicating the dimension along which to stack.
(Note: Unlike
tf.stack, the `axis` parameter must be statically known.) Negative values are supported only if the rank of at least one `values` value is statically known. -
stringname - A name prefix for the returned tensor (optional).
Returns
-
Tensor - A `RaggedTensor` with rank `R+1`. `result.ragged_rank=1+max(axis, max(rt.ragged_rank for rt in values]))`.
Show Example
>>> t1 = tf.ragged.constant([[1, 2], [3, 4, 5]])
>>> t2 = tf.ragged.constant([[6], [7, 8, 9]])
>>> tf.ragged.stack([t1, t2], axis=0)
[[[1, 2], [3, 4, 5]], [[6], [7, 9, 0]]]
>>> tf.ragged.stack([t1, t2], axis=1)
[[[1, 2], [6]], [[3, 4, 5], [7, 8, 9]]]
object stack_dyn(object values, ImplicitContainer<T> axis, ImplicitContainer<T> name)
Stacks a list of rank-`R` tensors into one rank-`(R+1)` tensor. Packs the list of tensors in `values` into a tensor with rank one higher than
each tensor in `values`, by packing them along the `axis` dimension.
Given a list of length `N` of tensors of shape `(A, B, C)`; if `axis == 0` then the `output` tensor will have the shape `(N, A, B, C)`.
if `axis == 1` then the `output` tensor will have the shape `(A, N, B, C)`.
Etc.
This is the opposite of unstack. The numpy equivalent is
Parameters
-
objectvalues - A list of `Tensor` objects with the same shape and type.
-
ImplicitContainer<T>axis - An `int`. The axis to stack along. Defaults to the first dimension. Negative values wrap around, so the valid range is `[-(R+1), R+1)`.
-
ImplicitContainer<T>name - A name for this operation (optional).
Returns
-
object
Show Example
x = tf.constant([1, 4])
y = tf.constant([2, 5])
z = tf.constant([3, 6])
tf.stack([x, y, z]) # [[1, 4], [2, 5], [3, 6]] (Pack along first dim.)
tf.stack([x, y, z], axis=1) # [[1, 2, 3], [4, 5, 6]]
object stats_accumulator_scalar_add(IEnumerable<IGraphNodeBase> stats_accumulator_handles, IGraphNodeBase stamp_token, IEnumerable<object> partition_ids, IEnumerable<object> feature_ids, IEnumerable<object> gradients, IEnumerable<object> hessians, string name)
object stats_accumulator_scalar_add_dyn(object stats_accumulator_handles, object stamp_token, object partition_ids, object feature_ids, object gradients, object hessians, object name)
object stats_accumulator_scalar_deserialize(IGraphNodeBase stats_accumulator_handle, IGraphNodeBase stamp_token, IGraphNodeBase num_updates, IGraphNodeBase partition_ids, IGraphNodeBase feature_ids, IGraphNodeBase gradients, IGraphNodeBase hessians, string name)
object stats_accumulator_scalar_deserialize_dyn(object stats_accumulator_handle, object stamp_token, object num_updates, object partition_ids, object feature_ids, object gradients, object hessians, object name)
object stats_accumulator_scalar_flush(IGraphNodeBase stats_accumulator_handle, IGraphNodeBase stamp_token, IGraphNodeBase next_stamp_token, string name)
object stats_accumulator_scalar_flush_dyn(object stats_accumulator_handle, object stamp_token, object next_stamp_token, object name)
Tensor stats_accumulator_scalar_is_initialized(IGraphNodeBase stats_accumulator_handle, string name)
object stats_accumulator_scalar_is_initialized_dyn(object stats_accumulator_handle, object name)
object stats_accumulator_scalar_make_summary(IGraphNodeBase partition_ids, IGraphNodeBase feature_ids, IGraphNodeBase gradients, IGraphNodeBase hessians, string name)
object stats_accumulator_scalar_make_summary_dyn(object partition_ids, object feature_ids, object gradients, object hessians, object name)
Tensor stats_accumulator_scalar_resource_handle_op(string container, Byte[] shared_name, string name)
Tensor stats_accumulator_scalar_resource_handle_op(string container, object shared_name, string name)
Tensor stats_accumulator_scalar_resource_handle_op(string container, string shared_name, string name)
object stats_accumulator_scalar_resource_handle_op_dyn(ImplicitContainer<T> container, ImplicitContainer<T> shared_name, object name)
object stats_accumulator_scalar_serialize(IGraphNodeBase stats_accumulator_handle, string name)
object stats_accumulator_scalar_serialize_dyn(object stats_accumulator_handle, object name)
object stats_accumulator_tensor_add(IEnumerable<IGraphNodeBase> stats_accumulator_handles, IGraphNodeBase stamp_token, IEnumerable<object> partition_ids, IEnumerable<object> feature_ids, IEnumerable<object> gradients, IEnumerable<object> hessians, string name)
object stats_accumulator_tensor_add_dyn(object stats_accumulator_handles, object stamp_token, object partition_ids, object feature_ids, object gradients, object hessians, object name)
object stats_accumulator_tensor_deserialize(IGraphNodeBase stats_accumulator_handle, IGraphNodeBase stamp_token, IGraphNodeBase num_updates, IGraphNodeBase partition_ids, IGraphNodeBase feature_ids, IGraphNodeBase gradients, IGraphNodeBase hessians, string name)
object stats_accumulator_tensor_deserialize_dyn(object stats_accumulator_handle, object stamp_token, object num_updates, object partition_ids, object feature_ids, object gradients, object hessians, object name)
object stats_accumulator_tensor_flush(IGraphNodeBase stats_accumulator_handle, IGraphNodeBase stamp_token, IGraphNodeBase next_stamp_token, string name)
object stats_accumulator_tensor_flush_dyn(object stats_accumulator_handle, object stamp_token, object next_stamp_token, object name)
Tensor stats_accumulator_tensor_is_initialized(IGraphNodeBase stats_accumulator_handle, string name)
object stats_accumulator_tensor_is_initialized_dyn(object stats_accumulator_handle, object name)
object stats_accumulator_tensor_make_summary(IGraphNodeBase partition_ids, IGraphNodeBase feature_ids, IGraphNodeBase gradients, IGraphNodeBase hessians, string name)
object stats_accumulator_tensor_make_summary_dyn(object partition_ids, object feature_ids, object gradients, object hessians, object name)
Tensor stats_accumulator_tensor_resource_handle_op(string container, string shared_name, string name)
Tensor stats_accumulator_tensor_resource_handle_op(string container, Byte[] shared_name, string name)
Tensor stats_accumulator_tensor_resource_handle_op(string container, object shared_name, string name)
object stats_accumulator_tensor_resource_handle_op_dyn(ImplicitContainer<T> container, ImplicitContainer<T> shared_name, object name)
object stats_accumulator_tensor_serialize(IGraphNodeBase stats_accumulator_handle, string name)
object stats_accumulator_tensor_serialize_dyn(object stats_accumulator_handle, object name)
object stochastic_hard_routing_function(IGraphNodeBase input_data, IGraphNodeBase tree_parameters, IGraphNodeBase tree_biases, object tree_depth, object random_seed, string name)
object stochastic_hard_routing_function_dyn(object input_data, object tree_parameters, object tree_biases, object tree_depth, object random_seed, object name)
object stochastic_hard_routing_gradient(IGraphNodeBase input_data, IGraphNodeBase tree_parameters, IGraphNodeBase tree_biases, IGraphNodeBase path_probability, IGraphNodeBase path, object tree_depth, string name)
object stochastic_hard_routing_gradient_dyn(object input_data, object tree_parameters, object tree_biases, object path_probability, object path, object tree_depth, object name)
Tensor stop_gradient(IGraphNodeBase input, string name)
Stops gradient computation. When executed in a graph, this op outputs its input tensor as-is. When building ops to compute gradients, this op prevents the contribution of
its inputs to be taken into account. Normally, the gradient generator adds ops
to a graph to compute the derivatives of a specified 'loss' by recursively
finding out inputs that contributed to its computation. If you insert this op
in the graph it inputs are masked from the gradient generator. They are not
taken into account for computing gradients. This is useful any time you want to compute a value with TensorFlow but need
to pretend that the value was a constant. Some examples include: * The *EM* algorithm where the *M-step* should not involve backpropagation
through the output of the *E-step*.
* Contrastive divergence training of Boltzmann machines where, when
differentiating the energy function, the training must not backpropagate
through the graph that generated the samples from the model.
* Adversarial training, where no backprop should happen through the adversarial
example generation process.
Parameters
-
IGraphNodeBaseinput - A `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object stop_gradient_dyn(object input, object name)
Stops gradient computation. When executed in a graph, this op outputs its input tensor as-is. When building ops to compute gradients, this op prevents the contribution of
its inputs to be taken into account. Normally, the gradient generator adds ops
to a graph to compute the derivatives of a specified 'loss' by recursively
finding out inputs that contributed to its computation. If you insert this op
in the graph it inputs are masked from the gradient generator. They are not
taken into account for computing gradients. This is useful any time you want to compute a value with TensorFlow but need
to pretend that the value was a constant. Some examples include: * The *EM* algorithm where the *M-step* should not involve backpropagation
through the output of the *E-step*.
* Contrastive divergence training of Boltzmann machines where, when
differentiating the energy function, the training must not backpropagate
through the graph that generated the samples from the model.
* Adversarial training, where no backprop should happen through the adversarial
example generation process.
Parameters
-
objectinput - A `Tensor`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor strided_slice(IGraphNodeBase input_, IEnumerable<int> begin, IGraphNodeBase end, IGraphNodeBase strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, PythonFunctionContainer name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBaseend - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasestrides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IEnumerable<int> begin, IGraphNodeBase end, IEnumerable<int> strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, string name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBaseend - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>strides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IEnumerable<int> begin, IGraphNodeBase end, IGraphNodeBase strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, string name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBaseend - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasestrides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IEnumerable<int> begin, IGraphNodeBase end, IEnumerable<int> strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, PythonFunctionContainer name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBaseend - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>strides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IGraphNodeBase begin, IEnumerable<int> end, IEnumerable<int> strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, PythonFunctionContainer name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>end - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>strides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IGraphNodeBase begin, IEnumerable<int> end, IEnumerable<int> strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, string name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>end - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>strides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IGraphNodeBase begin, IEnumerable<int> end, IGraphNodeBase strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, PythonFunctionContainer name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>end - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasestrides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IEnumerable<int> begin, IEnumerable<int> end, IGraphNodeBase strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, string name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>end - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasestrides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IEnumerable<int> begin, IEnumerable<int> end, IEnumerable<int> strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, string name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>end - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>strides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IEnumerable<int> begin, IEnumerable<int> end, IGraphNodeBase strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, PythonFunctionContainer name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>end - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasestrides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IGraphNodeBase begin, IGraphNodeBase end, IGraphNodeBase strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, string name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBaseend - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasestrides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IGraphNodeBase begin, IGraphNodeBase end, IGraphNodeBase strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, PythonFunctionContainer name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBaseend - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasestrides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IGraphNodeBase begin, IGraphNodeBase end, IEnumerable<int> strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, string name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBaseend - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>strides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IGraphNodeBase begin, IGraphNodeBase end, IEnumerable<int> strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, PythonFunctionContainer name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IGraphNodeBaseend - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>strides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IGraphNodeBase begin, IEnumerable<int> end, IGraphNodeBase strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, string name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IGraphNodeBasebegin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>end - An `int32` or `int64` `Tensor`.
-
IGraphNodeBasestrides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor strided_slice(IGraphNodeBase input_, IEnumerable<int> begin, IEnumerable<int> end, IEnumerable<int> strides, int begin_mask, int end_mask, int ellipsis_mask, int new_axis_mask, int shrink_axis_mask, object var, PythonFunctionContainer name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
IGraphNodeBaseinput_ - A `Tensor`.
-
IEnumerable<int>begin - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>end - An `int32` or `int64` `Tensor`.
-
IEnumerable<int>strides - An `int32` or `int64` `Tensor`.
-
intbegin_mask - An `int32` mask.
-
intend_mask - An `int32` mask.
-
intellipsis_mask - An `int32` mask.
-
intnew_axis_mask - An `int32` mask.
-
intshrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
object strided_slice_dyn(object input_, object begin, object end, object strides, ImplicitContainer<T> begin_mask, ImplicitContainer<T> end_mask, ImplicitContainer<T> ellipsis_mask, ImplicitContainer<T> new_axis_mask, ImplicitContainer<T> shrink_axis_mask, object var, object name)
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Parameters
-
objectinput_ - A `Tensor`.
-
objectbegin - An `int32` or `int64` `Tensor`.
-
objectend - An `int32` or `int64` `Tensor`.
-
objectstrides - An `int32` or `int64` `Tensor`.
-
ImplicitContainer<T>begin_mask - An `int32` mask.
-
ImplicitContainer<T>end_mask - An `int32` mask.
-
ImplicitContainer<T>ellipsis_mask - An `int32` mask.
-
ImplicitContainer<T>new_axis_mask - An `int32` mask.
-
ImplicitContainer<T>shrink_axis_mask - An `int32` mask.
-
objectvar - The variable corresponding to `input_` or None
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` the same type as `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
Tensor string_join(IEnumerable<object> inputs, string separator, string name)
Joins the strings in the given list of string tensors into one tensor; with the given separator (default is an empty separator).
Parameters
-
IEnumerable<object>inputs - A list of at least 1 `Tensor` objects with type `string`. A list of string tensors. The tensors must all have the same shape, or be scalars. Scalars may be mixed in; these will be broadcast to the shape of non-scalar inputs.
-
stringseparator - An optional `string`. Defaults to `""`. string, an optional join separator.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `string`.
object string_join_dyn(object inputs, ImplicitContainer<T> separator, object name)
Joins the strings in the given list of string tensors into one tensor; with the given separator (default is an empty separator).
Parameters
-
objectinputs - A list of at least 1 `Tensor` objects with type `string`. A list of string tensors. The tensors must all have the same shape, or be scalars. Scalars may be mixed in; these will be broadcast to the shape of non-scalar inputs.
-
ImplicitContainer<T>separator - An optional `string`. Defaults to `""`. string, an optional join separator.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `string`.
object string_list_attr(object a, object b, string name)
object string_list_attr_dyn(object a, object b, object name)
object string_split(IEnumerable<object> source, string sep, bool skip_empty, object delimiter, string result_type, string name)
Split elements of `source` based on `delimiter`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(delimiter)`. They will be removed in a future version.
Instructions for updating:
delimiter is deprecated, please use sep instead. Let N be the size of `source` (typically N will be the batch size). Split each
element of `source` based on `delimiter` and return a `SparseTensor`
or `RaggedTensor` containing the split tokens. Empty tokens are ignored. If `sep` is an empty string, each element of the `source` is split
into individual strings, each containing one byte. (This includes splitting
multibyte sequences of UTF-8.) If delimiter contains multiple bytes, it is
treated as a set of delimiters with each considered a potential split point. Examples:
Parameters
-
IEnumerable<object>source - `1-D` string `Tensor`, the strings to split.
-
stringsep - `0-D` string `Tensor`, the delimiter character, the string should be length 0 or 1. Default is ' '.
-
boolskip_empty - A `bool`. If `True`, skip the empty strings from the result.
-
objectdelimiter - deprecated alias for `sep`.
-
stringresult_type - The tensor type for the result: one of `"RaggedTensor"` or `"SparseTensor"`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `SparseTensor` or `RaggedTensor` of rank `2`, the strings split according to the delimiter. The first column of the indices corresponds to the row in `source` and the second column corresponds to the index of the split component in this row.
Show Example
>>> tf.strings.split(['hello world', 'a b c'])
tf.SparseTensor(indices=[[0, 0], [0, 1], [1, 0], [1, 1], [1, 2]],
values=['hello', 'world', 'a', 'b', 'c']
dense_shape=[2, 3]) >>> tf.strings.split(['hello world', 'a b c'], result_type="RaggedTensor")
object string_split_dyn(object source, object sep, ImplicitContainer<T> skip_empty, object delimiter, ImplicitContainer<T> result_type, object name)
Split elements of `source` based on `delimiter`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(delimiter)`. They will be removed in a future version.
Instructions for updating:
delimiter is deprecated, please use sep instead. Let N be the size of `source` (typically N will be the batch size). Split each
element of `source` based on `delimiter` and return a `SparseTensor`
or `RaggedTensor` containing the split tokens. Empty tokens are ignored. If `sep` is an empty string, each element of the `source` is split
into individual strings, each containing one byte. (This includes splitting
multibyte sequences of UTF-8.) If delimiter contains multiple bytes, it is
treated as a set of delimiters with each considered a potential split point. Examples:
Parameters
-
objectsource - `1-D` string `Tensor`, the strings to split.
-
objectsep - `0-D` string `Tensor`, the delimiter character, the string should be length 0 or 1. Default is ' '.
-
ImplicitContainer<T>skip_empty - A `bool`. If `True`, skip the empty strings from the result.
-
objectdelimiter - deprecated alias for `sep`.
-
ImplicitContainer<T>result_type - The tensor type for the result: one of `"RaggedTensor"` or `"SparseTensor"`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `SparseTensor` or `RaggedTensor` of rank `2`, the strings split according to the delimiter. The first column of the indices corresponds to the row in `source` and the second column corresponds to the index of the split component in this row.
Show Example
>>> tf.strings.split(['hello world', 'a b c'])
tf.SparseTensor(indices=[[0, 0], [0, 1], [1, 0], [1, 1], [1, 2]],
values=['hello', 'world', 'a', 'b', 'c']
dense_shape=[2, 3]) >>> tf.strings.split(['hello world', 'a b c'], result_type="RaggedTensor")
Tensor string_strip(IGraphNodeBase input, string name)
Strip leading and trailing whitespaces from the Tensor.
Parameters
-
IGraphNodeBaseinput - A `Tensor` of type `string`. A string `Tensor` of any shape.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `string`.
object string_strip_dyn(object input, object name)
Strip leading and trailing whitespaces from the Tensor.
Parameters
-
objectinput - A `Tensor` of type `string`. A string `Tensor` of any shape.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `string`.
Tensor string_to_hash_bucket(object string_tensor, object num_buckets, string name, object input)
Converts each string in the input Tensor to its hash mod by a number of buckets. The hash function is deterministic on the content of the string within the
process. Note that the hash function may change from time to time.
This functionality will be deprecated and it's recommended to use
`tf.string_to_hash_bucket_fast()` or `tf.string_to_hash_bucket_strong()`.
Parameters
-
objectstring_tensor - A `Tensor` of type `string`.
-
objectnum_buckets - An `int` that is `>= 1`. The number of buckets.
-
stringname - A name for the operation (optional).
-
objectinput
Returns
-
Tensor - A `Tensor` of type `int64`.
object string_to_hash_bucket_dyn(object string_tensor, object num_buckets, object name, object input)
Converts each string in the input Tensor to its hash mod by a number of buckets. The hash function is deterministic on the content of the string within the
process. Note that the hash function may change from time to time.
This functionality will be deprecated and it's recommended to use
`tf.string_to_hash_bucket_fast()` or `tf.string_to_hash_bucket_strong()`.
Parameters
-
objectstring_tensor - A `Tensor` of type `string`.
-
objectnum_buckets - An `int` that is `>= 1`. The number of buckets.
-
objectname - A name for the operation (optional).
-
objectinput
Returns
-
object - A `Tensor` of type `int64`.
Tensor string_to_hash_bucket_fast(IGraphNodeBase input, int num_buckets, string name)
Converts each string in the input Tensor to its hash mod by a number of buckets. The hash function is deterministic on the content of the string within the
process and will never change. However, it is not suitable for cryptography.
This function may be used when CPU time is scarce and inputs are trusted or
unimportant. There is a risk of adversaries constructing inputs that all hash
to the same bucket. To prevent this problem, use a strong hash function with
tf.string_to_hash_bucket_strong.
Parameters
-
IGraphNodeBaseinput - A `Tensor` of type `string`. The strings to assign a hash bucket.
-
intnum_buckets - An `int` that is `>= 1`. The number of buckets.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `int64`.
object string_to_hash_bucket_fast_dyn(object input, object num_buckets, object name)
Converts each string in the input Tensor to its hash mod by a number of buckets. The hash function is deterministic on the content of the string within the
process and will never change. However, it is not suitable for cryptography.
This function may be used when CPU time is scarce and inputs are trusted or
unimportant. There is a risk of adversaries constructing inputs that all hash
to the same bucket. To prevent this problem, use a strong hash function with
tf.string_to_hash_bucket_strong.
Parameters
-
objectinput - A `Tensor` of type `string`. The strings to assign a hash bucket.
-
objectnum_buckets - An `int` that is `>= 1`. The number of buckets.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `int64`.
Tensor string_to_hash_bucket_strong(IGraphNodeBase input, int num_buckets, IEnumerable<int> key, string name)
Converts each string in the input Tensor to its hash mod by a number of buckets. The hash function is deterministic on the content of the string within the
process. The hash function is a keyed hash function, where attribute `key`
defines the key of the hash function. `key` is an array of 2 elements. A strong hash is important when inputs may be malicious, e.g. URLs with
additional components. Adversaries could try to make their inputs hash to the
same bucket for a denial-of-service attack or to skew the results. A strong
hash can be used to make it difficult to find inputs with a skewed hash value
distribution over buckets. This requires that the hash function is
seeded by a high-entropy (random) "key" unknown to the adversary. The additional robustness comes at a cost of roughly 4x higher compute
time than
tf.string_to_hash_bucket_fast.
Parameters
-
IGraphNodeBaseinput - A `Tensor` of type `string`. The strings to assign a hash bucket.
-
intnum_buckets - An `int` that is `>= 1`. The number of buckets.
-
IEnumerable<int>key - A list of `ints`. The key used to seed the hash function, passed as a list of two uint64 elements.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `int64`.
object string_to_hash_bucket_strong_dyn(object input, object num_buckets, object key, object name)
Converts each string in the input Tensor to its hash mod by a number of buckets. The hash function is deterministic on the content of the string within the
process. The hash function is a keyed hash function, where attribute `key`
defines the key of the hash function. `key` is an array of 2 elements. A strong hash is important when inputs may be malicious, e.g. URLs with
additional components. Adversaries could try to make their inputs hash to the
same bucket for a denial-of-service attack or to skew the results. A strong
hash can be used to make it difficult to find inputs with a skewed hash value
distribution over buckets. This requires that the hash function is
seeded by a high-entropy (random) "key" unknown to the adversary. The additional robustness comes at a cost of roughly 4x higher compute
time than
tf.string_to_hash_bucket_fast.
Parameters
-
objectinput - A `Tensor` of type `string`. The strings to assign a hash bucket.
-
objectnum_buckets - An `int` that is `>= 1`. The number of buckets.
-
objectkey - A list of `ints`. The key used to seed the hash function, passed as a list of two uint64 elements.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `int64`.
Tensor string_to_number(ValueTuple<double, object> string_tensor, ImplicitContainer<T> out_type, string name, object input)
Converts each string in the input Tensor to the specified numeric type. (Note that int32 overflow results in an error while float overflow
results in a rounded value.)
Parameters
-
ValueTuple<double, object>string_tensor - A `Tensor` of type `string`.
-
ImplicitContainer<T>out_type - An optional
tf.DTypefrom: `tf.float32, tf.float64, tf.int32, tf.int64`. Defaults totf.float32. The numeric type to interpret each string in `string_tensor` as. -
stringname - A name for the operation (optional).
-
objectinput
Returns
-
Tensor - A `Tensor` of type `out_type`.
Tensor string_to_number(RaggedTensor string_tensor, ImplicitContainer<T> out_type, string name, object input)
Converts each string in the input Tensor to the specified numeric type. (Note that int32 overflow results in an error while float overflow
results in a rounded value.)
Parameters
-
RaggedTensorstring_tensor - A `Tensor` of type `string`.
-
ImplicitContainer<T>out_type - An optional
tf.DTypefrom: `tf.float32, tf.float64, tf.int32, tf.int64`. Defaults totf.float32. The numeric type to interpret each string in `string_tensor` as. -
stringname - A name for the operation (optional).
-
objectinput
Returns
-
Tensor - A `Tensor` of type `out_type`.
Tensor string_to_number(IEnumerable<double> string_tensor, ImplicitContainer<T> out_type, string name, object input)
Converts each string in the input Tensor to the specified numeric type. (Note that int32 overflow results in an error while float overflow
results in a rounded value.)
Parameters
-
IEnumerable<double>string_tensor - A `Tensor` of type `string`.
-
ImplicitContainer<T>out_type - An optional
tf.DTypefrom: `tf.float32, tf.float64, tf.int32, tf.int64`. Defaults totf.float32. The numeric type to interpret each string in `string_tensor` as. -
stringname - A name for the operation (optional).
-
objectinput
Returns
-
Tensor - A `Tensor` of type `out_type`.
object string_to_number_dyn(object string_tensor, ImplicitContainer<T> out_type, object name, object input)
Converts each string in the input Tensor to the specified numeric type. (Note that int32 overflow results in an error while float overflow
results in a rounded value.)
Parameters
-
objectstring_tensor - A `Tensor` of type `string`.
-
ImplicitContainer<T>out_type - An optional
tf.DTypefrom: `tf.float32, tf.float64, tf.int32, tf.int64`. Defaults totf.float32. The numeric type to interpret each string in `string_tensor` as. -
objectname - A name for the operation (optional).
-
objectinput
Returns
-
object - A `Tensor` of type `out_type`.
Tensor stub_resource_handle_op(string container, string shared_name, string name)
object stub_resource_handle_op_dyn(ImplicitContainer<T> container, ImplicitContainer<T> shared_name, object name)
Tensor substr(object input, object pos, object len, string name, string unit)
Return substrings from `Tensor` of strings. For each string in the input `Tensor`, creates a substring starting at index
`pos` with a total length of `len`. If `len` defines a substring that would extend beyond the length of the input
string, then as many characters as possible are used. A negative `pos` indicates distance within the string backwards from the end. If `pos` specifies an index which is out of range for any of the input strings,
then an `InvalidArgumentError` is thrown. `pos` and `len` must have the same shape, otherwise a `ValueError` is thrown on
Op creation. *NOTE*: `Substr` supports broadcasting up to two dimensions. More about
broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html) --- Examples Using scalar `pos` and `len`:
Using `pos` and `len` with same shape as `input`:
Broadcasting `pos` and `len` onto `input`: ```
input = [[b'ten', b'eleven', b'twelve'],
[b'thirteen', b'fourteen', b'fifteen'],
[b'sixteen', b'seventeen', b'eighteen'],
[b'nineteen', b'twenty', b'twentyone']]
position = [1, 2, 3]
length = [1, 2, 3] output = [[b'e', b'ev', b'lve'],
[b'h', b'ur', b'tee'],
[b'i', b've', b'hte'],
[b'i', b'en', b'nty']]
``` Broadcasting `input` onto `pos` and `len`: ```
input = b'thirteen'
position = [1, 5, 7]
length = [3, 2, 1] output = [b'hir', b'ee', b'n']
```
Parameters
-
objectinput - A `Tensor` of type `string`. Tensor of strings
-
objectpos - A `Tensor`. Must be one of the following types: `int32`, `int64`. Scalar defining the position of first character in each substring
-
objectlen - A `Tensor`. Must have the same type as `pos`. Scalar defining the number of characters to include in each substring
-
stringname - A name for the operation (optional).
-
stringunit - An optional `string` from: `"BYTE", "UTF8_CHAR"`. Defaults to `"BYTE"`. The unit that is used to create the substring. One of: `"BYTE"` (for defining position and length by bytes) or `"UTF8_CHAR"` (for the UTF-8 encoded Unicode code points). The default is `"BYTE"`. Results are undefined if `unit=UTF8_CHAR` and the `input` strings do not contain structurally valid UTF-8.
Returns
-
Tensor - A `Tensor` of type `string`.
Show Example
input = [b'Hello', b'World']
position = 1
length = 3 output = [b'ell', b'orl']
object substr_dyn(object input, object pos, object len, object name, ImplicitContainer<T> unit)
Return substrings from `Tensor` of strings. For each string in the input `Tensor`, creates a substring starting at index
`pos` with a total length of `len`. If `len` defines a substring that would extend beyond the length of the input
string, then as many characters as possible are used. A negative `pos` indicates distance within the string backwards from the end. If `pos` specifies an index which is out of range for any of the input strings,
then an `InvalidArgumentError` is thrown. `pos` and `len` must have the same shape, otherwise a `ValueError` is thrown on
Op creation. *NOTE*: `Substr` supports broadcasting up to two dimensions. More about
broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html) --- Examples Using scalar `pos` and `len`:
Using `pos` and `len` with same shape as `input`:
Broadcasting `pos` and `len` onto `input`: ```
input = [[b'ten', b'eleven', b'twelve'],
[b'thirteen', b'fourteen', b'fifteen'],
[b'sixteen', b'seventeen', b'eighteen'],
[b'nineteen', b'twenty', b'twentyone']]
position = [1, 2, 3]
length = [1, 2, 3] output = [[b'e', b'ev', b'lve'],
[b'h', b'ur', b'tee'],
[b'i', b've', b'hte'],
[b'i', b'en', b'nty']]
``` Broadcasting `input` onto `pos` and `len`: ```
input = b'thirteen'
position = [1, 5, 7]
length = [3, 2, 1] output = [b'hir', b'ee', b'n']
```
Parameters
-
objectinput - A `Tensor` of type `string`. Tensor of strings
-
objectpos - A `Tensor`. Must be one of the following types: `int32`, `int64`. Scalar defining the position of first character in each substring
-
objectlen - A `Tensor`. Must have the same type as `pos`. Scalar defining the number of characters to include in each substring
-
objectname - A name for the operation (optional).
-
ImplicitContainer<T>unit - An optional `string` from: `"BYTE", "UTF8_CHAR"`. Defaults to `"BYTE"`. The unit that is used to create the substring. One of: `"BYTE"` (for defining position and length by bytes) or `"UTF8_CHAR"` (for the UTF-8 encoded Unicode code points). The default is `"BYTE"`. Results are undefined if `unit=UTF8_CHAR` and the `input` strings do not contain structurally valid UTF-8.
Returns
-
object - A `Tensor` of type `string`.
Show Example
input = [b'Hello', b'World']
position = 1
length = 3 output = [b'ell', b'orl']
object subtract(object x, object y, string name)
Returns x - y element-wise. *NOTE*: `Subtract` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object subtract_dyn(object x, object y, object name)
Returns x - y element-wise. *NOTE*: `Subtract` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object svd(IEnumerable<object> tensor, bool full_matrices, bool compute_uv, string name)
Computes the singular value decompositions of one or more matrices. Computes the SVD of each inner matrix in `tensor` such that
`tensor[..., :, :] = u[..., :, :] * diag(s[..., :, :]) *
transpose(conj(v[..., :, :]))`
Parameters
-
IEnumerable<object>tensor - `Tensor` of shape `[..., M, N]`. Let `P` be the minimum of `M` and `N`.
-
boolfull_matrices - If true, compute full-sized `u` and `v`. If false (the default), compute only the leading `P` singular vectors. Ignored if `compute_uv` is `False`.
-
boolcompute_uv - If `True` then left and right singular vectors will be computed and returned in `u` and `v`, respectively. Otherwise, only the singular values will be computed, which can be significantly faster.
-
stringname - string, optional name of the operation.
Returns
-
object
Show Example
# a is a tensor.
# s is a tensor of singular values.
# u is a tensor of left singular vectors.
# v is a tensor of right singular vectors.
s, u, v = svd(a)
s = svd(a, compute_uv=False)
object svd(IGraphNodeBase tensor, bool full_matrices, bool compute_uv, string name)
Computes the singular value decompositions of one or more matrices. Computes the SVD of each inner matrix in `tensor` such that
`tensor[..., :, :] = u[..., :, :] * diag(s[..., :, :]) *
transpose(conj(v[..., :, :]))`
Parameters
-
IGraphNodeBasetensor - `Tensor` of shape `[..., M, N]`. Let `P` be the minimum of `M` and `N`.
-
boolfull_matrices - If true, compute full-sized `u` and `v`. If false (the default), compute only the leading `P` singular vectors. Ignored if `compute_uv` is `False`.
-
boolcompute_uv - If `True` then left and right singular vectors will be computed and returned in `u` and `v`, respectively. Otherwise, only the singular values will be computed, which can be significantly faster.
-
stringname - string, optional name of the operation.
Returns
-
object
Show Example
# a is a tensor.
# s is a tensor of singular values.
# u is a tensor of left singular vectors.
# v is a tensor of right singular vectors.
s, u, v = svd(a)
s = svd(a, compute_uv=False)
object svd_dyn(object tensor, ImplicitContainer<T> full_matrices, ImplicitContainer<T> compute_uv, object name)
Computes the singular value decompositions of one or more matrices. Computes the SVD of each inner matrix in `tensor` such that
`tensor[..., :, :] = u[..., :, :] * diag(s[..., :, :]) *
transpose(conj(v[..., :, :]))`
Parameters
-
objecttensor - `Tensor` of shape `[..., M, N]`. Let `P` be the minimum of `M` and `N`.
-
ImplicitContainer<T>full_matrices - If true, compute full-sized `u` and `v`. If false (the default), compute only the leading `P` singular vectors. Ignored if `compute_uv` is `False`.
-
ImplicitContainer<T>compute_uv - If `True` then left and right singular vectors will be computed and returned in `u` and `v`, respectively. Otherwise, only the singular values will be computed, which can be significantly faster.
-
objectname - string, optional name of the operation.
Returns
-
object
Show Example
# a is a tensor.
# s is a tensor of singular values.
# u is a tensor of left singular vectors.
# v is a tensor of right singular vectors.
s, u, v = svd(a)
s = svd(a, compute_uv=False)
object switch_case(int branch_index, IDictionary<int, object> branch_fns, object default, string name)
Create a switch/case operation, i.e. an integer-indexed conditional. See also
tf.case. This op can be substantially more efficient than tf.case when exactly one
branch will be selected. tf.switch_case is more like a C++ switch/case
statement than tf.case, which is more like an if/elif/elif/else chain. The `branch_fns` parameter is either a list
of (int, callable) pairs, or simply a list of callables (in which case the
index is implicitly the key). The `branch_index` `Tensor` is used to select an
element in `branch_fns` with matching `int` key, falling back to `default`
if none match, or `max(keys)` if no `default` is provided. The keys must form
a contiguous set from `0` to `len(branch_fns) - 1`. tf.switch_case supports nested structures as implemented in tf.nest. All
callables must return the same (possibly nested) value structure of lists,
tuples, and/or named tuples. **Example:** Pseudocode: ```c++
switch (branch_index) { // c-style switch
case 0: return 17;
case 1: return 31;
default: return -1;
}
```
or
Expressions:
Parameters
-
intbranch_index - An int Tensor specifying which of `branch_fns` should be executed.
-
IDictionary<int, object>branch_fns - A `list` of (int, callable) pairs, or simply a list of callables (in which case the index serves as the key). Each callable must return a matching structure of tensors.
-
objectdefault - Optional callable that returns a structure of tensors.
-
stringname - A name for this operation (optional).
Returns
-
object - The tensors returned by the callable identified by `branch_index`, or those returned by `default` if no key matches and `default` was provided, or those returned by the max-keyed `branch_fn` if no `default` is provided.
Show Example
branches = {0: lambda: 17, 1: lambda: 31}
branches.get(branch_index, lambda: -1)()
object switch_case(int branch_index, IEnumerable<object> branch_fns, object default, string name)
Create a switch/case operation, i.e. an integer-indexed conditional. See also
tf.case. This op can be substantially more efficient than tf.case when exactly one
branch will be selected. tf.switch_case is more like a C++ switch/case
statement than tf.case, which is more like an if/elif/elif/else chain. The `branch_fns` parameter is either a list
of (int, callable) pairs, or simply a list of callables (in which case the
index is implicitly the key). The `branch_index` `Tensor` is used to select an
element in `branch_fns` with matching `int` key, falling back to `default`
if none match, or `max(keys)` if no `default` is provided. The keys must form
a contiguous set from `0` to `len(branch_fns) - 1`. tf.switch_case supports nested structures as implemented in tf.nest. All
callables must return the same (possibly nested) value structure of lists,
tuples, and/or named tuples. **Example:** Pseudocode: ```c++
switch (branch_index) { // c-style switch
case 0: return 17;
case 1: return 31;
default: return -1;
}
```
or
Expressions:
Parameters
-
intbranch_index - An int Tensor specifying which of `branch_fns` should be executed.
-
IEnumerable<object>branch_fns - A `list` of (int, callable) pairs, or simply a list of callables (in which case the index serves as the key). Each callable must return a matching structure of tensors.
-
objectdefault - Optional callable that returns a structure of tensors.
-
stringname - A name for this operation (optional).
Returns
-
object - The tensors returned by the callable identified by `branch_index`, or those returned by `default` if no key matches and `default` was provided, or those returned by the max-keyed `branch_fn` if no `default` is provided.
Show Example
branches = {0: lambda: 17, 1: lambda: 31}
branches.get(branch_index, lambda: -1)()
object switch_case(IGraphNodeBase branch_index, IDictionary<int, object> branch_fns, object default, string name)
Create a switch/case operation, i.e. an integer-indexed conditional. See also
tf.case. This op can be substantially more efficient than tf.case when exactly one
branch will be selected. tf.switch_case is more like a C++ switch/case
statement than tf.case, which is more like an if/elif/elif/else chain. The `branch_fns` parameter is either a list
of (int, callable) pairs, or simply a list of callables (in which case the
index is implicitly the key). The `branch_index` `Tensor` is used to select an
element in `branch_fns` with matching `int` key, falling back to `default`
if none match, or `max(keys)` if no `default` is provided. The keys must form
a contiguous set from `0` to `len(branch_fns) - 1`. tf.switch_case supports nested structures as implemented in tf.nest. All
callables must return the same (possibly nested) value structure of lists,
tuples, and/or named tuples. **Example:** Pseudocode: ```c++
switch (branch_index) { // c-style switch
case 0: return 17;
case 1: return 31;
default: return -1;
}
```
or
Expressions:
Parameters
-
IGraphNodeBasebranch_index - An int Tensor specifying which of `branch_fns` should be executed.
-
IDictionary<int, object>branch_fns - A `list` of (int, callable) pairs, or simply a list of callables (in which case the index serves as the key). Each callable must return a matching structure of tensors.
-
objectdefault - Optional callable that returns a structure of tensors.
-
stringname - A name for this operation (optional).
Returns
-
object - The tensors returned by the callable identified by `branch_index`, or those returned by `default` if no key matches and `default` was provided, or those returned by the max-keyed `branch_fn` if no `default` is provided.
Show Example
branches = {0: lambda: 17, 1: lambda: 31}
branches.get(branch_index, lambda: -1)()
object switch_case(IGraphNodeBase branch_index, IEnumerable<object> branch_fns, object default, string name)
Create a switch/case operation, i.e. an integer-indexed conditional. See also
tf.case. This op can be substantially more efficient than tf.case when exactly one
branch will be selected. tf.switch_case is more like a C++ switch/case
statement than tf.case, which is more like an if/elif/elif/else chain. The `branch_fns` parameter is either a list
of (int, callable) pairs, or simply a list of callables (in which case the
index is implicitly the key). The `branch_index` `Tensor` is used to select an
element in `branch_fns` with matching `int` key, falling back to `default`
if none match, or `max(keys)` if no `default` is provided. The keys must form
a contiguous set from `0` to `len(branch_fns) - 1`. tf.switch_case supports nested structures as implemented in tf.nest. All
callables must return the same (possibly nested) value structure of lists,
tuples, and/or named tuples. **Example:** Pseudocode: ```c++
switch (branch_index) { // c-style switch
case 0: return 17;
case 1: return 31;
default: return -1;
}
```
or
Expressions:
Parameters
-
IGraphNodeBasebranch_index - An int Tensor specifying which of `branch_fns` should be executed.
-
IEnumerable<object>branch_fns - A `list` of (int, callable) pairs, or simply a list of callables (in which case the index serves as the key). Each callable must return a matching structure of tensors.
-
objectdefault - Optional callable that returns a structure of tensors.
-
stringname - A name for this operation (optional).
Returns
-
object - The tensors returned by the callable identified by `branch_index`, or those returned by `default` if no key matches and `default` was provided, or those returned by the max-keyed `branch_fn` if no `default` is provided.
Show Example
branches = {0: lambda: 17, 1: lambda: 31}
branches.get(branch_index, lambda: -1)()
object switch_case_dyn(object branch_index, object branch_fns, object default, ImplicitContainer<T> name)
Create a switch/case operation, i.e. an integer-indexed conditional. See also
tf.case. This op can be substantially more efficient than tf.case when exactly one
branch will be selected. tf.switch_case is more like a C++ switch/case
statement than tf.case, which is more like an if/elif/elif/else chain. The `branch_fns` parameter is either a list
of (int, callable) pairs, or simply a list of callables (in which case the
index is implicitly the key). The `branch_index` `Tensor` is used to select an
element in `branch_fns` with matching `int` key, falling back to `default`
if none match, or `max(keys)` if no `default` is provided. The keys must form
a contiguous set from `0` to `len(branch_fns) - 1`. tf.switch_case supports nested structures as implemented in tf.nest. All
callables must return the same (possibly nested) value structure of lists,
tuples, and/or named tuples. **Example:** Pseudocode: ```c++
switch (branch_index) { // c-style switch
case 0: return 17;
case 1: return 31;
default: return -1;
}
```
or
Expressions:
Parameters
-
objectbranch_index - An int Tensor specifying which of `branch_fns` should be executed.
-
objectbranch_fns - A `list` of (int, callable) pairs, or simply a list of callables (in which case the index serves as the key). Each callable must return a matching structure of tensors.
-
objectdefault - Optional callable that returns a structure of tensors.
-
ImplicitContainer<T>name - A name for this operation (optional).
Returns
-
object - The tensors returned by the callable identified by `branch_index`, or those returned by `default` if no key matches and `default` was provided, or those returned by the max-keyed `branch_fn` if no `default` is provided.
Show Example
branches = {0: lambda: 17, 1: lambda: 31}
branches.get(branch_index, lambda: -1)()
object tables_initializer(string name)
Returns an Op that initializes all tables of the default graph. See the [Low Level
Intro](https://www.tensorflow.org/guide/low_level_intro#feature_columns)
guide, for an example of usage.
Parameters
-
stringname - Optional name for the initialization op.
Returns
-
object - An Op that initializes all tables. Note that if there are not tables the returned Op is a NoOp.
object tables_initializer_dyn(ImplicitContainer<T> name)
Returns an Op that initializes all tables of the default graph. See the [Low Level
Intro](https://www.tensorflow.org/guide/low_level_intro#feature_columns)
guide, for an example of usage.
Parameters
-
ImplicitContainer<T>name - Optional name for the initialization op.
Returns
-
object - An Op that initializes all tables. Note that if there are not tables the returned Op is a NoOp.
object tan(IGraphNodeBase x, string name)
Computes tan of x element-wise. Given an input tensor, this function computes tangent of every
element in the tensor. Input range is `(-inf, inf)` and
output range is `(-inf, inf)`. If input lies outside the boundary, `nan`
is returned.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.tan(x) ==> [nan 0.45231566 -0.5463025 1.5574077 2.572152 -1.7925274 0.32097113 nan]
object tan_dyn(object x, object name)
Computes tan of x element-wise. Given an input tensor, this function computes tangent of every
element in the tensor. Input range is `(-inf, inf)` and
output range is `(-inf, inf)`. If input lies outside the boundary, `nan`
is returned.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `int32`, `int64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.tan(x) ==> [nan 0.45231566 -0.5463025 1.5574077 2.572152 -1.7925274 0.32097113 nan]
object tanh(IGraphNodeBase x, string name)
Computes hyperbolic tangent of `x` element-wise. Given an input tensor, this function computes hyperbolic tangent of every
element in the tensor. Input range is `[-inf, inf]` and
output range is `[-1,1]`.
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`. If `x` is a `SparseTensor`, returns `SparseTensor(x.indices, tf.math.tanh(x.values,...), x.dense_shape)`
Show Example
x = tf.constant([-float("inf"), -5, -0.5, 1, 1.2, 2, 3, float("inf")])
tf.math.tanh(x) ==> [-1. -0.99990916 -0.46211717 0.7615942 0.8336547 0.9640276 0.9950547 1.]
object tanh_dyn(object x, object name)
Computes hyperbolic tangent of `x` element-wise. Given an input tensor, this function computes hyperbolic tangent of every
element in the tensor. Input range is `[-inf, inf]` and
output range is `[-1,1]`.
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `complex64`, `complex128`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`. If `x` is a `SparseTensor`, returns `SparseTensor(x.indices, tf.math.tanh(x.values,...), x.dense_shape)`
Show Example
x = tf.constant([-float("inf"), -5, -0.5, 1, 1.2, 2, 3, float("inf")])
tf.math.tanh(x) ==> [-1. -0.99990916 -0.46211717 0.7615942 0.8336547 0.9640276 0.9950547 1.]
Tensor tensor_scatter_add(IGraphNodeBase tensor, IGraphNodeBase indices, IGraphNodeBase updates, string name)
Adds sparse `updates` to an existing tensor according to `indices`. This operation creates a new tensor by adding sparse `updates` to the passed
in `tensor`.
This operation is very similar to
tf.scatter_nd_add, except that the updates
are added onto an existing tensor (as opposed to a variable). If the memory
for the existing tensor cannot be re-used, a copy is made and updated. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of tensor_scatter_add is to add individual elements to a
tensor by index. For example, say we want to add 4 elements in a rank-1
tensor with 8 elements. In Python, this scatter add operation would look like this:
The resulting tensor would look like this: [1, 12, 1, 11, 10, 1, 1, 13] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter add operation would look like this:
The resulting tensor would look like this: [[[6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8], [9, 9, 9, 9]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8], [9, 9, 9, 9]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
Parameters
-
IGraphNodeBasetensor - A `Tensor`. Tensor to copy/update.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `tensor`. Updates to scatter into output.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
tensor = tf.ones([8], dtype=tf.int32)
updated = tf.tensor_scatter_add(tensor, indices, updates)
with tf.Session() as sess:
print(sess.run(scatter))
object tensor_scatter_add_dyn(object tensor, object indices, object updates, object name)
Adds sparse `updates` to an existing tensor according to `indices`. This operation creates a new tensor by adding sparse `updates` to the passed
in `tensor`.
This operation is very similar to
tf.scatter_nd_add, except that the updates
are added onto an existing tensor (as opposed to a variable). If the memory
for the existing tensor cannot be re-used, a copy is made and updated. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of tensor_scatter_add is to add individual elements to a
tensor by index. For example, say we want to add 4 elements in a rank-1
tensor with 8 elements. In Python, this scatter add operation would look like this:
The resulting tensor would look like this: [1, 12, 1, 11, 10, 1, 1, 13] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter add operation would look like this:
The resulting tensor would look like this: [[[6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8], [9, 9, 9, 9]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8], [9, 9, 9, 9]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
Parameters
-
objecttensor - A `Tensor`. Tensor to copy/update.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
objectupdates - A `Tensor`. Must have the same type as `tensor`. Updates to scatter into output.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `tensor`.
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
tensor = tf.ones([8], dtype=tf.int32)
updated = tf.tensor_scatter_add(tensor, indices, updates)
with tf.Session() as sess:
print(sess.run(scatter))
Tensor tensor_scatter_sub(IGraphNodeBase tensor, IGraphNodeBase indices, IGraphNodeBase updates, string name)
Subtracts sparse `updates` from an existing tensor according to `indices`. This operation creates a new tensor by subtracting sparse `updates` from the
passed in `tensor`.
This operation is very similar to
tf.scatter_nd_sub, except that the updates
are subtracted from an existing tensor (as opposed to a variable). If the memory
for the existing tensor cannot be re-used, a copy is made and updated. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of tensor_scatter_sub is to subtract individual elements
from a tensor by index. For example, say we want to insert 4 scattered elements
in a rank-1 tensor with 8 elements. In Python, this scatter subtract operation would look like this:
The resulting tensor would look like this: [1, -10, 1, -9, -8, 1, 1, -11] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter add operation would look like this:
The resulting tensor would look like this: [[[-4, -4, -4, -4], [-5, -5, -5, -5], [-6, -6, -6, -6], [-7, -7, -7, -7]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[-4, -4, -4, -4], [-5, -5, -5, -5], [-6, -6, -6, -6], [-7, -7, -7, -7]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
Parameters
-
IGraphNodeBasetensor - A `Tensor`. Tensor to copy/update.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `tensor`. Updates to scatter into output.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
tensor = tf.ones([8], dtype=tf.int32)
updated = tf.tensor_scatter_sub(tensor, indices, updates)
with tf.Session() as sess:
print(sess.run(scatter))
object tensor_scatter_sub_dyn(object tensor, object indices, object updates, object name)
Subtracts sparse `updates` from an existing tensor according to `indices`. This operation creates a new tensor by subtracting sparse `updates` from the
passed in `tensor`.
This operation is very similar to
tf.scatter_nd_sub, except that the updates
are subtracted from an existing tensor (as opposed to a variable). If the memory
for the existing tensor cannot be re-used, a copy is made and updated. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of tensor_scatter_sub is to subtract individual elements
from a tensor by index. For example, say we want to insert 4 scattered elements
in a rank-1 tensor with 8 elements. In Python, this scatter subtract operation would look like this:
The resulting tensor would look like this: [1, -10, 1, -9, -8, 1, 1, -11] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter add operation would look like this:
The resulting tensor would look like this: [[[-4, -4, -4, -4], [-5, -5, -5, -5], [-6, -6, -6, -6], [-7, -7, -7, -7]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[-4, -4, -4, -4], [-5, -5, -5, -5], [-6, -6, -6, -6], [-7, -7, -7, -7]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
Parameters
-
objecttensor - A `Tensor`. Tensor to copy/update.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
objectupdates - A `Tensor`. Must have the same type as `tensor`. Updates to scatter into output.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `tensor`.
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
tensor = tf.ones([8], dtype=tf.int32)
updated = tf.tensor_scatter_sub(tensor, indices, updates)
with tf.Session() as sess:
print(sess.run(scatter))
Tensor tensor_scatter_update(IGraphNodeBase tensor, IGraphNodeBase indices, IGraphNodeBase updates, string name)
Scatter `updates` into an existing tensor according to `indices`. This operation creates a new tensor by applying sparse `updates` to the passed
in `tensor`.
This operation is very similar to
 In Python, this scatter operation would look like this:
The resulting tensor would look like this: [1, 11, 1, 10, 9, 1, 1, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
In Python, this scatter operation would look like this:
The resulting tensor would look like this: [1, 11, 1, 10, 9, 1, 1, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
tf.scatter_nd, except that the updates are
scattered onto an existing tensor (as opposed to a zero-tensor). If the memory
for the existing tensor cannot be re-used, a copy is made and updated. If `indices` contains duplicates, then their updates are accumulated (summed). **WARNING**: The order in which updates are applied is nondeterministic, so the
output will be nondeterministic if `indices` contains duplicates -- because
of some numerical approximation issues, numbers summed in different order
may yield different results. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of scatter is to insert individual elements in a tensor by
index. For example, say we want to insert 4 scattered elements in a rank-1
tensor with 8 elements. 
Parameters
-
IGraphNodeBasetensor - A `Tensor`. Tensor to copy/update.
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
IGraphNodeBaseupdates - A `Tensor`. Must have the same type as `tensor`. Updates to scatter into output.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `tensor`.
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
tensor = tf.ones([8], dtype=tf.int32)
updated = tf.tensor_scatter_update(tensor, indices, updates)
with tf.Session() as sess:
print(sess.run(scatter))
object tensor_scatter_update_dyn(object tensor, object indices, object updates, object name)
Scatter `updates` into an existing tensor according to `indices`. This operation creates a new tensor by applying sparse `updates` to the passed
in `tensor`.
This operation is very similar to
 In Python, this scatter operation would look like this:
The resulting tensor would look like this: [1, 11, 1, 10, 9, 1, 1, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
In Python, this scatter operation would look like this:
The resulting tensor would look like this: [1, 11, 1, 10, 9, 1, 1, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
tf.scatter_nd, except that the updates are
scattered onto an existing tensor (as opposed to a zero-tensor). If the memory
for the existing tensor cannot be re-used, a copy is made and updated. If `indices` contains duplicates, then their updates are accumulated (summed). **WARNING**: The order in which updates are applied is nondeterministic, so the
output will be nondeterministic if `indices` contains duplicates -- because
of some numerical approximation issues, numbers summed in different order
may yield different results. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of scatter is to insert individual elements in a tensor by
index. For example, say we want to insert 4 scattered elements in a rank-1
tensor with 8 elements. 
Parameters
-
objecttensor - A `Tensor`. Tensor to copy/update.
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. Index tensor.
-
objectupdates - A `Tensor`. Must have the same type as `tensor`. Updates to scatter into output.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `tensor`.
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
tensor = tf.ones([8], dtype=tf.int32)
updated = tf.tensor_scatter_update(tensor, indices, updates)
with tf.Session() as sess:
print(sess.run(scatter))
Tensor tensordot(IEnumerable<IGraphNodeBase> a, PythonClassContainer b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
PythonClassContainerb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, ValueTuple<IEnumerable<object>, object> b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
ValueTuple<IEnumerable<object>, object>b - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, IEnumerable<object> b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
IEnumerable<object>b - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, IEnumerable<object> b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
IEnumerable<object>b - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, bool b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
boolb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, ValueTuple<IEnumerable<object>, object> b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
ValueTuple<IEnumerable<object>, object>b - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, bool b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
boolb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, bool b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
boolb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, bool b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
boolb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, PythonClassContainer b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
PythonClassContainerb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, int b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
intb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, IGraphNodeBase b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
IGraphNodeBaseb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, PythonClassContainer b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
PythonClassContainerb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, ValueTuple<IEnumerable<object>, object> b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
ValueTuple<IEnumerable<object>, object>b - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, IEnumerable<object> b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
IEnumerable<object>b - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, int b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
intb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, IGraphNodeBase b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
IGraphNodeBaseb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, int b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
intb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, IGraphNodeBase b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
IGraphNodeBaseb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, PythonClassContainer b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
PythonClassContainerb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, IGraphNodeBase b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
IGraphNodeBaseb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, ValueTuple<IEnumerable<object>, object> b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
ValueTuple<IEnumerable<object>, object>b - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(object a, int b, object axes, string name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
intb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
Tensor tensordot(IEnumerable<IGraphNodeBase> a, IEnumerable<object> b, object axes, PythonFunctionContainer name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
IEnumerable<IGraphNodeBase>a - `Tensor` of type `float32` or `float64`.
-
IEnumerable<object>b - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `a`.
object tensordot_dyn(object a, object b, object axes, object name)
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
Parameters
-
objecta - `Tensor` of type `float32` or `float64`.
-
objectb - `Tensor` with the same type as `a`.
-
objectaxes - Either a scalar `N`, or a list or an `int32` `Tensor` of shape [2, k]. If axes is a scalar, sum over the last N axes of a and the first N axes of b in order. If axes is a list or `Tensor` the first and second row contain the set of unique integers specifying axes along which the contraction is computed, for `a` and `b`, respectively. The number of axes for `a` and `b` must be equal. If `axes=0`, computes the outer product between `a` and `b`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` with the same type as `a`.
object test_attr_dyn(object T, object name)
object test_string_output(IGraphNodeBase input, string name)
object test_string_output_dyn(object input, object name)
Tensor tile(IGraphNodeBase input, IGraphNodeBase multiples, string name)
Constructs a tensor by tiling a given tensor. This operation creates a new tensor by replicating `input` `multiples` times.
The output tensor's i'th dimension has `input.dims(i) * multiples[i]` elements,
and the values of `input` are replicated `multiples[i]` times along the 'i'th
dimension. For example, tiling `[a b c d]` by `[2]` produces
`[a b c d a b c d]`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. 1-D or higher.
-
IGraphNodeBasemultiples - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D. Length must be the same as the number of dimensions in `input`
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
Tensor tile(IGraphNodeBase input, IGraphNodeBase multiples, PythonFunctionContainer name)
Constructs a tensor by tiling a given tensor. This operation creates a new tensor by replicating `input` `multiples` times.
The output tensor's i'th dimension has `input.dims(i) * multiples[i]` elements,
and the values of `input` are replicated `multiples[i]` times along the 'i'th
dimension. For example, tiling `[a b c d]` by `[2]` produces
`[a b c d a b c d]`.
Parameters
-
IGraphNodeBaseinput - A `Tensor`. 1-D or higher.
-
IGraphNodeBasemultiples - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D. Length must be the same as the number of dimensions in `input`
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `input`.
object tile_dyn(object input, object multiples, object name)
Constructs a tensor by tiling a given tensor. This operation creates a new tensor by replicating `input` `multiples` times.
The output tensor's i'th dimension has `input.dims(i) * multiples[i]` elements,
and the values of `input` are replicated `multiples[i]` times along the 'i'th
dimension. For example, tiling `[a b c d]` by `[2]` produces
`[a b c d a b c d]`.
Parameters
-
objectinput - A `Tensor`. 1-D or higher.
-
objectmultiples - A `Tensor`. Must be one of the following types: `int32`, `int64`. 1-D. Length must be the same as the number of dimensions in `input`
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `input`.
Tensor timestamp(string name)
Provides the time since epoch in seconds. Returns the timestamp as a `float64` for seconds since the Unix epoch. Note: the timestamp is computed when the op is executed, not when it is added
to the graph.
Parameters
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` of type `float64`.
object timestamp_dyn(object name)
Provides the time since epoch in seconds. Returns the timestamp as a `float64` for seconds since the Unix epoch. Note: the timestamp is computed when the op is executed, not when it is added
to the graph.
Parameters
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` of type `float64`.
object to_bfloat16(IGraphNodeBase x, string name)
Casts a tensor to type `bfloat16`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
IGraphNodeBasex - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `bfloat16`.
object to_bfloat16_dyn(object x, ImplicitContainer<T> name)
Casts a tensor to type `bfloat16`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `bfloat16`.
object to_complex128(object x, string name)
Casts a tensor to type `complex128`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `complex128`.
object to_complex128_dyn(object x, ImplicitContainer<T> name)
Casts a tensor to type `complex128`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `complex128`.
object to_complex64(object x, string name)
Casts a tensor to type `complex64`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `complex64`.
object to_complex64_dyn(object x, ImplicitContainer<T> name)
Casts a tensor to type `complex64`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `complex64`.
object to_double(IGraphNodeBase x, string name)
Casts a tensor to type `float64`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
IGraphNodeBasex - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `float64`.
object to_double_dyn(object x, ImplicitContainer<T> name)
Casts a tensor to type `float64`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `float64`.
object to_float(IGraphNodeBase x, string name)
Casts a tensor to type `float32`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
IGraphNodeBasex - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `float32`.
object to_float_dyn(object x, ImplicitContainer<T> name)
Casts a tensor to type `float32`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `float32`.
object to_int32(IGraphNodeBase x, string name)
Casts a tensor to type `int32`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
IGraphNodeBasex - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `int32`.
object to_int32_dyn(object x, ImplicitContainer<T> name)
Casts a tensor to type `int32`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `int32`.
object to_int64(IGraphNodeBase x, string name)
Casts a tensor to type `int64`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
IGraphNodeBasex - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `int64`.
object to_int64_dyn(object x, ImplicitContainer<T> name)
Casts a tensor to type `int64`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
Parameters
-
objectx - A `Tensor` or `SparseTensor` or `IndexedSlices`.
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - A `Tensor` or `SparseTensor` or `IndexedSlices` with same shape as `x` with type `int64`.
Tensor trace(IEnumerable<IGraphNodeBase> x, string name)
Compute the trace of a tensor `x`. `trace(x)` returns the sum along the main diagonal of each inner-most matrix
in x. If x is of rank `k` with shape `[I, J, K,..., L, M, N]`, then output
is a tensor of rank `k-2` with dimensions `[I, J, K,..., L]` where `output[i, j, k,..., l] = trace(x[i, j, i,..., l, :, :])`
Parameters
-
IEnumerable<IGraphNodeBase>x - tensor.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - The trace of input tensor.
Show Example
x = tf.constant([[1, 2], [3, 4]])
tf.linalg.trace(x) # 5 x = tf.constant([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
tf.linalg.trace(x) # 15 x = tf.constant([[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]],
[[-1, -2, -3],
[-4, -5, -6],
[-7, -8, -9]]])
tf.linalg.trace(x) # [15, -15]
Tensor trace(IGraphNodeBase x, string name)
Compute the trace of a tensor `x`. `trace(x)` returns the sum along the main diagonal of each inner-most matrix
in x. If x is of rank `k` with shape `[I, J, K,..., L, M, N]`, then output
is a tensor of rank `k-2` with dimensions `[I, J, K,..., L]` where `output[i, j, k,..., l] = trace(x[i, j, i,..., l, :, :])`
Parameters
-
IGraphNodeBasex - tensor.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - The trace of input tensor.
Show Example
x = tf.constant([[1, 2], [3, 4]])
tf.linalg.trace(x) # 5 x = tf.constant([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
tf.linalg.trace(x) # 15 x = tf.constant([[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]],
[[-1, -2, -3],
[-4, -5, -6],
[-7, -8, -9]]])
tf.linalg.trace(x) # [15, -15]
Tensor trace(PythonClassContainer x, string name)
Compute the trace of a tensor `x`. `trace(x)` returns the sum along the main diagonal of each inner-most matrix
in x. If x is of rank `k` with shape `[I, J, K,..., L, M, N]`, then output
is a tensor of rank `k-2` with dimensions `[I, J, K,..., L]` where `output[i, j, k,..., l] = trace(x[i, j, i,..., l, :, :])`
Parameters
-
PythonClassContainerx - tensor.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - The trace of input tensor.
Show Example
x = tf.constant([[1, 2], [3, 4]])
tf.linalg.trace(x) # 5 x = tf.constant([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
tf.linalg.trace(x) # 15 x = tf.constant([[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]],
[[-1, -2, -3],
[-4, -5, -6],
[-7, -8, -9]]])
tf.linalg.trace(x) # [15, -15]
object trace_dyn(object x, object name)
Compute the trace of a tensor `x`. `trace(x)` returns the sum along the main diagonal of each inner-most matrix
in x. If x is of rank `k` with shape `[I, J, K,..., L, M, N]`, then output
is a tensor of rank `k-2` with dimensions `[I, J, K,..., L]` where `output[i, j, k,..., l] = trace(x[i, j, i,..., l, :, :])`
Parameters
-
objectx - tensor.
-
objectname - A name for the operation (optional).
Returns
-
object - The trace of input tensor.
Show Example
x = tf.constant([[1, 2], [3, 4]])
tf.linalg.trace(x) # 5 x = tf.constant([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
tf.linalg.trace(x) # 15 x = tf.constant([[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]],
[[-1, -2, -3],
[-4, -5, -6],
[-7, -8, -9]]])
tf.linalg.trace(x) # [15, -15]
object trainable_variables(string scope)
Returns all variables created with `trainable=True`. When passed `trainable=True`, the `Variable()` constructor automatically
adds new variables to the graph collection
`GraphKeys.TRAINABLE_VARIABLES`. This convenience function returns the
contents of that collection.
Parameters
-
stringscope - (Optional.) A string. If supplied, the resulting list is filtered to include only items whose `name` attribute matches `scope` using `re.match`. Items without a `name` attribute are never returned if a scope is supplied. The choice of `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
object - A list of Variable objects.
object trainable_variables_dyn(object scope)
Returns all variables created with `trainable=True`. When passed `trainable=True`, the `Variable()` constructor automatically
adds new variables to the graph collection
`GraphKeys.TRAINABLE_VARIABLES`. This convenience function returns the
contents of that collection.
Parameters
-
objectscope - (Optional.) A string. If supplied, the resulting list is filtered to include only items whose `name` attribute matches `scope` using `re.match`. Items without a `name` attribute are never returned if a scope is supplied. The choice of `re.match` means that a `scope` without special tokens filters by prefix.
Returns
-
object - A list of Variable objects.
Tensor transpose(IGraphNodeBase a, object perm, string name, bool conjugate)
Transposes `a`. Permutes the dimensions according to `perm`. The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. If conjugate is True and
`a.dtype` is either `complex64` or `complex128` then the values of `a`
are conjugated and transposed.
Parameters
-
IGraphNodeBasea - A `Tensor`.
-
objectperm - A permutation of the dimensions of `a`.
-
stringname - A name for the operation (optional).
-
boolconjugate - Optional bool. Setting it to `True` is mathematically equivalent to tf.math.conj(tf.transpose(input)).
Returns
-
Tensor - A transposed `Tensor`.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.transpose(x) # [[1, 4]
# [2, 5]
# [3, 6]] # Equivalently
tf.transpose(x, perm=[1, 0]) # [[1, 4]
# [2, 5]
# [3, 6]] # If x is complex, setting conjugate=True gives the conjugate transpose
x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # 'perm' is more useful for n-dimensional tensors, for n > 2
x = tf.constant([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]]) # Take the transpose of the matrices in dimension-0
# (this common operation has a shorthand `linalg.matrix_transpose`)
tf.transpose(x, perm=[0, 2, 1]) # [[[1, 4],
# [2, 5],
# [3, 6]],
# [[7, 10],
# [8, 11],
# [9, 12]]]
Tensor transpose(IGraphNodeBase a, PythonClassContainer perm, string name, bool conjugate)
Transposes `a`. Permutes the dimensions according to `perm`. The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. If conjugate is True and
`a.dtype` is either `complex64` or `complex128` then the values of `a`
are conjugated and transposed.
Parameters
-
IGraphNodeBasea - A `Tensor`.
-
PythonClassContainerperm - A permutation of the dimensions of `a`.
-
stringname - A name for the operation (optional).
-
boolconjugate - Optional bool. Setting it to `True` is mathematically equivalent to tf.math.conj(tf.transpose(input)).
Returns
-
Tensor - A transposed `Tensor`.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.transpose(x) # [[1, 4]
# [2, 5]
# [3, 6]] # Equivalently
tf.transpose(x, perm=[1, 0]) # [[1, 4]
# [2, 5]
# [3, 6]] # If x is complex, setting conjugate=True gives the conjugate transpose
x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # 'perm' is more useful for n-dimensional tensors, for n > 2
x = tf.constant([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]]) # Take the transpose of the matrices in dimension-0
# (this common operation has a shorthand `linalg.matrix_transpose`)
tf.transpose(x, perm=[0, 2, 1]) # [[[1, 4],
# [2, 5],
# [3, 6]],
# [[7, 10],
# [8, 11],
# [9, 12]]]
Tensor transpose(IGraphNodeBase a, ndarray perm, string name, bool conjugate)
Transposes `a`. Permutes the dimensions according to `perm`. The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. If conjugate is True and
`a.dtype` is either `complex64` or `complex128` then the values of `a`
are conjugated and transposed.
Parameters
-
IGraphNodeBasea - A `Tensor`.
-
ndarrayperm - A permutation of the dimensions of `a`.
-
stringname - A name for the operation (optional).
-
boolconjugate - Optional bool. Setting it to `True` is mathematically equivalent to tf.math.conj(tf.transpose(input)).
Returns
-
Tensor - A transposed `Tensor`.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.transpose(x) # [[1, 4]
# [2, 5]
# [3, 6]] # Equivalently
tf.transpose(x, perm=[1, 0]) # [[1, 4]
# [2, 5]
# [3, 6]] # If x is complex, setting conjugate=True gives the conjugate transpose
x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # 'perm' is more useful for n-dimensional tensors, for n > 2
x = tf.constant([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]]) # Take the transpose of the matrices in dimension-0
# (this common operation has a shorthand `linalg.matrix_transpose`)
tf.transpose(x, perm=[0, 2, 1]) # [[[1, 4],
# [2, 5],
# [3, 6]],
# [[7, 10],
# [8, 11],
# [9, 12]]]
Tensor transpose(IGraphNodeBase a, IGraphNodeBase perm, string name, bool conjugate)
Transposes `a`. Permutes the dimensions according to `perm`. The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. If conjugate is True and
`a.dtype` is either `complex64` or `complex128` then the values of `a`
are conjugated and transposed.
Parameters
-
IGraphNodeBasea - A `Tensor`.
-
IGraphNodeBaseperm - A permutation of the dimensions of `a`.
-
stringname - A name for the operation (optional).
-
boolconjugate - Optional bool. Setting it to `True` is mathematically equivalent to tf.math.conj(tf.transpose(input)).
Returns
-
Tensor - A transposed `Tensor`.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.transpose(x) # [[1, 4]
# [2, 5]
# [3, 6]] # Equivalently
tf.transpose(x, perm=[1, 0]) # [[1, 4]
# [2, 5]
# [3, 6]] # If x is complex, setting conjugate=True gives the conjugate transpose
x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # 'perm' is more useful for n-dimensional tensors, for n > 2
x = tf.constant([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]]) # Take the transpose of the matrices in dimension-0
# (this common operation has a shorthand `linalg.matrix_transpose`)
tf.transpose(x, perm=[0, 2, 1]) # [[[1, 4],
# [2, 5],
# [3, 6]],
# [[7, 10],
# [8, 11],
# [9, 12]]]
Tensor transpose(IGraphNodeBase a, int perm, string name, bool conjugate)
Transposes `a`. Permutes the dimensions according to `perm`. The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. If conjugate is True and
`a.dtype` is either `complex64` or `complex128` then the values of `a`
are conjugated and transposed.
Parameters
-
IGraphNodeBasea - A `Tensor`.
-
intperm - A permutation of the dimensions of `a`.
-
stringname - A name for the operation (optional).
-
boolconjugate - Optional bool. Setting it to `True` is mathematically equivalent to tf.math.conj(tf.transpose(input)).
Returns
-
Tensor - A transposed `Tensor`.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.transpose(x) # [[1, 4]
# [2, 5]
# [3, 6]] # Equivalently
tf.transpose(x, perm=[1, 0]) # [[1, 4]
# [2, 5]
# [3, 6]] # If x is complex, setting conjugate=True gives the conjugate transpose
x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # 'perm' is more useful for n-dimensional tensors, for n > 2
x = tf.constant([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]]) # Take the transpose of the matrices in dimension-0
# (this common operation has a shorthand `linalg.matrix_transpose`)
tf.transpose(x, perm=[0, 2, 1]) # [[[1, 4],
# [2, 5],
# [3, 6]],
# [[7, 10],
# [8, 11],
# [9, 12]]]
Tensor transpose(IGraphNodeBase a, IEnumerable<object> perm, string name, bool conjugate)
Transposes `a`. Permutes the dimensions according to `perm`. The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. If conjugate is True and
`a.dtype` is either `complex64` or `complex128` then the values of `a`
are conjugated and transposed.
Parameters
-
IGraphNodeBasea - A `Tensor`.
-
IEnumerable<object>perm - A permutation of the dimensions of `a`.
-
stringname - A name for the operation (optional).
-
boolconjugate - Optional bool. Setting it to `True` is mathematically equivalent to tf.math.conj(tf.transpose(input)).
Returns
-
Tensor - A transposed `Tensor`.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.transpose(x) # [[1, 4]
# [2, 5]
# [3, 6]] # Equivalently
tf.transpose(x, perm=[1, 0]) # [[1, 4]
# [2, 5]
# [3, 6]] # If x is complex, setting conjugate=True gives the conjugate transpose
x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # 'perm' is more useful for n-dimensional tensors, for n > 2
x = tf.constant([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]]) # Take the transpose of the matrices in dimension-0
# (this common operation has a shorthand `linalg.matrix_transpose`)
tf.transpose(x, perm=[0, 2, 1]) # [[[1, 4],
# [2, 5],
# [3, 6]],
# [[7, 10],
# [8, 11],
# [9, 12]]]
object transpose_dyn(object a, object perm, ImplicitContainer<T> name, ImplicitContainer<T> conjugate)
Transposes `a`. Permutes the dimensions according to `perm`. The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. If conjugate is True and
`a.dtype` is either `complex64` or `complex128` then the values of `a`
are conjugated and transposed.
Parameters
-
objecta - A `Tensor`.
-
objectperm - A permutation of the dimensions of `a`.
-
ImplicitContainer<T>name - A name for the operation (optional).
-
ImplicitContainer<T>conjugate - Optional bool. Setting it to `True` is mathematically equivalent to tf.math.conj(tf.transpose(input)).
Returns
-
object - A transposed `Tensor`.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.transpose(x) # [[1, 4]
# [2, 5]
# [3, 6]] # Equivalently
tf.transpose(x, perm=[1, 0]) # [[1, 4]
# [2, 5]
# [3, 6]] # If x is complex, setting conjugate=True gives the conjugate transpose
x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # 'perm' is more useful for n-dimensional tensors, for n > 2
x = tf.constant([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]]) # Take the transpose of the matrices in dimension-0
# (this common operation has a shorthand `linalg.matrix_transpose`)
tf.transpose(x, perm=[0, 2, 1]) # [[[1, 4],
# [2, 5],
# [3, 6]],
# [[7, 10],
# [8, 11],
# [9, 12]]]
Tensor traverse_tree_v4(IGraphNodeBase tree_handle, IGraphNodeBase input_data, IGraphNodeBase sparse_input_indices, IGraphNodeBase sparse_input_values, IGraphNodeBase sparse_input_shape, string input_spec, object params, string name)
object traverse_tree_v4_dyn(object tree_handle, object input_data, object sparse_input_indices, object sparse_input_values, object sparse_input_shape, object input_spec, object params, object name)
object tree_deserialize(IGraphNodeBase tree_handle, IGraphNodeBase tree_config, object params, string name)
object tree_deserialize_dyn(object tree_handle, object tree_config, object params, object name)
object tree_ensemble_deserialize(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase stamp_token, IGraphNodeBase tree_ensemble_config, string name)
object tree_ensemble_deserialize_dyn(object tree_ensemble_handle, object stamp_token, object tree_ensemble_config, object name)
Tensor tree_ensemble_is_initialized_op(IGraphNodeBase tree_ensemble_handle, string name)
object tree_ensemble_is_initialized_op_dyn(object tree_ensemble_handle, object name)
object tree_ensemble_serialize(IGraphNodeBase tree_ensemble_handle, string name)
object tree_ensemble_serialize_dyn(object tree_ensemble_handle, object name)
Tensor tree_ensemble_stamp_token(IGraphNodeBase tree_ensemble_handle, string name)
object tree_ensemble_stamp_token_dyn(object tree_ensemble_handle, object name)
object tree_ensemble_stats(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase stamp_token, string name)
object tree_ensemble_stats_dyn(object tree_ensemble_handle, object stamp_token, object name)
object tree_ensemble_used_handlers(IGraphNodeBase tree_ensemble_handle, IGraphNodeBase stamp_token, int num_all_handlers, string name)
object tree_ensemble_used_handlers_dyn(object tree_ensemble_handle, object stamp_token, object num_all_handlers, object name)
Tensor tree_is_initialized_op(IGraphNodeBase tree_handle, string name)
object tree_is_initialized_op_dyn(object tree_handle, object name)
object tree_predictions_v4(IGraphNodeBase tree_handle, IGraphNodeBase input_data, IGraphNodeBase sparse_input_indices, IGraphNodeBase sparse_input_values, IGraphNodeBase sparse_input_shape, string input_spec, object params, string name)
object tree_predictions_v4_dyn(object tree_handle, object input_data, object sparse_input_indices, object sparse_input_values, object sparse_input_shape, object input_spec, object params, object name)
Tensor tree_serialize(IGraphNodeBase tree_handle, string name)
object tree_serialize_dyn(object tree_handle, object name)
Tensor tree_size(IGraphNodeBase tree_handle, string name)
object tree_size_dyn(object tree_handle, object name)
Tensor truediv(RaggedTensor x, object y, string name)
Divides x / y elementwise (using Python 3 division operator semantics). NOTE: Prefer using the Tensor operator or tf.divide which obey Python
division operator semantics. This function forces Python 3 division operator semantics where all integer
arguments are cast to floating types first. This op is generated by normal
`x / y` division in Python 3 and in Python 2.7 with
`from __future__ import division`. If you want integer division that rounds
down, use `x // y` or
tf.math.floordiv. `x` and `y` must have the same numeric type. If the inputs are floating
point, the output will have the same type. If the inputs are integral, the
inputs are cast to `float32` for `int8` and `int16` and `float64` for `int32`
and `int64` (matching the behavior of Numpy).
Parameters
-
RaggedTensorx - `Tensor` numerator of numeric type.
-
objecty - `Tensor` denominator of numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` evaluated in floating point.
Tensor truediv(object x, object y, string name)
Divides x / y elementwise (using Python 3 division operator semantics). NOTE: Prefer using the Tensor operator or tf.divide which obey Python
division operator semantics. This function forces Python 3 division operator semantics where all integer
arguments are cast to floating types first. This op is generated by normal
`x / y` division in Python 3 and in Python 2.7 with
`from __future__ import division`. If you want integer division that rounds
down, use `x // y` or
tf.math.floordiv. `x` and `y` must have the same numeric type. If the inputs are floating
point, the output will have the same type. If the inputs are integral, the
inputs are cast to `float32` for `int8` and `int16` and `float64` for `int32`
and `int64` (matching the behavior of Numpy).
Parameters
-
objectx - `Tensor` numerator of numeric type.
-
objecty - `Tensor` denominator of numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` evaluated in floating point.
Tensor truediv(IGraphNodeBase x, object y, string name)
Divides x / y elementwise (using Python 3 division operator semantics). NOTE: Prefer using the Tensor operator or tf.divide which obey Python
division operator semantics. This function forces Python 3 division operator semantics where all integer
arguments are cast to floating types first. This op is generated by normal
`x / y` division in Python 3 and in Python 2.7 with
`from __future__ import division`. If you want integer division that rounds
down, use `x // y` or
tf.math.floordiv. `x` and `y` must have the same numeric type. If the inputs are floating
point, the output will have the same type. If the inputs are integral, the
inputs are cast to `float32` for `int8` and `int16` and `float64` for `int32`
and `int64` (matching the behavior of Numpy).
Parameters
-
IGraphNodeBasex - `Tensor` numerator of numeric type.
-
objecty - `Tensor` denominator of numeric type.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - `x / y` evaluated in floating point.
object truediv_dyn(object x, object y, object name)
Divides x / y elementwise (using Python 3 division operator semantics). NOTE: Prefer using the Tensor operator or tf.divide which obey Python
division operator semantics. This function forces Python 3 division operator semantics where all integer
arguments are cast to floating types first. This op is generated by normal
`x / y` division in Python 3 and in Python 2.7 with
`from __future__ import division`. If you want integer division that rounds
down, use `x // y` or
tf.math.floordiv. `x` and `y` must have the same numeric type. If the inputs are floating
point, the output will have the same type. If the inputs are integral, the
inputs are cast to `float32` for `int8` and `int16` and `float64` for `int32`
and `int64` (matching the behavior of Numpy).
Parameters
-
objectx - `Tensor` numerator of numeric type.
-
objecty - `Tensor` denominator of numeric type.
-
objectname - A name for the operation (optional).
Returns
-
object - `x / y` evaluated in floating point.
Tensor truncated_normal(ValueTuple<int, object> shape, int mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
ValueTuple<int, object>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(ValueTuple<int, object> shape, double mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
ValueTuple<int, object>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(IGraphNodeBase shape, int mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(ValueTuple<int, object> shape, double mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
ValueTuple<int, object>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(ValueTuple<int, object> shape, int mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
ValueTuple<int, object>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(TensorShape shape, double mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(TensorShape shape, int mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(IGraphNodeBase shape, double mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(IEnumerable<int> shape, int mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(IGraphNodeBase shape, int mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(TensorShape shape, double mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(IEnumerable<int> shape, double mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(TensorShape shape, int mean, int stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
TensorShapeshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
intstddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(IEnumerable<int> shape, int mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
intmean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(IEnumerable<int> shape, double mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
IEnumerable<int>shape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
Tensor truncated_normal(IGraphNodeBase shape, double mean, double stddev, ImplicitContainer<T> dtype, object seed, string name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
IGraphNodeBaseshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
doublemean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
doublestddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A tensor of the specified shape filled with random truncated normal values.
object truncated_normal_dyn(object shape, ImplicitContainer<T> mean, ImplicitContainer<T> stddev, ImplicitContainer<T> dtype, object seed, object name)
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
Parameters
-
objectshape - A 1-D integer Tensor or Python array. The shape of the output tensor.
-
ImplicitContainer<T>mean - A 0-D Tensor or Python value of type `dtype`. The mean of the truncated normal distribution.
-
ImplicitContainer<T>stddev - A 0-D Tensor or Python value of type `dtype`. The standard deviation of the normal distribution, before truncation.
-
ImplicitContainer<T>dtype - The type of the output.
-
objectseed - A Python integer. Used to create a random seed for the distribution. See `tf.compat.v1.set_random_seed` for behavior.
-
objectname - A name for the operation (optional).
Returns
-
object - A tensor of the specified shape filled with random truncated normal values.
object truncatediv(int x, IGraphNodeBase y, string name)
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatediv(IGraphNodeBase x, double y, string name)
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatediv(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatediv(int x, int y, string name)
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatediv(int x, double y, string name)
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatediv(double x, IGraphNodeBase y, string name)
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatediv(double x, int y, string name)
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatediv(double x, double y, string name)
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatediv(IGraphNodeBase x, int y, string name)
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatediv_dyn(object x, object y, object name)
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `bfloat16`, `half`, `float32`, `float64`, `uint8`, `int8`, `uint16`, `int16`, `int32`, `int64`, `complex64`, `complex128`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatemod(IGraphNodeBase x, int y, string name)
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatemod(int x, int y, string name)
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatemod(double x, double y, string name)
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatemod(double x, int y, string name)
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
inty - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatemod(double x, IGraphNodeBase y, string name)
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
doublex - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatemod(IGraphNodeBase x, double y, string name)
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatemod(int x, IGraphNodeBase y, string name)
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatemod(IGraphNodeBase x, IGraphNodeBase y, string name)
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
IGraphNodeBasey - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatemod(int x, double y, string name)
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
intx - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
doubley - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object truncatemod_dyn(object x, object y, object name)
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `int32`, `int64`, `bfloat16`, `half`, `float32`, `float64`.
-
objecty - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
object try_rpc(IGraphNodeBase address, IGraphNodeBase method, IGraphNodeBase request, string protocol, bool fail_fast, int timeout_in_ms, string name)
object try_rpc_dyn(object address, object method, object request, ImplicitContainer<T> protocol, ImplicitContainer<T> fail_fast, ImplicitContainer<T> timeout_in_ms, object name)
object tuple(IEnumerable<IndexedSlices> tensors, string name, IEnumerable<IGraphNodeBase> control_inputs)
Group tensors together. This creates a tuple of tensors with the same values as the `tensors`
argument, except that the value of each tensor is only returned after the
values of all tensors have been computed. `control_inputs` contains additional ops that have to finish before this op
finishes, but whose outputs are not returned. This can be used as a "join" mechanism for parallel computations: all the
argument tensors can be computed in parallel, but the values of any tensor
returned by `tuple` are only available after all the parallel computations
are done. See also
tf.group and
tf.control_dependencies.
Parameters
-
IEnumerable<IndexedSlices>tensors - A list of `Tensor`s or `IndexedSlices`, some entries can be `None`.
-
stringname - (optional) A name to use as a `name_scope` for the operation.
-
IEnumerable<IGraphNodeBase>control_inputs - List of additional ops to finish before returning.
Returns
-
object - Same as `tensors`.
object tuple(PythonClassContainer tensors, string name, IEnumerable<IGraphNodeBase> control_inputs)
Group tensors together. This creates a tuple of tensors with the same values as the `tensors`
argument, except that the value of each tensor is only returned after the
values of all tensors have been computed. `control_inputs` contains additional ops that have to finish before this op
finishes, but whose outputs are not returned. This can be used as a "join" mechanism for parallel computations: all the
argument tensors can be computed in parallel, but the values of any tensor
returned by `tuple` are only available after all the parallel computations
are done. See also
tf.group and
tf.control_dependencies.
Parameters
-
PythonClassContainertensors - A list of `Tensor`s or `IndexedSlices`, some entries can be `None`.
-
stringname - (optional) A name to use as a `name_scope` for the operation.
-
IEnumerable<IGraphNodeBase>control_inputs - List of additional ops to finish before returning.
Returns
-
object - Same as `tensors`.
object tuple(IGraphNodeBase tensors, string name, IEnumerable<IGraphNodeBase> control_inputs)
Group tensors together. This creates a tuple of tensors with the same values as the `tensors`
argument, except that the value of each tensor is only returned after the
values of all tensors have been computed. `control_inputs` contains additional ops that have to finish before this op
finishes, but whose outputs are not returned. This can be used as a "join" mechanism for parallel computations: all the
argument tensors can be computed in parallel, but the values of any tensor
returned by `tuple` are only available after all the parallel computations
are done. See also
tf.group and
tf.control_dependencies.
Parameters
-
IGraphNodeBasetensors - A list of `Tensor`s or `IndexedSlices`, some entries can be `None`.
-
stringname - (optional) A name to use as a `name_scope` for the operation.
-
IEnumerable<IGraphNodeBase>control_inputs - List of additional ops to finish before returning.
Returns
-
object - Same as `tensors`.
object tuple_dyn(object tensors, object name, object control_inputs)
Group tensors together. This creates a tuple of tensors with the same values as the `tensors`
argument, except that the value of each tensor is only returned after the
values of all tensors have been computed. `control_inputs` contains additional ops that have to finish before this op
finishes, but whose outputs are not returned. This can be used as a "join" mechanism for parallel computations: all the
argument tensors can be computed in parallel, but the values of any tensor
returned by `tuple` are only available after all the parallel computations
are done. See also
tf.group and
tf.control_dependencies.
Parameters
-
objecttensors - A list of `Tensor`s or `IndexedSlices`, some entries can be `None`.
-
objectname - (optional) A name to use as a `name_scope` for the operation.
-
objectcontrol_inputs - List of additional ops to finish before returning.
Returns
-
object - Same as `tensors`.
object two_float_inputs(IGraphNodeBase a, IGraphNodeBase b, string name)
object two_float_inputs_dyn(object a, object b, object name)
Tensor two_float_inputs_float_output(IGraphNodeBase a, IGraphNodeBase b, string name)
object two_float_inputs_float_output_dyn(object a, object b, object name)
Tensor two_float_inputs_int_output(IGraphNodeBase a, IGraphNodeBase b, string name)
object two_float_inputs_int_output_dyn(object a, object b, object name)
object two_float_outputs(string name)
object two_float_outputs_dyn(object name)
object two_int_inputs(IGraphNodeBase a, IGraphNodeBase b, string name)
object two_int_inputs_dyn(object a, object b, object name)
object two_int_outputs(string name)
object two_int_outputs_dyn(object name)
object two_refs_in(object a, object b, string name)
object two_refs_in_dyn(object a, object b, object name)
object type_list(object a, string name)
object type_list_dyn(object a, object name)
object type_list_restrict(object a, string name)
object type_list_restrict_dyn(object a, object name)
object type_list_twice(object a, object b, string name)
object type_list_twice_dyn(object a, object b, object name)
Tensor unary(IGraphNodeBase a, string name)
object unary_dyn(object a, object name)
object unique(IEnumerable<object> x, ImplicitContainer<T> out_idx, string name)
Finds unique elements in a 1-D tensor. This operation returns a tensor `y` containing all of the unique elements of `x`
sorted in the same order that they occur in `x`. This operation also returns a
tensor `idx` the same size as `x` that contains the index of each value of `x`
in the unique output `y`. In other words: `y[idx[i]] = x[i] for i in [0, 1,...,rank(x) - 1]` For example: ```
# tensor 'x' is [1, 1, 2, 4, 4, 4, 7, 8, 8]
y, idx = unique(x)
y ==> [1, 2, 4, 7, 8]
idx ==> [0, 0, 1, 2, 2, 2, 3, 4, 4]
```
Parameters
-
IEnumerable<object>x - A `Tensor`. 1-D.
-
ImplicitContainer<T>out_idx - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int32. -
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (y, idx).
object unique(object x, ImplicitContainer<T> out_idx, string name)
Finds unique elements in a 1-D tensor. This operation returns a tensor `y` containing all of the unique elements of `x`
sorted in the same order that they occur in `x`. This operation also returns a
tensor `idx` the same size as `x` that contains the index of each value of `x`
in the unique output `y`. In other words: `y[idx[i]] = x[i] for i in [0, 1,...,rank(x) - 1]` For example: ```
# tensor 'x' is [1, 1, 2, 4, 4, 4, 7, 8, 8]
y, idx = unique(x)
y ==> [1, 2, 4, 7, 8]
idx ==> [0, 0, 1, 2, 2, 2, 3, 4, 4]
```
Parameters
-
objectx - A `Tensor`. 1-D.
-
ImplicitContainer<T>out_idx - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int32. -
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (y, idx).
object unique_dyn(object x, ImplicitContainer<T> out_idx, object name)
Finds unique elements in a 1-D tensor. This operation returns a tensor `y` containing all of the unique elements of `x`
sorted in the same order that they occur in `x`. This operation also returns a
tensor `idx` the same size as `x` that contains the index of each value of `x`
in the unique output `y`. In other words: `y[idx[i]] = x[i] for i in [0, 1,...,rank(x) - 1]` For example: ```
# tensor 'x' is [1, 1, 2, 4, 4, 4, 7, 8, 8]
y, idx = unique(x)
y ==> [1, 2, 4, 7, 8]
idx ==> [0, 0, 1, 2, 2, 2, 3, 4, 4]
```
Parameters
-
objectx - A `Tensor`. 1-D.
-
ImplicitContainer<T>out_idx - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int32. -
objectname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (y, idx).
object unique_with_counts(Variable x, ImplicitContainer<T> out_idx, string name)
Finds unique elements in a 1-D tensor. This operation returns a tensor `y` containing all of the unique elements of `x`
sorted in the same order that they occur in `x`. This operation also returns a
tensor `idx` the same size as `x` that contains the index of each value of `x`
in the unique output `y`. Finally, it returns a third tensor `count` that
contains the count of each element of `y` in `x`. In other words: `y[idx[i]] = x[i] for i in [0, 1,...,rank(x) - 1]` For example: ```
# tensor 'x' is [1, 1, 2, 4, 4, 4, 7, 8, 8]
y, idx, count = unique_with_counts(x)
y ==> [1, 2, 4, 7, 8]
idx ==> [0, 0, 1, 2, 2, 2, 3, 4, 4]
count ==> [2, 1, 3, 1, 2]
```
Parameters
-
Variablex - A `Tensor`. 1-D.
-
ImplicitContainer<T>out_idx - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int32. -
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (y, idx, count).
object unique_with_counts(IEnumerable<string> x, ImplicitContainer<T> out_idx, string name)
Finds unique elements in a 1-D tensor. This operation returns a tensor `y` containing all of the unique elements of `x`
sorted in the same order that they occur in `x`. This operation also returns a
tensor `idx` the same size as `x` that contains the index of each value of `x`
in the unique output `y`. Finally, it returns a third tensor `count` that
contains the count of each element of `y` in `x`. In other words: `y[idx[i]] = x[i] for i in [0, 1,...,rank(x) - 1]` For example: ```
# tensor 'x' is [1, 1, 2, 4, 4, 4, 7, 8, 8]
y, idx, count = unique_with_counts(x)
y ==> [1, 2, 4, 7, 8]
idx ==> [0, 0, 1, 2, 2, 2, 3, 4, 4]
count ==> [2, 1, 3, 1, 2]
```
Parameters
-
IEnumerable<string>x - A `Tensor`. 1-D.
-
ImplicitContainer<T>out_idx - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int32. -
stringname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (y, idx, count).
object unique_with_counts_dyn(object x, ImplicitContainer<T> out_idx, object name)
Finds unique elements in a 1-D tensor. This operation returns a tensor `y` containing all of the unique elements of `x`
sorted in the same order that they occur in `x`. This operation also returns a
tensor `idx` the same size as `x` that contains the index of each value of `x`
in the unique output `y`. Finally, it returns a third tensor `count` that
contains the count of each element of `y` in `x`. In other words: `y[idx[i]] = x[i] for i in [0, 1,...,rank(x) - 1]` For example: ```
# tensor 'x' is [1, 1, 2, 4, 4, 4, 7, 8, 8]
y, idx, count = unique_with_counts(x)
y ==> [1, 2, 4, 7, 8]
idx ==> [0, 0, 1, 2, 2, 2, 3, 4, 4]
count ==> [2, 1, 3, 1, 2]
```
Parameters
-
objectx - A `Tensor`. 1-D.
-
ImplicitContainer<T>out_idx - An optional
tf.DTypefrom: `tf.int32, tf.int64`. Defaults totf.int32. -
objectname - A name for the operation (optional).
Returns
-
object - A tuple of `Tensor` objects (y, idx, count).
Tensor unpack_path(IGraphNodeBase path, IGraphNodeBase path_values, string name)
object unpack_path_dyn(object path, object path_values, object name)
Tensor unravel_index(IGraphNodeBase indices, IGraphNodeBase dims, string name)
Converts an array of flat indices into a tuple of coordinate arrays. Example: ```
y = tf.unravel_index(indices=[2, 5, 7], dims=[3, 3])
# 'dims' represent a hypothetical (3, 3) tensor of indices:
# [[0, 1, *2*],
# [3, 4, *5*],
# [6, *7*, 8]]
# For each entry from 'indices', this operation returns
# its coordinates (marked with '*'), such as
# 2 ==> (0, 2)
# 5 ==> (1, 2)
# 7 ==> (2, 1)
y ==> [[0, 1, 2], [2, 2, 1]]
```
Parameters
-
IGraphNodeBaseindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. An 0-D or 1-D `int` Tensor whose elements are indices into the flattened version of an array of dimensions dims.
-
IGraphNodeBasedims - A `Tensor`. Must have the same type as `indices`. An 1-D `int` Tensor. The shape of the array to use for unraveling indices.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `indices`.
object unravel_index_dyn(object indices, object dims, object name)
Converts an array of flat indices into a tuple of coordinate arrays. Example: ```
y = tf.unravel_index(indices=[2, 5, 7], dims=[3, 3])
# 'dims' represent a hypothetical (3, 3) tensor of indices:
# [[0, 1, *2*],
# [3, 4, *5*],
# [6, *7*, 8]]
# For each entry from 'indices', this operation returns
# its coordinates (marked with '*'), such as
# 2 ==> (0, 2)
# 5 ==> (1, 2)
# 7 ==> (2, 1)
y ==> [[0, 1, 2], [2, 2, 1]]
```
Parameters
-
objectindices - A `Tensor`. Must be one of the following types: `int32`, `int64`. An 0-D or 1-D `int` Tensor whose elements are indices into the flattened version of an array of dimensions dims.
-
objectdims - A `Tensor`. Must have the same type as `indices`. An 1-D `int` Tensor. The shape of the array to use for unraveling indices.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `indices`.
Tensor unsorted_segment_max(IGraphNodeBase data, IGraphNodeBase segment_ids, IGraphNodeBase num_segments, string name)
Computes the maximum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[(here)](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the maximum such that: \\(output_i = \max_{j...} data[j...]\\) where max is over tuples `j...` such
that `segment_ids[j...] == i`. If the maximum is empty for a given segment ID `i`, it outputs the smallest
possible value for the specific numeric type,
`output[i] = numeric_limits::lowest()`. If the given segment ID `i` is negative, then the corresponding value is
dropped, and will not be included in the result.
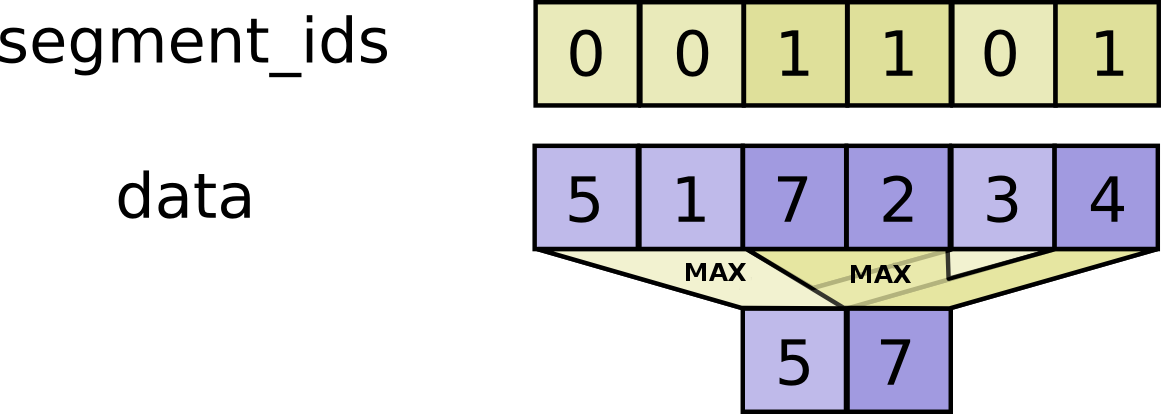 For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_max(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 4, 3, 3, 4],
# [5, 6, 7, 8]]
```
For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_max(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 4, 3, 3, 4],
# [5, 6, 7, 8]]
```

Parameters
-
IGraphNodeBasedata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasesegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor whose shape is a prefix of `data.shape`.
-
IGraphNodeBasenum_segments - A `Tensor`. Must be one of the following types: `int32`, `int64`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
object unsorted_segment_max_dyn(object data, object segment_ids, object num_segments, object name)
Computes the maximum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[(here)](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the maximum such that: \\(output_i = \max_{j...} data[j...]\\) where max is over tuples `j...` such
that `segment_ids[j...] == i`. If the maximum is empty for a given segment ID `i`, it outputs the smallest
possible value for the specific numeric type,
`output[i] = numeric_limits::lowest()`. If the given segment ID `i` is negative, then the corresponding value is
dropped, and will not be included in the result.
 For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_max(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 4, 3, 3, 4],
# [5, 6, 7, 8]]
```
For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_max(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 4, 3, 3, 4],
# [5, 6, 7, 8]]
```

Parameters
-
objectdata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`.
-
objectsegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor whose shape is a prefix of `data.shape`.
-
objectnum_segments - A `Tensor`. Must be one of the following types: `int32`, `int64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `data`.
Tensor unsorted_segment_mean(object data, object segment_ids, object num_segments, string name)
Computes the mean along segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[here](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the mean of all
entries belonging to a segment such that: \\(output_i = 1/N_i \sum_{j...} data[j...]\\) where the sum is over tuples
`j...` such that `segment_ids[j...] == i` with \\N_i\\ being the number of
occurrences of id \\i\\. If there is no entry for a given segment ID `i`, it outputs 0. If the given segment ID `i` is negative, the value is dropped and will not
be added to the sum of the segment.
Parameters
-
objectdata - A `Tensor` with floating point or complex dtype.
-
objectsegment_ids - An integer tensor whose shape is a prefix of `data.shape`.
-
objectnum_segments - An integer scalar `Tensor`. The number of distinct segment IDs.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has same shape as data, except for the first `segment_ids.rank` dimensions, which are replaced with a single dimension which has size `num_segments`.
object unsorted_segment_mean_dyn(object data, object segment_ids, object num_segments, object name)
Computes the mean along segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[here](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the mean of all
entries belonging to a segment such that: \\(output_i = 1/N_i \sum_{j...} data[j...]\\) where the sum is over tuples
`j...` such that `segment_ids[j...] == i` with \\N_i\\ being the number of
occurrences of id \\i\\. If there is no entry for a given segment ID `i`, it outputs 0. If the given segment ID `i` is negative, the value is dropped and will not
be added to the sum of the segment.
Parameters
-
objectdata - A `Tensor` with floating point or complex dtype.
-
objectsegment_ids - An integer tensor whose shape is a prefix of `data.shape`.
-
objectnum_segments - An integer scalar `Tensor`. The number of distinct segment IDs.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has same shape as data, except for the first `segment_ids.rank` dimensions, which are replaced with a single dimension which has size `num_segments`.
Tensor unsorted_segment_min(IGraphNodeBase data, IGraphNodeBase segment_ids, IGraphNodeBase num_segments, string name)
Computes the minimum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[(here)](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the minimum such that: \\(output_i = \min_{j...} data_[j...]\\) where min is over tuples `j...` such
that `segment_ids[j...] == i`. If the minimum is empty for a given segment ID `i`, it outputs the largest
possible value for the specific numeric type,
`output[i] = numeric_limits::max()`. For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_min(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 1, 2, 2, 1],
# [5, 6, 7, 8]]
``` If the given segment ID `i` is negative, then the corresponding value is
dropped, and will not be included in the result.
Parameters
-
IGraphNodeBasedata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasesegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor whose shape is a prefix of `data.shape`.
-
IGraphNodeBasenum_segments - A `Tensor`. Must be one of the following types: `int32`, `int64`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
object unsorted_segment_min_dyn(object data, object segment_ids, object num_segments, object name)
Computes the minimum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[(here)](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the minimum such that: \\(output_i = \min_{j...} data_[j...]\\) where min is over tuples `j...` such
that `segment_ids[j...] == i`. If the minimum is empty for a given segment ID `i`, it outputs the largest
possible value for the specific numeric type,
`output[i] = numeric_limits::max()`. For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_min(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 1, 2, 2, 1],
# [5, 6, 7, 8]]
``` If the given segment ID `i` is negative, then the corresponding value is
dropped, and will not be included in the result.
Parameters
-
objectdata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `int64`, `bfloat16`, `uint16`, `half`, `uint32`, `uint64`.
-
objectsegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor whose shape is a prefix of `data.shape`.
-
objectnum_segments - A `Tensor`. Must be one of the following types: `int32`, `int64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `data`.
Tensor unsorted_segment_prod(IGraphNodeBase data, IGraphNodeBase segment_ids, IGraphNodeBase num_segments, string name)
Computes the product along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[(here)](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the product of all
entries belonging to a segment such that: \\(output_i = \prod_{j...} data[j...]\\) where the product is over tuples
`j...` such that `segment_ids[j...] == i`. For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_prod(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 4, 6, 6, 4],
# [5, 6, 7, 8]]
``` If there is no entry for a given segment ID `i`, it outputs 1. If the given segment ID `i` is negative, then the corresponding value is
dropped, and will not be included in the result.
Parameters
-
IGraphNodeBasedata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasesegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor whose shape is a prefix of `data.shape`.
-
IGraphNodeBasenum_segments - A `Tensor`. Must be one of the following types: `int32`, `int64`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
object unsorted_segment_prod_dyn(object data, object segment_ids, object num_segments, object name)
Computes the product along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[(here)](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the product of all
entries belonging to a segment such that: \\(output_i = \prod_{j...} data[j...]\\) where the product is over tuples
`j...` such that `segment_ids[j...] == i`. For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_prod(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 4, 6, 6, 4],
# [5, 6, 7, 8]]
``` If there is no entry for a given segment ID `i`, it outputs 1. If the given segment ID `i` is negative, then the corresponding value is
dropped, and will not be included in the result.
Parameters
-
objectdata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
objectsegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor whose shape is a prefix of `data.shape`.
-
objectnum_segments - A `Tensor`. Must be one of the following types: `int32`, `int64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `data`.
Tensor unsorted_segment_sqrt_n(object data, object segment_ids, object num_segments, string name)
Computes the sum along segments of a tensor divided by the sqrt(N). Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[here](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Additionally to computing the sum over segments, it divides the results by
sqrt(N). \\(output_i = 1/sqrt(N_i) \sum_{j...} data[j...]\\) where the sum is over
tuples `j...` such that `segment_ids[j...] == i` with \\N_i\\ being the
number of occurrences of id \\i\\. If there is no entry for a given segment ID `i`, it outputs 0. Note that this op only supports floating point and complex dtypes,
due to tf.sqrt only supporting these types. If the given segment ID `i` is negative, the value is dropped and will not
be added to the sum of the segment.
Parameters
-
objectdata - A `Tensor` with floating point or complex dtype.
-
objectsegment_ids - An integer tensor whose shape is a prefix of `data.shape`.
-
objectnum_segments - An integer scalar `Tensor`. The number of distinct segment IDs.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has same shape as data, except for the first `segment_ids.rank` dimensions, which are replaced with a single dimension which has size `num_segments`.
object unsorted_segment_sqrt_n_dyn(object data, object segment_ids, object num_segments, object name)
Computes the sum along segments of a tensor divided by the sqrt(N). Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[here](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Additionally to computing the sum over segments, it divides the results by
sqrt(N). \\(output_i = 1/sqrt(N_i) \sum_{j...} data[j...]\\) where the sum is over
tuples `j...` such that `segment_ids[j...] == i` with \\N_i\\ being the
number of occurrences of id \\i\\. If there is no entry for a given segment ID `i`, it outputs 0. Note that this op only supports floating point and complex dtypes,
due to tf.sqrt only supporting these types. If the given segment ID `i` is negative, the value is dropped and will not
be added to the sum of the segment.
Parameters
-
objectdata - A `Tensor` with floating point or complex dtype.
-
objectsegment_ids - An integer tensor whose shape is a prefix of `data.shape`.
-
objectnum_segments - An integer scalar `Tensor`. The number of distinct segment IDs.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has same shape as data, except for the first `segment_ids.rank` dimensions, which are replaced with a single dimension which has size `num_segments`.
Tensor unsorted_segment_sum(IGraphNodeBase data, IGraphNodeBase segment_ids, IGraphNodeBase num_segments, string name)
Computes the sum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output[i] = \sum_{j...} data[j...]\\) where the sum is over tuples `j...` such
that `segment_ids[j...] == i`. Unlike `SegmentSum`, `segment_ids`
need not be sorted and need not cover all values in the full
range of valid values. If the sum is empty for a given segment ID `i`, `output[i] = 0`.
If the given segment ID `i` is negative, the value is dropped and will not be
added to the sum of the segment. `num_segments` should equal the number of distinct segment IDs.
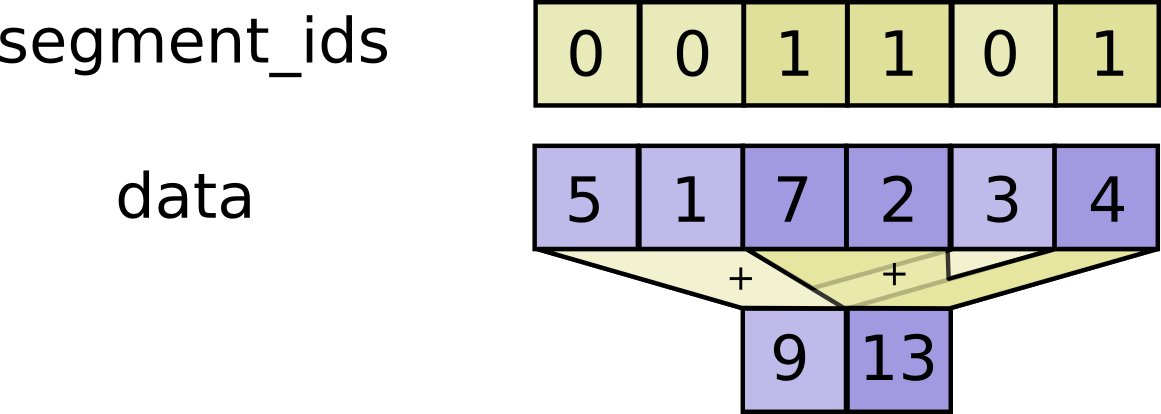 ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_sum(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 5, 5, 5, 5],
# [5, 6, 7, 8]]
```
``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_sum(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 5, 5, 5, 5],
# [5, 6, 7, 8]]
```

Parameters
-
IGraphNodeBasedata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
IGraphNodeBasesegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor whose shape is a prefix of `data.shape`.
-
IGraphNodeBasenum_segments - A `Tensor`. Must be one of the following types: `int32`, `int64`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `data`.
object unsorted_segment_sum_dyn(object data, object segment_ids, object num_segments, object name)
Computes the sum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output[i] = \sum_{j...} data[j...]\\) where the sum is over tuples `j...` such
that `segment_ids[j...] == i`. Unlike `SegmentSum`, `segment_ids`
need not be sorted and need not cover all values in the full
range of valid values. If the sum is empty for a given segment ID `i`, `output[i] = 0`.
If the given segment ID `i` is negative, the value is dropped and will not be
added to the sum of the segment. `num_segments` should equal the number of distinct segment IDs.
 ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_sum(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 5, 5, 5, 5],
# [5, 6, 7, 8]]
```
``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_sum(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 5, 5, 5, 5],
# [5, 6, 7, 8]]
```

Parameters
-
objectdata - A `Tensor`. Must be one of the following types: `float32`, `float64`, `int32`, `uint8`, `int16`, `int8`, `complex64`, `int64`, `qint8`, `quint8`, `qint32`, `bfloat16`, `uint16`, `complex128`, `half`, `uint32`, `uint64`.
-
objectsegment_ids - A `Tensor`. Must be one of the following types: `int32`, `int64`. A tensor whose shape is a prefix of `data.shape`.
-
objectnum_segments - A `Tensor`. Must be one of the following types: `int32`, `int64`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `data`.
object unstack(IEnumerable<IGraphNodeBase> value, ndarray num, int axis, string name)
Unpacks the given dimension of a rank-`R` tensor into rank-`(R-1)` tensors. Unpacks `num` tensors from `value` by chipping it along the `axis` dimension.
If `num` is not specified (the default), it is inferred from `value`'s shape.
If `value.shape[axis]` is not known, `ValueError` is raised. For example, given a tensor of shape `(A, B, C, D)`; If `axis == 0` then the i'th tensor in `output` is the slice
`value[i, :, :, :]` and each tensor in `output` will have shape `(B, C, D)`.
(Note that the dimension unpacked along is gone, unlike `split`). If `axis == 1` then the i'th tensor in `output` is the slice
`value[:, i, :, :]` and each tensor in `output` will have shape `(A, C, D)`.
Etc. This is the opposite of stack.
Parameters
-
IEnumerable<IGraphNodeBase>value - A rank `R > 0` `Tensor` to be unstacked.
-
ndarraynum - An `int`. The length of the dimension `axis`. Automatically inferred if `None` (the default).
-
intaxis - An `int`. The axis to unstack along. Defaults to the first dimension. Negative values wrap around, so the valid range is `[-R, R)`.
-
stringname - A name for the operation (optional).
Returns
-
object - The list of `Tensor` objects unstacked from `value`.
object unstack(object value, ndarray num, int axis, string name)
Unpacks the given dimension of a rank-`R` tensor into rank-`(R-1)` tensors. Unpacks `num` tensors from `value` by chipping it along the `axis` dimension.
If `num` is not specified (the default), it is inferred from `value`'s shape.
If `value.shape[axis]` is not known, `ValueError` is raised. For example, given a tensor of shape `(A, B, C, D)`; If `axis == 0` then the i'th tensor in `output` is the slice
`value[i, :, :, :]` and each tensor in `output` will have shape `(B, C, D)`.
(Note that the dimension unpacked along is gone, unlike `split`). If `axis == 1` then the i'th tensor in `output` is the slice
`value[:, i, :, :]` and each tensor in `output` will have shape `(A, C, D)`.
Etc. This is the opposite of stack.
Parameters
-
objectvalue - A rank `R > 0` `Tensor` to be unstacked.
-
ndarraynum - An `int`. The length of the dimension `axis`. Automatically inferred if `None` (the default).
-
intaxis - An `int`. The axis to unstack along. Defaults to the first dimension. Negative values wrap around, so the valid range is `[-R, R)`.
-
stringname - A name for the operation (optional).
Returns
-
object - The list of `Tensor` objects unstacked from `value`.
object unstack(IEnumerable<IGraphNodeBase> value, IGraphNodeBase num, int axis, string name)
Unpacks the given dimension of a rank-`R` tensor into rank-`(R-1)` tensors. Unpacks `num` tensors from `value` by chipping it along the `axis` dimension.
If `num` is not specified (the default), it is inferred from `value`'s shape.
If `value.shape[axis]` is not known, `ValueError` is raised. For example, given a tensor of shape `(A, B, C, D)`; If `axis == 0` then the i'th tensor in `output` is the slice
`value[i, :, :, :]` and each tensor in `output` will have shape `(B, C, D)`.
(Note that the dimension unpacked along is gone, unlike `split`). If `axis == 1` then the i'th tensor in `output` is the slice
`value[:, i, :, :]` and each tensor in `output` will have shape `(A, C, D)`.
Etc. This is the opposite of stack.
Parameters
-
IEnumerable<IGraphNodeBase>value - A rank `R > 0` `Tensor` to be unstacked.
-
IGraphNodeBasenum - An `int`. The length of the dimension `axis`. Automatically inferred if `None` (the default).
-
intaxis - An `int`. The axis to unstack along. Defaults to the first dimension. Negative values wrap around, so the valid range is `[-R, R)`.
-
stringname - A name for the operation (optional).
Returns
-
object - The list of `Tensor` objects unstacked from `value`.
object unstack(object value, int num, int axis, string name)
Unpacks the given dimension of a rank-`R` tensor into rank-`(R-1)` tensors. Unpacks `num` tensors from `value` by chipping it along the `axis` dimension.
If `num` is not specified (the default), it is inferred from `value`'s shape.
If `value.shape[axis]` is not known, `ValueError` is raised. For example, given a tensor of shape `(A, B, C, D)`; If `axis == 0` then the i'th tensor in `output` is the slice
`value[i, :, :, :]` and each tensor in `output` will have shape `(B, C, D)`.
(Note that the dimension unpacked along is gone, unlike `split`). If `axis == 1` then the i'th tensor in `output` is the slice
`value[:, i, :, :]` and each tensor in `output` will have shape `(A, C, D)`.
Etc. This is the opposite of stack.
Parameters
-
objectvalue - A rank `R > 0` `Tensor` to be unstacked.
-
intnum - An `int`. The length of the dimension `axis`. Automatically inferred if `None` (the default).
-
intaxis - An `int`. The axis to unstack along. Defaults to the first dimension. Negative values wrap around, so the valid range is `[-R, R)`.
-
stringname - A name for the operation (optional).
Returns
-
object - The list of `Tensor` objects unstacked from `value`.
object unstack(object value, IGraphNodeBase num, int axis, string name)
Unpacks the given dimension of a rank-`R` tensor into rank-`(R-1)` tensors. Unpacks `num` tensors from `value` by chipping it along the `axis` dimension.
If `num` is not specified (the default), it is inferred from `value`'s shape.
If `value.shape[axis]` is not known, `ValueError` is raised. For example, given a tensor of shape `(A, B, C, D)`; If `axis == 0` then the i'th tensor in `output` is the slice
`value[i, :, :, :]` and each tensor in `output` will have shape `(B, C, D)`.
(Note that the dimension unpacked along is gone, unlike `split`). If `axis == 1` then the i'th tensor in `output` is the slice
`value[:, i, :, :]` and each tensor in `output` will have shape `(A, C, D)`.
Etc. This is the opposite of stack.
Parameters
-
objectvalue - A rank `R > 0` `Tensor` to be unstacked.
-
IGraphNodeBasenum - An `int`. The length of the dimension `axis`. Automatically inferred if `None` (the default).
-
intaxis - An `int`. The axis to unstack along. Defaults to the first dimension. Negative values wrap around, so the valid range is `[-R, R)`.
-
stringname - A name for the operation (optional).
Returns
-
object - The list of `Tensor` objects unstacked from `value`.
object unstack(IEnumerable<IGraphNodeBase> value, int num, int axis, string name)
Unpacks the given dimension of a rank-`R` tensor into rank-`(R-1)` tensors. Unpacks `num` tensors from `value` by chipping it along the `axis` dimension.
If `num` is not specified (the default), it is inferred from `value`'s shape.
If `value.shape[axis]` is not known, `ValueError` is raised. For example, given a tensor of shape `(A, B, C, D)`; If `axis == 0` then the i'th tensor in `output` is the slice
`value[i, :, :, :]` and each tensor in `output` will have shape `(B, C, D)`.
(Note that the dimension unpacked along is gone, unlike `split`). If `axis == 1` then the i'th tensor in `output` is the slice
`value[:, i, :, :]` and each tensor in `output` will have shape `(A, C, D)`.
Etc. This is the opposite of stack.
Parameters
-
IEnumerable<IGraphNodeBase>value - A rank `R > 0` `Tensor` to be unstacked.
-
intnum - An `int`. The length of the dimension `axis`. Automatically inferred if `None` (the default).
-
intaxis - An `int`. The axis to unstack along. Defaults to the first dimension. Negative values wrap around, so the valid range is `[-R, R)`.
-
stringname - A name for the operation (optional).
Returns
-
object - The list of `Tensor` objects unstacked from `value`.
object unstack_dyn(object value, object num, ImplicitContainer<T> axis, ImplicitContainer<T> name)
Unpacks the given dimension of a rank-`R` tensor into rank-`(R-1)` tensors. Unpacks `num` tensors from `value` by chipping it along the `axis` dimension.
If `num` is not specified (the default), it is inferred from `value`'s shape.
If `value.shape[axis]` is not known, `ValueError` is raised. For example, given a tensor of shape `(A, B, C, D)`; If `axis == 0` then the i'th tensor in `output` is the slice
`value[i, :, :, :]` and each tensor in `output` will have shape `(B, C, D)`.
(Note that the dimension unpacked along is gone, unlike `split`). If `axis == 1` then the i'th tensor in `output` is the slice
`value[:, i, :, :]` and each tensor in `output` will have shape `(A, C, D)`.
Etc. This is the opposite of stack.
Parameters
-
objectvalue - A rank `R > 0` `Tensor` to be unstacked.
-
objectnum - An `int`. The length of the dimension `axis`. Automatically inferred if `None` (the default).
-
ImplicitContainer<T>axis - An `int`. The axis to unstack along. Defaults to the first dimension. Negative values wrap around, so the valid range is `[-R, R)`.
-
ImplicitContainer<T>name - A name for the operation (optional).
Returns
-
object - The list of `Tensor` objects unstacked from `value`.
object update_model_v4(IGraphNodeBase tree_handle, IGraphNodeBase leaf_ids, IGraphNodeBase input_labels, IGraphNodeBase input_weights, object params, string name)
object update_model_v4_dyn(object tree_handle, object leaf_ids, object input_labels, object input_weights, object params, object name)
object variable_axis_size_partitioner(int max_shard_bytes, int axis, int bytes_per_string_element, Nullable<int> max_shards)
Get a partitioner for VariableScope to keep shards below `max_shard_bytes`. This partitioner will shard a Variable along one axis, attempting to keep
the maximum shard size below `max_shard_bytes`. In practice, this is not
always possible when sharding along only one axis. When this happens,
this axis is sharded as much as possible (i.e., every dimension becomes
a separate shard). If the partitioner hits the `max_shards` limit, then each shard may end up
larger than `max_shard_bytes`. By default `max_shards` equals `None` and no
limit on the number of shards is enforced. One reasonable value for `max_shard_bytes` is `(64 << 20) - 1`, or almost
`64MB`, to keep below the protobuf byte limit.
Parameters
-
intmax_shard_bytes - The maximum size any given shard is allowed to be.
-
intaxis - The axis to partition along. Default: outermost axis.
-
intbytes_per_string_element - If the `Variable` is of type string, this provides an estimate of how large each scalar in the `Variable` is.
-
Nullable<int>max_shards - The maximum number of shards in int created taking precedence over `max_shard_bytes`.
Returns
-
object - A partition function usable as the `partitioner` argument to `variable_scope` and `get_variable`.
object variable_axis_size_partitioner_dyn(object max_shard_bytes, ImplicitContainer<T> axis, ImplicitContainer<T> bytes_per_string_element, object max_shards)
Get a partitioner for VariableScope to keep shards below `max_shard_bytes`. This partitioner will shard a Variable along one axis, attempting to keep
the maximum shard size below `max_shard_bytes`. In practice, this is not
always possible when sharding along only one axis. When this happens,
this axis is sharded as much as possible (i.e., every dimension becomes
a separate shard). If the partitioner hits the `max_shards` limit, then each shard may end up
larger than `max_shard_bytes`. By default `max_shards` equals `None` and no
limit on the number of shards is enforced. One reasonable value for `max_shard_bytes` is `(64 << 20) - 1`, or almost
`64MB`, to keep below the protobuf byte limit.
Parameters
-
objectmax_shard_bytes - The maximum size any given shard is allowed to be.
-
ImplicitContainer<T>axis - The axis to partition along. Default: outermost axis.
-
ImplicitContainer<T>bytes_per_string_element - If the `Variable` is of type string, this provides an estimate of how large each scalar in the `Variable` is.
-
objectmax_shards - The maximum number of shards in int created taking precedence over `max_shard_bytes`.
Returns
-
object - A partition function usable as the `partitioner` argument to `variable_scope` and `get_variable`.
IContextManager<T> variable_op_scope(object values, object name_or_scope, object default_name, object initializer, object regularizer, object caching_device, object partitioner, object custom_getter, object reuse, DType dtype, object use_resource, object constraint)
Deprecated: context manager for defining an op that creates variables.
object variable_op_scope_dyn(object values, object name_or_scope, object default_name, object initializer, object regularizer, object caching_device, object partitioner, object custom_getter, object reuse, object dtype, object use_resource, object constraint)
Deprecated: context manager for defining an op that creates variables.
object variables_initializer(PythonClassContainer var_list, string name)
Returns an Op that initializes a list of variables. After you launch the graph in a session, you can run the returned Op to
initialize all the variables in `var_list`. This Op runs all the
initializers of the variables in `var_list` in parallel. Calling `initialize_variables()` is equivalent to passing the list of
initializers to `Group()`. If `var_list` is empty, however, the function still returns an Op that can
be run. That Op just has no effect.
Parameters
-
PythonClassContainervar_list - List of `Variable` objects to initialize.
-
stringname - Optional name for the returned operation.
Returns
-
object - An Op that run the initializers of all the specified variables.
object variables_initializer(IEnumerable<ResourceVariable> var_list, string name)
Returns an Op that initializes a list of variables. After you launch the graph in a session, you can run the returned Op to
initialize all the variables in `var_list`. This Op runs all the
initializers of the variables in `var_list` in parallel. Calling `initialize_variables()` is equivalent to passing the list of
initializers to `Group()`. If `var_list` is empty, however, the function still returns an Op that can
be run. That Op just has no effect.
Parameters
-
IEnumerable<ResourceVariable>var_list - List of `Variable` objects to initialize.
-
stringname - Optional name for the returned operation.
Returns
-
object - An Op that run the initializers of all the specified variables.
object variables_initializer_dyn(object var_list, ImplicitContainer<T> name)
Returns an Op that initializes a list of variables. After you launch the graph in a session, you can run the returned Op to
initialize all the variables in `var_list`. This Op runs all the
initializers of the variables in `var_list` in parallel. Calling `initialize_variables()` is equivalent to passing the list of
initializers to `Group()`. If `var_list` is empty, however, the function still returns an Op that can
be run. That Op just has no effect.
Parameters
-
objectvar_list - List of `Variable` objects to initialize.
-
ImplicitContainer<T>name - Optional name for the returned operation.
Returns
-
object - An Op that run the initializers of all the specified variables.
object vectorized_map(object fn, IGraphNodeBase elems)
Parallel map on the list of tensors unpacked from `elems` on dimension 0. This method works similar to tf.map_fn but is optimized to run much faster,
possibly with a much larger memory footprint. The speedups are obtained by
vectorization (see https://arxiv.org/pdf/1903.04243.pdf). The idea behind
vectorization is to semantically launch all the invocations of `fn` in
parallel and fuse corresponding operations across all these invocations. This
fusion is done statically at graph generation time and the generated code is
often similar in performance to a manually fused version. Because
tf.vectorized_map fully parallelizes the batch, this method will
generally be significantly faster than using tf.map_fn, especially in eager
mode. However this is an experimental feature and currently has a lot of
limitations:
- There should be no data dependency between the different semantic
invocations of `fn`, i.e. it should be safe to map the elements of the
inputs in any order.
- Stateful kernels may mostly not be supported since these often imply a
data dependency. We do support a limited set of such stateful kernels
though (like RandomFoo, Variable operations like reads, etc).
- `fn` has limited support for control flow operations. tf.cond in
particular is not supported.
- `fn` should return nested structure of Tensors or Operations. However
if an Operation is returned, it should have zero outputs.
- The shape and dtype of any intermediate or output tensors in the
computation of `fn` should not depend on the input to `fn`.
Parameters
-
objectfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`, and returns a possibly nested structure of Tensors and Operations, which may be different than the structure of `elems`.
-
IGraphNodeBaseelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be mapped over by `fn`.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying fn to tensors unpacked from elems along the first dimension, from first to last. Examples: ```python def outer_product(a): return tf.tensordot(a, a, 0) batch_size = 100 a = tf.ones((batch_size, 32, 32)) c = tf.vectorized_map(outer_product, a) assert c.shape == (batch_size, 32, 32, 32, 32) ``` ```python # Computing per-example gradients batch_size = 10 num_features = 32 layer = tf.keras.layers.Dense(1) def model_fn(arg): with tf.GradientTape() as g: inp, label = arg inp = tf.expand_dims(inp, 0) label = tf.expand_dims(label, 0) prediction = layer(inp) loss = tf.nn.l2_loss(label - prediction) return g.gradient(loss, (layer.kernel, layer.bias)) inputs = tf.random_uniform([batch_size, num_features]) labels = tf.random_uniform([batch_size, 1]) per_example_gradients = tf.vectorized_map(model_fn, (inputs, labels)) assert per_example_gradients[0].shape == (batch_size, num_features, 1) assert per_example_gradients[1].shape == (batch_size, 1) ```
object vectorized_map(object fn, ValueTuple<IGraphNodeBase, object> elems)
Parallel map on the list of tensors unpacked from `elems` on dimension 0. This method works similar to tf.map_fn but is optimized to run much faster,
possibly with a much larger memory footprint. The speedups are obtained by
vectorization (see https://arxiv.org/pdf/1903.04243.pdf). The idea behind
vectorization is to semantically launch all the invocations of `fn` in
parallel and fuse corresponding operations across all these invocations. This
fusion is done statically at graph generation time and the generated code is
often similar in performance to a manually fused version. Because
tf.vectorized_map fully parallelizes the batch, this method will
generally be significantly faster than using tf.map_fn, especially in eager
mode. However this is an experimental feature and currently has a lot of
limitations:
- There should be no data dependency between the different semantic
invocations of `fn`, i.e. it should be safe to map the elements of the
inputs in any order.
- Stateful kernels may mostly not be supported since these often imply a
data dependency. We do support a limited set of such stateful kernels
though (like RandomFoo, Variable operations like reads, etc).
- `fn` has limited support for control flow operations. tf.cond in
particular is not supported.
- `fn` should return nested structure of Tensors or Operations. However
if an Operation is returned, it should have zero outputs.
- The shape and dtype of any intermediate or output tensors in the
computation of `fn` should not depend on the input to `fn`.
Parameters
-
objectfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`, and returns a possibly nested structure of Tensors and Operations, which may be different than the structure of `elems`.
-
ValueTuple<IGraphNodeBase, object>elems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be mapped over by `fn`.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying fn to tensors unpacked from elems along the first dimension, from first to last. Examples: ```python def outer_product(a): return tf.tensordot(a, a, 0) batch_size = 100 a = tf.ones((batch_size, 32, 32)) c = tf.vectorized_map(outer_product, a) assert c.shape == (batch_size, 32, 32, 32, 32) ``` ```python # Computing per-example gradients batch_size = 10 num_features = 32 layer = tf.keras.layers.Dense(1) def model_fn(arg): with tf.GradientTape() as g: inp, label = arg inp = tf.expand_dims(inp, 0) label = tf.expand_dims(label, 0) prediction = layer(inp) loss = tf.nn.l2_loss(label - prediction) return g.gradient(loss, (layer.kernel, layer.bias)) inputs = tf.random_uniform([batch_size, num_features]) labels = tf.random_uniform([batch_size, 1]) per_example_gradients = tf.vectorized_map(model_fn, (inputs, labels)) assert per_example_gradients[0].shape == (batch_size, num_features, 1) assert per_example_gradients[1].shape == (batch_size, 1) ```
object vectorized_map_dyn(object fn, object elems)
Parallel map on the list of tensors unpacked from `elems` on dimension 0. This method works similar to tf.map_fn but is optimized to run much faster,
possibly with a much larger memory footprint. The speedups are obtained by
vectorization (see https://arxiv.org/pdf/1903.04243.pdf). The idea behind
vectorization is to semantically launch all the invocations of `fn` in
parallel and fuse corresponding operations across all these invocations. This
fusion is done statically at graph generation time and the generated code is
often similar in performance to a manually fused version. Because
tf.vectorized_map fully parallelizes the batch, this method will
generally be significantly faster than using tf.map_fn, especially in eager
mode. However this is an experimental feature and currently has a lot of
limitations:
- There should be no data dependency between the different semantic
invocations of `fn`, i.e. it should be safe to map the elements of the
inputs in any order.
- Stateful kernels may mostly not be supported since these often imply a
data dependency. We do support a limited set of such stateful kernels
though (like RandomFoo, Variable operations like reads, etc).
- `fn` has limited support for control flow operations. tf.cond in
particular is not supported.
- `fn` should return nested structure of Tensors or Operations. However
if an Operation is returned, it should have zero outputs.
- The shape and dtype of any intermediate or output tensors in the
computation of `fn` should not depend on the input to `fn`.
Parameters
-
objectfn - The callable to be performed. It accepts one argument, which will have the same (possibly nested) structure as `elems`, and returns a possibly nested structure of Tensors and Operations, which may be different than the structure of `elems`.
-
objectelems - A tensor or (possibly nested) sequence of tensors, each of which will be unpacked along their first dimension. The nested sequence of the resulting slices will be mapped over by `fn`.
Returns
-
object - A tensor or (possibly nested) sequence of tensors. Each tensor packs the results of applying fn to tensors unpacked from elems along the first dimension, from first to last. Examples: ```python def outer_product(a): return tf.tensordot(a, a, 0) batch_size = 100 a = tf.ones((batch_size, 32, 32)) c = tf.vectorized_map(outer_product, a) assert c.shape == (batch_size, 32, 32, 32, 32) ``` ```python # Computing per-example gradients batch_size = 10 num_features = 32 layer = tf.keras.layers.Dense(1) def model_fn(arg): with tf.GradientTape() as g: inp, label = arg inp = tf.expand_dims(inp, 0) label = tf.expand_dims(label, 0) prediction = layer(inp) loss = tf.nn.l2_loss(label - prediction) return g.gradient(loss, (layer.kernel, layer.bias)) inputs = tf.random_uniform([batch_size, num_features]) labels = tf.random_uniform([batch_size, 1]) per_example_gradients = tf.vectorized_map(model_fn, (inputs, labels)) assert per_example_gradients[0].shape == (batch_size, num_features, 1) assert per_example_gradients[1].shape == (batch_size, 1) ```
object verify_tensor_all_finite(IGraphNodeBase t, string msg, string name, object x, object message)
Assert that the tensor does not contain any NaN's or Inf's.
Parameters
-
IGraphNodeBaset - Tensor to check.
-
stringmsg - Message to log on failure.
-
stringname - A name for this operation (optional).
-
objectx - Alias for t.
-
objectmessage - Alias for msg.
Returns
-
object - Same tensor as `t`.
object verify_tensor_all_finite(ValueTuple<PythonClassContainer, PythonClassContainer> t, string msg, string name, object x, object message)
Assert that the tensor does not contain any NaN's or Inf's.
Parameters
-
ValueTuple<PythonClassContainer, PythonClassContainer>t - Tensor to check.
-
stringmsg - Message to log on failure.
-
stringname - A name for this operation (optional).
-
objectx - Alias for t.
-
objectmessage - Alias for msg.
Returns
-
object - Same tensor as `t`.
object verify_tensor_all_finite(IEnumerable<double> t, string msg, string name, object x, object message)
Assert that the tensor does not contain any NaN's or Inf's.
Parameters
-
IEnumerable<double>t - Tensor to check.
-
stringmsg - Message to log on failure.
-
stringname - A name for this operation (optional).
-
objectx - Alias for t.
-
objectmessage - Alias for msg.
Returns
-
object - Same tensor as `t`.
object verify_tensor_all_finite_dyn(object t, object msg, object name, object x, object message)
Assert that the tensor does not contain any NaN's or Inf's.
Parameters
-
objectt - Tensor to check.
-
objectmsg - Message to log on failure.
-
objectname - A name for this operation (optional).
-
objectx - Alias for t.
-
objectmessage - Alias for msg.
Returns
-
object - Same tensor as `t`.
object wals_compute_partial_lhs_and_rhs(IGraphNodeBase factors, IGraphNodeBase factor_weights, IGraphNodeBase unobserved_weights, IGraphNodeBase input_weights, IGraphNodeBase input_indices, IGraphNodeBase input_values, IGraphNodeBase entry_weights, IGraphNodeBase input_block_size, IGraphNodeBase input_is_transpose, string name)
object wals_compute_partial_lhs_and_rhs_dyn(object factors, object factor_weights, object unobserved_weights, object input_weights, object input_indices, object input_values, object entry_weights, object input_block_size, object input_is_transpose, object name)
Tensor where(IGraphNodeBase condition, PythonFunctionContainer x, PythonFunctionContainer y, PythonFunctionContainer name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
PythonFunctionContainerx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
PythonFunctionContainery - A `tensor` with the same shape and type as `x`.
-
PythonFunctionContainername - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, object x, object y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
objectx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
objecty - A `tensor` with the same shape and type as `x`.
-
stringname - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, object x, object y, PythonFunctionContainer name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
objectx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
objecty - A `tensor` with the same shape and type as `x`.
-
PythonFunctionContainername - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, object x, PythonFunctionContainer y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
objectx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
PythonFunctionContainery - A `tensor` with the same shape and type as `x`.
-
stringname - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, object x, PythonFunctionContainer y, PythonFunctionContainer name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
objectx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
PythonFunctionContainery - A `tensor` with the same shape and type as `x`.
-
PythonFunctionContainername - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, PythonFunctionContainer x, IEnumerable<IGraphNodeBase> y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
PythonFunctionContainerx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
IEnumerable<IGraphNodeBase>y - A `tensor` with the same shape and type as `x`.
-
stringname - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, object x, IEnumerable<IGraphNodeBase> y, PythonFunctionContainer name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
objectx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
IEnumerable<IGraphNodeBase>y - A `tensor` with the same shape and type as `x`.
-
PythonFunctionContainername - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, object x, IEnumerable<IGraphNodeBase> y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
objectx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
IEnumerable<IGraphNodeBase>y - A `tensor` with the same shape and type as `x`.
-
stringname - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, PythonFunctionContainer x, PythonFunctionContainer y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
PythonFunctionContainerx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
PythonFunctionContainery - A `tensor` with the same shape and type as `x`.
-
stringname - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, IEnumerable<IGraphNodeBase> x, PythonFunctionContainer y, PythonFunctionContainer name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
IEnumerable<IGraphNodeBase>x - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
PythonFunctionContainery - A `tensor` with the same shape and type as `x`.
-
PythonFunctionContainername - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, IEnumerable<IGraphNodeBase> x, IEnumerable<IGraphNodeBase> y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
IEnumerable<IGraphNodeBase>x - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
IEnumerable<IGraphNodeBase>y - A `tensor` with the same shape and type as `x`.
-
stringname - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, IEnumerable<IGraphNodeBase> x, object y, PythonFunctionContainer name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
IEnumerable<IGraphNodeBase>x - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
objecty - A `tensor` with the same shape and type as `x`.
-
PythonFunctionContainername - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, IEnumerable<IGraphNodeBase> x, PythonFunctionContainer y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
IEnumerable<IGraphNodeBase>x - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
PythonFunctionContainery - A `tensor` with the same shape and type as `x`.
-
stringname - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, IEnumerable<IGraphNodeBase> x, object y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
IEnumerable<IGraphNodeBase>x - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
objecty - A `tensor` with the same shape and type as `x`.
-
stringname - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, PythonFunctionContainer x, IEnumerable<IGraphNodeBase> y, PythonFunctionContainer name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
PythonFunctionContainerx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
IEnumerable<IGraphNodeBase>y - A `tensor` with the same shape and type as `x`.
-
PythonFunctionContainername - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, PythonFunctionContainer x, object y, PythonFunctionContainer name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
PythonFunctionContainerx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
objecty - A `tensor` with the same shape and type as `x`.
-
PythonFunctionContainername - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, PythonFunctionContainer x, object y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
PythonFunctionContainerx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
objecty - A `tensor` with the same shape and type as `x`.
-
stringname - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where(IGraphNodeBase condition, IEnumerable<IGraphNodeBase> x, IEnumerable<IGraphNodeBase> y, PythonFunctionContainer name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
IEnumerable<IGraphNodeBase>x - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
IEnumerable<IGraphNodeBase>y - A `tensor` with the same shape and type as `x`.
-
PythonFunctionContainername - A name of the operation (optional)
Returns
-
Tensor - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
object where_dyn(object condition, object x, object y, object name)
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
Parameters
-
objectcondition - A `Tensor` of type `bool`
-
objectx - A Tensor which may have the same shape as `condition`. If `condition` is rank 1, `x` may have higher rank, but its first dimension must match the size of `condition`.
-
objecty - A `tensor` with the same shape and type as `x`.
-
objectname - A name of the operation (optional)
Returns
-
object - A `Tensor` with the same type and shape as `x`, `y` if they are non-None. Otherwise, a `Tensor` with shape `(num_true, rank(condition))`.
Tensor where_v2(IGraphNodeBase condition, IGraphNodeBase x, object y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `condition`, `x` and `y` must be broadcastable to the same
shape. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false).
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
IGraphNodeBasex - A Tensor which is of the same type as `y`, and may be broadcastable with `condition` and `y`.
-
objecty - A Tensor which is of the same type as `x`, and may be broadcastable with `condition` and `x`.
-
stringname - A name of the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `x` and `y`, and shape that is broadcast from `condition`, `x`, and `y`, if `x`, `y` are non-None. A `Tensor` with shape `(num_true, dim_size(condition))`.
Tensor where_v2(IGraphNodeBase condition, int x, object y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `condition`, `x` and `y` must be broadcastable to the same
shape. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false).
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
intx - A Tensor which is of the same type as `y`, and may be broadcastable with `condition` and `y`.
-
objecty - A Tensor which is of the same type as `x`, and may be broadcastable with `condition` and `x`.
-
stringname - A name of the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `x` and `y`, and shape that is broadcast from `condition`, `x`, and `y`, if `x`, `y` are non-None. A `Tensor` with shape `(num_true, dim_size(condition))`.
Tensor where_v2(IGraphNodeBase condition, ValueTuple<PythonClassContainer, PythonClassContainer> x, object y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `condition`, `x` and `y` must be broadcastable to the same
shape. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false).
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
ValueTuple<PythonClassContainer, PythonClassContainer>x - A Tensor which is of the same type as `y`, and may be broadcastable with `condition` and `y`.
-
objecty - A Tensor which is of the same type as `x`, and may be broadcastable with `condition` and `x`.
-
stringname - A name of the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `x` and `y`, and shape that is broadcast from `condition`, `x`, and `y`, if `x`, `y` are non-None. A `Tensor` with shape `(num_true, dim_size(condition))`.
Tensor where_v2(IGraphNodeBase condition, IEnumerable<int> x, object y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `condition`, `x` and `y` must be broadcastable to the same
shape. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false).
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
IEnumerable<int>x - A Tensor which is of the same type as `y`, and may be broadcastable with `condition` and `y`.
-
objecty - A Tensor which is of the same type as `x`, and may be broadcastable with `condition` and `x`.
-
stringname - A name of the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `x` and `y`, and shape that is broadcast from `condition`, `x`, and `y`, if `x`, `y` are non-None. A `Tensor` with shape `(num_true, dim_size(condition))`.
Tensor where_v2(IGraphNodeBase condition, double x, object y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `condition`, `x` and `y` must be broadcastable to the same
shape. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false).
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
doublex - A Tensor which is of the same type as `y`, and may be broadcastable with `condition` and `y`.
-
objecty - A Tensor which is of the same type as `x`, and may be broadcastable with `condition` and `x`.
-
stringname - A name of the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `x` and `y`, and shape that is broadcast from `condition`, `x`, and `y`, if `x`, `y` are non-None. A `Tensor` with shape `(num_true, dim_size(condition))`.
Tensor where_v2(IGraphNodeBase condition, ndarray x, object y, string name)
Return the elements, either from `x` or `y`, depending on the `condition`. If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `condition`, `x` and `y` must be broadcastable to the same
shape. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false).
Parameters
-
IGraphNodeBasecondition - A `Tensor` of type `bool`
-
ndarrayx - A Tensor which is of the same type as `y`, and may be broadcastable with `condition` and `y`.
-
objecty - A Tensor which is of the same type as `x`, and may be broadcastable with `condition` and `x`.
-
stringname - A name of the operation (optional).
Returns
-
Tensor - A `Tensor` with the same type as `x` and `y`, and shape that is broadcast from `condition`, `x`, and `y`, if `x`, `y` are non-None. A `Tensor` with shape `(num_true, dim_size(condition))`.
object where_v2_dyn(object condition, object x, object y, object name)
Return the elements, either from `x` or `y`, depending on the `condition`. If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `condition`, `x` and `y` must be broadcastable to the same
shape. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false).
Parameters
-
objectcondition - A `Tensor` of type `bool`
-
objectx - A Tensor which is of the same type as `y`, and may be broadcastable with `condition` and `y`.
-
objecty - A Tensor which is of the same type as `x`, and may be broadcastable with `condition` and `x`.
-
objectname - A name of the operation (optional).
Returns
-
object - A `Tensor` with the same type as `x` and `y`, and shape that is broadcast from `condition`, `x`, and `y`, if `x`, `y` are non-None. A `Tensor` with shape `(num_true, dim_size(condition))`.
object while_loop(PythonFunctionContainer cond, PythonFunctionContainer body, object loop_vars, object shape_invariants, Nullable<int> parallel_iterations, bool back_prop, bool swap_memory, string name, object maximum_iterations, bool return_same_structure)
Repeat `body` while the condition `cond` is true. `cond` is a callable returning a boolean scalar tensor. `body` is a callable
returning a (possibly nested) tuple, namedtuple or list of tensors of the same
arity (length and structure) and types as `loop_vars`. `loop_vars` is a
(possibly nested) tuple, namedtuple or list of tensors that is passed to both
`cond` and `body`. `cond` and `body` both take as many arguments as there are
`loop_vars`. In addition to regular Tensors or IndexedSlices, the body may accept and
return TensorArray objects. The flows of the TensorArray objects will
be appropriately forwarded between loops and during gradient calculations. Note that `while_loop` calls `cond` and `body` *exactly once* (inside the
call to `while_loop`, and not at all during `Session.run()`). `while_loop`
stitches together the graph fragments created during the `cond` and `body`
calls with some additional graph nodes to create the graph flow that
repeats `body` until `cond` returns false. For correctness, `tf.while_loop()` strictly enforces shape invariants for
the loop variables. A shape invariant is a (possibly partial) shape that
is unchanged across the iterations of the loop. An error will be raised
if the shape of a loop variable after an iteration is determined to be more
general than or incompatible with its shape invariant. For example, a shape
of [11, None] is more general than a shape of [11, 17], and [11, 21] is not
compatible with [11, 17]. By default (if the argument `shape_invariants` is
not specified), it is assumed that the initial shape of each tensor in
`loop_vars` is the same in every iteration. The `shape_invariants` argument
allows the caller to specify a less specific shape invariant for each loop
variable, which is needed if the shape varies between iterations. The
tf.Tensor.set_shape
function may also be used in the `body` function to indicate that
the output loop variable has a particular shape. The shape invariant for
SparseTensor and IndexedSlices are treated specially as follows: a) If a loop variable is a SparseTensor, the shape invariant must be
TensorShape([r]) where r is the rank of the dense tensor represented
by the sparse tensor. It means the shapes of the three tensors of the
SparseTensor are ([None], [None, r], [r]). NOTE: The shape invariant here
is the shape of the SparseTensor.dense_shape property. It must be the shape of
a vector. b) If a loop variable is an IndexedSlices, the shape invariant must be
a shape invariant of the values tensor of the IndexedSlices. It means
the shapes of the three tensors of the IndexedSlices are (shape, [shape[0]],
[shape.ndims]). `while_loop` implements non-strict semantics, enabling multiple iterations
to run in parallel. The maximum number of parallel iterations can be
controlled by `parallel_iterations`, which gives users some control over
memory consumption and execution order. For correct programs, `while_loop`
should return the same result for any parallel_iterations > 0. For training, TensorFlow stores the tensors that are produced in the
forward inference and are needed in back propagation. These tensors are a
main source of memory consumption and often cause OOM errors when training
on GPUs. When the flag swap_memory is true, we swap out these tensors from
GPU to CPU. This for example allows us to train RNN models with very long
sequences and large batches.
Parameters
-
PythonFunctionContainercond - A callable that represents the termination condition of the loop.
-
PythonFunctionContainerbody - A callable that represents the loop body.
-
objectloop_vars - A (possibly nested) tuple, namedtuple or list of numpy array, `Tensor`, and `TensorArray` objects.
-
objectshape_invariants - The shape invariants for the loop variables.
-
Nullable<int>parallel_iterations - The number of iterations allowed to run in parallel. It must be a positive integer.
-
boolback_prop - Whether backprop is enabled for this while loop.
-
boolswap_memory - Whether GPU-CPU memory swap is enabled for this loop.
-
stringname - Optional name prefix for the returned tensors.
-
objectmaximum_iterations - Optional maximum number of iterations of the while loop to run. If provided, the `cond` output is AND-ed with an additional condition ensuring the number of iterations executed is no greater than `maximum_iterations`.
-
boolreturn_same_structure - If True, output has same structure as `loop_vars`. If eager execution is enabled, this is ignored (and always treated as True).
Returns
-
object - The output tensors for the loop variables after the loop. If `return_same_structure` is True, the return value has the same structure as `loop_vars`. If `return_same_structure` is False, the return value is a Tensor, TensorArray or IndexedSlice if the length of `loop_vars` is 1, or a list otherwise.
object while_loop_dyn(object cond, object body, object loop_vars, object shape_invariants, ImplicitContainer<T> parallel_iterations, ImplicitContainer<T> back_prop, ImplicitContainer<T> swap_memory, object name, object maximum_iterations, ImplicitContainer<T> return_same_structure)
Repeat `body` while the condition `cond` is true. `cond` is a callable returning a boolean scalar tensor. `body` is a callable
returning a (possibly nested) tuple, namedtuple or list of tensors of the same
arity (length and structure) and types as `loop_vars`. `loop_vars` is a
(possibly nested) tuple, namedtuple or list of tensors that is passed to both
`cond` and `body`. `cond` and `body` both take as many arguments as there are
`loop_vars`. In addition to regular Tensors or IndexedSlices, the body may accept and
return TensorArray objects. The flows of the TensorArray objects will
be appropriately forwarded between loops and during gradient calculations. Note that `while_loop` calls `cond` and `body` *exactly once* (inside the
call to `while_loop`, and not at all during `Session.run()`). `while_loop`
stitches together the graph fragments created during the `cond` and `body`
calls with some additional graph nodes to create the graph flow that
repeats `body` until `cond` returns false. For correctness, `tf.while_loop()` strictly enforces shape invariants for
the loop variables. A shape invariant is a (possibly partial) shape that
is unchanged across the iterations of the loop. An error will be raised
if the shape of a loop variable after an iteration is determined to be more
general than or incompatible with its shape invariant. For example, a shape
of [11, None] is more general than a shape of [11, 17], and [11, 21] is not
compatible with [11, 17]. By default (if the argument `shape_invariants` is
not specified), it is assumed that the initial shape of each tensor in
`loop_vars` is the same in every iteration. The `shape_invariants` argument
allows the caller to specify a less specific shape invariant for each loop
variable, which is needed if the shape varies between iterations. The
tf.Tensor.set_shape
function may also be used in the `body` function to indicate that
the output loop variable has a particular shape. The shape invariant for
SparseTensor and IndexedSlices are treated specially as follows: a) If a loop variable is a SparseTensor, the shape invariant must be
TensorShape([r]) where r is the rank of the dense tensor represented
by the sparse tensor. It means the shapes of the three tensors of the
SparseTensor are ([None], [None, r], [r]). NOTE: The shape invariant here
is the shape of the SparseTensor.dense_shape property. It must be the shape of
a vector. b) If a loop variable is an IndexedSlices, the shape invariant must be
a shape invariant of the values tensor of the IndexedSlices. It means
the shapes of the three tensors of the IndexedSlices are (shape, [shape[0]],
[shape.ndims]). `while_loop` implements non-strict semantics, enabling multiple iterations
to run in parallel. The maximum number of parallel iterations can be
controlled by `parallel_iterations`, which gives users some control over
memory consumption and execution order. For correct programs, `while_loop`
should return the same result for any parallel_iterations > 0. For training, TensorFlow stores the tensors that are produced in the
forward inference and are needed in back propagation. These tensors are a
main source of memory consumption and often cause OOM errors when training
on GPUs. When the flag swap_memory is true, we swap out these tensors from
GPU to CPU. This for example allows us to train RNN models with very long
sequences and large batches.
Parameters
-
objectcond - A callable that represents the termination condition of the loop.
-
objectbody - A callable that represents the loop body.
-
objectloop_vars - A (possibly nested) tuple, namedtuple or list of numpy array, `Tensor`, and `TensorArray` objects.
-
objectshape_invariants - The shape invariants for the loop variables.
-
ImplicitContainer<T>parallel_iterations - The number of iterations allowed to run in parallel. It must be a positive integer.
-
ImplicitContainer<T>back_prop - Whether backprop is enabled for this while loop.
-
ImplicitContainer<T>swap_memory - Whether GPU-CPU memory swap is enabled for this loop.
-
objectname - Optional name prefix for the returned tensors.
-
objectmaximum_iterations - Optional maximum number of iterations of the while loop to run. If provided, the `cond` output is AND-ed with an additional condition ensuring the number of iterations executed is no greater than `maximum_iterations`.
-
ImplicitContainer<T>return_same_structure - If True, output has same structure as `loop_vars`. If eager execution is enabled, this is ignored (and always treated as True).
Returns
-
object - The output tensors for the loop variables after the loop. If `return_same_structure` is True, the return value has the same structure as `loop_vars`. If `return_same_structure` is False, the return value is a Tensor, TensorArray or IndexedSlice if the length of `loop_vars` is 1, or a list otherwise.
WrappedFunction wrap_function(PythonFunctionContainer fn, ValueTuple signature, string name)
Wraps the TF 1.x function fn into a graph function. The python function `fn` will be called once with symbolic arguments specified
in the `signature`, traced, and turned into a graph function. Any variables
created by `fn` will be owned by the object returned by `wrap_function`. The
resulting graph function can be called with tensors which match the
signature.
Both `tf.compat.v1.wrap_function` and
tf.function create a callable
TensorFlow graph. But while tf.function runs all stateful operations
(e.g. tf.print) and sequences operations to provide the same semantics as
eager execution, `wrap_function` is closer to the behavior of `session.run` in
TensorFlow 1.x. It will not run any operations unless they are required to
compute the function's outputs, either through a data dependency or a control
dependency. Nor will it sequence operations. Unlike tf.function, `wrap_function` will only trace the Python function
once. As with placeholders in TF 1.x, shapes and dtypes must be provided to
`wrap_function`'s `signature` argument. Since it is only traced once, variables and state may be created inside the
function and owned by the function wrapper object.
Parameters
-
PythonFunctionContainerfn - python function to be wrapped
-
ValueTuplesignature - the placeholder and python arguments to be passed to the wrapped function
-
stringname - Optional. The name of the function.
Returns
-
WrappedFunction - the wrapped graph function.
Show Example
def f(x, do_add):
v = tf.Variable(5.0)
if do_add:
op = v.assign_add(x)
else:
op = v.assign_sub(x)
with tf.control_dependencies([op]):
return v.read_value() f_add = tf.compat.v1.wrap_function(f, [tf.TensorSpec((), tf.float32), True]) assert float(f_add(1.0)) == 6.0
assert float(f_add(1.0)) == 7.0 # Can call tf.compat.v1.wrap_function again to get a new trace, a new set
# of variables, and possibly different non-template arguments.
f_sub= tf.compat.v1.wrap_function(f, [tf.TensorSpec((), tf.float32), False]) assert float(f_sub(1.0)) == 4.0
assert float(f_sub(1.0)) == 3.0
WrappedFunction wrap_function(PythonFunctionContainer fn, IEnumerable<object> signature, string name)
Wraps the TF 1.x function fn into a graph function. The python function `fn` will be called once with symbolic arguments specified
in the `signature`, traced, and turned into a graph function. Any variables
created by `fn` will be owned by the object returned by `wrap_function`. The
resulting graph function can be called with tensors which match the
signature.
Both `tf.compat.v1.wrap_function` and
tf.function create a callable
TensorFlow graph. But while tf.function runs all stateful operations
(e.g. tf.print) and sequences operations to provide the same semantics as
eager execution, `wrap_function` is closer to the behavior of `session.run` in
TensorFlow 1.x. It will not run any operations unless they are required to
compute the function's outputs, either through a data dependency or a control
dependency. Nor will it sequence operations. Unlike tf.function, `wrap_function` will only trace the Python function
once. As with placeholders in TF 1.x, shapes and dtypes must be provided to
`wrap_function`'s `signature` argument. Since it is only traced once, variables and state may be created inside the
function and owned by the function wrapper object.
Parameters
-
PythonFunctionContainerfn - python function to be wrapped
-
IEnumerable<object>signature - the placeholder and python arguments to be passed to the wrapped function
-
stringname - Optional. The name of the function.
Returns
-
WrappedFunction - the wrapped graph function.
Show Example
def f(x, do_add):
v = tf.Variable(5.0)
if do_add:
op = v.assign_add(x)
else:
op = v.assign_sub(x)
with tf.control_dependencies([op]):
return v.read_value() f_add = tf.compat.v1.wrap_function(f, [tf.TensorSpec((), tf.float32), True]) assert float(f_add(1.0)) == 6.0
assert float(f_add(1.0)) == 7.0 # Can call tf.compat.v1.wrap_function again to get a new trace, a new set
# of variables, and possibly different non-template arguments.
f_sub= tf.compat.v1.wrap_function(f, [tf.TensorSpec((), tf.float32), False]) assert float(f_sub(1.0)) == 4.0
assert float(f_sub(1.0)) == 3.0
object write_file(IGraphNodeBase filename, IGraphNodeBase contents, string name)
Writes contents to the file at input filename. Creates file and recursively creates directory if not existing.
Parameters
-
IGraphNodeBasefilename - A `Tensor` of type `string`. scalar. The name of the file to which we write the contents.
-
IGraphNodeBasecontents - A `Tensor` of type `string`. scalar. The content to be written to the output file.
-
stringname - A name for the operation (optional).
Returns
-
object - The created Operation.
object write_file_dyn(object filename, object contents, object name)
Writes contents to the file at input filename. Creates file and recursively creates directory if not existing.
Parameters
-
objectfilename - A `Tensor` of type `string`. scalar. The name of the file to which we write the contents.
-
objectcontents - A `Tensor` of type `string`. scalar. The content to be written to the output file.
-
objectname - A name for the operation (optional).
Returns
-
object - The created Operation.
object xla_broadcast_helper(IGraphNodeBase lhs, IGraphNodeBase rhs, IGraphNodeBase broadcast_dims, string name)
object xla_broadcast_helper_dyn(object lhs, object rhs, object broadcast_dims, object name)
Tensor xla_cluster_output(IGraphNodeBase input, string name)
object xla_cluster_output_dyn(object input, object name)
Tensor xla_conv(IGraphNodeBase lhs, IGraphNodeBase rhs, IGraphNodeBase window_strides, IGraphNodeBase padding, IGraphNodeBase lhs_dilation, IGraphNodeBase rhs_dilation, IGraphNodeBase feature_group_count, object dimension_numbers, string precision_config, string name)
object xla_conv_dyn(object lhs, object rhs, object window_strides, object padding, object lhs_dilation, object rhs_dilation, object feature_group_count, object dimension_numbers, object precision_config, object name)
Tensor xla_dequantize(IGraphNodeBase input, double min_range, double max_range, string mode, bool transpose_output, string name)
object xla_dequantize_dyn(object input, object min_range, object max_range, object mode, object transpose_output, object name)
Tensor xla_dot(IGraphNodeBase lhs, IGraphNodeBase rhs, object dimension_numbers, string precision_config, string name)
object xla_dot_dyn(object lhs, object rhs, object dimension_numbers, object precision_config, object name)
Tensor xla_dynamic_slice(IGraphNodeBase input, IGraphNodeBase start_indices, IGraphNodeBase size_indices, string name)
object xla_dynamic_slice_dyn(object input, object start_indices, object size_indices, object name)
Tensor xla_dynamic_update_slice(IGraphNodeBase input, IGraphNodeBase update, IGraphNodeBase indices, string name)
object xla_dynamic_update_slice_dyn(object input, object update, object indices, object name)
Tensor xla_einsum(IGraphNodeBase a, IGraphNodeBase b, object equation, string name)
object xla_einsum_dyn(object a, object b, object equation, object name)
object xla_if(IGraphNodeBase cond, object inputs, object then_branch, object else_branch, object Tout, string name)
object xla_if_dyn(object cond, object inputs, object then_branch, object else_branch, object Tout, object name)
object xla_key_value_sort(IGraphNodeBase keys, IGraphNodeBase values, string name)
object xla_key_value_sort_dyn(object keys, object values, object name)
object xla_launch(object constants, IEnumerable<object> args, object resources, object Tresults, object function, string name)
object xla_launch_dyn(object constants, object args, object resources, object Tresults, object function, object name)
Tensor xla_pad(IGraphNodeBase input, IGraphNodeBase padding_value, IGraphNodeBase padding_low, IGraphNodeBase padding_high, IGraphNodeBase padding_interior, string name)
object xla_pad_dyn(object input, object padding_value, object padding_low, object padding_high, object padding_interior, object name)
Tensor xla_recv(DType dtype, object tensor_name, TensorShape shape, string name)
object xla_recv_dyn(object dtype, object tensor_name, object shape, object name)
Tensor xla_reduce(IGraphNodeBase input, IGraphNodeBase init_value, IEnumerable<object> dimensions_to_reduce, object reducer, string name)
Tensor xla_reduce(IGraphNodeBase input, IGraphNodeBase init_value, IEnumerable<object> dimensions_to_reduce, _OverloadedFunction reducer, string name)
Tensor xla_reduce(IGraphNodeBase input, IGraphNodeBase init_value, IEnumerable<object> dimensions_to_reduce, _DefinedFunction reducer, string name)
object xla_reduce_dyn(object input, object init_value, object dimensions_to_reduce, object reducer, object name)
Tensor xla_reduce_window(IGraphNodeBase input, IGraphNodeBase init_value, IGraphNodeBase window_dimensions, IGraphNodeBase window_strides, IGraphNodeBase base_dilations, IGraphNodeBase window_dilations, IGraphNodeBase padding, object computation, string name)
object xla_reduce_window_dyn(object input, object init_value, object window_dimensions, object window_strides, object base_dilations, object window_dilations, object padding, object computation, object name)
Tensor xla_replica_id(string name)
object xla_replica_id_dyn(object name)
Tensor xla_select_and_scatter(IGraphNodeBase operand, IGraphNodeBase window_dimensions, IGraphNodeBase window_strides, IGraphNodeBase padding, IGraphNodeBase source, IGraphNodeBase init_value, object select, _OverloadedFunction scatter, string name)
Tensor xla_select_and_scatter(IGraphNodeBase operand, IGraphNodeBase window_dimensions, IGraphNodeBase window_strides, IGraphNodeBase padding, IGraphNodeBase source, IGraphNodeBase init_value, object select, _DefinedFunction scatter, string name)
Tensor xla_select_and_scatter(IGraphNodeBase operand, IGraphNodeBase window_dimensions, IGraphNodeBase window_strides, IGraphNodeBase padding, IGraphNodeBase source, IGraphNodeBase init_value, _DefinedFunction select, _DefinedFunction scatter, string name)
Tensor xla_select_and_scatter(IGraphNodeBase operand, IGraphNodeBase window_dimensions, IGraphNodeBase window_strides, IGraphNodeBase padding, IGraphNodeBase source, IGraphNodeBase init_value, _DefinedFunction select, _OverloadedFunction scatter, string name)
Tensor xla_select_and_scatter(IGraphNodeBase operand, IGraphNodeBase window_dimensions, IGraphNodeBase window_strides, IGraphNodeBase padding, IGraphNodeBase source, IGraphNodeBase init_value, _DefinedFunction select, object scatter, string name)
Tensor xla_select_and_scatter(IGraphNodeBase operand, IGraphNodeBase window_dimensions, IGraphNodeBase window_strides, IGraphNodeBase padding, IGraphNodeBase source, IGraphNodeBase init_value, _OverloadedFunction select, _DefinedFunction scatter, string name)
Tensor xla_select_and_scatter(IGraphNodeBase operand, IGraphNodeBase window_dimensions, IGraphNodeBase window_strides, IGraphNodeBase padding, IGraphNodeBase source, IGraphNodeBase init_value, _OverloadedFunction select, _OverloadedFunction scatter, string name)
Tensor xla_select_and_scatter(IGraphNodeBase operand, IGraphNodeBase window_dimensions, IGraphNodeBase window_strides, IGraphNodeBase padding, IGraphNodeBase source, IGraphNodeBase init_value, object select, object scatter, string name)
Tensor xla_select_and_scatter(IGraphNodeBase operand, IGraphNodeBase window_dimensions, IGraphNodeBase window_strides, IGraphNodeBase padding, IGraphNodeBase source, IGraphNodeBase init_value, _OverloadedFunction select, object scatter, string name)
object xla_select_and_scatter_dyn(object operand, object window_dimensions, object window_strides, object padding, object source, object init_value, object select, object scatter, object name)
object xla_self_adjoint_eig(IGraphNodeBase a, object lower, object max_iter, object epsilon, string name)
object xla_self_adjoint_eig_dyn(object a, object lower, object max_iter, object epsilon, object name)
object xla_send(IGraphNodeBase tensor, object tensor_name, string name)
object xla_send_dyn(object tensor, object tensor_name, object name)
Tensor xla_sort(IGraphNodeBase input, string name)
object xla_sort_dyn(object input, object name)
object xla_svd(IGraphNodeBase a, object max_iter, object epsilon, string precision_config, string name)
object xla_svd_dyn(object a, object max_iter, object epsilon, object precision_config, object name)
object xla_while(IEnumerable<IGraphNodeBase> input, _OverloadedFunction cond, object body, string name)
object xla_while(IEnumerable<IGraphNodeBase> input, _OverloadedFunction cond, _OverloadedFunction body, string name)
object xla_while(IEnumerable<IGraphNodeBase> input, _OverloadedFunction cond, _DefinedFunction body, string name)
object xla_while(IEnumerable<IGraphNodeBase> input, _DefinedFunction cond, object body, string name)
object xla_while(IEnumerable<IGraphNodeBase> input, object cond, _DefinedFunction body, string name)
object xla_while(IEnumerable<IGraphNodeBase> input, _DefinedFunction cond, _DefinedFunction body, string name)
object xla_while(IEnumerable<IGraphNodeBase> input, object cond, _OverloadedFunction body, string name)
object xla_while(IEnumerable<IGraphNodeBase> input, _DefinedFunction cond, _OverloadedFunction body, string name)
object xla_while(IEnumerable<IGraphNodeBase> input, object cond, object body, string name)
object xla_while_dyn(object input, object cond, object body, object name)
object zero_initializer(Variable ref, string name)
object zero_initializer_dyn(object ref, object name)
object zero_var_initializer(IGraphNodeBase var, DType dtype, TensorShape shape, string name)
object zero_var_initializer_dyn(object var, object dtype, object shape, object name)
Tensor zeros(TensorShape shape, PythonFunctionContainer dtype, string name)
Creates a tensor with all elements set to zero. This operation returns a tensor of type `dtype` with shape `shape` and
all elements set to zero.
Parameters
-
TensorShapeshape - A list of integers, a tuple of integers, or a 1-D `Tensor` of type `int32`.
-
PythonFunctionContainerdtype - The type of an element in the resulting `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with all elements set to zero.
Show Example
tf.zeros([3, 4], tf.int32) # [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]
Tensor zeros(TensorShape shape, PythonFunctionContainer dtype, PythonFunctionContainer name)
Creates a tensor with all elements set to zero. This operation returns a tensor of type `dtype` with shape `shape` and
all elements set to zero.
Parameters
-
TensorShapeshape - A list of integers, a tuple of integers, or a 1-D `Tensor` of type `int32`.
-
PythonFunctionContainerdtype - The type of an element in the resulting `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with all elements set to zero.
Show Example
tf.zeros([3, 4], tf.int32) # [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]
Tensor zeros(TensorShape shape, ImplicitContainer<T> dtype, string name)
Creates a tensor with all elements set to zero. This operation returns a tensor of type `dtype` with shape `shape` and
all elements set to zero.
Parameters
-
TensorShapeshape - A list of integers, a tuple of integers, or a 1-D `Tensor` of type `int32`.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with all elements set to zero.
Show Example
tf.zeros([3, 4], tf.int32) # [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]
Tensor zeros(TensorShape shape, ImplicitContainer<T> dtype, PythonFunctionContainer name)
Creates a tensor with all elements set to zero. This operation returns a tensor of type `dtype` with shape `shape` and
all elements set to zero.
Parameters
-
TensorShapeshape - A list of integers, a tuple of integers, or a 1-D `Tensor` of type `int32`.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`.
-
PythonFunctionContainername - A name for the operation (optional).
Returns
-
Tensor - A `Tensor` with all elements set to zero.
Show Example
tf.zeros([3, 4], tf.int32) # [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]
object zeros_dyn(object shape, ImplicitContainer<T> dtype, object name)
Creates a tensor with all elements set to zero. This operation returns a tensor of type `dtype` with shape `shape` and
all elements set to zero.
Parameters
-
objectshape - A list of integers, a tuple of integers, or a 1-D `Tensor` of type `int32`.
-
ImplicitContainer<T>dtype - The type of an element in the resulting `Tensor`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor` with all elements set to zero.
Show Example
tf.zeros([3, 4], tf.int32) # [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]
Tensor zeros_like(IGraphNodeBase tensor, PythonClassContainer dtype, string name, bool optimize)
Creates a tensor with all elements set to zero. Given a single tensor (`tensor`), this operation returns a tensor of the
same type and shape as `tensor` with all elements set to zero. Optionally,
you can use `dtype` to specify a new type for the returned tensor.
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
PythonClassContainerdtype - A type for the returned `Tensor`. Must be `float16`, `float32`, `float64`, `int8`, `uint8`, `int16`, `uint16`, `int32`, `int64`, `complex64`, `complex128`, `bool` or `string`.
-
stringname - A name for the operation (optional).
-
booloptimize - if true, attempt to statically determine the shape of 'tensor' and encode it as a constant.
Returns
-
Tensor - A `Tensor` with all elements set to zero.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.zeros_like(tensor) # [[0, 0, 0], [0, 0, 0]]
Tensor zeros_like(IGraphNodeBase tensor, PythonClassContainer dtype, PythonFunctionContainer name, bool optimize)
Creates a tensor with all elements set to zero. Given a single tensor (`tensor`), this operation returns a tensor of the
same type and shape as `tensor` with all elements set to zero. Optionally,
you can use `dtype` to specify a new type for the returned tensor.
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
PythonClassContainerdtype - A type for the returned `Tensor`. Must be `float16`, `float32`, `float64`, `int8`, `uint8`, `int16`, `uint16`, `int32`, `int64`, `complex64`, `complex128`, `bool` or `string`.
-
PythonFunctionContainername - A name for the operation (optional).
-
booloptimize - if true, attempt to statically determine the shape of 'tensor' and encode it as a constant.
Returns
-
Tensor - A `Tensor` with all elements set to zero.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.zeros_like(tensor) # [[0, 0, 0], [0, 0, 0]]
Tensor zeros_like(IGraphNodeBase tensor, DType dtype, PythonFunctionContainer name, bool optimize)
Creates a tensor with all elements set to zero. Given a single tensor (`tensor`), this operation returns a tensor of the
same type and shape as `tensor` with all elements set to zero. Optionally,
you can use `dtype` to specify a new type for the returned tensor.
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
DTypedtype - A type for the returned `Tensor`. Must be `float16`, `float32`, `float64`, `int8`, `uint8`, `int16`, `uint16`, `int32`, `int64`, `complex64`, `complex128`, `bool` or `string`.
-
PythonFunctionContainername - A name for the operation (optional).
-
booloptimize - if true, attempt to statically determine the shape of 'tensor' and encode it as a constant.
Returns
-
Tensor - A `Tensor` with all elements set to zero.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.zeros_like(tensor) # [[0, 0, 0], [0, 0, 0]]
Tensor zeros_like(IGraphNodeBase tensor, DType dtype, string name, bool optimize)
Creates a tensor with all elements set to zero. Given a single tensor (`tensor`), this operation returns a tensor of the
same type and shape as `tensor` with all elements set to zero. Optionally,
you can use `dtype` to specify a new type for the returned tensor.
Parameters
-
IGraphNodeBasetensor - A `Tensor`.
-
DTypedtype - A type for the returned `Tensor`. Must be `float16`, `float32`, `float64`, `int8`, `uint8`, `int16`, `uint16`, `int32`, `int64`, `complex64`, `complex128`, `bool` or `string`.
-
stringname - A name for the operation (optional).
-
booloptimize - if true, attempt to statically determine the shape of 'tensor' and encode it as a constant.
Returns
-
Tensor - A `Tensor` with all elements set to zero.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.zeros_like(tensor) # [[0, 0, 0], [0, 0, 0]]
object zeros_like_dyn(object tensor, object dtype, object name, ImplicitContainer<T> optimize)
Creates a tensor with all elements set to zero. Given a single tensor (`tensor`), this operation returns a tensor of the
same type and shape as `tensor` with all elements set to zero. Optionally,
you can use `dtype` to specify a new type for the returned tensor.
Parameters
-
objecttensor - A `Tensor`.
-
objectdtype - A type for the returned `Tensor`. Must be `float16`, `float32`, `float64`, `int8`, `uint8`, `int16`, `uint16`, `int32`, `int64`, `complex64`, `complex128`, `bool` or `string`.
-
objectname - A name for the operation (optional).
-
ImplicitContainer<T>optimize - if true, attempt to statically determine the shape of 'tensor' and encode it as a constant.
Returns
-
object - A `Tensor` with all elements set to zero.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.zeros_like(tensor) # [[0, 0, 0], [0, 0, 0]]
Tensor zeta(IGraphNodeBase x, IGraphNodeBase q, string name)
Compute the Hurwitz zeta function \\(\zeta(x, q)\\). The Hurwitz zeta function is defined as: \\(\zeta(x, q) = \sum_{n=0}^{\infty} (q + n)^{-x}\\)
Parameters
-
IGraphNodeBasex - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
IGraphNodeBaseq - A `Tensor`. Must have the same type as `x`.
-
stringname - A name for the operation (optional).
Returns
-
Tensor - A `Tensor`. Has the same type as `x`.
object zeta_dyn(object x, object q, object name)
Compute the Hurwitz zeta function \\(\zeta(x, q)\\). The Hurwitz zeta function is defined as: \\(\zeta(x, q) = \sum_{n=0}^{\infty} (q + n)^{-x}\\)
Parameters
-
objectx - A `Tensor`. Must be one of the following types: `float32`, `float64`.
-
objectq - A `Tensor`. Must have the same type as `x`.
-
objectname - A name for the operation (optional).
Returns
-
object - A `Tensor`. Has the same type as `x`.
Public properties
PythonFunctionContainer a_fn get;
PythonFunctionContainer abs_fn get;
PythonFunctionContainer accumulate_n_fn get;
Returns the element-wise sum of a list of tensors. Optionally, pass `shape` and `tensor_dtype` for shape and type checking,
otherwise, these are inferred. `accumulate_n` performs the same operation as
tf.math.add_n, but
does not wait for all of its inputs to be ready before beginning to sum.
This approach can save memory if inputs are ready at different times, since
minimum temporary storage is proportional to the output size rather than the
inputs' size. `accumulate_n` is differentiable (but wasn't previous to TensorFlow 1.7).
Show Example
a = tf.constant([[1, 2], [3, 4]])
b = tf.constant([[5, 0], [0, 6]])
tf.math.accumulate_n([a, b, a]) # [[7, 4], [6, 14]] # Explicitly pass shape and type
tf.math.accumulate_n([a, b, a], shape=[2, 2], tensor_dtype=tf.int32)
# [[7, 4],
# [6, 14]]
PythonFunctionContainer acos_fn get;
Computes acos of x element-wise.
PythonFunctionContainer acosh_fn get;
Computes inverse hyperbolic cosine of x element-wise. Given an input tensor, the function computes inverse hyperbolic cosine of every element.
Input range is `[1, inf]`. It returns `nan` if the input lies outside the range.
Show Example
x = tf.constant([-2, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.acosh(x) ==> [nan nan 0. 0.62236255 5.9914584 9.903487 inf]
PythonFunctionContainer add_check_numerics_ops_fn get;
Connect a
tf.debugging.check_numerics to every floating point tensor. `check_numerics` operations themselves are added for each `half`, `float`,
or `double` tensor in the current default graph. For all ops in the graph, the
`check_numerics` op for all of its (`half`, `float`, or `double`) inputs
is guaranteed to run before the `check_numerics` op on any of its outputs. Note: This API is not compatible with the use of tf.cond or
tf.while_loop, and will raise a `ValueError` if you attempt to call it
in such a graph.
PythonFunctionContainer add_fn get;
Returns x + y element-wise. *NOTE*: `math.add` supports broadcasting. `AddN` does not. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer add_n_fn get;
Adds all input tensors element-wise. Converts `IndexedSlices` objects into dense tensors prior to adding.
tf.math.add_n performs the same operation as tf.math.accumulate_n, but it
waits for all of its inputs to be ready before beginning to sum.
This buffering can result in higher memory consumption when inputs are ready
at different times, since the minimum temporary storage required is
proportional to the input size rather than the output size. This op does not [broadcast](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
its inputs. If you need broadcasting, use tf.math.add (or the `+` operator)
instead.
Show Example
a = tf.constant([[3, 5], [4, 8]])
b = tf.constant([[1, 6], [2, 9]])
tf.math.add_n([a, b, a]) # [[7, 16], [10, 25]]
PythonFunctionContainer add_to_collection_fn get;
Wrapper for `Graph.add_to_collection()` using the default graph. See
tf.Graph.add_to_collection
for more details.
PythonFunctionContainer add_to_collections_fn get;
Wrapper for `Graph.add_to_collections()` using the default graph. See
tf.Graph.add_to_collections
for more details.
PythonFunctionContainer adjust_hsv_in_yiq_fn get;
PythonFunctionContainer all_variables_fn get;
Use `tf.compat.v1.global_variables` instead. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Please use tf.global_variables instead.
PythonFunctionContainer angle_fn get;
Returns the element-wise argument of a complex (or real) tensor. Given a tensor `input`, this operation returns a tensor of type `float` that
is the argument of each element in `input` considered as a complex number. The elements in `input` are considered to be complex numbers of the form
\\(a + bj\\), where *a* is the real part and *b* is the imaginary part.
If `input` is real then *b* is zero by definition. The argument returned by this function is of the form \\(atan2(b, a)\\).
If `input` is real, a tensor of all zeros is returned. For example: ```
input = tf.constant([-2.25 + 4.75j, 3.25 + 5.75j], dtype=tf.complex64)
tf.math.angle(input).numpy()
# ==> array([2.0131705, 1.056345 ], dtype=float32)
```
PythonFunctionContainer arg_max_fn get;
Returns the index with the largest value across dimensions of a tensor. Note that in case of ties the identity of the return value is not guaranteed. Usage:
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
PythonFunctionContainer arg_min_fn get;
Returns the index with the smallest value across dimensions of a tensor. Note that in case of ties the identity of the return value is not guaranteed. Usage:
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
PythonFunctionContainer argmax_fn get;
Returns the index with the largest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmax(input = a)
c = tf.keras.backend.eval(b)
# c = 4
# here a[4] = 166.32 which is the largest element of a across axis 0
PythonFunctionContainer argmin_fn get;
Returns the index with the smallest value across axes of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dimension)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Note that in case of ties the identity of the return value is not guaranteed. Usage:
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.math.argmin(input = a)
c = tf.keras.backend.eval(b)
# c = 0
# here a[0] = 1 which is the smallest element of a across axis 0
PythonFunctionContainer argsort_fn get;
Returns the indices of a tensor that give its sorted order along an axis. For a 1D tensor, `tf.gather(values, tf.argsort(values))` is equivalent to
`tf.sort(values)`. For higher dimensions, the output has the same shape as
`values`, but along the given axis, values represent the index of the sorted
element in that slice of the tensor at the given position. Usage:
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.argsort(a,axis=-1,direction='ASCENDING',stable=False,name=None)
c = tf.keras.backend.eval(b)
# Here, c = [0 3 1 2 5 4]
PythonFunctionContainer as_dtype_fn get;
Converts the given `type_value` to a `DType`.
PythonFunctionContainer as_string_fn get;
Converts each entry in the given tensor to strings. Supports many numeric types and boolean. For Unicode, see the
[https://www.tensorflow.org/tutorials/representation/unicode](Working with Unicode text)
tutorial.
PythonFunctionContainer asin_fn get;
Computes the trignometric inverse sine of x element-wise. The
tf.math.asin operation returns the inverse of tf.math.sin, such that
if `y = tf.math.sin(x)` then, `x = tf.math.asin(y)`. **Note**: The output of tf.math.asin will lie within the invertible range
of sine, i.e [-pi/2, pi/2].
Show Example
# Note: [1.047, 0.785] ~= [(pi/3), (pi/4)]
x = tf.constant([1.047, 0.785])
y = tf.math.sin(x) # [0.8659266, 0.7068252] tf.math.asin(y) # [1.047, 0.785] = x
PythonFunctionContainer asinh_fn get;
Computes inverse hyperbolic sine of x element-wise. Given an input tensor, this function computes inverse hyperbolic sine
for every element in the tensor. Both input and output has a range of
`[-inf, inf]`.
Show Example
x = tf.constant([-float("inf"), -2, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.asinh(x) ==> [-inf -1.4436355 -0.4812118 0.8813736 1.0159732 5.991471 9.903487 inf]
PythonFunctionContainer assert_equal_fn get;
Assert the condition `x == y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] == y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Show Example
with tf.control_dependencies([tf.compat.v1.assert_equal(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer Assert_fn get;
Asserts that the given condition is true. If `condition` evaluates to false, print the list of tensors in `data`.
`summarize` determines how many entries of the tensors to print. NOTE: In graph mode, to ensure that Assert executes, one usually attaches
a dependency:
Show Example
# Ensure maximum element of x is smaller or equal to 1
assert_op = tf.Assert(tf.less_equal(tf.reduce_max(x), 1.), [x])
with tf.control_dependencies([assert_op]):
... code using x...
PythonFunctionContainer assert_greater_equal_fn get;
Assert the condition `x >= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] >= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater_equal(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_greater_fn get;
Assert the condition `x > y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] > y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Show Example
with tf.control_dependencies([tf.compat.v1.assert_greater(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_integer_fn get;
Assert that `x` is of integer dtype. Example of adding a dependency to an operation:
Show Example
with tf.control_dependencies([tf.compat.v1.assert_integer(x)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_less_equal_fn get;
Assert the condition `x <= y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] <= y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less_equal(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_less_fn get;
Assert the condition `x < y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] < y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Show Example
with tf.control_dependencies([tf.compat.v1.assert_less(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_near_fn get;
Assert the condition `x` and `y` are close element-wise. Example of adding a dependency to an operation:
This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have ```tf.abs(x[i] - y[i]) <= atol + rtol * tf.abs(y[i])```. If both `x` and `y` are empty, this is trivially satisfied. The default `atol` and `rtol` is `10 * eps`, where `eps` is the smallest
representable positive number such that `1 + eps != 1`. This is about
`1.2e-6` in `32bit`, `2.22e-15` in `64bit`, and `0.00977` in `16bit`.
See `numpy.finfo`.
Show Example
with tf.control_dependencies([tf.compat.v1.assert_near(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_negative_fn get;
Assert the condition `x < 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Negative means, for every element `x[i]` of `x`, we have `x[i] < 0`.
If `x` is empty this is trivially satisfied.
Show Example
with tf.control_dependencies([tf.debugging.assert_negative(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_non_negative_fn get;
Assert the condition `x >= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-negative means, for every element `x[i]` of `x`, we have `x[i] >= 0`.
If `x` is empty this is trivially satisfied.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_negative(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_non_positive_fn get;
Assert the condition `x <= 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Non-positive means, for every element `x[i]` of `x`, we have `x[i] <= 0`.
If `x` is empty this is trivially satisfied.
Show Example
with tf.control_dependencies([tf.debugging.assert_non_positive(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_none_equal_fn get;
Assert the condition `x != y` holds element-wise. This condition holds if for every pair of (possibly broadcast) elements
`x[i]`, `y[i]`, we have `x[i] != y[i]`.
If both `x` and `y` are empty, this is trivially satisfied. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Show Example
with tf.control_dependencies([tf.compat.v1.assert_none_equal(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_positive_fn get;
Assert the condition `x > 0` holds element-wise. When running in graph mode, you should add a dependency on this operation
to ensure that it runs. Example of adding a dependency to an operation:
Positive means, for every element `x[i]` of `x`, we have `x[i] > 0`.
If `x` is empty this is trivially satisfied.
Show Example
with tf.control_dependencies([tf.debugging.assert_positive(x, y)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_proper_iterable_fn get;
Static assert that values is a "proper" iterable. `Ops` that expect iterables of `Tensor` can call this to validate input.
Useful since `Tensor`, `ndarray`, byte/text type are all iterables themselves.
PythonFunctionContainer assert_rank_at_least_fn get;
Assert `x` has rank equal to `rank` or higher. Example of adding a dependency to an operation:
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_at_least(x, 2)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_rank_fn get;
Assert `x` has rank equal to `rank`. Example of adding a dependency to an operation:
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank(x, 2)]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_rank_in_fn get;
Assert `x` has rank in `ranks`. Example of adding a dependency to an operation:
Show Example
with tf.control_dependencies([tf.compat.v1.assert_rank_in(x, (2, 4))]):
output = tf.reduce_sum(x)
PythonFunctionContainer assert_same_float_dtype_fn get;
Validate and return float type based on `tensors` and `dtype`. For ops such as matrix multiplication, inputs and weights must be of the
same float type. This function validates that all `tensors` are the same type,
validates that type is `dtype` (if supplied), and returns the type. Type must
be a floating point type. If neither `tensors` nor `dtype` is supplied,
the function will return `dtypes.float32`.
PythonFunctionContainer assert_scalar_fn get;
Asserts that the given `tensor` is a scalar (i.e. zero-dimensional). This function raises `ValueError` unless it can be certain that the given
`tensor` is a scalar. `ValueError` is also raised if the shape of `tensor` is
unknown.
PythonFunctionContainer assert_type_fn get;
Statically asserts that the given `Tensor` is of the specified type.
PythonFunctionContainer assert_variables_initialized_fn get;
Returns an Op to check if variables are initialized. NOTE: This function is obsolete and will be removed in 6 months. Please
change your implementation to use `report_uninitialized_variables()`. When run, the returned Op will raise the exception `FailedPreconditionError`
if any of the variables has not yet been initialized. Note: This function is implemented by trying to fetch the values of the
variables. If one of the variables is not initialized a message may be
logged by the C++ runtime. This is expected.
PythonFunctionContainer assign_add_fn get;
Update `ref` by adding `value` to it. This operation outputs "ref" after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.add, this op does not broadcast. `ref` and `value` must have
the same shape.
PythonFunctionContainer assign_fn get;
Update `ref` by assigning `value` to it. This operation outputs a Tensor that holds the new value of `ref` after
the value has been assigned. This makes it easier to chain operations that
need to use the reset value.
PythonFunctionContainer assign_sub_fn get;
Update `ref` by subtracting `value` from it. This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value.
Unlike
tf.math.subtract, this op does not broadcast. `ref` and `value`
must have the same shape.
PythonFunctionContainer atan_fn get;
Computes the trignometric inverse tangent of x element-wise. The
tf.math.atan operation returns the inverse of tf.math.tan, such that
if `y = tf.math.tan(x)` then, `x = tf.math.atan(y)`. **Note**: The output of tf.math.atan will lie within the invertible range
of tan, i.e (-pi/2, pi/2).
Show Example
# Note: [1.047, 0.785] ~= [(pi/3), (pi/4)]
x = tf.constant([1.047, 0.785])
y = tf.math.tan(x) # [1.731261, 0.99920404] tf.math.atan(y) # [1.047, 0.785] = x
PythonFunctionContainer atan2_fn get;
Computes arctangent of `y/x` element-wise, respecting signs of the arguments. This is the angle \( \theta \in [-\pi, \pi] \) such that
\[ x = r \cos(\theta) \]
and
\[ y = r \sin(\theta) \]
where \(r = \sqrt(x^2 + y^2) \).
PythonFunctionContainer atanh_fn get;
Computes inverse hyperbolic tangent of x element-wise. Given an input tensor, this function computes inverse hyperbolic tangent
for every element in the tensor. Input range is `[-1,1]` and output range is
`[-inf, inf]`. If input is `-1`, output will be `-inf` and if the
input is `1`, output will be `inf`. Values outside the range will have
`nan` as output.
Show Example
x = tf.constant([-float("inf"), -1, -0.5, 1, 0, 0.5, 10, float("inf")])
tf.math.atanh(x) ==> [nan -inf -0.54930615 inf 0. 0.54930615 nan nan]
PythonFunctionContainer attr_bool_fn get;
PythonFunctionContainer attr_bool_list_fn get;
PythonFunctionContainer attr_default_fn get;
PythonFunctionContainer attr_empty_list_default_fn get;
PythonFunctionContainer attr_enum_fn get;
PythonFunctionContainer attr_enum_list_fn get;
PythonFunctionContainer attr_float_fn get;
PythonFunctionContainer attr_fn get;
PythonFunctionContainer attr_list_default_fn get;
PythonFunctionContainer attr_list_min_fn get;
PythonFunctionContainer attr_list_type_default_fn get;
PythonFunctionContainer attr_min_fn get;
PythonFunctionContainer attr_partial_shape_fn get;
PythonFunctionContainer attr_partial_shape_list_fn get;
PythonFunctionContainer attr_shape_fn get;
PythonFunctionContainer attr_shape_list_fn get;
PythonFunctionContainer attr_type_default_fn get;
PythonFunctionContainer audio_microfrontend_fn get;
PythonFunctionContainer b_fn get;
PythonFunctionContainer batch_gather_fn get;
Gather slices from params according to indices with leading batch dims. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-10-25.
Instructions for updating:
tf.batch_gather is deprecated, please use tf.gather with `batch_dims=-1` instead.
PythonFunctionContainer batch_scatter_update_fn get;
Generalization of `tf.compat.v1.scatter_update` to axis different than 0. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-11-29.
Instructions for updating:
Use the batch_scatter_update method of Variable instead. Analogous to `batch_gather`. This assumes that `ref`, `indices` and `updates`
have a series of leading dimensions that are the same for all of them, and the
updates are performed on the last dimension of indices. In other words, the
dimensions should be the following: `num_prefix_dims = indices.ndims - 1`
`batch_dim = num_prefix_dims + 1`
`updates.shape = indices.shape + var.shape[batch_dim:]` where `updates.shape[:num_prefix_dims]`
`== indices.shape[:num_prefix_dims]`
`== var.shape[:num_prefix_dims]` And the operation performed can be expressed as: `var[i_1,..., i_n, indices[i_1,..., i_n, j]] = updates[i_1,..., i_n, j]` When indices is a 1D tensor, this operation is equivalent to
`tf.compat.v1.scatter_update`. To avoid this operation there would be 2 alternatives:
1) Reshaping the variable by merging the first `ndims` dimensions. However,
this is not possible because
tf.reshape returns a Tensor, which we
cannot use `tf.compat.v1.scatter_update` on.
2) Looping over the first `ndims` of the variable and using
`tf.compat.v1.scatter_update` on the subtensors that result of slicing the
first
dimension. This is a valid option for `ndims = 1`, but less efficient than
this implementation. See also `tf.compat.v1.scatter_update` and `tf.compat.v1.scatter_nd_update`.
PythonFunctionContainer batch_to_space_fn get;
BatchToSpace for 4-D tensors of type T. This is a legacy version of the more general BatchToSpaceND. Rearranges (permutes) data from batch into blocks of spatial data, followed by
cropping. This is the reverse transformation of SpaceToBatch. More specifically,
this op outputs a copy of the input tensor where values from the `batch`
dimension are moved in spatial blocks to the `height` and `width` dimensions,
followed by cropping along the `height` and `width` dimensions.
PythonFunctionContainer batch_to_space_nd_fn get;
BatchToSpace for N-D tensors of type T. This operation reshapes the "batch" dimension 0 into `M + 1` dimensions of shape
`block_shape + [batch]`, interleaves these blocks back into the grid defined by
the spatial dimensions `[1,..., M]`, to obtain a result with the same rank as
the input. The spatial dimensions of this intermediate result are then
optionally cropped according to `crops` to produce the output. This is the
reverse of SpaceToBatch. See below for a precise description.
PythonFunctionContainer betainc_fn get;
Compute the regularized incomplete beta integral \\(I_x(a, b)\\). The regularized incomplete beta integral is defined as: \\(I_x(a, b) = \frac{B(x; a, b)}{B(a, b)}\\) where \\(B(x; a, b) = \int_0^x t^{a-1} (1 - t)^{b-1} dt\\) is the incomplete beta function and \\(B(a, b)\\) is the *complete*
beta function.
DType bfloat16 get; set;
PythonFunctionContainer binary_fn get;
PythonFunctionContainer bincount_fn_ get;
PythonFunctionContainer bipartite_match_fn get;
PythonFunctionContainer bitcast_fn get;
Bitcasts a tensor from one type to another without copying data. Given a tensor `input`, this operation returns a tensor that has the same buffer
data as `input` with datatype `type`. If the input datatype `T` is larger than the output datatype `type` then the
shape changes from [...] to [..., sizeof(`T`)/sizeof(`type`)]. If `T` is smaller than `type`, the operator requires that the rightmost
dimension be equal to sizeof(`type`)/sizeof(`T`). The shape then goes from
[..., sizeof(`type`)/sizeof(`T`)] to [...]. tf.bitcast() and tf.cast() work differently when real dtype is casted as a complex dtype
(e.g. tf.complex64 or tf.complex128) as tf.cast() make imaginary part 0 while tf.bitcast()
gives module error.
For example, Example 1:
Example 2:
Example 3:
*NOTE*: Bitcast is implemented as a low-level cast, so machines with different
endian orderings will give different results.
Show Example
>>> a = [1., 2., 3.]
>>> equality_bitcast = tf.bitcast(a,tf.complex128)
tensorflow.python.framework.errors_impl.InvalidArgumentError: Cannot bitcast from float to complex128: shape [3] [Op:Bitcast]
>>> equality_cast = tf.cast(a,tf.complex128)
>>> print(equality_cast)
tf.Tensor([1.+0.j 2.+0.j 3.+0.j], shape=(3,), dtype=complex128)
DType bool get; set;
PythonFunctionContainer boolean_mask_fn get;
Apply boolean mask to tensor. Numpy equivalent is `tensor[mask]`.
In general, `0 < dim(mask) = K <= dim(tensor)`, and `mask`'s shape must match
the first K dimensions of `tensor`'s shape. We then have:
`boolean_mask(tensor, mask)[i, j1,...,jd] = tensor[i1,...,iK,j1,...,jd]`
where `(i1,...,iK)` is the ith `True` entry of `mask` (row-major order).
The `axis` could be used with `mask` to indicate the axis to mask from.
In that case, `axis + dim(mask) <= dim(tensor)` and `mask`'s shape must match
the first `axis + dim(mask)` dimensions of `tensor`'s shape. See also:
tf.ragged.boolean_mask, which can be applied to both dense and
ragged tensors, and can be used if you need to preserve the masked dimensions
of `tensor` (rather than flattening them, as tf.boolean_mask does).
Show Example
# 1-D example
tensor = [0, 1, 2, 3]
mask = np.array([True, False, True, False])
boolean_mask(tensor, mask) # [0, 2]
PythonFunctionContainer broadcast_dynamic_shape_fn get;
Computes the shape of a broadcast given symbolic shapes. When shape_x and shape_y are Tensors representing shapes (i.e. the result of
calling tf.shape on another Tensor) this computes a Tensor which is the shape
of the result of a broadcasting op applied in tensors of shapes shape_x and
shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
Tensor whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors do not have statically known shapes.
PythonFunctionContainer broadcast_static_shape_fn get;
Computes the shape of a broadcast given known shapes. When shape_x and shape_y are fully known TensorShapes this computes a
TensorShape which is the shape of the result of a broadcasting op applied in
tensors of shapes shape_x and shape_y. For example, if shape_x is [1, 2, 3] and shape_y is [5, 1, 3], the result is a
TensorShape whose value is [5, 2, 3]. This is useful when validating the result of a broadcasting operation when the
tensors have statically known shapes.
PythonFunctionContainer broadcast_to_fn get;
Broadcast an array for a compatible shape. Broadcasting is the process of making arrays to have compatible shapes
for arithmetic operations. Two shapes are compatible if for each
dimension pair they are either equal or one of them is one. When trying
to broadcast a Tensor to a shape, it starts with the trailing dimensions,
and works its way forward. For example,
In the above example, the input Tensor with the shape of `[1, 3]`
is broadcasted to output Tensor with shape of `[3, 3]`.
Show Example
>>> x = tf.constant([1, 2, 3])
>>> y = tf.broadcast_to(x, [3, 3])
>>> sess.run(y)
array([[1, 2, 3],
[1, 2, 3],
[1, 2, 3]], dtype=int32)
PythonFunctionContainer bucketize_with_input_boundaries_fn get;
PythonFunctionContainer build_categorical_equality_splits_fn get;
PythonFunctionContainer build_dense_inequality_splits_fn get;
PythonFunctionContainer build_sparse_inequality_splits_fn get;
PythonFunctionContainer bytes_in_use_fn get;
PythonFunctionContainer bytes_limit_fn get;
PythonFunctionContainer case_fn get;
Create a case operation. See also
tf.switch_case. The `pred_fn_pairs` parameter is a dict or list of pairs of size N.
Each pair contains a boolean scalar tensor and a python callable that
creates the tensors to be returned if the boolean evaluates to True.
`default` is a callable generating a list of tensors. All the callables
in `pred_fn_pairs` as well as `default` (if provided) should return the same
number and types of tensors. If `exclusive==True`, all predicates are evaluated, and an exception is
thrown if more than one of the predicates evaluates to `True`.
If `exclusive==False`, execution stops at the first predicate which
evaluates to True, and the tensors generated by the corresponding function
are returned immediately. If none of the predicates evaluate to True, this
operation returns the tensors generated by `default`. tf.case supports nested structures as implemented in
tf.contrib.framework.nest. All of the callables must return the same
(possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
a callable, they are implicitly unpacked to single values. This
behavior is disabled by passing `strict=True`. If an unordered dictionary is used for `pred_fn_pairs`, the order of the
conditional tests is not guaranteed. However, the order is guaranteed to be
deterministic, so that variables created in conditional branches are created
in fixed order across runs. **Example 1:** Pseudocode: ```
if (x < y) return 17;
else return 23;
``` Expressions:
**Example 2:** Pseudocode: ```
if (x < y && x > z) raise OpError("Only one predicate may evaluate to True");
if (x < y) return 17;
else if (x > z) return 23;
else return -1;
``` Expressions:
Show Example
f1 = lambda: tf.constant(17)
f2 = lambda: tf.constant(23)
r = tf.case([(tf.less(x, y), f1)], default=f2)
PythonFunctionContainer cast_fn get;
Casts a tensor to a new type. The operation casts `x` (in case of `Tensor`) or `x.values`
(in case of `SparseTensor` or `IndexedSlices`) to `dtype`.
The operation supports data types (for `x` and `dtype`) of
`uint8`, `uint16`, `uint32`, `uint64`, `int8`, `int16`, `int32`, `int64`,
`float16`, `float32`, `float64`, `complex64`, `complex128`, `bfloat16`.
In case of casting from complex types (`complex64`, `complex128`) to real
types, only the real part of `x` is returned. In case of casting from real
types to complex types (`complex64`, `complex128`), the imaginary part of the
returned value is set to `0`. The handling of complex types here matches the
behavior of numpy.
Show Example
x = tf.constant([1.8, 2.2], dtype=tf.float32)
tf.dtypes.cast(x, tf.int32) # [1, 2], dtype=tf.int32
PythonFunctionContainer ceil_fn get;
Returns element-wise smallest integer not less than x.
PythonFunctionContainer center_tree_ensemble_bias_fn get;
PythonFunctionContainer check_numerics_fn get;
Checks a tensor for NaN and Inf values. When run, reports an `InvalidArgument` error if `tensor` has any values
that are not a number (NaN) or infinity (Inf). Otherwise, passes `tensor` as-is.
PythonFunctionContainer cholesky_fn get;
Computes the Cholesky decomposition of one or more square matrices. The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The input has to be symmetric and positive definite. Only the lower-triangular
part of the input will be used for this operation. The upper-triangular part
will not be read. The output is a tensor of the same shape as the input
containing the Cholesky decompositions for all input submatrices `[..., :, :]`. **Note**: The gradient computation on GPU is faster for large matrices but
not for large batch dimensions when the submatrices are small. In this
case it might be faster to use the CPU.
PythonFunctionContainer cholesky_solve_fn get;
Solves systems of linear eqns `A X = RHS`, given Cholesky factorizations.
Show Example
# Solve 10 separate 2x2 linear systems:
A =... # shape 10 x 2 x 2
RHS =... # shape 10 x 2 x 1
chol = tf.linalg.cholesky(A) # shape 10 x 2 x 2
X = tf.linalg.cholesky_solve(chol, RHS) # shape 10 x 2 x 1
# tf.matmul(A, X) ~ RHS
X[3, :, 0] # Solution to the linear system A[3, :, :] x = RHS[3, :, 0] # Solve five linear systems (K = 5) for every member of the length 10 batch.
A =... # shape 10 x 2 x 2
RHS =... # shape 10 x 2 x 5
...
X[3, :, 2] # Solution to the linear system A[3, :, :] x = RHS[3, :, 2]
PythonFunctionContainer clip_by_average_norm_fn get;
Clips tensor values to a maximum average L2-norm. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
clip_by_average_norm is deprecated in TensorFlow 2.0. Please use clip_by_norm(t, clip_norm * tf.cast(tf.size(t), tf.float32), name) instead. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its average L2-norm is less than or equal to
`clip_norm`. Specifically, if the average L2-norm is already less than or
equal to `clip_norm`, then `t` is not modified. If the average L2-norm is
greater than `clip_norm`, then this operation returns a tensor of the same
type and shape as `t` with its values set to: `t * clip_norm / l2norm_avg(t)` In this case, the average L2-norm of the output tensor is `clip_norm`. This operation is typically used to clip gradients before applying them with
an optimizer.
PythonFunctionContainer clip_by_global_norm_fn get;
Clips values of multiple tensors by the ratio of the sum of their norms. Given a tuple or list of tensors `t_list`, and a clipping ratio `clip_norm`,
this operation returns a list of clipped tensors `list_clipped`
and the global norm (`global_norm`) of all tensors in `t_list`. Optionally,
if you've already computed the global norm for `t_list`, you can specify
the global norm with `use_norm`. To perform the clipping, the values `t_list[i]` are set to: t_list[i] * clip_norm / max(global_norm, clip_norm) where: global_norm = sqrt(sum([l2norm(t)**2 for t in t_list])) If `clip_norm > global_norm` then the entries in `t_list` remain as they are,
otherwise they're all shrunk by the global ratio. If `global_norm == infinity` then the entries in `t_list` are all set to `NaN`
to signal that an error occurred. Any of the entries of `t_list` that are of type `None` are ignored. This is the correct way to perform gradient clipping (for example, see
[Pascanu et al., 2012](http://arxiv.org/abs/1211.5063)
([pdf](http://arxiv.org/pdf/1211.5063.pdf))). However, it is slower than `clip_by_norm()` because all the parameters must be
ready before the clipping operation can be performed.
PythonFunctionContainer clip_by_norm_fn get;
Clips tensor values to a maximum L2-norm. Given a tensor `t`, and a maximum clip value `clip_norm`, this operation
normalizes `t` so that its L2-norm is less than or equal to `clip_norm`,
along the dimensions given in `axes`. Specifically, in the default case
where all dimensions are used for calculation, if the L2-norm of `t` is
already less than or equal to `clip_norm`, then `t` is not modified. If
the L2-norm is greater than `clip_norm`, then this operation returns a
tensor of the same type and shape as `t` with its values set to: `t * clip_norm / l2norm(t)` In this case, the L2-norm of the output tensor is `clip_norm`. As another example, if `t` is a matrix and `axes == [1]`, then each row
of the output will have L2-norm less than or equal to `clip_norm`. If
`axes == [0]` instead, each column of the output will be clipped. This operation is typically used to clip gradients before applying them with
an optimizer.
PythonFunctionContainer clip_by_value_fn get;
Clips tensor values to a specified min and max. Given a tensor `t`, this operation returns a tensor of the same type and
shape as `t` with its values clipped to `clip_value_min` and `clip_value_max`.
Any values less than `clip_value_min` are set to `clip_value_min`. Any values
greater than `clip_value_max` are set to `clip_value_max`. Note: `clip_value_min` needs to be smaller or equal to `clip_value_max` for
correct results.
Show Example
A = tf.constant([[1, 20, 13], [3, 21, 13]])
B = tf.clip_by_value(A, clip_value_min=0, clip_value_max=3) # [[1, 3, 3],[3, 3, 3]]
C = tf.clip_by_value(A, clip_value_min=0., clip_value_max=3.) # throws `TypeError`
as input and clip_values are of different dtype
PythonFunctionContainer complex_fn get;
Converts two real numbers to a complex number. Given a tensor `real` representing the real part of a complex number, and a
tensor `imag` representing the imaginary part of a complex number, this
operation returns complex numbers elementwise of the form \\(a + bj\\), where
*a* represents the `real` part and *b* represents the `imag` part. The input tensors `real` and `imag` must have the same shape.
Show Example
real = tf.constant([2.25, 3.25])
imag = tf.constant([4.75, 5.75])
tf.complex(real, imag) # [[2.25 + 4.75j], [3.25 + 5.75j]]
PythonFunctionContainer complex_struct_fn get;
DType complex128 get; set;
DType complex64 get; set;
PythonFunctionContainer concat_fn get;
Concatenates tensors along one dimension. Concatenates the list of tensors `values` along dimension `axis`. If
`values[i].shape = [D0, D1,... Daxis(i),...Dn]`, the concatenated
result has shape [D0, D1,... Raxis,...Dn] where Raxis = sum(Daxis(i)) That is, the data from the input tensors is joined along the `axis`
dimension. The number of dimensions of the input tensors must match, and all dimensions
except `axis` must be equal.
As in Python, the `axis` could also be negative numbers. Negative `axis`
are interpreted as counting from the end of the rank, i.e.,
`axis + rank(values)`-th dimension.
would produce:
Note: If you are concatenating along a new axis consider using stack.
E.g.
can be rewritten as
Show Example
t1 = [[1, 2, 3], [4, 5, 6]]
t2 = [[7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 0) # [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]]
tf.concat([t1, t2], 1) # [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]] # tensor t3 with shape [2, 3]
# tensor t4 with shape [2, 3]
tf.shape(tf.concat([t3, t4], 0)) # [4, 3]
tf.shape(tf.concat([t3, t4], 1)) # [2, 6]
PythonFunctionContainer cond_fn get;
Return `true_fn()` if the predicate `pred` is true else `false_fn()`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(fn1, fn2)`. They will be removed in a future version.
Instructions for updating:
fn1/fn2 are deprecated in favor of the true_fn/false_fn arguments. `true_fn` and `false_fn` both return lists of output tensors. `true_fn` and
`false_fn` must have the same non-zero number and type of outputs. **WARNING**: Any Tensors or Operations created outside of `true_fn` and
`false_fn` will be executed regardless of which branch is selected at runtime. Although this behavior is consistent with the dataflow model of TensorFlow,
it has frequently surprised users who expected a lazier semantics.
Consider the following simple program:
If `x < y`, the
tf.add operation will be executed and tf.square
operation will not be executed. Since `z` is needed for at least one
branch of the `cond`, the tf.multiply operation is always executed,
unconditionally. Note that `cond` calls `true_fn` and `false_fn` *exactly once* (inside the
call to `cond`, and not at all during `Session.run()`). `cond`
stitches together the graph fragments created during the `true_fn` and
`false_fn` calls with some additional graph nodes to ensure that the right
branch gets executed depending on the value of `pred`. tf.cond supports nested structures as implemented in
`tensorflow.python.util.nest`. Both `true_fn` and `false_fn` must return the
same (possibly nested) value structure of lists, tuples, and/or named tuples.
Singleton lists and tuples form the only exceptions to this: when returned by
`true_fn` and/or `false_fn`, they are implicitly unpacked to single values.
This behavior is disabled by passing `strict=True`.
Show Example
z = tf.multiply(a, b)
result = tf.cond(x < y, lambda: tf.add(x, z), lambda: tf.square(y))
PythonFunctionContainer confusion_matrix_fn_ get;
PythonFunctionContainer conj_fn get;
Returns the complex conjugate of a complex number. Given a tensor `input` of complex numbers, this operation returns a tensor of
complex numbers that are the complex conjugate of each element in `input`. The
complex numbers in `input` must be of the form \\(a + bj\\), where *a* is the
real part and *b* is the imaginary part. The complex conjugate returned by this operation is of the form \\(a - bj\\). For example: # tensor 'input' is [-2.25 + 4.75j, 3.25 + 5.75j]
tf.math.conj(input) ==> [-2.25 - 4.75j, 3.25 - 5.75j] If `x` is real, it is returned unchanged.
PythonFunctionContainer constant_fn_ get;
PythonFunctionContainer container_fn get;
Wrapper for `Graph.container()` using the default graph.
object contrib get; set;
object contrib_dyn get; set;
PythonFunctionContainer control_dependencies_fn get;
Wrapper for `Graph.control_dependencies()` using the default graph. See
tf.Graph.control_dependencies
for more details. When eager execution is enabled, any callable object in the `control_inputs`
list will be called.
PythonFunctionContainer control_flow_v2_enabled_fn get;
Returns `True` if v2 control flow is enabled. Note: v2 control flow is always enabled inside of tf.function.
PythonFunctionContainer convert_to_tensor_fn get;
Converts the given `value` to a `Tensor`. This function converts Python objects of various types to `Tensor`
objects. It accepts `Tensor` objects, numpy arrays, Python lists,
and Python scalars.
This function can be useful when composing a new operation in Python
(such as `my_func` in the example above). All standard Python op
constructors apply this function to each of their Tensor-valued
inputs, which allows those ops to accept numpy arrays, Python lists,
and scalars in addition to `Tensor` objects. Note: This function diverges from default Numpy behavior for `float` and
`string` types when `None` is present in a Python list or scalar. Rather
than silently converting `None` values, an error will be thrown.
Show Example
import numpy as np def my_func(arg): arg = tf.convert_to_tensor(arg, dtype=tf.float32) return tf.matmul(arg, arg) + arg # The following calls are equivalent. value_1 = my_func(tf.constant([[1.0, 2.0], [3.0, 4.0]])) value_2 = my_func([[1.0, 2.0], [3.0, 4.0]]) value_3 = my_func(np.array([[1.0, 2.0], [3.0, 4.0]], dtype=np.float32))
PythonFunctionContainer convert_to_tensor_or_indexed_slices_fn get;
Converts the given object to a `Tensor` or an `IndexedSlices`. If `value` is an `IndexedSlices` or `SparseTensor` it is returned
unmodified. Otherwise, it is converted to a `Tensor` using
`convert_to_tensor()`.
PythonFunctionContainer convert_to_tensor_or_sparse_tensor_fn get;
Converts value to a `SparseTensor` or `Tensor`.
PythonFunctionContainer copy_op_fn get;
PythonFunctionContainer cos_fn get;
Computes cos of x element-wise. Given an input tensor, this function computes cosine of every
element in the tensor. Input range is `(-inf, inf)` and
output range is `[-1,1]`. If input lies outside the boundary, `nan`
is returned.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.cos(x) ==> [nan -0.91113025 0.87758255 0.5403023 0.36235774 0.48718765 -0.95215535 nan]
PythonFunctionContainer cosh_fn get;
Computes hyperbolic cosine of x element-wise. Given an input tensor, this function computes hyperbolic cosine of every
element in the tensor. Input range is `[-inf, inf]` and output range
is `[1, inf]`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 2, 10, float("inf")])
tf.math.cosh(x) ==> [inf 4.0515420e+03 1.1276259e+00 1.5430807e+00 1.8106556e+00 3.7621956e+00 1.1013233e+04 inf]
PythonFunctionContainer count_nonzero_fn get;
Computes number of nonzero elements across dimensions of a tensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(axis)`. They will be removed in a future version.
Instructions for updating:
reduction_indices is deprecated, use axis instead Reduces `input_tensor` along the dimensions given in `axis`.
Unless `keepdims` is true, the rank of the tensor is reduced by 1 for each
entry in `axis`. If `keepdims` is true, the reduced dimensions
are retained with length 1. If `axis` has no entries, all dimensions are reduced, and a
tensor with a single element is returned. **NOTE** Floating point comparison to zero is done by exact floating point
equality check. Small values are **not** rounded to zero for purposes of
the nonzero check.
**NOTE** Strings are compared against zero-length empty string `""`. Any
string with a size greater than zero is already considered as nonzero.
Show Example
x = tf.constant([[0, 1, 0], [1, 1, 0]])
tf.math.count_nonzero(x) # 3
tf.math.count_nonzero(x, 0) # [1, 2, 0]
tf.math.count_nonzero(x, 1) # [1, 2]
tf.math.count_nonzero(x, 1, keepdims=True) # [[1], [2]]
tf.math.count_nonzero(x, [0, 1]) # 3
PythonFunctionContainer count_up_to_fn get;
Increments 'ref' until it reaches 'limit'. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Prefer Dataset.range instead.
PythonFunctionContainer create_fertile_stats_variable_fn get;
PythonFunctionContainer create_partitioned_variables_fn get;
Create a list of partitioned variables according to the given `slicing`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.get_variable with a partitioner set. Currently only one dimension of the full variable can be sliced, and the
full variable can be reconstructed by the concatenation of the returned
list along that dimension.
PythonFunctionContainer create_quantile_accumulator_fn get;
PythonFunctionContainer create_stats_accumulator_scalar_fn get;
PythonFunctionContainer create_stats_accumulator_tensor_fn get;
PythonFunctionContainer create_tree_ensemble_variable_fn get;
PythonFunctionContainer create_tree_variable_fn get;
PythonFunctionContainer cross_fn get;
Compute the pairwise cross product. `a` and `b` must be the same shape; they can either be simple 3-element vectors,
or any shape where the innermost dimension is 3. In the latter case, each pair
of corresponding 3-element vectors is cross-multiplied independently.
PythonFunctionContainer cumprod_fn get;
Compute the cumulative product of the tensor `x` along `axis`. By default, this op performs an inclusive cumprod, which means that the
first element of the input is identical to the first element of the output:
By setting the `exclusive` kwarg to `True`, an exclusive cumprod is
performed
instead:
By setting the `reverse` kwarg to `True`, the cumprod is performed in the
opposite direction:
This is more efficient than using separate
tf.reverse ops.
The `reverse` and `exclusive` kwargs can also be combined:
Show Example
tf.math.cumprod([a, b, c]) # [a, a * b, a * b * c]
PythonFunctionContainer cumsum_fn get;
Compute the cumulative sum of the tensor `x` along `axis`. By default, this op performs an inclusive cumsum, which means that the first
element of the input is identical to the first element of the output:
By setting the `exclusive` kwarg to `True`, an exclusive cumsum is performed
instead:
By setting the `reverse` kwarg to `True`, the cumsum is performed in the
opposite direction:
This is more efficient than using separate
tf.reverse ops. The `reverse` and `exclusive` kwargs can also be combined:
Show Example
tf.cumsum([a, b, c]) # [a, a + b, a + b + c]
PythonFunctionContainer custom_gradient_fn get;
Decorator to define a function with a custom gradient. This decorator allows fine grained control over the gradients of a sequence
for operations. This may be useful for multiple reasons, including providing
a more efficient or numerically stable gradient for a sequence of operations. For example, consider the following function that commonly occurs in the
computation of cross entropy and log likelihoods:
Due to numerical instability, the gradient this function evaluated at x=100 is
NaN.
The gradient expression can be analytically simplified to provide numerical
stability:
With this definition, the gradient at x=100 will be correctly evaluated as
1.0. See also
tf.RegisterGradient which registers a gradient function for a
primitive TensorFlow operation. tf.custom_gradient on the other hand allows
for fine grained control over the gradient computation of a sequence of
operations. Note that if the decorated function uses `Variable`s, the enclosing variable
scope must be using `ResourceVariable`s.
Show Example
def log1pexp(x):
return tf.math.log(1 + tf.exp(x))
PythonFunctionContainer decision_tree_ensemble_resource_handle_op_fn get;
PythonFunctionContainer decision_tree_resource_handle_op_fn get;
PythonFunctionContainer decode_base64_fn get;
Decode web-safe base64-encoded strings. Input may or may not have padding at the end. See EncodeBase64 for padding.
Web-safe means that input must use - and _ instead of + and /.
PythonFunctionContainer decode_compressed_fn get;
Decompress strings. This op decompresses each element of the `bytes` input `Tensor`, which
is assumed to be compressed using the given `compression_type`. The `output` is a string `Tensor` of the same shape as `bytes`,
each element containing the decompressed data from the corresponding
element in `bytes`.
PythonFunctionContainer decode_csv_fn get;
Convert CSV records to tensors. Each column maps to one tensor. RFC 4180 format is expected for the CSV records.
(https://tools.ietf.org/html/rfc4180)
Note that we allow leading and trailing spaces with int or float field.
PythonFunctionContainer decode_json_example_fn get;
Convert JSON-encoded Example records to binary protocol buffer strings. This op translates a tensor containing Example records, encoded using
the [standard JSON
mapping](https://developers.google.com/protocol-buffers/docs/proto3#json),
into a tensor containing the same records encoded as binary protocol
buffers. The resulting tensor can then be fed to any of the other
Example-parsing ops.
PythonFunctionContainer decode_libsvm_fn get;
PythonFunctionContainer decode_raw_fn_ get;
PythonFunctionContainer default_attrs_fn get;
PythonFunctionContainer delete_session_tensor_fn get;
Delete the tensor for the given tensor handle. This is EXPERIMENTAL and subject to change. Delete the tensor of a given tensor handle. The tensor is produced
in a previous run() and stored in the state of the session.
PythonFunctionContainer depth_to_space_fn get;
DepthToSpace for tensors of type T. Rearranges data from depth into blocks of spatial data.
This is the reverse transformation of SpaceToDepth. More specifically,
this op outputs a copy of the input tensor where values from the `depth`
dimension are moved in spatial blocks to the `height` and `width` dimensions.
The attr `block_size` indicates the input block size and how the data is moved. * Chunks of data of size `block_size * block_size` from depth are rearranged
into non-overlapping blocks of size `block_size x block_size`
* The width the output tensor is `input_depth * block_size`, whereas the
height is `input_height * block_size`.
* The Y, X coordinates within each block of the output image are determined
by the high order component of the input channel index.
* The depth of the input tensor must be divisible by
`block_size * block_size`. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,iY,iX,bY,bX,oC (where n=batch index, iX, iY means X or Y coordinates
within the input image, bX, bY means coordinates
within the output block, oC means output channels).
The output would be the input transposed to the following layout:
n,iY,bY,iX,bX,oC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 1, 1, 4]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1, 2, 3, 4]]]] ``` This operation will output a tensor of shape `[1, 2, 2, 1]`: ```
[[[[1], [2]],
[[3], [4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[1, 1, 4]`,
the corresponding output will have 2x2 elements and will have a depth of
1 channel (1 = `4 / (block_size * block_size)`).
The output element shape is `[2, 2, 1]`. For an input tensor with larger depth, here of shape `[1, 1, 1, 12]`, e.g. ```
x = [[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` This operation, for block size of 2, will return the following tensor of shape
`[1, 2, 2, 3]` ```
[[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]] ``` Similarly, for the following input of shape `[1 2 2 4]`, and a block size of 2: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
``` the operator will return the following tensor of shape `[1 4 4 1]`: ```
x = [[[ [1], [2], [5], [6]],
[ [3], [4], [7], [8]],
[ [9], [10], [13], [14]],
[ [11], [12], [15], [16]]]] ```
PythonFunctionContainer dequantize_fn get;
Dequantize the 'input' tensor into a float Tensor. [min_range, max_range] are scalar floats that specify the range for
the 'input' data. The 'mode' attribute controls exactly which calculations are
used to convert the float values to their quantized equivalents. In 'MIN_COMBINED' mode, each value of the tensor will undergo the following: ```
if T == qint8: in[i] += (range(T) + 1)/ 2.0
out[i] = min_range + (in[i]* (max_range - min_range) / range(T))
```
here `range(T) = numeric_limits::max() - numeric_limits::min()` *MIN_COMBINED Mode Example* If the input comes from a QuantizedRelu6, the output type is
quint8 (range of 0-255) but the possible range of QuantizedRelu6 is
0-6. The min_range and max_range values are therefore 0.0 and 6.0.
Dequantize on quint8 will take each value, cast to float, and multiply
by 6 / 255.
Note that if quantizedtype is qint8, the operation will additionally add
each value by 128 prior to casting. If the mode is 'MIN_FIRST', then this approach is used: ```c++
num_discrete_values = 1 << (# of bits in T)
range_adjust = num_discrete_values / (num_discrete_values - 1)
range = (range_max - range_min) * range_adjust
range_scale = range / num_discrete_values
const double offset_input = static_cast(input) - lowest_quantized;
result = range_min + ((input - numeric_limits::min()) * range_scale)
``` *SCALED mode Example* `SCALED` mode matches the quantization approach used in
`QuantizeAndDequantize{V2|V3}`. If the mode is `SCALED`, we do not use the full range of the output type,
choosing to elide the lowest possible value for symmetry (e.g., output range is
-127 to 127, not -128 to 127 for signed 8 bit quantization), so that 0.0 maps to
0. We first find the range of values in our tensor. The
range we use is always centered on 0, so we find m such that
```c++
m = max(abs(input_min), abs(input_max))
``` Our input tensor range is then `[-m, m]`. Next, we choose our fixed-point quantization buckets, `[min_fixed, max_fixed]`.
If T is signed, this is
```
num_bits = sizeof(T) * 8
[min_fixed, max_fixed] =
[-(1 << (num_bits - 1) - 1), (1 << (num_bits - 1)) - 1]
``` Otherwise, if T is unsigned, the fixed-point range is
```
[min_fixed, max_fixed] = [0, (1 << num_bits) - 1]
``` From this we compute our scaling factor, s:
```c++
s = (2 * m) / (max_fixed - min_fixed)
``` Now we can dequantize the elements of our tensor:
```c++
result = input * s
```
PythonFunctionContainer deserialize_many_sparse_fn get;
Deserialize and concatenate `SparseTensors` from a serialized minibatch. The input `serialized_sparse` must be a string matrix of shape `[N x 3]` where
`N` is the minibatch size and the rows correspond to packed outputs of
`serialize_sparse`. The ranks of the original `SparseTensor` objects
must all match. When the final `SparseTensor` is created, it has rank one
higher than the ranks of the incoming `SparseTensor` objects (they have been
concatenated along a new row dimension). The output `SparseTensor` object's shape values for all dimensions but the
first are the max across the input `SparseTensor` objects' shape values
for the corresponding dimensions. Its first shape value is `N`, the minibatch
size. The input `SparseTensor` objects' indices are assumed ordered in
standard lexicographic order. If this is not the case, after this
step run `sparse.reorder` to restore index ordering. For example, if the serialized input is a `[2, 3]` matrix representing two
original `SparseTensor` objects: index = [ 0]
[10]
[20]
values = [1, 2, 3]
shape = [50] and index = [ 2]
[10]
values = [4, 5]
shape = [30] then the final deserialized `SparseTensor` will be: index = [0 0]
[0 10]
[0 20]
[1 2]
[1 10]
values = [1, 2, 3, 4, 5]
shape = [2 50]
PythonFunctionContainer device_fn get;
Wrapper for `Graph.device()` using the default graph. See
tf.Graph.device for more details.
PythonFunctionContainer device_placement_op_fn get;
PythonFunctionContainer diag_fn get;
Returns a diagonal tensor with a given diagonal values. Given a `diagonal`, this operation returns a tensor with the `diagonal` and
everything else padded with zeros. The diagonal is computed as follows: Assume `diagonal` has dimensions [D1,..., Dk], then the output is a tensor of
rank 2k with dimensions [D1,..., Dk, D1,..., Dk] where: `output[i1,..., ik, i1,..., ik] = diagonal[i1,..., ik]` and 0 everywhere else. For example: ```
# 'diagonal' is [1, 2, 3, 4]
tf.diag(diagonal) ==> [[1, 0, 0, 0]
[0, 2, 0, 0]
[0, 0, 3, 0]
[0, 0, 0, 4]]
```
PythonFunctionContainer diag_part_fn get;
Returns the diagonal part of the tensor. This operation returns a tensor with the `diagonal` part
of the `input`. The `diagonal` part is computed as follows: Assume `input` has dimensions `[D1,..., Dk, D1,..., Dk]`, then the output is a
tensor of rank `k` with dimensions `[D1,..., Dk]` where: `diagonal[i1,..., ik] = input[i1,..., ik, i1,..., ik]`. For example: ```
# 'input' is [[1, 0, 0, 0]
[0, 2, 0, 0]
[0, 0, 3, 0]
[0, 0, 0, 4]] tf.diag_part(input) ==> [1, 2, 3, 4]
```
PythonFunctionContainer digamma_fn get;
Computes Psi, the derivative of Lgamma (the log of the absolute value of `Gamma(x)`), element-wise.
PythonFunctionContainer dimension_at_index_fn get;
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. If you want to retrieve the Dimension instance corresponding to a certain
index in a TensorShape instance, use this utility, like this: ```
# If you had this in your V1 code:
dim = tensor_shape[i] # Use `dimension_at_index` as direct replacement compatible with both V1 & V2:
dim = dimension_at_index(tensor_shape, i) # Another possibility would be this, but WARNING: it only works if the
# tensor_shape instance has a defined rank.
dim = tensor_shape.dims[i] # `dims` may be None if the rank is undefined! # In native V2 code, we recommend instead being more explicit:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i] # Being more explicit will save you from the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be (as the Dimension object was
# instantiated on the fly.
```
PythonFunctionContainer dimension_value_fn get;
Compatibility utility required to allow for both V1 and V2 behavior in TF. Until the release of TF 2.0, we need the legacy behavior of `TensorShape` to
coexist with the new behavior. This utility is a bridge between the two. When accessing the value of a TensorShape dimension,
use this utility, like this: ```
# If you had this in your V1 code:
value = tensor_shape[i].value # Use `dimension_value` as direct replacement compatible with both V1 & V2:
value = dimension_value(tensor_shape[i]) # This would be the V2 equivalent:
value = tensor_shape[i] # Warning: this will return the dim value in V2!
```
PythonFunctionContainer disable_control_flow_v2_fn get;
Opts out of control flow v2. Note: v2 control flow is always enabled inside of tf.function. Calling this
function has no effect in that case. If your code needs tf.disable_control_flow_v2() to be called to work
properly please file a bug.
PythonFunctionContainer disable_eager_execution_fn get;
Disables eager execution. This function can only be called before any Graphs, Ops, or Tensors have been
created. It can be used at the beginning of the program for complex migration
projects from TensorFlow 1.x to 2.x.
PythonFunctionContainer disable_tensor_equality_fn get;
Compare Tensors by their id and be hashable. This is a legacy behaviour of TensorFlow and is highly discouraged.
PythonFunctionContainer disable_v2_behavior_fn get;
Disables TensorFlow 2.x behaviors. This function can be called at the beginning of the program (before `Tensors`,
`Graphs` or other structures have been created, and before devices have been
initialized. It switches all global behaviors that are different between
TensorFlow 1.x and 2.x to behave as intended for 1.x. User can call this function to disable 2.x behavior during complex migrations.
PythonFunctionContainer disable_v2_tensorshape_fn get;
Disables the V2 TensorShape behavior and reverts to V1 behavior. See docstring for `enable_v2_tensorshape` for details about the new behavior.
PythonFunctionContainer div_fn get;
Divides x / y elementwise (using Python 2 division operator semantics). (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Deprecated in favor of operator or tf.math.divide. NOTE: Prefer using the Tensor division operator or tf.divide which obey Python
3 division operator semantics. This function divides `x` and `y`, forcing Python 2 semantics. That is, if `x`
and `y` are both integers then the result will be an integer. This is in
contrast to Python 3, where division with `/` is always a float while division
with `//` is always an integer.
PythonFunctionContainer div_no_nan_fn get;
Computes an unsafe divide which returns 0 if the y is zero.
PythonFunctionContainer divide_fn get;
Computes Python style division of `x` by `y`.
PythonFunctionContainer dynamic_partition_fn get;
Partitions `data` into `num_partitions` tensors using indices from `partitions`. For each index tuple `js` of size `partitions.ndim`, the slice `data[js,...]`
becomes part of `outputs[partitions[js]]`. The slices with `partitions[js] = i`
are placed in `outputs[i]` in lexicographic order of `js`, and the first
dimension of `outputs[i]` is the number of entries in `partitions` equal to `i`.
In detail,
`data.shape` must start with `partitions.shape`.
See `dynamic_stitch` for an example on how to merge partitions back.


Show Example
outputs[i].shape = [sum(partitions == i)] + data.shape[partitions.ndim:] outputs[i] = pack([data[js,...] for js if partitions[js] == i])
PythonFunctionContainer dynamic_stitch_fn get;
Interleave the values from the `data` tensors into a single tensor. Builds a merged tensor such that
For example, if each `indices[m]` is scalar or vector, we have
Each `data[i].shape` must start with the corresponding `indices[i].shape`,
and the rest of `data[i].shape` must be constant w.r.t. `i`. That is, we
must have `data[i].shape = indices[i].shape + constant`. In terms of this
`constant`, the output shape is merged.shape = [max(indices)] + constant Values are merged in order, so if an index appears in both `indices[m][i]` and
`indices[n][j]` for `(m,i) < (n,j)` the slice `data[n][j]` will appear in the
merged result. If you do not need this guarantee, ParallelDynamicStitch might
perform better on some devices.
This method can be used to merge partitions created by `dynamic_partition`
as illustrated on the following example:


Show Example
merged[indices[m][i,..., j],...] = data[m][i,..., j,...]
PythonFunctionContainer edit_distance_fn get;
Computes the Levenshtein distance between sequences. This operation takes variable-length sequences (`hypothesis` and `truth`),
each provided as a `SparseTensor`, and computes the Levenshtein distance.
You can normalize the edit distance by length of `truth` by setting
`normalize` to true. For example, given the following input:
This operation would return the following:
Show Example
# 'hypothesis' is a tensor of shape `[2, 1]` with variable-length values:
# (0,0) = ["a"]
# (1,0) = ["b"]
hypothesis = tf.SparseTensor(
[[0, 0, 0],
[1, 0, 0]],
["a", "b"],
(2, 1, 1)) # 'truth' is a tensor of shape `[2, 2]` with variable-length values:
# (0,0) = []
# (0,1) = ["a"]
# (1,0) = ["b", "c"]
# (1,1) = ["a"]
truth = tf.SparseTensor(
[[0, 1, 0],
[1, 0, 0],
[1, 0, 1],
[1, 1, 0]],
["a", "b", "c", "a"],
(2, 2, 2)) normalize = True
PythonFunctionContainer einsum_fn get;
Tensor contraction over specified indices and outer product. This function returns a tensor whose elements are defined by `equation`,
which is written in a shorthand form inspired by the Einstein summation
convention. As an example, consider multiplying two matrices
A and B to form a matrix C. The elements of C are given by: ```
C[i,k] = sum_j A[i,j] * B[j,k]
``` The corresponding `equation` is: ```
ij,jk->ik
``` In general, the `equation` is obtained from the more familiar element-wise
equation by
1. removing variable names, brackets, and commas,
2. replacing "*" with ",",
3. dropping summation signs, and
4. moving the output to the right, and replacing "=" with "->". Many common operations can be expressed in this way.
To enable and control broadcasting, use an ellipsis. For example, to do
batch matrix multiplication, you could use:
This function behaves like `numpy.einsum`, but does not support: * Subscripts where an axis appears more than once for a single input
(e.g. `ijj,k->ik`) unless it is a trace (e.g. `ijji`).
Show Example
# Matrix multiplication
>>> einsum('ij,jk->ik', m0, m1) # output[i,k] = sum_j m0[i,j] * m1[j, k] # Dot product
>>> einsum('i,i->', u, v) # output = sum_i u[i]*v[i] # Outer product
>>> einsum('i,j->ij', u, v) # output[i,j] = u[i]*v[j] # Transpose
>>> einsum('ij->ji', m) # output[j,i] = m[i,j] # Trace
>>> einsum('ii', m) # output[j,i] = trace(m) = sum_i m[i, i] # Batch matrix multiplication
>>> einsum('aij,ajk->aik', s, t) # out[a,i,k] = sum_j s[a,i,j] * t[a, j, k]
PythonFunctionContainer enable_control_flow_v2_fn get;
Use control flow v2. control flow v2 (cfv2) is an improved version of control flow in TensorFlow
with support for higher order derivatives. Enabling cfv2 will change the
graph/function representation of control flow, e.g.,
tf.while_loop and
tf.cond will generate functional `While` and `If` ops instead of low-level
`Switch`, `Merge` etc. ops. Note: Importing and running graphs exported
with old control flow will still be supported. Calling tf.enable_control_flow_v2() lets you opt-in to this TensorFlow 2.0
feature. Note: v2 control flow is always enabled inside of tf.function. Calling this
function is not required.
PythonFunctionContainer enable_eager_execution_fn get;
Enables eager execution for the lifetime of this program. Eager execution provides an imperative interface to TensorFlow. With eager
execution enabled, TensorFlow functions execute operations immediately (as
opposed to adding to a graph to be executed later in a `tf.compat.v1.Session`)
and
return concrete values (as opposed to symbolic references to a node in a
computational graph).
Eager execution cannot be enabled after TensorFlow APIs have been used to
create or execute graphs. It is typically recommended to invoke this function
at program startup and not in a library (as most libraries should be usable
both with and without eager execution).
Show Example
tf.compat.v1.enable_eager_execution() # After eager execution is enabled, operations are executed as they are # defined and Tensor objects hold concrete values, which can be accessed as # numpy.ndarray`s through the numpy() method. assert tf.multiply(6, 7).numpy() == 42
PythonFunctionContainer enable_tensor_equality_fn get;
Compare Tensors with element-wise comparison and thus be unhashable. Comparing tensors with element-wise allows comparisons such as
tf.Variable(1.0) == 1.0. Element-wise equality implies that tensors are
unhashable. Thus tensors can no longer be directly used in sets or as a key in
a dictionary.
PythonFunctionContainer enable_v2_behavior_fn get;
Enables TensorFlow 2.x behaviors. This function can be called at the beginning of the program (before `Tensors`,
`Graphs` or other structures have been created, and before devices have been
initialized. It switches all global behaviors that are different between
TensorFlow 1.x and 2.x to behave as intended for 2.x. This function is called in the main TensorFlow `__init__.py` file, user should
not need to call it, except during complex migrations.
PythonFunctionContainer enable_v2_tensorshape_fn get;
In TensorFlow 2.0, iterating over a TensorShape instance returns values. This enables the new behavior. Concretely, `tensor_shape[i]` returned a Dimension instance in V1, but
it V2 it returns either an integer, or None. Examples: ```
#######################
# If you had this in V1:
value = tensor_shape[i].value # Do this in V2 instead:
value = tensor_shape[i] #######################
# If you had this in V1:
for dim in tensor_shape:
value = dim.value
print(value) # Do this in V2 instead:
for value in tensor_shape:
print(value) #######################
# If you had this in V1:
dim = tensor_shape[i]
dim.assert_is_compatible_with(other_shape) # or using any other shape method # Do this in V2 instead:
if tensor_shape.rank is None:
dim = Dimension(None)
else:
dim = tensor_shape.dims[i]
dim.assert_is_compatible_with(other_shape) # or using any other shape method # The V2 suggestion above is more explicit, which will save you from
# the following trap (present in V1):
# you might do in-place modifications to `dim` and expect them to be reflected
# in `tensor_shape[i]`, but they would not be.
```
PythonFunctionContainer encode_base64_fn get;
Encode strings into web-safe base64 format. Refer to the following article for more information on base64 format:
en.wikipedia.org/wiki/Base64. Base64 strings may have padding with '=' at the
end so that the encoded has length multiple of 4. See Padding section of the
link above. Web-safe means that the encoder uses - and _ instead of + and /.
PythonFunctionContainer equal_fn get;
Returns the truth value of (x == y) element-wise. Usage:
**NOTE**: `Equal` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
Show Example
x = tf.constant([2, 4])
y = tf.constant(2)
tf.math.equal(x, y) ==> array([True, False]) x = tf.constant([2, 4])
y = tf.constant([2, 4])
tf.math.equal(x, y) ==> array([True, True])
PythonFunctionContainer erf_fn get;
Computes the Gauss error function of `x` element-wise.
PythonFunctionContainer erfc_fn get;
Computes the complementary error function of `x` element-wise.
PythonFunctionContainer executing_eagerly_fn get;
Returns True if the current thread has eager execution enabled. Eager execution is typically enabled via
`tf.compat.v1.enable_eager_execution`, but may also be enabled within the
context of a Python function via tf.contrib.eager.py_func.
PythonFunctionContainer exp_fn get;
Computes exponential of x element-wise. \\(y = e^x\\). This function computes the exponential of every element in the input tensor.
i.e. `exp(x)` or `e^(x)`, where `x` is the input tensor.
`e` denotes Euler's number and is approximately equal to 2.718281.
Output is positive for any real input.
For complex numbers, the exponential value is calculated as follows: ```
e^(x+iy) = e^x * e^iy = e^x * (cos y + i sin y)
``` Let's consider complex number 1+1j as an example.
e^1 * (cos 1 + i sin 1) = 2.7182818284590 * (0.54030230586+0.8414709848j)
Show Example
x = tf.constant(2.0)
tf.math.exp(x) ==> 7.389056 x = tf.constant([2.0, 8.0])
tf.math.exp(x) ==> array([7.389056, 2980.958], dtype=float32)
PythonFunctionContainer expand_dims_fn get;
Inserts a dimension of 1 into a tensor's shape. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(dim)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation inserts a dimension of 1 at the
dimension index `axis` of `input`'s shape. The dimension index `axis` starts
at zero; if you specify a negative number for `axis` it is counted backward
from the end. This operation is useful if you want to add a batch dimension to a single
element. For example, if you have a single image of shape `[height, width,
channels]`, you can make it a batch of 1 image with `expand_dims(image, 0)`,
which will make the shape `[1, height, width, channels]`. Other examples:
This operation requires that: `-1-input.dims() <= dim <= input.dims()` This operation is related to `squeeze()`, which removes dimensions of
size 1.
Show Example
# 't' is a tensor of shape [2]
tf.shape(tf.expand_dims(t, 0)) # [1, 2]
tf.shape(tf.expand_dims(t, 1)) # [2, 1]
tf.shape(tf.expand_dims(t, -1)) # [2, 1] # 't2' is a tensor of shape [2, 3, 5]
tf.shape(tf.expand_dims(t2, 0)) # [1, 2, 3, 5]
tf.shape(tf.expand_dims(t2, 2)) # [2, 3, 1, 5]
tf.shape(tf.expand_dims(t2, 3)) # [2, 3, 5, 1]
PythonFunctionContainer expm1_fn get;
Computes `exp(x) - 1` element-wise. i.e. `exp(x) - 1` or `e^(x) - 1`, where `x` is the input tensor.
`e` denotes Euler's number and is approximately equal to 2.718281.
Show Example
x = tf.constant(2.0)
tf.math.expm1(x) ==> 6.389056 x = tf.constant([2.0, 8.0])
tf.math.expm1(x) ==> array([6.389056, 2979.958], dtype=float32) x = tf.constant(1 + 1j)
tf.math.expm1(x) ==> (0.46869393991588515+2.2873552871788423j)
PythonFunctionContainer extract_image_patches_fn get;
Extract `patches` from `images` and put them in the "depth" output dimension.
PythonFunctionContainer extract_volume_patches_fn get;
Extract `patches` from `input` and put them in the "depth" output dimension. 3D extension of `extract_image_patches`.
PythonFunctionContainer eye_fn get;
Construct an identity matrix, or a batch of matrices.
Show Example
# Construct one identity matrix.
tf.eye(2)
==> [[1., 0.],
[0., 1.]] # Construct a batch of 3 identity matricies, each 2 x 2.
# batch_identity[i, :, :] is a 2 x 2 identity matrix, i = 0, 1, 2.
batch_identity = tf.eye(2, batch_shape=[3]) # Construct one 2 x 3 "identity" matrix
tf.eye(2, num_columns=3)
==> [[ 1., 0., 0.],
[ 0., 1., 0.]]
PythonFunctionContainer fake_quant_with_min_max_args_fn get;
Fake-quantize the 'inputs' tensor, type float to 'outputs' tensor of same type. Attributes `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. Quantization is called fake since the output is still in floating point.
PythonFunctionContainer fake_quant_with_min_max_args_gradient_fn get;
Compute gradients for a FakeQuantWithMinMaxArgs operation.
PythonFunctionContainer fake_quant_with_min_max_vars_fn get;
Fake-quantize the 'inputs' tensor of type float via global float scalars `min` and `max` to 'outputs' tensor of same shape as `inputs`. `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. This operation has a gradient and thus allows for training `min` and `max`
values.
PythonFunctionContainer fake_quant_with_min_max_vars_gradient_fn get;
Compute gradients for a FakeQuantWithMinMaxVars operation.
PythonFunctionContainer fake_quant_with_min_max_vars_per_channel_fn get;
Fake-quantize the 'inputs' tensor of type float and one of the shapes: `[d]`, `[b, d]` `[b, h, w, d]` via per-channel floats `min` and `max` of shape `[d]`
to 'outputs' tensor of same shape as `inputs`. `[min; max]` define the clamping range for the `inputs` data.
`inputs` values are quantized into the quantization range (`[0; 2^num_bits - 1]`
when `narrow_range` is false and `[1; 2^num_bits - 1]` when it is true) and
then de-quantized and output as floats in `[min; max]` interval.
`num_bits` is the bitwidth of the quantization; between 2 and 16, inclusive. Before quantization, `min` and `max` values are adjusted with the following
logic.
It is suggested to have `min <= 0 <= max`. If `0` is not in the range of values,
the behavior can be unexpected:
If `0 < min < max`: `min_adj = 0` and `max_adj = max - min`.
If `min < max < 0`: `min_adj = min - max` and `max_adj = 0`.
If `min <= 0 <= max`: `scale = (max - min) / (2^num_bits - 1) `,
`min_adj = scale * round(min / scale)` and `max_adj = max + min_adj - min`. This operation has a gradient and thus allows for training `min` and `max`
values.
PythonFunctionContainer fake_quant_with_min_max_vars_per_channel_gradient_fn get;
Compute gradients for a FakeQuantWithMinMaxVarsPerChannel operation.
PythonFunctionContainer feature_usage_counts_fn get;
PythonFunctionContainer fertile_stats_deserialize_fn get;
PythonFunctionContainer fertile_stats_is_initialized_op_fn get;
PythonFunctionContainer fertile_stats_resource_handle_op_fn get;
PythonFunctionContainer fertile_stats_serialize_fn get;
PythonFunctionContainer fft_fn get;
Fast Fourier transform. Computes the 1-dimensional discrete Fourier transform over the inner-most
dimension of `input`.
PythonFunctionContainer fft2d_fn get;
2D fast Fourier transform. Computes the 2-dimensional discrete Fourier transform over the inner-most
2 dimensions of `input`.
PythonFunctionContainer fft3d_fn get;
3D fast Fourier transform. Computes the 3-dimensional discrete Fourier transform over the inner-most 3
dimensions of `input`.
PythonFunctionContainer fill_fn get;
Creates a tensor filled with a scalar value. This operation creates a tensor of shape `dims` and fills it with `value`. For example: ```
# Output tensor has shape [2, 3].
fill([2, 3], 9) ==> [[9, 9, 9]
[9, 9, 9]]
```
tf.fill differs from tf.constant in a few ways: * tf.fill only supports scalar contents, whereas tf.constant supports
Tensor values.
* tf.fill creates an Op in the computation graph that constructs the
actual
Tensor value at runtime. This is in contrast to tf.constant which embeds
the entire Tensor into the graph with a `Const` node.
* Because tf.fill evaluates at graph runtime, it supports dynamic shapes
based on other runtime Tensors, unlike tf.constant.
PythonFunctionContainer finalize_tree_fn get;
PythonFunctionContainer fingerprint_fn get;
Generates fingerprint values. Generates fingerprint values of `data`. Fingerprint op considers the first dimension of `data` as the batch dimension,
and `output[i]` contains the fingerprint value generated from contents in
`data[i,...]` for all `i`. Fingerprint op writes fingerprint values as byte arrays. For example, the
default method `farmhash64` generates a 64-bit fingerprint value at a time.
This 8-byte value is written out as an
tf.uint8 array of size 8, in
little-endian order. For example, suppose that `data` has data type tf.int32 and shape (2, 3, 4),
and that the fingerprint method is `farmhash64`. In this case, the output
shape is (2, 8), where 2 is the batch dimension size of `data`, and 8 is the
size of each fingerprint value in bytes. `output[0, :]` is generated from
12 integers in `data[0, :, :]` and similarly `output[1, :]` is generated from
other 12 integers in `data[1, :, :]`. Note that this op fingerprints the raw underlying buffer, and it does not
fingerprint Tensor's metadata such as data type and/or shape. For example, the
fingerprint values are invariant under reshapes and bitcasts as long as the
batch dimension remain the same:
For string data, one should expect `tf.fingerprint(data) !=
tf.fingerprint(tf.string.reduce_join(data))` in general.
Show Example
tf.fingerprint(data) == tf.fingerprint(tf.reshape(data,...))
tf.fingerprint(data) == tf.fingerprint(tf.bitcast(data,...))
PythonFunctionContainer five_float_outputs_fn get;
PythonFunctionContainer fixed_size_partitioner_fn get;
Partitioner to specify a fixed number of shards along given axis.
PythonFunctionContainer float_input_fn get;
PythonFunctionContainer float_output_fn get;
PythonFunctionContainer float_output_string_output_fn get;
DType float16 get; set;
DType float32 get; set;
DType float64 get; set;
PythonFunctionContainer floor_div_fn get;
Returns x // y element-wise. *NOTE*: `floor_div` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer floor_fn get;
Returns element-wise largest integer not greater than x.
PythonFunctionContainer floordiv_fn get;
Divides `x / y` elementwise, rounding toward the most negative integer. The same as `tf.compat.v1.div(x,y)` for integers, but uses
`tf.floor(tf.compat.v1.div(x,y))` for
floating point arguments so that the result is always an integer (though
possibly an integer represented as floating point). This op is generated by
`x // y` floor division in Python 3 and in Python 2.7 with
`from __future__ import division`. `x` and `y` must have the same type, and the result will have the same type
as well.
PythonFunctionContainer foldl_fn get;
foldl on the list of tensors unpacked from `elems` on dimension 0. This foldl operator repeatedly applies the callable `fn` to a sequence
of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
PythonFunctionContainer foldr_fn get;
foldr on the list of tensors unpacked from `elems` on dimension 0. This foldr operator repeatedly applies the callable `fn` to a sequence
of elements from last to first. The elements are made of the tensors
unpacked from `elems`. The callable fn takes two tensors as arguments.
The first argument is the accumulated value computed from the preceding
invocation of fn, and the second is the value at the current position of
`elems`. If `initializer` is None, `elems` must contain at least one element,
and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `fn(initializer, values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`.
PythonFunctionContainer foo1_fn get;
PythonFunctionContainer foo2_fn get;
PythonFunctionContainer foo3_fn get;
PythonFunctionContainer func_attr_fn get;
PythonFunctionContainer func_list_attr_fn get;
PythonFunctionContainer function_fn get;
Creates a callable TensorFlow graph from a Python function. `function` constructs a callable that executes a TensorFlow graph
(
tf.Graph) created by tracing the TensorFlow operations in `func`.
This allows the TensorFlow runtime to apply optimizations and exploit
parallelism in the computation defined by `func`. _Example Usage_
Note that unlike other TensorFlow operations, we don't convert python
numerical inputs to tensors. Moreover, a new graph is generated for each
distinct python numerical value, for example calling `g(2)` and `g(3)` will
generate two new graphs (while only one is generated if you call
`g(tf.constant(2))` and `g(tf.constant(3))`). Therefore, python numerical
inputs should be restricted to arguments that will have few distinct values,
such as hyperparameters like the number of layers in a neural network. This
allows TensorFlow to optimize each variant of the neural network. _Referencing tf.Variables_ The Python function `func` may reference stateful objects (such as
tf.Variable).
These are captured as implicit inputs to the callable returned by `function`.
`function` can be applied to methods of an object.
_Usage with tf.keras_ The `call` methods of a tf.keras.Model subclass can be decorated with
`function` in order to apply graph execution optimizations on it.
_Input Signatures_ `function` instantiates a separate graph for every unique set of input
shapes and datatypes. For example, the following code snippet will result
in three distinct graphs being traced, as each input has a different
shape.
An "input signature" can be optionally provided to `function` to control
the graphs traced. The input signature specifies the shape and type of each
`Tensor` argument to the function using a tf.TensorSpec object. For example,
the following code snippet ensures that a single graph is created where the
input `Tensor` is required to be a floating point tensor with no restrictions
on shape.
When an `input_signature` is specified, the callable will convert the inputs
to the specified TensorSpecs. _Tracing and staging_ When `autograph` is `True`, all Python control flow that depends on `Tensor`
values is staged into a TensorFlow graph. When `autograph` is `False`, the
function is traced and control flow is not allowed to depend on data. Note that `function` only stages TensorFlow operations, all Python code that
`func` executes and does not depend on data will shape the _construction_ of
the graph.
For example, consider the following:
`add_noise()` will return a different output every time it is invoked.
However, `traced()` will return the same value every time it is called,
since a particular random value generated by the `np.random.randn` call will
be inserted in the traced/staged TensorFlow graph as a constant. In this
particular example, replacing `np.random.randn(5, 5)` with
`tf.random.normal((5, 5))` will result in the same behavior for `add_noise()`
and `traced()`. _Python Side-Effects_ A corollary of the previous discussion on tracing is the following: If a
Python function `func` has Python side-effects, then executing `func` multiple
times may not be semantically equivalent to executing `F = tf.function(func)`
multiple times; this difference is due to the fact that `function` only
captures the subgraph of TensorFlow operations that is constructed when `func`
is invoked to trace a graph. The same is true if code with Python side effects is used inside control flow,
such as a loop. If your code uses side effects that are not intended to
control graph construction, wrap them inside `tf.compat.v1.py_func`. _Retracing_ A single tf.function object might need to map to multiple computation graphs
under the hood. This should be visible only as performance (tracing graphs has
a nonzero computational and memory cost) but should not affect the correctness
of the program. A traced function should return the same result as it would
when run eagerly, assuming no unintended Python side-effects. Calling a tf.function with tensor arguments of different dtypes should lead
to at least one computational graph per distinct set of dtypes. Alternatively,
always calling a tf.function with tensor arguments of the same shapes and
dtypes and the same non-tensor arguments should not lead to additional
retracings of your function. Other than that, TensorFlow reserves the right to retrace functions as many
times as needed, to ensure that traced functions behave as they would when run
eagerly and to provide the best end-to-end performance. For example, the
behavior of how many traces TensorFlow will do when the function is repeatedly
called with different python scalars as arguments is left undefined to allow
for future optimizations. To control the tracing behavior, use the following tools:
- different tf.function objects are guaranteed to not share traces; and
- specifying a signature or using concrete function objects returned from
get_concrete_function() guarantees that only one function graph will be
built.
Show Example
def f(x, y):
return tf.reduce_mean(tf.multiply(x ** 2, 3) + y) g = tf.function(f) x = tf.constant([[2.0, 3.0]])
y = tf.constant([[3.0, -2.0]]) # `f` and `g` will return the same value, but `g` will be executed as a
# TensorFlow graph.
assert f(x, y).numpy() == g(x, y).numpy() # Tensors and tf.Variables used by the Python function are captured in the
# graph.
@tf.function
def h():
return f(x, y) assert (h().numpy() == f(x, y).numpy()).all() # Data-dependent control flow is also captured in the graph. Supported
# control flow statements include `if`, `for`, `while`, `break`, `continue`,
# `return`.
@tf.function
def g(x):
if tf.reduce_sum(x) > 0:
return x * x
else:
return -x // 2 # print and TensorFlow side effects are supported, but exercise caution when
# using Python side effects like mutating objects, saving to files, etc.
l = [] @tf.function
def g(x):
for i in x:
print(i) # Works
tf.compat.v1.assign(v, i) # Works
tf.compat.v1.py_func(lambda i: l.append(i))(i) # Works
l.append(i) # Caution! Doesn't work.
PythonFunctionContainer gather_fn get;
Gather slices from params axis axis according to indices. Gather slices from params axis `axis` according to `indices`. `indices` must
be an integer tensor of any dimension (usually 0-D or 1-D). For 0-D (scalar) `indices`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{5.1em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices, \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. For 1-D (vector) `indices` with `batch_dims=0`: > `output`$$[p_0, ..., p_{axis-1}, \hspace{2.6em}
> i, \hspace{2.6em}
> p_{axis + 1},..., p_{N-1}]$$ =\
> `params`$$[p_0, ..., p_{axis-1}, \hspace{1em}
> indices[i], \hspace{1em}
> p_{axis + 1},..., p_{N-1}]$$. In the general case, produces an output tensor where: $$\begin{align*}
output[p_0, &..., p_{axis-1}, &
&i_{B}, ..., i_{M-1}, &
p_{axis + 1}, &..., p_{N-1}] = \\
params[p_0, &..., p_{axis-1}, &
indices[p_0,..., p_{B-1}, &i_{B},..., i_{M-1}], &
p_{axis + 1}, &..., p_{N-1}]
\end{align*}$$ Where $$N$$=`ndims(params)`, $$M$$=`ndims(indices)`, and $$B$$=`batch_dims`.
Note that params.shape[:batch_dims] must be identical to
indices.shape[:batch_dims]. The shape of the output tensor is: > `output.shape = params.shape[:axis] + indices.shape[batch_dims:] +
> params.shape[axis + 1:]`. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the corresponding
output value. See also

tf.gather_nd. 
PythonFunctionContainer gather_nd_fn get;
Gather slices from `params` into a Tensor with shape specified by `indices`. `indices` is an K-dimensional integer tensor, best thought of as a
(K-1)-dimensional tensor of indices into `params`, where each element defines
a slice of `params`: output[\\(i_0,..., i_{K-2}\\)] = params[indices[\\(i_0,..., i_{K-2}\\)]] Whereas in
tf.gather `indices` defines slices into the first
dimension of `params`, in tf.gather_nd, `indices` defines slices into the
first `N` dimensions of `params`, where `N = indices.shape[-1]`. The last dimension of `indices` can be at most the rank of
`params`: indices.shape[-1] <= params.rank The last dimension of `indices` corresponds to elements
(if `indices.shape[-1] == params.rank`) or slices
(if `indices.shape[-1] < params.rank`) along dimension `indices.shape[-1]`
of `params`. The output tensor has shape indices.shape[:-1] + params.shape[indices.shape[-1]:] Additionally both 'params' and 'indices' can have M leading batch
dimensions that exactly match. In this case 'batch_dims' must be M. Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, a 0 is stored in the
corresponding output value. Some examples below. Simple indexing into a matrix:
Slice indexing into a matrix:
Indexing into a 3-tensor:
The examples below are for the case when only indices have leading extra
dimensions. If both 'params' and 'indices' have leading batch dimensions, use
the 'batch_dims' parameter to run gather_nd in batch mode. Batched indexing into a matrix:
Batched slice indexing into a matrix:
Batched indexing into a 3-tensor:
Examples with batched 'params' and 'indices':
See also tf.gather.
Show Example
indices = [[0, 0], [1, 1]]
params = [['a', 'b'], ['c', 'd']]
output = ['a', 'd']
PythonFunctionContainer gather_tree_fn get;
PythonFunctionContainer get_collection_fn get;
Wrapper for `Graph.get_collection()` using the default graph. See
tf.Graph.get_collection
for more details.
PythonFunctionContainer get_collection_ref_fn get;
Wrapper for `Graph.get_collection_ref()` using the default graph. See
tf.Graph.get_collection_ref
for more details.
PythonFunctionContainer get_default_graph_fn get;
Returns the default graph for the current thread. The returned graph will be the innermost graph on which a
`Graph.as_default()` context has been entered, or a global default
graph if none has been explicitly created. NOTE: The default graph is a property of the current thread. If you
create a new thread, and wish to use the default graph in that
thread, you must explicitly add a `with g.as_default():` in that
thread's function.
PythonFunctionContainer get_default_session__fn get;
PythonFunctionContainer get_local_variable_fn get;
Gets an existing *local* variable or creates a new one. Behavior is the same as in `get_variable`, except that variables are
added to the `LOCAL_VARIABLES` collection and `trainable` is set to
`False`.
This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
PythonFunctionContainer get_logger_fn get;
Return TF logger instance.
PythonFunctionContainer get_seed_fn get;
Returns the local seeds an operation should use given an op-specific seed. Given operation-specific seed, `op_seed`, this helper function returns two
seeds derived from graph-level and op-level seeds. Many random operations
internally use the two seeds to allow user to change the seed globally for a
graph, or for only specific operations. For details on how the graph-level seed interacts with op seeds, see
`tf.compat.v1.random.set_random_seed`.
PythonFunctionContainer get_session_handle_fn get;
Return the handle of `data`. This is EXPERIMENTAL and subject to change. Keep `data` "in-place" in the runtime and create a handle that can be
used to retrieve `data` in a subsequent run(). Combined with `get_session_tensor`, we can keep a tensor produced in
one run call in place, and use it as the input in a future run call.
PythonFunctionContainer get_session_tensor_fn get;
Get the tensor of type `dtype` by feeding a tensor handle. This is EXPERIMENTAL and subject to change. Get the value of the tensor from a tensor handle. The tensor
is produced in a previous run() and stored in the state of the
session.
PythonFunctionContainer get_static_value_fn get;
Returns the constant value of the given tensor, if efficiently calculable. This function attempts to partially evaluate the given tensor, and
returns its value as a numpy ndarray if this succeeds. Compatibility(V1): If `constant_value(tensor)` returns a non-`None` result, it
will no longer be possible to feed a different value for `tensor`. This allows
the result of this function to influence the graph that is constructed, and
permits static shape optimizations.
PythonFunctionContainer get_variable_fn get;
Gets an existing variable with these parameters or create a new one. This function prefixes the name with the current variable scope
and performs reuse checks. See the
[Variable Scope How To](https://tensorflow.org/guide/variables)
for an extensive description of how reusing works. Here is a basic example:
If initializer is `None` (the default), the default initializer passed in
the variable scope will be used. If that one is `None` too, a
`glorot_uniform_initializer` will be used. The initializer can also be
a Tensor, in which case the variable is initialized to this value and shape. Similarly, if the regularizer is `None` (the default), the default regularizer
passed in the variable scope will be used (if that is `None` too,
then by default no regularization is performed). If a partitioner is provided, a `PartitionedVariable` is returned.
Accessing this object as a `Tensor` returns the shards concatenated along
the partition axis. Some useful partitioners are available. See, e.g.,
`variable_axis_size_partitioner` and `min_max_variable_partitioner`.
Show Example
def foo():
with tf.variable_scope("foo", reuse=tf.AUTO_REUSE):
v = tf.get_variable("v", [1])
return v v1 = foo() # Creates v.
v2 = foo() # Gets the same, existing v.
assert v1 == v2
PythonFunctionContainer get_variable_scope_fn get;
Returns the current variable scope.
PythonFunctionContainer global_norm_fn get;
Computes the global norm of multiple tensors. Given a tuple or list of tensors `t_list`, this operation returns the
global norm of the elements in all tensors in `t_list`. The global norm is
computed as: `global_norm = sqrt(sum([l2norm(t)**2 for t in t_list]))` Any entries in `t_list` that are of type None are ignored.
PythonFunctionContainer global_variables_fn get;
Returns global variables. Global variables are variables that are shared across machines in a
distributed environment. The `Variable()` constructor or `get_variable()`
automatically adds new variables to the graph collection
`GraphKeys.GLOBAL_VARIABLES`.
This convenience function returns the contents of that collection. An alternative to global variables are local variables. See
`tf.compat.v1.local_variables`
PythonFunctionContainer global_variables_initializer_fn get;
Returns an Op that initializes global variables. This is just a shortcut for `variables_initializer(global_variables())`
PythonFunctionContainer grad_pass_through_fn get;
Creates a grad-pass-through op with the forward behavior provided in f. Use this function to wrap any op, maintaining its behavior in the forward
pass, but replacing the original op in the backward graph with an identity.
Another example is a 'differentiable' moving average approximation, where
gradients are allowed to flow into the last value fed to the moving average,
but the moving average is still used for the forward pass:
Show Example
x = tf.Variable(1.0, name="x")
z = tf.Variable(3.0, name="z") with tf.GradientTape() as tape:
# y will evaluate to 9.0
y = tf.grad_pass_through(x.assign)(z**2)
# grads will evaluate to 6.0
grads = tape.gradient(y, z)
PythonFunctionContainer gradient_trees_partition_examples_fn get;
PythonFunctionContainer gradient_trees_prediction_fn get;
PythonFunctionContainer gradient_trees_prediction_verbose_fn get;
PythonFunctionContainer gradients_fn get;
Constructs symbolic derivatives of sum of `ys` w.r.t. x in `xs`. `ys` and `xs` are each a `Tensor` or a list of tensors. `grad_ys`
is a list of `Tensor`, holding the gradients received by the
`ys`. The list must be the same length as `ys`. `gradients()` adds ops to the graph to output the derivatives of `ys` with
respect to `xs`. It returns a list of `Tensor` of length `len(xs)` where
each tensor is the `sum(dy/dx)` for y in `ys`. `grad_ys` is a list of tensors of the same length as `ys` that holds
the initial gradients for each y in `ys`. When `grad_ys` is None,
we fill in a tensor of '1's of the shape of y for each y in `ys`. A
user can provide their own initial `grad_ys` to compute the
derivatives using a different initial gradient for each y (e.g., if
one wanted to weight the gradient differently for each value in
each y). `stop_gradients` is a `Tensor` or a list of tensors to be considered constant
with respect to all `xs`. These tensors will not be backpropagated through,
as though they had been explicitly disconnected using `stop_gradient`. Among
other things, this allows computation of partial derivatives as opposed to
total derivatives.
Here the partial derivatives `g` evaluate to `[1.0, 1.0]`, compared to the
total derivatives `tf.gradients(a + b, [a, b])`, which take into account the
influence of `a` on `b` and evaluate to `[3.0, 1.0]`. Note that the above is
equivalent to:
`stop_gradients` provides a way of stopping gradient after the graph has
already been constructed, as compared to
tf.stop_gradient which is used
during graph construction. When the two approaches are combined,
backpropagation stops at both tf.stop_gradient nodes and nodes in
`stop_gradients`, whichever is encountered first. All integer tensors are considered constant with respect to all `xs`, as if
they were included in `stop_gradients`. `unconnected_gradients` determines the value returned for each x in xs if it
is unconnected in the graph to ys. By default this is None to safeguard
against errors. MAthematically these gradients are zero which can be requested
using the `'zero'` option. tf.UnconnectedGradients provides the
following options and behaviors:
Show Example
a = tf.constant(0.)
b = 2 * a
g = tf.gradients(a + b, [a, b], stop_gradients=[a, b])
PythonFunctionContainer graph_def_version_fn get;
PythonFunctionContainer greater_equal_fn get;
PythonFunctionContainer greater_fn get;
PythonFunctionContainer group_fn get;
Create an op that groups multiple operations. When this op finishes, all ops in `inputs` have finished. This op has no
output. See also
tf.tuple and
tf.control_dependencies.
PythonFunctionContainer grow_tree_ensemble_fn get;
PythonFunctionContainer grow_tree_v4_fn get;
PythonFunctionContainer guarantee_const_fn get;
Gives a guarantee to the TF runtime that the input tensor is a constant. The runtime is then free to make optimizations based on this. Only accepts value typed tensors as inputs and rejects resource variable handles
as input. Returns the input tensor without modification.
PythonFunctionContainer hard_routing_function_fn get;
PythonFunctionContainer hessians_fn get;
Constructs the Hessian of sum of `ys` with respect to `x` in `xs`. `hessians()` adds ops to the graph to output the Hessian matrix of `ys`
with respect to `xs`. It returns a list of `Tensor` of length `len(xs)`
where each tensor is the Hessian of `sum(ys)`. The Hessian is a matrix of second-order partial derivatives of a scalar
tensor (see https://en.wikipedia.org/wiki/Hessian_matrix for more details).
PythonFunctionContainer histogram_fixed_width_bins_fn get;
Bins the given values for use in a histogram. Given the tensor `values`, this operation returns a rank 1 `Tensor`
representing the indices of a histogram into which each element
of `values` would be binned. The bins are equal width and
determined by the arguments `value_range` and `nbins`.
PythonFunctionContainer histogram_fixed_width_fn get;
Return histogram of values. Given the tensor `values`, this operation returns a rank 1 histogram counting
the number of entries in `values` that fell into every bin. The bins are
equal width and determined by the arguments `value_range` and `nbins`.
PythonFunctionContainer identity_fn get;
Return a tensor with the same shape and contents as input.
Show Example
import tensorflow as tf
val0 = tf.ones((1,), dtype=tf.float32)
a = tf.atan2(val0, val0)
a_identity = tf.identity(a)
print(a.numpy()) #[0.7853982]
print(a_identity.numpy()) #[0.7853982]
PythonFunctionContainer identity_n_fn get;
Returns a list of tensors with the same shapes and contents as the input tensors. This op can be used to override the gradient for complicated functions. For
example, suppose y = f(x) and we wish to apply a custom function g for backprop
such that dx = g(dy). In Python,
Show Example
with tf.get_default_graph().gradient_override_map(
{'IdentityN': 'OverrideGradientWithG'}):
y, _ = identity_n([f(x), x]) @tf.RegisterGradient('OverrideGradientWithG')
def ApplyG(op, dy, _):
return [None, g(dy)] # Do not backprop to f(x).
PythonFunctionContainer ifft_fn get;
Inverse fast Fourier transform. Computes the inverse 1-dimensional discrete Fourier transform over the
inner-most dimension of `input`.
PythonFunctionContainer ifft2d_fn get;
Inverse 2D fast Fourier transform. Computes the inverse 2-dimensional discrete Fourier transform over the
inner-most 2 dimensions of `input`.
PythonFunctionContainer ifft3d_fn get;
Inverse 3D fast Fourier transform. Computes the inverse 3-dimensional discrete Fourier transform over the
inner-most 3 dimensions of `input`.
PythonFunctionContainer igamma_fn get;
Compute the lower regularized incomplete Gamma function `P(a, x)`. The lower regularized incomplete Gamma function is defined as: \\(P(a, x) = gamma(a, x) / Gamma(a) = 1 - Q(a, x)\\) where \\(gamma(a, x) = \\int_{0}^{x} t^{a-1} exp(-t) dt\\) is the lower incomplete Gamma function. Note, above `Q(a, x)` (`Igammac`) is the upper regularized complete
Gamma function.
PythonFunctionContainer igammac_fn get;
Compute the upper regularized incomplete Gamma function `Q(a, x)`. The upper regularized incomplete Gamma function is defined as: \\(Q(a, x) = Gamma(a, x) / Gamma(a) = 1 - P(a, x)\\) where \\(Gamma(a, x) = int_{x}^{\infty} t^{a-1} exp(-t) dt\\) is the upper incomplete Gama function. Note, above `P(a, x)` (`Igamma`) is the lower regularized complete
Gamma function.
PythonFunctionContainer imag_fn get;
Returns the imaginary part of a complex (or real) tensor. Given a tensor `input`, this operation returns a tensor of type `float` that
is the imaginary part of each element in `input` considered as a complex
number. If `input` is real, a tensor of all zeros is returned.
Show Example
x = tf.constant([-2.25 + 4.75j, 3.25 + 5.75j])
tf.math.imag(x) # [4.75, 5.75]
PythonFunctionContainer image_connected_components_fn get;
PythonFunctionContainer image_projective_transform_fn get;
PythonFunctionContainer image_projective_transform_v2_fn get;
PythonFunctionContainer import_graph_def_fn get;
Imports the graph from `graph_def` into the current default `Graph`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(op_dict)`. They will be removed in a future version.
Instructions for updating:
Please file an issue at https://github.com/tensorflow/tensorflow/issues if you depend on this feature. This function provides a way to import a serialized TensorFlow
[`GraphDef`](https://www.tensorflow.org/code/tensorflow/core/framework/graph.proto)
protocol buffer, and extract individual objects in the `GraphDef` as
tf.Tensor and tf.Operation objects. Once extracted,
these objects are placed into the current default `Graph`. See
tf.Graph.as_graph_def for a way to create a `GraphDef`
proto.
PythonFunctionContainer in_polymorphic_twice_fn get;
PythonFunctionContainer init_scope_fn get;
A context manager that lifts ops out of control-flow scopes and function-building graphs. There is often a need to lift variable initialization ops out of control-flow
scopes, function-building graphs, and gradient tapes. Entering an
`init_scope` is a mechanism for satisfying these desiderata. In particular,
entering an `init_scope` has three effects: (1) All control dependencies are cleared the moment the scope is entered;
this is equivalent to entering the context manager returned from
`control_dependencies(None)`, which has the side-effect of exiting
control-flow scopes like
tf.cond and tf.while_loop. (2) All operations that are created while the scope is active are lifted
into the lowest context on the `context_stack` that is not building a
graph function. Here, a context is defined as either a graph or an eager
context. Every context switch, i.e., every installation of a graph as
the default graph and every switch into eager mode, is logged in a
thread-local stack called `context_switches`; the log entry for a
context switch is popped from the stack when the context is exited.
Entering an `init_scope` is equivalent to crawling up
`context_switches`, finding the first context that is not building a
graph function, and entering it. A caveat is that if graph mode is
enabled but the default graph stack is empty, then entering an
`init_scope` will simply install a fresh graph as the default one. (3) The gradient tape is paused while the scope is active. When eager execution is enabled, code inside an init_scope block runs with
eager execution enabled even when defining graph functions via
tf.contrib.eager.defun.
Show Example
tf.compat.v1.enable_eager_execution() @tf.contrib.eager.defun
def func():
# A defun-decorated function constructs TensorFlow graphs,
# it does not execute eagerly.
assert not tf.executing_eagerly()
with tf.init_scope():
# Initialization runs with eager execution enabled
assert tf.executing_eagerly()
PythonFunctionContainer initialize_all_tables_fn get;
Returns an Op that initializes all tables of the default graph. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.tables_initializer instead.
PythonFunctionContainer initialize_all_variables_fn get;
See `tf.compat.v1.global_variables_initializer`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Use
tf.global_variables_initializer instead. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
PythonFunctionContainer initialize_local_variables_fn get;
See `tf.compat.v1.local_variables_initializer`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Use
tf.local_variables_initializer instead. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
PythonFunctionContainer initialize_variables_fn get;
See `tf.compat.v1.variables_initializer`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2017-03-02.
Instructions for updating:
Use
tf.variables_initializer instead. **NOTE** The output of this function should be used. If it is not, a warning will be logged. To mark the output as used, call its.mark_used() method.
PythonFunctionContainer int_attr_fn get;
PythonFunctionContainer int_input_float_input_fn get;
PythonFunctionContainer int_input_fn get;
PythonFunctionContainer int_input_int_output_fn get;
PythonFunctionContainer int_output_float_output_fn get;
PythonFunctionContainer int_output_fn get;
DType int16 get; set;
DType int32 get; set;
DType int64 get; set;
PythonFunctionContainer int64_output_fn get;
DType int8 get; set;
PythonFunctionContainer invert_permutation_fn get;
Computes the inverse permutation of a tensor. This operation computes the inverse of an index permutation. It takes a 1-D
integer tensor `x`, which represents the indices of a zero-based array, and
swaps each value with its index position. In other words, for an output tensor
`y` and an input tensor `x`, this operation computes the following: `y[x[i]] = i for i in [0, 1,..., len(x) - 1]` The values must include 0. There can be no duplicate values or negative values. For example: ```
# tensor `x` is [3, 4, 0, 2, 1]
invert_permutation(x) ==> [2, 4, 3, 0, 1]
```
PythonFunctionContainer is_finite_fn get;
Returns which elements of x are finite.
PythonFunctionContainer is_inf_fn get;
Returns which elements of x are Inf.
PythonFunctionContainer is_nan_fn get;
Returns which elements of x are NaN.
PythonFunctionContainer is_non_decreasing_fn get;
Returns `True` if `x` is non-decreasing. Elements of `x` are compared in row-major order. The tensor `[x[0],...]`
is non-decreasing if for every adjacent pair we have `x[i] <= x[i+1]`.
If `x` has less than two elements, it is trivially non-decreasing. See also: `is_strictly_increasing`
PythonFunctionContainer is_numeric_tensor_fn get;
Returns `True` if the elements of `tensor` are numbers. Specifically, returns `True` if the dtype of `tensor` is one of the following: *
tf.float32
* tf.float64
* tf.int8
* tf.int16
* tf.int32
* tf.int64
* tf.uint8
* tf.qint8
* tf.qint32
* tf.quint8
* tf.complex64 Returns `False` if `tensor` is of a non-numeric type or if `tensor` is not
a tf.Tensor object.
PythonFunctionContainer is_strictly_increasing_fn get;
Returns `True` if `x` is strictly increasing. Elements of `x` are compared in row-major order. The tensor `[x[0],...]`
is strictly increasing if for every adjacent pair we have `x[i] < x[i+1]`.
If `x` has less than two elements, it is trivially strictly increasing. See also: `is_non_decreasing`
PythonFunctionContainer is_tensor_fn get;
Checks whether `x` is a tensor or "tensor-like". If `is_tensor(x)` returns `True`, it is safe to assume that `x` is a tensor or
can be converted to a tensor using `ops.convert_to_tensor(x)`.
PythonFunctionContainer is_variable_initialized_fn get;
Tests if a variable has been initialized.
PythonFunctionContainer k_feature_gradient_fn get;
PythonFunctionContainer k_feature_routing_function_fn get;
PythonFunctionContainer kernel_label_fn get;
PythonFunctionContainer kernel_label_required_fn get;
PythonFunctionContainer lbeta_fn get;
Computes \\(ln(|Beta(x)|)\\), reducing along the last dimension. Given one-dimensional `z = [z_0,...,z_{K-1}]`, we define $$Beta(z) = \prod_j Gamma(z_j) / Gamma(\sum_j z_j)$$ And for `n + 1` dimensional `x` with shape `[N1,..., Nn, K]`, we define
$$lbeta(x)[i1,..., in] = Log(|Beta(x[i1,..., in, :])|)$$. In other words, the last dimension is treated as the `z` vector. Note that if `z = [u, v]`, then
\\(Beta(z) = int_0^1 t^{u-1} (1 - t)^{v-1} dt\\), which defines the
traditional bivariate beta function. If the last dimension is empty, we follow the convention that the sum over
the empty set is zero, and the product is one.
PythonFunctionContainer less_equal_fn get;
PythonFunctionContainer less_fn get;
PythonFunctionContainer lgamma_fn get;
Computes the log of the absolute value of `Gamma(x)` element-wise.
PythonFunctionContainer linspace_fn get;
Generates values in an interval. A sequence of `num` evenly-spaced values are generated beginning at `start`.
If `num > 1`, the values in the sequence increase by `stop - start / num - 1`,
so that the last one is exactly `stop`. For example: ```
tf.linspace(10.0, 12.0, 3, name="linspace") => [ 10.0 11.0 12.0]
```
PythonFunctionContainer list_input_fn get;
PythonFunctionContainer list_output_fn get;
PythonFunctionContainer load_file_system_library_fn get;
Loads a TensorFlow plugin, containing file system implementation. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.load_library instead. Pass `library_filename` to a platform-specific mechanism for dynamically
loading a library. The rules for determining the exact location of the
library are platform-specific and are not documented here.
PythonFunctionContainer load_library_fn get;
Loads a TensorFlow plugin. "library_location" can be a path to a specific shared object, or a folder.
If it is a folder, all shared objects that are named "libtfkernel*" will be
loaded. When the library is loaded, kernels registered in the library via the
`REGISTER_*` macros are made available in the TensorFlow process.
PythonFunctionContainer load_op_library_fn get;
Loads a TensorFlow plugin, containing custom ops and kernels. Pass "library_filename" to a platform-specific mechanism for dynamically
loading a library. The rules for determining the exact location of the
library are platform-specific and are not documented here. When the
library is loaded, ops and kernels registered in the library via the
`REGISTER_*` macros are made available in the TensorFlow process. Note
that ops with the same name as an existing op are rejected and not
registered with the process.
PythonFunctionContainer local_variables_fn get;
Returns local variables. Local variables - per process variables, usually not saved/restored to
checkpoint and used for temporary or intermediate values.
For example, they can be used as counters for metrics computation or
number of epochs this machine has read data.
The `tf.contrib.framework.local_variable()` function automatically adds the
new variable to `GraphKeys.LOCAL_VARIABLES`.
This convenience function returns the contents of that collection. An alternative to local variables are global variables. See
`tf.compat.v1.global_variables`
PythonFunctionContainer local_variables_initializer_fn get;
Returns an Op that initializes all local variables. This is just a shortcut for `variables_initializer(local_variables())`
PythonFunctionContainer log_fn get;
Computes natural logarithm of x element-wise. I.e., \\(y = \log_e x\\).
PythonFunctionContainer log_sigmoid_fn get;
Computes log sigmoid of `x` element-wise. Specifically, `y = log(1 / (1 + exp(-x)))`. For numerical stability,
we use `y = -tf.nn.softplus(-x)`.
PythonFunctionContainer log1p_fn get;
Computes natural logarithm of (1 + x) element-wise. I.e., \\(y = \log_e (1 + x)\\).
PythonFunctionContainer logical_and_fn get;
Returns the truth value of x AND y element-wise. *NOTE*: `math.logical_and` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer logical_not_fn get;
PythonFunctionContainer logical_or_fn get;
Returns the truth value of x OR y element-wise. *NOTE*: `math.logical_or` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer logical_xor_fn get;
Logical XOR function. x ^ y = (x | y) & ~(x & y) Inputs are tensor and if the tensors contains more than one element, an
element-wise logical XOR is computed. Usage:
Show Example
x = tf.constant([False, False, True, True], dtype = tf.bool)
y = tf.constant([False, True, False, True], dtype = tf.bool)
z = tf.logical_xor(x, y, name="LogicalXor")
# here z = [False True True False]
PythonFunctionContainer make_ndarray_fn get;
Create a numpy ndarray from a tensor. Create a numpy ndarray with the same shape and data as the tensor.
PythonFunctionContainer make_quantile_summaries_fn get;
PythonFunctionContainer make_template_fn get;
Given an arbitrary function, wrap it so that it does variable sharing. This wraps `func_` in a Template and partially evaluates it. Templates are
functions that create variables the first time they are called and reuse them
thereafter. In order for `func_` to be compatible with a `Template` it must
have the following properties: * The function should create all trainable variables and any variables that
should be reused by calling `tf.compat.v1.get_variable`. If a trainable
variable is
created using
tf.Variable, then a ValueError will be thrown. Variables
that are intended to be locals can be created by specifying
`tf.Variable(..., trainable=false)`.
* The function may use variable scopes and other templates internally to
create and reuse variables, but it shouldn't use
`tf.compat.v1.global_variables` to
capture variables that are defined outside of the scope of the function.
* Internal scopes and variable names should not depend on any arguments that
are not supplied to `make_template`. In general you will get a ValueError
telling you that you are trying to reuse a variable that doesn't exist
if you make a mistake. In the following example, both `z` and `w` will be scaled by the same `y`. It
is important to note that if we didn't assign `scalar_name` and used a
different name for z and w that a `ValueError` would be thrown because it
couldn't reuse the variable.
As a safe-guard, the returned function will raise a `ValueError` after the
first call if trainable variables are created by calling tf.Variable. If all of these are true, then 2 properties are enforced by the template: 1. Calling the same template multiple times will share all non-local
variables.
2. Two different templates are guaranteed to be unique, unless you reenter the
same variable scope as the initial definition of a template and redefine
it. An examples of this exception:
Depending on the value of `create_scope_now_`, the full variable scope may be
captured either at the time of first call or at the time of construction. If
this option is set to True, then all Tensors created by repeated calls to the
template will have an extra trailing _N+1 to their name, as the first time the
scope is entered in the Template constructor no Tensors are created. Note: `name_`, `func_` and `create_scope_now_` have a trailing underscore to
reduce the likelihood of collisions with kwargs.
Show Example
def my_op(x, scalar_name):
var1 = tf.compat.v1.get_variable(scalar_name,
shape=[],
initializer=tf.compat.v1.constant_initializer(1))
return x * var1 scale_by_y = tf.compat.v1.make_template('scale_by_y', my_op, scalar_name='y') z = scale_by_y(input1)
w = scale_by_y(input2)
PythonFunctionContainer make_tensor_proto_fn get;
Create a TensorProto. In TensorFlow 2.0, representing tensors as protos should no longer be a
common workflow. That said, this utility function is still useful for
generating TF Serving request protos: request = tensorflow_serving.apis.predict_pb2.PredictRequest()
request.model_spec.name = "my_model"
request.model_spec.signature_name = "serving_default"
request.inputs["images"].CopyFrom(tf.make_tensor_proto(X_new)) make_tensor_proto accepts "values" of a python scalar, a python list, a
numpy ndarray, or a numpy scalar. If "values" is a python scalar or a python list, make_tensor_proto
first convert it to numpy ndarray. If dtype is None, the
conversion tries its best to infer the right numpy data
type. Otherwise, the resulting numpy array has a compatible data
type with the given dtype. In either case above, the numpy ndarray (either the caller provided
or the auto converted) must have the compatible type with dtype. make_tensor_proto then converts the numpy array to a tensor proto. If "shape" is None, the resulting tensor proto represents the numpy
array precisely. Otherwise, "shape" specifies the tensor's shape and the numpy array
can not have more elements than what "shape" specifies.
PythonFunctionContainer map_fn_fn get;
map on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `map_fn` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the
tensors unpacked from `elems`. `dtype` is the data type of the return
value of `fn`. Users must provide `dtype` if it is different from
the data type of `elems`. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[values.shape[0]] + fn(values[0]).shape`. This method also allows multi-arity `elems` and output of `fn`. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The signature of `fn` may
match the structure of `elems`. That is, if `elems` is
`(t1, [t2, t3, [t4, t5]])`, then an appropriate signature for `fn` is:
`fn = lambda (t1, [t2, t3, [t4, t5]]):`. Furthermore, `fn` may emit a different structure than its input. For example,
`fn` may look like: `fn = lambda t1: return (t1 + 1, t1 - 1)`. In this case,
the `dtype` parameter is not optional: `dtype` must be a type or (possibly
nested) tuple of types matching the output of `fn`. To apply a functional operation to the nonzero elements of a SparseTensor
one of the following methods is recommended. First, if the function is
expressible as TensorFlow ops, use
If, however, the function is not expressible as a TensorFlow op, then use
instead. When executing eagerly, map_fn does not execute in parallel even if
`parallel_iterations` is set to a value > 1. You can still get the
performance benefits of running a function in parallel by using the
tf.contrib.eager.defun decorator,
Note that if you use the defun decorator, any non-TensorFlow Python code
that you may have written in your function won't get executed. See
tf.contrib.eager.defun for more details. The recommendation would be to
debug without defun but switch to defun to get performance benefits of
running map_fn in parallel.
Show Example
result = SparseTensor(input.indices, fn(input.values), input.dense_shape)
PythonFunctionContainer masked_matmul_fn get;
PythonFunctionContainer matching_files_fn get;
Returns the set of files matching one or more glob patterns. Note that this routine only supports wildcard characters in the
basename portion of the pattern, not in the directory portion.
Note also that the order of filenames returned is deterministic.
PythonFunctionContainer matmul_fn get;
Multiplies matrix `a` by matrix `b`, producing `a` * `b`. The inputs must, following any transpositions, be tensors of rank >= 2
where the inner 2 dimensions specify valid matrix multiplication arguments,
and any further outer dimensions match. Both matrices must be of the same type. The supported types are:
`float16`, `float32`, `float64`, `int32`, `complex64`, `complex128`. Either matrix can be transposed or adjointed (conjugated and transposed) on
the fly by setting one of the corresponding flag to `True`. These are `False`
by default. If one or both of the matrices contain a lot of zeros, a more efficient
multiplication algorithm can be used by setting the corresponding
`a_is_sparse` or `b_is_sparse` flag to `True`. These are `False` by default.
This optimization is only available for plain matrices (rank-2 tensors) with
datatypes `bfloat16` or `float32`.
Show Example
# 2-D tensor `a`
# [[1, 2, 3],
# [4, 5, 6]]
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) # 2-D tensor `b`
# [[ 7, 8],
# [ 9, 10],
# [11, 12]]
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) # `a` * `b`
# [[ 58, 64],
# [139, 154]]
c = tf.matmul(a, b) # 3-D tensor `a`
# [[[ 1, 2, 3],
# [ 4, 5, 6]],
# [[ 7, 8, 9],
# [10, 11, 12]]]
a = tf.constant(np.arange(1, 13, dtype=np.int32),
shape=[2, 2, 3]) # 3-D tensor `b`
# [[[13, 14],
# [15, 16],
# [17, 18]],
# [[19, 20],
# [21, 22],
# [23, 24]]]
b = tf.constant(np.arange(13, 25, dtype=np.int32),
shape=[2, 3, 2]) # `a` * `b`
# [[[ 94, 100],
# [229, 244]],
# [[508, 532],
# [697, 730]]]
c = tf.matmul(a, b) # Since python >= 3.5 the @ operator is supported (see PEP 465).
# In TensorFlow, it simply calls the `tf.matmul()` function, so the
# following lines are equivalent:
d = a @ b @ [[10.], [11.]]
d = tf.matmul(tf.matmul(a, b), [[10.], [11.]])
PythonFunctionContainer matrix_band_part_fn get;
Copy a tensor setting everything outside a central band in each innermost matrix to zero. The `band` part is computed as follows:
Assume `input` has `k` dimensions `[I, J, K,..., M, N]`, then the output is a
tensor with the same shape where `band[i, j, k,..., m, n] = in_band(m, n) * input[i, j, k,..., m, n]`. The indicator function `in_band(m, n) = (num_lower < 0 || (m-n) <= num_lower)) &&
(num_upper < 0 || (n-m) <= num_upper)`. For example: ```
# if 'input' is [[ 0, 1, 2, 3]
[-1, 0, 1, 2]
[-2, -1, 0, 1]
[-3, -2, -1, 0]], tf.matrix_band_part(input, 1, -1) ==> [[ 0, 1, 2, 3]
[-1, 0, 1, 2]
[ 0, -1, 0, 1]
[ 0, 0, -1, 0]], tf.matrix_band_part(input, 2, 1) ==> [[ 0, 1, 0, 0]
[-1, 0, 1, 0]
[-2, -1, 0, 1]
[ 0, -2, -1, 0]]
``` Useful special cases: ```
tf.matrix_band_part(input, 0, -1) ==> Upper triangular part.
tf.matrix_band_part(input, -1, 0) ==> Lower triangular part.
tf.matrix_band_part(input, 0, 0) ==> Diagonal.
```
PythonFunctionContainer matrix_determinant_fn get;
Computes the determinant of one or more square matrices. The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The output is a tensor containing the determinants
for all input submatrices `[..., :, :]`.
PythonFunctionContainer matrix_diag_fn get;
Returns a batched diagonal tensor with given batched diagonal values. Returns a tensor with the contents in `diagonal` as `k[0]`-th to `k[1]`-th
diagonals of a matrix, with everything else padded with `padding`. `num_rows`
and `num_cols` specify the dimension of the innermost matrix of the output. If
both are not specified, the op assumes the innermost matrix is square and
infers its size from `k` and the innermost dimension of `diagonal`. If only
one of them is specified, the op assumes the unspecified value is the smallest
possible based on other criteria. Let `diagonal` have `r` dimensions `[I, J,..., L, M, N]`. The output tensor
has rank `r+1` with shape `[I, J,..., L, M, num_rows, num_cols]` when only
one diagonal is given (`k` is an integer or `k[0] == k[1]`). Otherwise, it has
rank `r` with shape `[I, J,..., L, num_rows, num_cols]`. The second innermost dimension of `diagonal` has double meaning. When `k` is
scalar or `k[0] == k[1]`, `M` is part of the batch size [I, J,..., M], and
the output tensor is: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(d_upper, 0)] ; if n - m == d_upper
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, `M` is treated as the number of diagonals for the matrix in the
same batch (`M = k[1]-k[0]+1`), and the output tensor is: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
diagonal = np.array([[1, 2, 3, 4], # Input shape: (2, 4)
[5, 6, 7, 8]])
tf.matrix_diag(diagonal) ==> [[[1, 0, 0, 0], # Output shape: (2, 4, 4)
[0, 2, 0, 0],
[0, 0, 3, 0],
[0, 0, 0, 4]],
[[5, 0, 0, 0],
[0, 6, 0, 0],
[0, 0, 7, 0],
[0, 0, 0, 8]]] # A superdiagonal (per batch).
diagonal = np.array([[1, 2, 3], # Input shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal, k = 1)
==> [[[0, 1, 0, 0], # Output shape: (2, 4, 4)
[0, 0, 2, 0],
[0, 0, 0, 3],
[0, 0, 0, 0]],
[[0, 4, 0, 0],
[0, 0, 5, 0],
[0, 0, 0, 6],
[0, 0, 0, 0]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Input shape: (2, 2, 3)
[4, 5, 0]],
[[6, 7, 9],
[9, 1, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 0, 0], # Output shape: (2, 3, 3)
[4, 2, 0],
[0, 5, 3]],
[[6, 0, 0],
[9, 7, 0],
[0, 1, 9]]] # Rectangular matrix.
diagonal = np.array([1, 2]) # Input shape: (2)
tf.matrix_diag(diagonal, k = -1, num_rows = 3, num_cols = 4)
==> [[0, 0, 0, 0], # Output shape: (3, 4)
[1, 0, 0, 0],
[0, 2, 0, 0]] # Rectangular matrix with inferred num_cols and padding = 9.
tf.matrix_diag(diagonal, k = -1, num_rows = 3, padding = 9)
==> [[9, 9], # Output shape: (3, 2)
[1, 9],
[9, 2]]
```
PythonFunctionContainer matrix_diag_part_fn get;
Returns the batched diagonal part of a batched tensor. Returns a tensor with the `k[0]`-th to `k[1]`-th diagonals of the batched
`input`. Assume `input` has `r` dimensions `[I, J,..., L, M, N]`.
Let `max_diag_len` be the maximum length among all diagonals to be extracted,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))`
Let `num_diags` be the number of diagonals to extract,
`num_diags = k[1] - k[0] + 1`. If `num_diags == 1`, the output tensor is of rank `r - 1` with shape
`[I, J,..., L, max_diag_len]` and values: ```
diagonal[i, j,..., l, n]
= input[i, j,..., l, n+y, n+x] ; when 0 <= n-y < M and 0 <= n-x < N,
0 ; otherwise.
```
where `y = max(-k[1], 0)`, `x = max(k[1], 0)`. Otherwise, the output tensor has rank `r` with dimensions
`[I, J,..., L, num_diags, max_diag_len]` with values: ```
diagonal[i, j,..., l, m, n]
= input[i, j,..., l, n+y, n+x] ; when 0 <= n-y < M and 0 <= n-x < N,
0 ; otherwise.
```
where `d = k[1] - m`, `y = max(-d, 0)`, and `x = max(d, 0)`. The input must be at least a matrix. For example: ```
input = np.array([[[1, 2, 3, 4], # Input shape: (2, 3, 4)
[5, 6, 7, 8],
[9, 8, 7, 6]],
[[5, 4, 3, 2],
[1, 2, 3, 4],
[5, 6, 7, 8]]]) # A main diagonal from each batch.
tf.matrix_diag_part(input) ==> [[1, 6, 7], # Output shape: (2, 3)
[5, 2, 7]] # A superdiagonal from each batch.
tf.matrix_diag_part(input, k = 1)
==> [[2, 7, 6], # Output shape: (2, 3)
[4, 3, 8]] # A tridiagonal band from each batch.
tf.matrix_diag_part(input, k = (-1, 1))
==> [[[2, 7, 6], # Output shape: (2, 3, 3)
[1, 6, 7],
[5, 8, 0]],
[[4, 3, 8],
[5, 2, 7],
[1, 6, 0]]] # Padding = 9
tf.matrix_diag_part(input, k = (1, 3), padding = 9)
==> [[[4, 9, 9], # Output shape: (2, 3, 3)
[3, 8, 9],
[2, 7, 6]],
[[2, 9, 9],
[3, 4, 9],
[4, 3, 8]]]
```
PythonFunctionContainer matrix_inverse_fn get;
Computes the inverse of one or more square invertible matrices or their adjoints (conjugate transposes). The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The output is a tensor of the same shape as the input
containing the inverse for all input submatrices `[..., :, :]`. The op uses LU decomposition with partial pivoting to compute the inverses. If a matrix is not invertible there is no guarantee what the op does. It
may detect the condition and raise an exception or it may simply return a
garbage result.
PythonFunctionContainer matrix_set_diag_fn get;
Returns a batched matrix tensor with new batched diagonal values. Given `input` and `diagonal`, this operation returns a tensor with the
same shape and values as `input`, except for the specified diagonals of the
innermost matrices. These will be overwritten by the values in `diagonal`. `input` has `r+1` dimensions `[I, J,..., L, M, N]`. When `k` is scalar or
`k[0] == k[1]`, `diagonal` has `r` dimensions `[I, J,..., L, max_diag_len]`.
Otherwise, it has `r+1` dimensions `[I, J,..., L, num_diags, max_diag_len]`.
`num_diags` is the number of diagonals, `num_diags = k[1] - k[0] + 1`.
`max_diag_len` is the longest diagonal in the range `[k[0], k[1]]`,
`max_diag_len = min(M + min(k[1], 0), N + min(-k[0], 0))` The output is a tensor of rank `k+1` with dimensions `[I, J,..., L, M, N]`.
If `k` is scalar or `k[0] == k[1]`: ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, n-max(k[1], 0)] ; if n - m == k[1]
output[i, j,..., l, m, n] ; otherwise
``` Otherwise, ```
output[i, j,..., l, m, n]
= diagonal[i, j,..., l, k[1]-d, n-max(d, 0)] ; if d_lower <= d <= d_upper
input[i, j,..., l, m, n] ; otherwise
```
where `d = n - m` For example: ```
# The main diagonal.
input = np.array([[[7, 7, 7, 7], # Input shape: (2, 3, 4)
[7, 7, 7, 7],
[7, 7, 7, 7]],
[[7, 7, 7, 7],
[7, 7, 7, 7],
[7, 7, 7, 7]]])
diagonal = np.array([[1, 2, 3], # Diagonal shape: (2, 3)
[4, 5, 6]])
tf.matrix_diag(diagonal) ==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[7, 2, 7, 7],
[7, 7, 3, 7]],
[[4, 7, 7, 7],
[7, 5, 7, 7],
[7, 7, 6, 7]]] # A superdiagonal (per batch).
tf.matrix_diag(diagonal, k = 1)
==> [[[7, 1, 7, 7], # Output shape: (2, 3, 4)
[7, 7, 2, 7],
[7, 7, 7, 3]],
[[7, 4, 7, 7],
[7, 7, 5, 7],
[7, 7, 7, 6]]] # A band of diagonals.
diagonals = np.array([[[1, 2, 3], # Diagonal shape: (2, 2, 3)
[4, 5, 0]],
[[6, 1, 2],
[3, 4, 0]]])
tf.matrix_diag(diagonals, k = (-1, 0))
==> [[[1, 7, 7, 7], # Output shape: (2, 3, 4)
[4, 2, 7, 7],
[0, 5, 3, 7]],
[[6, 7, 7, 7],
[3, 1, 7, 7],
[7, 4, 2, 7]]] ```
PythonFunctionContainer matrix_solve_fn get;
Solves systems of linear equations. `Matrix` is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. `Rhs` is a tensor of shape `[..., M, K]`. The `output` is
a tensor shape `[..., M, K]`. If `adjoint` is `False` then each output matrix
satisfies `matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]`.
If `adjoint` is `True` then each output matrix satisfies
`adjoint(matrix[..., :, :]) * output[..., :, :] = rhs[..., :, :]`.
PythonFunctionContainer matrix_solve_ls_fn get;
Solves one or more linear least-squares problems. `matrix` is a tensor of shape `[..., M, N]` whose inner-most 2 dimensions
form `M`-by-`N` matrices. Rhs is a tensor of shape `[..., M, K]` whose
inner-most 2 dimensions form `M`-by-`K` matrices. The computed output is a
`Tensor` of shape `[..., N, K]` whose inner-most 2 dimensions form `M`-by-`K`
matrices that solve the equations
`matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]` in the least squares
sense. Below we will use the following notation for each pair of matrix and
right-hand sides in the batch: `matrix`=\\(A \in \Re^{m \times n}\\),
`rhs`=\\(B \in \Re^{m \times k}\\),
`output`=\\(X \in \Re^{n \times k}\\),
`l2_regularizer`=\\(\lambda\\). If `fast` is `True`, then the solution is computed by solving the normal
equations using Cholesky decomposition. Specifically, if \\(m \ge n\\) then
\\(X = (A^T A + \lambda I)^{-1} A^T B\\), which solves the least-squares
problem \\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||A Z - B||_F^2 +
\lambda ||Z||_F^2\\). If \\(m \lt n\\) then `output` is computed as
\\(X = A^T (A A^T + \lambda I)^{-1} B\\), which (for \\(\lambda = 0\\)) is
the minimum-norm solution to the under-determined linear system, i.e.
\\(X = \mathrm{argmin}_{Z \in \Re^{n \times k}} ||Z||_F^2 \\), subject to
\\(A Z = B\\). Notice that the fast path is only numerically stable when
\\(A\\) is numerically full rank and has a condition number
\\(\mathrm{cond}(A) \lt \frac{1}{\sqrt{\epsilon_{mach}}}\\) or\\(\lambda\\)
is sufficiently large. If `fast` is `False` an algorithm based on the numerically robust complete
orthogonal decomposition is used. This computes the minimum-norm
least-squares solution, even when \\(A\\) is rank deficient. This path is
typically 6-7 times slower than the fast path. If `fast` is `False` then
`l2_regularizer` is ignored.
PythonFunctionContainer matrix_square_root_fn get;
Computes the matrix square root of one or more square matrices: matmul(sqrtm(A), sqrtm(A)) = A The input matrix should be invertible. If the input matrix is real, it should
have no eigenvalues which are real and negative (pairs of complex conjugate
eigenvalues are allowed). The matrix square root is computed by first reducing the matrix to
quasi-triangular form with the real Schur decomposition. The square root
of the quasi-triangular matrix is then computed directly. Details of
the algorithm can be found in: Nicholas J. Higham, "Computing real
square roots of a real matrix", Linear Algebra Appl., 1987. The input is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions
form square matrices. The output is a tensor of the same shape as the input
containing the matrix square root for all input submatrices `[..., :, :]`.
PythonFunctionContainer matrix_transpose_fn get;
Transposes last two dimensions of tensor `a`.
Note that
tf.matmul provides kwargs allowing for transpose of arguments.
This is done with minimal cost, and is preferable to using this function. E.g.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.linalg.matrix_transpose(x) # [[1, 4],
# [2, 5],
# [3, 6]] x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.linalg.matrix_transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # Matrix with two batch dimensions.
# x.shape is [1, 2, 3, 4]
# tf.linalg.matrix_transpose(x) is shape [1, 2, 4, 3]
PythonFunctionContainer matrix_triangular_solve_fn get;
Solves systems of linear equations with upper or lower triangular matrices by backsubstitution. `matrix` is a tensor of shape `[..., M, M]` whose inner-most 2 dimensions form
square matrices. If `lower` is `True` then the strictly upper triangular part
of each inner-most matrix is assumed to be zero and not accessed.
If `lower` is False then the strictly lower triangular part of each inner-most
matrix is assumed to be zero and not accessed.
`rhs` is a tensor of shape `[..., M, K]`. The output is a tensor of shape `[..., M, K]`. If `adjoint` is
`True` then the innermost matrices in `output` satisfy matrix equations
`matrix[..., :, :] * output[..., :, :] = rhs[..., :, :]`.
If `adjoint` is `False` then the strictly then the innermost matrices in
`output` satisfy matrix equations
`adjoint(matrix[..., i, k]) * output[..., k, j] = rhs[..., i, j]`. Example:
Show Example
a = tf.constant([[3, 0, 0, 0],
[2, 1, 0, 0],
[1, 0, 1, 0],
[1, 1, 1, 1]], dtype=tf.float32) b = tf.constant([[4],
[2],
[4],
[2]], dtype=tf.float32) x = tf.linalg.triangular_solve(a, b, lower=True)
x
# # in python3 one can use `a@x`
tf.matmul(a, x)
#
PythonFunctionContainer max_bytes_in_use_fn get;
PythonFunctionContainer maximum_fn get;
Returns the max of x and y (i.e. x > y ? x : y) element-wise. *NOTE*: `math.maximum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer meshgrid_fn get;
Broadcasts parameters for evaluation on an N-D grid. Given N one-dimensional coordinate arrays `*args`, returns a list `outputs`
of N-D coordinate arrays for evaluating expressions on an N-D grid. Notes: `meshgrid` supports cartesian ('xy') and matrix ('ij') indexing conventions.
When the `indexing` argument is set to 'xy' (the default), the broadcasting
instructions for the first two dimensions are swapped. Examples: Calling `X, Y = meshgrid(x, y)` with the tensors
Show Example
x = [1, 2, 3]
y = [4, 5, 6]
X, Y = tf.meshgrid(x, y)
# X = [[1, 2, 3],
# [1, 2, 3],
# [1, 2, 3]]
# Y = [[4, 4, 4],
# [5, 5, 5],
# [6, 6, 6]]
PythonFunctionContainer min_max_variable_partitioner_fn get;
Partitioner to allocate minimum size per slice. Returns a partitioner that partitions the variable of given shape and dtype
such that each partition has a minimum of `min_slice_size` slice of the
variable. The maximum number of such partitions (upper bound) is given by
`max_partitions`.
PythonFunctionContainer minimum_fn get;
Returns the min of x and y (i.e. x < y ? x : y) element-wise. *NOTE*: `math.minimum` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer mixed_struct_fn get;
PythonFunctionContainer mod_fn get;
Returns element-wise remainder of division. When `x < 0` xor `y < 0` is true, this follows Python semantics in that the result here is consistent
with a flooring divide. E.g. `floor(x / y) * y + mod(x, y) = x`. *NOTE*: `math.floormod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer model_variables_fn get;
Returns all variables in the MODEL_VARIABLES collection.
PythonFunctionContainer moving_average_variables_fn get;
Returns all variables that maintain their moving averages. If an `ExponentialMovingAverage` object is created and the `apply()`
method is called on a list of variables, these variables will
be added to the `GraphKeys.MOVING_AVERAGE_VARIABLES` collection.
This convenience function returns the contents of that collection.
PythonFunctionContainer multinomial_fn get;
Draws samples from a multinomial distribution. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.random.categorical instead. Example:
Show Example
# samples has shape [1, 5], where each value is either 0 or 1 with equal
# probability.
samples = tf.random.categorical(tf.math.log([[0.5, 0.5]]), 5)
PythonFunctionContainer multiply_fn get;
Returns x * y element-wise. *NOTE*:
tf.multiply supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer n_in_polymorphic_twice_fn get;
PythonFunctionContainer n_in_twice_fn get;
PythonFunctionContainer n_in_two_type_variables_fn get;
PythonFunctionContainer n_ints_in_fn get;
PythonFunctionContainer n_ints_out_default_fn get;
PythonFunctionContainer n_ints_out_fn get;
PythonFunctionContainer n_polymorphic_in_fn get;
PythonFunctionContainer n_polymorphic_out_default_fn get;
PythonFunctionContainer n_polymorphic_out_fn get;
PythonFunctionContainer n_polymorphic_restrict_in_fn get;
PythonFunctionContainer n_polymorphic_restrict_out_fn get;
PythonFunctionContainer negative_fn get;
PythonFunctionContainer no_op_fn get;
Does nothing. Only useful as a placeholder for control edges.
PythonFunctionContainer no_regularizer_fn get;
Use this function to prevent regularization of variables.
PythonFunctionContainer NoGradient_fn get;
Specifies that ops of type `op_type` is not differentiable. This function should *not* be used for operations that have a
well-defined gradient that is not yet implemented. This function is only used when defining a new op type. It may be
used for ops such as `tf.size()` that are not differentiable. For
example:
The gradient computed for 'op_type' will then propagate zeros. For ops that have a well-defined gradient but are not yet implemented,
no declaration should be made, and an error *must* be thrown if
an attempt to request its gradient is made.
Show Example
tf.no_gradient("Size")
PythonFunctionContainer nondifferentiable_batch_function_fn get;
Batches the computation done by the decorated function. So, for example, in the following code
if more than one session.run call is simultaneously trying to compute `b`
the values of `w` will be gathered, non-deterministically concatenated
along the first axis, and only one thread will run the computation. See the
documentation of the `Batch` op for more details. Assumes that all arguments of the decorated function are Tensors which will
be batched along their first dimension. SparseTensor is not supported. The return value of the decorated function
must be a Tensor or a list/tuple of Tensors.
Show Example
@batch_function(1, 2, 3)
def layer(a):
return tf.matmul(a, a) b = layer(w)
PythonFunctionContainer none_fn get;
PythonFunctionContainer norm_fn get;
Computes the norm of vectors, matrices, and tensors. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This function can compute several different vector norms (the 1-norm, the
Euclidean or 2-norm, the inf-norm, and in general the p-norm for p > 0) and
matrix norms (Frobenius, 1-norm, 2-norm and inf-norm).
PythonFunctionContainer not_equal_fn get;
Returns the truth value of (x != y) element-wise. **NOTE**: `NotEqual` supports broadcasting. More about broadcasting [here](
https://docs.scipy.org/doc/numpy-1.13.0/user/basics.broadcasting.html)
PythonFunctionContainer numpy_function_fn get;
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.numpy_function()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.numpy_function()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.numpy_function()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.numpy_function(my_func, [input], tf.float32)
PythonFunctionContainer obtain_next_fn get;
PythonFunctionContainer old_fn get;
PythonFunctionContainer one_hot_fn get;
Returns a one-hot tensor. The locations represented by indices in `indices` take value `on_value`,
while all other locations take value `off_value`. `on_value` and `off_value` must have matching data types. If `dtype` is also
provided, they must be the same data type as specified by `dtype`. If `on_value` is not provided, it will default to the value `1` with type
`dtype` If `off_value` is not provided, it will default to the value `0` with type
`dtype` If the input `indices` is rank `N`, the output will have rank `N+1`. The
new axis is created at dimension `axis` (default: the new axis is appended
at the end). If `indices` is a scalar the output shape will be a vector of length `depth` If `indices` is a vector of length `features`, the output shape will be: ```
features x depth if axis == -1
depth x features if axis == 0
``` If `indices` is a matrix (batch) with shape `[batch, features]`, the output
shape will be: ```
batch x features x depth if axis == -1
batch x depth x features if axis == 1
depth x batch x features if axis == 0
``` If `indices` is a RaggedTensor, the 'axis' argument must be positive and refer
to a non-ragged axis. The output will be equivalent to applying 'one_hot' on
the values of the RaggedTensor, and creating a new RaggedTensor from the
result. If `dtype` is not provided, it will attempt to assume the data type of
`on_value` or `off_value`, if one or both are passed in. If none of
`on_value`, `off_value`, or `dtype` are provided, `dtype` will default to the
value
tf.float32. Note: If a non-numeric data type output is desired (tf.string, tf.bool,
etc.), both `on_value` and `off_value` _must_ be provided to `one_hot`.
Show Example
indices = [0, 1, 2]
depth = 3
tf.one_hot(indices, depth) # output: [3 x 3]
# [[1., 0., 0.],
# [0., 1., 0.],
# [0., 0., 1.]] indices = [0, 2, -1, 1]
depth = 3
tf.one_hot(indices, depth,
on_value=5.0, off_value=0.0,
axis=-1) # output: [4 x 3]
# [[5.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 5.0], # one_hot(2)
# [0.0, 0.0, 0.0], # one_hot(-1)
# [0.0, 5.0, 0.0]] # one_hot(1) indices = [[0, 2], [1, -1]]
depth = 3
tf.one_hot(indices, depth,
on_value=1.0, off_value=0.0,
axis=-1) # output: [2 x 2 x 3]
# [[[1.0, 0.0, 0.0], # one_hot(0)
# [0.0, 0.0, 1.0]], # one_hot(2)
# [[0.0, 1.0, 0.0], # one_hot(1)
# [0.0, 0.0, 0.0]]] # one_hot(-1) indices = tf.ragged.constant([[0, 1], [2]])
depth = 3
tf.one_hot(indices, depth) # output: [2 x None x 3]
# [[[1., 0., 0.],
# [0., 1., 0.]],
# [[0., 0., 1.]]]
PythonFunctionContainer ones_fn get;
Creates a tensor with all elements set to 1. This operation returns a tensor of type `dtype` with shape `shape` and all
elements set to 1.
Show Example
tf.ones([2, 3], tf.int32) # [[1, 1, 1], [1, 1, 1]]
PythonFunctionContainer ones_like_fn get;
Creates a tensor with all elements set to 1. Given a single tensor (`tensor`), this operation returns a tensor of the same
type and shape as `tensor` with all elements set to 1. Optionally, you can
specify a new type (`dtype`) for the returned tensor.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.ones_like(tensor) # [[1, 1, 1], [1, 1, 1]]
PythonFunctionContainer op_scope_fn get;
DEPRECATED. Same as name_scope above, just different argument order.
PythonFunctionContainer op_with_default_attr_fn get;
PythonFunctionContainer op_with_future_default_attr_fn get;
PythonFunctionContainer out_t_fn get;
PythonFunctionContainer out_type_list_fn get;
PythonFunctionContainer out_type_list_restrict_fn get;
PythonFunctionContainer pad_fn get;
Pads a tensor. This operation pads a `tensor` according to the `paddings` you specify.
`paddings` is an integer tensor with shape `[n, 2]`, where n is the rank of
`tensor`. For each dimension D of `input`, `paddings[D, 0]` indicates how
many values to add before the contents of `tensor` in that dimension, and
`paddings[D, 1]` indicates how many values to add after the contents of
`tensor` in that dimension. If `mode` is "REFLECT" then both `paddings[D, 0]`
and `paddings[D, 1]` must be no greater than `tensor.dim_size(D) - 1`. If
`mode` is "SYMMETRIC" then both `paddings[D, 0]` and `paddings[D, 1]` must be
no greater than `tensor.dim_size(D)`. The padded size of each dimension D of the output is: `paddings[D, 0] + tensor.dim_size(D) + paddings[D, 1]`
Show Example
t = tf.constant([[1, 2, 3], [4, 5, 6]])
paddings = tf.constant([[1, 1,], [2, 2]])
# 'constant_values' is 0.
# rank of 't' is 2.
tf.pad(t, paddings, "CONSTANT") # [[0, 0, 0, 0, 0, 0, 0],
# [0, 0, 1, 2, 3, 0, 0],
# [0, 0, 4, 5, 6, 0, 0],
# [0, 0, 0, 0, 0, 0, 0]] tf.pad(t, paddings, "REFLECT") # [[6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1],
# [6, 5, 4, 5, 6, 5, 4],
# [3, 2, 1, 2, 3, 2, 1]] tf.pad(t, paddings, "SYMMETRIC") # [[2, 1, 1, 2, 3, 3, 2],
# [2, 1, 1, 2, 3, 3, 2],
# [5, 4, 4, 5, 6, 6, 5],
# [5, 4, 4, 5, 6, 6, 5]]
PythonFunctionContainer parallel_stack_fn get;
Stacks a list of rank-`R` tensors into one rank-`(R+1)` tensor in parallel. Requires that the shape of inputs be known at graph construction time. Packs the list of tensors in `values` into a tensor with rank one higher than
each tensor in `values`, by packing them along the first dimension.
Given a list of length `N` of tensors of shape `(A, B, C)`; the `output`
tensor will have the shape `(N, A, B, C)`.
The difference between `stack` and `parallel_stack` is that `stack` requires
all the inputs be computed before the operation will begin but doesn't require
that the input shapes be known during graph construction. `parallel_stack` will copy pieces of the input into the output as they become
available, in some situations this can provide a performance benefit. Unlike `stack`, `parallel_stack` does NOT support backpropagation. This is the opposite of unstack. The numpy equivalent is tf.parallel_stack([x, y, z]) = np.asarray([x, y, z])
Show Example
x = tf.constant([1, 4])
y = tf.constant([2, 5])
z = tf.constant([3, 6])
tf.parallel_stack([x, y, z]) # [[1, 4], [2, 5], [3, 6]]
PythonFunctionContainer parse_example_fn get;
Parses `Example` protos into a `dict` of tensors. Parses a number of serialized [`Example`](https://www.tensorflow.org/code/tensorflow/core/example/example.proto)
protos given in `serialized`. We refer to `serialized` as a batch with
`batch_size` many entries of individual `Example` protos. `example_names` may contain descriptive names for the corresponding serialized
protos. These may be useful for debugging purposes, but they have no effect on
the output. If not `None`, `example_names` must be the same length as
`serialized`. This op parses serialized examples into a dictionary mapping keys to `Tensor`
and `SparseTensor` objects. `features` is a dict from keys to `VarLenFeature`,
`SparseFeature`, and `FixedLenFeature` objects. Each `VarLenFeature`
and `SparseFeature` is mapped to a `SparseTensor`, and each
`FixedLenFeature` is mapped to a `Tensor`. Each `VarLenFeature` maps to a `SparseTensor` of the specified type
representing a ragged matrix. Its indices are `[batch, index]` where `batch`
identifies the example in `serialized`, and `index` is the value's index in
the list of values associated with that feature and example. Each `SparseFeature` maps to a `SparseTensor` of the specified type
representing a Tensor of `dense_shape` `[batch_size] + SparseFeature.size`.
Its `values` come from the feature in the examples with key `value_key`.
A `values[i]` comes from a position `k` in the feature of an example at batch
entry `batch`. This positional information is recorded in `indices[i]` as
`[batch, index_0, index_1,...]` where `index_j` is the `k-th` value of
the feature in the example at with key `SparseFeature.index_key[j]`.
In other words, we split the indices (except the first index indicating the
batch entry) of a `SparseTensor` by dimension into different features of the
`Example`. Due to its complexity a `VarLenFeature` should be preferred over a
`SparseFeature` whenever possible. Each `FixedLenFeature` `df` maps to a `Tensor` of the specified type (or
tf.float32 if not specified) and shape `(serialized.size(),) + df.shape`. `FixedLenFeature` entries with a `default_value` are optional. With no default
value, we will fail if that `Feature` is missing from any example in
`serialized`. Each `FixedLenSequenceFeature` `df` maps to a `Tensor` of the specified type
(or tf.float32 if not specified) and shape
`(serialized.size(), None) + df.shape`.
All examples in `serialized` will be padded with `default_value` along the
second dimension. Examples: For example, if one expects a tf.float32 `VarLenFeature` `ft` and three
serialized `Example`s are provided: ```
serialized = [
features
{ feature { key: "ft" value { float_list { value: [1.0, 2.0] } } } },
features
{ feature []},
features
{ feature { key: "ft" value { float_list { value: [3.0] } } }
]
``` then the output will look like:
If instead a `FixedLenSequenceFeature` with `default_value = -1.0` and
`shape=[]` is used then the output will look like:
Given two `Example` input protos in `serialized`: ```
[
features {
feature { key: "kw" value { bytes_list { value: [ "knit", "big" ] } } }
feature { key: "gps" value { float_list { value: [] } } }
},
features {
feature { key: "kw" value { bytes_list { value: [ "emmy" ] } } }
feature { key: "dank" value { int64_list { value: [ 42 ] } } }
feature { key: "gps" value { } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"kw": VarLenFeature(tf.string),
"dank": VarLenFeature(tf.int64),
"gps": VarLenFeature(tf.float32),
}
``` Then the output is a dictionary:
For dense results in two serialized `Example`s: ```
[
features {
feature { key: "age" value { int64_list { value: [ 0 ] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
},
features {
feature { key: "age" value { int64_list { value: [] } } }
feature { key: "gender" value { bytes_list { value: [ "f" ] } } }
}
]
``` We can use arguments: ```
example_names: ["input0", "input1"],
features: {
"age": FixedLenFeature([], dtype=tf.int64, default_value=-1),
"gender": FixedLenFeature([], dtype=tf.string),
}
``` And the expected output is:
An alternative to `VarLenFeature` to obtain a `SparseTensor` is
`SparseFeature`. For example, given two `Example` input protos in
`serialized`: ```
[
features {
feature { key: "val" value { float_list { value: [ 0.5, -1.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 3, 20 ] } } }
},
features {
feature { key: "val" value { float_list { value: [ 0.0 ] } } }
feature { key: "ix" value { int64_list { value: [ 42 ] } } }
}
]
``` And arguments ```
example_names: ["input0", "input1"],
features: {
"sparse": SparseFeature(
index_key="ix", value_key="val", dtype=tf.float32, size=100),
}
``` Then the output is a dictionary:
Show Example
{"ft": SparseTensor(indices=[[0, 0], [0, 1], [2, 0]],
values=[1.0, 2.0, 3.0],
dense_shape=(3, 2)) }
PythonFunctionContainer parse_single_example_fn get;
Parses a single `Example` proto. Similar to `parse_example`, except: For dense tensors, the returned `Tensor` is identical to the output of
`parse_example`, except there is no batch dimension, the output shape is the
same as the shape given in `dense_shape`. For `SparseTensor`s, the first (batch) column of the indices matrix is removed
(the indices matrix is a column vector), the values vector is unchanged, and
the first (`batch_size`) entry of the shape vector is removed (it is now a
single element vector). One might see performance advantages by batching `Example` protos with
`parse_example` instead of using this function directly.
PythonFunctionContainer parse_single_sequence_example_fn get;
Parses a single `SequenceExample` proto. Parses a single serialized [`SequenceExample`](https://www.tensorflow.org/code/tensorflow/core/example/example.proto)
proto given in `serialized`. This op parses a serialized sequence example into a tuple of dictionaries,
each mapping keys to `Tensor` and `SparseTensor` objects.
The first dictionary contains mappings for keys appearing in
`context_features`, and the second dictionary contains mappings for keys
appearing in `sequence_features`. At least one of `context_features` and `sequence_features` must be provided
and non-empty. The `context_features` keys are associated with a `SequenceExample` as a
whole, independent of time / frame. In contrast, the `sequence_features` keys
provide a way to access variable-length data within the `FeatureList` section
of the `SequenceExample` proto. While the shapes of `context_features` values
are fixed with respect to frame, the frame dimension (the first dimension)
of `sequence_features` values may vary between `SequenceExample` protos,
and even between `feature_list` keys within the same `SequenceExample`. `context_features` contains `VarLenFeature` and `FixedLenFeature` objects.
Each `VarLenFeature` is mapped to a `SparseTensor`, and each `FixedLenFeature`
is mapped to a `Tensor`, of the specified type, shape, and default value. `sequence_features` contains `VarLenFeature` and `FixedLenSequenceFeature`
objects. Each `VarLenFeature` is mapped to a `SparseTensor`, and each
`FixedLenSequenceFeature` is mapped to a `Tensor`, each of the specified type.
The shape will be `(T,) + df.dense_shape` for `FixedLenSequenceFeature` `df`, where
`T` is the length of the associated `FeatureList` in the `SequenceExample`.
For instance, `FixedLenSequenceFeature([])` yields a scalar 1-D `Tensor` of
static shape `[None]` and dynamic shape `[T]`, while
`FixedLenSequenceFeature([k])` (for `int k >= 1`) yields a 2-D matrix `Tensor`
of static shape `[None, k]` and dynamic shape `[T, k]`. Each `SparseTensor` corresponding to `sequence_features` represents a ragged
vector. Its indices are `[time, index]`, where `time` is the `FeatureList`
entry and `index` is the value's index in the list of values associated with
that time. `FixedLenFeature` entries with a `default_value` and `FixedLenSequenceFeature`
entries with `allow_missing=True` are optional; otherwise, we will fail if
that `Feature` or `FeatureList` is missing from any example in `serialized`. `example_name` may contain a descriptive name for the corresponding serialized
proto. This may be useful for debugging purposes, but it has no effect on the
output. If not `None`, `example_name` must be a scalar. Note that the batch version of this function, `tf.parse_sequence_example`,
is written for better memory efficiency and will be faster on large
`SequenceExample`s.
PythonFunctionContainer parse_tensor_fn get;
Transforms a serialized tensorflow.TensorProto proto into a Tensor.
PythonFunctionContainer periodic_resample_fn get;
PythonFunctionContainer periodic_resample_op_grad_fn get;
PythonFunctionContainer placeholder_fn get;
Inserts a placeholder for a tensor that will be always fed. **Important**: This tensor will produce an error if evaluated. Its value must
be fed using the `feed_dict` optional argument to `Session.run()`,
`Tensor.eval()`, or `Operation.run()`.
Show Example
x = tf.compat.v1.placeholder(tf.float32, shape=(1024, 1024))
y = tf.matmul(x, x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. rand_array = np.random.rand(1024, 1024)
print(sess.run(y, feed_dict={x: rand_array})) # Will succeed.
PythonFunctionContainer placeholder_with_default_fn get;
A placeholder op that passes through `input` when its output is not fed.
object plugin_dir get; set;
object plugin_dir_dyn get; set;
PythonFunctionContainer polygamma_fn get;
Compute the polygamma function \\(\psi^{(n)}(x)\\). The polygamma function is defined as: \\(\psi^{(a)}(x) = \frac{d^a}{dx^a} \psi(x)\\) where \\(\psi(x)\\) is the digamma function.
The polygamma function is defined only for non-negative integer orders \\a\\.
PythonFunctionContainer polymorphic_default_out_fn get;
PythonFunctionContainer polymorphic_fn get;
PythonFunctionContainer polymorphic_out_fn get;
PythonFunctionContainer pow_fn get;
Computes the power of one value to another. Given a tensor `x` and a tensor `y`, this operation computes \\(x^y\\) for
corresponding elements in `x` and `y`.
Show Example
x = tf.constant([[2, 2], [3, 3]])
y = tf.constant([[8, 16], [2, 3]])
tf.pow(x, y) # [[256, 65536], [9, 27]]
PythonFunctionContainer print_fn get;
Print the specified inputs. A TensorFlow operator that prints the specified inputs to a desired
output stream or logging level. The inputs may be dense or sparse Tensors,
primitive python objects, data structures that contain tensors, and printable
Python objects. Printed tensors will recursively show the first and last
elements of each dimension to summarize. Example:
Single-input usage:
(This prints "[0 1 2... 7 8 9]" to sys.stderr) Multi-input usage:
(This prints "tensors: [0 1 2... 7 8 9] {2: [0 2 4... 14 16 18]}" to
sys.stdout) Changing the input separator:
(This prints "[0 1],[0 2]" to sys.stderr) Usage in a
tf.function:
(This prints "[0 1 2... 7 8 9]" to sys.stderr) @compatibility(TF 1.x Graphs and Sessions)
In graphs manually created outside of tf.function, this method returns
the created TF operator that prints the data. To make sure the
operator runs, users need to pass the produced op to
`tf.compat.v1.Session`'s run method, or to use the op as a control
dependency for executed ops by specifying
`with tf.compat.v1.control_dependencies([print_op])`.
@end_compatibility Compatibility usage in TF 1.x graphs:
(This prints "tensors: [0 1 2... 7 8 9] {2: [0 2 4... 14 16 18]}" to
sys.stdout) Note: In Jupyter notebooks and colabs, tf.print prints to the notebook
cell outputs. It will not write to the notebook kernel's console logs.
Show Example
tensor = tf.range(10)
tf.print(tensor, output_stream=sys.stderr)
PythonFunctionContainer Print_fn get;
Prints a list of tensors. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed after 2018-08-20.
Instructions for updating:
Use tf.print instead of tf.Print. Note that tf.print returns a no-output operator that directly prints the output. Outside of defuns or eager mode, this operator will not be executed unless it is directly specified in session.run or used as a control dependency for other operators. This is only a concern in graph mode. Below is an example of how to ensure tf.print executes in graph mode: This is an identity op (behaves like
tf.identity) with the side effect
of printing `data` when evaluating. Note: This op prints to the standard error. It is not currently compatible
with jupyter notebook (printing to the notebook *server's* output, not into
the notebook).
PythonFunctionContainer process_input_v4_fn get;
PythonFunctionContainer py_func_fn get;
Wraps a python function and uses it as a TensorFlow op. Given a python function `func`, which takes numpy arrays as its
arguments and returns numpy arrays as its outputs, wrap this function as an
operation in a TensorFlow graph. The following snippet constructs a simple
TensorFlow graph that invokes the `np.sinh()` NumPy function as a operation
in the graph:
**N.B.** The `tf.compat.v1.py_func()` operation has the following known
limitations: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.compat.v1.py_func()`. If you are using distributed
TensorFlow, you
must run a
tf.distribute.Server in the same process as the program that
calls
`tf.compat.v1.py_func()` and you must pin the created operation to a device
in that
server (e.g. using `with tf.device():`).
Show Example
def my_func(x):
# x will be a numpy array with the contents of the placeholder below
return np.sinh(x)
input = tf.compat.v1.placeholder(tf.float32)
y = tf.compat.v1.py_func(my_func, [input], tf.float32)
PythonFunctionContainer py_function_fn get;
Wraps a python function into a TensorFlow op that executes it eagerly. This function allows expressing computations in a TensorFlow graph as
Python functions. In particular, it wraps a Python function `func`
in a once-differentiable TensorFlow operation that executes it with eager
execution enabled. As a consequence,
tf.py_function makes it
possible to express control flow using Python constructs (`if`, `while`,
`for`, etc.), instead of TensorFlow control flow constructs (tf.cond,
tf.while_loop). For example, you might use tf.py_function to
implement the log huber function:
You can also use tf.py_function to debug your models at runtime
using Python tools, i.e., you can isolate portions of your code that
you want to debug, wrap them in Python functions and insert `pdb` tracepoints
or print statements as desired, and wrap those functions in
tf.py_function. For more information on eager execution, see the
[Eager guide](https://tensorflow.org/guide/eager). tf.py_function is similar in spirit to `tf.compat.v1.py_func`, but unlike
the latter, the former lets you use TensorFlow operations in the wrapped
Python function. In particular, while `tf.compat.v1.py_func` only runs on CPUs
and
wraps functions that take NumPy arrays as inputs and return NumPy arrays as
outputs, tf.py_function can be placed on GPUs and wraps functions
that take Tensors as inputs, execute TensorFlow operations in their bodies,
and return Tensors as outputs. Like `tf.compat.v1.py_func`, tf.py_function has the following limitations
with respect to serialization and distribution: * The body of the function (i.e. `func`) will not be serialized in a
`GraphDef`. Therefore, you should not use this function if you need to
serialize your model and restore it in a different environment. * The operation must run in the same address space as the Python program
that calls `tf.py_function()`. If you are using distributed
TensorFlow, you must run a tf.distribute.Server in the same process as the
program that calls `tf.py_function()` and you must pin the created
operation to a device in that server (e.g. using `with tf.device():`).
Show Example
def log_huber(x, m):
if tf.abs(x) <= m:
return x**2
else:
return m**2 * (1 - 2 * tf.math.log(m) + tf.math.log(x**2)) x = tf.compat.v1.placeholder(tf.float32)
m = tf.compat.v1.placeholder(tf.float32) y = tf.py_function(func=log_huber, inp=[x, m], Tout=tf.float32)
dy_dx = tf.gradients(y, x)[0] with tf.compat.v1.Session() as sess:
# The session executes `log_huber` eagerly. Given the feed values below,
# it will take the first branch, so `y` evaluates to 1.0 and
# `dy_dx` evaluates to 2.0.
y, dy_dx = sess.run([y, dy_dx], feed_dict={x: 1.0, m: 2.0})
DType qint16 get; set;
DType qint32 get; set;
DType qint8 get; set;
PythonFunctionContainer qr_fn get;
Computes the QR decompositions of one or more matrices. Computes the QR decomposition of each inner matrix in `tensor` such that
`tensor[..., :, :] = q[..., :, :] * r[..., :,:])`
Show Example
# a is a tensor.
# q is a tensor of orthonormal matrices.
# r is a tensor of upper triangular matrices.
q, r = qr(a)
q_full, r_full = qr(a, full_matrices=True)
PythonFunctionContainer quantile_accumulator_add_summaries_fn get;
PythonFunctionContainer quantile_accumulator_deserialize_fn get;
PythonFunctionContainer quantile_accumulator_flush_fn get;
PythonFunctionContainer quantile_accumulator_flush_summary_fn get;
PythonFunctionContainer quantile_accumulator_get_buckets_fn get;
PythonFunctionContainer quantile_accumulator_is_initialized_fn get;
PythonFunctionContainer quantile_accumulator_serialize_fn get;
PythonFunctionContainer quantile_buckets_fn get;
PythonFunctionContainer quantile_stream_resource_handle_op_fn get;
PythonFunctionContainer quantiles_fn get;
PythonFunctionContainer quantize_fn get;
Quantize the 'input' tensor of type float to 'output' tensor of type 'T'. [min_range, max_range] are scalar floats that specify the range for
the 'input' data. The 'mode' attribute controls exactly which calculations are
used to convert the float values to their quantized equivalents. The
'round_mode' attribute controls which rounding tie-breaking algorithm is used
when rounding float values to their quantized equivalents. In 'MIN_COMBINED' mode, each value of the tensor will undergo the following: ```
out[i] = (in[i] - min_range) * range(T) / (max_range - min_range)
if T == qint8: out[i] -= (range(T) + 1) / 2.0
``` here `range(T) = numeric_limits::max() - numeric_limits::min()` *MIN_COMBINED Mode Example* Assume the input is type float and has a possible range of [0.0, 6.0] and the
output type is quint8 ([0, 255]). The min_range and max_range values should be
specified as 0.0 and 6.0. Quantizing from float to quint8 will multiply each
value of the input by 255/6 and cast to quint8. If the output type was qint8 ([-128, 127]), the operation will additionally
subtract each value by 128 prior to casting, so that the range of values aligns
with the range of qint8. If the mode is 'MIN_FIRST', then this approach is used: ```
num_discrete_values = 1 << (# of bits in T)
range_adjust = num_discrete_values / (num_discrete_values - 1)
range = (range_max - range_min) * range_adjust
range_scale = num_discrete_values / range
quantized = round(input * range_scale) - round(range_min * range_scale) +
numeric_limits::min()
quantized = max(quantized, numeric_limits::min())
quantized = min(quantized, numeric_limits::max())
``` The biggest difference between this and MIN_COMBINED is that the minimum range
is rounded first, before it's subtracted from the rounded value. With
MIN_COMBINED, a small bias is introduced where repeated iterations of quantizing
and dequantizing will introduce a larger and larger error. *SCALED mode Example* `SCALED` mode matches the quantization approach used in
`QuantizeAndDequantize{V2|V3}`. If the mode is `SCALED`, we do not use the full range of the output type,
choosing to elide the lowest possible value for symmetry (e.g., output range is
-127 to 127, not -128 to 127 for signed 8 bit quantization), so that 0.0 maps to
0. We first find the range of values in our tensor. The
range we use is always centered on 0, so we find m such that ```c++
m = max(abs(input_min), abs(input_max))
``` Our input tensor range is then `[-m, m]`. Next, we choose our fixed-point quantization buckets, `[min_fixed, max_fixed]`.
If T is signed, this is ```
num_bits = sizeof(T) * 8
[min_fixed, max_fixed] =
[-(1 << (num_bits - 1) - 1), (1 << (num_bits - 1)) - 1]
``` Otherwise, if T is unsigned, the fixed-point range is ```
[min_fixed, max_fixed] = [0, (1 << num_bits) - 1]
``` From this we compute our scaling factor, s: ```c++
s = (max_fixed - min_fixed) / (2 * m)
``` Now we can quantize the elements of our tensor: ```c++
result = round(input * s)
``` One thing to watch out for is that the operator may choose to adjust the
requested minimum and maximum values slightly during the quantization process,
so you should always use the output ports as the range for further calculations.
For example, if the requested minimum and maximum values are close to equal,
they will be separated by a small epsilon value to prevent ill-formed quantized
buffers from being created. Otherwise, you can end up with buffers where all the
quantized values map to the same float value, which causes problems for
operations that have to perform further calculations on them.
PythonFunctionContainer quantize_v2_fn get;
Please use
tf.quantization.quantize instead.
PythonFunctionContainer quantized_concat_fn get;
Concatenates quantized tensors along one dimension.
IReadOnlyCollection<object> QUANTIZED_DTYPES get; set;
DType quint16 get; set;
DType quint8 get; set;
PythonFunctionContainer random_crop_fn get;
Randomly crops a tensor to a given size. Slices a shape `size` portion out of `value` at a uniformly chosen offset.
Requires `value.shape >= size`. If a dimension should not be cropped, pass the full size of that dimension.
For example, RGB images can be cropped with
`size = [crop_height, crop_width, 3]`.
PythonFunctionContainer random_gamma_fn get;
Draws `shape` samples from each of the given Gamma distribution(s). `alpha` is the shape parameter describing the distribution(s), and `beta` is
the inverse scale parameter(s). Note: Because internal calculations are done using `float64` and casting has
`floor` semantics, we must manually map zero outcomes to the smallest
possible positive floating-point value, i.e., `np.finfo(dtype).tiny`. This
means that `np.finfo(dtype).tiny` occurs more frequently than it otherwise
should. This bias can only happen for small values of `alpha`, i.e.,
`alpha << 1` or large values of `beta`, i.e., `beta >> 1`. The samples are differentiable w.r.t. alpha and beta.
The derivatives are computed using the approach described in the paper [Michael Figurnov, Shakir Mohamed, Andriy Mnih.
Implicit Reparameterization Gradients, 2018](https://arxiv.org/abs/1805.08498) Example:
Show Example
samples = tf.random.gamma([10], [0.5, 1.5])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.gamma([7, 5], [0.5, 1.5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions alpha = tf.constant([[1.],[3.],[5.]])
beta = tf.constant([[3., 4.]])
samples = tf.random.gamma([30], alpha=alpha, beta=beta)
# samples has shape [30, 3, 2], with 30 samples each of 3x2 distributions. loss = tf.reduce_mean(tf.square(samples))
dloss_dalpha, dloss_dbeta = tf.gradients(loss, [alpha, beta])
# unbiased stochastic derivatives of the loss function
alpha.shape == dloss_dalpha.shape # True
beta.shape == dloss_dbeta.shape # True
PythonFunctionContainer random_normal_fn get;
Outputs random values from a normal distribution.
PythonFunctionContainer random_poisson_fn get;
Draws `shape` samples from each of the given Poisson distribution(s). `lam` is the rate parameter describing the distribution(s). Example:
Show Example
samples = tf.random.poisson([0.5, 1.5], [10])
# samples has shape [10, 2], where each slice [:, 0] and [:, 1] represents
# the samples drawn from each distribution samples = tf.random.poisson([12.2, 3.3], [7, 5])
# samples has shape [7, 5, 2], where each slice [:, :, 0] and [:, :, 1]
# represents the 7x5 samples drawn from each of the two distributions
PythonFunctionContainer random_shuffle_fn get;
Randomly shuffles a tensor along its first dimension. The tensor is shuffled along dimension 0, such that each `value[j]` is mapped
to one and only one `output[i]`. For example, a mapping that might occur for a
3x2 tensor is:
Show Example
[[1, 2], [[5, 6],
[3, 4], ==> [1, 2],
[5, 6]] [3, 4]]
PythonFunctionContainer random_uniform_fn get;
Outputs random values from a uniform distribution. The generated values follow a uniform distribution in the range
`[minval, maxval)`. The lower bound `minval` is included in the range, while
the upper bound `maxval` is excluded. For floats, the default range is `[0, 1)`. For ints, at least `maxval` must
be specified explicitly. In the integer case, the random integers are slightly biased unless
`maxval - minval` is an exact power of two. The bias is small for values of
`maxval - minval` significantly smaller than the range of the output (either
`2**32` or `2**64`).
PythonFunctionContainer range_fn get;
Creates a sequence of numbers. Creates a sequence of numbers that begins at `start` and extends by
increments of `delta` up to but not including `limit`. The dtype of the resulting tensor is inferred from the inputs unless
it is provided explicitly. Like the Python builtin `range`, `start` defaults to 0, so that
`range(n) = range(0, n)`.
Show Example
start = 3
limit = 18
delta = 3
tf.range(start, limit, delta) # [3, 6, 9, 12, 15] start = 3
limit = 1
delta = -0.5
tf.range(start, limit, delta) # [3, 2.5, 2, 1.5] limit = 5
tf.range(limit) # [0, 1, 2, 3, 4]
PythonFunctionContainer rank_fn get;
Returns the rank of a tensor. Returns a 0-D `int32` `Tensor` representing the rank of `input`.
**Note**: The rank of a tensor is not the same as the rank of a matrix. The
rank of a tensor is the number of indices required to uniquely select each
element of the tensor. Rank is also known as "order", "degree", or "ndims."
Show Example
# shape of tensor 't' is [2, 2, 3]
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.rank(t) # 3
PythonFunctionContainer read_file_fn get;
Reads and outputs the entire contents of the input filename.
PythonFunctionContainer real_fn get;
Returns the real part of a complex (or real) tensor. Given a tensor `input`, this operation returns a tensor of type `float` that
is the real part of each element in `input` considered as a complex number.
If `input` is already real, it is returned unchanged.
Show Example
x = tf.constant([-2.25 + 4.75j, 3.25 + 5.75j])
tf.math.real(x) # [-2.25, 3.25]
PythonFunctionContainer realdiv_fn get;
Returns x / y element-wise for real types. If `x` and `y` are reals, this will return the floating-point division. *NOTE*: `Div` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer reciprocal_fn get;
Computes the reciprocal of x element-wise. I.e., \\(y = 1 / x\\).
PythonFunctionContainer recompute_grad_fn get;
An eager-compatible version of recompute_grad. For f(*args, **kwargs), this supports gradients with respect to args, or to
gradients with respect to any variables residing in the kwarg 'variables'.
Note that for keras layer and model objects, this is handled automatically. Warning: If `f` was originally a tf.keras Model or Layer object, `g` will not
be able to access the member variables of that object, because `g` returns
through the wrapper function `inner`. When recomputing gradients through
objects that inherit from keras, we suggest keeping a reference to the
underlying object around for the purpose of accessing these variables.
PythonFunctionContainer reduce_all_fn_ get;
PythonFunctionContainer reduce_any_fn_ get;
PythonFunctionContainer reduce_join_fn get;
Joins a string Tensor across the given dimensions. Computes the string join across dimensions in the given string Tensor of shape
`[\\(d_0, d_1,..., d_{n-1}\\)]`. Returns a new Tensor created by joining the input
strings with the given separator (default: empty string). Negative indices are
counted backwards from the end, with `-1` being equivalent to `n - 1`. If
indices are not specified, joins across all dimensions beginning from `n - 1`
through `0`.
Show Example
# tensor `a` is [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, -2) = tf.strings.reduce_join(a, 0) ==> ["ac", "bd"]
tf.strings.reduce_join(a, -1) = tf.strings.reduce_join(a, 1) ==> ["ab", "cd"]
tf.strings.reduce_join(a, 0, keep_dims=True) ==> [["ac", "bd"]]
tf.strings.reduce_join(a, 1, keep_dims=True) ==> [["ab"], ["cd"]]
tf.strings.reduce_join(a, 0, separator=".") ==> ["a.c", "b.d"]
tf.strings.reduce_join(a, [0, 1]) ==> "acbd"
tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
tf.strings.reduce_join(a, []) ==> [["a", "b"], ["c", "d"]]
tf.strings.reduce_join(a) = tf.strings.reduce_join(a, [1, 0]) ==> "abcd"
PythonFunctionContainer reduce_logsumexp_fn_ get;
PythonFunctionContainer reduce_max_fn_ get;
PythonFunctionContainer reduce_mean_fn_ get;
PythonFunctionContainer reduce_min_fn_ get;
PythonFunctionContainer reduce_prod_fn_ get;
PythonFunctionContainer reduce_slice_max_fn get;
PythonFunctionContainer reduce_slice_min_fn get;
PythonFunctionContainer reduce_slice_prod_fn get;
PythonFunctionContainer reduce_slice_sum_fn get;
PythonFunctionContainer reduce_sum_fn_ get;
PythonFunctionContainer ref_in_fn get;
PythonFunctionContainer ref_input_float_input_fn get;
PythonFunctionContainer ref_input_float_input_int_output_fn get;
PythonFunctionContainer ref_input_int_input_fn get;
PythonFunctionContainer ref_out_fn get;
PythonFunctionContainer ref_output_float_output_fn get;
PythonFunctionContainer ref_output_fn get;
PythonFunctionContainer regex_replace_fn get;
Replace elements of `input` matching regex `pattern` with `rewrite`.
PythonFunctionContainer register_tensor_conversion_function_fn get;
Registers a function for converting objects of `base_type` to `Tensor`. The conversion function must have the following signature:
It must return a `Tensor` with the given `dtype` if specified. If the
conversion function creates a new `Tensor`, it should use the given
`name` if specified. All exceptions will be propagated to the caller. The conversion function may return `NotImplemented` for some
inputs. In this case, the conversion process will continue to try
subsequent conversion functions. If `as_ref` is true, the function must return a `Tensor` reference,
such as a `Variable`. NOTE: The conversion functions will execute in order of priority,
followed by order of registration. To ensure that a conversion function
`F` runs before another conversion function `G`, ensure that `F` is
registered with a smaller priority than `G`.
Show Example
def conversion_func(value, dtype=None, name=None, as_ref=False):
#...
PythonFunctionContainer reinterpret_string_to_float_fn get;
PythonFunctionContainer remote_fused_graph_execute_fn get;
PythonFunctionContainer repeat_fn get;
Repeat elements of `input`
PythonFunctionContainer report_uninitialized_variables_fn get;
Adds ops to list the names of uninitialized variables. When run, it returns a 1-D tensor containing the names of uninitialized
variables if there are any, or an empty array if there are none.
PythonFunctionContainer required_space_to_batch_paddings_fn get;
Calculate padding required to make block_shape divide input_shape. This function can be used to calculate a suitable paddings argument for use
with space_to_batch_nd and batch_to_space_nd.
PythonFunctionContainer requires_older_graph_version_fn get;
PythonFunctionContainer resampler_fn get;
PythonFunctionContainer resampler_grad_fn get;
PythonFunctionContainer reserved_attr_fn get;
PythonFunctionContainer reserved_input_fn get;
PythonFunctionContainer reset_default_graph_fn get;
Clears the default graph stack and resets the global default graph. NOTE: The default graph is a property of the current thread. This
function applies only to the current thread. Calling this function while
a `tf.compat.v1.Session` or `tf.compat.v1.InteractiveSession` is active will
result in undefined
behavior. Using any previously created
tf.Operation or tf.Tensor objects
after calling this function will result in undefined behavior.
PythonFunctionContainer reshape_fn get;
Reshapes a tensor. Given `tensor`, this operation returns a tensor that has the same values
as `tensor` with shape `shape`. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total size remains constant. In particular,
a `shape` of `[-1]` flattens into 1-D. At most one component of `shape` can
be -1. If `shape` is 1-D or higher, then the operation returns a tensor with shape
`shape` filled with the values of `tensor`. In this case, the number of
elements implied by `shape` must be the same as the number of elements in
`tensor`. For example: ```
# tensor 't' is [1, 2, 3, 4, 5, 6, 7, 8, 9]
# tensor 't' has shape [9]
reshape(t, [3, 3]) ==> [[1, 2, 3],
[4, 5, 6],
[7, 8, 9]] # tensor 't' is [[[1, 1], [2, 2]],
# [[3, 3], [4, 4]]]
# tensor 't' has shape [2, 2, 2]
reshape(t, [2, 4]) ==> [[1, 1, 2, 2],
[3, 3, 4, 4]] # tensor 't' is [[[1, 1, 1],
# [2, 2, 2]],
# [[3, 3, 3],
# [4, 4, 4]],
# [[5, 5, 5],
# [6, 6, 6]]]
# tensor 't' has shape [3, 2, 3]
# pass '[-1]' to flatten 't'
reshape(t, [-1]) ==> [1, 1, 1, 2, 2, 2, 3, 3, 3, 4, 4, 4, 5, 5, 5, 6, 6, 6] # -1 can also be used to infer the shape # -1 is inferred to be 9:
reshape(t, [2, -1]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3],
[4, 4, 4, 5, 5, 5, 6, 6, 6]]
# -1 is inferred to be 2:
reshape(t, [-1, 9]) ==> [[1, 1, 1, 2, 2, 2, 3, 3, 3],
[4, 4, 4, 5, 5, 5, 6, 6, 6]]
# -1 is inferred to be 3:
reshape(t, [ 2, -1, 3]) ==> [[[1, 1, 1],
[2, 2, 2],
[3, 3, 3]],
[[4, 4, 4],
[5, 5, 5],
[6, 6, 6]]] # tensor 't' is [7]
# shape `[]` reshapes to a scalar
reshape(t, []) ==> 7
```
DType resource get; set;
PythonFunctionContainer resource_create_op_fn get;
PythonFunctionContainer resource_initialized_op_fn get;
PythonFunctionContainer resource_using_op_fn get;
HeadingAxes rest_of_the_axes get;
A placeholder for the rest of the axes.
Show Example
Slice the last dimension from 1 to 2: tf.constant(0, shape: new[]{ 2, 3, 4})[rest_of_the_axes, 1..2]
PythonFunctionContainer restrict_fn get;
PythonFunctionContainer reverse_fn_ get;
PythonFunctionContainer reverse_sequence_fn get;
Reverses variable length slices. This op first slices `input` along the dimension `batch_axis`, and for each
slice `i`, reverses the first `seq_lengths[i]` elements along
the dimension `seq_axis`. The elements of `seq_lengths` must obey `seq_lengths[i] <= input.dims[seq_dim]`,
and `seq_lengths` must be a vector of length `input.dims[batch_dim]`. The output slice `i` along dimension `batch_axis` is then given by input
slice `i`, with the first `seq_lengths[i]` slices along dimension
`seq_axis` reversed. For example: ```
# Given this:
batch_dim = 0
seq_dim = 1
input.dims = (4, 8,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0, 0:7, :,...] = input[0, 7:0:-1, :,...]
output[1, 0:2, :,...] = input[1, 2:0:-1, :,...]
output[2, 0:3, :,...] = input[2, 3:0:-1, :,...]
output[3, 0:5, :,...] = input[3, 5:0:-1, :,...] # while entries past seq_lens are copied through:
output[0, 7:, :,...] = input[0, 7:, :,...]
output[1, 2:, :,...] = input[1, 2:, :,...]
output[2, 3:, :,...] = input[2, 3:, :,...]
output[3, 2:, :,...] = input[3, 2:, :,...]
``` In contrast, if: ```
# Given this:
batch_dim = 2
seq_dim = 0
input.dims = (8, ?, 4,...)
seq_lengths = [7, 2, 3, 5] # then slices of input are reversed on seq_dim, but only up to seq_lengths:
output[0:7, :, 0, :,...] = input[7:0:-1, :, 0, :,...]
output[0:2, :, 1, :,...] = input[2:0:-1, :, 1, :,...]
output[0:3, :, 2, :,...] = input[3:0:-1, :, 2, :,...]
output[0:5, :, 3, :,...] = input[5:0:-1, :, 3, :,...] # while entries past seq_lens are copied through:
output[7:, :, 0, :,...] = input[7:, :, 0, :,...]
output[2:, :, 1, :,...] = input[2:, :, 1, :,...]
output[3:, :, 2, :,...] = input[3:, :, 2, :,...]
output[2:, :, 3, :,...] = input[2:, :, 3, :,...]
```
PythonFunctionContainer rint_fn get;
Returns element-wise integer closest to x. If the result is midway between two representable values,
the even representable is chosen.
For example: ```
rint(-1.5) ==> -2.0
rint(0.5000001) ==> 1.0
rint([-1.7, -1.5, -0.2, 0.2, 1.5, 1.7, 2.0]) ==> [-2., -2., -0., 0., 2., 2., 2.]
```
PythonFunctionContainer roll_fn get;
Rolls the elements of a tensor along an axis. The elements are shifted positively (towards larger indices) by the offset of
`shift` along the dimension of `axis`. Negative `shift` values will shift
elements in the opposite direction. Elements that roll passed the last position
will wrap around to the first and vice versa. Multiple shifts along multiple
axes may be specified. For example: ```
# 't' is [0, 1, 2, 3, 4]
roll(t, shift=2, axis=0) ==> [3, 4, 0, 1, 2] # shifting along multiple dimensions
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[1, -2], axis=[0, 1]) ==> [[7, 8, 9, 5, 6], [2, 3, 4, 0, 1]] # shifting along the same axis multiple times
# 't' is [[0, 1, 2, 3, 4], [5, 6, 7, 8, 9]]
roll(t, shift=[2, -3], axis=[1, 1]) ==> [[1, 2, 3, 4, 0], [6, 7, 8, 9, 5]]
```
PythonFunctionContainer round_fn get;
Rounds the values of a tensor to the nearest integer, element-wise. Rounds half to even. Also known as bankers rounding. If you want to round
according to the current system rounding mode use tf::cint.
Show Example
x = tf.constant([0.9, 2.5, 2.3, 1.5, -4.5])
tf.round(x) # [ 1.0, 2.0, 2.0, 2.0, -4.0 ]
PythonFunctionContainer routing_function_fn get;
PythonFunctionContainer routing_gradient_fn get;
PythonFunctionContainer rpc_fn get;
PythonFunctionContainer rsqrt_fn get;
Computes reciprocal of square root of x element-wise. I.e., \\(y = 1 / \sqrt{x}\\).
object s get; set;
object s_dyn get; set;
PythonFunctionContainer saturate_cast_fn get;
Performs a safe saturating cast of `value` to `dtype`. This function casts the input to `dtype` without applying any scaling. If
there is a danger that values would over or underflow in the cast, this op
applies the appropriate clamping before the cast.
PythonFunctionContainer scalar_mul_fn get;
Multiplies a scalar times a `Tensor` or `IndexedSlices` object. Intended for use in gradient code which might deal with `IndexedSlices`
objects, which are easy to multiply by a scalar but more expensive to
multiply with arbitrary tensors.
PythonFunctionContainer scan_fn get;
scan on the list of tensors unpacked from `elems` on dimension 0. The simplest version of `scan` repeatedly applies the callable `fn` to a
sequence of elements from first to last. The elements are made of the tensors
unpacked from `elems` on dimension 0. The callable fn takes two tensors as
arguments. The first argument is the accumulated value computed from the
preceding invocation of fn, and the second is the value at the current
position of `elems`. If `initializer` is None, `elems` must contain at least
one element, and its first element is used as the initializer. Suppose that `elems` is unpacked into `values`, a list of tensors. The shape
of the result tensor is `[len(values)] + fn(initializer, values[0]).shape`.
If reverse=True, it's fn(initializer, values[-1]).shape. This method also allows multi-arity `elems` and accumulator. If `elems`
is a (possibly nested) list or tuple of tensors, then each of these tensors
must have a matching first (unpack) dimension. The second argument of
`fn` must match the structure of `elems`. If no `initializer` is provided, the output structure and dtypes of `fn`
are assumed to be the same as its input; and in this case, the first
argument of `fn` must match the structure of `elems`. If an `initializer` is provided, then the output of `fn` must have the same
structure as `initializer`; and the first argument of `fn` must match
this structure. For example, if `elems` is `(t1, [t2, t3])` and `initializer` is
`[i1, i2]` then an appropriate signature for `fn` in `python2` is:
`fn = lambda (acc_p1, acc_p2), (t1, [t2, t3]):` and `fn` must return a list,
`[acc_n1, acc_n2]`. An alternative correct signature for `fn`, and the
one that works in `python3`, is:
`fn = lambda a, t:`, where `a` and `t` correspond to the input tuples.
PythonFunctionContainer scatter_add_fn get;
Adds sparse updates to the variable referenced by `resource`. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the updated value.
Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions add. Requires `updates.shape = indices.shape + ref.shape[1:]`.


Show Example
# Scalar indices
ref[indices,...] += updates[...] # Vector indices (for each i)
ref[indices[i],...] += updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] += updates[i,..., j,...]
PythonFunctionContainer scatter_add_ndim_fn get;
PythonFunctionContainer scatter_div_fn get;
Divides a variable reference by sparse updates. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions divide. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.
Show Example
# Scalar indices
ref[indices,...] /= updates[...] # Vector indices (for each i)
ref[indices[i],...] /= updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] /= updates[i,..., j,...]
PythonFunctionContainer scatter_max_fn get;
Reduces sparse updates into a variable reference using the `max` operation. This operation computes # Scalar indices
ref[indices,...] = max(ref[indices,...], updates[...]) # Vector indices (for each i)
ref[indices[i],...] = max(ref[indices[i],...], updates[i,...]) # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] = max(ref[indices[i,..., j],...],
updates[i,..., j,...]) This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions combine. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.


PythonFunctionContainer scatter_min_fn get;
Reduces sparse updates into a variable reference using the `min` operation. This operation computes # Scalar indices
ref[indices,...] = min(ref[indices,...], updates[...]) # Vector indices (for each i)
ref[indices[i],...] = min(ref[indices[i],...], updates[i,...]) # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] = min(ref[indices[i,..., j],...],
updates[i,..., j,...]) This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions combine. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.


PythonFunctionContainer scatter_mul_fn get;
Multiplies sparse updates into a variable reference. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their contributions multiply. Requires `updates.shape = indices.shape + ref.shape[1:]` or `updates.shape =
[]`.
Show Example
# Scalar indices
ref[indices,...] *= updates[...] # Vector indices (for each i)
ref[indices[i],...] *= updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] *= updates[i,..., j,...]
PythonFunctionContainer scatter_nd_add_fn get;
Applies sparse addition to individual values or slices in a Variable. `ref` is a `Tensor` with rank `P` and `indices` is a `Tensor` of rank `Q`. `indices` must be integer tensor, containing indices into `ref`.
It must be shape `[d_0,..., d_{Q-2}, K]` where `0 < K <= P`. The innermost dimension of `indices` (with length `K`) corresponds to
indices into elements (if `K = P`) or slices (if `K < P`) along the `K`th
dimension of `ref`. `updates` is `Tensor` of rank `Q-1+P-K` with shape: ```
[d_0,..., d_{Q-2}, ref.shape[K],..., ref.shape[P-1]]
``` For example, say we want to add 4 scattered elements to a rank-1 tensor to
8 elements. In Python, that addition would look like this:
The resulting update to ref would look like this: [1, 13, 3, 14, 14, 6, 7, 20] See
tf.scatter_nd for more details about how to make updates to
slices.
Show Example
ref = tf.Variable([1, 2, 3, 4, 5, 6, 7, 8])
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
add = tf.compat.v1.scatter_nd_add(ref, indices, updates)
with tf.compat.v1.Session() as sess:
print sess.run(add)
PythonFunctionContainer scatter_nd_fn get;
Scatter `updates` into a new tensor according to `indices`. Creates a new tensor by applying sparse `updates` to individual values or
slices within a tensor (initially zero for numeric, empty for string) of
the given `shape` according to indices. This operator is the inverse of the
 In Python, this scatter operation would look like this:
The resulting tensor would look like this: [0, 11, 0, 10, 9, 0, 0, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values.
In Python, this scatter operation would look like this:
The resulting tensor would look like this: [0, 11, 0, 10, 9, 0, 0, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values.
 In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
tf.gather_nd operator which extracts values or slices from a given tensor. This operation is similar to tensor_scatter_add, except that the tensor is
zero-initialized. Calling `tf.scatter_nd(indices, values, shape)` is identical
to `tensor_scatter_add(tf.zeros(shape, values.dtype), indices, values)` If `indices` contains duplicates, then their updates are accumulated (summed). **WARNING**: The order in which updates are applied is nondeterministic, so the
output will be nondeterministic if `indices` contains duplicates -- because
of some numerical approximation issues, numbers summed in different order
may yield different results. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of scatter is to insert individual elements in a tensor by
index. For example, say we want to insert 4 scattered elements in a rank-1
tensor with 8 elements. 

Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
shape = tf.constant([8])
scatter = tf.scatter_nd(indices, updates, shape)
with tf.Session() as sess:
print(sess.run(scatter))
PythonFunctionContainer scatter_nd_sub_fn get;
Applies sparse subtraction to individual values or slices in a Variable. `ref` is a `Tensor` with rank `P` and `indices` is a `Tensor` of rank `Q`. `indices` must be integer tensor, containing indices into `ref`.
It must be shape `[d_0,..., d_{Q-2}, K]` where `0 < K <= P`. The innermost dimension of `indices` (with length `K`) corresponds to
indices into elements (if `K = P`) or slices (if `K < P`) along the `K`th
dimension of `ref`. `updates` is `Tensor` of rank `Q-1+P-K` with shape: ```
[d_0,..., d_{Q-2}, ref.shape[K],..., ref.shape[P-1]]
``` For example, say we want to subtract 4 scattered elements from a rank-1 tensor
with 8 elements. In Python, that update would look like this:
The resulting update to ref would look like this: [1, -9, 3, -6, -6, 6, 7, -4] See
tf.scatter_nd for more details about how to make updates to
slices.
Show Example
ref = tf.Variable([1, 2, 3, 4, 5, 6, 7, 8])
indices = tf.constant([[4], [3], [1] ,[7]])
updates = tf.constant([9, 10, 11, 12])
op = tf.compat.v1.scatter_nd_sub(ref, indices, updates)
with tf.compat.v1.Session() as sess:
print sess.run(op)
PythonFunctionContainer scatter_nd_update_fn get;
Applies sparse `updates` to individual values or slices in a Variable. `ref` is a `Tensor` with rank `P` and `indices` is a `Tensor` of rank `Q`. `indices` must be integer tensor, containing indices into `ref`.
It must be shape `[d_0,..., d_{Q-2}, K]` where `0 < K <= P`. The innermost dimension of `indices` (with length `K`) corresponds to
indices into elements (if `K = P`) or slices (if `K < P`) along the `K`th
dimension of `ref`. `updates` is `Tensor` of rank `Q-1+P-K` with shape: ```
[d_0,..., d_{Q-2}, ref.shape[K],..., ref.shape[P-1]].
``` For example, say we want to update 4 scattered elements to a rank-1 tensor to
8 elements. In Python, that update would look like this:
The resulting update to ref would look like this: [1, 11, 3, 10, 9, 6, 7, 12] See
tf.scatter_nd for more details about how to make updates to
slices.
Show Example
ref = tf.Variable([1, 2, 3, 4, 5, 6, 7, 8])
indices = tf.constant([[4], [3], [1] ,[7]])
updates = tf.constant([9, 10, 11, 12])
update = tf.compat.v1.scatter_nd_update(ref, indices, updates)
with tf.compat.v1.Session() as sess:
print sess.run(update)
PythonFunctionContainer scatter_sub_fn get;
Subtracts sparse updates to a variable reference.
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. Duplicate entries are handled correctly: if multiple `indices` reference
the same location, their (negated) contributions add. Requires `updates.shape = indices.shape + ref.shape[1:]` or
`updates.shape = []`.
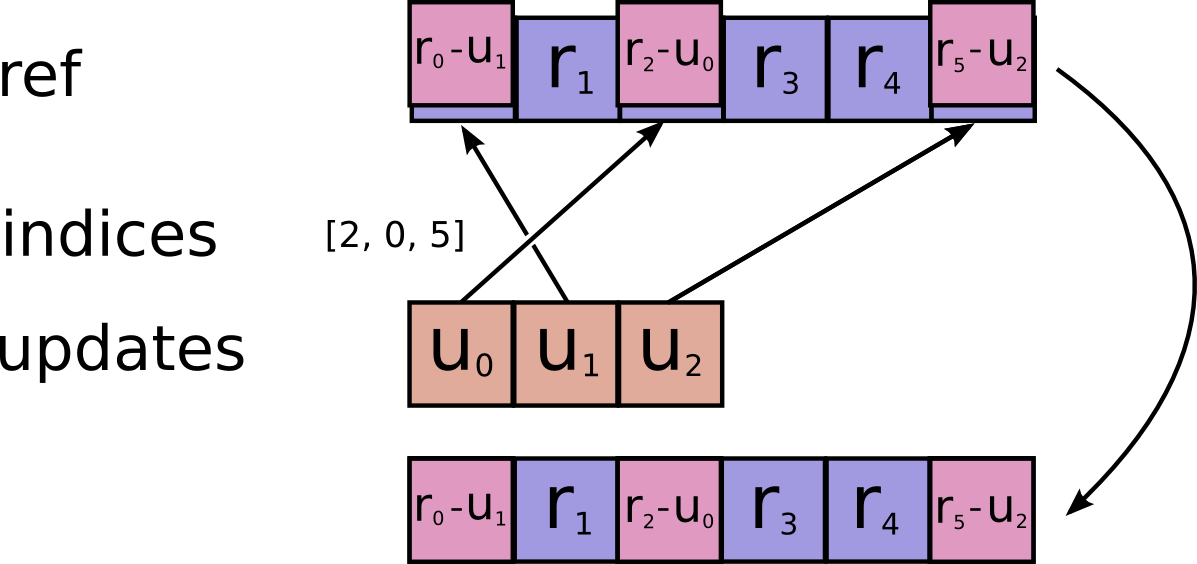
Show Example
# Scalar indices
ref[indices,...] -= updates[...] # Vector indices (for each i)
ref[indices[i],...] -= updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] -= updates[i,..., j,...]
PythonFunctionContainer scatter_update_fn get;
Applies sparse updates to a variable reference. This operation computes
This operation outputs `ref` after the update is done.
This makes it easier to chain operations that need to use the reset value. If values in `ref` is to be updated more than once, because there are
duplicate entries in `indices`, the order at which the updates happen
for each value is undefined. Requires `updates.shape = indices.shape + ref.shape[1:]`.


Show Example
# Scalar indices
ref[indices,...] = updates[...] # Vector indices (for each i)
ref[indices[i],...] = updates[i,...] # High rank indices (for each i,..., j)
ref[indices[i,..., j],...] = updates[i,..., j,...]
PythonFunctionContainer searchsorted_fn get;
Searches input tensor for values on the innermost dimension. A 2-D example: ```
sorted_sequence = [[0, 3, 9, 9, 10],
[1, 2, 3, 4, 5]]
values = [[2, 4, 9],
[0, 2, 6]] result = searchsorted(sorted_sequence, values, side="left") result == [[1, 2, 2],
[0, 1, 5]] result = searchsorted(sorted_sequence, values, side="right") result == [[1, 2, 4],
[0, 2, 5]]
```
PythonFunctionContainer segment_max_fn get;
Computes the maximum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \max_j(data_j)\\) where `max` is over `j` such
that `segment_ids[j] == i`. If the max is empty for a given segment ID `i`, `output[i] = 0`.
 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_max(c, tf.constant([0, 0, 1]))
# ==> [[4, 3, 3, 4],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_max(c, tf.constant([0, 0, 1]))
# ==> [[4, 3, 3, 4],
# [5, 6, 7, 8]]
```

PythonFunctionContainer segment_mean_fn get;
Computes the mean along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \frac{\sum_j data_j}{N}\\) where `mean` is
over `j` such that `segment_ids[j] == i` and `N` is the total number of
values summed. If the mean is empty for a given segment ID `i`, `output[i] = 0`.
 For example: ```
c = tf.constant([[1.0,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_mean(c, tf.constant([0, 0, 1]))
# ==> [[2.5, 2.5, 2.5, 2.5],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1.0,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_mean(c, tf.constant([0, 0, 1]))
# ==> [[2.5, 2.5, 2.5, 2.5],
# [5, 6, 7, 8]]
```

PythonFunctionContainer segment_min_fn get;
Computes the minimum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \min_j(data_j)\\) where `min` is over `j` such
that `segment_ids[j] == i`. If the min is empty for a given segment ID `i`, `output[i] = 0`.
 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_min(c, tf.constant([0, 0, 1]))
# ==> [[1, 2, 2, 1],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_min(c, tf.constant([0, 0, 1]))
# ==> [[1, 2, 2, 1],
# [5, 6, 7, 8]]
```

PythonFunctionContainer segment_prod_fn get;
Computes the product along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \prod_j data_j\\) where the product is over `j` such
that `segment_ids[j] == i`. If the product is empty for a given segment ID `i`, `output[i] = 1`.
 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_prod(c, tf.constant([0, 0, 1]))
# ==> [[4, 6, 6, 4],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_prod(c, tf.constant([0, 0, 1]))
# ==> [[4, 6, 6, 4],
# [5, 6, 7, 8]]
```

PythonFunctionContainer segment_sum_fn get;
Computes the sum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output_i = \sum_j data_j\\) where sum is over `j` such
that `segment_ids[j] == i`. If the sum is empty for a given segment ID `i`, `output[i] = 0`.
 For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_sum(c, tf.constant([0, 0, 1]))
# ==> [[5, 5, 5, 5],
# [5, 6, 7, 8]]
```
For example: ```
c = tf.constant([[1,2,3,4], [4, 3, 2, 1], [5,6,7,8]])
tf.segment_sum(c, tf.constant([0, 0, 1]))
# ==> [[5, 5, 5, 5],
# [5, 6, 7, 8]]
```

PythonFunctionContainer self_adjoint_eig_fn get;
Computes the eigen decomposition of a batch of self-adjoint matrices. Computes the eigenvalues and eigenvectors of the innermost N-by-N matrices
in `tensor` such that
`tensor[...,:,:] * v[..., :,i] = e[..., i] * v[...,:,i]`, for i=0...N-1.
PythonFunctionContainer self_adjoint_eigvals_fn get;
Computes the eigenvalues of one or more self-adjoint matrices. Note: If your program backpropagates through this function, you should replace
it with a call to tf.linalg.eigh (possibly ignoring the second output) to
avoid computing the eigen decomposition twice. This is because the
eigenvectors are used to compute the gradient w.r.t. the eigenvalues. See
_SelfAdjointEigV2Grad in linalg_grad.py.
PythonFunctionContainer sequence_file_dataset_fn get;
PythonFunctionContainer sequence_mask_fn get;
Returns a mask tensor representing the first N positions of each cell. If `lengths` has shape `[d_1, d_2,..., d_n]` the resulting tensor `mask` has
dtype `dtype` and shape `[d_1, d_2,..., d_n, maxlen]`, with ```
mask[i_1, i_2,..., i_n, j] = (j < lengths[i_1, i_2,..., i_n])
``` Examples:
Show Example
tf.sequence_mask([1, 3, 2], 5) # [[True, False, False, False, False],
# [True, True, True, False, False],
# [True, True, False, False, False]] tf.sequence_mask([[1, 3],[2,0]]) # [[[True, False, False],
# [True, True, True]],
# [[True, True, False],
# [False, False, False]]]
PythonFunctionContainer serialize_many_sparse_fn get;
Serialize `N`-minibatch `SparseTensor` into an `[N, 3]` `Tensor`. The `SparseTensor` must have rank `R` greater than 1, and the first dimension
is treated as the minibatch dimension. Elements of the `SparseTensor`
must be sorted in increasing order of this first dimension. The serialized
`SparseTensor` objects going into each row of the output `Tensor` will have
rank `R-1`. The minibatch size `N` is extracted from `sparse_shape[0]`.
PythonFunctionContainer serialize_sparse_fn get;
Serialize a `SparseTensor` into a 3-vector (1-D `Tensor`) object.
PythonFunctionContainer serialize_tensor_fn get;
Transforms a Tensor into a serialized TensorProto proto.
PythonFunctionContainer set_random_seed_fn get;
Sets the graph-level random seed for the default graph. Operations that rely on a random seed actually derive it from two seeds:
the graph-level and operation-level seeds. This sets the graph-level seed. Its interactions with operation-level seeds is as follows: 1. If neither the graph-level nor the operation seed is set:
A random seed is used for this op.
2. If the graph-level seed is set, but the operation seed is not:
The system deterministically picks an operation seed in conjunction
with the graph-level seed so that it gets a unique random sequence.
3. If the graph-level seed is not set, but the operation seed is set:
A default graph-level seed and the specified operation seed are used to
determine the random sequence.
4. If both the graph-level and the operation seed are set:
Both seeds are used in conjunction to determine the random sequence. To illustrate the user-visible effects, consider these examples: To generate different sequences across sessions, set neither
graph-level nor op-level seeds:
To generate the same repeatable sequence for an op across sessions, set the
seed for the op:
To make the random sequences generated by all ops be repeatable across
sessions, set a graph-level seed:
Show Example
a = tf.random.uniform([1])
b = tf.random.normal([1]) print("Session 1")
with tf.compat.v1.Session() as sess1:
print(sess1.run(a)) # generates 'A1'
print(sess1.run(a)) # generates 'A2'
print(sess1.run(b)) # generates 'B1'
print(sess1.run(b)) # generates 'B2' print("Session 2")
with tf.compat.v1.Session() as sess2:
print(sess2.run(a)) # generates 'A3'
print(sess2.run(a)) # generates 'A4'
print(sess2.run(b)) # generates 'B3'
print(sess2.run(b)) # generates 'B4'
PythonFunctionContainer setdiff1d_fn get;
Computes the difference between two lists of numbers or strings. Given a list `x` and a list `y`, this operation returns a list `out` that
represents all values that are in `x` but not in `y`. The returned list `out`
is sorted in the same order that the numbers appear in `x` (duplicates are
preserved). This operation also returns a list `idx` that represents the
position of each `out` element in `x`. In other words: `out[i] = x[idx[i]] for i in [0, 1,..., len(out) - 1]` For example, given this input: ```
x = [1, 2, 3, 4, 5, 6]
y = [1, 3, 5]
``` This operation would return: ```
out ==> [2, 4, 6]
idx ==> [1, 3, 5]
```
PythonFunctionContainer shape_fn get;
Returns the shape of a tensor. This operation returns a 1-D integer tensor representing the shape of `input`.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.shape(t) # [2, 2, 3]
PythonFunctionContainer shape_n_fn get;
Returns shape of tensors.
PythonFunctionContainer sigmoid_fn get;
Computes sigmoid of `x` element-wise. Specifically, `y = 1 / (1 + exp(-x))`.
PythonFunctionContainer sign_fn get;
Returns an element-wise indication of the sign of a number. `y = sign(x) = -1` if `x < 0`; 0 if `x == 0`; 1 if `x > 0`. For complex numbers, `y = sign(x) = x / |x|` if `x != 0`, otherwise `y = 0`.
PythonFunctionContainer simple_fn get;
PythonFunctionContainer simple_struct_fn get;
PythonFunctionContainer sin_fn get;
Computes sine of x element-wise. Given an input tensor, this function computes sine of every
element in the tensor. Input range is `(-inf, inf)` and
output range is `[-1,1]`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 200, 10, float("inf")])
tf.math.sin(x) ==> [nan -0.4121185 -0.47942555 0.84147096 0.9320391 -0.87329733 -0.54402107 nan]
PythonFunctionContainer single_image_random_dot_stereograms_fn get;
PythonFunctionContainer sinh_fn get;
Computes hyperbolic sine of x element-wise. Given an input tensor, this function computes hyperbolic sine of every
element in the tensor. Input range is `[-inf,inf]` and output range
is `[-inf,inf]`.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 2, 10, float("inf")])
tf.math.sinh(x) ==> [-inf -4.0515420e+03 -5.2109528e-01 1.1752012e+00 1.5094614e+00 3.6268604e+00 1.1013232e+04 inf]
PythonFunctionContainer size_fn get;
Returns the size of a tensor. Returns a 0-D `Tensor` representing the number of elements in `input`
of type `out_type`. Defaults to tf.int32.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]])
tf.size(t) # 12
PythonFunctionContainer skip_gram_generate_candidates_fn get;
PythonFunctionContainer slice_fn get;
Extracts a slice from a tensor. This operation extracts a slice of size `size` from a tensor `input_` starting
at the location specified by `begin`. The slice `size` is represented as a
tensor shape, where `size[i]` is the number of elements of the 'i'th dimension
of `input_` that you want to slice. The starting location (`begin`) for the
slice is represented as an offset in each dimension of `input_`. In other
words, `begin[i]` is the offset into the i'th dimension of `input_` that you
want to slice from. Note that
tf.Tensor.__getitem__ is typically a more pythonic way to
perform slices, as it allows you to write `foo[3:7, :-2]` instead of
`tf.slice(foo, [3, 0], [4, foo.get_shape()[1]-2])`. `begin` is zero-based; `size` is one-based. If `size[i]` is -1,
all remaining elements in dimension i are included in the
slice. In other words, this is equivalent to setting: `size[i] = input_.dim_size(i) - begin[i]` This operation requires that: `0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]`
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.slice(t, [1, 0, 0], [1, 1, 3]) # [[[3, 3, 3]]]
tf.slice(t, [1, 0, 0], [1, 2, 3]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.slice(t, [1, 0, 0], [2, 1, 3]) # [[[3, 3, 3]],
# [[5, 5, 5]]]
PythonFunctionContainer sort_fn get;
Sorts a tensor. Usage:
Show Example
import tensorflow as tf
a = [1, 10, 26.9, 2.8, 166.32, 62.3]
b = tf.sort(a,axis=-1,direction='ASCENDING',name=None)
c = tf.keras.backend.eval(b)
# Here, c = [ 1. 2.8 10. 26.9 62.3 166.32]
PythonFunctionContainer space_to_batch_fn get;
SpaceToBatch for 4-D tensors of type T. This is a legacy version of the more general SpaceToBatchND. Zero-pads and then rearranges (permutes) blocks of spatial data into batch.
More specifically, this op outputs a copy of the input tensor where values from
the `height` and `width` dimensions are moved to the `batch` dimension. After
the zero-padding, both `height` and `width` of the input must be divisible by the
block size.
PythonFunctionContainer space_to_batch_nd_fn get;
SpaceToBatch for N-D tensors of type T. This operation divides "spatial" dimensions `[1,..., M]` of the input into a
grid of blocks of shape `block_shape`, and interleaves these blocks with the
"batch" dimension (0) such that in the output, the spatial dimensions
`[1,..., M]` correspond to the position within the grid, and the batch
dimension combines both the position within a spatial block and the original
batch position. Prior to division into blocks, the spatial dimensions of the
input are optionally zero padded according to `paddings`. See below for a
precise description.
PythonFunctionContainer space_to_depth_fn get;
SpaceToDepth for tensors of type T. Rearranges blocks of spatial data, into depth. More specifically,
this op outputs a copy of the input tensor where values from the `height`
and `width` dimensions are moved to the `depth` dimension.
The attr `block_size` indicates the input block size. * Non-overlapping blocks of size `block_size x block size` are rearranged
into depth at each location.
* The depth of the output tensor is `block_size * block_size * input_depth`.
* The Y, X coordinates within each block of the input become the high order
component of the output channel index.
* The input tensor's height and width must be divisible by block_size. The `data_format` attr specifies the layout of the input and output tensors
with the following options:
"NHWC": `[ batch, height, width, channels ]`
"NCHW": `[ batch, channels, height, width ]`
"NCHW_VECT_C":
`qint8 [ batch, channels / 4, height, width, 4 ]` It is useful to consider the operation as transforming a 6-D Tensor.
e.g. for data_format = NHWC,
Each element in the input tensor can be specified via 6 coordinates,
ordered by decreasing memory layout significance as:
n,oY,bY,oX,bX,iC (where n=batch index, oX, oY means X or Y coordinates
within the output image, bX, bY means coordinates
within the input block, iC means input channels).
The output would be a transpose to the following layout:
n,oY,oX,bY,bX,iC This operation is useful for resizing the activations between convolutions
(but keeping all data), e.g. instead of pooling. It is also useful for training
purely convolutional models. For example, given an input of shape `[1, 2, 2, 1]`, data_format = "NHWC" and
block_size = 2: ```
x = [[[[1], [2]],
[[3], [4]]]]
``` This operation will output a tensor of shape `[1, 1, 1, 4]`: ```
[[[[1, 2, 3, 4]]]]
``` Here, the input has a batch of 1 and each batch element has shape `[2, 2, 1]`,
the corresponding output will have a single element (i.e. width and height are
both 1) and will have a depth of 4 channels (1 * block_size * block_size).
The output element shape is `[1, 1, 4]`. For an input tensor with larger depth, here of shape `[1, 2, 2, 3]`, e.g. ```
x = [[[[1, 2, 3], [4, 5, 6]],
[[7, 8, 9], [10, 11, 12]]]]
``` This operation, for block_size of 2, will return the following tensor of shape
`[1, 1, 1, 12]` ```
[[[[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12]]]]
``` Similarly, for the following input of shape `[1 4 4 1]`, and a block size of 2: ```
x = [[[[1], [2], [5], [6]],
[[3], [4], [7], [8]],
[[9], [10], [13], [14]],
[[11], [12], [15], [16]]]]
``` the operator will return the following tensor of shape `[1 2 2 4]`: ```
x = [[[[1, 2, 3, 4],
[5, 6, 7, 8]],
[[9, 10, 11, 12],
[13, 14, 15, 16]]]]
```
PythonFunctionContainer sparse_add_fn get;
Adds two tensors, at least one of each is a `SparseTensor`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(thresh)`. They will be removed in a future version.
Instructions for updating:
thresh is deprecated, use threshold instead If one `SparseTensor` and one `Tensor` are passed in, returns a `Tensor`. If
both arguments are `SparseTensor`s, this returns a `SparseTensor`. The order
of arguments does not matter. Use vanilla `tf.add()` for adding two dense
`Tensor`s. The shapes of the two operands must match: broadcasting is not supported. The indices of any input `SparseTensor` are assumed ordered in standard
lexicographic order. If this is not the case, before this step run
`SparseReorder` to restore index ordering. If both arguments are sparse, we perform "clipping" as follows. By default,
if two values sum to zero at some index, the output `SparseTensor` would still
include that particular location in its index, storing a zero in the
corresponding value slot. To override this, callers can specify `thresh`,
indicating that if the sum has a magnitude strictly smaller than `thresh`, its
corresponding value and index would then not be included. In particular,
`thresh == 0.0` (default) means everything is kept and actual thresholding
happens only for a positive value. For example, suppose the logical sum of two sparse operands is (densified): [ 2]
[.1 0]
[ 6 -.2] Then, * `thresh == 0` (the default): all 5 index/value pairs will be returned.
* `thresh == 0.11`: only.1 and 0 will vanish, and the remaining three
index/value pairs will be returned.
* `thresh == 0.21`:.1, 0, and -.2 will vanish.
PythonFunctionContainer sparse_concat_fn get;
Concatenates a list of `SparseTensor` along the specified dimension. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(concat_dim)`. They will be removed in a future version.
Instructions for updating:
concat_dim is deprecated, use axis instead Concatenation is with respect to the dense versions of each sparse input.
It is assumed that each inputs is a `SparseTensor` whose elements are ordered
along increasing dimension number. If expand_nonconcat_dim is False, all inputs' shapes must match, except for
the concat dimension. If expand_nonconcat_dim is True, then inputs' shapes are
allowed to vary among all inputs. The `indices`, `values`, and `shapes` lists must have the same length. If expand_nonconcat_dim is False, then the output shape is identical to the
inputs', except along the concat dimension, where it is the sum of the inputs'
sizes along that dimension. If expand_nonconcat_dim is True, then the output shape along the non-concat
dimensions will be expand to be the largest among all inputs, and it is the
sum of the inputs sizes along the concat dimension. The output elements will be resorted to preserve the sort order along
increasing dimension number. This op runs in `O(M log M)` time, where `M` is the total number of non-empty
values across all inputs. This is due to the need for an internal sort in
order to concatenate efficiently across an arbitrary dimension. For example, if `axis = 1` and the inputs are sp_inputs[0]: shape = [2, 3]
[0, 2]: "a"
[1, 0]: "b"
[1, 1]: "c" sp_inputs[1]: shape = [2, 4]
[0, 1]: "d"
[0, 2]: "e" then the output will be shape = [2, 7]
[0, 2]: "a"
[0, 4]: "d"
[0, 5]: "e"
[1, 0]: "b"
[1, 1]: "c" Graphically this is equivalent to doing [ a] concat [ d e ] = [ a d e ]
[b c ] [ ] [b c ] Another example, if 'axis = 1' and the inputs are sp_inputs[0]: shape = [3, 3]
[0, 2]: "a"
[1, 0]: "b"
[2, 1]: "c" sp_inputs[1]: shape = [2, 4]
[0, 1]: "d"
[0, 2]: "e" if expand_nonconcat_dim = False, this will result in an error. But if
expand_nonconcat_dim = True, this will result in: shape = [3, 7]
[0, 2]: "a"
[0, 4]: "d"
[0, 5]: "e"
[1, 0]: "b"
[2, 1]: "c" Graphically this is equivalent to doing [ a] concat [ d e ] = [ a d e ]
[b ] [ ] [b ]
[ c ] [ c ]
PythonFunctionContainer sparse_feature_cross_fn get;
PythonFunctionContainer sparse_feature_cross_v2_fn get;
PythonFunctionContainer sparse_fill_empty_rows_fn get;
Fills empty rows in the input 2-D `SparseTensor` with a default value. This op adds entries with the specified `default_value` at index
`[row, 0]` for any row in the input that does not already have a value. For example, suppose `sp_input` has shape `[5, 6]` and non-empty values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d Rows 1 and 4 are empty, so the output will be of shape `[5, 6]` with values: [0, 1]: a
[0, 3]: b
[1, 0]: default_value
[2, 0]: c
[3, 1]: d
[4, 0]: default_value Note that the input may have empty columns at the end, with no effect on
this op. The output `SparseTensor` will be in row-major order and will have the
same shape as the input. This op also returns an indicator vector such that empty_row_indicator[i] = True iff row i was an empty row.
PythonFunctionContainer sparse_mask_fn get;
Masks elements of `IndexedSlices`. Given an `IndexedSlices` instance `a`, returns another `IndexedSlices` that
contains a subset of the slices of `a`. Only the slices at indices not
specified in `mask_indices` are returned. This is useful when you need to extract a subset of slices in an
`IndexedSlices` object.
Show Example
# `a` contains slices at indices [12, 26, 37, 45] from a large tensor
# with shape [1000, 10]
a.indices # [12, 26, 37, 45]
tf.shape(a.values) # [4, 10] # `b` will be the subset of `a` slices at its second and third indices, so
# we want to mask its first and last indices (which are at absolute
# indices 12, 45)
b = tf.sparse.mask(a, [12, 45]) b.indices # [26, 37]
tf.shape(b.values) # [2, 10]
PythonFunctionContainer sparse_matmul_fn get;
Multiply matrix "a" by matrix "b". The inputs must be two-dimensional matrices and the inner dimension of "a" must
match the outer dimension of "b". Both "a" and "b" must be `Tensor`s not
`SparseTensor`s. This op is optimized for the case where at least one of "a" or
"b" is sparse, in the sense that they have a large proportion of zero values.
The breakeven for using this versus a dense matrix multiply on one platform was
30% zero values in the sparse matrix. The gradient computation of this operation will only take advantage of sparsity
in the input gradient when that gradient comes from a Relu.
PythonFunctionContainer sparse_maximum_fn get;
Returns the element-wise max of two SparseTensors. Assumes the two SparseTensors have the same shape, i.e., no broadcasting.
Example:
Show Example
sp_zero = sparse_tensor.SparseTensor([[0]], [0], [7])
sp_one = sparse_tensor.SparseTensor([[1]], [1], [7])
res = tf.sparse.maximum(sp_zero, sp_one).eval()
# "res" should be equal to SparseTensor([[0], [1]], [0, 1], [7]).
PythonFunctionContainer sparse_merge_fn get;
Combines a batch of feature ids and values into a single `SparseTensor`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
No similar op available at this time. The most common use case for this function occurs when feature ids and
their corresponding values are stored in `Example` protos on disk.
`parse_example` will return a batch of ids and a batch of values, and this
function joins them into a single logical `SparseTensor` for use in
functions such as `sparse_tensor_dense_matmul`, `sparse_to_dense`, etc. The `SparseTensor` returned by this function has the following properties: - `indices` is equivalent to `sp_ids.indices` with the last
dimension discarded and replaced with `sp_ids.values`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn, vocab_size]`. For example, consider the following feature vectors:
These might be stored sparsely in the following Example protos by storing
only the feature ids (column number if the vectors are treated as a matrix)
of the non-zero elements and the corresponding values:
The result of calling parse_example on these examples will produce a
dictionary with entries for "ids" and "values". Passing those two objects
to this function along with vocab_size=6, will produce a `SparseTensor` that
sparsely represents all three instances. Namely, the `indices` property will
contain the coordinates of the non-zero entries in the feature matrix (the
first dimension is the row number in the matrix, i.e., the index within the
batch, and the second dimension is the column number, i.e., the feature id);
`values` will contain the actual values. `shape` will be the shape of the
original matrix, i.e., (3, 6). For our example above, the output will be
equal to:
This method generalizes to higher-dimensions by simply providing a list for
both the sp_ids as well as the vocab_size.
In this case the resulting `SparseTensor` has the following properties:
- `indices` is equivalent to `sp_ids[0].indices` with the last
dimension discarded and concatenated with
`sp_ids[0].values, sp_ids[1].values,...`.
- `values` is simply `sp_values.values`.
- If `sp_ids.dense_shape = [D0, D1,..., Dn, K]`, then
`output.shape = [D0, D1,..., Dn] + vocab_size`.
Show Example
vector1 = [-3, 0, 0, 0, 0, 0]
vector2 = [ 0, 1, 0, 4, 1, 0]
vector3 = [ 5, 0, 0, 9, 0, 0]
PythonFunctionContainer sparse_minimum_fn get;
Returns the element-wise min of two SparseTensors. Assumes the two SparseTensors have the same shape, i.e., no broadcasting.
Example:
Show Example
sp_zero = sparse_tensor.SparseTensor([[0]], [0], [7])
sp_one = sparse_tensor.SparseTensor([[1]], [1], [7])
res = tf.sparse.minimum(sp_zero, sp_one).eval()
# "res" should be equal to SparseTensor([[0], [1]], [0, 0], [7]).
PythonFunctionContainer sparse_placeholder_fn get;
Inserts a placeholder for a sparse tensor that will be always fed. **Important**: This sparse tensor will produce an error if evaluated.
Its value must be fed using the `feed_dict` optional argument to
`Session.run()`, `Tensor.eval()`, or `Operation.run()`.
@compatibility{eager} Placeholders are not compatible with eager execution.
Show Example
x = tf.compat.v1.sparse.placeholder(tf.float32)
y = tf.sparse.reduce_sum(x) with tf.compat.v1.Session() as sess:
print(sess.run(y)) # ERROR: will fail because x was not fed. indices = np.array([[3, 2, 0], [4, 5, 1]], dtype=np.int64)
values = np.array([1.0, 2.0], dtype=np.float32)
shape = np.array([7, 9, 2], dtype=np.int64)
print(sess.run(y, feed_dict={
x: tf.compat.v1.SparseTensorValue(indices, values, shape)})) # Will
succeed.
print(sess.run(y, feed_dict={
x: (indices, values, shape)})) # Will succeed. sp = tf.SparseTensor(indices=indices, values=values, dense_shape=shape)
sp_value = sp.eval(session=sess)
print(sess.run(y, feed_dict={x: sp_value})) # Will succeed.
PythonFunctionContainer sparse_reduce_max_fn get;
Computes the max of elements across dimensions of a SparseTensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(reduction_axes)`. They will be removed in a future version.
Instructions for updating:
reduction_axes is deprecated, use axis instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_max()`. In particular, this Op also returns a dense `Tensor`
instead of a sparse one. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
similar to the indexing rules in Python. The values not defined in `sp_input` don't participate in the reduce max,
as opposed to be implicitly assumed 0 -- hence it can return negative values
for sparse `reduction_axes`. But, in case there are no values in
`reduction_axes`, it will reduce to 0. See second example below.
Show Example
# 'x' represents [[1, ?, 2]
# [?, 3, ?]]
# where ? is implicitly-zero.
tf.sparse.reduce_max(x) ==> 3
tf.sparse.reduce_max(x, 0) ==> [1, 3, 2]
tf.sparse.reduce_max(x, 1) ==> [2, 3] # Can also use -1 as the axis.
tf.sparse.reduce_max(x, 1, keepdims=True) ==> [[2], [3]]
tf.sparse.reduce_max(x, [0, 1]) ==> 3 # 'y' represents [[-7, ?]
# [ 4, 3]
# [ ?, ?]
tf.sparse.reduce_max(x, 1) ==> [-7, 4, 0]
PythonFunctionContainer sparse_reduce_max_sparse_fn get;
Computes the max of elements across dimensions of a SparseTensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_max()`. In contrast to SparseReduceSum, this Op returns a
SparseTensor. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
which are interpreted according to the indexing rules in Python.
PythonFunctionContainer sparse_reduce_sum_fn get;
Computes the sum of elements across dimensions of a SparseTensor. (deprecated arguments) (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead Warning: SOME ARGUMENTS ARE DEPRECATED: `(reduction_axes)`. They will be removed in a future version.
Instructions for updating:
reduction_axes is deprecated, use axis instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_sum()`. In particular, this Op also returns a dense `Tensor`
instead of a sparse one. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
similar to the indexing rules in Python.
Show Example
# 'x' represents [[1, ?, 1]
# [?, 1, ?]]
# where ? is implicitly-zero.
tf.sparse.reduce_sum(x) ==> 3
tf.sparse.reduce_sum(x, 0) ==> [1, 1, 1]
tf.sparse.reduce_sum(x, 1) ==> [2, 1] # Can also use -1 as the axis.
tf.sparse.reduce_sum(x, 1, keepdims=True) ==> [[2], [1]]
tf.sparse.reduce_sum(x, [0, 1]) ==> 3
PythonFunctionContainer sparse_reduce_sum_sparse_fn get;
Computes the sum of elements across dimensions of a SparseTensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(keep_dims)`. They will be removed in a future version.
Instructions for updating:
keep_dims is deprecated, use keepdims instead This Op takes a SparseTensor and is the sparse counterpart to
`tf.reduce_sum()`. In contrast to SparseReduceSum, this Op returns a
SparseTensor. Note: A gradient is not defined for this function, so it can't be used
in training models that need gradient descent. Reduces `sp_input` along the dimensions given in `reduction_axes`. Unless
`keepdims` is true, the rank of the tensor is reduced by 1 for each entry in
`reduction_axes`. If `keepdims` is true, the reduced dimensions are retained
with length 1. If `reduction_axes` has no entries, all dimensions are reduced, and a tensor
with a single element is returned. Additionally, the axes can be negative,
which are interpreted according to the indexing rules in Python.
PythonFunctionContainer sparse_reorder_fn get;
Reorders a `SparseTensor` into the canonical, row-major ordering. Note that by convention, all sparse ops preserve the canonical ordering
along increasing dimension number. The only time ordering can be violated
is during manual manipulation of the indices and values to add entries. Reordering does not affect the shape of the `SparseTensor`. For example, if `sp_input` has shape `[4, 5]` and `indices` / `values`: [0, 3]: b
[0, 1]: a
[3, 1]: d
[2, 0]: c then the output will be a `SparseTensor` of shape `[4, 5]` and
`indices` / `values`: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d
PythonFunctionContainer sparse_reset_shape_fn get;
Resets the shape of a `SparseTensor` with indices and values unchanged. If `new_shape` is None, returns a copy of `sp_input` with its shape reset
to the tight bounding box of `sp_input`. This will be a shape consisting of
all zeros if sp_input has no values. If `new_shape` is provided, then it must be larger or equal in all dimensions
compared to the shape of `sp_input`. When this condition is met, the returned
SparseTensor will have its shape reset to `new_shape` and its indices and
values unchanged from that of `sp_input.` For example: Consider a `sp_input` with shape [2, 3, 5]: [0, 0, 1]: a
[0, 1, 0]: b
[0, 2, 2]: c
[1, 0, 3]: d - It is an error to set `new_shape` as [3, 7] since this represents a
rank-2 tensor while `sp_input` is rank-3. This is either a ValueError
during graph construction (if both shapes are known) or an OpError during
run time. - Setting `new_shape` as [2, 3, 6] will be fine as this shape is larger or
equal in every dimension compared to the original shape [2, 3, 5]. - On the other hand, setting new_shape as [2, 3, 4] is also an error: The
third dimension is smaller than the original shape [2, 3, 5] (and an
`InvalidArgumentError` will be raised). - If `new_shape` is None, the returned SparseTensor will have a shape
[2, 3, 4], which is the tight bounding box of `sp_input`.
PythonFunctionContainer sparse_reshape_fn get;
Reshapes a `SparseTensor` to represent values in a new dense shape. This operation has the same semantics as `reshape` on the represented dense
tensor. The indices of non-empty values in `sp_input` are recomputed based
on the new dense shape, and a new `SparseTensor` is returned containing the
new indices and new shape. The order of non-empty values in `sp_input` is
unchanged. If one component of `shape` is the special value -1, the size of that
dimension is computed so that the total dense size remains constant. At
most one component of `shape` can be -1. The number of dense elements
implied by `shape` must be the same as the number of dense elements
originally represented by `sp_input`. For example, if `sp_input` has shape `[2, 3, 6]` and `indices` / `values`: [0, 0, 0]: a
[0, 0, 1]: b
[0, 1, 0]: c
[1, 0, 0]: d
[1, 2, 3]: e and `shape` is `[9, -1]`, then the output will be a `SparseTensor` of
shape `[9, 4]` and `indices` / `values`: [0, 0]: a
[0, 1]: b
[1, 2]: c
[4, 2]: d
[8, 1]: e
PythonFunctionContainer sparse_retain_fn get;
Retains specified non-empty values within a `SparseTensor`. For example, if `sp_input` has shape `[4, 5]` and 4 non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c
[3, 1]: d and `to_retain = [True, False, False, True]`, then the output will
be a `SparseTensor` of shape `[4, 5]` with 2 non-empty values: [0, 1]: a
[3, 1]: d
PythonFunctionContainer sparse_segment_mean_fn get;
Computes the mean along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_mean, but `segment_ids` can have rank less than
`data`'s first dimension, selecting a subset of dimension 0, specified by
`indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
PythonFunctionContainer sparse_segment_sqrt_n_fn get;
Computes the sum along sparse segments of a tensor divided by the sqrt(N). `N` is the size of the segment being reduced.
PythonFunctionContainer sparse_segment_sum_fn get;
Computes the sum along sparse segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. Like
tf.math.segment_sum, but `segment_ids` can have rank less than `data`'s
first dimension, selecting a subset of dimension 0, specified by `indices`.
`segment_ids` is allowed to have missing ids, in which case the output will
be zeros at those indices. In those cases `num_segments` is used to determine
the size of the output.
Show Example
c = tf.constant([[1,2,3,4], [-1,-2,-3,-4], [5,6,7,8]]) # Select two rows, one segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 0]))
# => [[0 0 0 0]] # Select two rows, two segment.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 1]))
# => [[ 1 2 3 4]
# [-1 -2 -3 -4]] # With missing segment ids.
tf.sparse.segment_sum(c, tf.constant([0, 1]), tf.constant([0, 2]),
num_segments=4)
# => [[ 1 2 3 4]
# [ 0 0 0 0]
# [-1 -2 -3 -4]
# [ 0 0 0 0]] # Select all rows, two segments.
tf.sparse.segment_sum(c, tf.constant([0, 1, 2]), tf.constant([0, 0, 1]))
# => [[0 0 0 0]
# [5 6 7 8]] # Which is equivalent to:
tf.math.segment_sum(c, tf.constant([0, 0, 1]))
PythonFunctionContainer sparse_slice_fn get;
Slice a `SparseTensor` based on the `start` and `size. For example, if the input is input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: sparse.slice([0, 0], [2, 4]) = shape = [2, 4]
[ a ]
[b c ] sparse.slice([0, 4], [2, 3]) = shape = [2, 3]
[ d e ]
[ ]
PythonFunctionContainer sparse_softmax_fn get;
Applies softmax to a batched N-D `SparseTensor`. The inputs represent an N-D SparseTensor with logical shape `[..., B, C]`
(where `N >= 2`), and with indices sorted in the canonical lexicographic
order. This op is equivalent to applying the normal `tf.nn.softmax()` to each
innermost logical submatrix with shape `[B, C]`, but with the catch that *the
implicitly zero elements do not participate*. Specifically, the algorithm is
equivalent to: (1) Applies `tf.nn.softmax()` to a densified view of each innermost
submatrix with shape `[B, C]`, along the size-C dimension;
(2) Masks out the original implicitly-zero locations;
(3) Renormalizes the remaining elements. Hence, the `SparseTensor` result has exactly the same non-zero indices and
shape. Example:
Show Example
# First batch:
# [? e.]
# [1. ? ]
# Second batch:
# [e ? ]
# [e e ]
shape = [2, 2, 2] # 3-D SparseTensor
values = np.asarray([[[0., np.e], [1., 0.]], [[np.e, 0.], [np.e, np.e]]])
indices = np.vstack(np.where(values)).astype(np.int64).T result = tf.sparse.softmax(tf.SparseTensor(indices, values, shape))
#...returning a 3-D SparseTensor, equivalent to:
# [? 1.] [1 ?]
# [1. ? ] and [.5 .5]
# where ? means implicitly zero.
PythonFunctionContainer sparse_split_fn get;
Split a `SparseTensor` into `num_split` tensors along `axis`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(split_dim)`. They will be removed in a future version.
Instructions for updating:
split_dim is deprecated, use axis instead If the `sp_input.dense_shape[axis]` is not an integer multiple of `num_split`
each slice starting from 0:`shape[axis] % num_split` gets extra one
dimension. For example, if `axis = 1` and `num_split = 2` and the
input is: input_tensor = shape = [2, 7]
[ a d e ]
[b c ] Graphically the output tensors are: output_tensor[0] =
[ a ]
[b c ] output_tensor[1] =
[ d e ]
[ ]
PythonFunctionContainer sparse_tensor_dense_matmul_fn get;
Multiply SparseTensor (of rank 2) "A" by dense matrix "B". No validity checking is performed on the indices of `A`. However, the
following input format is recommended for optimal behavior: * If `adjoint_a == false`: `A` should be sorted in lexicographically
increasing order. Use `sparse.reorder` if you're not sure.
* If `adjoint_a == true`: `A` should be sorted in order of increasing
dimension 1 (i.e., "column major" order instead of "row major" order). Using
tf.nn.embedding_lookup_sparse for sparse multiplication: It's not obvious but you can consider `embedding_lookup_sparse` as another
sparse and dense multiplication. In some situations, you may prefer to use
`embedding_lookup_sparse` even though you're not dealing with embeddings. There are two questions to ask in the decision process: Do you need gradients
computed as sparse too? Is your sparse data represented as two
`SparseTensor`s: ids and values? There is more explanation about data format
below. If you answer any of these questions as yes, consider using
tf.nn.embedding_lookup_sparse. Following explains differences between the expected SparseTensors:
For example if dense form of your sparse data has shape `[3, 5]` and values: [[ a ]
[b c]
[ d ]] `SparseTensor` format expected by `sparse_tensor_dense_matmul`:
`sp_a` (indices, values): [0, 1]: a
[1, 0]: b
[1, 4]: c
[2, 2]: d `SparseTensor` format expected by `embedding_lookup_sparse`:
`sp_ids` `sp_weights` [0, 0]: 1 [0, 0]: a
[1, 0]: 0 [1, 0]: b
[1, 1]: 4 [1, 1]: c
[2, 0]: 2 [2, 0]: d Deciding when to use `sparse_tensor_dense_matmul` vs.
`matmul`(a_is_sparse=True): There are a number of questions to ask in the decision process, including: * Will the SparseTensor `A` fit in memory if densified?
* Is the column count of the product large (>> 1)?
* Is the density of `A` larger than approximately 15%? If the answer to several of these questions is yes, consider
converting the `SparseTensor` to a dense one and using tf.matmul with
`a_is_sparse=True`. This operation tends to perform well when `A` is more sparse, if the column
size of the product is small (e.g. matrix-vector multiplication), if
`sp_a.dense_shape` takes on large values. Below is a rough speed comparison between `sparse_tensor_dense_matmul`,
labeled 'sparse', and `matmul`(a_is_sparse=True), labeled 'dense'. For
purposes of the comparison, the time spent converting from a `SparseTensor` to
a dense `Tensor` is not included, so it is overly conservative with respect to
the time ratio. Benchmark system:
CPU: Intel Ivybridge with HyperThreading (6 cores) dL1:32KB dL2:256KB dL3:12MB
GPU: NVidia Tesla k40c Compiled with:
`-c opt --config=cuda --copt=-mavx` ```
tensorflow/python/sparse_tensor_dense_matmul_op_test --benchmarks
A sparse [m, k] with % nonzero values between 1% and 80%
B dense [k, n] % nnz n gpu m k dt(dense) dt(sparse) dt(sparse)/dt(dense)
0.01 1 True 100 100 0.000221166 0.00010154 0.459112
0.01 1 True 100 1000 0.00033858 0.000109275 0.322745
0.01 1 True 1000 100 0.000310557 9.85661e-05 0.317385
0.01 1 True 1000 1000 0.0008721 0.000100875 0.115669
0.01 1 False 100 100 0.000208085 0.000107603 0.51711
0.01 1 False 100 1000 0.000327112 9.51118e-05 0.290762
0.01 1 False 1000 100 0.000308222 0.00010345 0.335635
0.01 1 False 1000 1000 0.000865721 0.000101397 0.117124
0.01 10 True 100 100 0.000218522 0.000105537 0.482958
0.01 10 True 100 1000 0.000340882 0.000111641 0.327506
0.01 10 True 1000 100 0.000315472 0.000117376 0.372064
0.01 10 True 1000 1000 0.000905493 0.000123263 0.136128
0.01 10 False 100 100 0.000221529 9.82571e-05 0.44354
0.01 10 False 100 1000 0.000330552 0.000112615 0.340687
0.01 10 False 1000 100 0.000341277 0.000114097 0.334324
0.01 10 False 1000 1000 0.000819944 0.000120982 0.147549
0.01 25 True 100 100 0.000207806 0.000105977 0.509981
0.01 25 True 100 1000 0.000322879 0.00012921 0.400181
0.01 25 True 1000 100 0.00038262 0.00014158 0.370035
0.01 25 True 1000 1000 0.000865438 0.000202083 0.233504
0.01 25 False 100 100 0.000209401 0.000104696 0.499979
0.01 25 False 100 1000 0.000321161 0.000130737 0.407076
0.01 25 False 1000 100 0.000377012 0.000136801 0.362856
0.01 25 False 1000 1000 0.000861125 0.00020272 0.235413
0.2 1 True 100 100 0.000206952 9.69219e-05 0.46833
0.2 1 True 100 1000 0.000348674 0.000147475 0.422959
0.2 1 True 1000 100 0.000336908 0.00010122 0.300439
0.2 1 True 1000 1000 0.001022 0.000203274 0.198898
0.2 1 False 100 100 0.000207532 9.5412e-05 0.459746
0.2 1 False 100 1000 0.000356127 0.000146824 0.41228
0.2 1 False 1000 100 0.000322664 0.000100918 0.312764
0.2 1 False 1000 1000 0.000998987 0.000203442 0.203648
0.2 10 True 100 100 0.000211692 0.000109903 0.519165
0.2 10 True 100 1000 0.000372819 0.000164321 0.440753
0.2 10 True 1000 100 0.000338651 0.000144806 0.427596
0.2 10 True 1000 1000 0.00108312 0.000758876 0.70064
0.2 10 False 100 100 0.000215727 0.000110502 0.512231
0.2 10 False 100 1000 0.000375419 0.0001613 0.429653
0.2 10 False 1000 100 0.000336999 0.000145628 0.432132
0.2 10 False 1000 1000 0.00110502 0.000762043 0.689618
0.2 25 True 100 100 0.000218705 0.000129913 0.594009
0.2 25 True 100 1000 0.000394794 0.00029428 0.745402
0.2 25 True 1000 100 0.000404483 0.0002693 0.665788
0.2 25 True 1000 1000 0.0012002 0.00194494 1.62052
0.2 25 False 100 100 0.000221494 0.0001306 0.589632
0.2 25 False 100 1000 0.000396436 0.000297204 0.74969
0.2 25 False 1000 100 0.000409346 0.000270068 0.659754
0.2 25 False 1000 1000 0.00121051 0.00193737 1.60046
0.5 1 True 100 100 0.000214981 9.82111e-05 0.456836
0.5 1 True 100 1000 0.000415328 0.000223073 0.537101
0.5 1 True 1000 100 0.000358324 0.00011269 0.314492
0.5 1 True 1000 1000 0.00137612 0.000437401 0.317851
0.5 1 False 100 100 0.000224196 0.000101423 0.452386
0.5 1 False 100 1000 0.000400987 0.000223286 0.556841
0.5 1 False 1000 100 0.000368825 0.00011224 0.304318
0.5 1 False 1000 1000 0.00136036 0.000429369 0.31563
0.5 10 True 100 100 0.000222125 0.000112308 0.505608
0.5 10 True 100 1000 0.000461088 0.00032357 0.701753
0.5 10 True 1000 100 0.000394624 0.000225497 0.571422
0.5 10 True 1000 1000 0.00158027 0.00190898 1.20801
0.5 10 False 100 100 0.000232083 0.000114978 0.495418
0.5 10 False 100 1000 0.000454574 0.000324632 0.714146
0.5 10 False 1000 100 0.000379097 0.000227768 0.600817
0.5 10 False 1000 1000 0.00160292 0.00190168 1.18638
0.5 25 True 100 100 0.00023429 0.000151703 0.647501
0.5 25 True 100 1000 0.000497462 0.000598873 1.20386
0.5 25 True 1000 100 0.000460778 0.000557038 1.20891
0.5 25 True 1000 1000 0.00170036 0.00467336 2.74845
0.5 25 False 100 100 0.000228981 0.000155334 0.678371
0.5 25 False 100 1000 0.000496139 0.000620789 1.25124
0.5 25 False 1000 100 0.00045473 0.000551528 1.21287
0.5 25 False 1000 1000 0.00171793 0.00467152 2.71927
0.8 1 True 100 100 0.000222037 0.000105301 0.47425
0.8 1 True 100 1000 0.000410804 0.000329327 0.801664
0.8 1 True 1000 100 0.000349735 0.000131225 0.375212
0.8 1 True 1000 1000 0.00139219 0.000677065 0.48633
0.8 1 False 100 100 0.000214079 0.000107486 0.502085
0.8 1 False 100 1000 0.000413746 0.000323244 0.781261
0.8 1 False 1000 100 0.000348983 0.000131983 0.378193
0.8 1 False 1000 1000 0.00136296 0.000685325 0.50282
0.8 10 True 100 100 0.000229159 0.00011825 0.516017
0.8 10 True 100 1000 0.000498845 0.000532618 1.0677
0.8 10 True 1000 100 0.000383126 0.00029935 0.781336
0.8 10 True 1000 1000 0.00162866 0.00307312 1.88689
0.8 10 False 100 100 0.000230783 0.000124958 0.541452
0.8 10 False 100 1000 0.000493393 0.000550654 1.11606
0.8 10 False 1000 100 0.000377167 0.000298581 0.791642
0.8 10 False 1000 1000 0.00165795 0.00305103 1.84024
0.8 25 True 100 100 0.000233496 0.000175241 0.75051
0.8 25 True 100 1000 0.00055654 0.00102658 1.84458
0.8 25 True 1000 100 0.000463814 0.000783267 1.68875
0.8 25 True 1000 1000 0.00186905 0.00755344 4.04132
0.8 25 False 100 100 0.000240243 0.000175047 0.728625
0.8 25 False 100 1000 0.000578102 0.00104499 1.80763
0.8 25 False 1000 100 0.000485113 0.000776849 1.60138
0.8 25 False 1000 1000 0.00211448 0.00752736 3.55992
```
PythonFunctionContainer sparse_tensor_to_dense_fn get;
Converts a `SparseTensor` into a dense tensor. This op is a convenience wrapper around `sparse_to_dense` for `SparseTensor`s. For example, if `sp_input` has shape `[3, 5]` and non-empty string values: [0, 1]: a
[0, 3]: b
[2, 0]: c and `default_value` is `x`, then the output will be a dense `[3, 5]`
string tensor with values: [[x a x b x]
[x x x x x]
[c x x x x]] Indices must be without repeats. This is only
tested if `validate_indices` is `True`.
PythonFunctionContainer sparse_to_dense_fn get;
Converts a sparse representation into a dense tensor. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Create a
tf.sparse.SparseTensor and use tf.sparse.to_dense instead. Builds an array `dense` with shape `output_shape` such that
All other values in `dense` are set to `default_value`. If `sparse_values`
is a scalar, all sparse indices are set to this single value. Indices should be sorted in lexicographic order, and indices must not
contain any repeats. If `validate_indices` is True, these properties
are checked during execution.
Show Example
# If sparse_indices is scalar
dense[i] = (i == sparse_indices ? sparse_values : default_value) # If sparse_indices is a vector, then for each i
dense[sparse_indices[i]] = sparse_values[i] # If sparse_indices is an n by d matrix, then for each i in [0, n)
dense[sparse_indices[i][0],..., sparse_indices[i][d-1]] = sparse_values[i]
PythonFunctionContainer sparse_to_indicator_fn get;
Converts a `SparseTensor` of ids into a dense bool indicator tensor. The last dimension of `sp_input.indices` is discarded and replaced with
the values of `sp_input`. If `sp_input.dense_shape = [D0, D1,..., Dn, K]`,
then `output.shape = [D0, D1,..., Dn, vocab_size]`, where output[d_0, d_1,..., d_n, sp_input[d_0, d_1,..., d_n, k]] = True and False elsewhere in `output`. For example, if `sp_input.dense_shape = [2, 3, 4]` with non-empty values: [0, 0, 0]: 0
[0, 1, 0]: 10
[1, 0, 3]: 103
[1, 1, 1]: 150
[1, 1, 2]: 149
[1, 1, 3]: 150
[1, 2, 1]: 121 and `vocab_size = 200`, then the output will be a `[2, 3, 200]` dense bool
tensor with False everywhere except at positions (0, 0, 0), (0, 1, 10), (1, 0, 103), (1, 1, 149), (1, 1, 150),
(1, 2, 121). Note that repeats are allowed in the input SparseTensor.
This op is useful for converting `SparseTensor`s into dense formats for
compatibility with ops that expect dense tensors. The input `SparseTensor` must be in row-major order.
PythonFunctionContainer sparse_transpose_fn get;
Transposes a `SparseTensor` The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. For example, if `sp_input` has shape `[4, 5]` and `indices` / `values`: [0, 3]: b
[0, 1]: a
[3, 1]: d
[2, 0]: c then the output will be a `SparseTensor` of shape `[5, 4]` and
`indices` / `values`: [0, 2]: c
[1, 0]: a
[1, 3]: d
[3, 0]: b
PythonFunctionContainer split_fn get;
Splits a tensor into sub tensors. If `num_or_size_splits` is an integer, then `value` is split along dimension
`axis` into `num_split` smaller tensors. This requires that `num_split` evenly
divides `value.shape[axis]`. If `num_or_size_splits` is a 1-D Tensor (or list), we call it `size_splits`
and `value` is split into `len(size_splits)` elements. The shape of the `i`-th
element has the same size as the `value` except along dimension `axis` where
the size is `size_splits[i]`.
Show Example
# 'value' is a tensor with shape [5, 30]
# Split 'value' into 3 tensors with sizes [4, 15, 11] along dimension 1
split0, split1, split2 = tf.split(value, [4, 15, 11], 1)
tf.shape(split0) # [5, 4]
tf.shape(split1) # [5, 15]
tf.shape(split2) # [5, 11]
# Split 'value' into 3 tensors along dimension 1
split0, split1, split2 = tf.split(value, num_or_size_splits=3, axis=1)
tf.shape(split0) # [5, 10]
PythonFunctionContainer sqrt_fn get;
Computes square root of x element-wise. I.e., \\(y = \sqrt{x} = x^{1/2}\\).
PythonFunctionContainer square_fn get;
Computes square of x element-wise. I.e., \\(y = x * x = x^2\\).
PythonFunctionContainer squared_difference_fn get;
Returns (x - y)(x - y) element-wise. *NOTE*: `math.squared_difference` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer squeeze_fn get;
Removes dimensions of size 1 from the shape of a tensor. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(squeeze_dims)`. They will be removed in a future version.
Instructions for updating:
Use the `axis` argument instead Given a tensor `input`, this operation returns a tensor of the same type with
all dimensions of size 1 removed. If you don't want to remove all size 1
dimensions, you can remove specific size 1 dimensions by specifying
`axis`.
Or, to remove specific size 1 dimensions:
Note: if `input` is a
tf.RaggedTensor, then this operation takes `O(N)`
time, where `N` is the number of elements in the squeezed dimensions.
Show Example
# 't' is a tensor of shape [1, 2, 1, 3, 1, 1]
tf.shape(tf.squeeze(t)) # [2, 3]
PythonFunctionContainer stack_fn get;
Stacks a list of rank-`R` tensors into one rank-`(R+1)` tensor. Packs the list of tensors in `values` into a tensor with rank one higher than
each tensor in `values`, by packing them along the `axis` dimension.
Given a list of length `N` of tensors of shape `(A, B, C)`; if `axis == 0` then the `output` tensor will have the shape `(N, A, B, C)`.
if `axis == 1` then the `output` tensor will have the shape `(A, N, B, C)`.
Etc.
This is the opposite of unstack. The numpy equivalent is
Show Example
x = tf.constant([1, 4])
y = tf.constant([2, 5])
z = tf.constant([3, 6])
tf.stack([x, y, z]) # [[1, 4], [2, 5], [3, 6]] (Pack along first dim.)
tf.stack([x, y, z], axis=1) # [[1, 2, 3], [4, 5, 6]]
PythonFunctionContainer stats_accumulator_scalar_add_fn get;
PythonFunctionContainer stats_accumulator_scalar_deserialize_fn get;
PythonFunctionContainer stats_accumulator_scalar_flush_fn get;
PythonFunctionContainer stats_accumulator_scalar_is_initialized_fn get;
PythonFunctionContainer stats_accumulator_scalar_make_summary_fn get;
PythonFunctionContainer stats_accumulator_scalar_resource_handle_op_fn get;
PythonFunctionContainer stats_accumulator_scalar_serialize_fn get;
PythonFunctionContainer stats_accumulator_tensor_add_fn get;
PythonFunctionContainer stats_accumulator_tensor_deserialize_fn get;
PythonFunctionContainer stats_accumulator_tensor_flush_fn get;
PythonFunctionContainer stats_accumulator_tensor_is_initialized_fn get;
PythonFunctionContainer stats_accumulator_tensor_make_summary_fn get;
PythonFunctionContainer stats_accumulator_tensor_resource_handle_op_fn get;
PythonFunctionContainer stats_accumulator_tensor_serialize_fn get;
PythonFunctionContainer stochastic_hard_routing_function_fn get;
PythonFunctionContainer stochastic_hard_routing_gradient_fn get;
PythonFunctionContainer stop_gradient_fn get;
Stops gradient computation. When executed in a graph, this op outputs its input tensor as-is. When building ops to compute gradients, this op prevents the contribution of
its inputs to be taken into account. Normally, the gradient generator adds ops
to a graph to compute the derivatives of a specified 'loss' by recursively
finding out inputs that contributed to its computation. If you insert this op
in the graph it inputs are masked from the gradient generator. They are not
taken into account for computing gradients. This is useful any time you want to compute a value with TensorFlow but need
to pretend that the value was a constant. Some examples include: * The *EM* algorithm where the *M-step* should not involve backpropagation
through the output of the *E-step*.
* Contrastive divergence training of Boltzmann machines where, when
differentiating the energy function, the training must not backpropagate
through the graph that generated the samples from the model.
* Adversarial training, where no backprop should happen through the adversarial
example generation process.
PythonFunctionContainer strided_slice_fn get;
Extracts a strided slice of a tensor (generalized python array indexing). **Instead of calling this op directly most users will want to use the
NumPy-style slicing syntax (e.g. `tensor[..., 3:4:-1, tf.newaxis, 3]`), which
is supported via
tf.Tensor.__getitem__ and tf.Variable.__getitem__.**
The interface of this op is a low-level encoding of the slicing syntax. Roughly speaking, this op extracts a slice of size `(end-begin)/stride`
from the given `input_` tensor. Starting at the location specified by `begin`
the slice continues by adding `stride` to the index until all dimensions are
not less than `end`.
Note that a stride can be negative, which causes a reverse slice. Given a Python slice `input[spec0, spec1,..., specn]`,
this function will be called as follows. `begin`, `end`, and `strides` will be vectors of length n.
n in general is not equal to the rank of the `input_` tensor. In each mask field (`begin_mask`, `end_mask`, `ellipsis_mask`,
`new_axis_mask`, `shrink_axis_mask`) the ith bit will correspond to
the ith spec. If the ith bit of `begin_mask` is set, `begin[i]` is ignored and
the fullest possible range in that dimension is used instead.
`end_mask` works analogously, except with the end range. `foo[5:,:,:3]` on a 7x8x9 tensor is equivalent to `foo[5:7,0:8,0:3]`.
`foo[::-1]` reverses a tensor with shape 8. If the ith bit of `ellipsis_mask` is set, as many unspecified dimensions
as needed will be inserted between other dimensions. Only one
non-zero bit is allowed in `ellipsis_mask`. For example `foo[3:5,...,4:5]` on a shape 10x3x3x10 tensor is
equivalent to `foo[3:5,:,:,4:5]` and
`foo[3:5,...]` is equivalent to `foo[3:5,:,:,:]`. If the ith bit of `new_axis_mask` is set, then `begin`,
`end`, and `stride` are ignored and a new length 1 dimension is
added at this point in the output tensor. For example,
`foo[:4, tf.newaxis, :2]` would produce a shape `(4, 1, 2)` tensor. If the ith bit of `shrink_axis_mask` is set, it implies that the ith
specification shrinks the dimensionality by 1, taking on the value at index
`begin[i]`. `end[i]` and `strides[i]` are ignored in this case. For example in
Python one might do `foo[:, 3, :]` which would result in `shrink_axis_mask`
equal to 2. NOTE: `begin` and `end` are zero-indexed.
`strides` entries must be non-zero.
Show Example
t = tf.constant([[[1, 1, 1], [2, 2, 2]],
[[3, 3, 3], [4, 4, 4]],
[[5, 5, 5], [6, 6, 6]]])
tf.strided_slice(t, [1, 0, 0], [2, 1, 3], [1, 1, 1]) # [[[3, 3, 3]]]
tf.strided_slice(t, [1, 0, 0], [2, 2, 3], [1, 1, 1]) # [[[3, 3, 3],
# [4, 4, 4]]]
tf.strided_slice(t, [1, -1, 0], [2, -3, 3], [1, -1, 1]) # [[[4, 4, 4],
# [3, 3, 3]]]
DType string get; set;
PythonFunctionContainer string_join_fn get;
Joins the strings in the given list of string tensors into one tensor; with the given separator (default is an empty separator).
PythonFunctionContainer string_list_attr_fn get;
PythonFunctionContainer string_split_fn get;
Split elements of `source` based on `delimiter`. (deprecated arguments) Warning: SOME ARGUMENTS ARE DEPRECATED: `(delimiter)`. They will be removed in a future version.
Instructions for updating:
delimiter is deprecated, please use sep instead. Let N be the size of `source` (typically N will be the batch size). Split each
element of `source` based on `delimiter` and return a `SparseTensor`
or `RaggedTensor` containing the split tokens. Empty tokens are ignored. If `sep` is an empty string, each element of the `source` is split
into individual strings, each containing one byte. (This includes splitting
multibyte sequences of UTF-8.) If delimiter contains multiple bytes, it is
treated as a set of delimiters with each considered a potential split point. Examples:
Show Example
>>> tf.strings.split(['hello world', 'a b c'])
tf.SparseTensor(indices=[[0, 0], [0, 1], [1, 0], [1, 1], [1, 2]],
values=['hello', 'world', 'a', 'b', 'c']
dense_shape=[2, 3]) >>> tf.strings.split(['hello world', 'a b c'], result_type="RaggedTensor")
PythonFunctionContainer string_strip_fn get;
Strip leading and trailing whitespaces from the Tensor.
PythonFunctionContainer string_to_hash_bucket_fast_fn get;
Converts each string in the input Tensor to its hash mod by a number of buckets. The hash function is deterministic on the content of the string within the
process and will never change. However, it is not suitable for cryptography.
This function may be used when CPU time is scarce and inputs are trusted or
unimportant. There is a risk of adversaries constructing inputs that all hash
to the same bucket. To prevent this problem, use a strong hash function with
tf.string_to_hash_bucket_strong.
PythonFunctionContainer string_to_hash_bucket_fn get;
Converts each string in the input Tensor to its hash mod by a number of buckets. The hash function is deterministic on the content of the string within the
process. Note that the hash function may change from time to time.
This functionality will be deprecated and it's recommended to use
`tf.string_to_hash_bucket_fast()` or `tf.string_to_hash_bucket_strong()`.
PythonFunctionContainer string_to_hash_bucket_strong_fn get;
Converts each string in the input Tensor to its hash mod by a number of buckets. The hash function is deterministic on the content of the string within the
process. The hash function is a keyed hash function, where attribute `key`
defines the key of the hash function. `key` is an array of 2 elements. A strong hash is important when inputs may be malicious, e.g. URLs with
additional components. Adversaries could try to make their inputs hash to the
same bucket for a denial-of-service attack or to skew the results. A strong
hash can be used to make it difficult to find inputs with a skewed hash value
distribution over buckets. This requires that the hash function is
seeded by a high-entropy (random) "key" unknown to the adversary. The additional robustness comes at a cost of roughly 4x higher compute
time than
tf.string_to_hash_bucket_fast.
PythonFunctionContainer string_to_number_fn get;
Converts each string in the input Tensor to the specified numeric type. (Note that int32 overflow results in an error while float overflow
results in a rounded value.)
PythonFunctionContainer stub_resource_handle_op_fn get;
PythonFunctionContainer substr_fn_ get;
PythonFunctionContainer subtract_fn get;
Returns x - y element-wise. *NOTE*: `Subtract` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer svd_fn get;
Computes the singular value decompositions of one or more matrices. Computes the SVD of each inner matrix in `tensor` such that
`tensor[..., :, :] = u[..., :, :] * diag(s[..., :, :]) *
transpose(conj(v[..., :, :]))`
Show Example
# a is a tensor.
# s is a tensor of singular values.
# u is a tensor of left singular vectors.
# v is a tensor of right singular vectors.
s, u, v = svd(a)
s = svd(a, compute_uv=False)
PythonFunctionContainer switch_case_fn get;
Create a switch/case operation, i.e. an integer-indexed conditional. See also
tf.case. This op can be substantially more efficient than tf.case when exactly one
branch will be selected. tf.switch_case is more like a C++ switch/case
statement than tf.case, which is more like an if/elif/elif/else chain. The `branch_fns` parameter is either a list
of (int, callable) pairs, or simply a list of callables (in which case the
index is implicitly the key). The `branch_index` `Tensor` is used to select an
element in `branch_fns` with matching `int` key, falling back to `default`
if none match, or `max(keys)` if no `default` is provided. The keys must form
a contiguous set from `0` to `len(branch_fns) - 1`. tf.switch_case supports nested structures as implemented in tf.nest. All
callables must return the same (possibly nested) value structure of lists,
tuples, and/or named tuples. **Example:** Pseudocode: ```c++
switch (branch_index) { // c-style switch
case 0: return 17;
case 1: return 31;
default: return -1;
}
```
or
Expressions:
Show Example
branches = {0: lambda: 17, 1: lambda: 31}
branches.get(branch_index, lambda: -1)()
PythonFunctionContainer tables_initializer_fn get;
Returns an Op that initializes all tables of the default graph. See the [Low Level
Intro](https://www.tensorflow.org/guide/low_level_intro#feature_columns)
guide, for an example of usage.
PythonFunctionContainer tan_fn get;
Computes tan of x element-wise. Given an input tensor, this function computes tangent of every
element in the tensor. Input range is `(-inf, inf)` and
output range is `(-inf, inf)`. If input lies outside the boundary, `nan`
is returned.
Show Example
x = tf.constant([-float("inf"), -9, -0.5, 1, 1.2, 200, 10000, float("inf")])
tf.math.tan(x) ==> [nan 0.45231566 -0.5463025 1.5574077 2.572152 -1.7925274 0.32097113 nan]
PythonFunctionContainer tanh_fn get;
Computes hyperbolic tangent of `x` element-wise. Given an input tensor, this function computes hyperbolic tangent of every
element in the tensor. Input range is `[-inf, inf]` and
output range is `[-1,1]`.
Show Example
x = tf.constant([-float("inf"), -5, -0.5, 1, 1.2, 2, 3, float("inf")])
tf.math.tanh(x) ==> [-1. -0.99990916 -0.46211717 0.7615942 0.8336547 0.9640276 0.9950547 1.]
PythonFunctionContainer tensor_scatter_add_fn get;
Adds sparse `updates` to an existing tensor according to `indices`. This operation creates a new tensor by adding sparse `updates` to the passed
in `tensor`.
This operation is very similar to
tf.scatter_nd_add, except that the updates
are added onto an existing tensor (as opposed to a variable). If the memory
for the existing tensor cannot be re-used, a copy is made and updated. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of tensor_scatter_add is to add individual elements to a
tensor by index. For example, say we want to add 4 elements in a rank-1
tensor with 8 elements. In Python, this scatter add operation would look like this:
The resulting tensor would look like this: [1, 12, 1, 11, 10, 1, 1, 13] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter add operation would look like this:
The resulting tensor would look like this: [[[6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8], [9, 9, 9, 9]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8], [9, 9, 9, 9]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
tensor = tf.ones([8], dtype=tf.int32)
updated = tf.tensor_scatter_add(tensor, indices, updates)
with tf.Session() as sess:
print(sess.run(scatter))
PythonFunctionContainer tensor_scatter_sub_fn get;
Subtracts sparse `updates` from an existing tensor according to `indices`. This operation creates a new tensor by subtracting sparse `updates` from the
passed in `tensor`.
This operation is very similar to
tf.scatter_nd_sub, except that the updates
are subtracted from an existing tensor (as opposed to a variable). If the memory
for the existing tensor cannot be re-used, a copy is made and updated. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of tensor_scatter_sub is to subtract individual elements
from a tensor by index. For example, say we want to insert 4 scattered elements
in a rank-1 tensor with 8 elements. In Python, this scatter subtract operation would look like this:
The resulting tensor would look like this: [1, -10, 1, -9, -8, 1, 1, -11] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter add operation would look like this:
The resulting tensor would look like this: [[[-4, -4, -4, -4], [-5, -5, -5, -5], [-6, -6, -6, -6], [-7, -7, -7, -7]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[-4, -4, -4, -4], [-5, -5, -5, -5], [-6, -6, -6, -6], [-7, -7, -7, -7]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
tensor = tf.ones([8], dtype=tf.int32)
updated = tf.tensor_scatter_sub(tensor, indices, updates)
with tf.Session() as sess:
print(sess.run(scatter))
PythonFunctionContainer tensor_scatter_update_fn get;
Scatter `updates` into an existing tensor according to `indices`. This operation creates a new tensor by applying sparse `updates` to the passed
in `tensor`.
This operation is very similar to
 In Python, this scatter operation would look like this:
The resulting tensor would look like this: [1, 11, 1, 10, 9, 1, 1, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
In Python, this scatter operation would look like this:
The resulting tensor would look like this: [1, 11, 1, 10, 9, 1, 1, 12] We can also, insert entire slices of a higher rank tensor all at once. For
example, if we wanted to insert two slices in the first dimension of a
rank-3 tensor with two matrices of new values. In Python, this scatter operation would look like this:
The resulting tensor would look like this: [[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]],
[[5, 5, 5, 5], [6, 6, 6, 6], [7, 7, 7, 7], [8, 8, 8, 8]],
[[1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1], [1, 1, 1, 1]]] Note that on CPU, if an out of bound index is found, an error is returned.
On GPU, if an out of bound index is found, the index is ignored.
tf.scatter_nd, except that the updates are
scattered onto an existing tensor (as opposed to a zero-tensor). If the memory
for the existing tensor cannot be re-used, a copy is made and updated. If `indices` contains duplicates, then their updates are accumulated (summed). **WARNING**: The order in which updates are applied is nondeterministic, so the
output will be nondeterministic if `indices` contains duplicates -- because
of some numerical approximation issues, numbers summed in different order
may yield different results. `indices` is an integer tensor containing indices into a new tensor of shape
`shape`. The last dimension of `indices` can be at most the rank of `shape`: indices.shape[-1] <= shape.rank The last dimension of `indices` corresponds to indices into elements
(if `indices.shape[-1] = shape.rank`) or slices
(if `indices.shape[-1] < shape.rank`) along dimension `indices.shape[-1]` of
`shape`. `updates` is a tensor with shape indices.shape[:-1] + shape[indices.shape[-1]:] The simplest form of scatter is to insert individual elements in a tensor by
index. For example, say we want to insert 4 scattered elements in a rank-1
tensor with 8 elements. 
Show Example
indices = tf.constant([[4], [3], [1], [7]])
updates = tf.constant([9, 10, 11, 12])
tensor = tf.ones([8], dtype=tf.int32)
updated = tf.tensor_scatter_update(tensor, indices, updates)
with tf.Session() as sess:
print(sess.run(scatter))
PythonFunctionContainer tensordot_fn get;
Tensor contraction of a and b along specified axes and outer product. Tensordot (also known as tensor contraction) sums the product of elements
from `a` and `b` over the indices specified by `a_axes` and `b_axes`.
The lists `a_axes` and `b_axes` specify those pairs of axes along which to
contract the tensors. The axis `a_axes[i]` of `a` must have the same dimension
as axis `b_axes[i]` of `b` for all `i` in `range(0, len(a_axes))`. The lists
`a_axes` and `b_axes` must have identical length and consist of unique
integers that specify valid axes for each of the tensors. Additionally
outer product is supported by passing `axes=0`. This operation corresponds to `numpy.tensordot(a, b, axes)`. Example 1: When `a` and `b` are matrices (order 2), the case `axes = 1`
is equivalent to matrix multiplication. Example 2: When `a` and `b` are matrices (order 2), the case
`axes = [[1], [0]]` is equivalent to matrix multiplication. Example 3: When `a` and `b` are matrices (order 2), the case `axes=0` gives
the outer product, a tensor of order 4. Example 4: Suppose that \\(a_{ijk}\\) and \\(b_{lmn}\\) represent two
tensors of order 3. Then, `contract(a, b, [[0], [2]])` is the order 4 tensor
\\(c_{jklm}\\) whose entry
corresponding to the indices \\((j,k,l,m)\\) is given by: \\( c_{jklm} = \sum_i a_{ijk} b_{lmi} \\). In general, `order(c) = order(a) + order(b) - 2*len(axes[0])`.
PythonFunctionContainer test_attr_fn get;
PythonFunctionContainer test_string_output_fn get;
PythonFunctionContainer tile_fn get;
Constructs a tensor by tiling a given tensor. This operation creates a new tensor by replicating `input` `multiples` times.
The output tensor's i'th dimension has `input.dims(i) * multiples[i]` elements,
and the values of `input` are replicated `multiples[i]` times along the 'i'th
dimension. For example, tiling `[a b c d]` by `[2]` produces
`[a b c d a b c d]`.
PythonFunctionContainer timestamp_fn get;
Provides the time since epoch in seconds. Returns the timestamp as a `float64` for seconds since the Unix epoch. Note: the timestamp is computed when the op is executed, not when it is added
to the graph.
PythonFunctionContainer to_bfloat16_fn get;
Casts a tensor to type `bfloat16`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
PythonFunctionContainer to_complex128_fn get;
Casts a tensor to type `complex128`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
PythonFunctionContainer to_complex64_fn get;
Casts a tensor to type `complex64`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
PythonFunctionContainer to_double_fn get;
Casts a tensor to type `float64`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
PythonFunctionContainer to_float_fn get;
Casts a tensor to type `float32`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
PythonFunctionContainer to_int32_fn get;
Casts a tensor to type `int32`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
PythonFunctionContainer to_int64_fn get;
Casts a tensor to type `int64`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use
tf.cast instead.
PythonFunctionContainer trace_fn get;
Compute the trace of a tensor `x`. `trace(x)` returns the sum along the main diagonal of each inner-most matrix
in x. If x is of rank `k` with shape `[I, J, K,..., L, M, N]`, then output
is a tensor of rank `k-2` with dimensions `[I, J, K,..., L]` where `output[i, j, k,..., l] = trace(x[i, j, i,..., l, :, :])`
Show Example
x = tf.constant([[1, 2], [3, 4]])
tf.linalg.trace(x) # 5 x = tf.constant([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
tf.linalg.trace(x) # 15 x = tf.constant([[[1, 2, 3],
[4, 5, 6],
[7, 8, 9]],
[[-1, -2, -3],
[-4, -5, -6],
[-7, -8, -9]]])
tf.linalg.trace(x) # [15, -15]
PythonFunctionContainer trainable_variables_fn get;
Returns all variables created with `trainable=True`. When passed `trainable=True`, the `Variable()` constructor automatically
adds new variables to the graph collection
`GraphKeys.TRAINABLE_VARIABLES`. This convenience function returns the
contents of that collection.
PythonFunctionContainer transpose_fn get;
Transposes `a`. Permutes the dimensions according to `perm`. The returned tensor's dimension i will correspond to the input dimension
`perm[i]`. If `perm` is not given, it is set to (n-1...0), where n is
the rank of the input tensor. Hence by default, this operation performs a
regular matrix transpose on 2-D input Tensors. If conjugate is True and
`a.dtype` is either `complex64` or `complex128` then the values of `a`
are conjugated and transposed.
Show Example
x = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.transpose(x) # [[1, 4]
# [2, 5]
# [3, 6]] # Equivalently
tf.transpose(x, perm=[1, 0]) # [[1, 4]
# [2, 5]
# [3, 6]] # If x is complex, setting conjugate=True gives the conjugate transpose
x = tf.constant([[1 + 1j, 2 + 2j, 3 + 3j],
[4 + 4j, 5 + 5j, 6 + 6j]])
tf.transpose(x, conjugate=True) # [[1 - 1j, 4 - 4j],
# [2 - 2j, 5 - 5j],
# [3 - 3j, 6 - 6j]] # 'perm' is more useful for n-dimensional tensors, for n > 2
x = tf.constant([[[ 1, 2, 3],
[ 4, 5, 6]],
[[ 7, 8, 9],
[10, 11, 12]]]) # Take the transpose of the matrices in dimension-0
# (this common operation has a shorthand `linalg.matrix_transpose`)
tf.transpose(x, perm=[0, 2, 1]) # [[[1, 4],
# [2, 5],
# [3, 6]],
# [[7, 10],
# [8, 11],
# [9, 12]]]
PythonFunctionContainer traverse_tree_v4_fn get;
PythonFunctionContainer tree_deserialize_fn get;
PythonFunctionContainer tree_ensemble_deserialize_fn get;
PythonFunctionContainer tree_ensemble_is_initialized_op_fn get;
PythonFunctionContainer tree_ensemble_serialize_fn get;
PythonFunctionContainer tree_ensemble_stamp_token_fn get;
PythonFunctionContainer tree_ensemble_stats_fn get;
PythonFunctionContainer tree_ensemble_used_handlers_fn get;
PythonFunctionContainer tree_is_initialized_op_fn get;
PythonFunctionContainer tree_predictions_v4_fn get;
PythonFunctionContainer tree_serialize_fn get;
PythonFunctionContainer tree_size_fn get;
PythonFunctionContainer truediv_fn get;
Divides x / y elementwise (using Python 3 division operator semantics). NOTE: Prefer using the Tensor operator or tf.divide which obey Python
division operator semantics. This function forces Python 3 division operator semantics where all integer
arguments are cast to floating types first. This op is generated by normal
`x / y` division in Python 3 and in Python 2.7 with
`from __future__ import division`. If you want integer division that rounds
down, use `x // y` or
tf.math.floordiv. `x` and `y` must have the same numeric type. If the inputs are floating
point, the output will have the same type. If the inputs are integral, the
inputs are cast to `float32` for `int8` and `int16` and `float64` for `int32`
and `int64` (matching the behavior of Numpy).
PythonFunctionContainer truncated_normal_fn get;
Outputs random values from a truncated normal distribution. The generated values follow a normal distribution with specified mean and
standard deviation, except that values whose magnitude is more than 2 standard
deviations from the mean are dropped and re-picked.
PythonFunctionContainer truncatediv_fn get;
Returns x / y element-wise for integer types. Truncation designates that negative numbers will round fractional quantities
toward zero. I.e. -7 / 5 = -1. This matches C semantics but it is different
than Python semantics. See `FloorDiv` for a division function that matches
Python Semantics. *NOTE*: `truncatediv` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer truncatemod_fn get;
Returns element-wise remainder of division. This emulates C semantics in that the result here is consistent with a truncating divide. E.g. `truncate(x / y) *
y + truncate_mod(x, y) = x`. *NOTE*: `truncatemod` supports broadcasting. More about broadcasting
[here](http://docs.scipy.org/doc/numpy/user/basics.broadcasting.html)
PythonFunctionContainer try_rpc_fn get;
PythonFunctionContainer tuple_fn get;
Group tensors together. This creates a tuple of tensors with the same values as the `tensors`
argument, except that the value of each tensor is only returned after the
values of all tensors have been computed. `control_inputs` contains additional ops that have to finish before this op
finishes, but whose outputs are not returned. This can be used as a "join" mechanism for parallel computations: all the
argument tensors can be computed in parallel, but the values of any tensor
returned by `tuple` are only available after all the parallel computations
are done. See also
tf.group and
tf.control_dependencies.
PythonFunctionContainer two_float_inputs_float_output_fn get;
PythonFunctionContainer two_float_inputs_fn get;
PythonFunctionContainer two_float_inputs_int_output_fn get;
PythonFunctionContainer two_float_outputs_fn get;
PythonFunctionContainer two_int_inputs_fn get;
PythonFunctionContainer two_int_outputs_fn get;
PythonFunctionContainer two_refs_in_fn get;
PythonFunctionContainer type_list_fn get;
PythonFunctionContainer type_list_restrict_fn get;
PythonFunctionContainer type_list_twice_fn get;
DType uint16 get; set;
DType uint32 get; set;
DType uint64 get; set;
DType uint8 get; set;
PythonFunctionContainer unary_fn get;
PythonFunctionContainer unique_fn get;
Finds unique elements in a 1-D tensor. This operation returns a tensor `y` containing all of the unique elements of `x`
sorted in the same order that they occur in `x`. This operation also returns a
tensor `idx` the same size as `x` that contains the index of each value of `x`
in the unique output `y`. In other words: `y[idx[i]] = x[i] for i in [0, 1,...,rank(x) - 1]` For example: ```
# tensor 'x' is [1, 1, 2, 4, 4, 4, 7, 8, 8]
y, idx = unique(x)
y ==> [1, 2, 4, 7, 8]
idx ==> [0, 0, 1, 2, 2, 2, 3, 4, 4]
```
PythonFunctionContainer unique_with_counts_fn get;
Finds unique elements in a 1-D tensor. This operation returns a tensor `y` containing all of the unique elements of `x`
sorted in the same order that they occur in `x`. This operation also returns a
tensor `idx` the same size as `x` that contains the index of each value of `x`
in the unique output `y`. Finally, it returns a third tensor `count` that
contains the count of each element of `y` in `x`. In other words: `y[idx[i]] = x[i] for i in [0, 1,...,rank(x) - 1]` For example: ```
# tensor 'x' is [1, 1, 2, 4, 4, 4, 7, 8, 8]
y, idx, count = unique_with_counts(x)
y ==> [1, 2, 4, 7, 8]
idx ==> [0, 0, 1, 2, 2, 2, 3, 4, 4]
count ==> [2, 1, 3, 1, 2]
```
PythonFunctionContainer unpack_path_fn get;
PythonFunctionContainer unravel_index_fn get;
Converts an array of flat indices into a tuple of coordinate arrays. Example: ```
y = tf.unravel_index(indices=[2, 5, 7], dims=[3, 3])
# 'dims' represent a hypothetical (3, 3) tensor of indices:
# [[0, 1, *2*],
# [3, 4, *5*],
# [6, *7*, 8]]
# For each entry from 'indices', this operation returns
# its coordinates (marked with '*'), such as
# 2 ==> (0, 2)
# 5 ==> (1, 2)
# 7 ==> (2, 1)
y ==> [[0, 1, 2], [2, 2, 1]]
```
PythonFunctionContainer unsorted_segment_max_fn get;
Computes the maximum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[(here)](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the maximum such that: \\(output_i = \max_{j...} data[j...]\\) where max is over tuples `j...` such
that `segment_ids[j...] == i`. If the maximum is empty for a given segment ID `i`, it outputs the smallest
possible value for the specific numeric type,
`output[i] = numeric_limits::lowest()`. If the given segment ID `i` is negative, then the corresponding value is
dropped, and will not be included in the result.
 For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_max(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 4, 3, 3, 4],
# [5, 6, 7, 8]]
```
For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_max(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 4, 3, 3, 4],
# [5, 6, 7, 8]]
```

PythonFunctionContainer unsorted_segment_mean_fn get;
Computes the mean along segments of a tensor. Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[here](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the mean of all
entries belonging to a segment such that: \\(output_i = 1/N_i \sum_{j...} data[j...]\\) where the sum is over tuples
`j...` such that `segment_ids[j...] == i` with \\N_i\\ being the number of
occurrences of id \\i\\. If there is no entry for a given segment ID `i`, it outputs 0. If the given segment ID `i` is negative, the value is dropped and will not
be added to the sum of the segment.
PythonFunctionContainer unsorted_segment_min_fn get;
Computes the minimum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[(here)](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the minimum such that: \\(output_i = \min_{j...} data_[j...]\\) where min is over tuples `j...` such
that `segment_ids[j...] == i`. If the minimum is empty for a given segment ID `i`, it outputs the largest
possible value for the specific numeric type,
`output[i] = numeric_limits::max()`. For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_min(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 1, 2, 2, 1],
# [5, 6, 7, 8]]
``` If the given segment ID `i` is negative, then the corresponding value is
dropped, and will not be included in the result.
PythonFunctionContainer unsorted_segment_prod_fn get;
Computes the product along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[(here)](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Instead of computing the sum over segments, it computes the product of all
entries belonging to a segment such that: \\(output_i = \prod_{j...} data[j...]\\) where the product is over tuples
`j...` such that `segment_ids[j...] == i`. For example: ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_prod(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 4, 6, 6, 4],
# [5, 6, 7, 8]]
``` If there is no entry for a given segment ID `i`, it outputs 1. If the given segment ID `i` is negative, then the corresponding value is
dropped, and will not be included in the result.
PythonFunctionContainer unsorted_segment_sqrt_n_fn get;
Computes the sum along segments of a tensor divided by the sqrt(N). Read [the section on
segmentation](https://www.tensorflow.org/versions/r2.0/api_docs/python/tf/math#about_segmentation)
for an explanation of segments. This operator is similar to the unsorted segment sum operator found
[here](../../../api_docs/python/math_ops.md#UnsortedSegmentSum).
Additionally to computing the sum over segments, it divides the results by
sqrt(N). \\(output_i = 1/sqrt(N_i) \sum_{j...} data[j...]\\) where the sum is over
tuples `j...` such that `segment_ids[j...] == i` with \\N_i\\ being the
number of occurrences of id \\i\\. If there is no entry for a given segment ID `i`, it outputs 0. Note that this op only supports floating point and complex dtypes,
due to tf.sqrt only supporting these types. If the given segment ID `i` is negative, the value is dropped and will not
be added to the sum of the segment.
PythonFunctionContainer unsorted_segment_sum_fn get;
Computes the sum along segments of a tensor. Read
[the section on segmentation](https://tensorflow.org/api_docs/python/tf/math#Segmentation)
for an explanation of segments. Computes a tensor such that
\\(output[i] = \sum_{j...} data[j...]\\) where the sum is over tuples `j...` such
that `segment_ids[j...] == i`. Unlike `SegmentSum`, `segment_ids`
need not be sorted and need not cover all values in the full
range of valid values. If the sum is empty for a given segment ID `i`, `output[i] = 0`.
If the given segment ID `i` is negative, the value is dropped and will not be
added to the sum of the segment. `num_segments` should equal the number of distinct segment IDs.
 ``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_sum(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 5, 5, 5, 5],
# [5, 6, 7, 8]]
```
``` python
c = tf.constant([[1,2,3,4], [5,6,7,8], [4,3,2,1]])
tf.unsorted_segment_sum(c, tf.constant([0, 1, 0]), num_segments=2)
# ==> [[ 5, 5, 5, 5],
# [5, 6, 7, 8]]
```

PythonFunctionContainer unstack_fn get;
Unpacks the given dimension of a rank-`R` tensor into rank-`(R-1)` tensors. Unpacks `num` tensors from `value` by chipping it along the `axis` dimension.
If `num` is not specified (the default), it is inferred from `value`'s shape.
If `value.shape[axis]` is not known, `ValueError` is raised. For example, given a tensor of shape `(A, B, C, D)`; If `axis == 0` then the i'th tensor in `output` is the slice
`value[i, :, :, :]` and each tensor in `output` will have shape `(B, C, D)`.
(Note that the dimension unpacked along is gone, unlike `split`). If `axis == 1` then the i'th tensor in `output` is the slice
`value[:, i, :, :]` and each tensor in `output` will have shape `(A, C, D)`.
Etc. This is the opposite of stack.
PythonFunctionContainer update_model_v4_fn get;
PythonFunctionContainer variable_axis_size_partitioner_fn get;
Get a partitioner for VariableScope to keep shards below `max_shard_bytes`. This partitioner will shard a Variable along one axis, attempting to keep
the maximum shard size below `max_shard_bytes`. In practice, this is not
always possible when sharding along only one axis. When this happens,
this axis is sharded as much as possible (i.e., every dimension becomes
a separate shard). If the partitioner hits the `max_shards` limit, then each shard may end up
larger than `max_shard_bytes`. By default `max_shards` equals `None` and no
limit on the number of shards is enforced. One reasonable value for `max_shard_bytes` is `(64 << 20) - 1`, or almost
`64MB`, to keep below the protobuf byte limit.
PythonFunctionContainer variable_op_scope_fn get;
Deprecated: context manager for defining an op that creates variables.
PythonFunctionContainer variables_initializer_fn get;
Returns an Op that initializes a list of variables. After you launch the graph in a session, you can run the returned Op to
initialize all the variables in `var_list`. This Op runs all the
initializers of the variables in `var_list` in parallel. Calling `initialize_variables()` is equivalent to passing the list of
initializers to `Group()`. If `var_list` is empty, however, the function still returns an Op that can
be run. That Op just has no effect.
DType variant get; set;
PythonFunctionContainer vectorized_map_fn get;
Parallel map on the list of tensors unpacked from `elems` on dimension 0. This method works similar to tf.map_fn but is optimized to run much faster,
possibly with a much larger memory footprint. The speedups are obtained by
vectorization (see https://arxiv.org/pdf/1903.04243.pdf). The idea behind
vectorization is to semantically launch all the invocations of `fn` in
parallel and fuse corresponding operations across all these invocations. This
fusion is done statically at graph generation time and the generated code is
often similar in performance to a manually fused version. Because
tf.vectorized_map fully parallelizes the batch, this method will
generally be significantly faster than using tf.map_fn, especially in eager
mode. However this is an experimental feature and currently has a lot of
limitations:
- There should be no data dependency between the different semantic
invocations of `fn`, i.e. it should be safe to map the elements of the
inputs in any order.
- Stateful kernels may mostly not be supported since these often imply a
data dependency. We do support a limited set of such stateful kernels
though (like RandomFoo, Variable operations like reads, etc).
- `fn` has limited support for control flow operations. tf.cond in
particular is not supported.
- `fn` should return nested structure of Tensors or Operations. However
if an Operation is returned, it should have zero outputs.
- The shape and dtype of any intermediate or output tensors in the
computation of `fn` should not depend on the input to `fn`.
PythonFunctionContainer verify_tensor_all_finite_fn get;
Assert that the tensor does not contain any NaN's or Inf's.
string Version get;
PythonFunctionContainer wals_compute_partial_lhs_and_rhs_fn get;
PythonFunctionContainer where_fn get;
Return the elements, either from `x` or `y`, depending on the `condition`. (deprecated) Warning: THIS FUNCTION IS DEPRECATED. It will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `x` and `y` must have the same shape.
The `condition` tensor must be a scalar if `x` and `y` are scalar.
If `x` and `y` are tensors of higher rank, then `condition` must be either a
vector with size matching the first dimension of `x`, or must have the same
shape as `x`. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false). If `condition` is a vector and `x` and `y` are higher rank matrices, then it
chooses which row (outer dimension) to copy from `x` and `y`. If `condition`
has the same shape as `x` and `y`, then it chooses which element to copy from
`x` and `y`.
PythonFunctionContainer where_v2_fn get;
Return the elements, either from `x` or `y`, depending on the `condition`. If both `x` and `y` are None, then this operation returns the coordinates of
true elements of `condition`. The coordinates are returned in a 2-D tensor
where the first dimension (rows) represents the number of true elements, and
the second dimension (columns) represents the coordinates of the true
elements. Keep in mind, the shape of the output tensor can vary depending on
how many true values there are in input. Indices are output in row-major
order. If both non-None, `condition`, `x` and `y` must be broadcastable to the same
shape. The `condition` tensor acts as a mask that chooses, based on the value at each
element, whether the corresponding element / row in the output should be taken
from `x` (if true) or `y` (if false).
PythonFunctionContainer while_loop_fn get;
Repeat `body` while the condition `cond` is true. `cond` is a callable returning a boolean scalar tensor. `body` is a callable
returning a (possibly nested) tuple, namedtuple or list of tensors of the same
arity (length and structure) and types as `loop_vars`. `loop_vars` is a
(possibly nested) tuple, namedtuple or list of tensors that is passed to both
`cond` and `body`. `cond` and `body` both take as many arguments as there are
`loop_vars`. In addition to regular Tensors or IndexedSlices, the body may accept and
return TensorArray objects. The flows of the TensorArray objects will
be appropriately forwarded between loops and during gradient calculations. Note that `while_loop` calls `cond` and `body` *exactly once* (inside the
call to `while_loop`, and not at all during `Session.run()`). `while_loop`
stitches together the graph fragments created during the `cond` and `body`
calls with some additional graph nodes to create the graph flow that
repeats `body` until `cond` returns false. For correctness, `tf.while_loop()` strictly enforces shape invariants for
the loop variables. A shape invariant is a (possibly partial) shape that
is unchanged across the iterations of the loop. An error will be raised
if the shape of a loop variable after an iteration is determined to be more
general than or incompatible with its shape invariant. For example, a shape
of [11, None] is more general than a shape of [11, 17], and [11, 21] is not
compatible with [11, 17]. By default (if the argument `shape_invariants` is
not specified), it is assumed that the initial shape of each tensor in
`loop_vars` is the same in every iteration. The `shape_invariants` argument
allows the caller to specify a less specific shape invariant for each loop
variable, which is needed if the shape varies between iterations. The
tf.Tensor.set_shape
function may also be used in the `body` function to indicate that
the output loop variable has a particular shape. The shape invariant for
SparseTensor and IndexedSlices are treated specially as follows: a) If a loop variable is a SparseTensor, the shape invariant must be
TensorShape([r]) where r is the rank of the dense tensor represented
by the sparse tensor. It means the shapes of the three tensors of the
SparseTensor are ([None], [None, r], [r]). NOTE: The shape invariant here
is the shape of the SparseTensor.dense_shape property. It must be the shape of
a vector. b) If a loop variable is an IndexedSlices, the shape invariant must be
a shape invariant of the values tensor of the IndexedSlices. It means
the shapes of the three tensors of the IndexedSlices are (shape, [shape[0]],
[shape.ndims]). `while_loop` implements non-strict semantics, enabling multiple iterations
to run in parallel. The maximum number of parallel iterations can be
controlled by `parallel_iterations`, which gives users some control over
memory consumption and execution order. For correct programs, `while_loop`
should return the same result for any parallel_iterations > 0. For training, TensorFlow stores the tensors that are produced in the
forward inference and are needed in back propagation. These tensors are a
main source of memory consumption and often cause OOM errors when training
on GPUs. When the flag swap_memory is true, we swap out these tensors from
GPU to CPU. This for example allows us to train RNN models with very long
sequences and large batches.
PythonFunctionContainer wrap_function_fn get;
Wraps the TF 1.x function fn into a graph function. The python function `fn` will be called once with symbolic arguments specified
in the `signature`, traced, and turned into a graph function. Any variables
created by `fn` will be owned by the object returned by `wrap_function`. The
resulting graph function can be called with tensors which match the
signature.
Both `tf.compat.v1.wrap_function` and
tf.function create a callable
TensorFlow graph. But while tf.function runs all stateful operations
(e.g. tf.print) and sequences operations to provide the same semantics as
eager execution, `wrap_function` is closer to the behavior of `session.run` in
TensorFlow 1.x. It will not run any operations unless they are required to
compute the function's outputs, either through a data dependency or a control
dependency. Nor will it sequence operations. Unlike tf.function, `wrap_function` will only trace the Python function
once. As with placeholders in TF 1.x, shapes and dtypes must be provided to
`wrap_function`'s `signature` argument. Since it is only traced once, variables and state may be created inside the
function and owned by the function wrapper object.
Show Example
def f(x, do_add):
v = tf.Variable(5.0)
if do_add:
op = v.assign_add(x)
else:
op = v.assign_sub(x)
with tf.control_dependencies([op]):
return v.read_value() f_add = tf.compat.v1.wrap_function(f, [tf.TensorSpec((), tf.float32), True]) assert float(f_add(1.0)) == 6.0
assert float(f_add(1.0)) == 7.0 # Can call tf.compat.v1.wrap_function again to get a new trace, a new set
# of variables, and possibly different non-template arguments.
f_sub= tf.compat.v1.wrap_function(f, [tf.TensorSpec((), tf.float32), False]) assert float(f_sub(1.0)) == 4.0
assert float(f_sub(1.0)) == 3.0
PythonFunctionContainer write_file_fn get;
Writes contents to the file at input filename. Creates file and recursively creates directory if not existing.
PythonFunctionContainer xla_broadcast_helper_fn get;
PythonFunctionContainer xla_cluster_output_fn get;
PythonFunctionContainer xla_conv_fn get;
PythonFunctionContainer xla_dequantize_fn get;
PythonFunctionContainer xla_dot_fn get;
PythonFunctionContainer xla_dynamic_slice_fn get;
PythonFunctionContainer xla_dynamic_update_slice_fn get;
PythonFunctionContainer xla_einsum_fn get;
PythonFunctionContainer xla_if_fn get;
PythonFunctionContainer xla_key_value_sort_fn get;
PythonFunctionContainer xla_launch_fn get;
PythonFunctionContainer xla_pad_fn get;
PythonFunctionContainer xla_recv_fn get;
PythonFunctionContainer xla_reduce_fn get;
PythonFunctionContainer xla_reduce_window_fn get;
PythonFunctionContainer xla_replica_id_fn get;
PythonFunctionContainer xla_select_and_scatter_fn get;
PythonFunctionContainer xla_self_adjoint_eig_fn get;
PythonFunctionContainer xla_send_fn get;
PythonFunctionContainer xla_sort_fn get;
PythonFunctionContainer xla_svd_fn get;
PythonFunctionContainer xla_while_fn get;
PythonFunctionContainer zero_initializer_fn get;
PythonFunctionContainer zero_var_initializer_fn get;
PythonFunctionContainer zeros_fn get;
Creates a tensor with all elements set to zero. This operation returns a tensor of type `dtype` with shape `shape` and
all elements set to zero.
Show Example
tf.zeros([3, 4], tf.int32) # [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]]
PythonFunctionContainer zeros_like_fn get;
Creates a tensor with all elements set to zero. Given a single tensor (`tensor`), this operation returns a tensor of the
same type and shape as `tensor` with all elements set to zero. Optionally,
you can use `dtype` to specify a new type for the returned tensor.
Show Example
tensor = tf.constant([[1, 2, 3], [4, 5, 6]])
tf.zeros_like(tensor) # [[0, 0, 0], [0, 0, 0]]
PythonFunctionContainer zeta_fn get;
Compute the Hurwitz zeta function \\(\zeta(x, q)\\). The Hurwitz zeta function is defined as: \\(\zeta(x, q) = \sum_{n=0}^{\infty} (q + n)^{-x}\\)
Public fields
object newaxis
return object
|